Finite Element Study of Bio-Convective Stefan Blowing Ag-MgO/Water Hybrid Nanofluid Induced by Stretching Cylinder Utilizing Non-Fourier and Non-Fick’s Laws
Abstract
:1. Introduction
2. Nano-Materials and Modeling
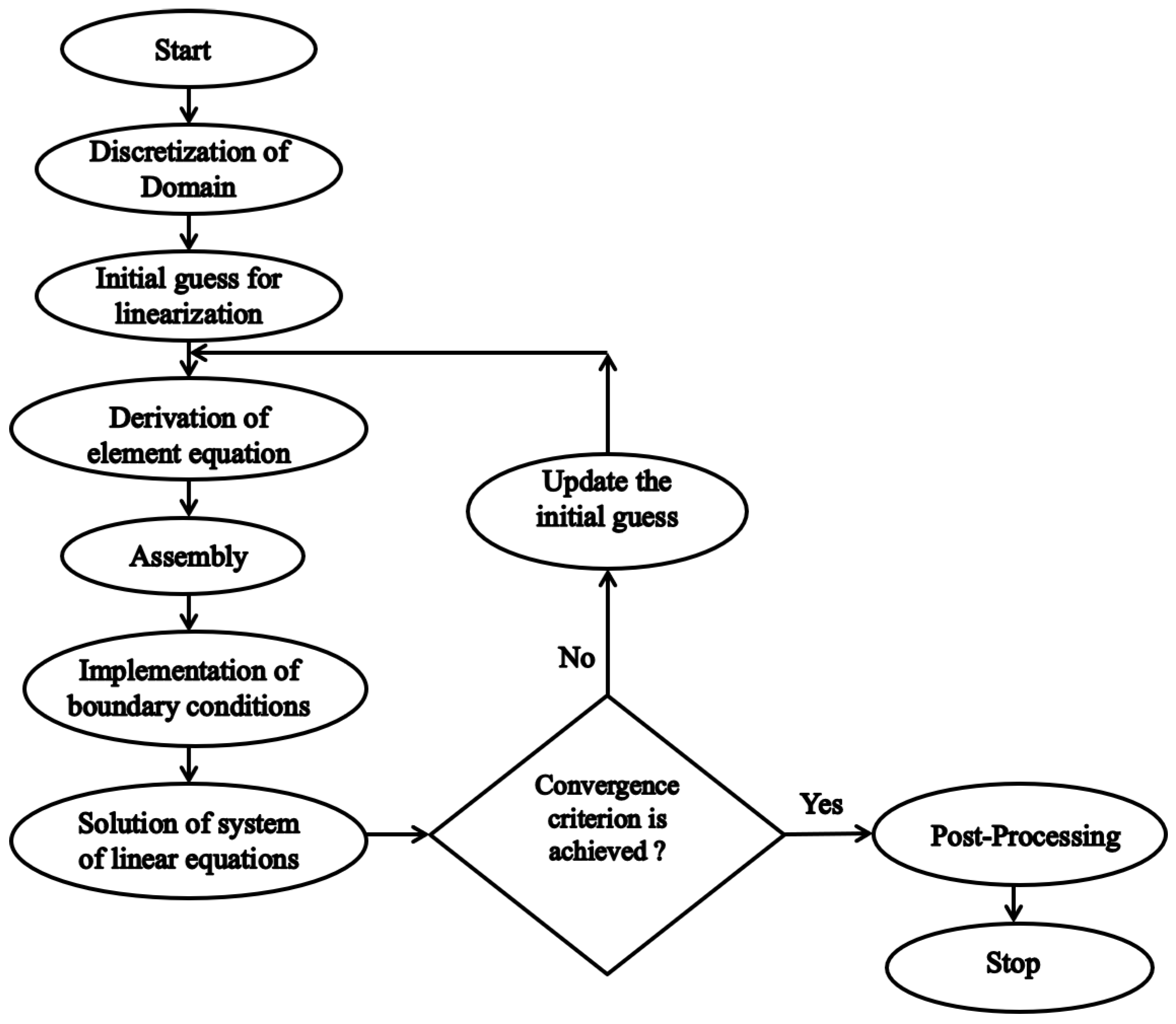
3. Numerical Method
4. Interpretation of Results
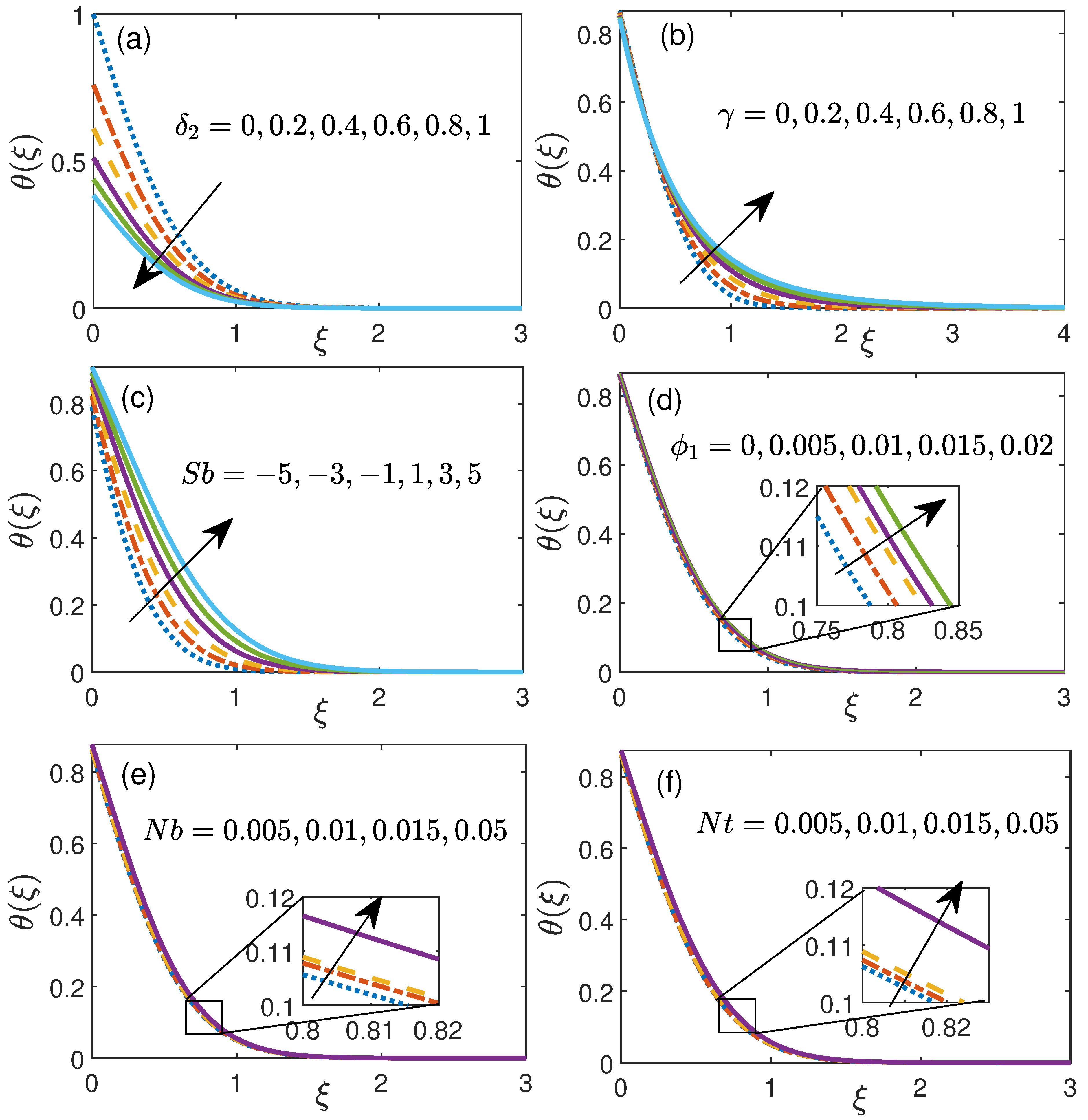
4.1. Influence of Physical Parameters on Velocity and Temperature Profiles
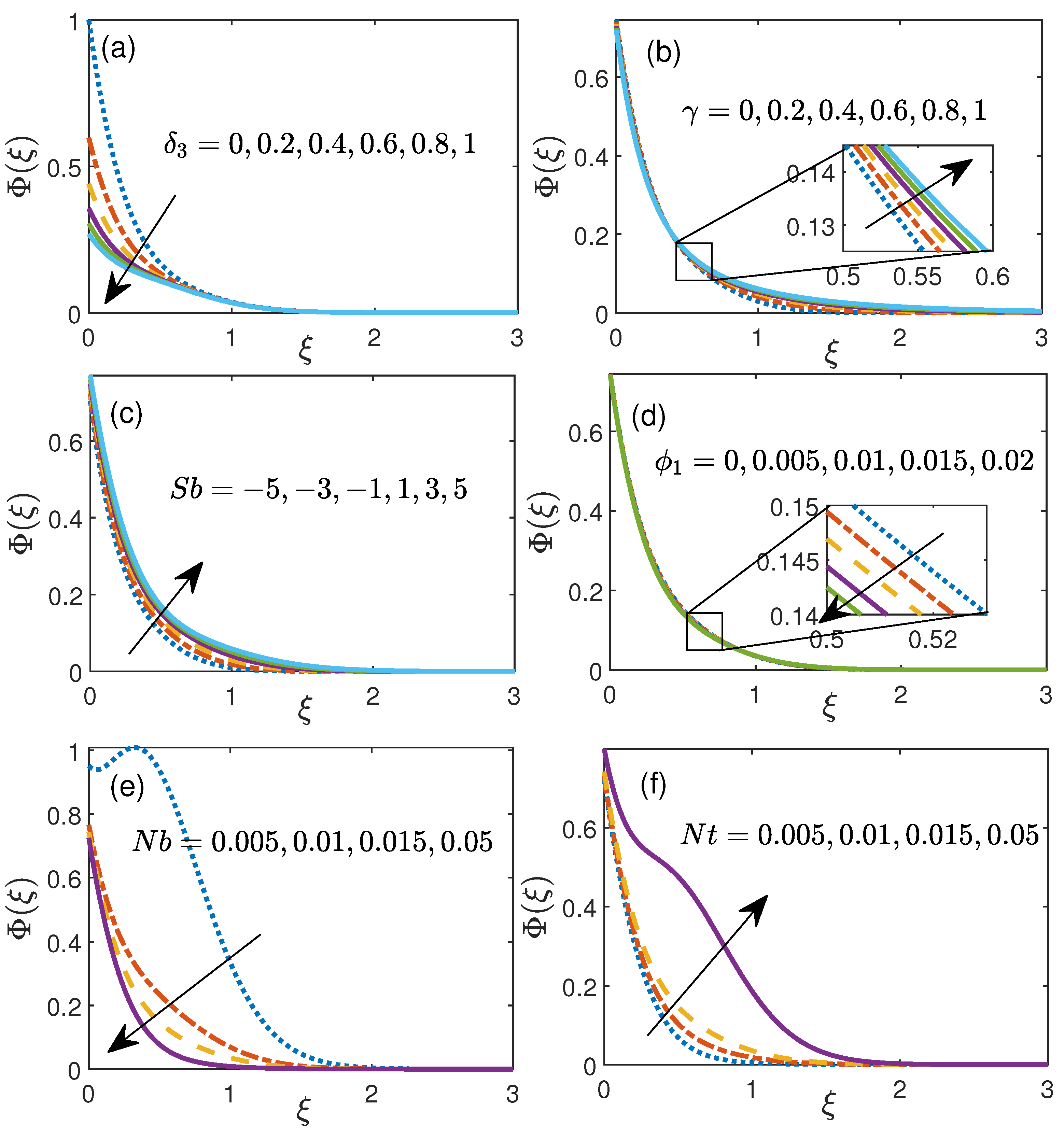
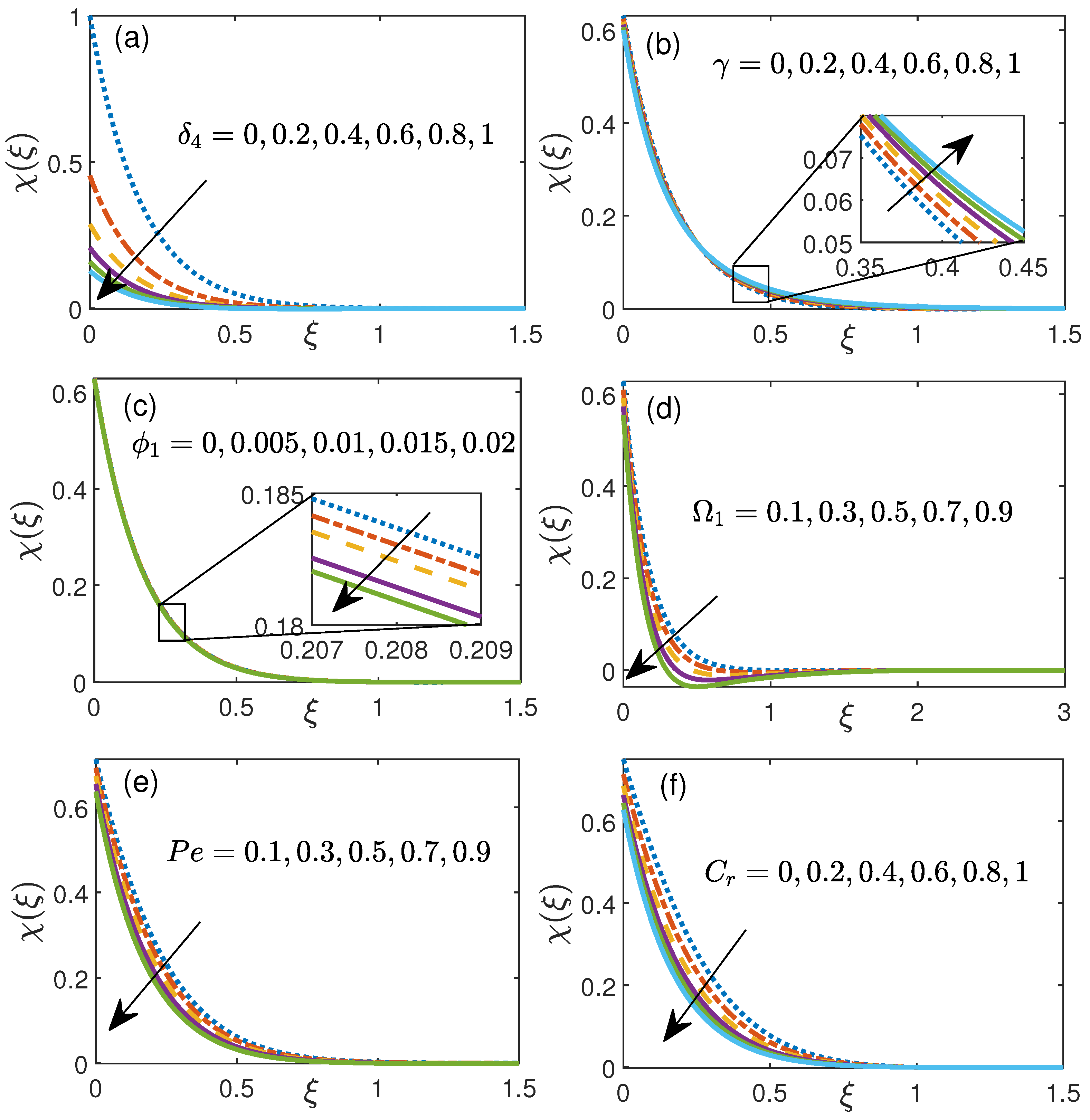
4.2. Impact of Controlling Parameters on Nanoparticle Volume Fraction and Motile Density Microorganisms Distribution
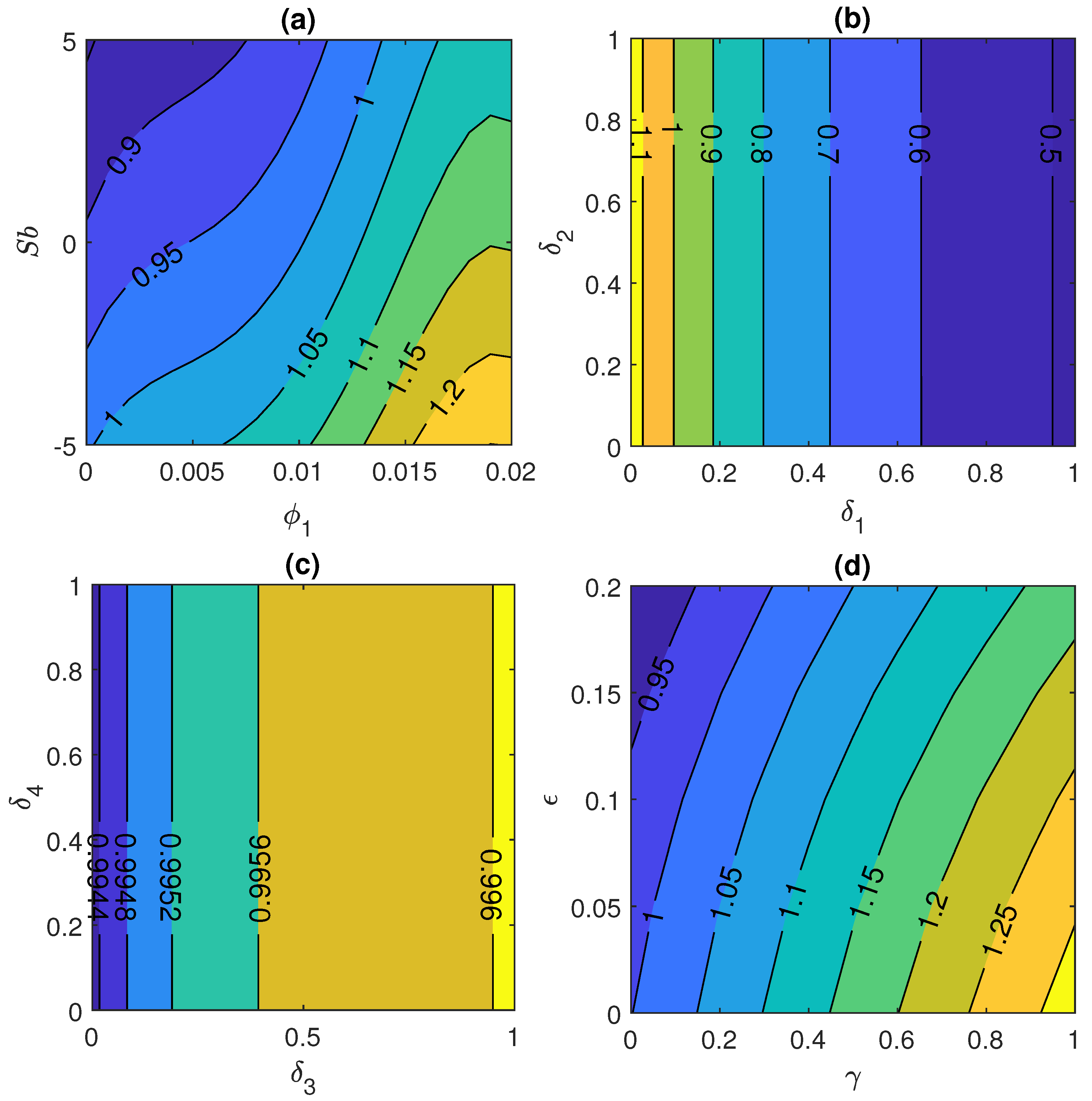
4.3. Influence on Skin Friction Coefficient and Nusselt Number with Different Controlling Parameter
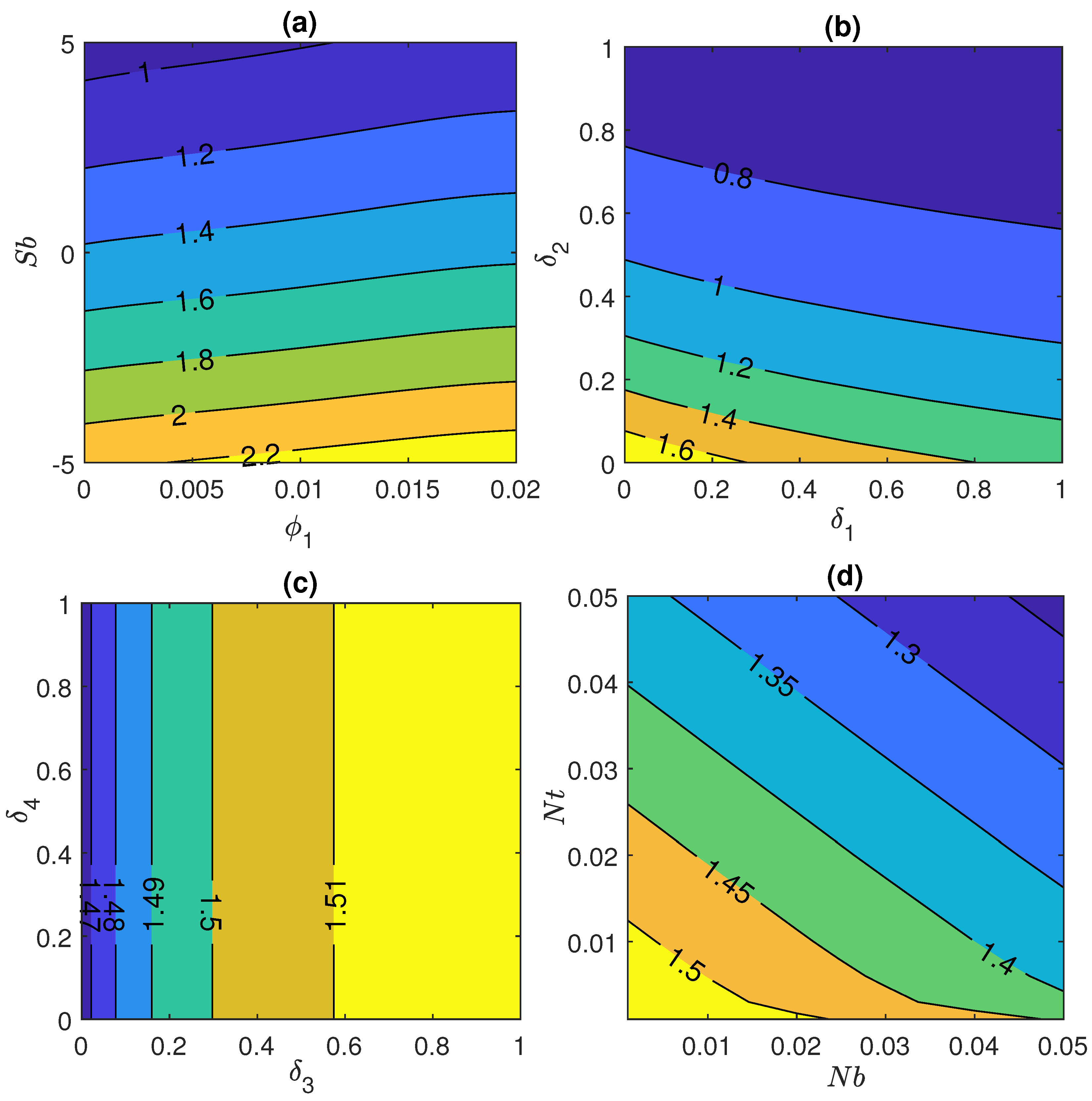
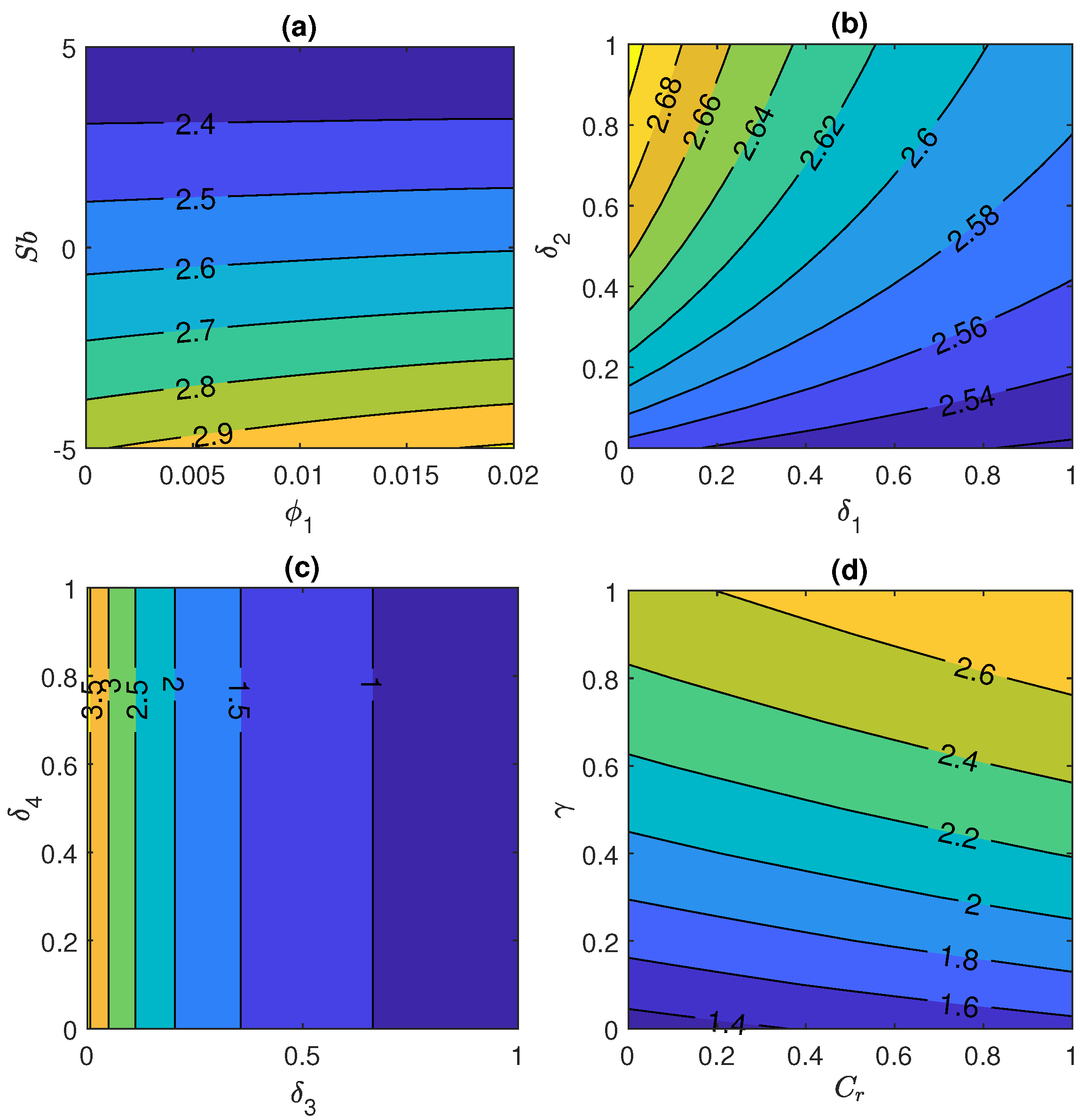
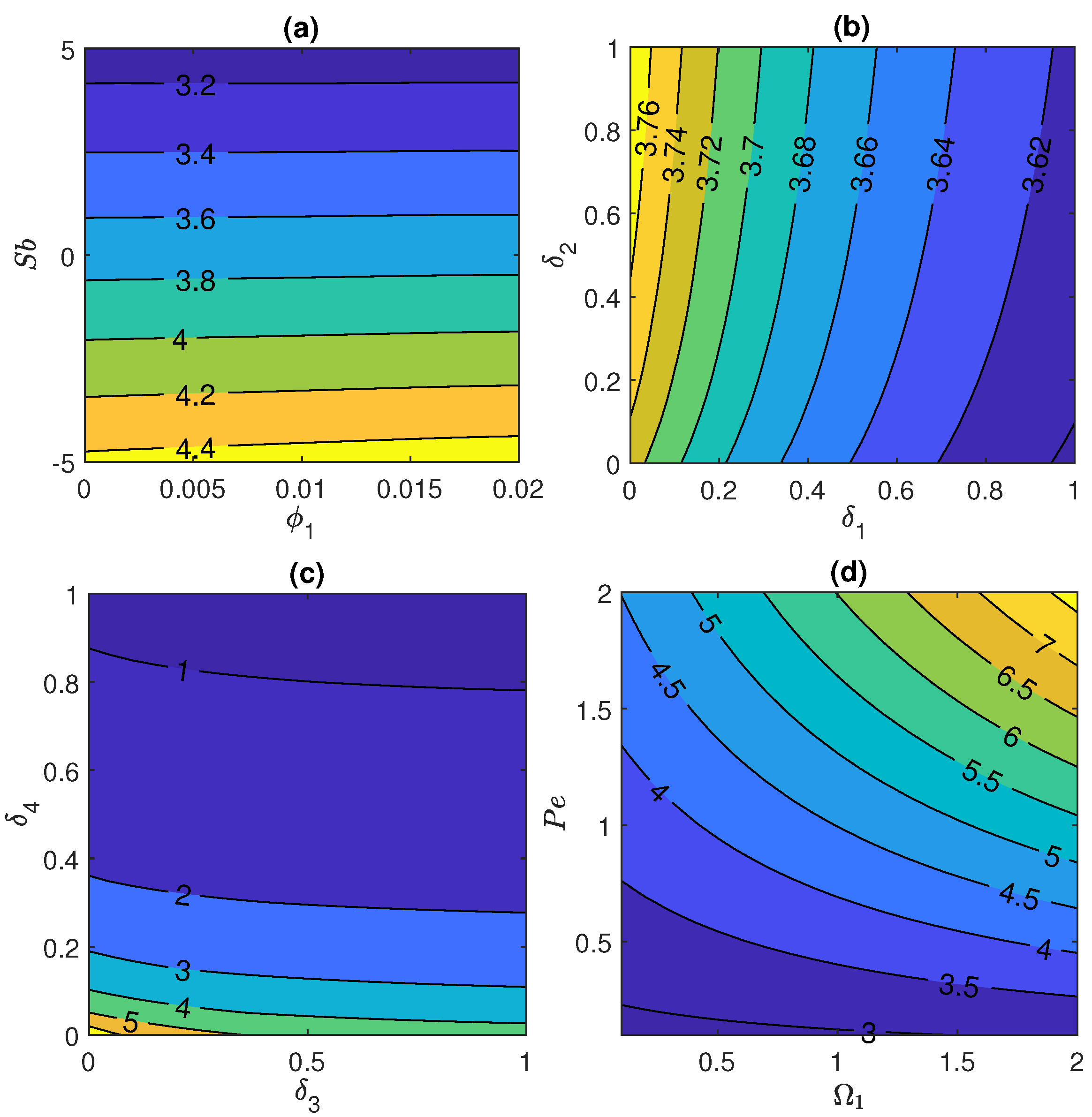
4.4. Impact of Prominent Physical Parameters on Sherwood Number and Motile Microorganism Number
5. Conclusions
- 1.
- Stefan blowing and initial nanoparticle volume fraction are found to have maximum impact on skin friction. The optimal (minimum) value of skin friction is recorded for the lower value of initial nanoparticle volume fraction and higher value of Stefan blowing parameter, which is required to have better flow performance and to avoid abrasion.
- 2.
- The consideration of velocity slip has a detrimental effect on skin friction to nearly 50% for the unit increment in its value. However, the skin friction are independent of variation in other slip conditions (thermal, nanoparticle and micro-organism).
- 3.
- Higher values of the free stream velocity reduce the skin friction but the curvature parameter has a contrary impact on it.
- 4.
- Heat transfer enhancement of upto 20% is noticed with increment of 2% of initial volume fraction of hybrid nanomaterials. With controlled nanoparticle volume fraction, the heat transfer can be optimized required for several industrial processings. Additionally, velocity and thermal slips have considerable impact on the Nusselt number.
- 5.
- The nanoparticle volume fraction upsurges with an extended zigzag motion of nanoparticles and the declined thermo-migration of nanoparticles.
- 6.
- The curvature parameter and chemically reactive nanoparticles both favor the mass transfer. Even the Sherwood number gets a boost with the increment in initial nanoparticle volume fraction.
- 7.
- An excellent agreement is noticed between the numerical results obtained from the Finite Element Method and MATLAB bvp5c routine.
Author Contributions
Funding
Conflicts of Interest
References
- Sakiadis, B.C. Boundary-layer behavior on continuous solid surfaces: I. Boundary-layer equations for two-dimensional and axisymmetric flow. AIChE J. 1961, 7, 26–28. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticles. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, San Diego, CA, USA, 12–17 November 1995. [Google Scholar]
- Buongiorno, J. Convective Transport in Nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Kuznetsov, A.; Nield, D. Natural convective boundary-layer flow of a nanofluid past a vertical plate: A revised model. Int. J. Therm. Sci. 2014, 77, 126–129. [Google Scholar] [CrossRef]
- Dhanai, R.; Rana, P.; Kumar, L. MHD mixed convection nanofluid flow and heat transfer over an inclined cylinder due to velocity and thermal slip effects: Buongiorno’s model. Powder Technol. 2016, 288, 140–150. [Google Scholar] [CrossRef]
- Swapna, G.; Kumar, L.; Rana, P.; Kumari, A.; Singh, B. Finite element study of radiative double-diffusive mixed convection magneto-micropolar flow in a porous medium with chemical reaction and convective condition. Alex. Eng. J. 2018, 57, 107–120. [Google Scholar] [CrossRef]
- Rana, P.; Bhargava, R.; Bég, O.A.; Kadir, A. Finite element analysis of viscoelastic nanofluid flow with energy dissipation and internal heat source/sink effects. Int. J. Appl. Comput. Math. 2017, 3, 1421–1447. [Google Scholar] [CrossRef]
- Vinita, V.; Poply, V. Impact of outer velocity MHD slip flow and heat transfer of nanofluid past a stretching cylinder. Mater. Today Proc. 2020, 26, 3429–3435. [Google Scholar] [CrossRef]
- Goyal, R.; Vinita; Sharma, N.; Bhargava, R. GFEM analysis of MHD nanofluid flow toward a power-law stretching sheet in the presence of thermodiffusive effect along with regression investigation. Heat Transf. 2021, 50, 234–256. [Google Scholar] [CrossRef]
- Vinita Poply, V.; Goyal, R.; Sharma, N. Analysis of the velocity, thermal, and concentration MHD slip flow over a nonlinear stretching cylinder in the presence of outer velocity. Heat Transf. 2021, 50, 1543–1569. [Google Scholar] [CrossRef]
- Vinita Poply, V.; Devi, R. A two-component modeling for free stream velocity in magnetohydrodynamic nanofluid flow with radiation and chemical reaction over a stretching cylinder. Heat Transf. 2020, 50, 3603–3619. [Google Scholar] [CrossRef]
- Khan, S.U.; Al-Khaled, K.; Aldabesh, A.; Awais, M.; Tlili, I. Bioconvection flow in accelerated couple stress nanoparticles with activation energy: Bio-fuel applications. Sci. Rep. 2021, 11, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Ramzan, M.; Shaheen, N.; Chung, J.D.; Kadry, S.; Chu, Y.M.; Howari, F. Impact of Newtonian heating and Fourier and Fick’s laws on a magnetohydrodynamic dusty Casson nanofluid flow with variable heat source/sink over a stretching cylinder. Sci. Rep. 2021, 11, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Fourier, J.B.J. Théorie Analytique de la Chaleur; Firmin Didot Père et Fils: Paris, France, 1822. [Google Scholar]
- Cattaneo, C. Sulla conduzione del calore. Atti Sem. Mat. Fis. Univ. Modena 1948, 3, 83–101. [Google Scholar]
- Christov, C. On frame indifferent formulation of the Maxwell–Cattaneo model of finite-speed heat conduction. Mech. Res. Commun. 2009, 36, 481–486. [Google Scholar] [CrossRef]
- Kumar, B.; Seth, G.; Singh, M.; Chamkha, A. Carbon nanotubes (CNTs)-based flow between two spinning discs with porous medium, Cattaneo—Christov (non-Fourier) model and convective thermal condition. J. Therm. Anal. Calorim. 2020. [Google Scholar] [CrossRef]
- Abid, N.; Ramzan, M.; Chung, J.D.; Kadry, S.; Chu, Y.M. Comparative analysis of magnetized partially ionized copper, copper oxide—Water and kerosene oil nanofluid flow with Cattaneo–Christov heat flux. Sci. Rep. 2020, 10, 1–14. [Google Scholar] [CrossRef]
- Lu, D.; Ramzan, M.; Mohammad, M.; Howari, F.; Chung, J.D. A thin film flow of nanofluid comprising carbon nanotubes influenced by Cattaneo-Christov heat flux and entropy generation. Coatings 2019, 9, 296. [Google Scholar] [CrossRef] [Green Version]
- Alamri, S.Z.; Khan, A.A.; Azeez, M.; Ellahi, R. Effects of mass transfer on MHD second grade fluid towards stretching cylinder: A novel perspective of Cattaneo–Christov heat flux model. Phys. Lett. A 2019, 383, 276–281. [Google Scholar] [CrossRef]
- Alebraheem, J.; Ramzan, M. Flow of nanofluid with Cattaneo—Christov heat flux model. Appl. Nanosci. 2019, 10, 2989–2999. [Google Scholar] [CrossRef]
- Ibrahim, W.; Hindebu, B. Magnetohydrodynamic (MHD) boundary layer flow of eyring-powell nanofluid past stretching cylinder with cattaneo-christov heat flux model. Nonlinear Eng. 2019, 8, 303–317. [Google Scholar] [CrossRef]
- Ahmad, S.; Nadeem, S.; Muhammad, N.; Khan, M.N. Cattaneo—Christov heat flux model for stagnation point flow of micropolar nanofluid toward a nonlinear stretching surface with slip effects. J. Therm. Anal. Calorim. 2020, 143, 1187–1199. [Google Scholar] [CrossRef]
- Rana, P.; Shukla, N.; Bég, O.A.; Kadir, A.; Singh, B. Unsteady electromagnetic radiative nanofluid stagnation-point flow from a stretching sheet with chemically reactive nanoparticles, Stefan blowing effect and entropy generation. Proc. Inst. Mech. Eng. Part N J. Nanomater. Nanoeng. Nanosyst. 2018, 232, 69–82. [Google Scholar] [CrossRef]
- Rana, P.; Shukla, N.; Bég, O.A.; Bhardwaj, A. Lie group analysis of nanofluid slip flow with Stefan blowing effect via modified Buongiorno’s Model: Entropy generation analysis. Differ. Equ. Dyn. Syst. 2021, 29, 193–210. [Google Scholar] [CrossRef]
- Gowda, R.P.; Kumar, R.N.; Prasannakumara, B.; Nagaraja, B.; Gireesha, B. Exploring magnetic dipole contribution on ferromagnetic nanofluid flow over a stretching sheet: An application of Stefan blowing. J. Mol. Liq. 2021, 335, 116215. [Google Scholar] [CrossRef]
- Mabood, F.; Rauf, A.; Prasannakumara, B.; Izadi, M.; Shehzad, S. Impacts of Stefan blowing and mass convention on flow of Maxwell nanofluid of variable thermal conductivity about a rotating disk. Chin. J. Phys. 2021, 71, 260–272. [Google Scholar] [CrossRef]
- Gowda, R.P.; Kumar, R.N.; Rauf, A.; Prasannakumara, B.; Shehzad, S. Magnetized flow of sutterby nanofluid through cattaneo-christov theory of heat diffusion and stefan blowing condition. Appl. Nanosci. 2021. [Google Scholar] [CrossRef]
- Madhukesh, J.; Kumar, R.N.; Gowda, R.P.; Prasannakumara, B.; Ramesh, G.; Khan, M.I.; Khan, S.U.; Chu, Y.M. Numerical simulation of AA7072-AA7075/water-based hybrid nanofluid flow over a curved stretching sheet with Newtonian heating: A non-Fourier heat flux model approach. J. Mol. Liq. 2021, 335, 116103. [Google Scholar] [CrossRef]
- Punith Gowda, R.J.; Naveen Kumar, R.; Jyothi, A.M.; Prasannakumara, B.C.; Sarris, I.E. Impact of binary chemical reaction and activation energy on heat and mass transfer of marangoni driven boundary layer flow of a non-Newtonian nanofluid. Processes 2021, 9, 702. [Google Scholar] [CrossRef]
- Yusuf, T.A.; Mabood, F.; Prasannakumara, B.; Sarris, I.E. Magneto-bioconvection flow of Williamson nanofluid over an inclined plate with gyrotactic microorganisms and entropy generation. Fluids 2021, 6, 109. [Google Scholar] [CrossRef]
- Rana, P.; Dhanai, R.; Kumar, L. MHD slip flow and heat transfer of Al2O3-water nanofluid over a horizontal shrinking cylinder using Buongiorno’s model: Effect of nanolayer and nanoparticle diameter. Adv. Powder Technol. 2017, 28, 1727–1738. [Google Scholar] [CrossRef]
- Esfe, M.H.; Amiri, M.K.; Alirezaie, A. Thermal conductivity of a hybrid nanofluid. J. Therm. Anal. Calorim. 2018, 134, 1113–1122. [Google Scholar] [CrossRef]
- Shah, T.R.; Ali, H.M. Applications of hybrid nanofluids in solar energy, practical limitations and challenges: A critical review. Sol. Energy 2019, 183, 173–203. [Google Scholar] [CrossRef]
- Rana, P. MHD convective heat transfer in the annulus between concentric cylinders utilizing nanoparticles and non-uniform heating. In AIP Conference Proceedings; AIP Publishing LLC: New York, NY, USA, 2020; Volume 2214, p. 020013. [Google Scholar]
- Aminian, E.; Moghadasi, H.; Saffari, H. Magnetic field effects on forced convection flow of a hybrid nanofluid in a cylinder filled with porous media: A numerical study. J. Therm. Anal. Calorim. 2020, 141, 2019–2031. [Google Scholar] [CrossRef]
- Gul, T.; Khan, A.; Bilal, M.; Alreshidi, N.A.; Mukhtar, S.; Shah, Z.; Kumam, P. Magnetic dipole impact on the hybrid nanofluid flow over an extending surface. Sci. Rep. 2020, 10, 1–13. [Google Scholar]
- Reddy, M.G.; Rani, M.S.; Kumar, K.G.; Prasannakumar, B.; Lokesh, H. Hybrid dusty fluid flow through a Cattaneo–Christov heat flux model. Phys. A Stat. Mech. Its Appl. 2020, 551, 123975. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Waini, I.; Zainal, N.A.; Hamzah, K.; Mohd Kasim, A.R. Hybrid nanofluid flow past a shrinking cylinder with prescribed surface heat flux. Symmetry 2020, 12, 1493. [Google Scholar] [CrossRef]
- Tassaddiq, A. Impact of Cattaneo-Christov heat flux model on MHD hybrid nano-micropolar fluid flow and heat transfer with viscous and joule dissipation effects. Sci. Rep. 2021, 11, 67. [Google Scholar] [CrossRef]
- Shah, Z.; Alzahrani, E.O.; Dawar, A.; Alghamdi, W.; Zaka Ullah, M. Entropy generation in MHD second-grade nanofluid thin film flow containing CNTs with Cattaneo-Christov heat flux model past an unsteady stretching sheet. Appl. Sci. 2020, 10, 2720. [Google Scholar] [CrossRef] [Green Version]
- Khan, U.; Ahmad, S.; Hayyat, A.; Khan, I.; Nisar, K.S.; Baleanu, D. On the Cattaneo–Christov heat flux model and OHAM analysis for three different types of nanofluids. Appl. Sci. 2020, 10, 886. [Google Scholar] [CrossRef] [Green Version]
- Jakeer, S.; Reddy, P.B.; Rashad, A.; Nabwey, H.A. Impact of heated obstacle position on magneto-hybrid nanofluid flow in a lid-driven porous cavity with Cattaneo-Christov heat flux pattern. Alex. Eng. J. 2021, 60, 821–835. [Google Scholar] [CrossRef]
- Esfe, M.H.; Arani, A.A.A.; Rezaie, M.; Yan, W.M.; Karimipour, A. Experimental determination of thermal conductivity and dynamic viscosity of Ag–MgO/water hybrid nanofluid. Int. Commun. Heat Mass Transf. 2015, 66, 189–195. [Google Scholar] [CrossRef]
- Ma, Y.; Mohebbi, R.; Rashidi, M.; Yang, Z. MHD convective heat transfer of Ag-MgO/water hybrid nanofluid in a channel with active heaters and coolers. Int. J. Heat Mass Transf. 2019, 137, 714–726. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. Impact of a rotating cone on forced convection of Ag–MgO/water hybrid nanofluid in a 3D multiple vented T-shaped cavity considering magnetic field effects. J. Therm. Anal. Calorim. 2020, 143, 1485–1501. [Google Scholar] [CrossRef]
- Pedley, T.; Hill, N.; Kessler, J. The growth of bioconvection patterns in a uniform suspension of gyrotactic micro-organisms. J. Fluid Mech. 1988, 195, 223–237. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khurana, M.; Rana, P.; Srivastava, S.; Yadav, S. Magneto-bio-thermal convection in rotating nanoliquid containing gyrotactic microorganism. J. Appl. Comput. Mech. 2021. [Google Scholar] [CrossRef]
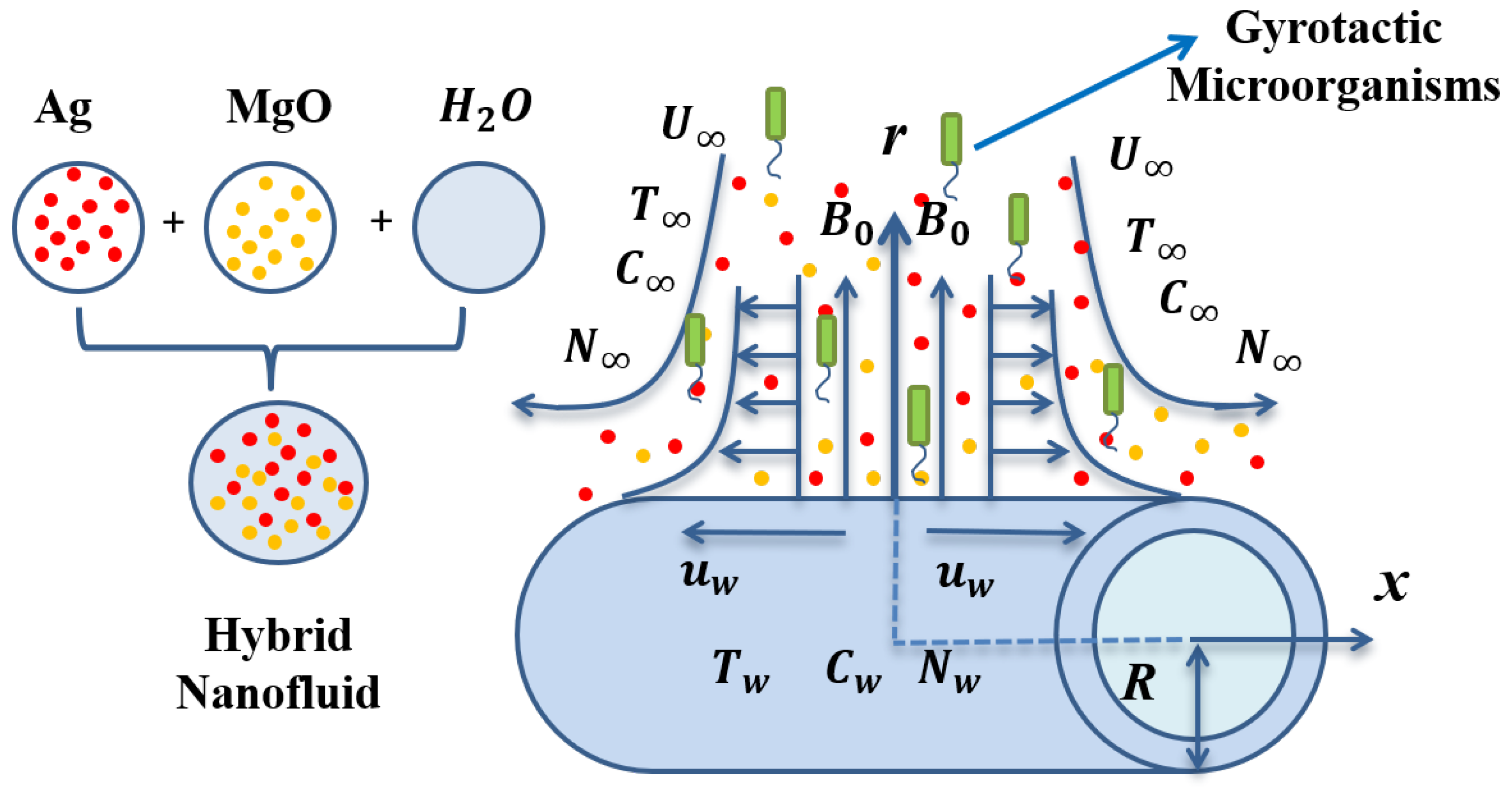

| Pure Water | |||
|---|---|---|---|
| (Kg/m) | 10,500 | 3560 | 997.1 |
| c (J/Kg K) | 235 | 955 | 4179 |
| k (W/m K) | 429 | 45 | 0.62 |
| (S/m) | ≈ | 0.05 | |
| (Kg/m S) | - | - | 8.55 × |
| Element Size | ||||||||
| 0.1 | 0.995848 | 1.482866 | 2.584126 | 3.731891 | 0.995449 | 1.483016 | 2.584130 | 3.731912 |
| 0.05 | 0.995469 | 1.483159 | 2.576088 | 3.716691 | 0.995070 | 1.483313 | 2.576094 | 3.716716 |
| 0.025 | 0.995375 | 1.483235 | 2.574064 | 3.712841 | 0.994975 | 1.483390 | 2.574071 | 3.712867 |
| 0.01 | 0.995348 | 1.483256 | 2.573496 | 3.711759 | 0.994949 | 1.483412 | 2.573503 | 3.711785 |
| 0.005 | 0.995344 | 1.483259 | 2.573415 | 3.711604 | 0.994945 | 1.483415 | 2.573422 | 3.711630 |
| Element Size | ||||||||
| 0.1 | 0.995390 | 1.483037 | 2.584131 | 3.731914 | 0.995380 | 1.483041 | 2.584131 | 3.731915 |
| 0.05 | 0.995011 | 1.483335 | 2.576095 | 3.716720 | 0.995002 | 1.483339 | 2.576095 | 3.716720 |
| 0.025 | 0.994916 | 1.483412 | 2.574072 | 3.712870 | 0.994907 | 1.483416 | 2.574072 | 3.712871 |
| 0.01 | 0.994890 | 1.483434 | 2.573504 | 3.711789 | 0.994880 | 1.483437 | 2.573504 | 3.711789 |
| 0.005 | 0.994886 | 1.483437 | 2.573423 | 3.711634 | 0.994876 | 1.483440 | 2.573423 | 3.711635 |
| Element Size | ||||||||
| 0.1 | 0.995288 | 1.482829 | 2.573205 | 3.700777 | 0.994889 | 1.482984 | 2.573212 | 3.700801 |
| 0.05 | 0.995329 | 1.483153 | 2.573335 | 3.704312 | 0.994930 | 1.483308 | 2.573342 | 3.704338 |
| 0.025 | 0.995340 | 1.483233 | 2.573374 | 3.707449 | 0.994940 | 1.483389 | 2.573381 | 3.707475 |
| 0.01 | 0.995342 | 1.483256 | 2.573386 | 3.709793 | 0.994943 | 1.483412 | 2.573393 | 3.709819 |
| 0.005 | 0.995343 | 1.483259 | 2.573387 | 3.710653 | 0.994944 | 1.483415 | 2.573394 | 3.710679 |
| Element Size | ||||||||
| 0.1 | 0.994830 | 1.483005 | 2.573213 | 3.700804 | 0.994820 | 1.483009 | 2.573213 | 3.700805 |
| 0.05 | 0.994871 | 1.483330 | 2.573343 | 3.704341 | 0.994861 | 1.483334 | 2.573344 | 3.704342 |
| 0.025 | 0.994881 | 1.483411 | 2.573382 | 3.707479 | 0.994872 | 1.483415 | 2.573383 | 3.707480 |
| 0.01 | 0.994884 | 1.483434 | 2.573394 | 3.709823 | 0.994875 | 1.483437 | 2.573394 | 3.709824 |
| 0.005 | 0.994885 | 1.483437 | 2.573395 | 3.710683 | 0.994875 | 1.483440 | 2.573396 | 3.710684 |
| FEM | MATLAB bvp5c | ||||
|---|---|---|---|---|---|
| −2 | 0.01 | 0.92401060 | 1.71063232 | 0.92401055 | 1.71063225 |
| −1 | 0.90400142 | 1.54416075 | 0.90400137 | 1.54416073 | |
| 0 | 0.88413285 | 1.38255544 | 0.88413281 | 1.38255547 | |
| 1 | 0.86454938 | 1.22697477 | 0.86454934 | 1.22697487 | |
| 2 | 0.84541153 | 1.07879608 | 0.84541149 | 1.07879626 | |
| 1 | 0 | 0.88744497 | 1.26305925 | 0.88744493 | 1.26305936 |
| 0.005 | 0.87633789 | 1.24418922 | 0.87633785 | 1.24418932 | |
| 0.015 | 0.82487969 | 1.21973533 | 0.82487965 | 1.21973542 | |
| 0.02 | 0.81263218 | 1.20750268 | 0.81263215 | 1.20750276 | |
| M | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0 | 0.1 | 0.1 | 0.1 | 0.01 | 0.958815 | 1.492518 | 2.574126 | 3.724582 |
| 0.2 | 1.029288 | 1.474745 | 2.572737 | 3.720466 | ||||
| 0.5 | 1.124164 | 1.450629 | 2.571015 | 3.714981 | ||||
| 1 | 1.261306 | 1.415459 | 2.568802 | 3.707166 | ||||
| −3 | 1.048829 | 1.910737 | 2.785927 | 4.166730 | ||||
| −1 | 1.012783 | 1.622628 | 2.643372 | 3.874408 | ||||
| 0 | 0.996462 | 1.495597 | 2.579568 | 3.736039 | ||||
| 1 | 0.981118 | 1.378151 | 2.519442 | 3.602502 | ||||
| 3 | 0.953033 | 1.168544 | 2.407608 | 3.349496 | ||||
| 0 | 0.961862 | 1.460638 | 2.545320 | 3.689000 | ||||
| 0.2 | 1.027009 | 1.506224 | 2.600866 | 3.755347 | ||||
| 0.5 | 1.118951 | 1.574069 | 2.679831 | 3.850559 | ||||
| 1 | 1.261265 | 1.683889 | 2.801731 | 3.998840 | ||||
| 0 | 1.033387 | 1.469748 | 2.572731 | 3.720044 | ||||
| 0.05 | 1.016872 | 1.475782 | 2.573006 | 3.721086 | ||||
| 0.1 | 0.994885 | 1.483438 | 2.573403 | 3.722471 | ||||
| 0.2 | 0.936694 | 1.502411 | 2.574580 | 3.726132 | ||||
| 0 | 0.906476 | 1.412154 | 2.556206 | 3.715626 | ||||
| 0.002 | 0.932973 | 1.428518 | 2.559989 | 3.717488 | ||||
| 0.01 | 0.994885 | 1.483438 | 2.573403 | 3.722471 | ||||
| 0.02 | 1.144794 | 1.553461 | 2.587661 | 3.730159 |
| 0 | 0.1 | 0.1 | 0.1 | 1 | 0.01 | 0.01 | 1.142372 | 1.545323 | 2.584920 | 3.749584 |
| 0.2 | 0.884582 | 1.432896 | 2.564600 | 3.700998 | ||||||
| 0.5 | 0.671345 | 1.321554 | 2.546924 | 3.655857 | ||||||
| 1 | 0.486269 | 1.203998 | 2.530404 | 3.611454 | ||||||
| 0 | 0.994904 | 1.712409 | 2.543340 | 3.713681 | ||||||
| 0.2 | 0.994871 | 1.307643 | 2.596794 | 3.729352 | ||||||
| 0.5 | 0.994843 | 0.963149 | 2.643405 | 3.743163 | ||||||
| 1 | 0.994818 | 0.668176 | 2.684117 | 3.755327 | ||||||
| 0 | 0.994276 | 1.465529 | 3.568595 | 4.044178 | ||||||
| 0.2 | 0.995230 | 1.493596 | 2.011039 | 3.531668 | ||||||
| 0.5 | 0.995718 | 1.508042 | 1.213800 | 3.249761 | ||||||
| 1 | 0.996014 | 1.516824 | 0.730580 | 3.072294 | ||||||
| 0 | 0.994885 | 1.483438 | 2.573403 | 5.845095 | ||||||
| 0.2 | 0.994885 | 1.483438 | 2.573403 | 2.730793 | ||||||
| 0.5 | 0.994885 | 1.483438 | 2.573403 | 1.517774 | ||||||
| 1 | 0.994885 | 1.483438 | 2.573403 | 0.872117 | ||||||
| 0 | 0.995640 | 1.492384 | 1.341482 | 2.486181 | ||||||
| 0.2 | 0.995427 | 1.489573 | 1.689495 | 2.852012 | ||||||
| 0.5 | 0.995181 | 1.486593 | 2.090375 | 3.255614 | ||||||
| 1 | 0.994885 | 1.483438 | 2.573403 | 3.722471 | ||||||
| 0.001 | 0.994773 | 1.509164 | 2.757261 | 3.777386 | ||||||
| 0.005 | 0.994825 | 1.497691 | 2.672910 | 3.751970 | ||||||
| 0.01 | 0.994885 | 1.483438 | 2.573403 | 3.722471 | ||||||
| 0.05 | 0.995236 | 1.373002 | 2.000487 | 3.575400 | ||||||
| 0.001 | 0.996163 | 1.527152 | 0.488376 | 3.054297 | ||||||
| 0.005 | 0.995024 | 1.503198 | 2.346370 | 3.651667 | ||||||
| 0.01 | 0.994885 | 1.483438 | 2.573403 | 3.722471 | ||||||
| 0.05 | 0.994775 | 1.338567 | 2.753463 | 3.778114 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rana, P.; Makkar, V.; Gupta, G. Finite Element Study of Bio-Convective Stefan Blowing Ag-MgO/Water Hybrid Nanofluid Induced by Stretching Cylinder Utilizing Non-Fourier and Non-Fick’s Laws. Nanomaterials 2021, 11, 1735. https://doi.org/10.3390/nano11071735
Rana P, Makkar V, Gupta G. Finite Element Study of Bio-Convective Stefan Blowing Ag-MgO/Water Hybrid Nanofluid Induced by Stretching Cylinder Utilizing Non-Fourier and Non-Fick’s Laws. Nanomaterials. 2021; 11(7):1735. https://doi.org/10.3390/nano11071735
Chicago/Turabian StyleRana, Puneet, Vinita Makkar, and Gaurav Gupta. 2021. "Finite Element Study of Bio-Convective Stefan Blowing Ag-MgO/Water Hybrid Nanofluid Induced by Stretching Cylinder Utilizing Non-Fourier and Non-Fick’s Laws" Nanomaterials 11, no. 7: 1735. https://doi.org/10.3390/nano11071735
APA StyleRana, P., Makkar, V., & Gupta, G. (2021). Finite Element Study of Bio-Convective Stefan Blowing Ag-MgO/Water Hybrid Nanofluid Induced by Stretching Cylinder Utilizing Non-Fourier and Non-Fick’s Laws. Nanomaterials, 11(7), 1735. https://doi.org/10.3390/nano11071735






