Impact of Nonlocality on Group Delay and Reflective Behavior Near Surface Plasmon Resonances in Otto Structure
Abstract
:1. Introduction
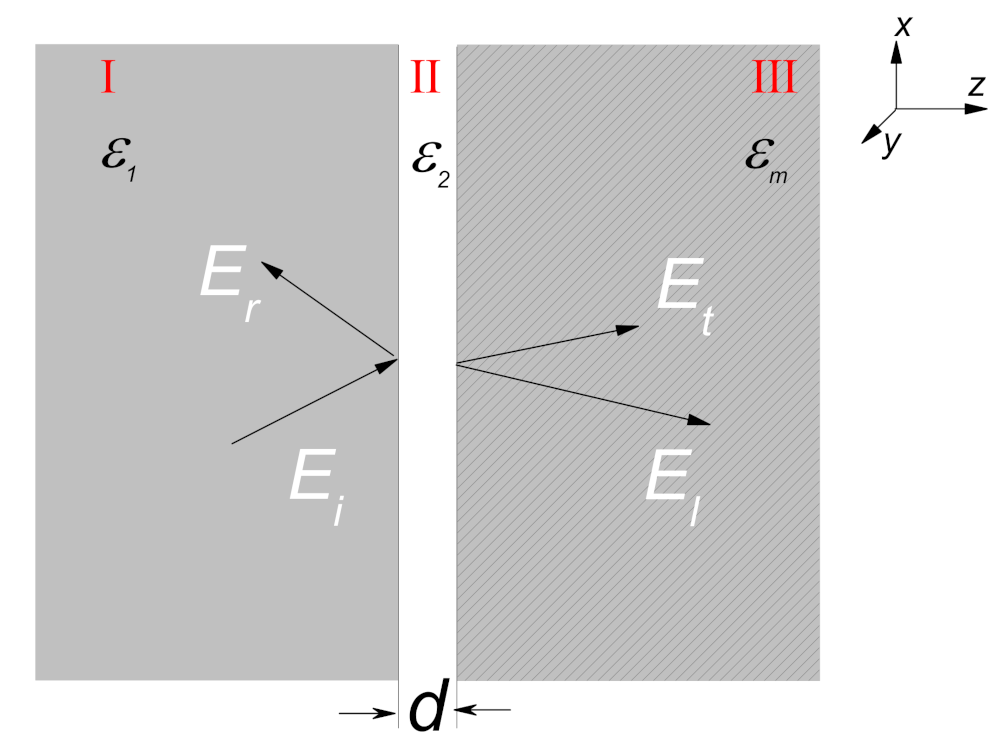
2. Materials and Methods
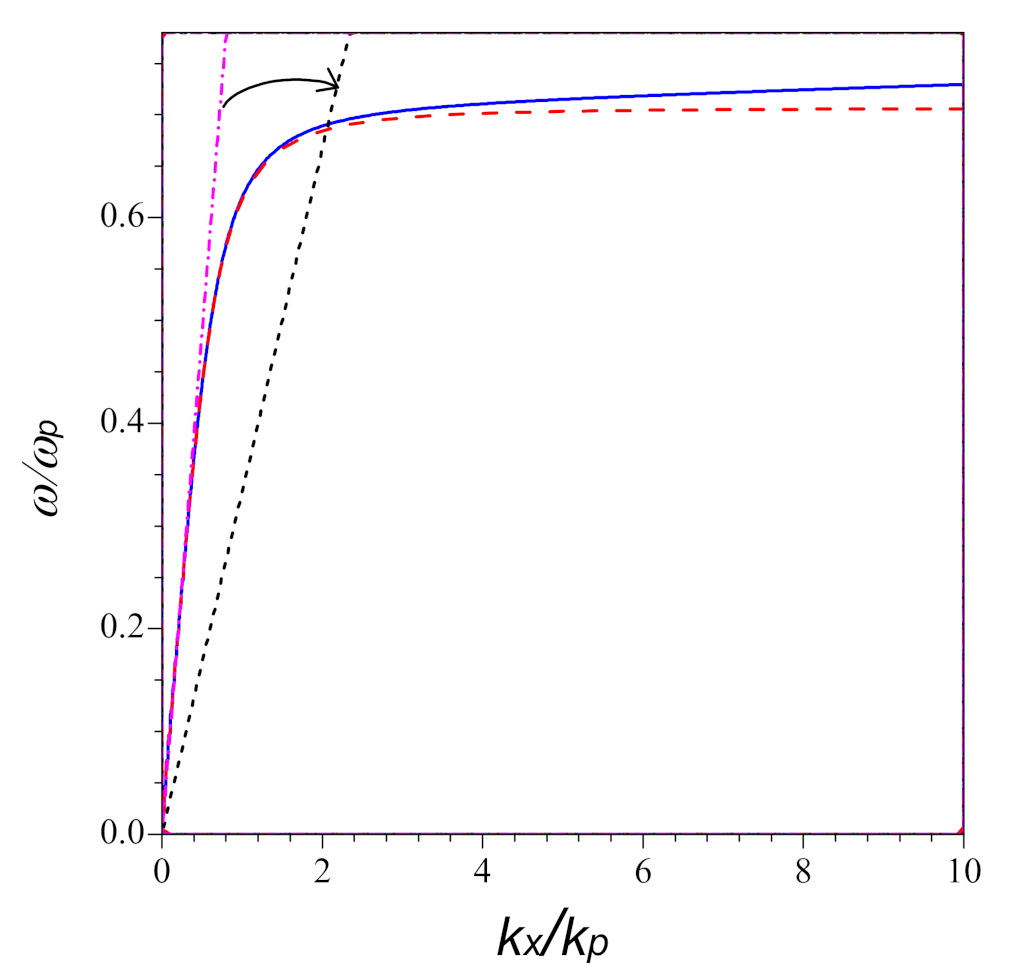
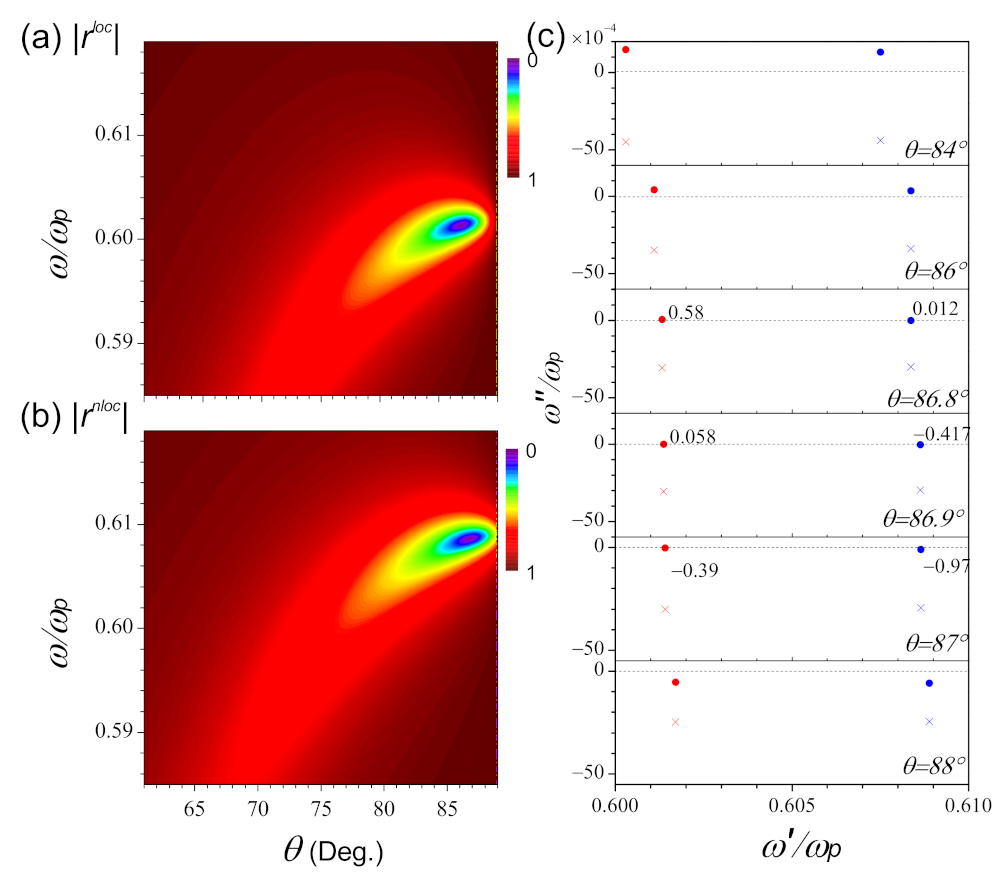
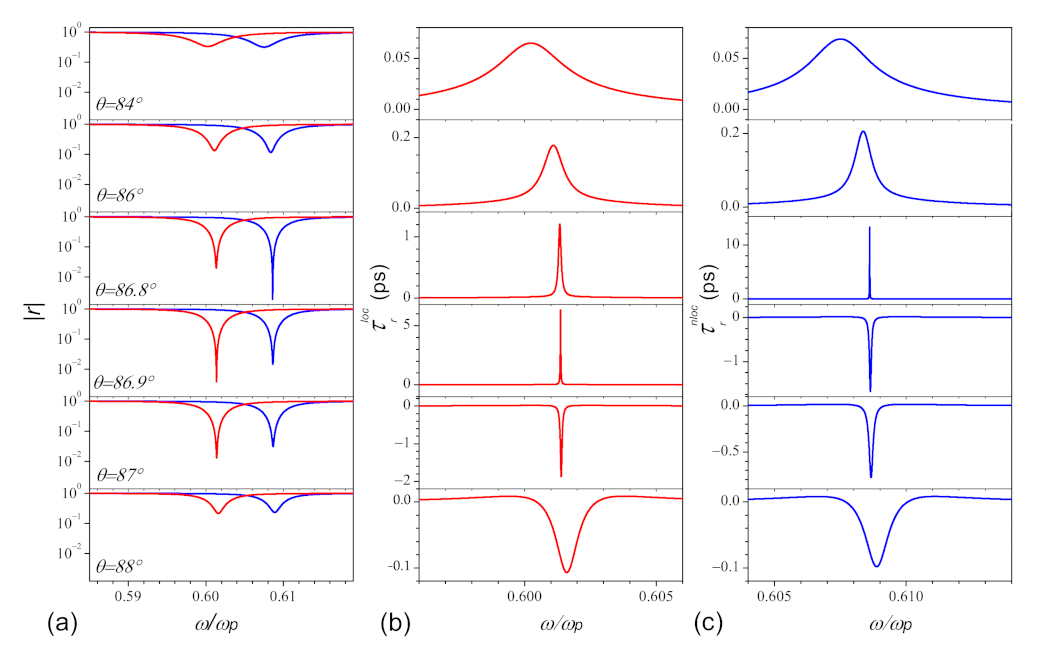
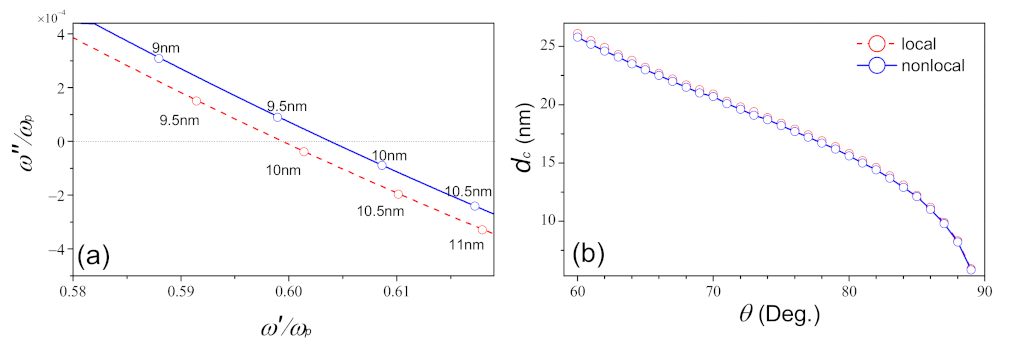
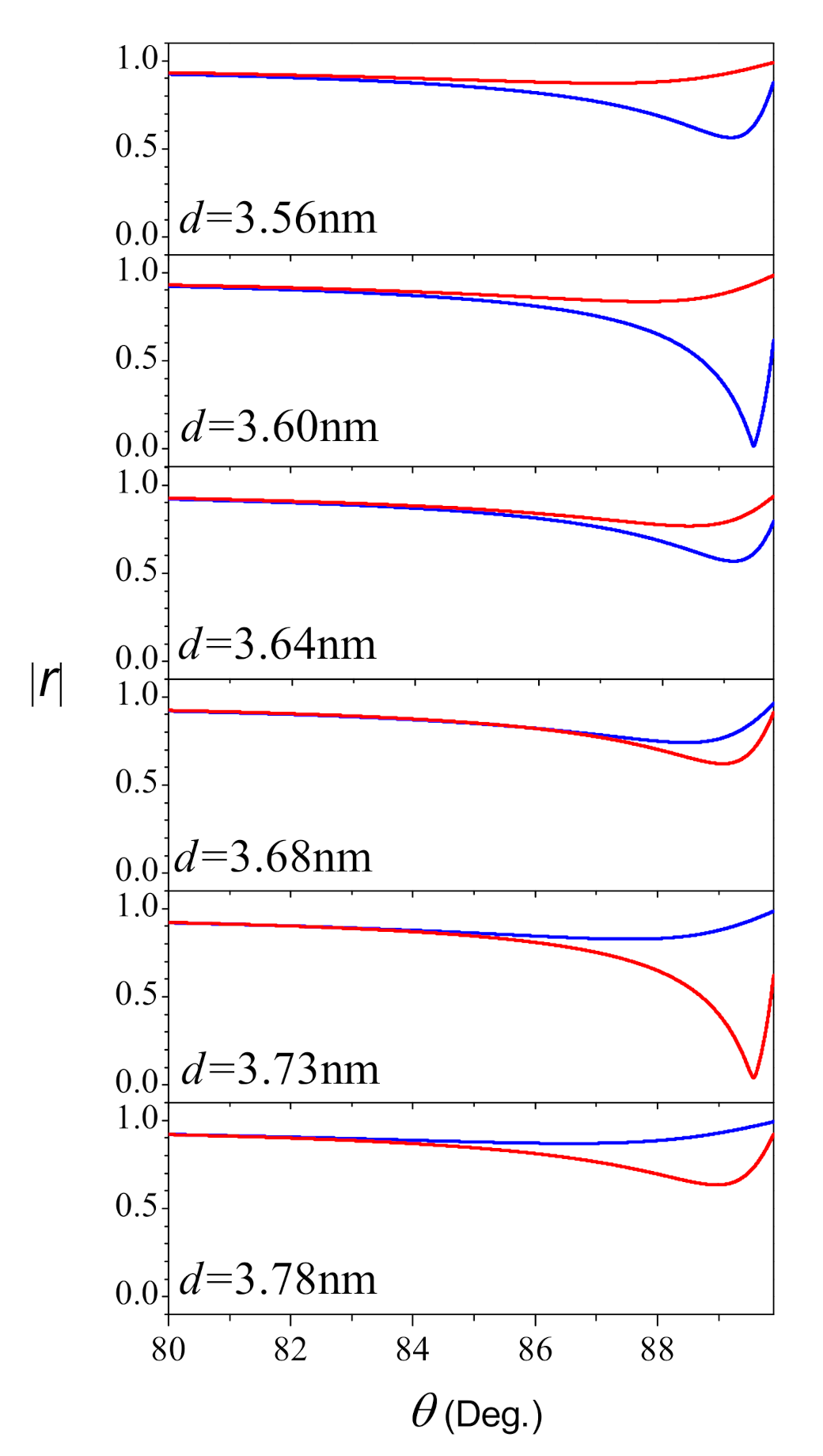
3. Numerical Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gaponenko, S.V. Introduction to Nanophotonics, 1st ed.; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Simovski, C.; Tretyakov, S. An Introduction to Metamaterials and Nanophotonics, 1st ed.; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Pitarke, J.M.; Silkin, V.M.; Chulkov, E.V.; Echenique, P.M. Theory of surface plasmons and surface-plasmon polaritons. Rep. Prog. Phys. 2007, 70, 1–87. [Google Scholar] [CrossRef]
- Jackson, J.D. Classical Electrodynamics, 3rd ed.; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Drude, P. Zur Elektronentheorie der Metalle. Ann. Phys. 1900, 306, 566–613. [Google Scholar] [CrossRef] [Green Version]
- Scholl, J.A.; Koh, A.L.K.; Dionne, J.A. Quantum plasmon resonances of individual metallic nanoparticles. Nature 2012, 483, 421–427. [Google Scholar] [CrossRef]
- Cha, H.; Yoon, J.H.; Yoon, S. Probing Quantum Plasmon Coupling Using Gold Nanoparticle Dimers with Tunable Interparticle Distances down to the Subnanometer Range. ACS Nano 2014, 8, 8554–8563. [Google Scholar] [CrossRef]
- Ciracì, C.; Hill, R.T.; Mock, J.J.; Urzhumov, Y.; Fernández-Domínguez, A.I.; Maier, S.A.; Pendry, J.B.; Chilkoti, A.; Smith, D.R. Probing the ultimate limits of plasmonic enhancement. Science 2012, 337, 1072–1074. [Google Scholar] [CrossRef] [Green Version]
- Mortensen, N.A.; Raza, S.; Wubs, M.; Sondergaard, T.; Bozhevolnyi, S.I. A generalized non-local optical response theory for plasmonic nanostructures. Nat. Commun. 2014, 5, 3809. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tsuei, K.D.; Plummer, E.W.; Liebsch, A.; Kempa, K.; Bakshi, P. Multipole plasmon modes at a metal surface. Phys. Rev. Lett. 1990, 64, 44–47. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Toscano, G.; Straubel, J.; Kwiatkowski, A.; Rockstuhl, C.; Evers, F.; Xu, H.X.; Mortensen, N.A.; Wubs, M. Resonance shifts and spill-out effects in self-consistent hydrodynamic nanoplasmonics. Nat. Commun. 2015, 6, 7132. [Google Scholar] [CrossRef] [Green Version]
- Ciracì, C.; Sala, F.D. Quantum Hydrodynamic Theory for Plasmonics: Impact of the electron density tail. Phys. Rev. B 2016, 93, 205405. [Google Scholar] [CrossRef] [Green Version]
- Bloch, F. Bremsvermögen von Atomen mit mehreren Elektronen. Z. Physik 1933, 81, 363–376. [Google Scholar] [CrossRef]
- McMahon, J.M.; Gray, S.K.; Schatz, G.C. Nonlocal Optical Response of Metal Nanostructures with Arbitrary Shape. Phys. Rev. Lett. 2009, 103, 097403. [Google Scholar] [CrossRef] [PubMed]
- Moreau, A.; Ciracì, C.; Smith, D.R. Impact of nonlocal response on metallodielectric multilayers and optical patch antennas. Phys. Rev. B 2013, 87, 045401. [Google Scholar] [CrossRef] [Green Version]
- Toscano, G.; Raza, S.; Jauho, A.P.; Mortensen, N.A.; Wubs, M. Modified field enhancement and extinction by plasmonic nanowire dimers due to nonlocal response. Opt. Express 2012, 20, 4176–4188. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Toscano, G.; Raza, S.; Xiao, S.; Wubs, M.; Jauho, A.P.; Bozhevolnyi, S.I.; Mortensen, N.A. Surface-enhanced raman spectroscopy: Nonlocal limitations. Opt. Lett. 2012, 37, 2538–2540. [Google Scholar] [CrossRef] [Green Version]
- Wiener, A.; Fernández-Domínguez, A.I.; Horsfield, A.P.; Pendry, J.B.; Maier, S.A. Nonlocal effects in the nanofocusing performance of plasmonic tips. Nano Lett. 2012, 12, 3308–3314. [Google Scholar] [CrossRef] [PubMed]
- Toscano, G.; Raza, S.; Yan, W.; Jeppesen, C.; Xiao, S.S.; Mubs, M.; Jauho, A.P.; Bozhevolnyi, S.I.; Mortensen, N.A. Nonlocal response in plasmonic waveguiding with extreme light confinement. Nanophotonics 2013, 2, 161–166. [Google Scholar] [CrossRef] [Green Version]
- Wiener, A.; Duan, H.G.; Bosman, M.; Horsfield, A.P.; Pendry, J.B.; Yang, J.K.W.; Maier, S.A.; Fernández-Domínguez, A.I. Electron-energy loss study of nonlocal effects in connected plasmonic nanoprisms. ACS Nano 2013, 7, 6287–6296. [Google Scholar] [CrossRef] [PubMed]
- Ciracì, C.; Poutrina, E.; Scalora, M.; Smith, D.R. Origin of second-harmonic generation enhancement in optical split-ring resonators. Phys. Rev. B 2012, 85, 201403. [Google Scholar] [CrossRef] [Green Version]
- Maack, J.R.; Mortensen, N.A.; Wubs, M. Size-dependent nonlocal effects in plasmonic semiconductor particles. Epl 2017, 119, 17003. [Google Scholar] [CrossRef]
- Benedicto, J.; Pollès, R.; Ciracì, C.; Centeno, E.; Smith, D.R.; Moreau, A. Numerical tool to take nonlocal effects into account in metallo-dielectric multilayers. J. Opt. Soc. Am. A 2015, 32, 1581–1588. [Google Scholar] [CrossRef] [PubMed]
- Pitelet, A.; Mallet, É.; Centeno, E.; Moreau, A. Fresnel coefficients and Fabry-Perot formula for spatially dispersive metallic layers. Phys. Rev. B 2017, 96, 041406. [Google Scholar] [CrossRef] [Green Version]
- Raza, S.; Christensen, T.; Wubs, M.; Bozhevolnyi, S.I.; Mortensen, N.A. Nonlocal response in thin-film waveguides: Loss versus nonlocality and breaking of complementarity. Phys. Rev. B 2013, 88, 115401. [Google Scholar] [CrossRef] [Green Version]
- Fernández-Domínguez, A.I.; Wiener, A.; García-Vidal, F.J.; Maier, S.A.; Pendry, J.B. Transformation-Optics Description of Nonlocal Effects in Plasmonic Nanostructures. Phys. Rev. Lett. 2012, 108, 106802. [Google Scholar] [CrossRef] [Green Version]
- Yang, F.; Wang, Y.T.; Huidobro, P.A.; Pendry, J.B. Nonlocal effects in singular plasmonic metasurfaces. Phys. Rev. B 2019, 99, 165423. [Google Scholar] [CrossRef] [Green Version]
- Dechaux, M.; Tichit, P.H.; Ciracì, C.; Benedicto, J.; Pollés, R.; Centeno, E.; Smith, D.R.; Moreau, A. Influence of spatial dispersion in metals on the optical response of deeply subwavelength slit arrays. Phys. Rev. B 2016, 93, 045413. [Google Scholar] [CrossRef] [Green Version]
- Dong, T.Y.; Yin, K.; Gao, X.K.; Ma, X.K. Generalized local analogue model for nonlocal plasmonic nanostructures based on multiple-fluid hydrodynamic framework. J. Phys. D Appl. Phys. 2020, 53, 295105. [Google Scholar] [CrossRef]
- Pilelet, A.; Mallet, E.; Ajib, R.; Lemaitre, C.; Centeno, E.; Moreau, A. Plasmonic enhancement of spatial dispersion effects in prism coupler experiments. Phys. Rev. B 2018, 98, 125418. [Google Scholar] [CrossRef] [Green Version]
- Dias, E.J.C.; Iranzo, D.A.; Gonçalves, P.A.D.; Hajati, Y.; Bludov, Y.V.; Jauho, A.P.; Mortensen, N.A.; Koppens, F.H.L.; Peres, N.M.R. Probing Nonlocal Effects in Metals with Graphene Plasmons. Phys. Rev. B 2018, 97, 245405. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Li, C.F. Negative group delay for Dirac particles traveling through a potential well. Phys. Rev. A 2003, 68, 052105. [Google Scholar] [CrossRef] [Green Version]
- Sánchez-Meroño, A.; Arias, J.; Sánchez-López, M.M. Negative Group Delay of Reflected Pulses on Microstrip Slabs and Bragg Reflectors. IEEE J. Quantum. Elect. 2010, 46, 546–553. [Google Scholar]
- Milonni, P.M. Fast Light, Slow Light and Left-Handed Light; Institute of Physics: Bristol, UK, 2005. [Google Scholar]
- Wang, L.; Wang, L.G.; Ye, L.H.; Al-Amri, M.; Zhu, S.Y.; Zubairy, M.S. Counterintuitive dispersion effect near surface plasmon resonances in Otto structures. Phys. Rev. A 2016, 94, 013806. [Google Scholar] [CrossRef]
- Li, E.P.; Chu, H.S. Plasmonic Nanoelectronics and Sensing; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
Short Biography of Authors
 | Lin Wang received the Ph.D. degree from the Institute of Optics, Department of Physics, Zhejiang University, Hangzhou, China, in 2017. From 2016 to 2017, she was a vsiting sudent with the Institute for Quantum Science and Engineering (IQSE) and Department of Physics and Astronomy, Texas A&M University, College Station, TX, USA. Currently, she is an associate researcher with Hangzhou Dianzi University. Her research includes nanophotonics and quantum optics. |
 | Shangqing Liang received the Ph.D. degree from the Institute of Optics, Department of Physics, Zhejiang University, Hangzhou, China, in 2017. Currently, he is a lecturer with Hangzhou Dianzi University. His research includes optics and atomic and molecular physics. |
 | Yuanguo Zhou received the Ph.D. degree from the Department of Electronic Science, Institute of Electromagnetics and Acoustics, Xiamen University, Xiamen, China, in 2017. From 2014 to 2015, he was a visiting student with the Department of Electrical and Computer Engineering, Duke University, Durham, NC, USA. From 2015 to 2016, he was a visiting student with the Department of Geology and Geophysics, Texas A&M University, College Station, TX, USA. He is currently an Associate Professor with the College of Communication and Information Engineering, Xi’an University of Science and Technology, Xi’an, China. His current research interests include computational electromagnetics and optics, inverse problems, mathematical methods, and deep learning technologies. |
 | Li-Gang Wang received the Ph.D. degree from the Hong Kong Baptist University in 2005. Between 2008 and 2010, he was a Research Assistant Professor at the Chinese University of Hong Kong. He also did his postdoctoral research associate in the Department of Physics and Astronomy at Texas A&M University from 2013 to 2014. He has published over 100 research papers on topics such as singular optics, beam/pulse propagations, optical coherence effects, optical tweezers, light propagation in photonic crystals and novel materials (metamaterials, graphene, etc), slow and fast-light propagations in various systems. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Liang, S.; Zhou, Y.; Wang, L.-G. Impact of Nonlocality on Group Delay and Reflective Behavior Near Surface Plasmon Resonances in Otto Structure. Nanomaterials 2021, 11, 1780. https://doi.org/10.3390/nano11071780
Wang L, Liang S, Zhou Y, Wang L-G. Impact of Nonlocality on Group Delay and Reflective Behavior Near Surface Plasmon Resonances in Otto Structure. Nanomaterials. 2021; 11(7):1780. https://doi.org/10.3390/nano11071780
Chicago/Turabian StyleWang, Lin, Shangqing Liang, Yuanguo Zhou, and Li-Gang Wang. 2021. "Impact of Nonlocality on Group Delay and Reflective Behavior Near Surface Plasmon Resonances in Otto Structure" Nanomaterials 11, no. 7: 1780. https://doi.org/10.3390/nano11071780





