Electronic and Magnetic Properties of Building Blocks of Mn and Fe Atomic Chains on Nb(110)
Abstract
1. Introduction
2. Computational Details
2.1. VASP Calculations
2.2. KKR Calculations
2.3. Spin Model
3. Results and Discussion
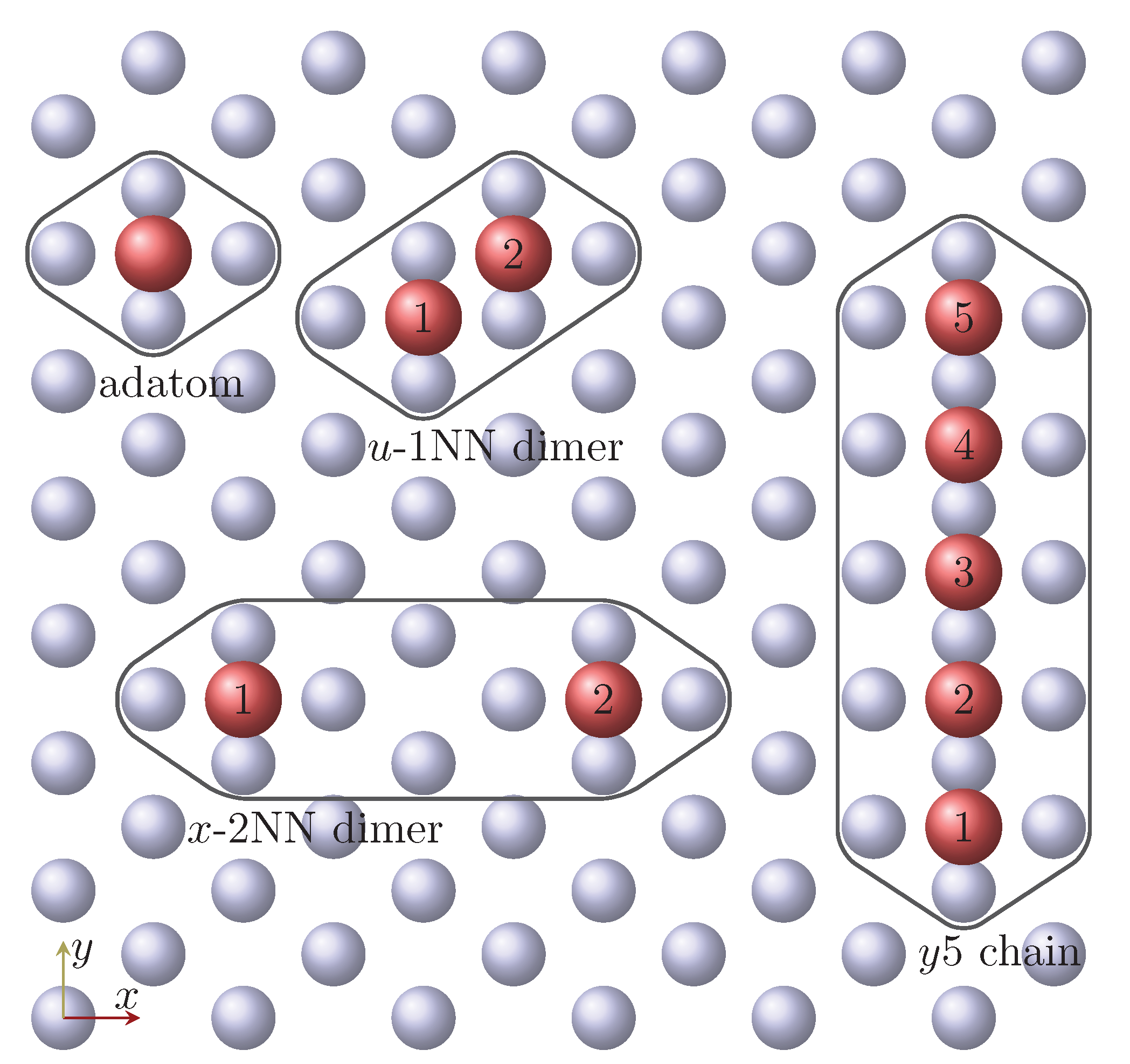
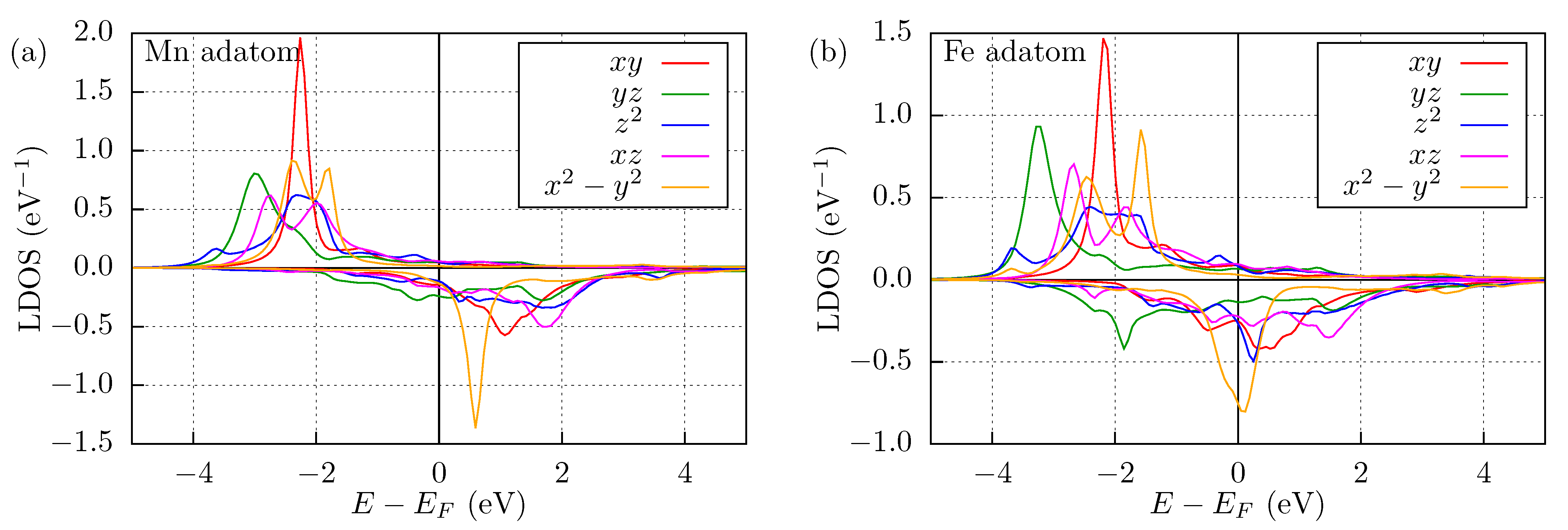
3.1. Mn and Fe Adatom
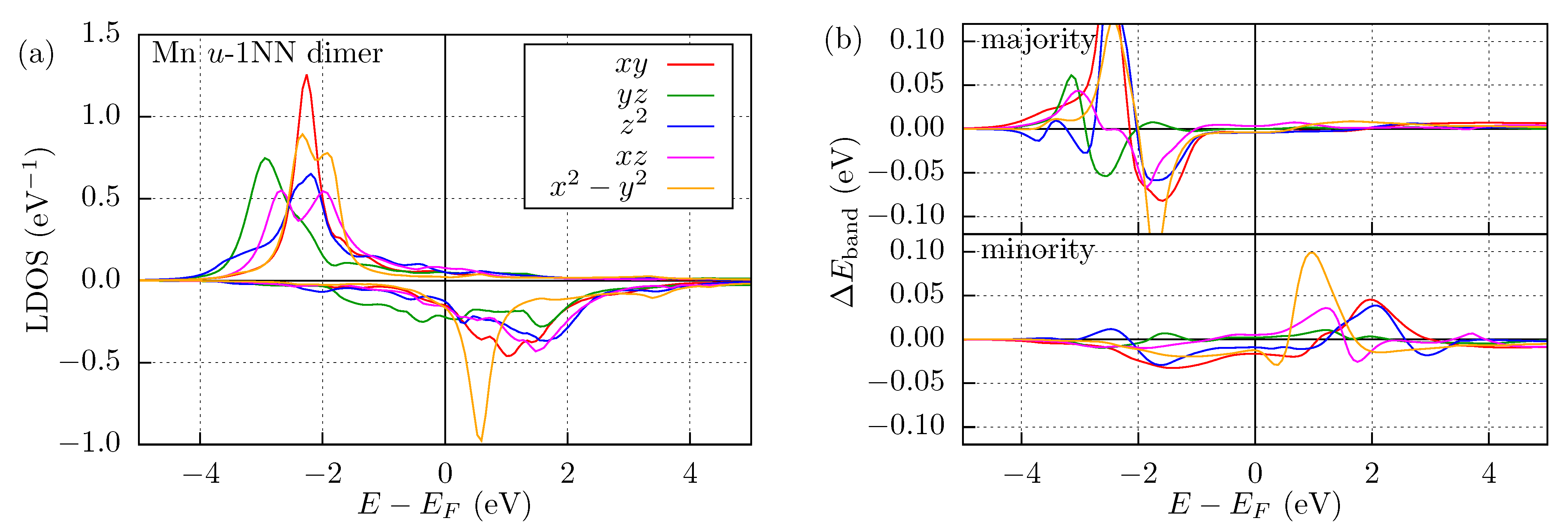
3.2. Mn and Fe Dimers
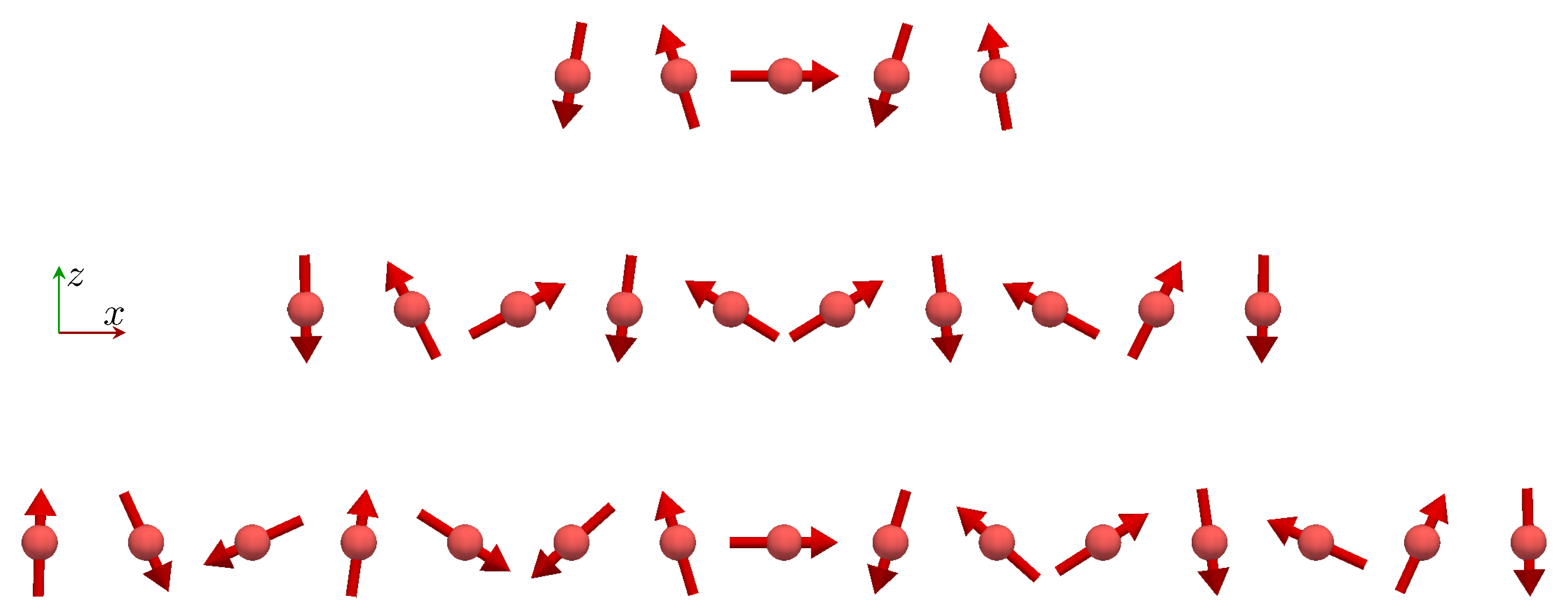
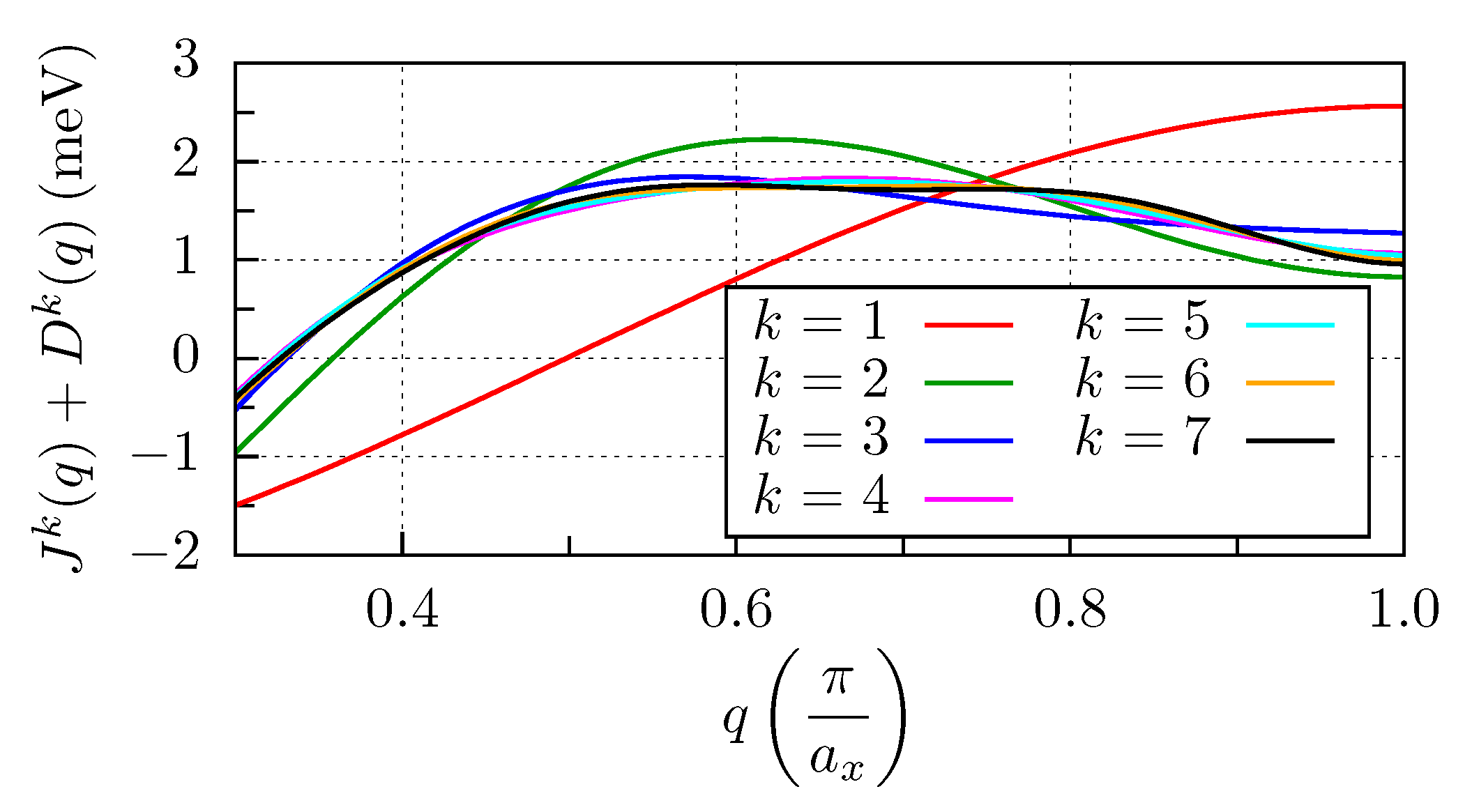
3.3. Mn and Fe Chains
4. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Dimer Spin Model Ground State

| Mn x-1NN | 179.93 | 179.94 | 179.84 | 0.10 | 0.00 | 179.90 | −0.0355 | 0.0000 | 0.9994 |
| Mn x-2NN | 179.04 | 179.29 | 179.66 | 0.96 | 0.00 | 179.04 | −0.0231 | 0.0000 | 0.9997 |
| Mn x-3NN | 178.16 | 176.55 | 179.69 | −1.82 | 0.00 | 178.18 | −0.0072 | 0.0000 | 1.0000 |
| Mn y-1NN | 0.36 | 0.40 | 0.03 | 0.00 | −0.37 | 0.37 | 0.0000 | −0.0451 | 0.9990 |
| Mn y-2NN | 172.24 | 170.44 | 179.55 | 0.00 | −7.86 | 172.13 | 0.0000 | −0.0293 | 0.9996 |
| Mn y-3NN | 178.04 | 171.39 | 178.40 | 0.00 | −1.95 | 178.05 | 0.0000 | −0.0237 | 0.9997 |
| Mn u-1NN | 179.46 | 179.41 | 179.90 | −0.47 | 0.26 | 179.46 | −0.0711 | −0.0969 | 0.9927 |
| Mn u-2NN | 5.24 | 5.34 | 0.26 | −5.25 | −0.51 | 5.27 | 0.0390 | −0.1049 | 0.9937 |
| Mn u-3NN | 172.90 | 172.60 | 179.35 | 2.84 | 6.53 | 172.88 | 0.0083 | −0.0649 | 0.9979 |
| Fe x-1NN | 178.04 | 177.98 | 177.65 | 1.96 | 0.00 | 178.04 | −0.0105 | 0.0000 | 0.9999 |
| Fe x-2NN | 178.93 | 178.76 | 179.94 | 1.07 | 0.00 | 178.93 | 0.0060 | 0.0000 | 1.0000 |
| Fe x-3NN | 173.94 | 171.73 | 179.94 | −6.07 | 0.00 | 173.93 | 0.0020 | 0.0000 | 1.0000 |
| Fe y-1NN | 0.05 | 0.12 | 0.04 | 0.00 | −0.07 | 0.07 | −0.0000 | −0.0177 | 0.9998 |
| Fe y-2NN | 0.01 | 0.09 | 2.03 | 0.00 | −0.02 | 0.02 | −0.0000 | −0.0104 | 0.9999 |
| Fe y-3NN | 174.67 | 169.13 | 179.60 | 0.00 | 5.28 | 174.72 | 0.0000 | 0.0073 | 1.0000 |
| Fe u-1NN | 4.00 | 4.06 | 0.09 | −3.75 | −1.43 | 4.01 | 0.0482 | −0.0841 | 0.9953 |
| Fe u-2NN | 4.95 | 4.91 | 0.32 | −4.95 | 0.52 | 4.98 | 0.0534 | −0.0590 | 0.9968 |
| Fe u-3NN | 177.60 | 177.73 | 179.66 | 0.14 | 2.40 | 177.59 | 0.0296 | −0.0294 | 0.9991 |
References
- Bogani, L.; Vindigni, A.; Sessoli, R.; Gatteschi, D. Single chain magnets: Where to from here? J. Mater. Chem. 2008, 18, 4750–4758. [Google Scholar] [CrossRef]
- Sun, H.L.; Wang, Z.M.; Gao, S. Strategies towards single-chain magnets. Coord. Chem. Rev. 2010, 254, 1081–1100. [Google Scholar] [CrossRef]
- Zhang, W.X.; Ishikawa, R.; Breedlove, B.; Yamashita, M. Single-chain magnets: Beyond the Glauber model. RSC Adv. 2013, 3, 3772–3798. [Google Scholar] [CrossRef]
- Yu, L. Bound state in superconductors with paramagnetic impurities. Acta Phys. Sin. 1965, 21, 75–91. [Google Scholar]
- Shiba, H. Classical spins in superconductors. Prog. Theor. Phys. 1968, 40, 435–451. [Google Scholar] [CrossRef]
- Rusinov, A. Superconductivity near a paramagnetic impurity. JETP Lett. 1969, 9, 85. [Google Scholar]
- Beck, P.; Schneider, L.; Rózsa, L.; Palotás, K.; Lászlóffy, A.; Szunyogh, L.; Wiebe, J.; Wiesendanger, R. Spin-orbit coupling induced splitting of Yu-Shiba-Rusinov states in antiferromagnetic dimers. Nat. Commun. 2021, 12, 2040. [Google Scholar] [CrossRef]
- Odobesko, A.; Di Sante, D.; Kowalski, A.; Wilfert, S.; Friedrich, F.; Thomale, R.; Sangiovanni, G.; Bode, M. Observation of tunable single-atom Yu-Shiba-Rusinov states. Phys. Rev. B 2020, 102, 174504. [Google Scholar] [CrossRef]
- Schneider, L.; Steinbrecher, M.; Rózsa, L.; Bouaziz, J.; Palotás, K.; dos Santos Dias, M.; Lounis, S.; Wiebe, J.; Wiesendanger, R. Magnetism and in-gap states of 3d transition metal atoms on superconducting Re. NPJ Quantum Mater. 2019, 4, 42. [Google Scholar] [CrossRef]
- Schneider, L.; Brinker, S.; Steinbrecher, M.; Hermenau, J.; Posske, T.; dos Santos Dias, M.; Lounis, S.; Wiesendanger, R.; Wiebe, J. Controlling in-gap end states by linking nonmagnetic atoms and artificially-constructed spin chains on superconductors. Nat. Commun. 2020, 11, 4707. [Google Scholar] [CrossRef]
- Kobiałka, A.; Piekarz, P.; Oleś, A.M.; Ptok, A. First-principles study of the nontrivial topological phase in chains of 3d transition metals. Phys. Rev. B 2020, 101, 205143. [Google Scholar] [CrossRef]
- Kim, H.; Palacio-Morales, A.; Posske, T.; Rózsa, L.; Palotás, K.; Szunyogh, L.; Thorwart, M.; Wiesendanger, R. Toward tailoring Majorana bound states in artificially constructed magnetic atom chains on elemental superconductors. Sci. Adv. 2018, 4, eaar5251. [Google Scholar] [CrossRef] [PubMed]
- Choi, D.J.; Lorente, N.; Wiebe, J.; von Bergmann, K.; Otte, A.F.; Heinrich, A.J. Colloquium: Atomic spin chains on surfaces. Rev. Mod. Phys. 2019, 91, 041001. [Google Scholar] [CrossRef]
- Schneider, L.; Beck, P.; Posske, T.; Crawford, D.; Mascot, E.; Rachel, S.; Wiesendanger, R.; Wiebe, J. Topological Shiba bands in artificial spin chains on superconductors. Nat. Phys. 2021. [Google Scholar] [CrossRef]
- Schneider, L.; Beck, P.; Neuhaus-Steinmetz, J.; Posske, T.; Wiebe, J.; Wiesendanger, R. Controlled length-dependent interaction of Majorana modes in Yu-Shiba-Rusinov chains. arXiv 2021, arXiv:2104.11503. [Google Scholar]
- Pawlak, R.; Hoffman, S.; Klinovaja, J.; Loss, D.; Meyer, E. Majorana fermions in magnetic chains. Prog. Part. Nucl. Phys. 2019, 107, 1–19. [Google Scholar] [CrossRef]
- Braunecker, B.; Simon, P. Interplay between Classical Magnetic Moments and Superconductivity in Quantum One-Dimensional Conductors: Toward a Self-Sustained Topological Majorana Phase. Phys. Rev. Lett. 2013, 111, 147202. [Google Scholar] [CrossRef]
- Vazifeh, M.M.; Franz, M. Self-Organized Topological State with Majorana Fermions. Phys. Rev. Lett. 2013, 111, 206802. [Google Scholar] [CrossRef]
- Klinovaja, J.; Stano, P.; Yazdani, A.; Loss, D. Topological Superconductivity and Majorana Fermions in RKKY Systems. Phys. Rev. Lett. 2013, 111, 186805. [Google Scholar] [CrossRef]
- Pientka, F.; Glazman, L.I.; von Oppen, F. Topological superconducting phase in helical Shiba chains. Phys. Rev. B 2013, 88, 155420. [Google Scholar] [CrossRef]
- Dzyaloshinsky, I. A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics. J. Phys. Chem. Solids 1958, 4, 241–255. [Google Scholar] [CrossRef]
- Moriya, T. Anisotropic Superexchange Interaction and Weak Ferromagnetism. Phys. Rev. 1960, 120, 91–98. [Google Scholar] [CrossRef]
- Rózsa, L.; Udvardi, L.; Szunyogh, L.; Szabó, I.A. Magnetic phase diagram of an Fe monolayer on W(110) and Ta(110) surfaces based on ab initio calculations. Phys. Rev. B 2015, 91, 144424. [Google Scholar] [CrossRef]
- Simon, E.; Rózsa, L.; Palotás, K.; Szunyogh, L. Magnetism of a Co monolayer on Pt(111) capped by overlayers of 5d elements: A spin-model study. Phys. Rev. B 2018, 97, 134405. [Google Scholar] [CrossRef]
- Lászlóffy, A.; Rózsa, L.; Palotás, K.; Udvardi, L.; Szunyogh, L. Magnetic structure of monatomic Fe chains on Re(0001): Emergence of chiral multispin interactions. Phys. Rev. B 2019, 99, 184430. [Google Scholar] [CrossRef]
- Bezerra-Neto, M.M.; Kvashnin, Y.O.; Bergman, A.; Muniz, R.B.; Eriksson, O.; Katsnelson, M.I.; Klautau, A.B. Incommensurate spin and orbital magnetism of Mn atomic chains on W(110) surface. arXiv 2021, arXiv:2105.00348. [Google Scholar]
- Kamber, U.; Bergman, A.; Eich, A.; Iuşan, D.; Steinbrecher, M.; Hauptmann, N.; Nordström, L.; Katsnelson, M.I.; Wegner, D.; Eriksson, O.; et al. Self-induced spin glass state in elemental and crystalline neodymium. Science 2020, 368, eaay6757. [Google Scholar] [CrossRef] [PubMed]
- Schneider, L.; Beck, P.; Wiebe, J.; Wiesendanger, R. Atomic-scale spin-polarization maps using functionalized superconducting probes. Sci. Adv. 2021, 7, eabd7302. [Google Scholar] [CrossRef]
- Lazarovits, B.; Szunyogh, L.; Weinberger, P. Magnetic properties of finite Co chains on Pt(111). Phys. Rev. B 2003, 67, 024415. [Google Scholar] [CrossRef]
- Lazarovits, B.; Szunyogh, L.; Weinberger, P.; Újfalussy, B. Magnetic properties of finite Fe chains at fcc Cu(001) and Cu(111) surfaces. Phys. Rev. B 2003, 68, 024433. [Google Scholar] [CrossRef]
- Újfalussy, B.; Lazarovits, B.; Szunyogh, L.; Stocks, G.M.; Weinberger, P. Ab initio spin dynamics applied to nanoparticles: Canted magnetism of a finite Co chain along a Pt ( 111 ) surface step edge. Phys. Rev. B 2004, 70, 100404. [Google Scholar] [CrossRef]
- Lazarovits, B.; Újfalussy, B.; Szunyogh, L.; Stocks, G.M.; Weinberger, P. Ab initio study of canted magnetism of finite atomic chains at surfaces. J. Phys. Condens. Matter 2004, 16, S5833–S5840. [Google Scholar] [CrossRef][Green Version]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Hafner, J. Ab-initiosimulations of materials using VASP: Density-functional theory and beyond. J. Comput. Chem. 2008, 29, 2044–2078. [Google Scholar] [CrossRef]
- Lazarovits, B.; Szunyogh, L.; Weinberger, P. Fully relativistic calculation of magnetic properties of Fe, Co, and Ni adclusters on Ag(100). Phys. Rev. B 2002, 65, 104441. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef]
- Ceperley, D.M.; Alder, B.J. Ground State of the Electron Gas by a Stochastic Method. Phys. Rev. Lett. 1980, 45, 566–569. [Google Scholar] [CrossRef]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef]
- Drautz, R.; Fähnle, M. Spin-cluster expansion: Parametrization of the general adiabatic magnetic energy surface with ab initio accuracy. Phys. Rev. B 2004, 69, 104404. [Google Scholar] [CrossRef]
- Szunyogh, L.; Udvardi, L.; Jackson, J.; Nowak, U.; Chantrell, R. Atomistic spin model based on a spin-cluster expansion technique: Application to the IrMn 3 /Co interface. Phys. Rev. B 2011, 83, 024401. [Google Scholar] [CrossRef]
- Deák, A.; Szunyogh, L.; Újfalussy, B. Thickness-dependent magnetic structure of ultrathin Fe/Ir(001) films: From spin-spiral states toward ferromagnetic order. Phys. Rev. B 2011, 84, 224413. [Google Scholar] [CrossRef]
- Lászlóffy, A.; Udvardi, L.; Szunyogh, L. Atomistic simulation of finite-temperature magnetism of nanoparticles: Application to cobalt clusters on Au(111). Phys. Rev. B 2017, 95, 184406. [Google Scholar] [CrossRef]
- Liechtenstein, A.I.; Katsnelson, M.I.; Antropov, V.P.; Gubanov, V.A. Local spin density funtional approach to the theory of exchange interactions in ferromagnetic metals and alloys. J. Magn. Magn. Mater. 1987, 67, 65–74. [Google Scholar] [CrossRef]
- Lloyd, P. Wave propagation through an assembly of spheres: II. The density of single-particle eigenstates. Proc. Phys. Soc. 1967, 90, 207. [Google Scholar] [CrossRef]
- Udvardi, L.; Szunyogh, L.; Palotás, K.; Weinberger, P. First-principles relativistic study of spin waves in thin magnetic films. Phys. Rev. B 2003, 68, 104436. [Google Scholar] [CrossRef]
- Antropov, V.P.; Katsnelson, M.I.; Harmon, B.N.; van Schilfgaarde, M.; Kusnezov, D. Spin dynamics in magnets: Equation of motion and finite temperature effects. Phys. Rev. B 1996, 54, 1019–1035. [Google Scholar] [CrossRef]

| Mn x-1NN | −7.13 | 0.00 | 0.01 | 0.29 | 0.16 | 179.93 | 179.90 |
| Mn x-2NN | −1.90 | 0.00 | −0.02 | 0.28 | 0.14 | 179.04 | 179.04 |
| Mn x-3NN | −0.45 | 0.00 | 0.03 | 0.28 | 0.14 | 178.16 | 178.18 |
| Mn y-1NN | 31.93 | 0.22 | 0.00 | 0.38 | 0.18 | 0.36 | 0.37 |
| Mn y-2NN | −1.04 | −0.17 | 0.00 | 0.28 | 0.16 | 172.24 | 172.13 |
| Mn y-3NN | −0.10 | −0.01 | 0.00 | 0.28 | 0.14 | 178.04 | 178.05 |
| Mn u-1NN | −33.00 | 0.10 | 0.32 | 0.34 | 0.24 | 179.46 | 179.46 |
| Mn u-2NN | 5.92 | 0.08 | −0.55 | 0.28 | 0.12 | 5.24 | 5.27 |
| Mn u-3NN | −1.32 | 0.15 | −0.08 | 0.28 | 0.12 | 172.90 | 172.88 |
| Fe x-1NN | −4.35 | 0.00 | −0.15 | 0.32 | 0.70 | 178.04 | 178.04 |
| Fe x-2NN | −2.92 | 0.00 | −0.06 | 0.29 | 0.67 | 178.93 | 178.93 |
| Fe x-3NN | −0.74 | 0.00 | 0.11 | 0.28 | 0.68 | 173.94 | 173.93 |
| Fe y-1NN | 33.30 | 0.07 | 0.00 | 0.29 | 0.73 | 0.05 | 0.07 |
| Fe y-2NN | 10.61 | 0.02 | 0.00 | 0.27 | 0.68 | 0.01 | 0.02 |
| Fe y-3NN | −0.73 | 0.14 | 0.00 | 0.29 | 0.68 | 174.67 | 174.72 |
| Fe u-1NN | 49.66 | 1.39 | −3.24 | 0.45 | 0.70 | 4.00 | 4.01 |
| Fe u-2NN | 9.85 | 0.00 | −0.85 | 0.36 | 0.77 | 4.95 | 4.98 |
| Fe u-3NN | −3.91 | 0.15 | −0.03 | 0.29 | 0.68 | 177.60 | 177.59 |
| s | p | f | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Mn x-1NN | −7.27 | −0.12 | 0.26 | 0.45 | 0.55 | −7.18 | −0.38 | −0.87 | 0.02 |
| Mn y-1NN | 31.75 | 0.16 | −0.55 | 2.47 | 18.66 | 12.15 | 0.87 | −1.99 | −0.02 |
| Mn u-1NN | −33.19 | −2.75 | 3.18 | −12.08 | 2.22 | −14.16 | 15.71 | −25.76 | 0.45 |
| Fe x-1NN | −4.59 | −0.05 | 0.11 | 1.41 | 1.47 | −7.05 | −0.70 | 0.20 | 0.01 |
| Fe y-1NN | 33.53 | 0.59 | −0.65 | 3.17 | 5.26 | 6.06 | −1.53 | 20.63 | −0.01 |
| Fe u-1NN | 50.01 | −0.26 | 0.12 | 16.82 | 1.44 | 0.33 | 15.74 | 15.81 | 0.02 |
| Mn x-1NN | 0.19 | 0.46 | −2.13 | 0.07 | −0.32 | −7.13 |
| Mn y-1NN | 3.24 | 11.40 | 7.32 | 0.26 | −0.39 | 31.99 |
| Mn u-1NN | −20.96 | 2.84 | −13.95 | 10.56 | −18.50 | −33.06 |
| Fe x-1NN | 1.08 | 0.65 | −2.20 | 0.42 | 0.66 | −4.13 |
| Fe y-1NN | 5.39 | −1.37 | 4.51 | −0.84 | 17.59 | 33.74 |
| Fe u-1NN | 10.78 | 1.35 | 0.50 | 13.80 | 21.18 | 49.94 |
| i | |||||||
|---|---|---|---|---|---|---|---|
| Mn | 1 | −6.87 | −0.00 | 0.07 | −1.28 | 0.31 | 0.16 |
| Mn | 8 | −6.70 | 0.00 | 0.11 | −1.15 | 0.34 | 0.18 |
| Mn | 1 | 29.09 | 0.24 | 0.00 | 2.31 | 0.41 | 0.23 |
| Mn | 8 | 27.14 | 0.30 | 0.00 | 2.14 | 0.57 | 0.32 |
| Mn | 1 | −35.56 | 0.38 | −0.55 | 2.71 | 0.39 | 0.26 |
| Mn | 8 | −38.15 | 0.45 | −1.50 | 2.58 | 0.49 | 0.40 |
| Fe | 1 | −3.41 | −0.00 | −0.04 | −2.02 | 0.32 | 0.71 |
| Fe | 8 | −2.56 | −0.00 | 0.01 | −1.74 | 0.36 | 0.76 |
| Fe | 1 | 25.42 | −0.19 | 0.00 | 10.00 | 0.23 | 0.73 |
| Fe | 8 | 18.57 | −0.41 | −0.00 | 9.64 | 0.18 | 0.77 |
| Fe | 1 | 34.11 | 0.82 | −2.52 | 1.54 | 0.45 | 0.74 |
| Fe | 8 | 18.00 | 0.53 | −1.68 | 3.80 | 0.51 | 0.72 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lászlóffy, A.; Palotás, K.; Rózsa, L.; Szunyogh, L. Electronic and Magnetic Properties of Building Blocks of Mn and Fe Atomic Chains on Nb(110). Nanomaterials 2021, 11, 1933. https://doi.org/10.3390/nano11081933
Lászlóffy A, Palotás K, Rózsa L, Szunyogh L. Electronic and Magnetic Properties of Building Blocks of Mn and Fe Atomic Chains on Nb(110). Nanomaterials. 2021; 11(8):1933. https://doi.org/10.3390/nano11081933
Chicago/Turabian StyleLászlóffy, András, Krisztián Palotás, Levente Rózsa, and László Szunyogh. 2021. "Electronic and Magnetic Properties of Building Blocks of Mn and Fe Atomic Chains on Nb(110)" Nanomaterials 11, no. 8: 1933. https://doi.org/10.3390/nano11081933
APA StyleLászlóffy, A., Palotás, K., Rózsa, L., & Szunyogh, L. (2021). Electronic and Magnetic Properties of Building Blocks of Mn and Fe Atomic Chains on Nb(110). Nanomaterials, 11(8), 1933. https://doi.org/10.3390/nano11081933







