Tailoring the Nonlinear Optical Response of Some Graphene Derivatives by Ultraviolet (UV) Irradiation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Synthesis and Characterization
2.2. In Situ UV Irradiation of G, GO, GF and GFH
2.3. Nonlinear Optical Measurements
3. Results and Discussion
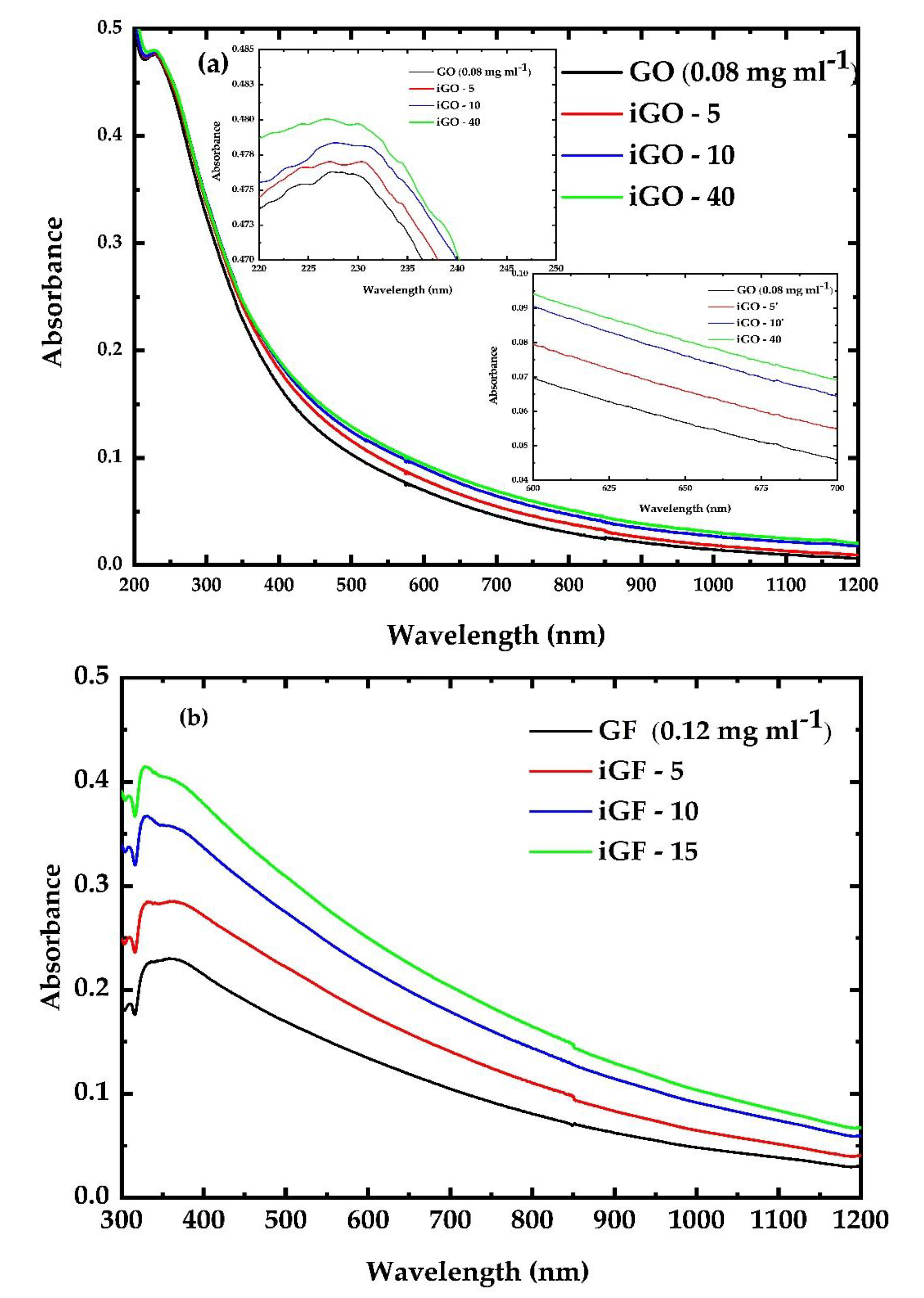
3.1. UV Irradiation Experiments of the G, GF, GO and GFH Dispersions
3.2. Measurements of the Nonlinear Optical (NLO) Properties
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Novoselov, K.; Geim, A.; Morozov, S.; Jiang, D.; Zhang, Y.; Dubonos, S.; Grigorieva, I.; Firsov, A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [Green Version]
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef] [Green Version]
- Iqbal, M.Z.; Rehman, A.-U. Recent progress in graphene incorporated solar cell devices. Sol. Energy 2018, 169, 634–647. [Google Scholar] [CrossRef]
- Bao, Q.; Loh, K.P. Graphene Photonics, Plasmonics, and Broadband Optoelectronic Devices. ACS Nano 2012, 6, 3677–3694. [Google Scholar] [CrossRef] [PubMed]
- Bokhari, S.W.; Siddique, A.H.; Sherrell, P.C.; Yue, X.; Karumbaiah, K.M.; Wei, S.; Ellis, A.V.; Wei, G. Advances in graphene-based supercapacitor electrodes. Energy Rep. 2020, 6, 2768–2784. [Google Scholar] [CrossRef]
- Yang, W.; Ni, M.; Ren, X.; Tian, Y.; Li, N.; Su, Y.; Zhang, X. Graphene in Supercapacitor Applications. Curr. Opin. Colloid Interface Sci. 2015, 20, 416–428. [Google Scholar] [CrossRef]
- Dai, C.; Sun, G.; Hu, L.; Xiao, Y.; Zhang, Z.; Qu, L. Recent progress in graphene-based electrodes for flexible batteries. Infomat 2020, 2, 509–526. [Google Scholar] [CrossRef] [Green Version]
- Han, T.-H.; Kim, H.; Kwon, S.-J.; Lee, T.-W. Graphene-based flexible electronic devices. Mater. Sci. Eng. R Rep. 2017, 118, 1–43. [Google Scholar] [CrossRef]
- Novodchuk, I.; Bajcsy, M.; Yavuz, M. Graphene-based field effect transistor biosensors for breast cancer detection: A review on biosensing strategies. Carbon 2021, 172, 431–453. [Google Scholar] [CrossRef]
- Ni, Z.; Yu, T.; Lu, Y.; Wang, Y.; Feng, Y.; Shen, Z. Uniaxial Strain on Graphene: Raman Spectroscopy Study and Band-Gap Opening. ACS Nano 2008, 2, 2301–2305. [Google Scholar] [CrossRef]
- Mohiuddin, T.; Lombardo, A.; Nair, R.; Bonetti, A.; Savini, G.; Jalil, R.; Bonini, N.; Basko, D.; Galiotis, C.; Marzari, N.; et al. Uniaxial strain in graphene by Raman spectroscopy: G peak splitting, Grüneisen parameters, and sample orientation. Phys. Rev. B 2009, 79, 205433. [Google Scholar] [CrossRef]
- Ohta, T.; Bostwick, A.; Seyller, T.; Horn, K.; Rotenberg, E. Controlling the Electronic Structure of Bilayer Graphene. Science 2006, 313, 951–954. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Tang, T.; Girit, C.; Hao, Z.; Martin, M.; Zettl, A.; Crommie, M.; Shen, Y.; Wang, F. Direct observation of a widely tunable bandgap in bilayer graphene. Nature 2009, 459, 820–823. [Google Scholar] [CrossRef]
- Zhou, S.; Gweon, G.; Fedorov, A.; de Heer, F.P.; Lee, W.; Guinea, F.; Castro Neto, A.H.; Lanzara, A. Substrate-induced bandgap opening in epitaxial graphene. Nat. Mater. 2007, 6, 770–775. [Google Scholar] [CrossRef] [Green Version]
- Balog, R.; Jørgensen, B.; Nilsson, L.; Andersen, M.; Rienks, E.; Bianchi, M.; Fanetti, M.; Lægsgaard, E.; Baraldi, A.; Lizzit, S.; et al. Bandgap opening in graphene induced by patterned hydrogen adsorption. Nat. Mater. 2010, 9, 315–319. [Google Scholar] [CrossRef] [PubMed]
- Park, J.; Yan, M. Covalent Functionalization of Graphene with Reactive Intermediates. Acc. Chem. Res. 2012, 46, 181–189. [Google Scholar] [CrossRef] [PubMed]
- Pašti, I.; Jovanović, A.; Dobrota, A.; Mentus, S.; Johansson, B.; Skorodumova, N. Atomic adsorption on graphene with a single vacancy: Systematic DFT study through the periodic table of elements. Phys. Chem. Chem. Phys. 2018, 20, 858–865. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Georgakilas, V.; Otyepka, M.; Bourlinos, A.; Chandra, V.; Kim, N.; Kemp, K.; Hobza, P.; Zboril, R.; Kim, K. Functionalization of Graphene: Covalent and Non-Covalent Approaches, Derivatives and Applications. Chem. Rev. 2012, 112, 6156–6214. [Google Scholar] [CrossRef] [PubMed]
- Kuila, T.; Bose, S.; Mishra, A.; Khanra, P.; Kim, N.; Lee, J. Chemical functionalization of graphene and its applications. Prog. Mater. Sci. 2012, 57, 1061–1105. [Google Scholar] [CrossRef]
- Bakandritsos, A.; Pykal, M.; Błoński, P.; Jakubec, P.; Chronopoulos, D.; Poláková, K.; Georgakilas, V.; Čépe, K.; Tomanec, O.; Ranc, V.; et al. Cyanographene and Graphene Acid: Emerging Derivatives Enabling High-Yield and Selective Functionalization of Graphene. ACS Nano 2017, 11, 982–2991. [Google Scholar] [CrossRef]
- Marcano, D.; Kosynkin, D.; Berlin, J.; Sinitskii, A.; Sun, Z.; Slesarev, A.; Alemany, L.; Lu, W.; Tour, J. Improved Synthesis of Graphene Oxide. ACS Nano 2010, 4, 4806–4814. [Google Scholar] [CrossRef] [PubMed]
- Zbořil, R.; Karlický, F.; Bourlinos, A.; Steriotis, T.; Stubos, A.; Georgakilas, V.; Šafářová, K.; Jančík, D.; Trapalis, C.; Otyepka, M. Graphene Fluoride: A Stable Stoichiometric Graphene Derivative and its Chemical Conversion to Graphene. Small 2010, 6, 2885–2891. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chronopoulos, D.; Bakandritsos, A.; Pykal, M.; Zbořil, R.; Otyepka, M. Chemistry, properties, and applications of fluorographene. Appl. Mater. Today 2017, 9, 60–70. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Müller, M.; Gilje, S.; Kaner, R.; Wallace, G. Processable aqueous dispersions of graphene nanosheets. Nat. Nanotechnol. 2008, 3, 101–105. [Google Scholar] [CrossRef] [PubMed]
- Su, C.; Loh, K. Carbocatalysts: Graphene Oxide and Its Derivatives. Acc. Chem. Res. 2012, 46, 2275–2285. [Google Scholar] [CrossRef]
- Eda, G.; Lin, Y.; Mattevi, C.; Yamaguchi, H.; Chen, H.; Chen, I.; Chen, C.; Chhowalla, M. Blue Photoluminescence from Chemically Derived Graphene Oxide. Adv. Mater. 2010, 22, 505–509. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Wang, L.; Gao, J.; Zhao, J.; Gao, X.; Chen, Z. Amorphous structural models for graphene oxides. Carbon 2012, 50, 1690–1698. [Google Scholar] [CrossRef]
- Shi, H.; Wang, C.; Sun, Z.; Zhou, Y.; Jin, K.; Redfern, S.; Yang, G. Tuning the nonlinear optical absorption of reduced graphene oxide by chemical reduction. Opt. Express 2014, 22, 19375. [Google Scholar] [CrossRef] [Green Version]
- Abid, S.P.; Islam, S.S.; Mishra, P.; Ahmad, S. Reduced graphene oxide (rGO) based wideband optical sensor and the role of Temperature, Defect States and Quantum Efficiency. Sci. Rep. 2018, 8, 3537. [Google Scholar] [CrossRef] [Green Version]
- Nair, R.; Ren, W.; Jalil, R.; Riaz, I.; Kravets, V.; Britnell, L.; Blake, P.; Schedin, F.; Mayorov, A.; Yuan, S.; et al. Fluorographene: A Two-Dimensional Counterpart of Teflon. Small 2010, 6, 2877–2884. [Google Scholar] [CrossRef]
- Zaoralová, D.; Hrubý, V.; Šedajová, V.; Mach, R.; Kupka, V.; Ugolotti, J.; Bakandritsos, A.; Medved’, M.; Otyepka, M. Tunable Synthesis of Nitrogen Doped Graphene from Fluorographene under Mild Conditions. ACS Sustain. Chem. Eng. 2020, 8, 4764–4772. [Google Scholar] [CrossRef]
- Papadakis, I.; Bouza, Z.; Couris, S.; Bourlinos, A.; Mouselimis, V.; Kouloumpis, A.; Gournis, D.; Bakandritsos, A.; Ugolotti, J.; Zboril, R. Hydrogenated Fluorographene: A 2D Counterpart of Graphane with Enhanced Nonlinear Optical Properties. J. Phys. Chem. C 2017, 121, 22567–22575. [Google Scholar] [CrossRef]
- Fedorov, E.V.; Grayfer, E.D.; Makotchenko, V.; Semenovich, N.A.; Shin, H.; Choi, J. Highly Exfoliated Graphite Fluoride as a Precursor for Graphene Fluoride Dispersions and Films. Croat. Chem. Acta 2012, 85, 107–112. [Google Scholar] [CrossRef]
- Bourlinos, A.; Georgakilas, V.; Zboril, R.; Steriotis, T.; Stubos, A. Liquid-Phase Exfoliation of Graphite towards Solubilized Graphenes. Small 2009, 5, 1841–1845. [Google Scholar] [CrossRef]
- Stavrou, M.; Dalamaras, I.; Karampitsos, N.; Couris, S. Determination of the Nonlinear Optical Properties of Single- and Few-Layered Graphene Dispersions under Femtosecond Laser Excitation: Electronic and Thermal Origin Contributions. J. Phys. Chem. C 2020, 124, 27241–27249. [Google Scholar] [CrossRef]
- Papadakis, I.; Bakandritsos, A.; Swain, A.; Szabo, T.; Couris, S. Effects of Size and Oxidation on the Nonlinear Optical Response and Optical Limiting of Graphene Oxide Sheets. J. Phys. Chem. C 2020, 124, 11265–11273. [Google Scholar] [CrossRef]
- Sheik-Bahae, M.; Said, A.A.; Wei, T.H.; Hagan, D.J.; Van Stryland, E.W. Sensitive Measurement of Optical Nonlinearities Using a Single Beam. IEEE J. Quant. Electr. 1990, 26, 760–769. [Google Scholar] [CrossRef] [Green Version]
- Dimiev, A.M.; Siegfied, E. Graphene Oxide: Fundamentals and Applications, 1st ed.; John Wiley & Sons, Ltd.: Chichester, UK, 2021; pp. 149–150. [Google Scholar]
- Trusovas, R.; Račiukaitis, G.; Niaura, G.; Barkauskas, J.; Valušis, G.; Pauliukaite, R. Recent Advances in Laser Utilization in the Chemical Modification of Graphene Oxide and Its Applications. Adv. Opt. Mater. 2015, 4, 37–65. [Google Scholar] [CrossRef]
- Trusovas, R.; Ratautas, K.; Račiukaitis, G.; Barkauskas, J.; Stankevičienė, I.; Niaura, G.; Mažeikienė, R. Reduction of graphite oxide to graphene with laser irradiation. Carbon 2013, 52, 574–582. [Google Scholar] [CrossRef]
- Wu, T.; Liu, S.; Li, H.; Wang, L.; Sun, X. Production of Reduced Graphene Oxide by UV Irradiation. J. Nanosci. Nanotechnol. 2011, 11, 10078–10081. [Google Scholar] [CrossRef]
- Potsi, G.; Bourlinos, A.B.; Mouselimis, V.; Polakova, K.; Chalmpes, N.; Gournis, D.; Kalytchuk, S.; Tomanec, O.; Błonski, P.; Medved’, M.; et al. Intrinsic Photo-Luminescence of Amine-Functionalized Graphene Derivatives for Bioimaging Applications. Appl. Mater. Today 2019, 17, 112–122. [Google Scholar] [CrossRef]
- Guérin, K.; Pinheiro, J.; Dubois, M.; Fawal, Z.; Masin, F.; Yazami, R.; Hamwi, A. Synthesis and Characterization of Highly Fluorinated Graphite Containing sp2 and sp3 Carbon. Chem. Mater. 2004, 16, 1786–1792. [Google Scholar] [CrossRef]
- Ren, M.; Wang, X.; Dong, C.; Li, B.; Liu, Y.; Chen, T.; Wu, P.; Cheng, Z.; Liu, X. Reduction and transformation of fluorinated graphene induced by ultraviolet irradiation. Phys. Chem. Chem. Phys. 2015, 17, 24056–24062. [Google Scholar] [CrossRef]
- Pumera, M.; Sofer, Z. Towards stoichiometric analogues of graphene: Graphane, fluorographene, graphol, graphene acid and others. Chem. Soc. Rev. 2017, 46, 4450–4463. [Google Scholar] [CrossRef] [Green Version]
- Papadakis, I.; Bouza, Z.; Couris, S.; Mouselimis, V.; Bourlinos, A. Dramatic Enhancement of the Nonlinear Optical Response of Hydrogenated Fluorographene: The Effect of Midgap States. J. Phys. Chem. C 2018, 122, 25573–25579. [Google Scholar] [CrossRef]
- Liaros, N.; Tucek, J.; Dimos, K.; Bakandritsos, A.; Andrikopoulos, K.; Gournis, D.; Zboril, R.; Couris, S. The effect of the degree of oxidation on broadband nonlinear absorption and ferromagnetic ordering in graphene oxide. Nanoscale 2016, 8, 2908–2917. [Google Scholar] [CrossRef]




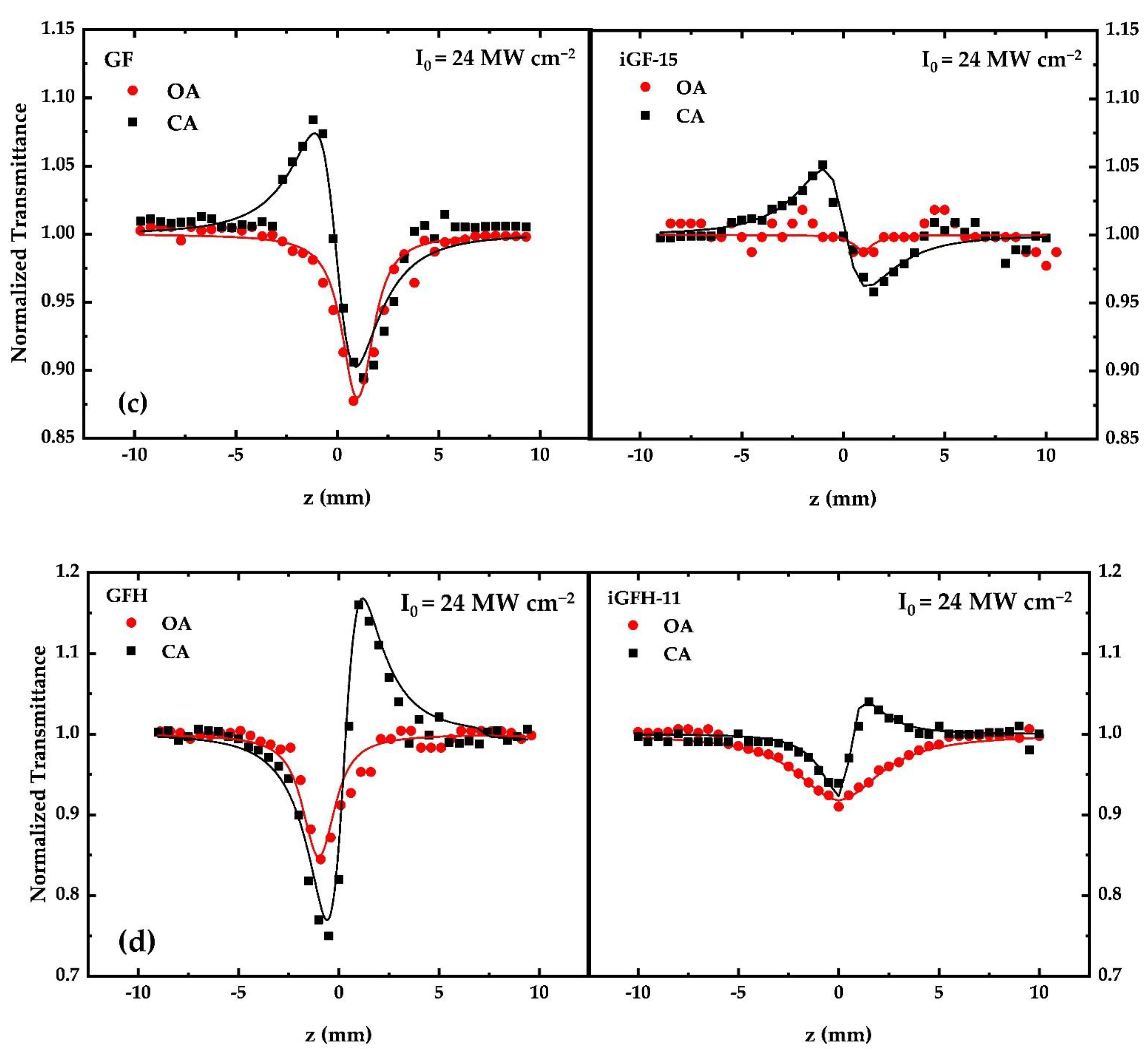

| Sample | β (×10−11 m W−1) | γ′ (×10−18 m2 W−1) | Imχ(3) (×10−13 esu) | Reχ(3) (×10−13 esu) | |χ(3)| (×10−13 esu) |
|---|---|---|---|---|---|
| G | 1240 ± 149 | 1440 ± 173 | 680 ± 79 | 1880 ± 221 | 2000 ± 313 |
| GO | 44 ± 5 | −81 ± 8 | 20 ± 2 | −91 ± 9 | 95 ± 9 |
| iGO-5 | 81 ± 10 | −100 ± 9 | 37 ± 4 | −112 ± 10 | 118 ± 11 |
| iGO-10 | 138 ± 12 | −125 ± 15 | 63 ± 6 | −140 ± 17 | 154 ± 18 |
| iGO-40 | 263 ± 20 | −263 ± 24 | 121 ± 9 | −294 ± 27 | 318 ± 28 |
| GF | 683 ± 72 | −1583 ± 177 | 367 ± 38 | −2050 ± 226 | 2083 ± 230 |
| iGF-5 | 475 ± 60 | −1317 ± 145 | 250 ± 32 | −1708 ± 185 | 1725 ± 187 |
| iGF-10 | 333 ± 32 | −1083 ± 115 | 175 ± 17 | −1408 ± 147 | 1417 ± 148 |
| iGF-15 | 192 ± 18 | −900 ± 85 | 100 ± 9 | −1158 ± 108 | 1168 ± 109 |
| GFH | 8067 ± 811 | 3700 ± 375 | 3867 ± 390 | 4333 ± 439 | 5807 ± 598 |
| iGFH-7 | 4000 ± 254 | 1800 ± 235 | 1933 ± 122 | 2107 ± 298 | 2867 ± 322 |
| iGFH-9 | 2000 ± 187 | 900 ± 90 | 967 ± 90 | 1067 ± 105 | 1433 ± 138 |
| iGFH-11 | 1033 ± 120 | 467 ± 41 | 497 ± 57 | 533 ± 48 | 730 ± 74 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stathis, A.; Bouza, Z.; Papadakis, I.; Couris, S. Tailoring the Nonlinear Optical Response of Some Graphene Derivatives by Ultraviolet (UV) Irradiation. Nanomaterials 2022, 12, 152. https://doi.org/10.3390/nano12010152
Stathis A, Bouza Z, Papadakis I, Couris S. Tailoring the Nonlinear Optical Response of Some Graphene Derivatives by Ultraviolet (UV) Irradiation. Nanomaterials. 2022; 12(1):152. https://doi.org/10.3390/nano12010152
Chicago/Turabian StyleStathis, Aristeidis, Zoi Bouza, Ioannis Papadakis, and Stelios Couris. 2022. "Tailoring the Nonlinear Optical Response of Some Graphene Derivatives by Ultraviolet (UV) Irradiation" Nanomaterials 12, no. 1: 152. https://doi.org/10.3390/nano12010152
APA StyleStathis, A., Bouza, Z., Papadakis, I., & Couris, S. (2022). Tailoring the Nonlinear Optical Response of Some Graphene Derivatives by Ultraviolet (UV) Irradiation. Nanomaterials, 12(1), 152. https://doi.org/10.3390/nano12010152







