Edge Doping Engineering of High-Performance Graphene Nanoribbon Molecular Spintronic Devices
Abstract
:1. Introduction
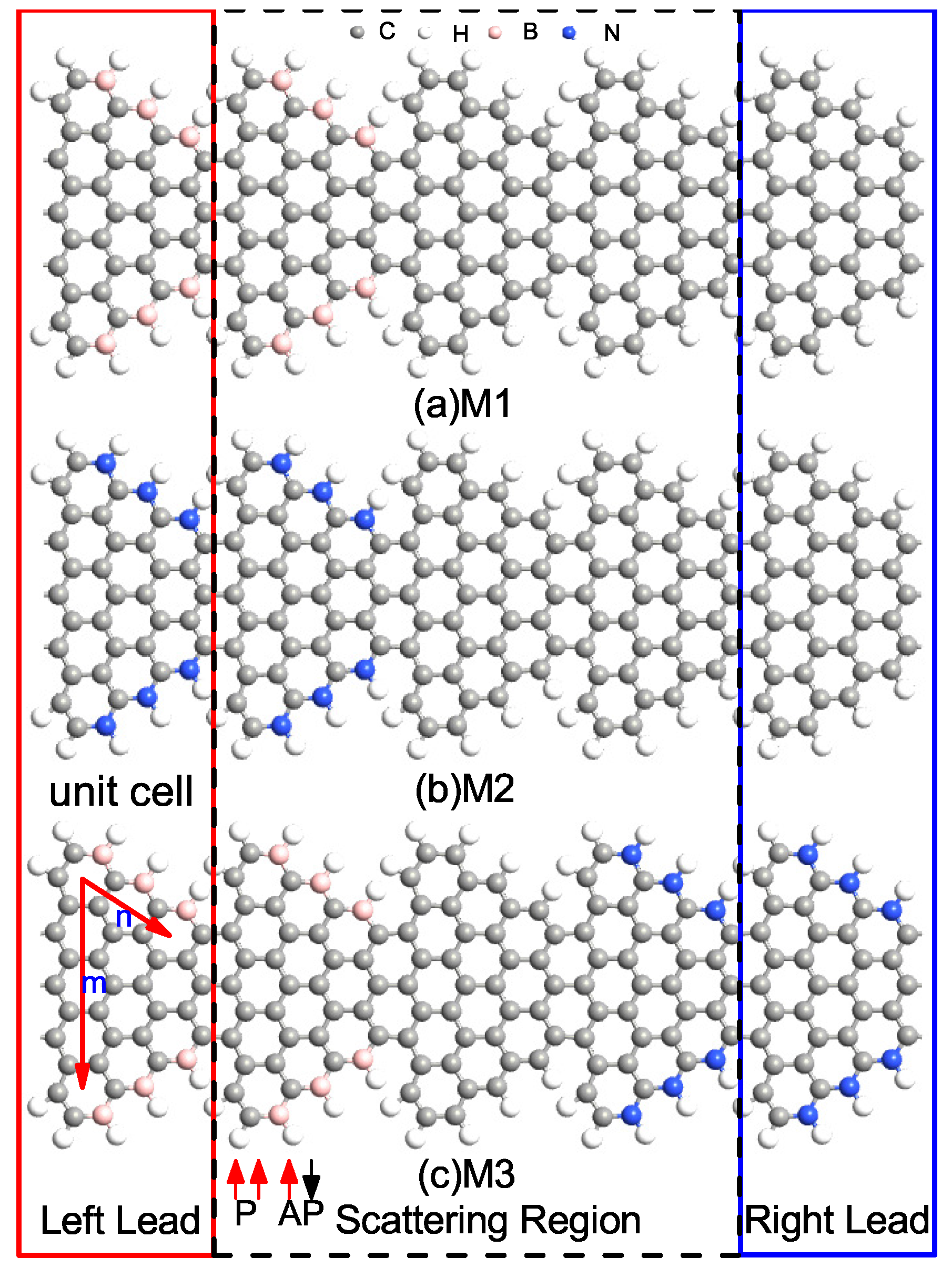
2. Computational Details
3. Results and Discussions
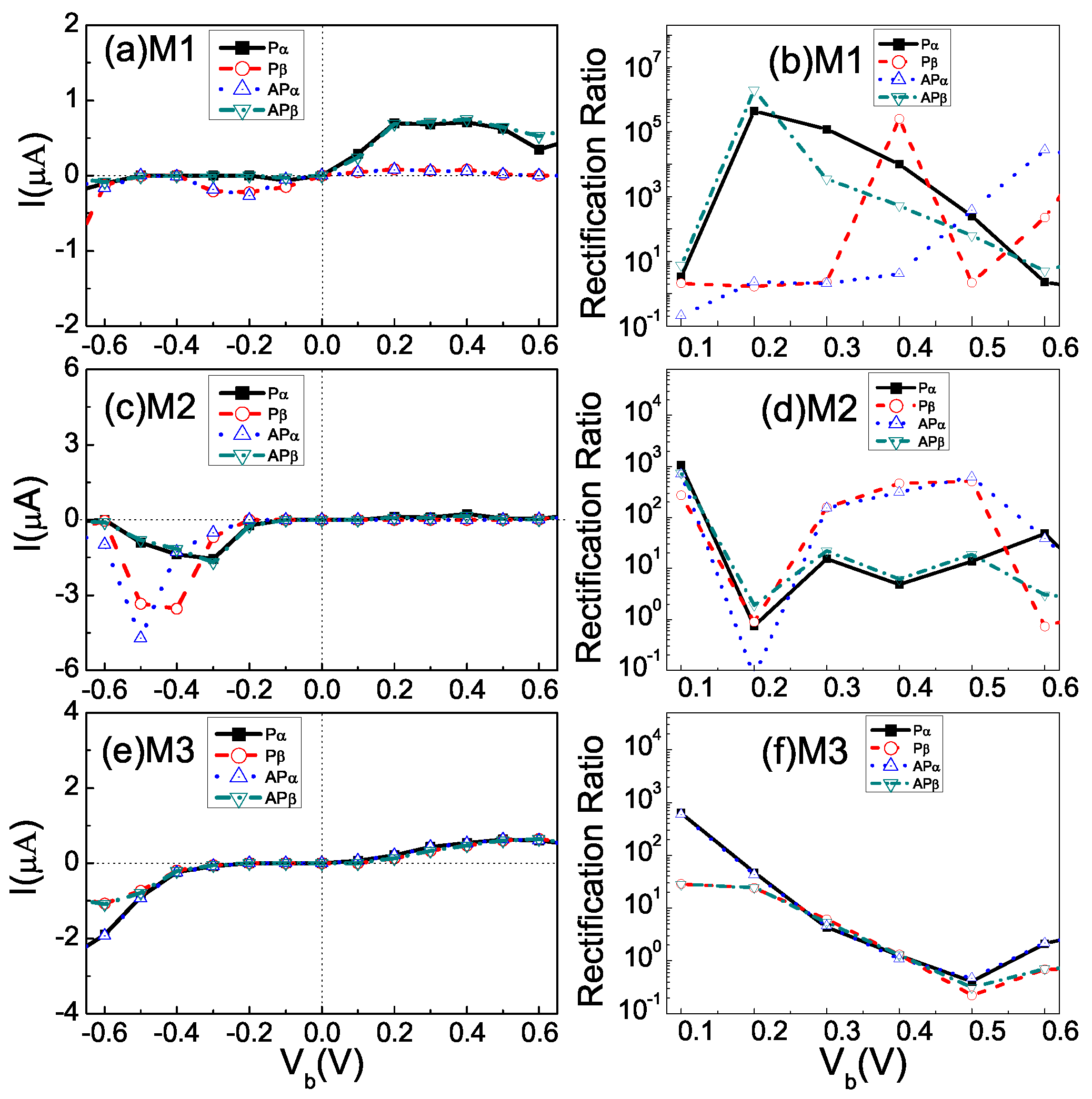
3.1. Spin-Resolved Tunneling Current, Rectification Ratio and Negative Differential Resistance Effect
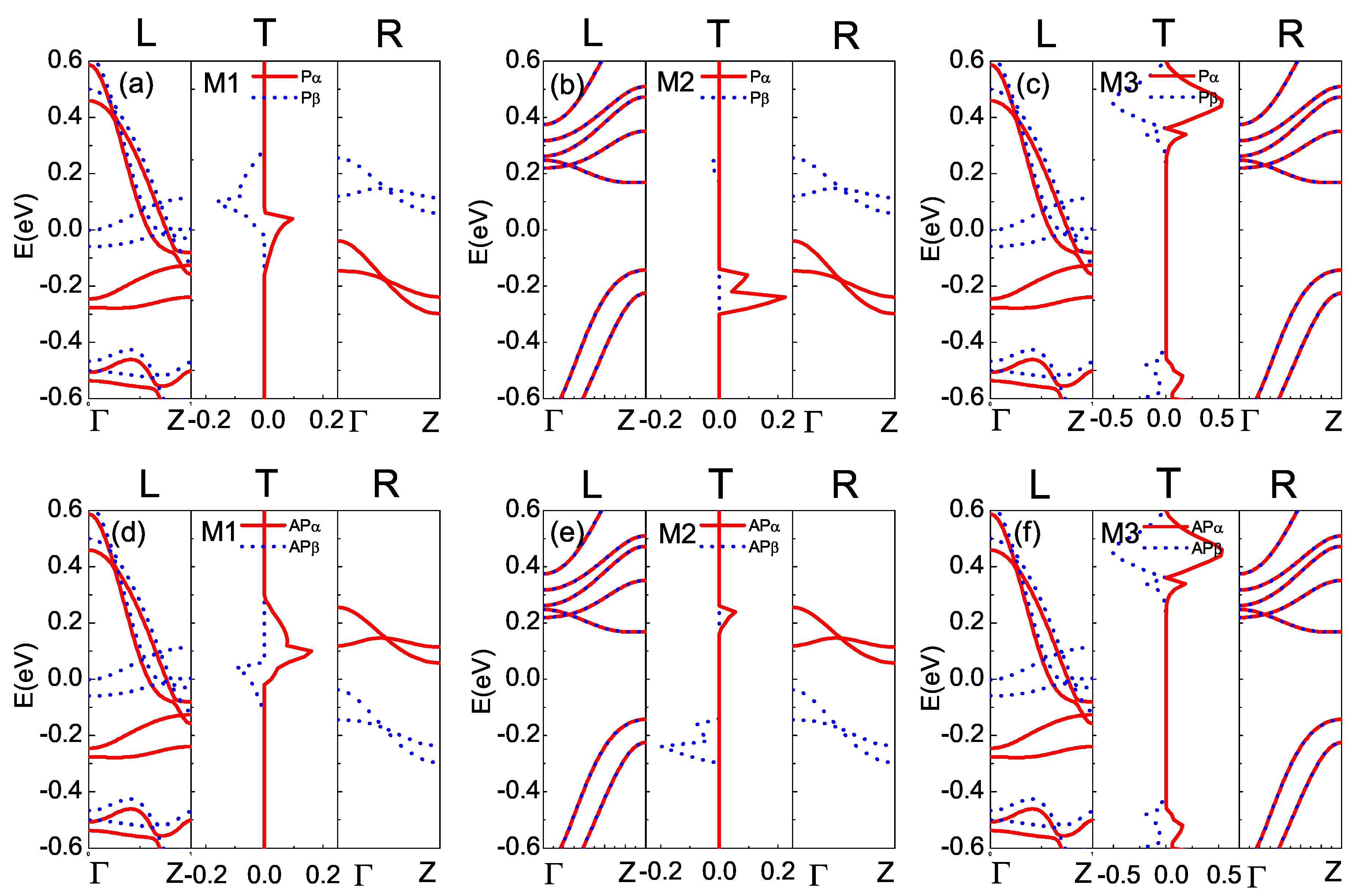
3.2. Electronic Band Structures of the Electrodes and Spin-Dependent Transmission Spectra
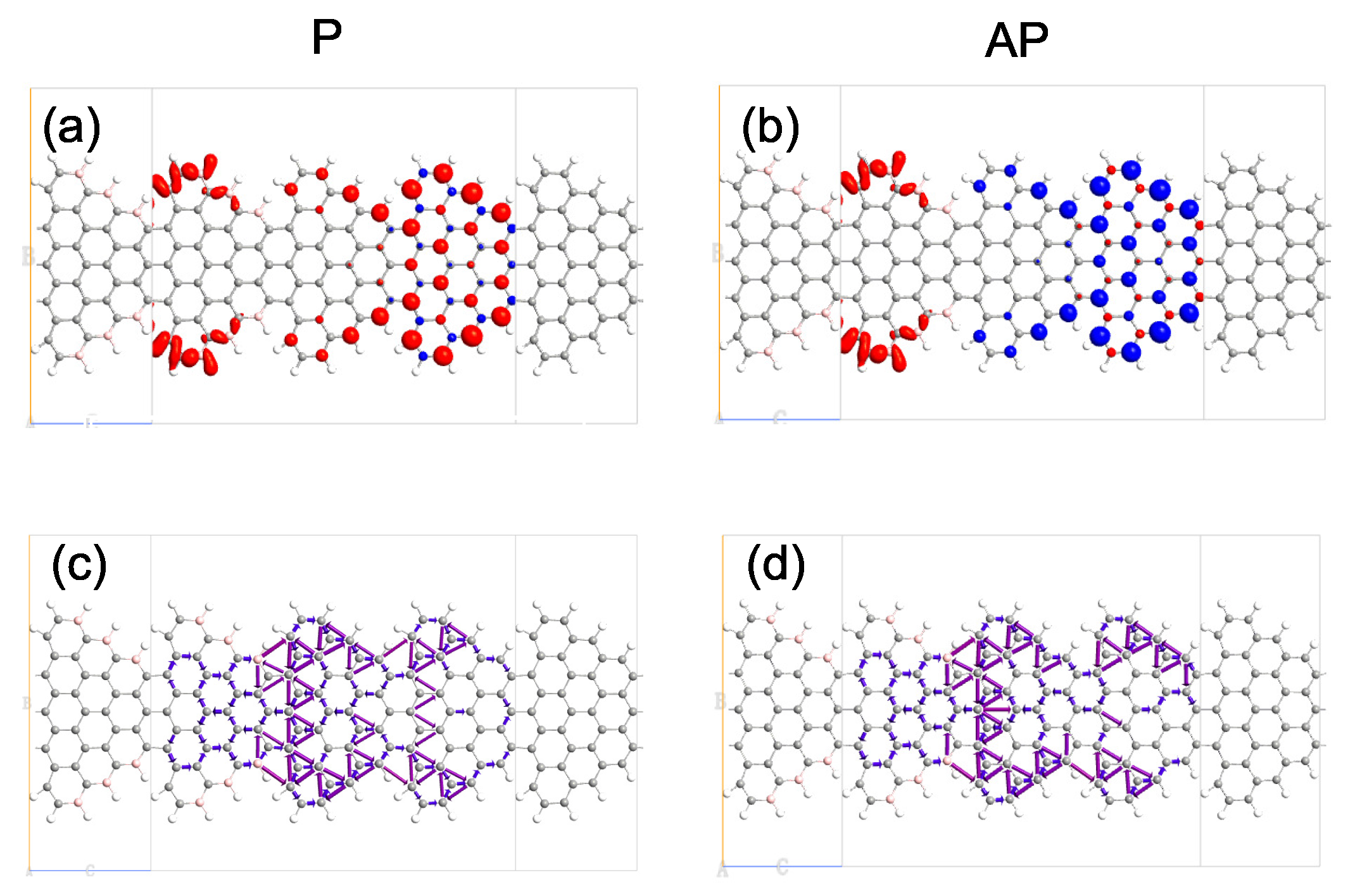
3.3. The Molecular Projected Self-Consistent Hamiltonian(MPSH), Spin Polarized Density, and Transmission Pathway
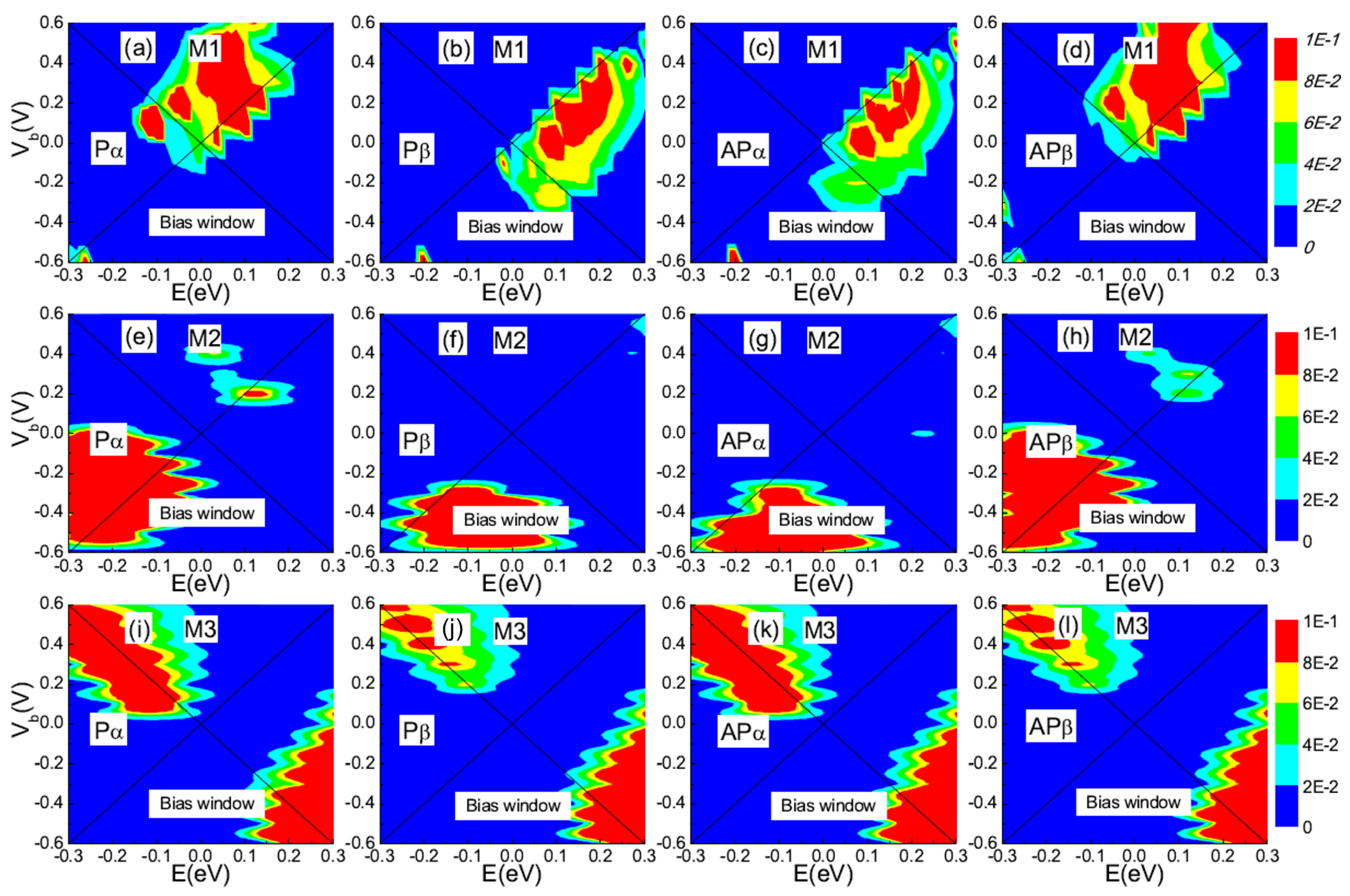
3.4. Electron Energy and Bias Voltage Dependence of the Spin-Resolved Transmission Spectrum
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, Q.H.; Zhao, P.; Chen, G. Magnetic Transport Properties of DBTAA-Based Nanodevices with Graphene Nanoribbon Electrodes. Org. Electron. 2015, 25, 308–316. [Google Scholar] [CrossRef]
- Jiang, B.; Zhou, Y.H.; Chen, C.Y.; Chen, K.Q. Designing Multi-Functional Devices Based on Two Benzene Rings Molecule Modulated with Co and N Atoms. Org. Electron. 2015, 23, 133–137. [Google Scholar] [CrossRef]
- Han, X.; Mi, W.; Wang, X. Large magnetoresistance and spin-polarized photocurrent in La2/3Sr1/3MnO3(Co)/quaterthiophene/ La2/3Sr1/3MnO3 organic magnetic tunnel junctions. J. Mater. Chem. C 2019, 7, 4079–4088. [Google Scholar] [CrossRef]
- Chen, X.; Hu, H.; Trasobares, J.; Nijhuis, C.A. Rectification Ratio and Tunneling Decay Coefficient Depend on the Contact Geometry Revealed by in Situ Imaging of the Formation of EGaIn Junctions. ACS Appl. Mater. Interfaces 2019, 11, 21018–21029. [Google Scholar] [CrossRef]
- Huang, J.; Xu, K.; Lei, S.L.; Su, H.B.; Yang, S.F.; Li, Q.X.; Yang, J.L. Iron-Phthalocyanine Molecular Junction with High Spin Filter Efficiency and Negative Differential Resistance. J. Chem. Phys. 2012, 136, 064707. [Google Scholar] [CrossRef]
- Dlubak, B.; Martin, M.B.; Deranlot, C.; Servet, B.; Xavier, S.; Mattana, R.; Sprinkle, M.; Berger, C.; Heer, W.A.D.; Petroff, F.; et al. Highly efficient spin transport in epitaxial graphene on SiC. Nat. Phys. 2012, 8, 557–561. [Google Scholar] [CrossRef]
- Zeng, M.; Shen, L.; Zhou, M.; Zhang, C.; Feng, Y. Graphene-based bipolar spin diode and spin transistor: Rectification and amplification of spin-polarized current. Phys. Rev. B 2011, 83, 115427. [Google Scholar] [CrossRef] [Green Version]
- Ang, Y.S.; Cao, L.; Ang, L.K. Physics of electron emission and injection in two-dimensional materials: Theory and simulation. Infomat 2021, 3, 502–535. [Google Scholar] [CrossRef]
- Wang, Q.; Cao, L.; Liang, S.-J.; Wu, W.; Wang, G.; Lee, C.H.; Ong, W.L.; Yang, H.Y.; Ang, L.K.; Yang, S.A.; et al. Efficient Ohmic contacts and built-in atomic sublayer protection in MoSi2N4 and WSi2N4 monolayers. npj 2D Mater. Appl. 2021, 5, 71. [Google Scholar] [CrossRef]
- Fiori, G.; Bonaccorso, F.; Iannaccone, G.; Palacios, T.; Neumaier, D.; Seabaugh, A.; Banerfee, S.K.; Colombo, L. Electronics based on two-dimensional materials. Nat. Nanotechnol. 2014, 9, 768. [Google Scholar]
- Roche, S.; Åkerman, J.; Beschoten, B.; Charlier, J.C.; Chshiev, M.; Dash, S.P.; Dlubak, B.; Fabian, J.; Fert, A.; Guimarães, M.; et al. Graphene spintronics: The European Flagship perspective. 2D Mater. 2015, 2, 030202. [Google Scholar] [CrossRef]
- Ang, Y.S.; Yang, S.A.; Zhang, C.; Ma, Z.; Ang, L.K. Valleytronics in merging Dirac cones: All-electric-controlled valley filter, valve, and universal reversible logic gate. Phys. Rev. B 2017, 96, 245410. [Google Scholar] [CrossRef] [Green Version]
- Ang, Y.S.; Sultan, S.; Zhang, C. Nonlinear optical spectrum of bilayer graphene in the terahertz regime. Appl. Phys. Lett. 2010, 97, 243110. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, C.; Hoang, N.V.; Phuc, H.V.; Sin, A.Y.; Nguyen, C.V. Two-Dimensional Boron Phosphide/MoGe2N4 van der Waals Heterostructure: A Promising Tunable Optoelectronic Material. J. Phys. Chem. Lett. 2021, 12, 5076. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Ang, Y.S.; Ang, L.K. High sensitivity surface plasmon resonance sensor based on two-dimensional MXene and transition metal dichalcogenide: A theoretical study. Nanomaterials 2019, 9, 165. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, X.; Ouyang, Y.; Li, X.; Wang, H.; Guo, J.; Dai, H. Room-temperature all-semiconducting sub-10-nm graphene nanoribbon field-effect transistors. Phys. Rev. Lett. 2008, 100, 206803. [Google Scholar] [CrossRef] [Green Version]
- Shi, Z.; Yang, R.; Zhang, L.; Wang, Y.; Liu, D.; Shi, D.; Zhang, G. Patterning Graphene with Zigzag Edges by Self Aligned Anisotropic Etching. Adv. Mater. 2011, 23, 3061–3065. [Google Scholar] [CrossRef] [PubMed]
- Jia, X.; Hofmann, M.; Meunier, V.; Sumpter, B.G.; Campos-Delgado, J.; Romo-Herrera, J.M.; Son, H.; Hsieh, Y.-P.; Reina, A.; Kong, J.; et al. Controlled formation of sharp zigzag and armchair edges in graphitic nanoribbons. Science 2009, 323, 1701–1705. [Google Scholar] [CrossRef]
- Jeon, S.; Han, P.; Jeong, J.; Hwang, W.S.; Hong, S.W. Highly aligned polymeric nanowire etch-mask lithography enabling the integration of graphene nanoribbon transistors. Nanomaterials 2021, 11, 33. [Google Scholar] [CrossRef] [PubMed]
- Son, Y.W.; Cohen, M.L.; Louie, S.G. Half-metallic graphene nanoribbons. Nature 2006, 444, 347–349. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Zhang, Z.; Zhu, Z.; Liang, B. Magnetic structure and Magnetic transport Properties of Graphene Nanoribbons with Sawtooth Zigzag Edges. Sci. Rep. 2014, 4, 7587. [Google Scholar] [CrossRef] [PubMed]
- Luo, M.; Li, B.L.; Li, D. Effects of divacancy and extended line defects on the thermal transport properties of graphene nanoribbons. Nanomaterials 2019, 9, 1609. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Esmaeili, M.; Jafari, M.R.; Sanaeepur, M. Negative differential resistance in nanoscale heterostructures based on zigzag graphene nanoribbons anti-symmetrically decorated with BN. Superlattices Microstruct. 2020, 145, 106584. [Google Scholar] [CrossRef]
- Hu, R.; Fan, Z.Q.; Fu, C.H.; Nie, L.Y.; Huang, W.R.; Zhang, Z.H. Structural stability, magneto-electronics and spin transport properties of triangular graphene nanoflake chains with edge oxidation. Carbon 2018, 126, 93–104. [Google Scholar] [CrossRef]
- Wang, Z.F.; Jin, S.; Liu, F. Spatially Separated Spin Carriers in Spin-Semiconducting Graphene Nanoribbons. PRL 2013, 111, 096803. [Google Scholar] [CrossRef] [Green Version]
- Zou, F.; Zhu, L.; Yao, K. Perfect spin filtering effect and negative differential behavior in phosphorus-doped zigzag graphene nanoribbons. Sci. Rep. 2015, 5, 15966. [Google Scholar] [CrossRef] [Green Version]
- Javan, M.; Jorjani, R.; Soltani, A.R. Theoretical study of nitrogen, boron, and co-doped (B, N) armchair graphene nanoribbons. J. Mol. Model. 2020, 26, 64. [Google Scholar] [CrossRef]
- Kim, W.Y.; Kim, K.S. Prediction of very large values of magnetoresistance in a graphene nanoribbon device. Nat. Nanotechnol. 2008, 3, 408–412. [Google Scholar] [CrossRef]
- Malki, M.; Uhrig, G.S. Tunable signal velocity in the integer quantum Hall effect of tailored graphene. J. Phys. Soc. Jpn. 2020, 89, 054705. [Google Scholar] [CrossRef]
- Poljak, M. Electron Mobility in Defective Nanoribbons of Monoelemental 2D Materials. IEEE Electron Device Lett. 2020, 41, 151–154. [Google Scholar] [CrossRef]
- Bronner, C.; Stremlau, S.; Gille, M.; Brauße, F.; Haase, A.; Hecht, S.; Tegeder, P. Aligning the band gap of graphene nanoribbons by monomer doping. Angew. Chem. Int. Ed. 2013, 52, 4422–4425. [Google Scholar] [CrossRef] [PubMed]
- Kawai, S.; Saito, S.; Osumi, S.; Yamaguchi, S.; Foster, A.S.; Spijker, P.; Meyer, E. Atomically controlled substitutional boron-doping of graphene nanoribbons. Nat. Commun. 2015, 6, 8098. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Zhang, Z.; Zhao, J.-G.; Ding, B.; Guo, Y.; Jin, C. Bipolar spin-filtering effect in B- or N-doped zigzag graphene nanoribbons with asymmetric edge hydrogenation. Phys. Lett. A 2015, 379, 2860–2865. [Google Scholar] [CrossRef]
- Rui, C.; Shao, C.; Liu, J.; Chen, A.; Zhu, K.; Shao, Q. Transport properties of B/P doped graphene nanoribbon field-effect transistor. Mater. Sci. Semicond. 2021, 130, 105826. [Google Scholar] [CrossRef]
- Dong, Y.-J.; Wang, X.-F.; Yang, S.-W.; Wu, X.-M. High performance current and spin diode of atomic carbon chain between transversely symmetric ribbon electrodes. Sci. Rep. 2014, 4, 6157. [Google Scholar] [CrossRef] [Green Version]
- Poljak, M.; Matić, M. Metallization-Induced Quantum Limits of Contact Resistance in Graphene Nanoribbons with One-Dimensional Contacts. Materials 2021, 14, 3670. [Google Scholar] [CrossRef] [PubMed]
- Poljak, M.; Matić, M.; Zeljko, A. Minimum contact resistance in monoelemental 2d material nanodevices with edge-contacts. IEEE Electron Device Lett. 2021, 42, 1240–1243. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, J.; Zhu, E.; Liao, L.; Lee, S.-J.; Ding, M.; Shakir, I.; Gambin, V.; Huang, Y.; Duan, X. Approaching the Schottky–Mott limit in van der Waals metal–semiconductor junctions. Nature 2018, 557, 696–700. [Google Scholar] [CrossRef]
- Lau, C.S.; Chee, J.Y.; Ang, Y.S.; Tong, S.W.; Cao, L.; Ooi, Z.E.; Wang, T.; Ang, L.K.; Wang, Y.; Chhowalla, M.; et al. Quantum Transport in Two-Dimensional WS2 with High-Efficiency Carrier Injection through Indium Alloy Contacts. ACS Nano 2020, 14, 13700–13708. [Google Scholar] [CrossRef]
- Liu, Y.; Stradins, P.; Wei, S.-H. Van der Waals metal-semiconductor junction: Weak Fermi level pinning enables effective tuning of Schottky barrier. Sci. Adv. 2016, 2, e1600069. [Google Scholar] [CrossRef] [Green Version]
- Taylor, J.; Guo, H.; Wang, J. Ab initio modeling of quantum transport properties of molecular electronic devices. Phys. Rev. B 2001, 63, 121104. [Google Scholar] [CrossRef] [Green Version]
- Brandbyge, M.; Mozos, J.L.; Ordejön, P.; Taylor, J.; Stokbro, K. Density-functional method for nonequilibrium electron transport. Phys. Rev. B 2001, 65, 165401. [Google Scholar]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Receipes, 3rd ed.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Sancho, M.P.L.; Sancho, J.M.L.; Rubio, J. Highly convergent schemes for the calculation of bulk and surface Green functions. J. Phys. F Met. Phys. 1985, 15, 851. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and Simple Analytic Representation of the Electron-Gas Correlation Energy. Phys. Rev. B 1992, 45, 13244. [Google Scholar] [CrossRef] [PubMed]
- Landauer, R. Electrical resistance of disordered one-dimensional lattices. Philos. Mag. 1970, 21, 863. [Google Scholar]
- Li, X.B.; Gao, H.; Wan, H.Q.; Li, H.L.; Zhou, G.H. A multi-functional molecular device based on oligo phenylenevinylene and graphene. Chem. Phys. Lett. 2014, 610, 298. [Google Scholar] [CrossRef]
- Zhu, L.; Zou, F.; Gao, J.H.; Fu, Y.S.; Gao, G.Y.; Fu, H.H.; Wu, M.H.; Lü, J.T.; Yao, K.L. The integrated spintronic functionalities of an individual high-spin state spin-crossover molecule between graphene nanoribbon electrodes. Nanotechnology 2015, 26, 315201. [Google Scholar] [CrossRef]
- Wan, H.; Zhou, B.; Chen, X.; Sun, C.Q.; Zhou, G.H. Switching, Dual Spin-Filtering Effects, and Negative Differential Resistance in a Carbon-Based Molecular Device. J. Phys. Chem. C 2012, 116, 2570–2574. [Google Scholar] [CrossRef]
- Wilhelm, J.; Walz, M.; Evers, F. Ab initio spin-flip conductance of hydrogenated graphene nanoribbons: Spin-orbit interaction and scattering with local impurity spins. Phys. Rev. B 2015, 92, 014405. [Google Scholar] [CrossRef] [Green Version]
- Abedi, A.; Sharifi, M.J. Impact of Phonon Scattering on the Negative-Differential-Resistance Behavior in Graphene Nanoribbon p-n Junctions. IEEE Trans. Electron Devices 2018, 65, 3033–3037. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, H.; Xiao, X.; Ang, Y.S. Edge Doping Engineering of High-Performance Graphene Nanoribbon Molecular Spintronic Devices. Nanomaterials 2022, 12, 56. https://doi.org/10.3390/nano12010056
Wan H, Xiao X, Ang YS. Edge Doping Engineering of High-Performance Graphene Nanoribbon Molecular Spintronic Devices. Nanomaterials. 2022; 12(1):56. https://doi.org/10.3390/nano12010056
Chicago/Turabian StyleWan, Haiqing, Xianbo Xiao, and Yee Sin Ang. 2022. "Edge Doping Engineering of High-Performance Graphene Nanoribbon Molecular Spintronic Devices" Nanomaterials 12, no. 1: 56. https://doi.org/10.3390/nano12010056
APA StyleWan, H., Xiao, X., & Ang, Y. S. (2022). Edge Doping Engineering of High-Performance Graphene Nanoribbon Molecular Spintronic Devices. Nanomaterials, 12(1), 56. https://doi.org/10.3390/nano12010056





