Structural and Parametric Identification of Knowm Memristors
Abstract
:1. Introduction
- The novel identification method is presented as a generalized process for a wide range of memristive elements.
- The proposed memristor model outperforms the existing ones in representing the switching threshold as a function of the state variables vector, making it possible to account for snapforward or snapback effects, frequency properties, and switching variability.
- The process and results of the parametric identification for the proposed memristor model are presented.
2. Materials and Methods
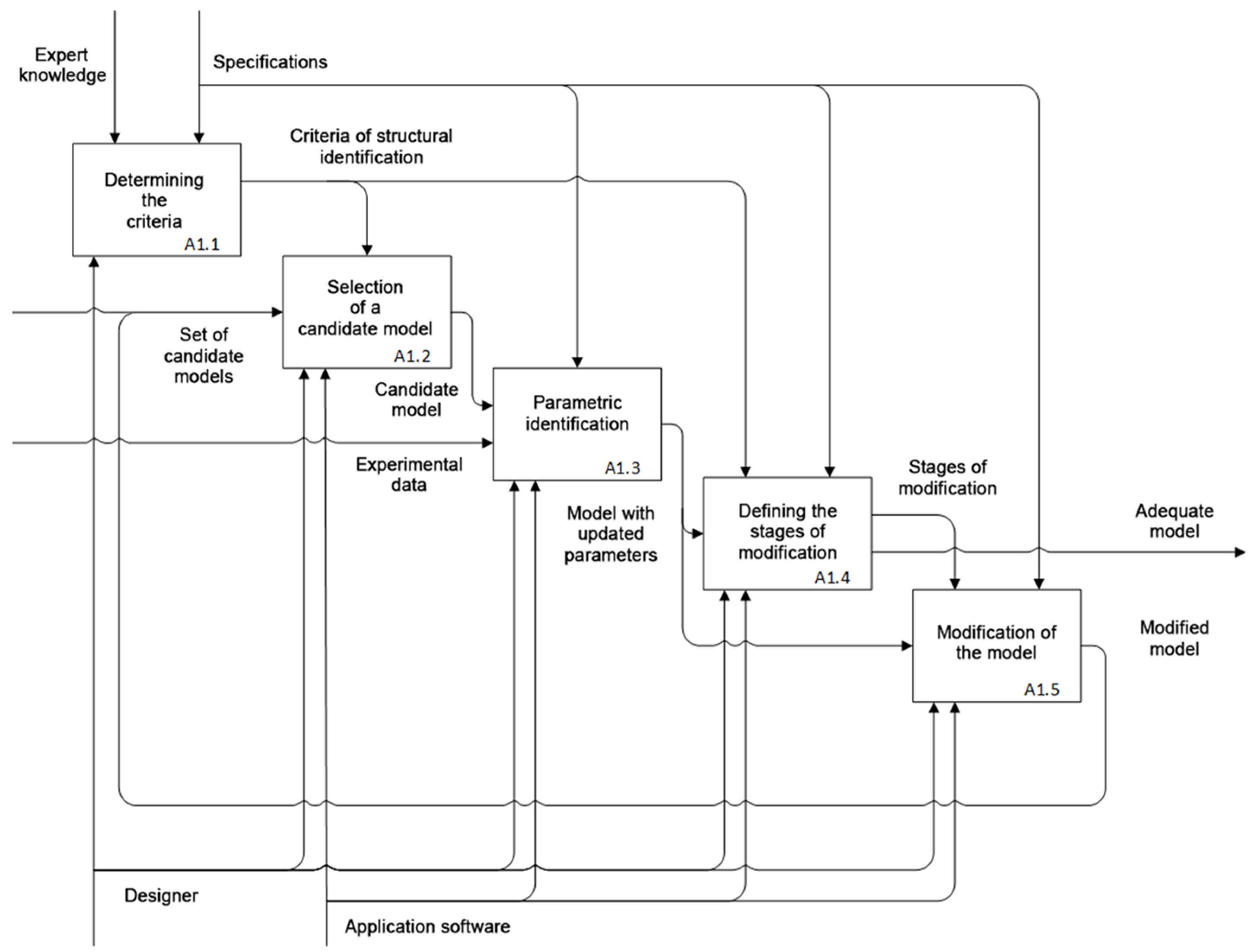
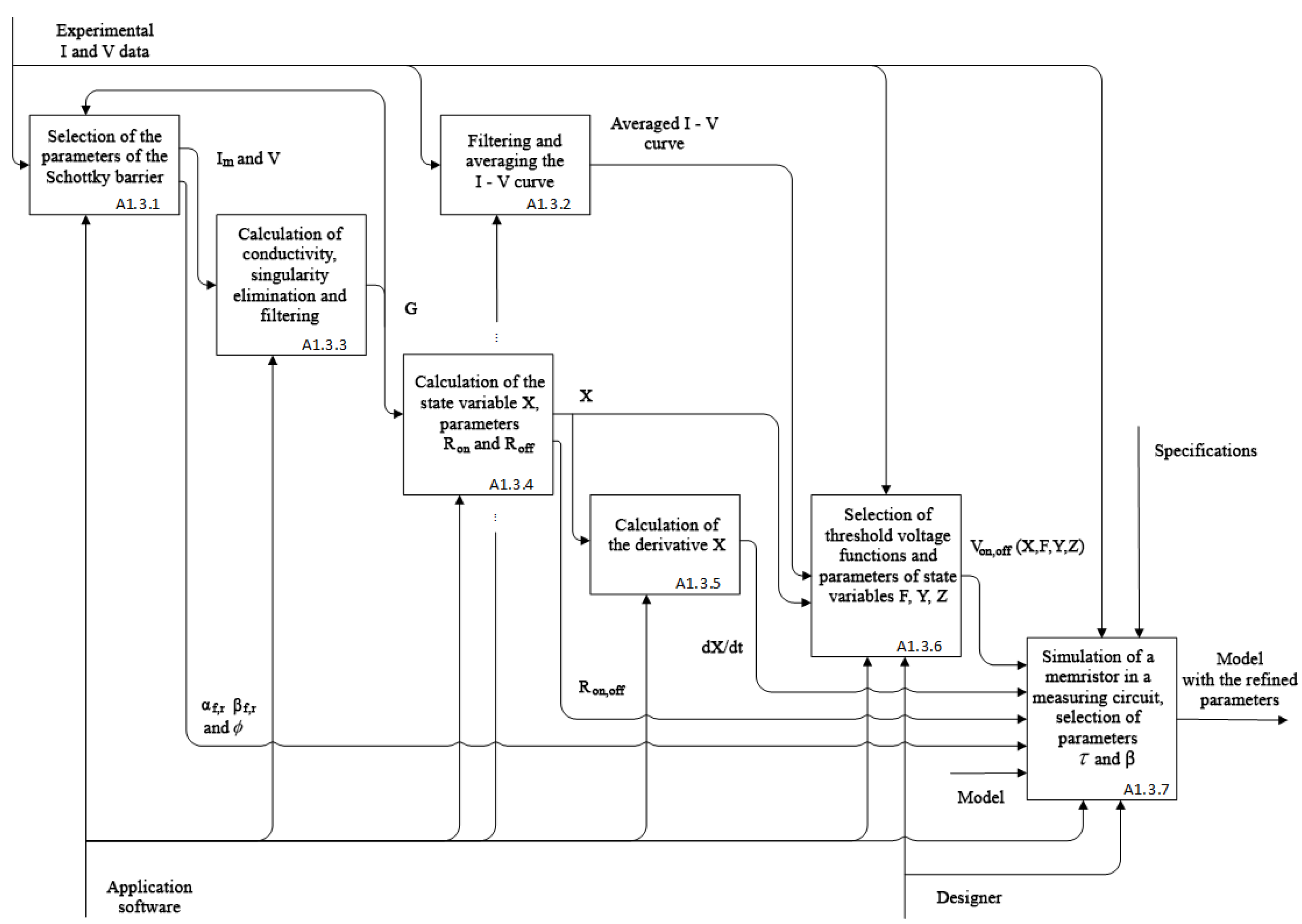
2.1. Procedure for Identification of Memristive Elements
2.2. Knowm Memristive Devices
2.3. Experimental Setup
2.4. Modeling Criteria
- 1
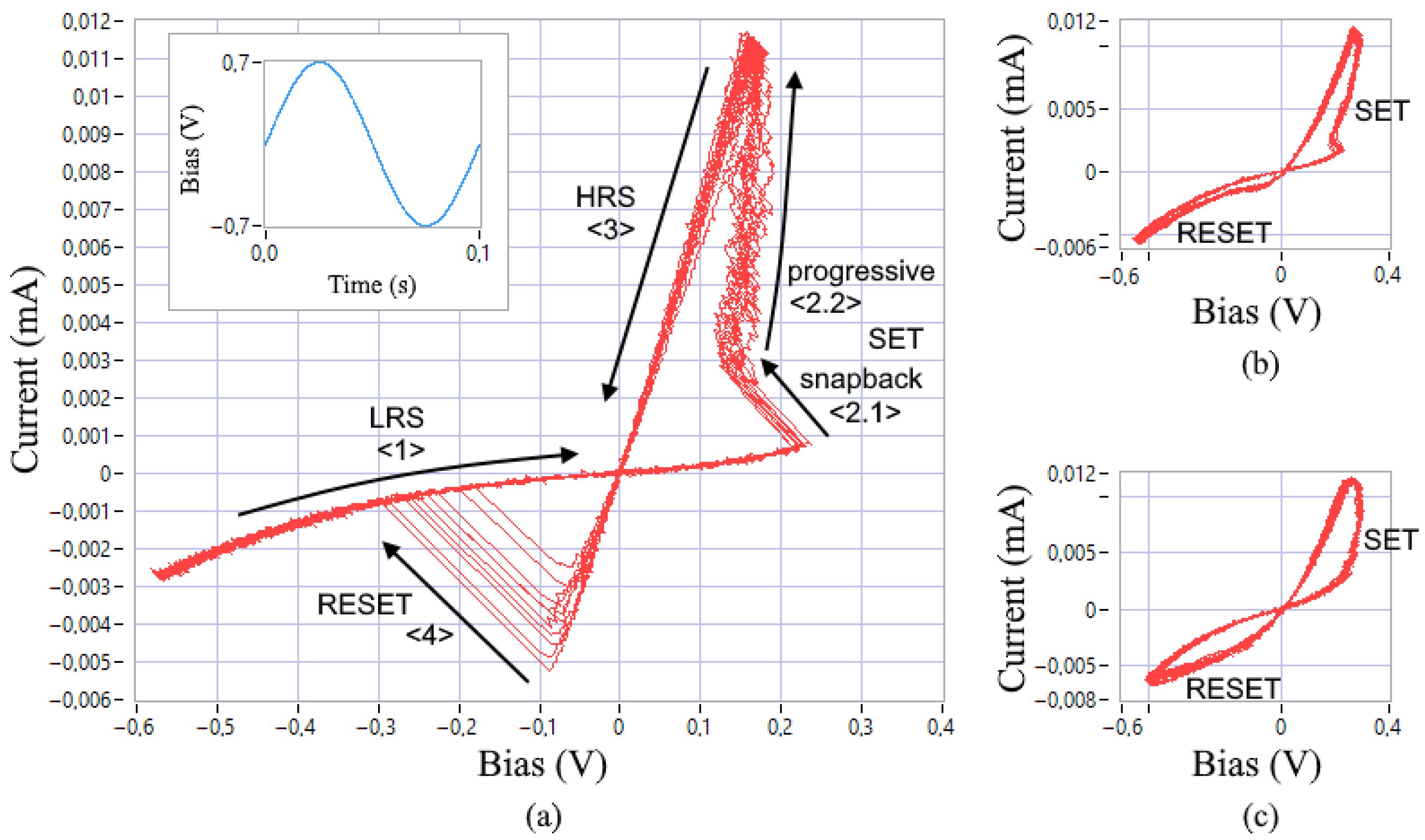
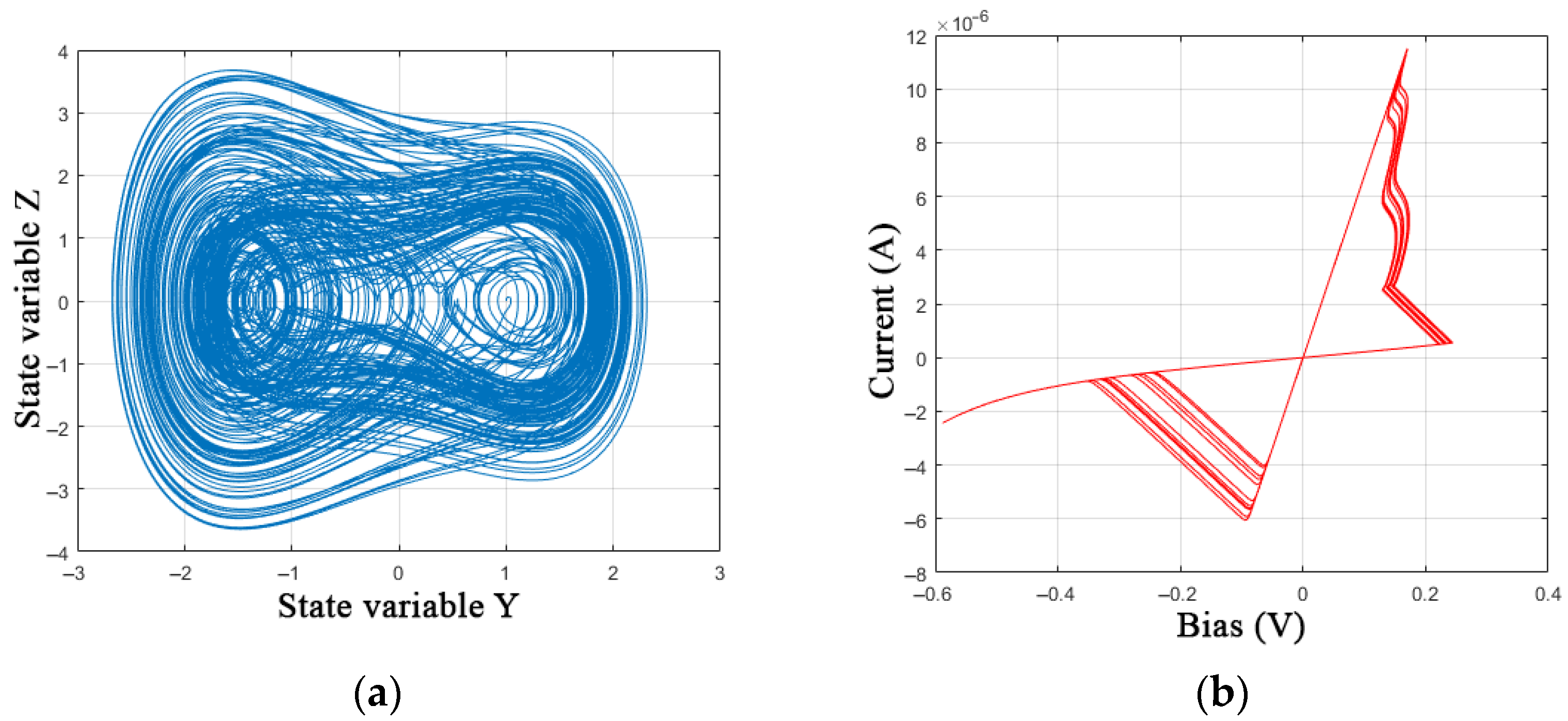
- Correspondence of the model’s I-V curve and the switching dynamics in the time domain to the experimental data of real devices. Therefore, in Figure 3a,b, the SET transition process of the device from HRS to LRS demonstrates a sharp current increase with a shift of the voltage switching boundary (snapback) at the initial stage <1>, in case (c) the SET transition looks smooth throughout the entire section. The reverse RESET process, which switches the device to HRS, can either be instantaneous (a), snapforward effect, or significantly slower (b) and (c). The symmetry of the I-V curve relative to the diagonal of the II and IV quarters is often violated. This can also be visualized in the time domain when AC voltage is applied. In addition, there is a visible curvature of the <1> section due to the metal-semiconductor/insulator barrier between the electrodes and the inner layers of the devices.
- 2
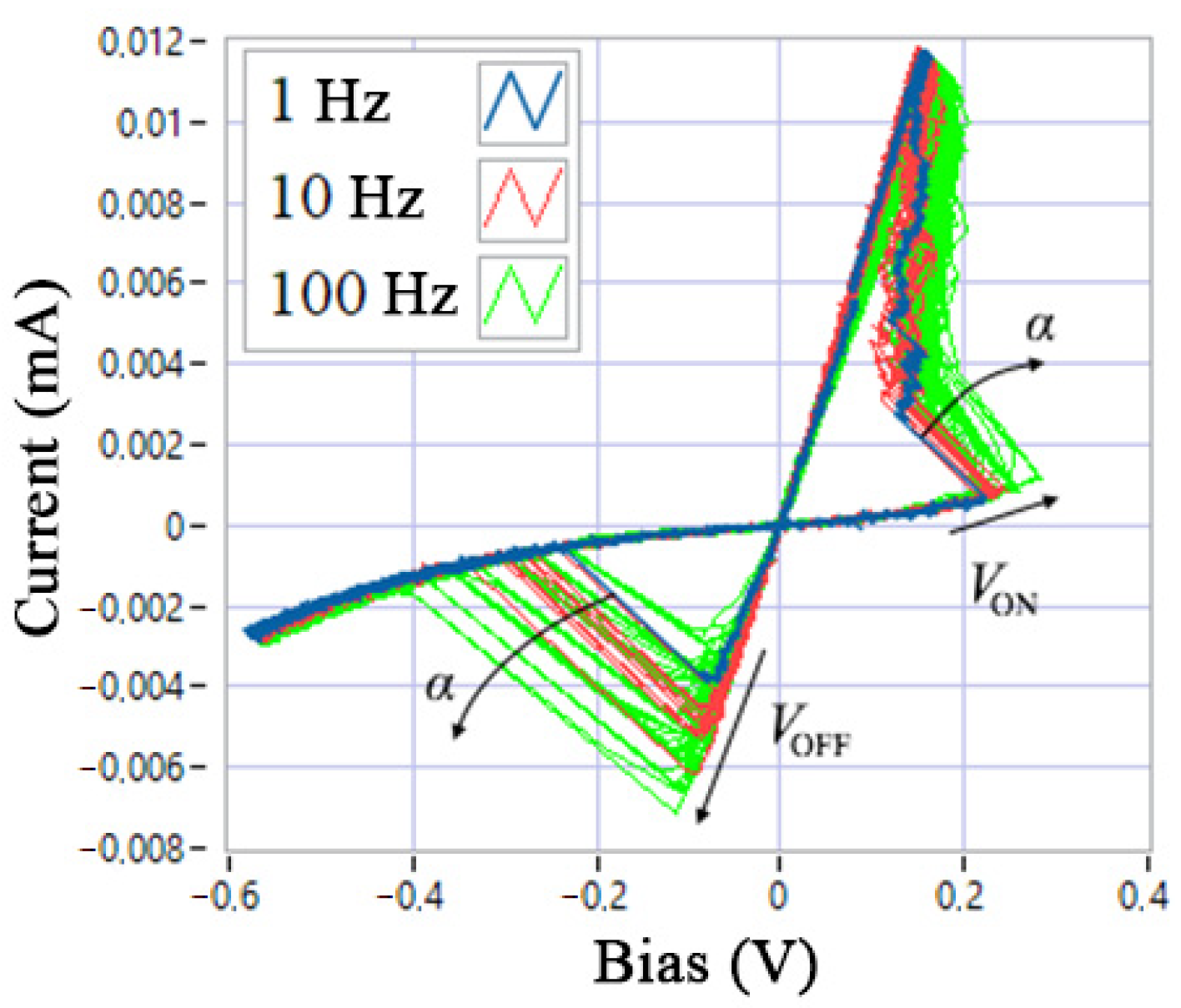
- Nonlinearity of the switching function. The origin of this nonlinearity in memristive devices based on redox reactions is explained by the nonlinear movement of ion vacancies or defects, accelerated by Joule heating. This property is characterized in that the resistance switching time of the SET and RESET processes decreases by orders of magnitude if the applied voltage pulse increases only several times. Thus, this criterion tests the model for a nonlinear dependence of the switching time on the input voltage.
- 3
- Suitability for modeling the complementary serial connection of two elements. One of the distinguishing features of such a connection is the presence of a common LRS when AC voltage is applied. This criterion serves as a check for the consistency of the memristive device model.
- 4
- Ability to set several states of resistance. The criterion is to identify more than two states of resistance of the memristive device between the LRS and HRS, providing multi-bit data storage.
- 5
- Dependence of SET (or RESET) switching from the current state of the resistance. According to this criterion, the voltage required to set the device to a lower resistance state should depend on the high resistance value in the current cycle and vice versa. Thus, the switching kinetics should be power-dependent.
- 6
- Reliable simulation of the memory fading effect. This dynamical phenomenon is well known in the theory of nonlinear systems. With suitable periodic exposure, the previous “history” of the memristive device is gradually erased.
- 7
- Compact representation of a continuous mathematical model, which determines the suitability of using its discrete version in the processes of large-system simulation, including neural networks, as well as digital hardware emulators of memristive circuits.
2.5. Candidate Memristor Models
2.5.1. Mean Metastable Switch Memristor Model
2.5.2. Generalized Mean Metastable Switch Memristor Model
3. Results
3.1. Criterial Analysis of Candidate Models
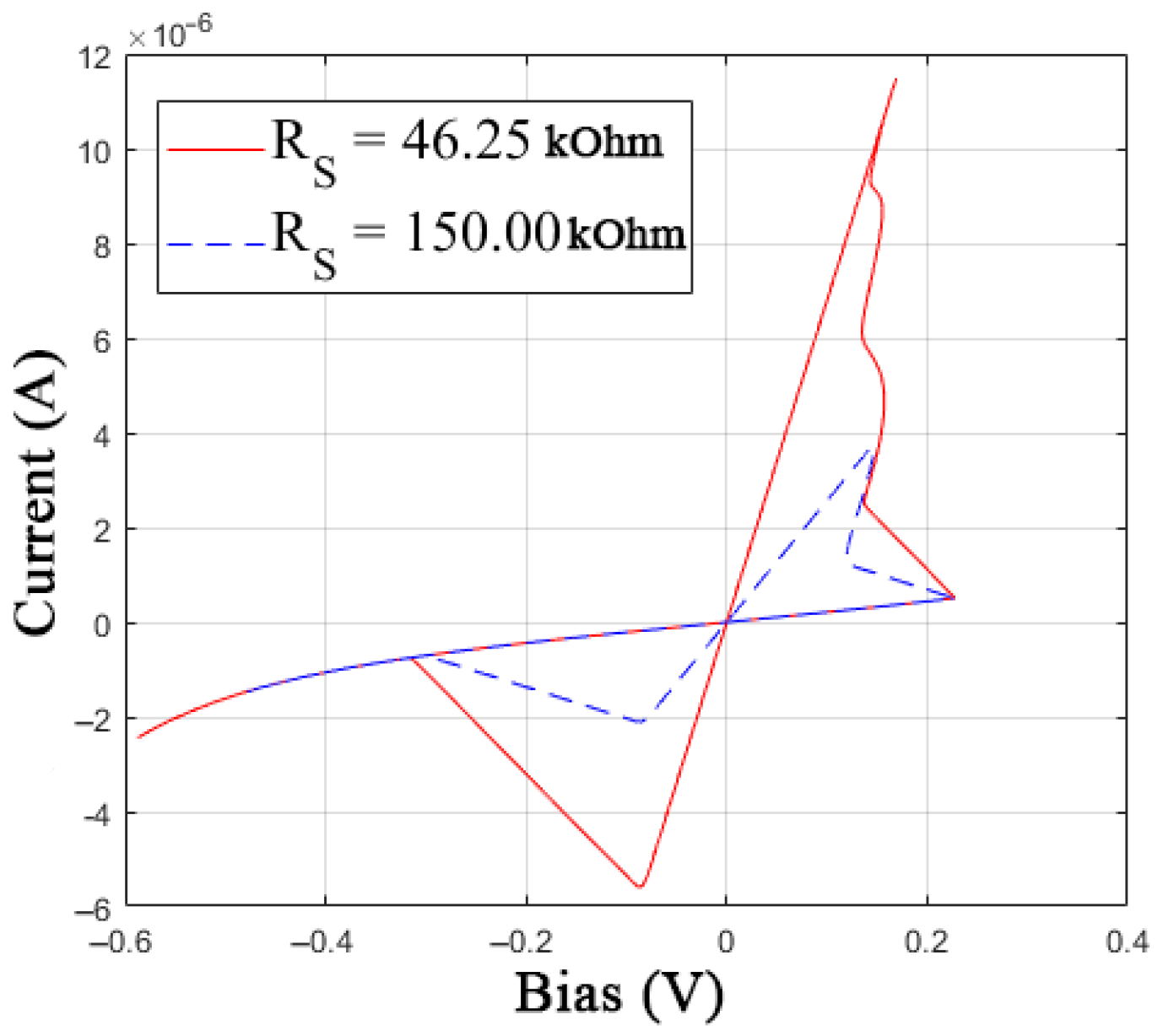
3.2. The Modification of Memristor Model
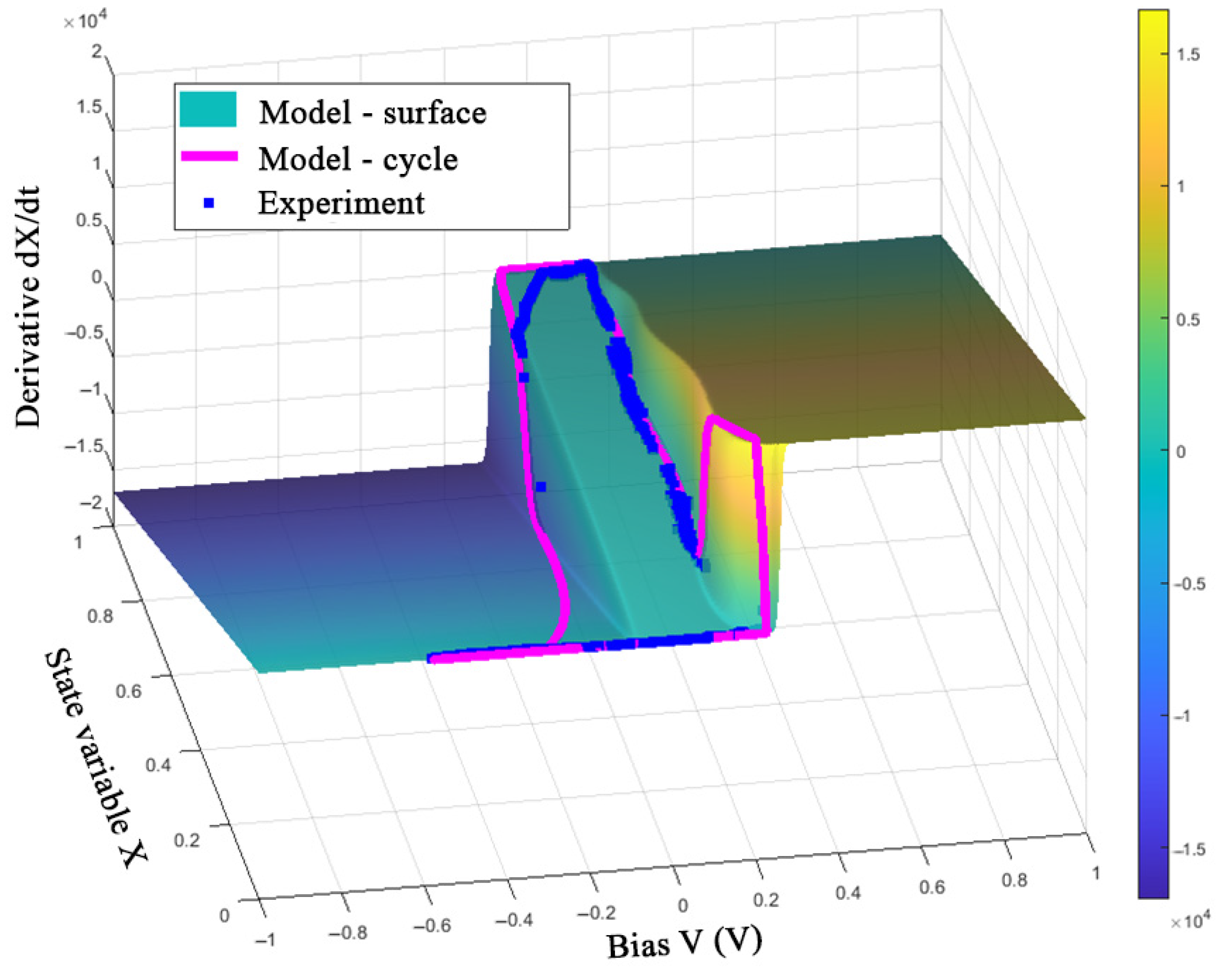
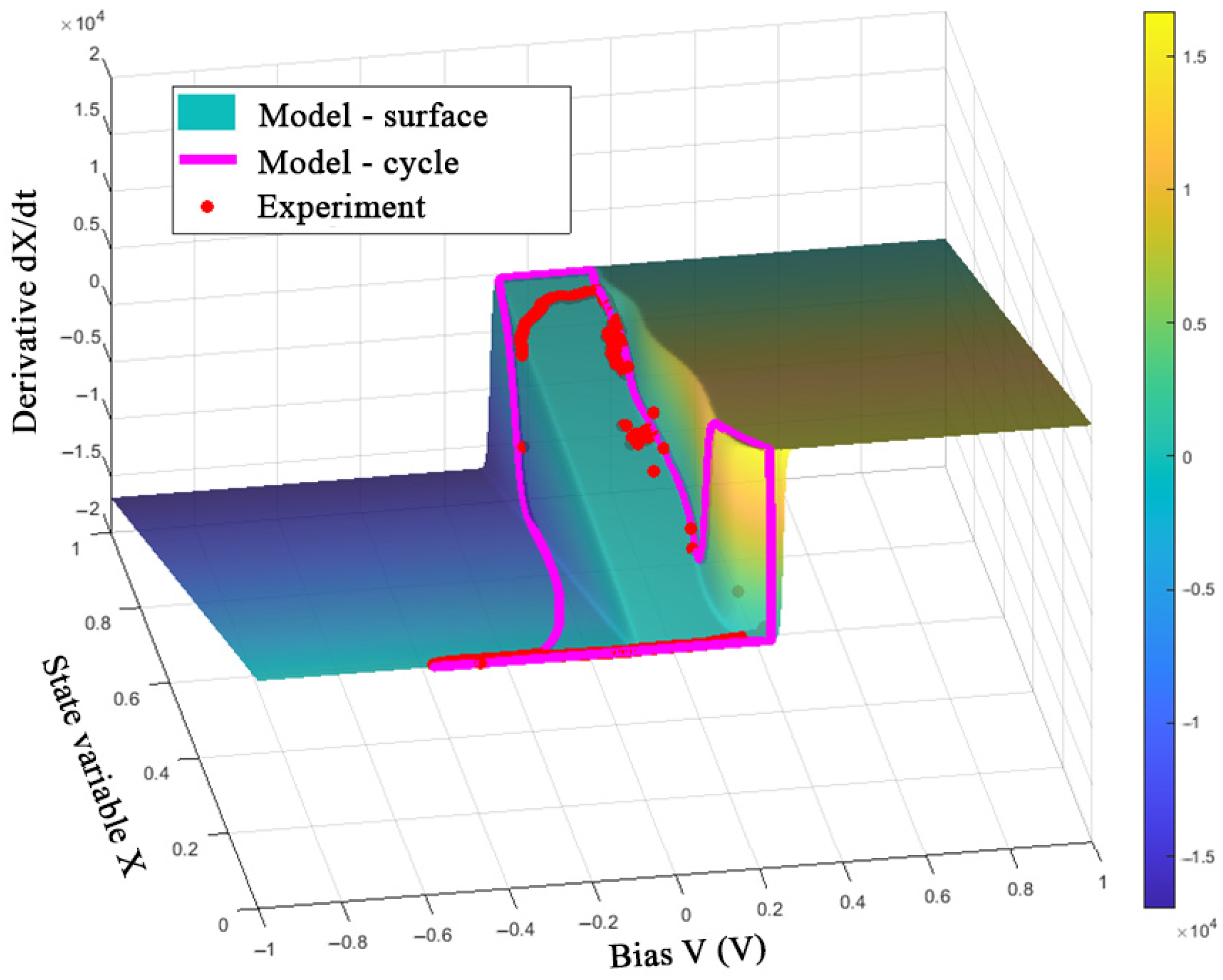
3.3. Parametric Identification
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chua, L. Memristor-the missing circuit element. IEEE Trans. Circuits Syst. 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Strukov, D.B.; Snider, G.S.; Stewart, D.R.; Williams, R.S. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef] [PubMed]
- Chua, L. If it’s pinched it’s a memristor. Semicond. Sci. Technol. 2014, 29, 104001. [Google Scholar] [CrossRef]
- Pan, F.; Gao, S.; Chen, C.; Song, C.; Zeng, F. Recent progress in resistive random access memories: Materials, switching mechanisms, and performance. Mater. Sci. Eng. R Rep. 2014, 83, 1–59. [Google Scholar] [CrossRef]
- Vourkas, I.; Sirakoulis, G.C. Emerging memristor-based logic circuit design approaches: A review. IEEE Circuits Syst. Mag. 2016, 16, 15–30. [Google Scholar] [CrossRef]
- Puppo, F.; Doucey, M.A.; Di Ventra, M.; De Micheli, G.; Carrara, S. Memristor-based devices for sensing. In Proceedings of the 2014 IEEE International Symposium on Circuits and Systems (ISCAS), Melbourne, VIC, Australia, 1–5 June 2014; pp. 2257–2260. [Google Scholar]
- James, A.P. An overview of memristive cryptography. Eur. Phys. J. Spec. Top. 2019, 228, 2301–2312. [Google Scholar] [CrossRef]
- Sun, J.; Zhao, X.; Fang, J.; Wang, Y. Autonomous memristor chaotic systems of infinite chaotic attractors and circuitry realization. Nonlinear Dyn. 2018, 94, 2879–2887. [Google Scholar] [CrossRef]
- Ziegler, M.; Wenger, C.; Chicca, E.; Kohlstedt, H. Tutorial: Concepts for closely mimicking biological learning with memristive devices: Principles to emulate cellular forms of learning. J. Appl. Phys. 2018, 124, 152003. [Google Scholar] [CrossRef]
- Thomas, A. Memristor-based neural networks. J. Phys. D Appl. Phys. 2013, 46, 093001. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.; Han, G.; Zeng, Z.; Wang, Y. Memristor-based neural network circuit of full-function Pavlov associative memory with time delay and variable learning rate. IEEE Trans. Cybern. 2020, 50, 2935–2945. [Google Scholar] [CrossRef]
- Sun, J.; Han, J.; Wang, Y.; Liu, P. Memristor-based neural network circuit of emotion congruent memory with mental fatigue and emotion inhibition. IEEE Trans. Biomed. Circuits Syst. 2021, 15, 606–616. [Google Scholar] [CrossRef] [PubMed]
- Menzel, S.; Böttger, U.; Wimmer, M.; Salinga, M. Physics of the switching kinetics in resistive memories. Adv. Funct. Mater. 2015, 25, 6306–6325. [Google Scholar] [CrossRef]
- Waser, R.; Dittmann, R.; Staikov, G.; Szot, K. Redox-based resistive switching memories–nanoionic mechanisms, prospects, and challenges. Adv. Mater. 2009, 21, 2632–2663. [Google Scholar] [CrossRef]
- Campbell, K.A. Self-directed channel memristor for high temperature operation. Microelectron. J. 2017, 59, 10–14. [Google Scholar] [CrossRef]
- Garda, B.; Galias, Z. Modeling Sinusoidally Driven Self-Directed Channel Memristors. In Proceedings of the 2018 International Conference on Signals and Electronic Systems (ICSES), Krakow, Poland, 10–12 September 2018; pp. 19–22. [Google Scholar]
- Kvatinsky, S.; Ramadan, M.; Friedman, E.G.; Kolodny, A. VTEAM: A General Model for Voltage-Controlled Memristors. IEEE Trans. Circuits Syst. II Express Briefs 2015, 62, 786–790. [Google Scholar] [CrossRef]
- Gomez, J.; Vourkas, I.; Abusleme, A. Exploring memristor multi-level tuning dependencies on the applied pulse properties via a low cost instrumentation setup. IEEE Access 2019, 7, 59413–59421. [Google Scholar] [CrossRef]
- Drake, K.; Lu, T.; Majumdar, M.; Kamrul, H.; Campbell, K.A. Comparison of the electrical response of Cu and Ag ion-conducting SDC memristors over the temperature range 6 K to 300 K. Micromachines 2019, 10, 663. [Google Scholar] [CrossRef] [Green Version]
- Bunnam, T.; Soltan, A.; Sokolov, D.; Maevsky, O.; Degenaar, P.; Yakovlev, A. Empirical Temperature Model of Self-Directed Channel Memristor. In Proceedings of the 2020 IEEE Sensors, Rotterdam, The Netherlands, 25–28 October 2020; pp. 1–4. [Google Scholar]
- Volos, C.; Nistazakis, H.; Pham, V.T.; Stouboulos, I. The first experimental evidence of chaos from a nonlinear circuit with a real memristor. In Proceedings of the 2020 9th International Conference on Modern Circuits and Systems Technologies (MOCAST), Bremen, Germany, 7–9 September 2020; pp. 1–4. [Google Scholar]
- Volos, C.K.; Pham, V.T.; Nistazakis, H.E.; Stouboulos, I.N. A dream that has come true: Chaos from a nonlinear circuit with a real memristor. Int. J. Bifurc. Chaos 2020, 30, 2030036. [Google Scholar] [CrossRef]
- Shinriki, M.; Yamamoto, M.; Mori, S. Multimode oscillations in a modified van der Pol oscillator containing a positive nonlinear conductance. Proc. IEEE 1981, 69, 394–395. [Google Scholar] [CrossRef]
- Minati, L.; Gambuzza, L.V.; Thio, W.J.; Sprott, J.C.; Frasca, M. A chaotic circuit based on a physical memristor. Chaos Solitons Fractals 2020, 138, 109990. [Google Scholar] [CrossRef]
- Sprott, J.C. A new chaotic jerk circuit. IEEE Trans. Circuits Syst. II Express Briefs 2011, 58, 240–243. [Google Scholar] [CrossRef]
- Molter, T.W.; Nugent, M.A. The generalized metastable switch memristor model. In Proceedings of the 2016 15th International Workshop on Cellular Nanoscale Networks and their Applications (CNNA), Dresden, Germany, 23–25 August 2016; pp. 1–2. [Google Scholar]
- The Mean Metastable Switch Memristor Model in Xyce. Available online: https://knowm.org/the-mean-metastable-switch-memristor-model-in-xyce/ (accessed on 26 December 2021).
- Knowm SDC Memristors. Available online: https://knowm.org/downloads/Knowm_Memristors.pdf (accessed on 26 December 2021).
- Lee, J.H.; Lim, D.H.; Jeong, H.; Ma, H.; Shi, L. Exploring cycle-to-cycle and device-to-device variation tolerance in MLC storage-based neural network training. IEEE Trans. Electron. Devices 2019, 66, 2172–2178. [Google Scholar] [CrossRef]
- Fantini, A.; Wouters, D.J.; Degraeve, R.; Goux, L.; Pantisano, L.; Kar, G.; Chen, Y.-Y.; Govoreanu, B.; Kittl, J.A.; Altimime, L.; et al. Intrinsic Switching Behavior in HfO2 RRAM by Fast Electrical Measurements on Novel 2R Test Structures. In Proceedings of the 2012 4th IEEE International Memory Workshop, Milan, Italy, 20–23 May 2012; pp. 1–4. [Google Scholar] [CrossRef]
- Goux, L.; Raghavan, N.; Fantini, A.; Nigon, R.; Strangio, S.; Degraeve, R.; Kar, G.; Chen, Y.Y.; De Stefano, F.; Afanas’ev, V.V.; et al. On the bipolar resistive-switching characteristics of Al2O3-and HfO2-based memory cells operated in the soft-breakdown regime. J. Appl. Phys. 2014, 116, 134502. [Google Scholar] [CrossRef]
- Niraula, D.; Karpov, V. Comprehensive numerical modeling of filamentary RRAM devices including voltage ramp-rate and cycle-to-cycle variations. J. Appl. Phys. 2018, 124, 174502. [Google Scholar] [CrossRef] [Green Version]
- Miranda, E.; Muñoz-Gorriz, J.; Suñé, J.; Fröhlich, K. SPICE model for the current-voltage characteristic of resistive switching devices including the snapback effect. Microelectron. Eng. 2019, 215, 110998. [Google Scholar] [CrossRef]
- Linn, E.; Siemon, A.; Waser, R.; Menzel, S. Applicability of Well-Established Memristive Models for Simulations of Resistive Switching Devices. IEEE Trans. Circuits Syst. 2014, 61, 2402–2410. [Google Scholar] [CrossRef] [Green Version]
- Menzel, S.; Siemon, A.; Ascoli, A.; Tetzlaff, R. Requirements and Challenges for Modelling Redox-based Memristive Devices. In Proceedings of the 2018 IEEE ISCAS, Florence, Italy, 27–30 May 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Nugent, M.A.; Molter, T.W. AHaH Computing–From Metastable Switches to Attractors to Machine Learning. PLoS ONE 2014, 9, e85175. [Google Scholar] [CrossRef]
- Patterson, G.A.; Suñé, J.; Miranda, E. SPICE simulation of memristive circuits based on memdiodes with sigmoidal threshold functions. Int. J. Circuit Theory Appl. 2018, 1, 39–49. [Google Scholar] [CrossRef]
- Jiang, Z.; Wu, Y.; Yu, S.; Yang, L.; Song, K.; Karim, Z.; Philip Wong, H.-S. A Compact Model for Metal–Oxide Resistive Random Access Memory With Experiment Verification. IEEE Trans. Electron. Devices 2016, 63, 1884–1892. [Google Scholar] [CrossRef]
- Čičo, K.; Jančovič, P.; Dérer, J.; Šmatko, V.; Rosova, A.; Blaho, M.; Hudec, B.; Gregušová, D.; Fröhlich, K. Resistive switching in nonplanar HfO2-based structures with variable series resistance. J. Vac. Sci. Technol. 2015, 33, 01A108. [Google Scholar] [CrossRef]
- Zhu, Y.; Zheng, K.; Wu, X.; Ang, L.K. Enhanced stability of filament-type resistive switching by interface engineering. Sci. Rep. 2017, 7, 43664. [Google Scholar] [CrossRef] [Green Version]
- Degraeve, R.; Roussel, P.; Goux, L.; Wouters, D.; Kittl, J.; Altimime, L.; Jurczak, M.; Groeseneken, G. Generic learning of TDDB applied to RRAM for improved understanding of conduction and switching mechanism through multiple filaments. In Proceedings of the 2010 International Electron Devices Meeting, San Francisco, CA, USA, 6–8 December 2010; pp. 28.4.1–28.4.4. [Google Scholar] [CrossRef]
- Agudov, N.; Safonov, A.; Krichigin, A.; Kharcheva, A.; Dubkov, A.; Valenti, D.; Guseinov, D.; Belov, A.; Mikhaylov, A.; Carollo, A.; et al. Nonstationary distributions and relaxation times in a stochastic model of memristor. J. Stat. Mech. Theory Exp. 2020, 2020, 024003. [Google Scholar] [CrossRef] [Green Version]
- Agudov, N.V.; Dubkov, A.A.; Safonov, A.V.; Krichigin, A.V.; Kharcheva, A.A.; Guseinov, D.V.; Koryazhkina, M.N.; Novikov, A.S.; Shishmakova, V.A.; Antonov, I.N.; et al. Stochastic model of memristor based on th length of conductive region. Chaos Solitons Fractals 2021, 150, 111131. [Google Scholar] [CrossRef]
- Naous, R.; Al-Shedivat, M.; Salama, K. Stochasticity Modeling in Memristors. IEEE Trans. Nanotechnol. 2015, 15, 15–28. [Google Scholar] [CrossRef] [Green Version]
- Alonso, F.; Maldonado, D.; Aguilera, A.; Roldan, J. Memristor variability and stochastic physical properties modeling from a multivariate time series approach. Chaos Solitons Fractals 2021, 143, 110461. [Google Scholar] [CrossRef]
- Driscoll, T.; Pershin, Y.V.; Basov, D.N.; Di Ventra, M. Chaotic memristor. Appl. Phys. A 2011, 102, 885–889. [Google Scholar] [CrossRef] [Green Version]
- Tutueva, A.V.; Nepomuceno, E.G.; Karimov, A.I.; Andreev, V.S.; Butusov, D.N. Adaptive chaotic maps and their application to pseudo-random numbers generation. Chaos Solitons Fractals 2020, 133, 109615. [Google Scholar] [CrossRef]
- Ignatov, M.; Ziegler, M.; Hansen, M.; Petraru, A.; Kohlstedt, H. A memristive spiking neuron with firing rate coding. Front. Neurosci. 2015, 9, 376. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, L.; He, Z.; Li, C.; Wen, S.; Chen, Y. Revisiting memristor properties. Int. J. Bifurcat. Chaos 2020, 30, 2050172. [Google Scholar] [CrossRef]












Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ostrovskii, V.; Fedoseev, P.; Bobrova, Y.; Butusov, D. Structural and Parametric Identification of Knowm Memristors. Nanomaterials 2022, 12, 63. https://doi.org/10.3390/nano12010063
Ostrovskii V, Fedoseev P, Bobrova Y, Butusov D. Structural and Parametric Identification of Knowm Memristors. Nanomaterials. 2022; 12(1):63. https://doi.org/10.3390/nano12010063
Chicago/Turabian StyleOstrovskii, Valerii, Petr Fedoseev, Yulia Bobrova, and Denis Butusov. 2022. "Structural and Parametric Identification of Knowm Memristors" Nanomaterials 12, no. 1: 63. https://doi.org/10.3390/nano12010063
APA StyleOstrovskii, V., Fedoseev, P., Bobrova, Y., & Butusov, D. (2022). Structural and Parametric Identification of Knowm Memristors. Nanomaterials, 12(1), 63. https://doi.org/10.3390/nano12010063







