Magnetic Dipole and Thermophoretic Particle Deposition Impact on Bioconvective Oldroyd-B Fluid Flow over a Stretching Surface with Cattaneo–Christov Heat Flux
Abstract
:1. Introduction
- What are the effects of relaxation retardation time on the velocity profile?
- How are temperature profiles affected by thermal stratification parameters?
- How is the concentration profile influenced by introducing thermophoretic particle deposition?
- How does magnetic dipole influence the skin friction coefficient?
- What is the effect of the highest swimming speed of microorganisms on the density number of motile microorganisms?
2. Mathematical Formulation
3. Magnetic Dipole
4. Thermophoretic Particle Deposition
5. Similarity Transformation
6. Quantities of Practical Interest
7. Numerical Solution
8. Results and Discussion
8.1. Velocity Profile
8.2. Temperature Profile
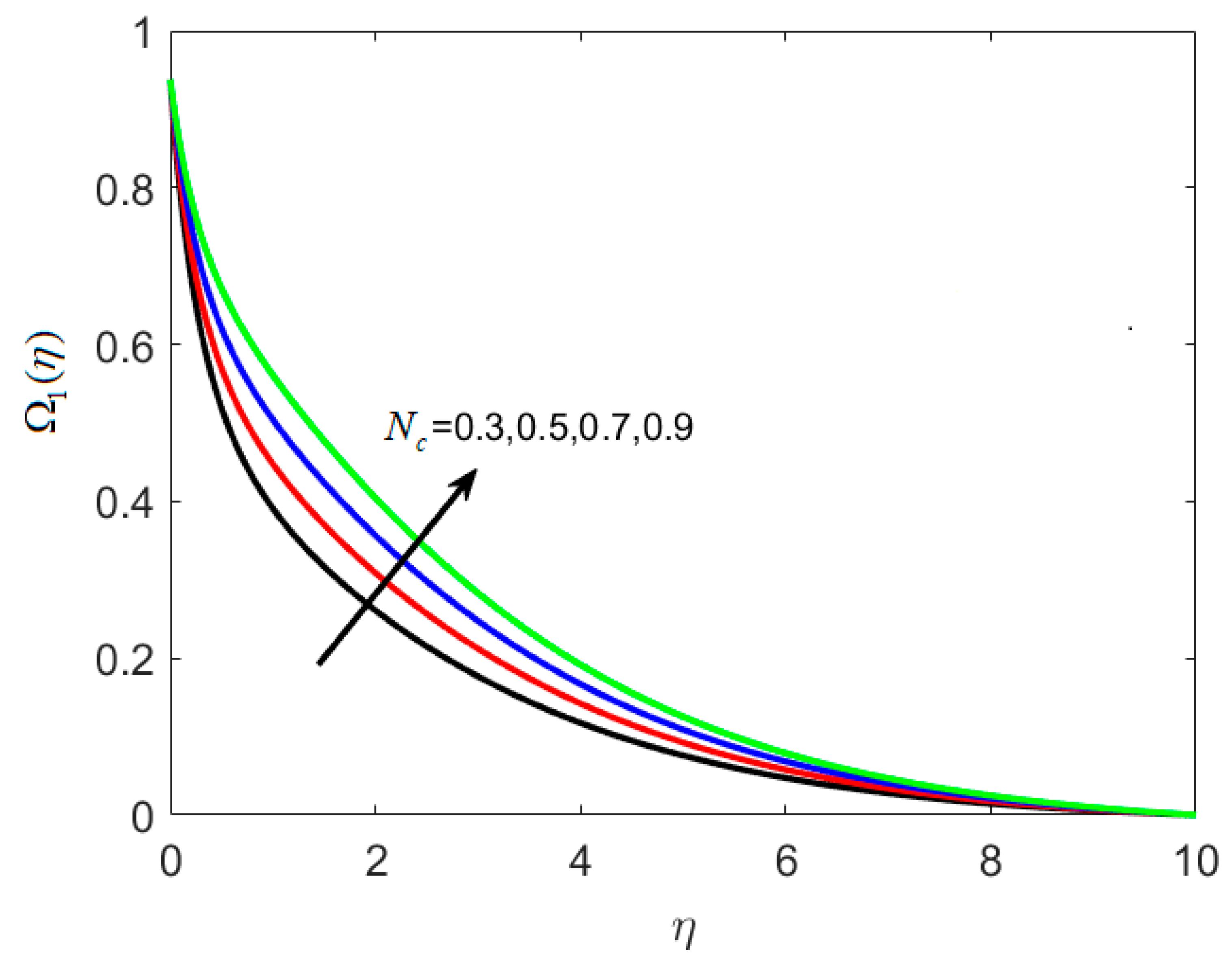
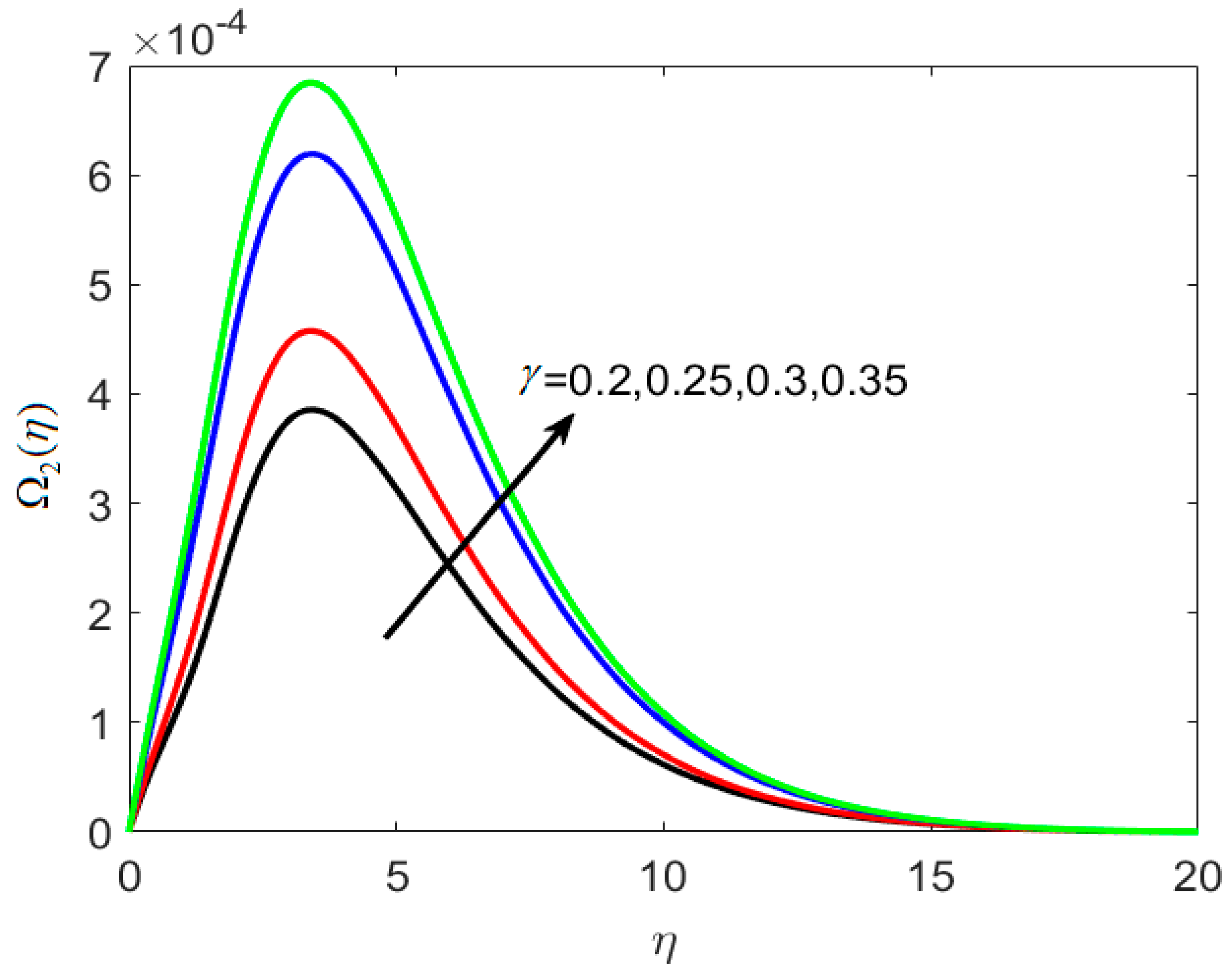
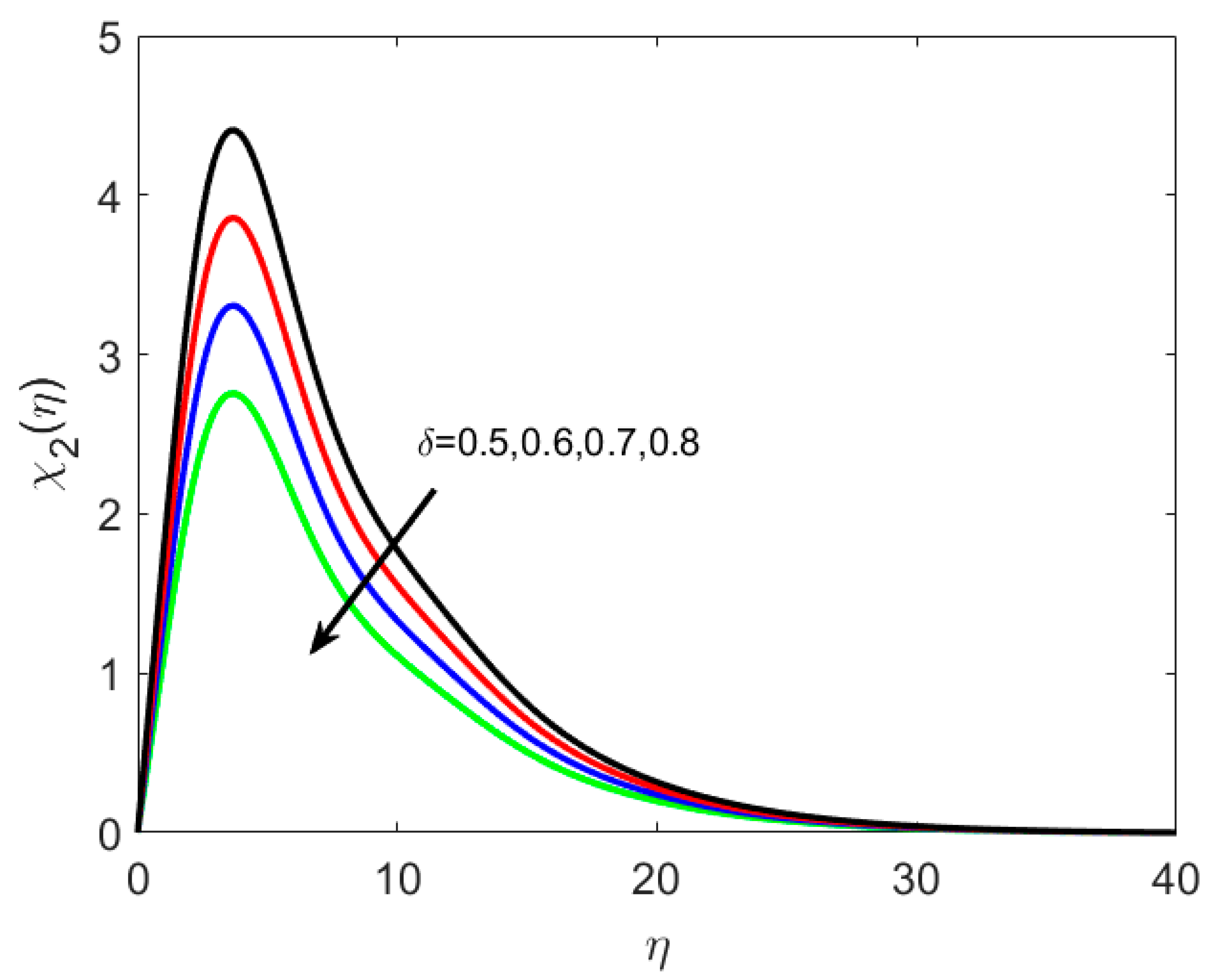
8.3. Concentration and Microorganism Profiles
9. Concluding Remarks
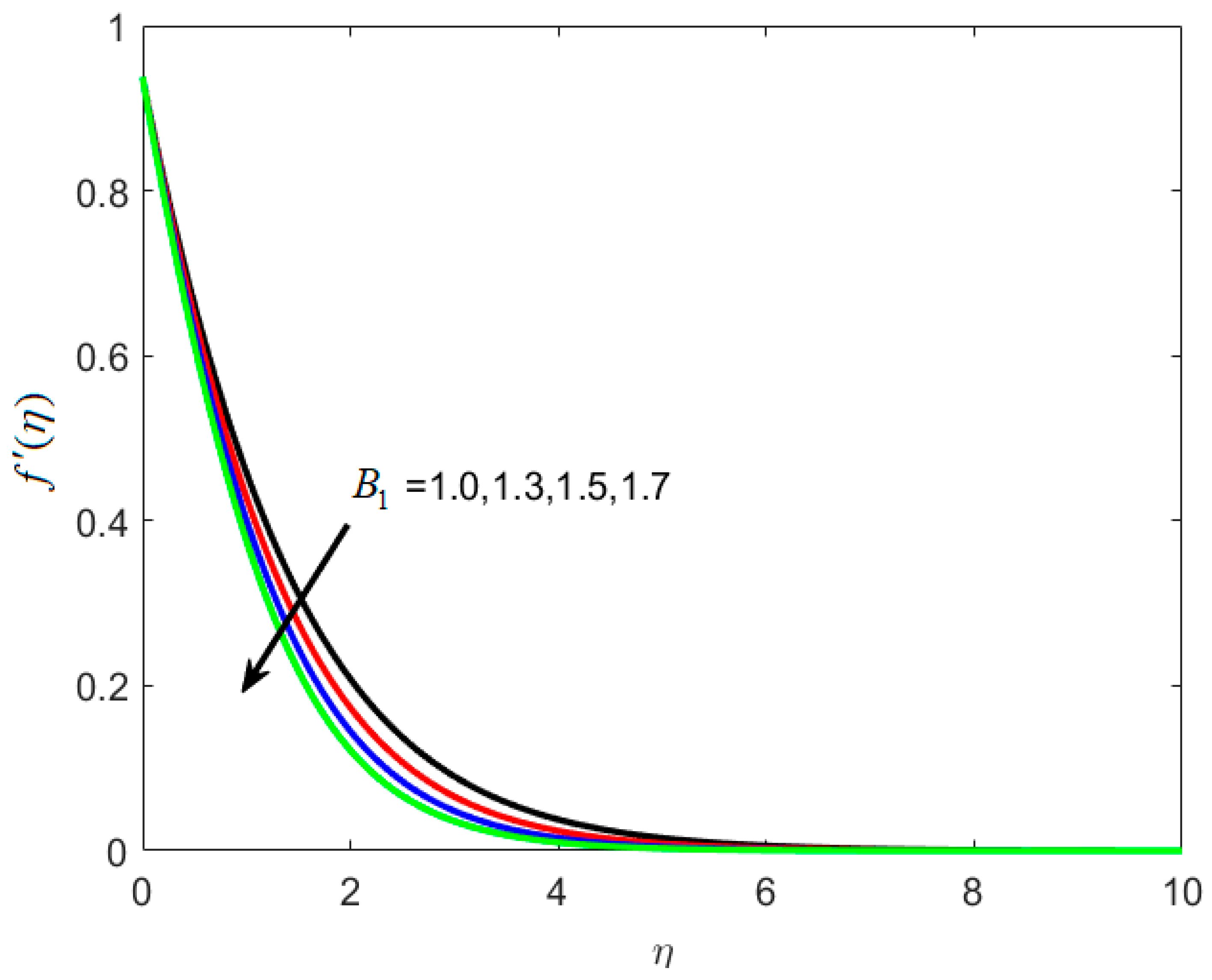
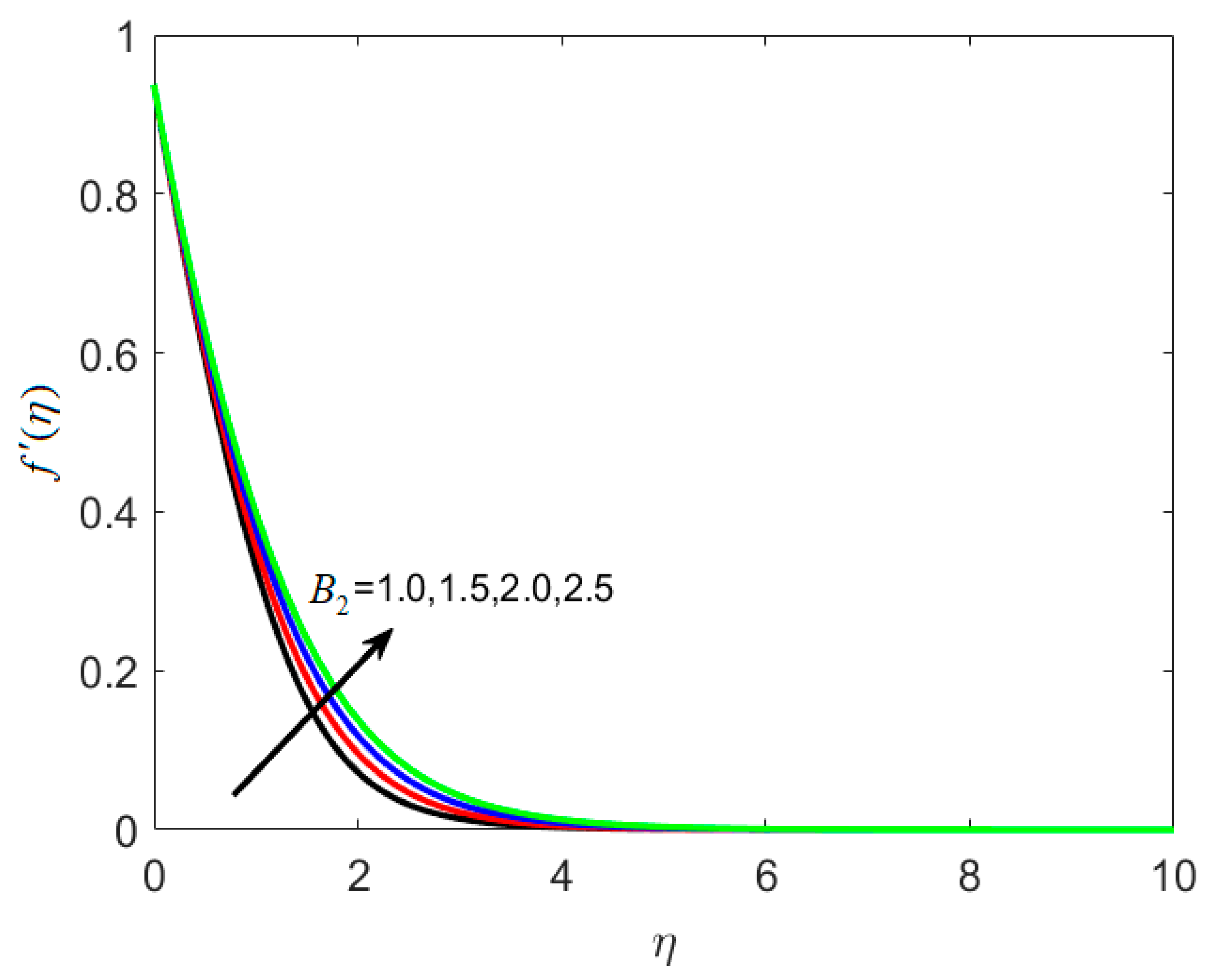
- The opposite behavior of velocity function is observed with increasing relaxation retardation time constants B1 and B2.
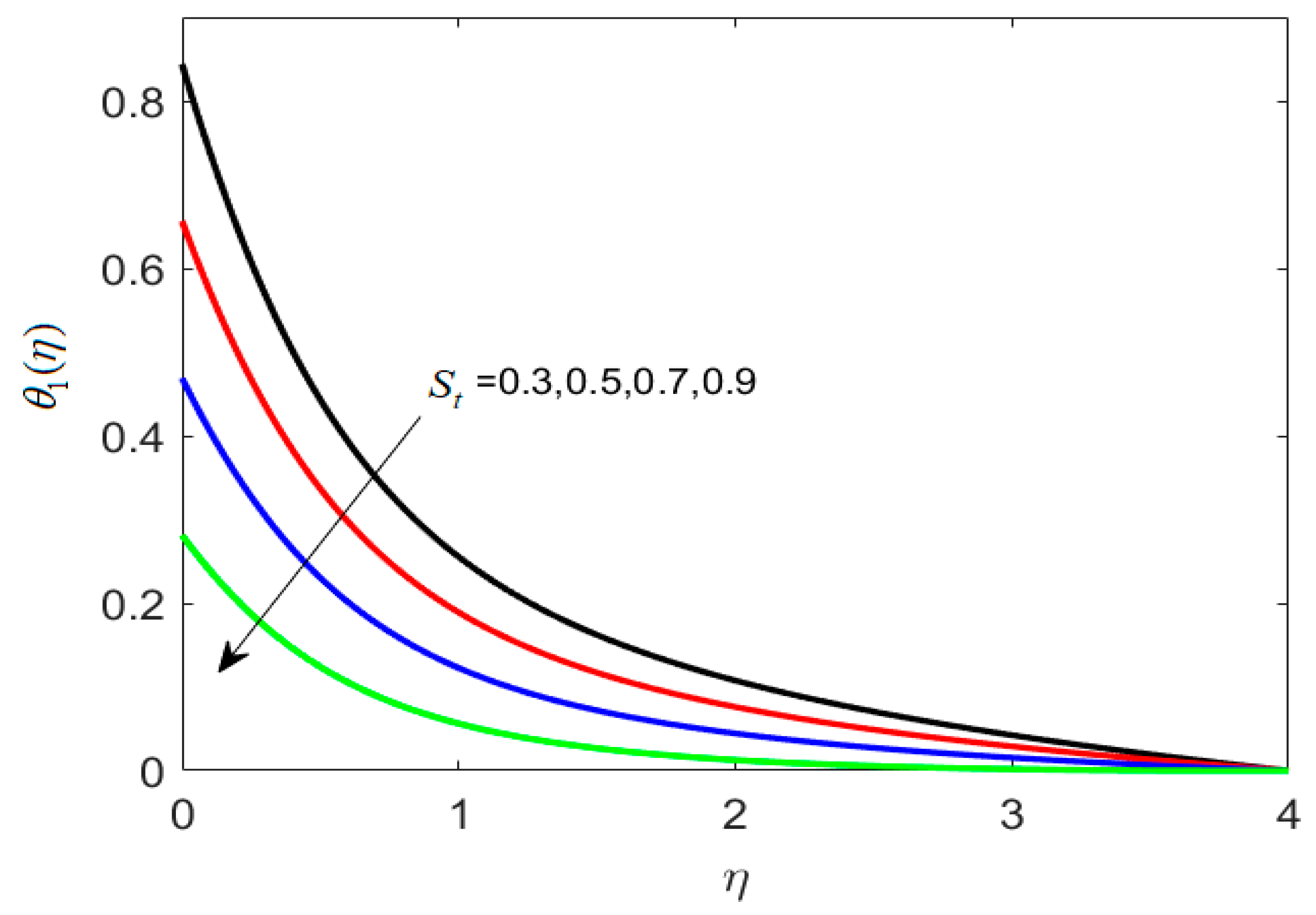
- Thermal stratification parameter St minimizes temperature profiles.
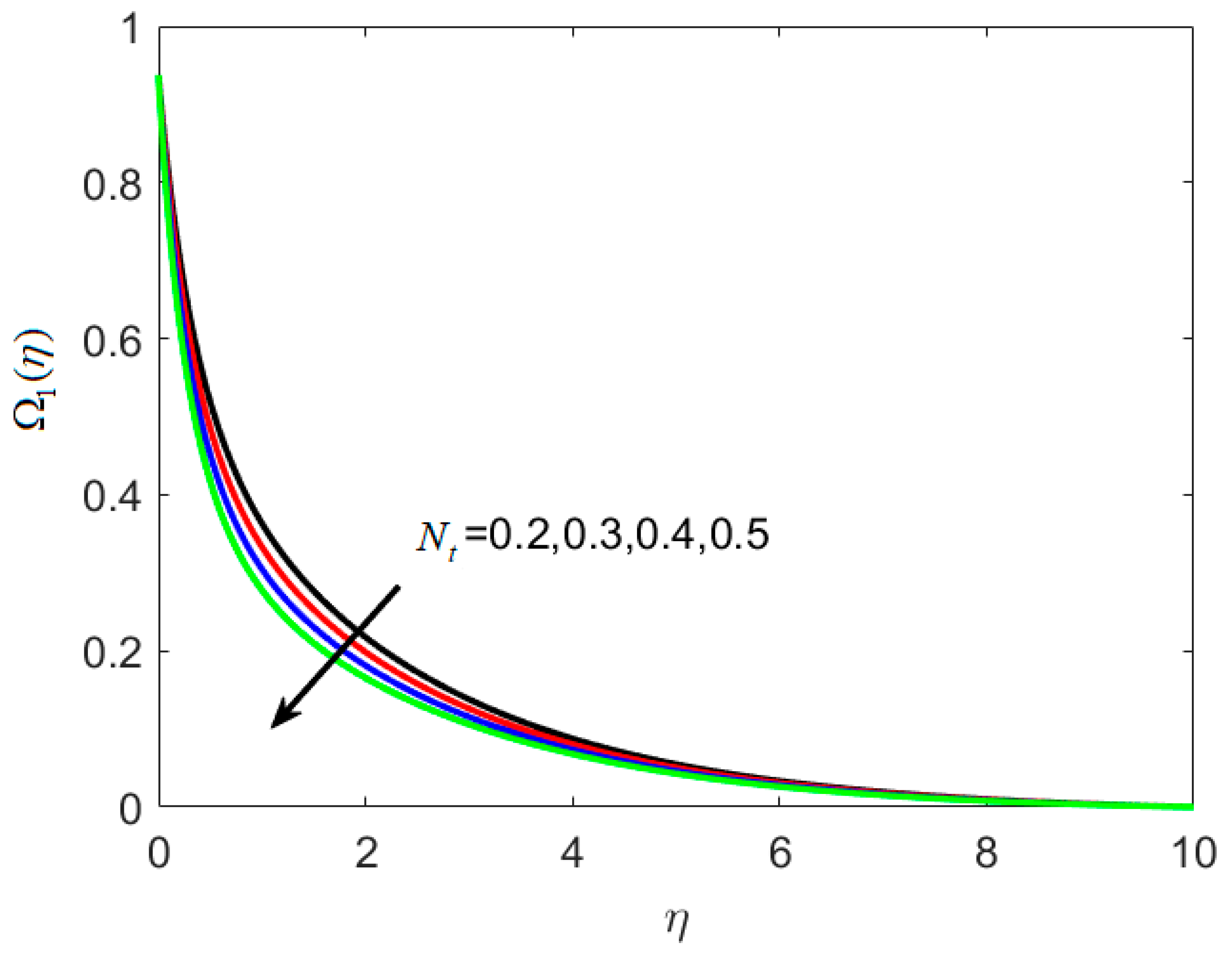
- and decrease with increasing Nt.
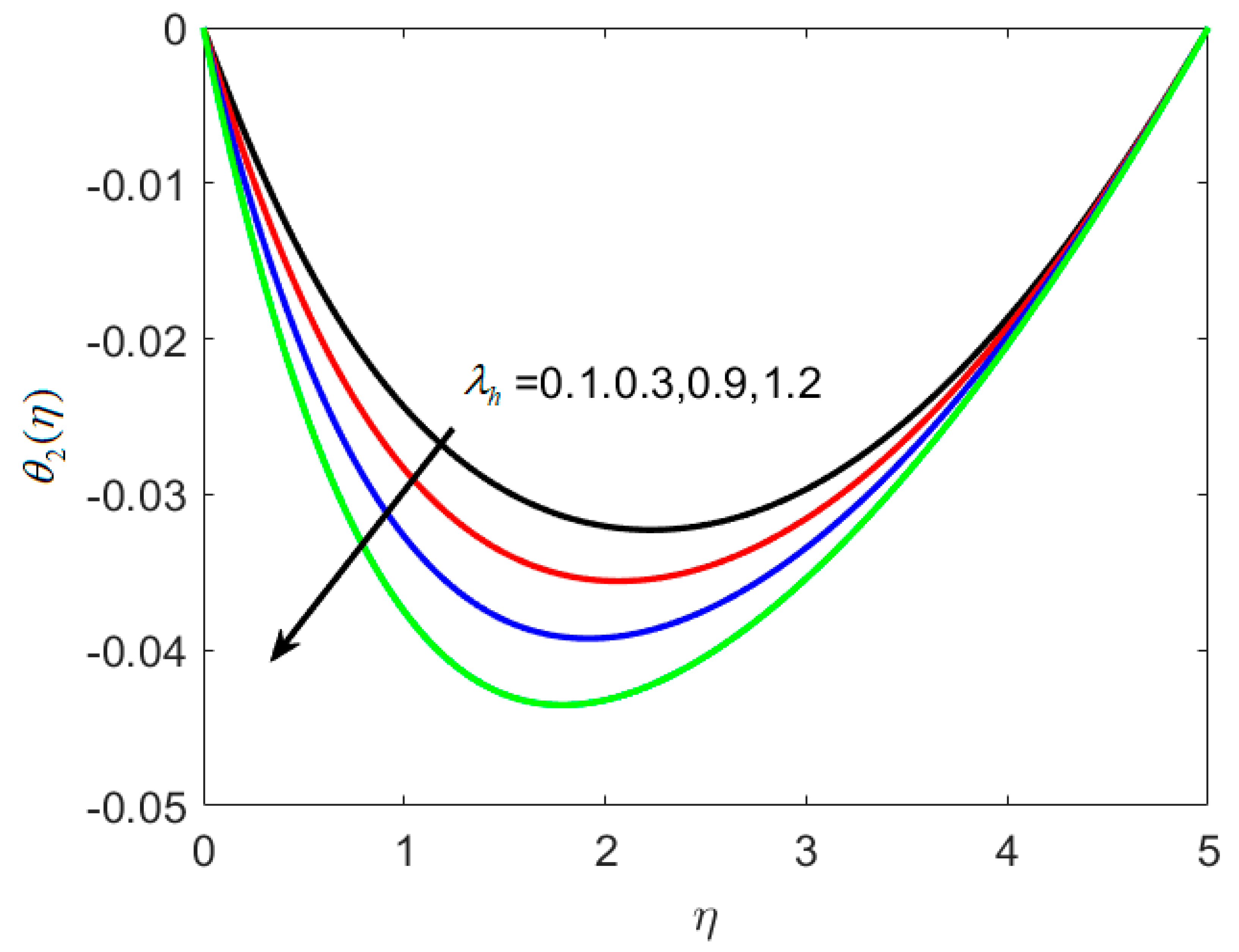
- Thermal relaxation parameter decreases the temperature profiles.
- Nu increases with increasing .
- Large estimations of decrease the concentration profile.
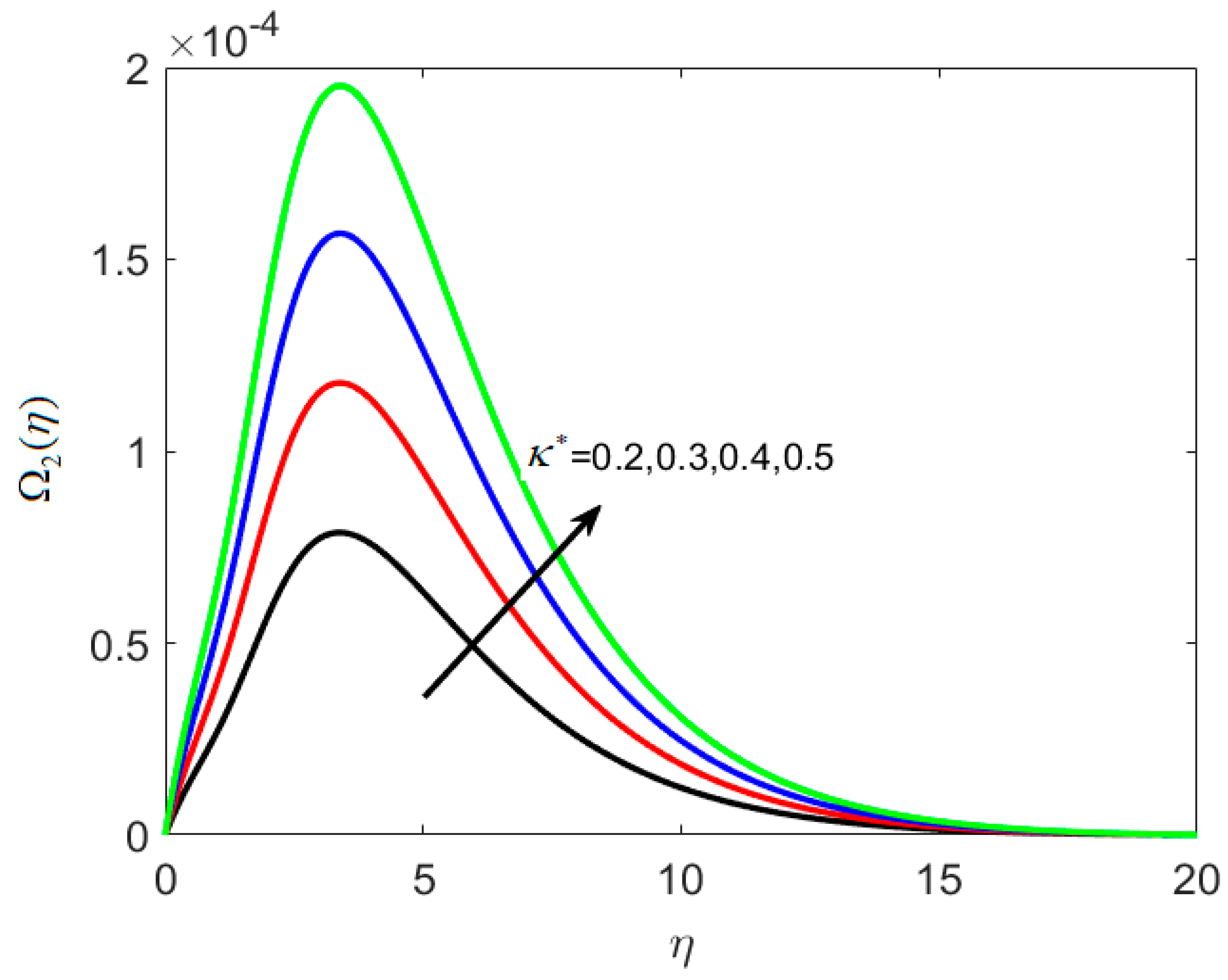
- Thermophoretic deposition velocity decreases with increasing Sc and κ*.
- The density number of motile microorganisms decreases with increasing Pe and Le.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Constant | Velocity components | ||
| Thermophoretic velocity | Thermophoretic deposition velocity | ||
| Coordinates axis | Concentration | ||
| Thermophoretic parameter | Non-dimensional thermophoretic deposition velocity | ||
| Dimensionless concentration ratio | Temperature | ||
| Chemotaxis constant | Greek symbols | ||
| Curie temperature | Viscous dissipation parameter | ||
| Highest swimming speed of microorganisms | Shear stress, surface heat flux, surface mass flux | ||
| Thermal conductivity | Thermal relaxation time coefficient | ||
| Magnetization | Free space permeability | ||
| Schmidt number | Relaxation, retardation times of material parameters | ||
| Dimensionless velocity | Gyromagnetic coefficient | ||
| Thermal stratification parameter | Strength of magnetic field | ||
| Traditional Lewis number | Dimensionless reaction rate constant | ||
| Distance | Solutal relaxation parameter | ||
| Dynamic viscosity | |||
| Magnetic field | Dimensionless temperature | ||
| Wall temperature | Ferromagnetic interaction parameter | ||
| , | Deborah numbers or dimensionless material parameters | Diffusive concentration of microorganisms at the wall | |
| Bioconvection Peclet number | , | Similarity variables | |
| Kinematic viscosity | |||
| Chemical reaction rate | Dimensionless distance | ||
| Prandtl number | Dimensionless concentration | ||
| Local Reynolds number | Scalar potential | ||
| Thermophoretic coefficient | Dimensionless curie temperature | ||
| Local Stranton number | Density | ||
| Diffusion coefficient | Fluid parameter | ||
| Local Nusselt number | Scalar potential | ||
| Density of motile microorganisms | Thermal relaxation parameter | ||
| Knudsen number | Dimensionless diffusive concentration of microorganisms | ||
| Constants | Dimensionless diffusive concentration of microorganisms | ||
| Reference temperature K | Thermal diffusivity | ||
| Specific heat capacity | |||
| Skin friction coefficient | |||
| Reference concentration |
References
- Oldroyd, J.G. On the formulation of rheological equations of state. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1950, 200, 523–541. [Google Scholar] [CrossRef]
- Ibrahim, W.; Sisay, G.; Gamachu, D. Mixed convection flow of Oldroyd-B nano fluid with Cattaneo–Christov heat and mass flux model with third order slip. AIP Adv. 2019, 9, 125023. [Google Scholar] [CrossRef] [Green Version]
- Hayat, T.; Imtiaz, M.; Alsaedi, A. Boundary layer flow of Oldroyd-B fluid by exponentially stretching sheet. Appl. Math. Mech. 2016, 37, 573–582. [Google Scholar] [CrossRef]
- Ramzan, M.; Howari, F.; Chung, J.D.; Kadry, S.; Chu, Y.-M. Irreversibility minimization analysis of ferromagnetic Oldroyd-B nanofluid flow under the influence of a magnetic dipole. Sci. Rep. 2021, 11, 4810. [Google Scholar] [CrossRef]
- Waqas, M.; Khan, M.I.; Hayat, T.; Alsaedi, A. Stratified flow of an Oldroyd-B nanoliquid with heat generation. Results Phys. 2017, 7, 2489–2496. [Google Scholar] [CrossRef]
- Shehzad, S.; Abbasi, F.; Hayat, T.; Alsaedi, A. Cattaneo–Christov heat flux model for Darcy-Forchheimer flow of an Oldroyd-B fluid with variable conductivity and non-linear convection. J. Mol. Liq. 2016, 224, 274–278. [Google Scholar] [CrossRef]
- Riaz, M.B.; Siddique, I.; Saeed, S.T.; Atangana, A. MHD Oldroyd-B Fluid with Slip Condition in view of Local and Nonlocal Kernels. J. Appl. Comput. Mech. 2020, 7, 116–127. [Google Scholar] [CrossRef]
- Hafeez, A.; Khan, M.; Ahmed, J. Stagnation point flow of radiative Oldroyd-B nanofluid over a rotating disk. Comput. Methods Programs Biomed. 2020, 191, 105342. [Google Scholar] [CrossRef]
- Ramzan, M.; Bilal, M.; Chung, J.D. Radiative Williamson nanofluid flow over a convectively heated Riga plate with chemical reaction-A numerical approach. Chin. J. Phys. 2017, 55, 1663–1673. [Google Scholar] [CrossRef]
- Lu, D.; Ramzan, M.; Bilal, M.; Chung, J.D.; Farooq, U.; Tahir, S. On three-dimensional MHD Oldroyd-B fluid flow with nonlinear thermal radiation and homogeneous–heterogeneous reaction. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 387. [Google Scholar] [CrossRef]
- Saqib, M.; Khan, I.; Chu, Y.-M.; Qushairi, A.; Shafie, S.; Nisar, K.S. Multiple Fractional Solutions for Magnetic Bio-Nanofluid Using Oldroyd-B Model in a Porous Medium with Ramped Wall Heating and Variable Velocity. Appl. Sci. 2020, 10, 3886. [Google Scholar] [CrossRef]
- Khan, M.N.; Nadeem, S.; Ullah, N.; Saleem, A. Theoretical treatment of radiative Oldroyd-B nanofluid with microorganism pass an exponentially stretching sheet. Surf. Interf. 2020, 21, 100686. [Google Scholar] [CrossRef]
- Waqas, H.; Imran, M.; Muhammad, T.; Sait, S.M.; Ellahi, R. Numerical investigation on bioconvection flow of Oldroyd-B nanofluid with nonlinear thermal radiation and motile microorganisms over rotating disk. J. Therm. Anal. Calorim. 2021, 145, 523–539. [Google Scholar] [CrossRef]
- Alam, M.; Rahman, M.; Sattar, M. Effects of variable suction and thermophoresis on steady MHD combined free-forced convective heat and mass transfer flow over a semi-infinite permeable inclined plate in the presence of thermal radiation. Int. J. Therm. Sci. 2008, 47, 758–765. [Google Scholar] [CrossRef]
- Damseh, R.A.; Tahat, M.S.; Benim, D.-I.H.A.C. Nonsimilar solutions of magnetohydrodynamic and thermophoresis particle deposition on mixed convection problem in porous media along a vertical surface with variable wall temperature. Prog. Comput. Fluid Dyn. Int. J. 2009, 9, 58. [Google Scholar] [CrossRef]
- Gowda, R.P.; Kumar, R.N.; Aldalbahi, A.; Issakhov, A.; Prasannakumara, B.; Rahimi-Gorji, M.; Rahaman, M. Thermophoretic particle deposition in time-dependent flow of hybrid nanofluid over rotating and vertically upward/ downward moving disk. Surf. Interf. 2021, 22, 100864. [Google Scholar] [CrossRef]
- Kumar, R.N.; Jyothi, A.; Alhumade, H.; Gowda, R.P.; Alam, M.M.; Ahmad, I.; Gorji, M.; Prasannakumara, B. Impact of magnetic dipole on thermophoretic particle deposition in the flow of Maxwell fluid over a stretching sheet. J. Mol. Liq. 2021, 334, 116494. [Google Scholar] [CrossRef]
- Kumar, R.N.; Gowda, R.J.P.; Madhukesh, J.K.; Prasannakumara, B.C.; Ramesh, G.K. Impact of thermophoretic particle deposition on heat and mass transfer across the dynamics of Casson fluid flow over a moving thin needle. Phys. Scr. 2021, 96, 075210. [Google Scholar] [CrossRef]
- Khan, N.A.; Sultan, F.; Khan, N.A. Heat and mass transfer of thermophoretic MHD flow of Powell–Eyring fluid over a vertical stretching sheet in the presence of chemical reaction and Joule heating. Int. J. Chem. React. Eng. 2015, 13, 37–49. [Google Scholar] [CrossRef]
- Alam, M.S.; Rahman, M.M.; Uddin, M.J.; Vajravelu, K. Numerical study of transient hydromagnetic forced convective slip flow over a porous rotating disk with thermophoresis. J. Nonlinear Evol. Equ. Appl. 2016, 2016, 1–23. [Google Scholar]
- Shehzad, S.; Alsaedi, A.; Hayat, T.; Alhuthali, M. Thermophoresis particle deposition in mixed convection three-dimensional radiative flow of an Oldroyd-B fluid. J. Taiwan Inst. Chem. Eng. 2014, 45, 787–794. [Google Scholar] [CrossRef]
- Doh, D.; Muthtamilselvan, M. Thermophoretic particle deposition on magnetohydrodynamic flow of micropolar fluid due to a rotating disk. Int. J. Mech. Sci. 2017, 130, 350–359. [Google Scholar] [CrossRef]
- Postelnicu, A. Thermophoresis particle deposition in natural convection over inclined surfaces in porous media. Int. J. Heat Mass Transf. 2012, 55, 2087–2094. [Google Scholar] [CrossRef]
- Neuringer, J.L. Some viscous flows of a saturated ferro-fluid under the combined influence of thermal and magnetic field gradients. Int. J. Non-Linear Mech. 1966, 1, 123–137. [Google Scholar] [CrossRef]
- Andersson, H.I.; Valnes, O.A. Flow of a heated ferrofluid over a stretching sheet in the presence of a magnetic dipole. Acta Mech. 1998, 128, 39–47. [Google Scholar] [CrossRef]
- Waqas, M.; Jabeen, S.; Hayat, T.; Khan, M.I.; Alsaedi, A. Modeling and analysis for magnetic dipole impact in nonlinear thermally radiating Carreau nanofluid flow subject to heat generation. J. Magn. Magn. Mater. 2019, 485, 197–204. [Google Scholar] [CrossRef]
- Gul, H.; Ramzan, M.; Nisar, K.S.; Mohamed, R.N.; Ghazwani, H.A.S. Performance-based comparison of Yamada–Ota and Hamilton–Crosser hybrid nanofluid flow models with magnetic dipole impact past a stretched surface. Sci. Rep. 2022, 12, 29. [Google Scholar] [CrossRef]
- Bognár, G.; Hriczó, K. Ferrofluid flow in magnetic field above stretching sheet with suction and injection. Math. Model. Anal. 2020, 25, 461–472. [Google Scholar] [CrossRef]
- Chen, S.B.; Shahmir, N.; Ramzan, M.; Sun, Y.L.; Aly, A.A.; Malik, M.Y. Thermophoretic particle deposition in the flow of dual stratified Casson fluid with magnetic dipole and generalized Fourier’s and Fick’s laws. Case Stud. Therm. Eng. 2021, 26, 101186. [Google Scholar] [CrossRef]
- Kefayati, G. Natural convection of ferrofluid in a linearly heated cavity utilizing LBM. J. Mol. Liq. 2014, 191, 1–9. [Google Scholar] [CrossRef]
- Ijaz, M.; Ayub, M. Simulation of magnetic dipole and dual stratification in radiative flow of ferromagnetic Maxwell fluid. Heliyon 2019, 5, e01465. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alshomrani, A.S.; Ramzan, M. Upshot of magnetic dipole on the flow of nanofluid along a stretched cylinder with gyrotactic microorganism in a stratified medium. Phys. Scr. 2019, 95, 025702. [Google Scholar] [CrossRef]
- Ahmad, S.; Khan, M.N.; Rehman, A.; Felemban, B.F.; Alqurashi, M.S.; Alharbi, F.M.; Alotaibi, F.; Galal, A.M. Analysis of Heat and Mass Transfer Features of Hybrid Casson Nanofluid Flow with the Magnetic Dipole Past a Stretched Cylinder. Appl. Sci. 2021, 11, 11203. [Google Scholar] [CrossRef]
- Shah, Z.; Vrinceanu, N.; Rooman, M.; Deebani, W.; Shutaywi, M. Mathematical Modelling of Ree-Eyring Nanofluid Using Koo-Kleinstreuer and Cattaneo–Christov Models on Chemically Reactive AA7072-AA7075 Alloys over a Magnetic Dipole Stretching Surface. Coatings 2022, 12, 391. [Google Scholar] [CrossRef]
- Nisar, K.S.; Khan, U.; Zaib, A.; Khan, I.; Baleanu, D. Exploration of aluminum and titanium alloys in the stream-wise and secondary flow directions comprising the significant impacts of magnetohydrodynamic and hybrid nanofluid. Crystals 2020, 10, 679. [Google Scholar] [CrossRef]
- Abbasi, F.M.; Shehzad, S.A.; Hayat, T.; Alhuthali, M.S. Mixed convection flow of jeffrey nanofluid with thermal radiation and double stratification. J. Hydrodyn. Ser. B 2016, 28, 840–849. [Google Scholar] [CrossRef]
- Sandeep, N.; Sulochana, C. Dual solutions for unsteady mixed convection flow of MHD micropolar fluid over a stretching/shrinking sheet with non-uniform heat source/sink. Eng. Sci. Technol. Int. J. 2015, 18, 738–745. [Google Scholar] [CrossRef] [Green Version]
- Ramzan, M.; Liaquet, A.; Kadry, S.; Yu, S.; Nam, Y.; Lu, D. Impact of Second-Order Slip and Double Stratification Coatings on 3D MHD Williamson Nanofluid Flow with Cattaneo–Christov Heat Flux. Coatings 2019, 9, 849. [Google Scholar] [CrossRef] [Green Version]
- Rehman, K.U.; Malik, M.; Salahuddin, T.; Naseer, M. Dual stratified mixed convection flow of Eyring-Powell fluid over an inclined stretching cylinder with heat generation/absorption effect. AIP Adv. 2016, 6, 075112. [Google Scholar] [CrossRef] [Green Version]
- Kandasamy, R.; Dharmalingam, R.; Prabhu, K.S. Thermal and solutal stratification on MHD nanofluid flow over a porous vertical plate. Alex. Eng. J. 2018, 57, 121–130. [Google Scholar] [CrossRef]
- Khan, M.; Rasheed, A.; Salahuddin, T.; Ali, S. Chemically reactive flow of hyperbolic tangent fluid flow having thermal radiation and double stratification embedded in porous medium. Ain Shams Eng. J. 2021, 12, 3209–3216. [Google Scholar] [CrossRef]
- Mallawi, F.; Bhuvaneswari, M.; Sivasankaran, S.; Eswaramoorthi, S. Impact of double-stratification on convective flow of a non-Newtonian liquid in a Riga plate with Cattaneo–Christov double-flux and thermal radiation. Ain Shams Eng. J. 2021, 12, 969–981. [Google Scholar] [CrossRef]
- Bilal, M.; Ramzan, M.; Mehmood, Y.; Alaoui, M.K.; Chinram, R. An entropy optimization study of non-Darcian magnetohydrodynamic Williamson nanofluid with nonlinear thermal radiation over a stratified sheet. Proc. Inst. Mech. Eng. Part E J. Process. Mech. Eng. 2021, 235, 1883–1894. [Google Scholar] [CrossRef]
- Ramzan, M.; Ullah, N.; Chung, J.D.; Lu, D.; Farooq, U. Buoyancy effects on the radiative magneto Micropolar nanofluid flow with double stratification, activation energy and binary chemical reaction. Sci. Rep. 2017, 7, 12901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bilal, M.; Ramzan, M.; Mehmood, Y.; Sajid, T.; Shah, S.; Malik, M.Y. A novel approach for EMHD Williamson nanofluid over nonlinear sheet with double stratification and Ohmic dissipation. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2021. [Google Scholar] [CrossRef]
- Pal, D.; Mondal, H. Hydromagnetic non-Darcy flow and heat transfer over a stretching sheet in the presence of thermal radiation and Ohmic dissipation. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1197–1209. [Google Scholar] [CrossRef]
- Tlili, I.; Naseer, S.; Ramzan, M.; Kadry, S.; Nam, Y. Effects of chemical species and nonlinear thermal radiation with 3D Maxwell nanofluid flow with double stratification—An analytical solution. Entropy 2020, 22, 453. [Google Scholar] [CrossRef] [Green Version]
- Zeeshan, A.; Majeed, A. Effect of magnetic dipole on radiative non-Darcian mixed convective flow over a stretching sheet in porous medium. J. Nanofluids 2016, 5, 617–626. [Google Scholar] [CrossRef]


| Authors | Oldroyd-B | Magnetic Dipole | Thermophoretic Particle Deposition | Cattaneo–Christov Heat Flux | Thermal Stratification | Gyrotactic Microorganisms | Chemical Reaction |
|---|---|---|---|---|---|---|---|
| [10] | Yes | No | No | Yes | Yes | No | Yes |
| [17] | No | Yes | Yes | No | No | No | Yes |
| [29] | No | Yes | Yes | Yes | Yes | No | No |
| Present | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| 0.5 | 1.1 | 0.1 | 1.2 | 0.1 | 0.1 | 0.3 | 1.1 | 1.1007748 |
| 0.6 | 1.0969643 | |||||||
| 0.7 | 1.0838647 | |||||||
| 1.2 | 1.1008176 | |||||||
| 1.3 | 1.1008605 | |||||||
| 0.2 | 1.1016806 | |||||||
| 0.3 | 1.1025864 | |||||||
| 1.3 | 1.1460540 | |||||||
| 1.4 | 1.1885233 | |||||||
| 0.2 | 1.1021934 | |||||||
| 0.3 | 1.1036116 | |||||||
| 0.2 | 1.1906204 | |||||||
| 0.3 | 1.2804782 | |||||||
| 0.4 | 1.1006387 | |||||||
| 0.5 | 1.1005585 | |||||||
| 1.2 | 1.1006819 | |||||||
| 1.3 | 1.1006387 | |||||||
| 1.1 | 0.20969592 | |||||||
| 1.2 | 0.2145712 |
| 0.7 | 1.3 | 0.1 | 0.4 | 1.5 | 1.4893254 |
| 0.8 | 1.5668322 | ||||
| 0.9 | 1.6394216 | ||||
| 1.4 | 1.4763646 | ||||
| 1.5 | 1.4634038 | ||||
| 0.2 | 1.4392334 | ||||
| 0.3 | 1.3787588 | ||||
| 0.5 | 1.3458035 | ||||
| 0.6 | 1.245990 | ||||
| 1.6 | 1.4864837 | ||||
| 1.7 | 1.4836393 |
| 0.2 | 0.5 | 1.1 | −0.28919802 |
| 0.3 | −0.28562933 | ||
| 0.4 | −0.2809328 | ||
| 0.6 | −0.34703762 | ||
| 0.7 | −0.40487721 | ||
| 1.2 | −0.31631026 | ||
| 1.3 | −0.3435266 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bashir, S.; Ramzan, M.; Ghazwani, H.A.S.; Nisar, K.S.; Saleel, C.A.; Abdelrahman, A. Magnetic Dipole and Thermophoretic Particle Deposition Impact on Bioconvective Oldroyd-B Fluid Flow over a Stretching Surface with Cattaneo–Christov Heat Flux. Nanomaterials 2022, 12, 2181. https://doi.org/10.3390/nano12132181
Bashir S, Ramzan M, Ghazwani HAS, Nisar KS, Saleel CA, Abdelrahman A. Magnetic Dipole and Thermophoretic Particle Deposition Impact on Bioconvective Oldroyd-B Fluid Flow over a Stretching Surface with Cattaneo–Christov Heat Flux. Nanomaterials. 2022; 12(13):2181. https://doi.org/10.3390/nano12132181
Chicago/Turabian StyleBashir, Seemab, Muhammad Ramzan, Hassan Ali S. Ghazwani, Kottakkaran Sooppy Nisar, C. Ahamed Saleel, and Anas Abdelrahman. 2022. "Magnetic Dipole and Thermophoretic Particle Deposition Impact on Bioconvective Oldroyd-B Fluid Flow over a Stretching Surface with Cattaneo–Christov Heat Flux" Nanomaterials 12, no. 13: 2181. https://doi.org/10.3390/nano12132181
APA StyleBashir, S., Ramzan, M., Ghazwani, H. A. S., Nisar, K. S., Saleel, C. A., & Abdelrahman, A. (2022). Magnetic Dipole and Thermophoretic Particle Deposition Impact on Bioconvective Oldroyd-B Fluid Flow over a Stretching Surface with Cattaneo–Christov Heat Flux. Nanomaterials, 12(13), 2181. https://doi.org/10.3390/nano12132181








