Polarization Control in Integrated Silicon Waveguides Using Semiconductor Nanowires
Abstract
:1. Introduction
2. InP Semiconductor Nanowires
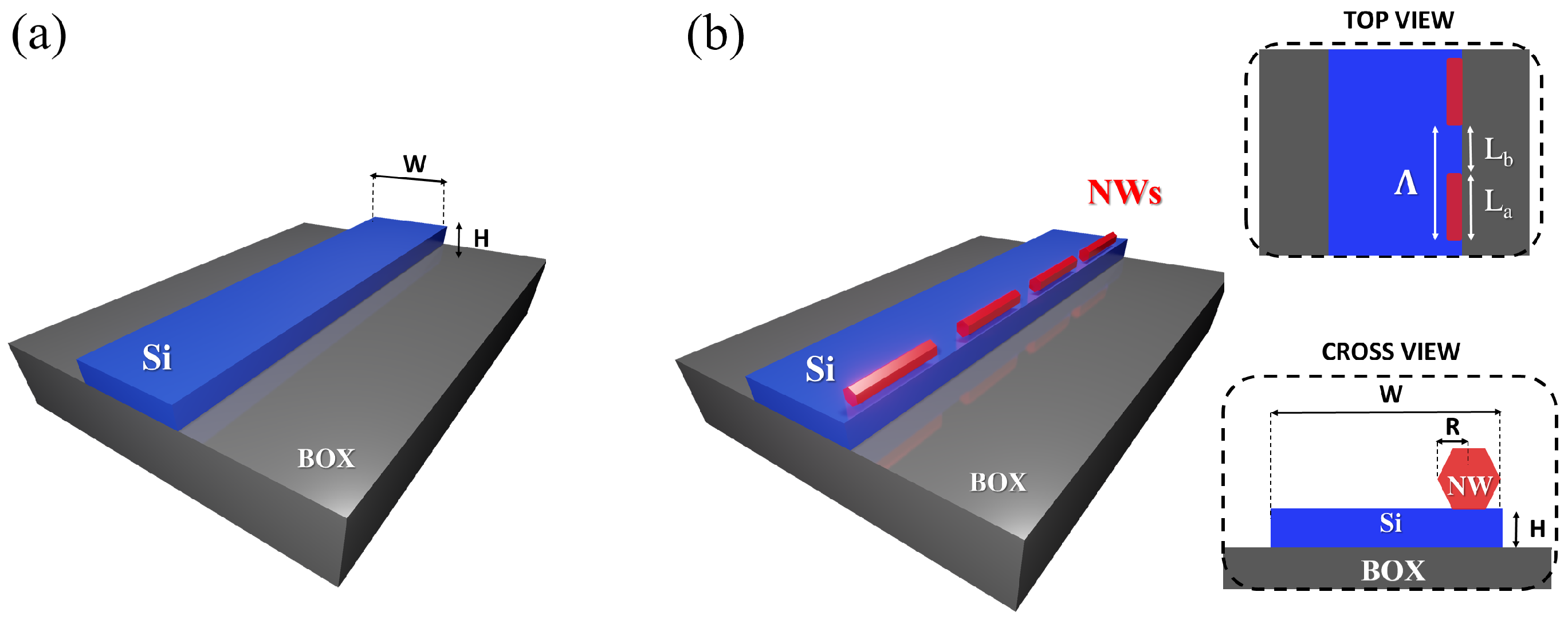
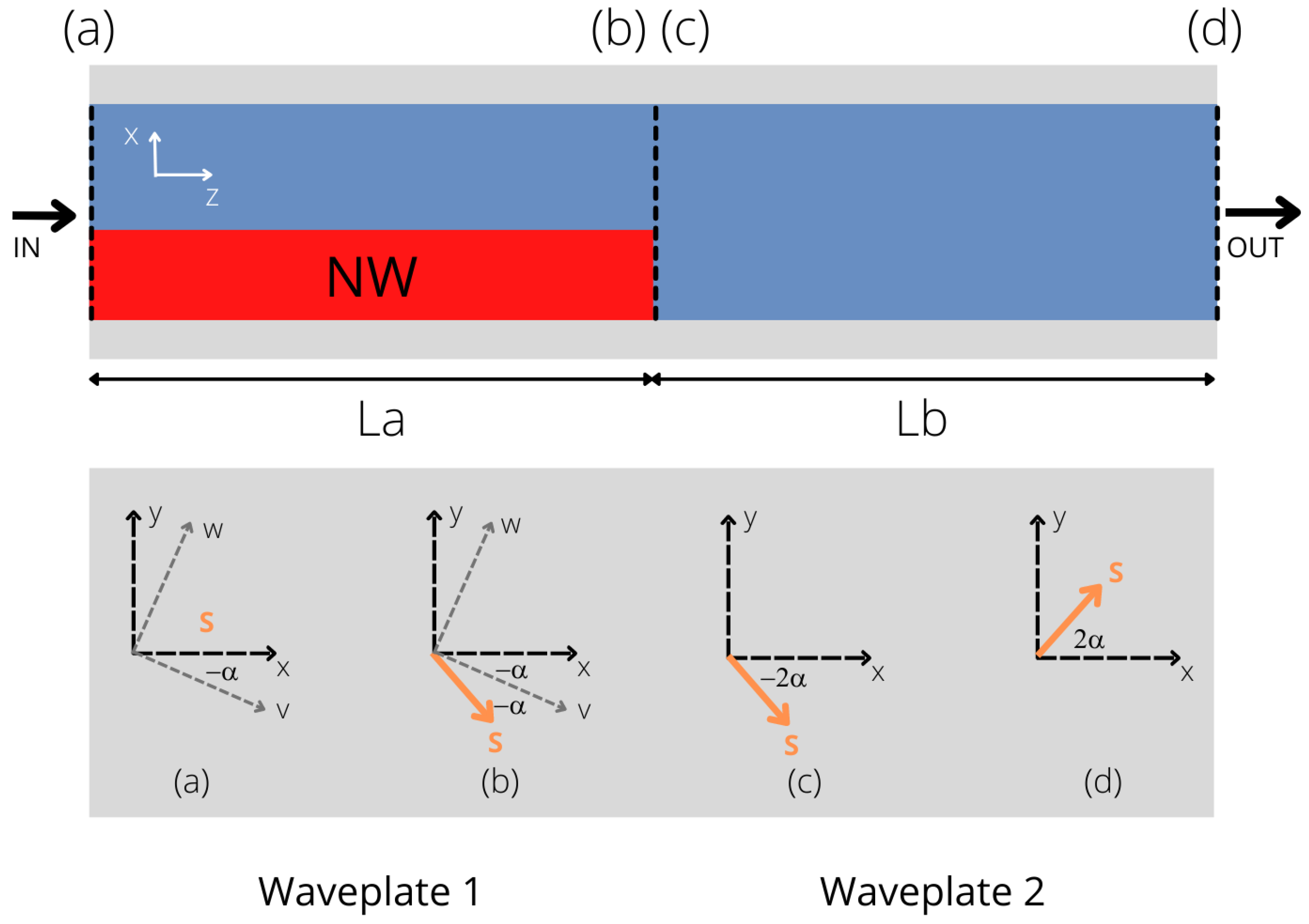
3. Theoretical Background, Device Configuration and Design Strategy
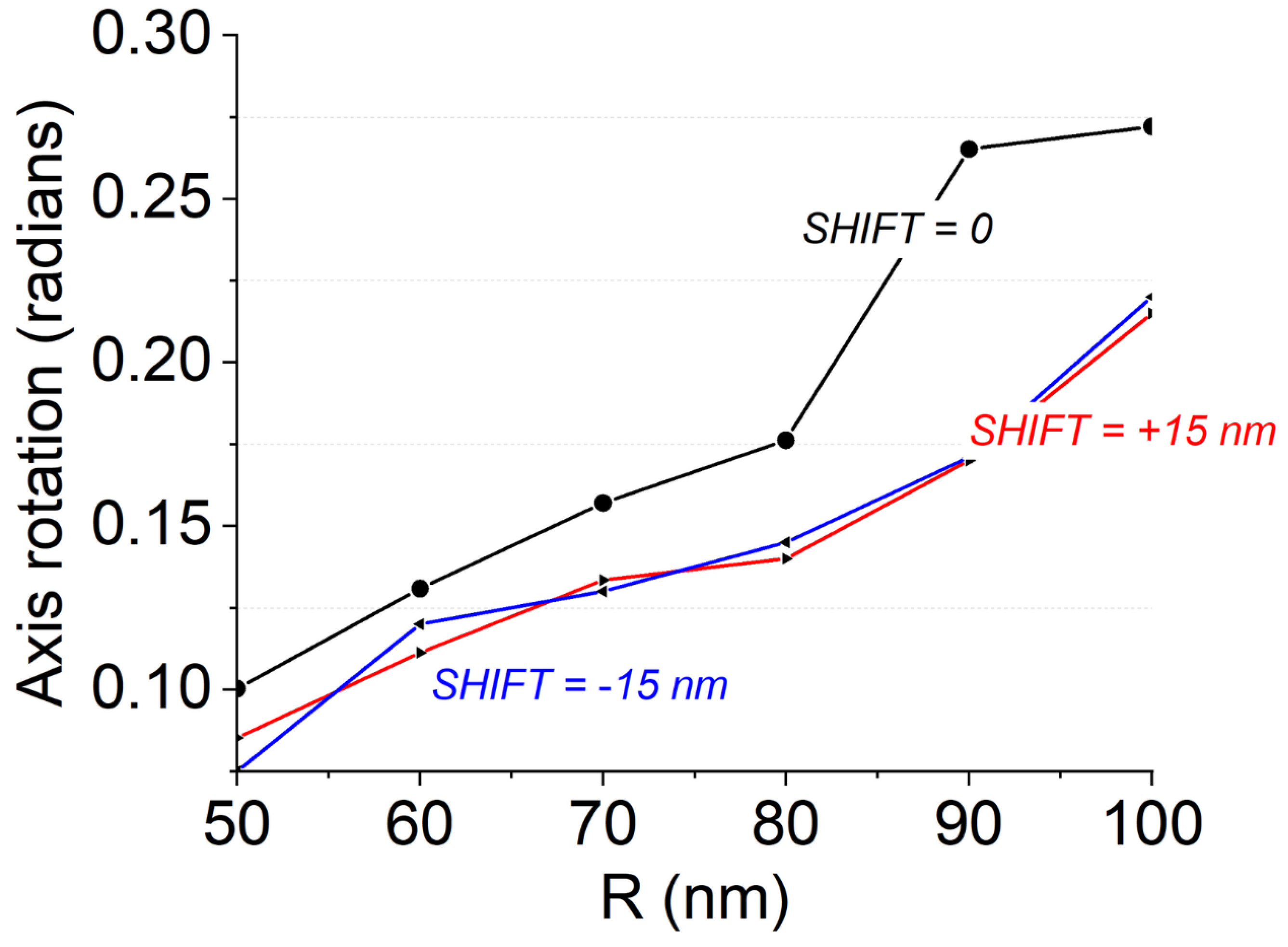
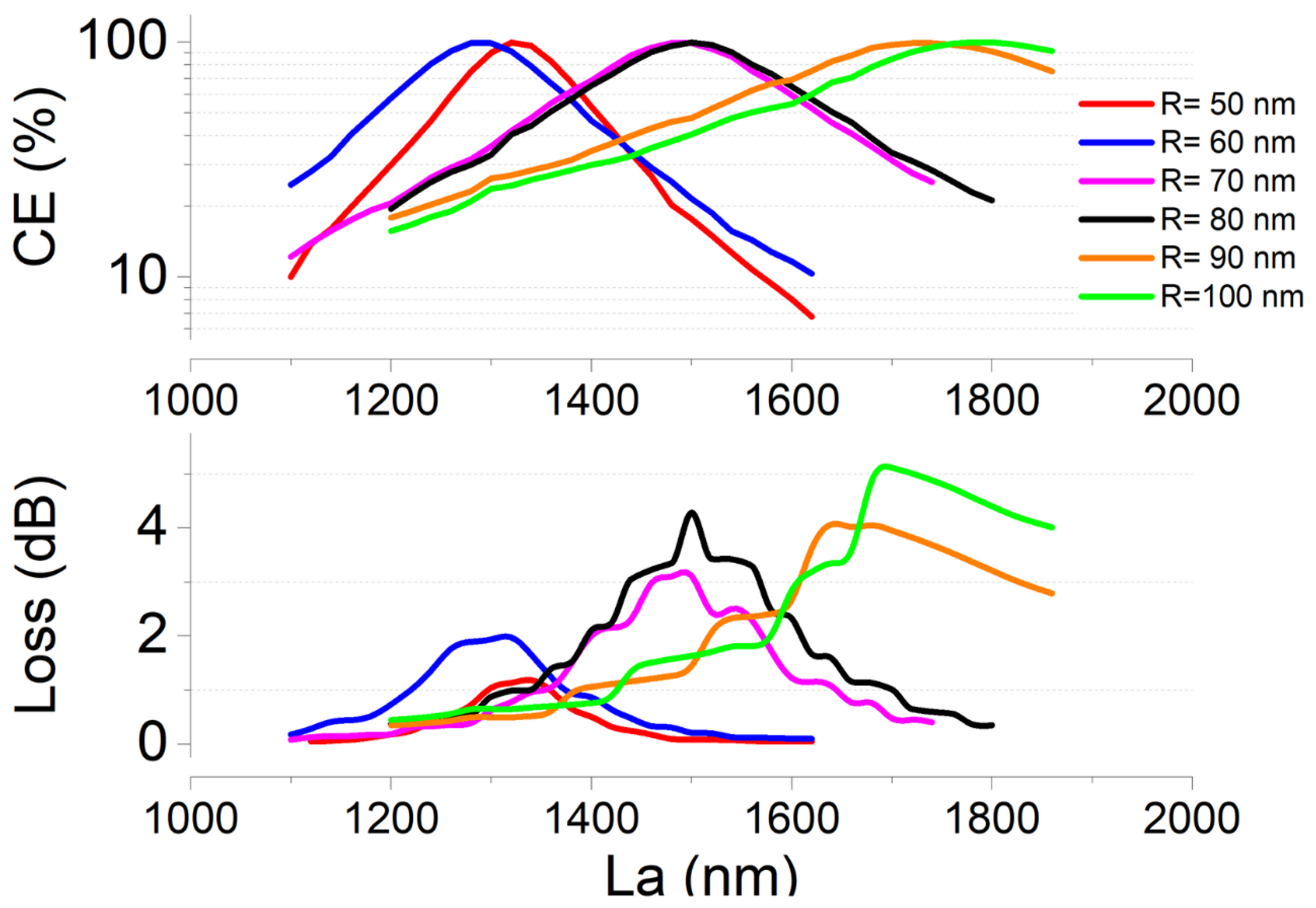
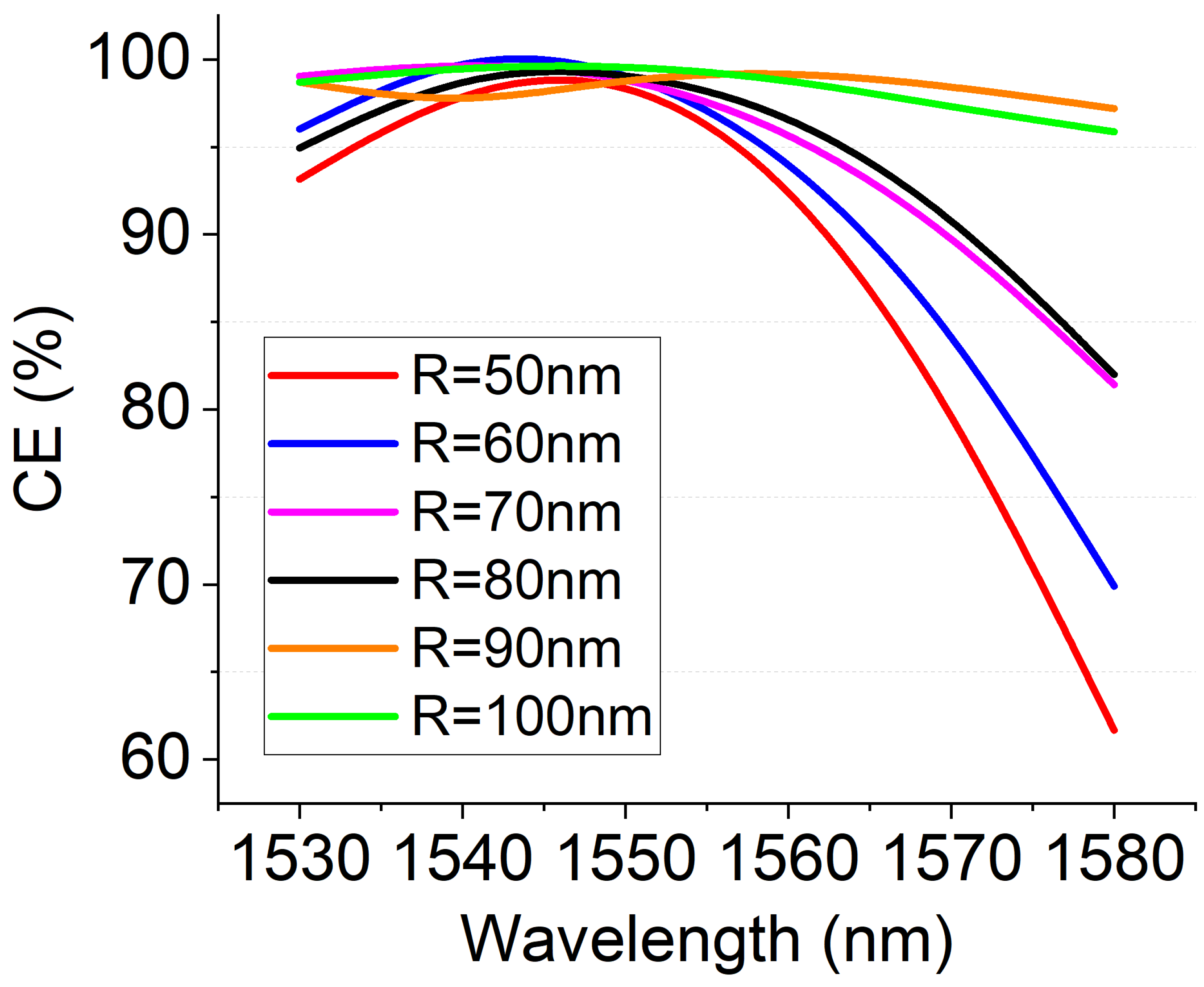
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shastri, B.J.; Tait, A.N.; Ferreira de Lima, T.; Nahmias, M.A.; Peng, H.T.; Prucnal, P.R. Principles of Neuromorphic Photonics; Springer: New York, NY, USA, 2018; pp. 83–118. [Google Scholar] [CrossRef] [Green Version]
- Doerr, C.R. Silicon photonic integration in telecommunications. Front. Phys. 2015, 3, 37. [Google Scholar] [CrossRef]
- Lacava, C.; Strain, M.J.; Minzioni, P.; Cristiani, I.; Sorel, M. Integrated nonlinear Mach Zehnder for 40 Gbit/s all-optical switching. Opt. Express 2013, 21, 21587. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Leuthold, J.; Koos, C.; Freude, W. Nonlinear silicon photonics. Nat. Photonics 2010, 4, 535–544. [Google Scholar] [CrossRef]
- Chagnon, M.; Spasojevic, M.; Adams, R.; Li, J.; Plant, D.V.; Chen, L.R. Wavelength Multicasting at 22-GBaud 16-QAM in a Silicon Nanowire Using Four-Wave Mixing. IEEE Photonics Technol. Lett. 2015, 27, 860–863. [Google Scholar] [CrossRef]
- Martelli, P.; Boffi, P.; Ferrario, M.; Marazzi, L.; Parolari, P.; Siano, R.; Pusino, V.; Minzioni, P.; Cristiani, I.; Langrock, C.; et al. All-optical wavelength conversion of a 100-Gb/s polarization-multiplexed signal. Opt. Express 2009, 17, 17758–17763. [Google Scholar] [CrossRef]
- Caspani, L.; Xiong, C.; Eggleton, B.J.; Bajoni, D.; Liscidini, M.; Galli, M.; Morandotti, R.; Moss, D.J. Integrated sources of photon quantum states based on nonlinear optics. Light. Sci. Appl. 2017, 6, e17100. [Google Scholar] [CrossRef] [PubMed]
- Larger, L.; Soriano, M.C.; Brunner, D.; Appeltant, L.; Gutierrez, J.M.; Pesquera, L.; Mirasso, C.R.; Fischer, I. Photonic information processing beyond Turing: An optoelectronic implementation of reservoir computing. Opt. Express 2012, 20, 3241. [Google Scholar] [CrossRef]
- Willner, A.E.; Khaleghi, S.; Chitgarha, M.R.; Yilmaz, O.F. All-optical signal processing. J. Light. Technol. 2014, 32, 660–680. [Google Scholar] [CrossRef]
- Kaplan, A.E.; Bellanca, G.; van Engelen, J.P.; Jiao, Y.; van der Tol, J.J.G.M.; Bassi, P. Experimental characterization of directional couplers in InP photonic membranes on silicon (IMOS). OSA Contin. 2019, 2, 2844–2854. [Google Scholar] [CrossRef]
- Dai, D.; Liu, L.; Gao, S.; Xu, D.X.; He, S. Polarization management for silicon photonic integrated circuits. Laser Photonics Rev. 2013, 7, 303–328. [Google Scholar] [CrossRef]
- Xu, D.X.; Janz, S.; Cheben, P. Design of polarization-insensitive ring resonators in silicon-on-insulator using MMI couplers and cladding stress engineering. IEEE Photonics Technol. Lett. 2006, 18, 343–345. [Google Scholar] [CrossRef]
- Liu, L.; Ding, Y.; Yvind, K.; Hvam, J.M. Silicon-on-insulator polarization splitting and rotating device for polarization diversity circuits. Opt. Express 2011, 19, 12646–12651. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Deng, H.; Yevick, D.O.; Brooks, C.; Jessop, P.E. Design rules for slanted-angle polarization rotators. J. Light. Technol. 2005, 23, 432–445. [Google Scholar] [CrossRef]
- Dai, D.; Tang, Y.; Bowers, J.E. Mode conversion in tapered submicron silicon ridge optical waveguides. Opt. Express 2012, 20, 13425. [Google Scholar] [CrossRef]
- Huang, W.; Mao, Z.M. Polarization Rotation in Periodic Loaded Rib Waveguides. J. Light. Technol. 1992, 10, 1825–1831. [Google Scholar] [CrossRef]
- van Dam, D.; Abujetas, D.R.; Paniagua-Domínguez, R.; Sánchez-Gil, J.A.; Bakkers, E.P.A.M.; Haverkort, J.E.M.; Gómez Rivas, J. Directional and Polarized Emission from Nanowire Arrays. Nano Lett. 2015, 15, 4557–4563. [Google Scholar] [CrossRef]
- Bermúdez-Ureña, E.; Tutuncuoglu, G.; Cuerda, J.; Smith, C.L.C.; Bravo-Abad, J.; Bozhevolnyi, S.I.; Fontcuberta i Morral, A.; García-Vidal, F.J.; Quidant, R. Plasmonic Waveguide-Integrated Nanowire Laser. Nano Lett. 2017, 17, 747–754. [Google Scholar] [CrossRef] [Green Version]
- Casadei, A.; Llado, E.A.; Amaduzzi, F.; Russo-Averchi, E.; Rüffer, D.; Heiss, M.; Negro, L.D.; Morral, A.F.I. Polarization response of nanowires à la carte. Sci. Rep. 2015, 5, 7651. [Google Scholar] [CrossRef] [Green Version]
- Jia, C.; Lin, Z.; Huang, Y.; Duan, X. Nanowire Electronics: From Nanoscale to Macroscale. Chem. Rev. 2019, 119, 9074–9135. [Google Scholar] [CrossRef]
- Sadre Momtaz, Z.; Servino, S.; Demontis, V.; Zannier, V.; Ercolani, D.; Rossi, F.; Rossella, F.; Sorba, L.; Beltram, F.; Roddaro, S. Orbital Tuning of Tunnel Coupling in InAs/InP Nanowire Quantum Dots. Nano Lett. 2020, 20, 1693–1699. [Google Scholar] [CrossRef] [Green Version]
- Yan, R.; Gargas, D.; Yang, P. Nanowire photonics. Nat. Photonics 2009, 3, 569–576. [Google Scholar] [CrossRef]
- Zagaglia, L.; Demontis, V.; Rossella, F.; Floris, F. Semiconductor nanowire arrays for optical sensing: A numerical insight on the impact of array periodicity and density. Nanotechnology 2021, 32, 335502. [Google Scholar] [CrossRef] [PubMed]
- Battiato, S.; Wu, S.; Zannier, V.; Bertoni, A.; Goldoni, G.; Li, A.; Xiao, S.; Han, X.D.; Beltram, F.; Sorba, L.; et al. Polychromatic emission in a wide energy range from InP-InAs-InP multi-shell nanowires. Nanotechnology 2019, 30, 194004. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.; Peng, K.; Battiato, S.; Zannier, V.; Bertoni, A.; Goldoni, G.; Xie, X.; Yang, J.; Xiao, S.; Qian, C.; et al. Anisotropies of the g-factor tensor and diamagnetic coefficient in crystal-phase quantum dots in InP nanowires. Nano Res. 2019, 12, 2842–2848. [Google Scholar] [CrossRef] [Green Version]
- Floris, F.; Fornasari, L.; Marini, A.; Bellani, V.; Banfi, F.; Roddaro, S.; Ercolani, D.; Rocci, M.; Beltram, F.; Cecchini, M.; et al. Self-Assembled InAs Nanowires as Optical Reflectors. Nanomaterials 2017, 7, 400. [Google Scholar] [CrossRef] [Green Version]
- Goktas, N.I.; Wilson, P.; Ghukasyan, A.; Wagner, D.; McNamee, S.; LaPierre, R. Nanowires for energy: A review. Appl. Phys. Rev. 2018, 5, 041305. [Google Scholar] [CrossRef]
- Rocci, M.; Demontis, V.; Prete, D.; Ercolani, D.; Sorba, L.; Beltram, F.; Pennelli, G.; Roddaro, S.; Rossella, F. Suspended InAs Nanowire-Based Devices for Thermal Conductivity Measurement Using the 3ω Method. J. Mater. Eng. Perform. 2018, 27, 6299–6305. [Google Scholar] [CrossRef]
- Tikhonov, E.S.; Shovkun, D.V.; Ercolani, D.; Rossella, F.; Rocci, M.; Sorba, L.; Roddaro, S.; Khrapai, V.S. Noise thermometry applied to thermoelectric measurements in InAs nanowires. Semicond. Sci. Technol. 2016, 31, 104001. [Google Scholar] [CrossRef] [Green Version]
- Demontis, V.; Rocci, M.; Donarelli, M.; Maiti, R.; Zannier, V.; Beltram, F.; Sorba, L.; Roddaro, S.; Rossella, F.; Baratto, C. Conductometric Sensing with Individual InAs Nanowires. Sensors 2019, 19, 2994. [Google Scholar] [CrossRef] [Green Version]
- Floris, F.; Fornasari, L.; Bellani, V.; Marini, A.; Banfi, F.; Marabelli, F.; Beltram, F.; Ercolani, D.; Battiato, S.; Sorba, L.; et al. Strong Modulations of Optical Reflectance in Tapered Core–Shell Nanowires. Materials 2019, 12, 3572. [Google Scholar] [CrossRef] [Green Version]
- Güniat, L.; Caroff, P.; i Morral, A.F. Vapor Phase Growth of Semiconductor Nanowires: Key Developments and Open Questions. Chem. Rev. 2019, 119, 8958–8971. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Demontis, V.; Zannier, V.; Sorba, L.; Rossella, F. Surface Nano-Patterning for The Bottom-Up Growth of III-V Semiconductor Nanowire Ordered Arrays. Nanomaterials 2021, 11, 2079. [Google Scholar] [CrossRef] [PubMed]
- Barrigón, E.; Heurlin, M.; Bi, Z.; Monemar, B.; Samuelson, L. Synthesis and Applications of III–V Nanowires. Chem. Rev. 2019, 119, 9170–9220. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.P.; Ci, L.; Bur, J.A.; Lin, S.Y.; Ajayan, P.M. Experimental observation of an extremely dark material made by a low-density nanotube array. Nano Lett. 2008, 8, 446–451. [Google Scholar] [CrossRef]
- Cai, W.; Chettiar, U.K.; Kildishev, A.V.; Shalaev, V.M. Optical cloaking with metamaterials. Nat. Photonics 2007, 1, 224–227. [Google Scholar] [CrossRef] [Green Version]
- Pendry, J.B.; Schurig, D.; Smith, D.R. Controlling electromagnetic fields. Science 2006, 312, 1780–1782. [Google Scholar] [CrossRef] [Green Version]
- Mauthe, S.; Baumgartner, Y.; Sousa, M.; Ding, Q.; Rossell, M.D.; Schenk, A.; Czornomaz, L.; Moselund, K.E. High-speed III-V nanowire photodetector monolithically integrated on Si. Nat. Commun. 2020, 11, 4565. [Google Scholar] [CrossRef]
- Stettner, T.; Kostenbader, T.; Ruhstorfer, D.; Bissinger, J.; Riedl, H.; Kaniber, M.; Koblmüller, G.; Finley, J.J. Direct Coupling of Coherent Emission from Site-Selectively Grown III–V Nanowire Lasers into Proximal Silicon Waveguides. ACS Photonics 2017, 4, 2537–2543. [Google Scholar] [CrossRef]
- Güniat, L.; Martí-Sánchez, S.; Garcia, O.; Boscardin, M.; Vindice, D.; Tappy, N.; Friedl, M.; Kim, W.; Zamani, M.; Francaviglia, L.; et al. III–V Integration on Si(100): Vertical Nanospades. ACS Nano 2019, 13, 5833–5840. [Google Scholar] [CrossRef] [Green Version]
- Vukajlovic-Plestina, J.; Kim, W.; Ghisalberti, L.; Varnavides, G.; Tütüncuoglu, G.; Potts, H.; Friedl, M.; Güniat, L.; Carter, W.C.; Dubrovskii, V.G.; et al. Fundamental aspects to localize self-catalyzed III-V nanowires on silicon. Nat. Commun. 2019, 10, 869. [Google Scholar] [CrossRef]
- Bian, Y.; Ren, Q.; Kang, L.; Yue, T.; Werner, P.L.; Werner, D.H. Deep-subwavelength light transmission in hybrid nanowire-loaded silicon nano-rib waveguides. Photonics Res. 2018, 6, 37. [Google Scholar] [CrossRef] [Green Version]
- Zagaglia, L.; Demontis, V.; Rossella, F.; Floris, F. Particle swarm optimization of GaAs-AlGaAS nanowire photonic crystals as two-dimensional diffraction gratings for light trapping. Nano Express 2022, 3, 021001. [Google Scholar] [CrossRef]
- Demontis, V.; Marini, A.; Floris, F.; Sorba, L.; Rossella, F. Engineering the optical reflectance of randomly arranged self-assembled semiconductor nanowires. AIP Conf. Proc. 2020, 2257, 020009. [Google Scholar] [CrossRef]
- Caridad, J.M.; McCloskey, D.; Rossella, F.; Bellani, V.; Donegan, J.F.; Krstić, V. Effective Wavelength Scaling of and Damping in Plasmonic Helical Antennae. ACS Photonics 2015, 2, 675–679. [Google Scholar] [CrossRef]
- Yan, Z.; Han, Y.; Lin, L.; Xue, Y.; Ma, C.; Ng, W.K.; Wong, K.S.; Lau, K.M. A monolithic InP/SOI platform for integrated photonics. Light. Sci. Appl. 2021, 10, 200. [Google Scholar] [CrossRef] [PubMed]
- Ye, X.; Zhang, Y.; Ru, C.; Luo, J.; Xie, S.; Sun, Y. Automated pick-place of silicon nanowires. IEEE Trans. Autom. Sci. Eng. 2013, 10, 554–561. [Google Scholar] [CrossRef]
- Yokoo, A.; Takiguchi, M.; Birowosuto, M.D.; Tateno, K.; Zhang, G.; Kuramochi, E.; Shinya, A.; Taniyama, H.; Notomi, M. Subwavelength Nanowire Lasers on a Silicon Photonic Crystal Operating at Telecom Wavelengths. ACS Photonics 2017, 4, 355–362. [Google Scholar] [CrossRef]
- Hurtado, A.; Jevtics, D.; Guilhabert, B.; Gao, Q.; Tan, H.H.; Jagadish, C.; Dawson, M.D. Novel nanoscale transfer printing technique for precise positioning of nanowire lasers. SPIE Newsroom 2017. [Google Scholar] [CrossRef] [Green Version]
- Dasgupta, N.P.; Sun, J.; Liu, C.; Brittman, S.; Andrews, S.C.; Lim, J.; Gao, H.; Yan, R.; Yang, P. 25th Anniversary Article: Semiconductor Nanowires—Synthesis, Characterization, and Applications. Adv. Mater. 2014, 26, 2137–2184. [Google Scholar] [CrossRef]
- Novotny, C.J.; Yu, P.K.L. Vertically aligned, catalyst-free InP nanowires grown by metalorganic chemical vapor deposition. Appl. Phys. Lett. 2005, 87, 203111. [Google Scholar] [CrossRef]
- Dick, K.A.; Caroff, P. Metal-seeded growth of III–V semiconductor nanowires: Towards gold-free synthesis. Nanoscale 2014, 6, 3006–3021. [Google Scholar] [CrossRef] [PubMed]
- Cui, Y.; Lauhon, L.J.; Gudiksen, M.S.; Wang, J.; Lieber, C.M. Diameter-controlled synthesis of single-crystal silicon nanowires. Appl. Phys. Lett. 2001, 78, 2214–2216. [Google Scholar] [CrossRef]
- McIntyre, P.; i Morral, A.F. Semiconductor nanowires: To grow or not to grow? Mater. Today Nano 2020, 9, 100058. [Google Scholar] [CrossRef]
- Kargar, F.; Debnath, B.; Kakko, J.P.; Säynätjoki, A.; Lipsanen, H.; Nika, D.L.; Lake, R.K.; Balandin, A.A. Direct observation of confined acoustic phonon polarization branches in free-standing semiconductor nanowires. Nat. Commun. 2016, 7, 13400. [Google Scholar] [CrossRef]
- Kitauchi, Y.; Kobayashi, Y.; Tomioka, K.; Hara, S.; Hiruma, K.; Fukui, T.; Motohisa, J. Structural transition in indium phosphide nanowires. Nano Lett. 2010, 10, 1699–1703. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaplan, A.E.; Vitali, V.; Demontis, V.; Rossella, F.; Fontana, A.; Cornia, S.; Petropoulos, P.; Bellani, V.; Lacava, C.; Cristiani, I. Polarization Control in Integrated Silicon Waveguides Using Semiconductor Nanowires. Nanomaterials 2022, 12, 2438. https://doi.org/10.3390/nano12142438
Kaplan AE, Vitali V, Demontis V, Rossella F, Fontana A, Cornia S, Petropoulos P, Bellani V, Lacava C, Cristiani I. Polarization Control in Integrated Silicon Waveguides Using Semiconductor Nanowires. Nanomaterials. 2022; 12(14):2438. https://doi.org/10.3390/nano12142438
Chicago/Turabian StyleKaplan, Ali Emre, Valerio Vitali, Valeria Demontis, Francesco Rossella, Andrea Fontana, Samuele Cornia, Periklis Petropoulos, Vittorio Bellani, Cosimo Lacava, and Ilaria Cristiani. 2022. "Polarization Control in Integrated Silicon Waveguides Using Semiconductor Nanowires" Nanomaterials 12, no. 14: 2438. https://doi.org/10.3390/nano12142438
APA StyleKaplan, A. E., Vitali, V., Demontis, V., Rossella, F., Fontana, A., Cornia, S., Petropoulos, P., Bellani, V., Lacava, C., & Cristiani, I. (2022). Polarization Control in Integrated Silicon Waveguides Using Semiconductor Nanowires. Nanomaterials, 12(14), 2438. https://doi.org/10.3390/nano12142438








