Band Structure Near the Dirac Point in HgTe Quantum Wells with Critical Thickness
Abstract
:1. Introduction
2. Experimental Section
2.1. HgTe Quantum Wells
2.2. Magneto-Optical Technique
3. Modeling
3.1. Optical Drude Conductivity
3.2. Reconstructing the Band Structure
3.3. k·p Model
4. Results
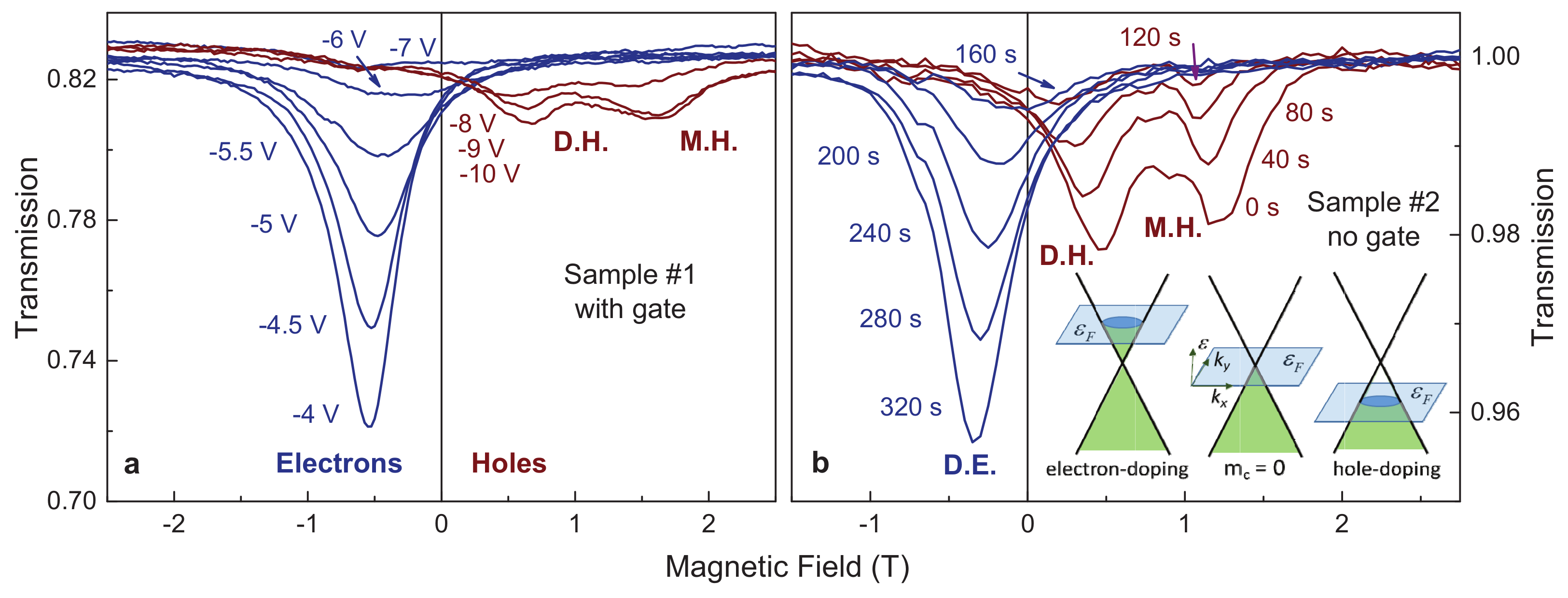
4.1. Cyclotron Resonance
4.2. Drude Parameters
4.3. Electronic Band Structure
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kvon, Z.D.; Danilov, S.N.; Kozlov, D.A.; Zoth, C.; Mikhailov, N.N.; Dvoretskii, S.A.; Ganichev, D.S. Cyclotron resonance of Dirac fermions in HgTe quantum wells. JETP Lett. 2012, 94, 816. [Google Scholar] [CrossRef]
- Bernevig, B.A.; Hughes, T.L.; Zhang, S.-C. Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science 2006, 314, 1757. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- König, M.; Wiedmann, S.; Brüne, C.; Roth, A.; Buhmann, H.; Molenkamp, L.W.; Qi, X.-L.; Zhang, S.-C. Quantum spin Hall insulator state in HgTe quantum wells. Science 2007, 318, 766. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fu, L.; Kane, C.L. Topological insulators with inversion symmetry. Phys. Rev. B 2007, 76, 045302. [Google Scholar] [CrossRef] [Green Version]
- Brüne, C.; Liu, C.X.; Novik, E.G.; Hankiewicz, E.M.; Buhmann, H.; Chen, Y.L.; Qi, X.L.; Shen, Z.X.; Zhang, S.C.; Molenkamp, L.W. Quantum Hall effect from the topological surface states of strained bulk HgTe. Phys. Rev. Lett. 2011, 106, 126803. [Google Scholar] [CrossRef]
- Gospodarič, J.; Dziom, V.; Shuvaev, A.; Dobretsova, A.A.; Mikhailov, N.N.; Kvon, Z.D.; Novik, E.G.; Pimenov, A. Band structure of a HgTe-based three-dimensional topological insulator. Phys. Rev. B 2020, 102, 115113. [Google Scholar] [CrossRef]
- Rogalski, A. Infrared detectors: Status and trends. Prog. Quantum Electron. 2003, 27, 59. [Google Scholar] [CrossRef]
- Ruffenach, S.; Kadykov, A.; Rumyantsev, V.V.; Torres, J.; Coquillat, D.; However, D.; Krishtopenko, S.S.; Consejo, C.; Knap, W.; Winnerl, S.; et al. HgCdTe-based heterostructures for terahertz photonics. APL Mater. 2017, 5, 035503. [Google Scholar] [CrossRef] [Green Version]
- Liu, B.; Sharma, M.; Yu, J.; Shendre, S.; Hettiarachchi, C.; Sharma, A.; Yeltik, A.; Wang, L.; Sun, H.; Dang, C.; et al. Light- emitting diodes with cu-doped colloidal quantum wells: From ultrapure green, tunable dual-emission to white light. Small 2019, 15, 1901983. [Google Scholar] [CrossRef]
- Kvon, Z.D.; Olshanetsky, E.B.; Kozlov, D.A.; Mikhailov, N.N.; Dvoretskii, S.A. Two-dimensional electron-hole system in a HgTe-based quantum well. JETP Lett. 2008, 87, 502. [Google Scholar] [CrossRef]
- Ortner, K.; Zhang, X.C.; Pfeuffer-Jeschke, A.; Becker, C.R.; Landwehr, G.; Molenkamp, L.W. Valence band structure of HgTe/Hg1 x Cdx Te single quantum wells. Phys. Rev. B 2002, 66, 075322. [Google Scholar] [CrossRef]
- Gospodarič, J.; Shuvaev, A.; Mikhailov, N.N.; Kvon, Z.D.; Novik, E.G.; Pimenov, A. Energy spectrum of semimetallic HgTe quantum wells. Phys. Rev. B 2021, 104, 115307. [Google Scholar] [CrossRef]
- Damascelli, A.; Hussain, Z.; Shen, Z.X. Angle-resolved photoemission studies of the cuprate superconductors. Rev. Mod. Phys. 2003, 75, 473. [Google Scholar] [CrossRef] [Green Version]
- Shuvaev, A.M.; Dziom, V.; Mikhailov, N.N.; Kvon, Z.D.; Shao, Y.; Basov, D.N.; Pimenov, A. Band structure of a two-dimensional Dirac semimetal from cyclotron resonance. Phys. Rev. B 2017, 96, 155434. [Google Scholar] [CrossRef] [Green Version]
- Varavin, V.; Dvoretskii, S.; Mikhailov, N.; Remesnik, V.; Sabinina, I.; Sidorov, Y.; Shvets, V.; Yakushev, M.; Latyshev, A. Molecular beam epitaxy of CdHgTe: Current state and horizons, Optoelectron. Instrum. Data Process. 2020, 56, 456. [Google Scholar]
- McRae, A.; Tayari, V.; Porter, J.; Champagne, A. Giant electron-hole transport asymmetry in ultra-short quantum transistors. Nat. Commun. 2017, 8, 15491. [Google Scholar] [CrossRef] [Green Version]
- However, D.; Mittendorff, M.; Consejo, C.; Teppe, F.; Mikhailov, N.; Dvoretskii, S.; Faugeras, C.; Winnerl, S.; Helm, M.; Knap, W.; et al. Suppressed Auger scattering and tunable light emission of Landau-quantized massless Kane electrons. Nat. Photon. 2019, 13, 783. [Google Scholar]
- Neto, A.H.C.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.; Chernikov, A.; Glazov, M.M.; Heinz, T.F.; Marie, X.; Amand, T.; Urbaszek, B. Colloquium: Excitons in atomically thin transition metal dichalcogenides. Rev. Mod. Phys. 2018, 90, 021001. [Google Scholar] [CrossRef] [Green Version]
- Yu, J.; Dang, C. Colloidal metal chalcogenide quantum wells for laser applications. Cell Rep. Phys. Sci. 2021, 2, 100308. [Google Scholar] [CrossRef]
- Ikonnikov, A.V.; Zholudev, M.S.; Spirin, K.E.; Lastovkin, A.A.; Maremyanin, K.V.; Aleshkin, V.Y.; Gavrilenko, V.I.; Drachenko, O.; Helm, M.; Wosnitza, J.; et al. Cyclotron resonance and interband optical transitions in HgTe/CdTe (0 1 3) quantum well heterostructures. Semicond. Sci. Technol. 2011, 26, 125011. [Google Scholar] [CrossRef]
- Olbrich, P.; Zoth, C.; Vierling, P.; Dantscher, K.-M.; Budkin, G.V.; Tarasenko, S.A.; Bel’kov, V.V.; Kozlov, D.A.; Kvon, Z.D.; Mikhailov, N.N.; et al. Giant photocurrents in a Dirac fermion system at cyclotron resonance. Phys. Rev. B 2013, 87, 235439. [Google Scholar] [CrossRef] [Green Version]
- Zoth, C.; Olbrich, P.; Vierling, P.; Dantscher, K.-M.; Bel’kov, V.V.; Semina, M.A.; Glazov, M.M.; Golub, L.E.; Kozlov, D.A.; Kvon, Z.D.; et al. Quantum oscillations of photocurrents in HgTe quantum wells with Dirac and parabolic dispersions. Phys. Rev. B 2014, 90, 205415. [Google Scholar] [CrossRef] [Green Version]
- Dziom, V.; Shuvaev, A.; Mikhailov, N.N.; Pimenov, A. Terahertz properties of Dirac fermions in HgTe films with optical doping. 2D Mater. 2017, 4, 024005. [Google Scholar] [CrossRef] [Green Version]
- Shuvaev, A.M.; Astakhov, G.V.; Brüne, C.; Buhmann, H.; Molenkamp, L.W.; Pimenov, A. Terahertz magneto-optical spectroscopy in HgTe thin films. Semicond. Sci. Technol. 2012, 27, 124004. [Google Scholar] [CrossRef]
- Novik, E.G.; Pfeuffer-Jeschke, A.; Jungwirth, T.; Latussek, V.; Becker, C.R.; Landwehr, G.; Buhmann, H.; Molenkamp, L.W. Band structure of semimagnetic Hg1 yMnyTe quantum wells. Phys. Rev. B 2005, 72, 035321. [Google Scholar] [CrossRef] [Green Version]
- Tarasenko, S.A.; Durnev, M.V.; Nestoklon, M.O.; Ivchenko, E.L.; Luo, J.-W.; Zunger, A. Split Dirac cones in HgTe/CdTe quantum wells due to symmetry-enforced level anticrossing at interfaces. Phys. Rev. B 2015, 91, 081302. [Google Scholar] [CrossRef] [Green Version]
- Winkler, R. Spin-Orbit Coupling Effects in Two-Dimensional Electron and Hole Systems; Springer Tracts in Modern Physics; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Gusev, G.M.; Kvon, Z.D.; Kozlov, D.A.; Olshanetsky, E.B.; Entin, M.V.; Mikhailov, N.N. Transport through the network of topological channels in HgTe based quantum well. 2D Mater. 2021, 9, 015021. [Google Scholar] [CrossRef]
- Kozlov, D.A.; Kvon, Z.D.; Mikhailov, N.N.; Dvoretskii, S.A. Quantum Hall effect in a system of gapless Dirac fermions in HgTe quantum wells. JETP Lett. 2015, 100, 724. [Google Scholar] [CrossRef]
- Kozlov, D.A.; Savchenko, M.L.; Ziegler, J.; Kvon, Z.D.; Mikhailov, N.N.; Dvoretskii, S.A.; Weiss, D. Capacitance spectroscopy of a system of gapless Dirac fermions in a HgTe quantum well. JETP Lett. 2016, 104, 859. [Google Scholar] [CrossRef]
- Dobretsova, A.A.; Kvon, Z.D.; Braginskii, L.S.; Entin, M.V.; Mikhailov, N.N. Mobility of Dirac electrons in HgTe quantum wells. JETP Lett. 2016, 104, 388. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197. [Google Scholar] [CrossRef] [PubMed]
- Kvon, Z.-D.; Danilov, S.N.; Mikhailov, N.N.; Dvoretsky, S.A.; Prettl, W.; Ganichev, S.D. Cyclotron resonance photoconductivity of a two-dimensional electron gas in HgTe quantum wells. Physica E 2008, 40, 1885–1887. [Google Scholar] [CrossRef] [Green Version]
- Ikonnikov, A.; Lastovkin, A.; Spirin, K.; Zholudev, M.; Rumyantsev, V.; Maremyanin, K.; Antonov, A.; Aleshkin, V.; Gavrilenko, V.; Dvoretskii, S.; et al. Terahertz spectroscopy of quantum well narrow-bandgap HgTe/CdTe- based heterostructures. JETP Lett. 2010, 92, 756. [Google Scholar] [CrossRef]
- Kozlov, D.A.; Kvon, Z.D.; Mikhailov, N.N.; Dvoretsky, S.A. Weak localization of Dirac fermions in HgTe quantum wells. JETP Lett. 2013, 96, 730. [Google Scholar] [CrossRef]
- Minkov, G.M.; Aleshkin, V.Y.; Rut, O.E.; Sherstobitov, A.A.; Germanenko, A.V.; Dvoretski, S.A.; Mikhailov, N.N. Valence band energy spectrum of HgTe quantum wells with an inverted band structure. Phys. Rev. B 2017, 96, 035310. [Google Scholar] [CrossRef] [Green Version]
- Durnev, M.V.; Tarasenko, S.A. Optical properties of helical edge channels in zinc-blende-type topological insulators: Selection rules, circular and linear dichroism, circular and linear photocurrents. J. Phys. Cond. Matter 2019, 31, 035301. [Google Scholar] [CrossRef] [Green Version]
- Durnev, M.V.; Tarasenko, S.A. Edge photogalvanic effect caused by optical alignment of carrier momenta in two-dimensional Dirac materials. Phys. Rev. B 2021, 103, 165411. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shuvaev, A.; Dziom, V.; Gospodarič, J.; Novik, E.G.; Dobretsova, A.A.; Mikhailov, N.N.; Kvon, Z.D.; Pimenov, A. Band Structure Near the Dirac Point in HgTe Quantum Wells with Critical Thickness. Nanomaterials 2022, 12, 2492. https://doi.org/10.3390/nano12142492
Shuvaev A, Dziom V, Gospodarič J, Novik EG, Dobretsova AA, Mikhailov NN, Kvon ZD, Pimenov A. Band Structure Near the Dirac Point in HgTe Quantum Wells with Critical Thickness. Nanomaterials. 2022; 12(14):2492. https://doi.org/10.3390/nano12142492
Chicago/Turabian StyleShuvaev, Alexey, Vlad Dziom, Jan Gospodarič, Elena G. Novik, Alena A. Dobretsova, Nikolay N. Mikhailov, Ze Don Kvon, and Andrei Pimenov. 2022. "Band Structure Near the Dirac Point in HgTe Quantum Wells with Critical Thickness" Nanomaterials 12, no. 14: 2492. https://doi.org/10.3390/nano12142492
APA StyleShuvaev, A., Dziom, V., Gospodarič, J., Novik, E. G., Dobretsova, A. A., Mikhailov, N. N., Kvon, Z. D., & Pimenov, A. (2022). Band Structure Near the Dirac Point in HgTe Quantum Wells with Critical Thickness. Nanomaterials, 12(14), 2492. https://doi.org/10.3390/nano12142492






