Quantum Coherence and Total Phase in Semiconductor Microcavities for Multi-Photon Excitation
Abstract
:1. Introduction
2. Physical Model
3. Coherence, Fidelity and Total Phase
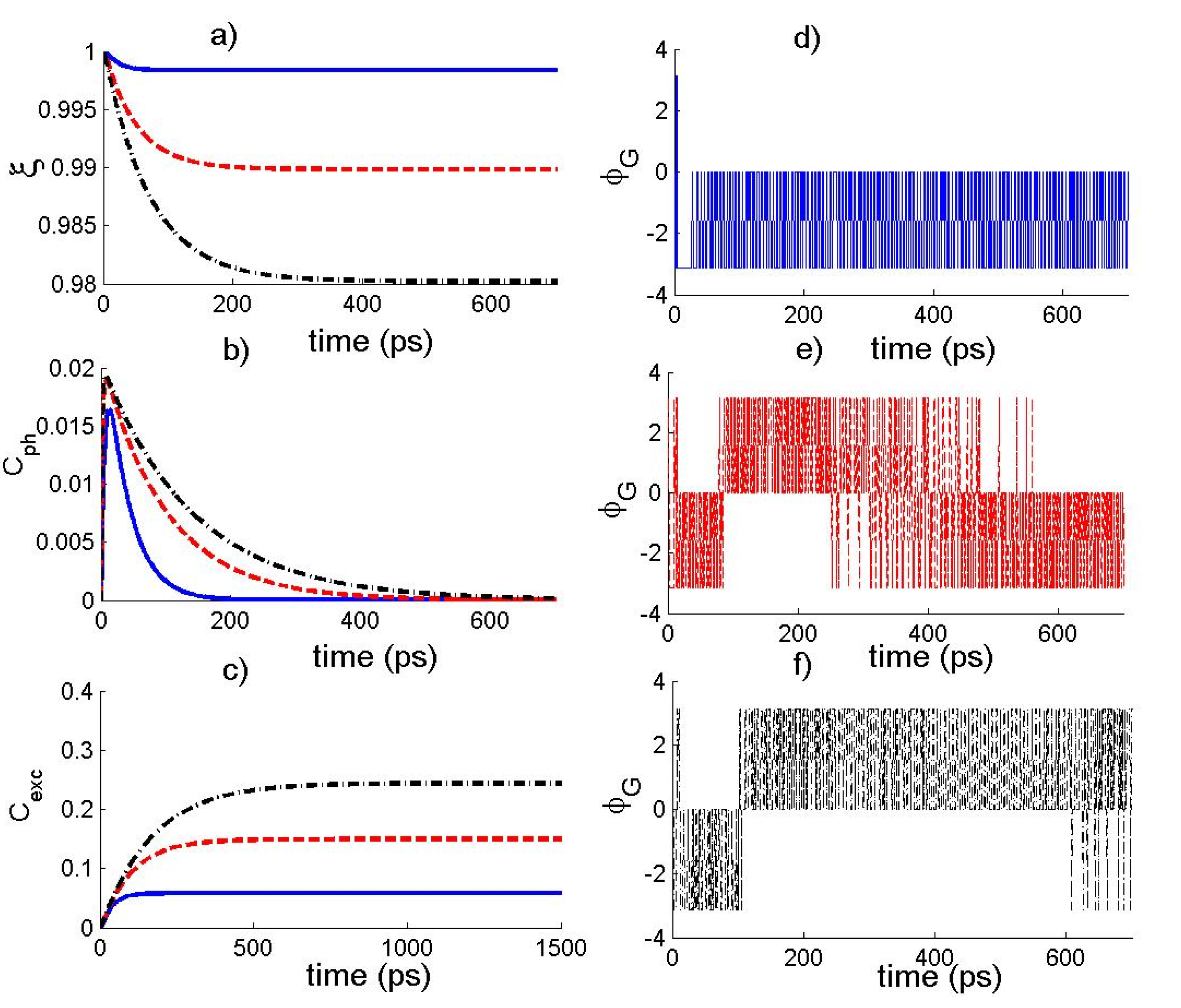
4. Numerical Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Walls, D.F.; Millburn, G.J. Quantum Optics; Springer: New York, NY, USA, 2010. [Google Scholar]
- Levi, F.; Mintert, F. A quantitative theory of coherent delocalization. New J. Phys. 2014, 16, 033007. [Google Scholar] [CrossRef]
- Bera, M.N.; Qureshi, T.; Siddiqui, M.A.; Pati, A.K. Duality of quantum coherence and path distinguishability. Phys. Rev. A 2015, 92, 012118. [Google Scholar] [CrossRef] [Green Version]
- Monda, D.; Datta, C.; Sazim, S. Quantum coherence sets the quantum speed limit for mixed states. Phys. Lett. A 2016, 380, 689–695. [Google Scholar] [CrossRef] [Green Version]
- Shao, L.H.; Xi, Z.J.; Fan, H.; Li, Y.M. Fidelity and trace-norm distances for quantifying coherence. Phys. Rev. A 2015, 91, 042120. [Google Scholar] [CrossRef] [Green Version]
- Yuan, X.; Zhou, H.Y.; Cao, Z.; Ma, X.F. Intrinsic randomness as a measure of quantum coherence. Phys. Rev. A 2015, 92, 022124. [Google Scholar] [CrossRef] [Green Version]
- Rana, S.; Parashar, P.; Lewenstein, M. Trace-distance measure of coherence. Phys. Rev. A 2016, 93, 012110. [Google Scholar] [CrossRef] [Green Version]
- Chitambar, E.; Gour, G. Critical examination of incoherent operations and a physically consistent resource theory of quantum coherence. Phys. Rev. Lett. 2016, 117, 030401. [Google Scholar] [CrossRef] [Green Version]
- Winter, A.; Yang, D. Operational resource theory of coherence. Phys. Rev. Lett. 2016, 116, 120404. [Google Scholar] [CrossRef] [Green Version]
- Baumgratz, T.; Cramer, M.; Plenio, M.B. Quantifying coherence. Phys. Rev. Lett. 2014, 113, 140401. [Google Scholar] [CrossRef] [Green Version]
- Streltsov, A.; Singh, U.; Dhar, H.S.; Bera, M.N.; Adesso, G. Measuring quantum coherence with entanglement. Phys. Rev. Lett. 2015, 115, 020403. [Google Scholar] [CrossRef] [Green Version]
- Napoli, C.; Bromley, T.R.; Cianciaruso, M.; Piani, M.; Johnston, N.; Adesso, G. Robustness of coherence: An operational and observable measure of quantum coherence. Phys. Rev. Lett. 2016, 116, 150502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- El-Qahtani, Z.M.H.; Abdel-Khalek, S.; Berrada, K. Quantum Coherence and Degree of Mixedness for a System of Two Superconducting Qubits Under Decohe\rence Conditions. J. Russ. Laser Res. 2022, 43, 139. [Google Scholar] [CrossRef]
- Li, B.-M.; Hu, M.-L.; Fan, H. Nonlocal advantage of quantum coherence and entanglement of two spins under intrinsic decoherence. Chin. Phys. B 2021, 30, 070307. [Google Scholar] [CrossRef]
- Du, S.P.; Bai, Z.F.; Qi, X.F. Coherence measures and optimal conversion for coherent states. Quantum Inf. Comput. 2015, 15, 1307. [Google Scholar] [CrossRef]
- Korotkov, A.N.; Keane, K. Decoherence suppression by quantum measurement reversal. Phys. Rev. A 2010, 81, 040103. [Google Scholar] [CrossRef] [Green Version]
- Ming, F.; Song, X.-K.; Ling, J.; Ye, L.; Wang, D. Quantification of quantumness in neutrino oscillations. Eur. Phys. J. C 2020, 80, 275. [Google Scholar] [CrossRef]
- Yuan, X.; Bai, G.; Peng, T.; Ma, X. Quantum uncertainty relation using coherence. Phys. Rev. A 2017, 96, 032313. [Google Scholar] [CrossRef] [Green Version]
- Xie, B.; Ming, F.; Wang, D.; Ye, L.; Chen, J. Optimized entropic uncertainty relations for multiple measurements. Phys. Rev. A 2021, 104, 062204. [Google Scholar] [CrossRef]
- Ming, F.; Wang, D.; Fan, X.-G.; Shi, W.; Ye, L.; Chen, J. Improved tripartite uncertainty relation with quantum memory. Phys. Rev. A 2020, 102, 012206. [Google Scholar] [CrossRef]
- Yang, Y.; Sun, W.; Shi, W.; Ming, F.; Wang, D.; Ye, L. Dynamical characteristic of measurement uncertainty under Heisenberg spin models with Dzyaloshinskii–Moriya interactions. Front. Phys. 2019, 14, 31601. [Google Scholar] [CrossRef]
- Pancharatnam, S. Generalized theory of interference and its applications. Proc. Indian Acad. Sci. A 1956, 44, 247. [Google Scholar] [CrossRef]
- Berry, M.V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. London Ser. A 1984, 392, 45. [Google Scholar]
- Jordan, T.F. Berry phases for partial cycles. Phys. Rev. A 1988, 38, 1590. [Google Scholar] [CrossRef] [PubMed]
- Samuel, J.; Bhandari, R. General setting for Berry’s phase. Phys. Rev. Lett. 1988, 60, 2339. [Google Scholar] [CrossRef] [PubMed]
- Berry, M.V. The adiabatic phase and Pancharatnam’s phase for polarized light. J. Mod. Opt. 1987, 34, 1401. [Google Scholar] [CrossRef]
- Weinfurter, H.; Banudrek, G. Measurement of Berry’s phase for noncyclic evolution. Phys. Rev. Lett. 1990, 64, 1318. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.-S.; Li, H.-Z. Observable effects of the quantum adiabatic phase for noncyclic evolution. Phys. Rev. B 1988, 38, 11907. [Google Scholar] [CrossRef]
- Tarasov, V.E. Quantum computer with mixed states and four-valued logic. J. Phys. A 2002, 35, 5207. [Google Scholar] [CrossRef] [Green Version]
- Ekert, A.K.; Ericsson, M.; Hayden, P.; Inamori, H.; Jones, J.A.; Oi, D.K.L.; Vedral, V. Geometric quantum computation. J. Mod. Opt. 2000, 47, 2501. [Google Scholar] [CrossRef]
- Abdel-Aty, M. The Pancharatnam phase of a two-level atom in the presence of another two-level atom in a cavity. J. Opt. B 2003, 5, 349. [Google Scholar] [CrossRef]
- Lawande, Q.V.; Lawande, S.V.; Joshi, A. Pancharatnam phase for a system of a two-level atom interacting with a quantized field in a cavity. Phys. Lett. A 1999, 251, 164. [Google Scholar] [CrossRef]
- Berrada, K.; Ooi, H.R.; Abdel-Khalek, A. Geometric phase and entanglement of Raman photon pairs in the presence of photonic band gap. J. Appl. Phys. 2015, 117, 124904. [Google Scholar] [CrossRef] [Green Version]
- Pati, A. Geometric phases for mixed states during unitary and non-unitary evolutions. Int. J. Quantum Inf. 2003, 1, 135. [Google Scholar] [CrossRef]
- Scully, M.O.; Zubairy, M.S. Quantum Optics; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Gerry, C.; Knight, P. Introductory Quantum Optics; Cambridge University Press: Cambridge, NY, USA, 2006. [Google Scholar]
- Pieczarka, M.; Estrecho, E.; Boozarjmehr, M.; Bleu, O.; Steger, M.; West, K.; Pfeiffer, L.N.; Snoke, D.W.; Levinsen, J.; Parish, M.M.; et al. Observation of quantum depletion in a non-equilibrium exciton–polariton condensate. Nat. Commun. 2020, 11, 429. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Berger, B.; Asmann, M.; Driben, R.; Meier, T.; Schneider, C.; Hofling, S.; Schumacher, S. Realization of all-optical vortex switching in exciton-polariton condensates. Nat. Commun. 2020, 11, 897. [Google Scholar] [CrossRef] [Green Version]
- Estrecho, E.; Gao, T.; Bobrovska, N.; Fraser, M.D.; Steger, M.; Pfeiffer, L.; West, K.; Liew, T.C.H.; Matuszewski, M.; Snoke, D.W.; et al. Direct measurement of polariton-polariton interaction strength in the Thomas-Fermi regime of exciton-polariton condensation. Nat. Commun. 2018, 9, 1. [Google Scholar] [CrossRef] [Green Version]
- Klaas, M.; Schlottmann, E.; Flayac, H.; Laussy, F.P.; Gericke, F.; Schmidt, M.; Helversen, M.v.; Beyer, J.; Brodbeck, S.; Suchomel, H.; et al. Photon-Number-Resolved Measurement of an Exciton-Polariton Condensate. Phys. Rev. Lett. 2018, 121, 047401. [Google Scholar] [CrossRef] [Green Version]
- Adiyatullin, A.F.; Anderson, M.D.; Busi, P.V.; Abbaspour, H.; Andre, R.; Portella-Oberli, M.T.; Deveaud, B. Temporally resolved second-order photon correlations of exciton-polariton Bose-Einstein condensate formation. Appl. Phys. Lett. 2015, 107, 221107. [Google Scholar] [CrossRef] [Green Version]
- Carreno, J.C.L.; SanchezMunoz, C.; Sanvitto, D.; del Valle, E.; Laussy, F.P. Exciting Polaritons with Quantum Light. Phys. Rev. Lett. 2015, 115, 196402. [Google Scholar] [CrossRef] [Green Version]
- Delteil, A.; Fink, T.; Schade, A.; Hofling, S.; Schneider, C.; Imamoglu, A. Towards polariton blockade of confined exciton-polaritons. Nat. Mater. 2019, 18, 219. [Google Scholar] [CrossRef] [Green Version]
- Munoz-Matutano, G.; Wood, A.; Johnsson, M.; Vidal, X.; Baragiola, B.Q.; Reinhard, A.; Lemaitre, A.; Bloch, J.; Amo, A.; Nogues, G.; et al. Emergence of quantum correlations from interacting fibre-cavity polaritons. Nat. Mater. 2019, 18, 213. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cuevas, A.; Carreno, J.C.L.; Silva, B.; de Giorgi, M.; Suarez-Forero, D.G.; Munoz, C.S.; Fieramosca, A.; Cardano, F.; Marrucci, L.; Tasco, V.; et al. Carbon Nanotube Devices for Quantum Technology—PMC. Sci. Adv. 2018, 4, eaao6814. [Google Scholar] [CrossRef] [Green Version]
- Baas, A.; Karr, J.P.; Eleuch, H.; Giacobino, E. Optical bistability in semiconductor microcavities. Phys. Rev. A 2004, 69, 023809. [Google Scholar] [CrossRef] [Green Version]
- Luders, C.; Pukrop, M.; Rozas, E.; Schneider, C.; Hofling, S.; Sperling, J.; Schumacher, S.; Asmann, M. Quantifying Quantum Coherence in Polariton Condensates. Phys. Rev. X Quantum 2021, 2, 030320. [Google Scholar] [CrossRef]
- Ciuti, C.; Savona, V.; Piermarocchi, C. Threshold behavior in the collision broadening of microcavity polaritons. Phys. Rev. B 1998, 58, R10123. [Google Scholar] [CrossRef]
- Tassone, F.; Yamamoto, Y. Exciton-exciton scattering dynamics in a semiconductor microcavity and stimulated scattering into polaritons. Phys. Rev. B 1999, 59, 10830. [Google Scholar] [CrossRef]
- Haug, H. On the phase transitions for the electronic excitations in semiconductors. Z. Phys. B 1976, 24, 351. [Google Scholar] [CrossRef]
- Hanamura, E. Theory of Many Wannier Excitons. J. Phys. Soc. Jpn. 1974, 37, 1545. [Google Scholar] [CrossRef]
- Naguyen, A.B. Exciton-induced squeezed state of light in semiconductors. Phys. Rev. B 1993, 48, 11732. [Google Scholar]
- Eleuch, H. Quantum Trajectories and Autocorrelation Function in Semiconductor Microcavity. Appl. Math. Inf. Sci. 2009, 3, 185. [Google Scholar]
- Giacobino, E.; Karr, J.-P.; Messin, G.; Eleuch, H.; Baas, A. Quantum optical effects in semiconductor microcavities. Comptes Rendus Phys. 2002, 3, 41. [Google Scholar] [CrossRef]
- Ciuti, C.; Schwendimann, P.; Deveaud, B.; Quattropani, A. Theory of the angle-resonant polariton amplifier. Phys. Rev. B 2000, 62, R4825. [Google Scholar] [CrossRef]
- Eleuch, H. Photon statistics of light in semiconductor microcavities. J. Phys. B 2008, 41, 055502. [Google Scholar] [CrossRef]
- Eleuch, H.; Bennaceur, R.J. An optical soliton pair among absorbing three-level atoms. Opt. A 2003, 5, 528. [Google Scholar] [CrossRef]
- Louisell, W.H. Quantum Statistical Properties of Radiation; Wiley: New York, NY, USA, 1973. [Google Scholar]
- Bousse, N.E.; Miller, J.M.L.; Alter, A.L.; Cameron, C.P.; Kwon, H.K.; Vukasin, G.D.; Kenny, T.W. Negative nonlinear dissipation in microelectromechanical beams. J. Microelectromech. Syst. 2020, 29, 954. [Google Scholar] [CrossRef]
- Eleuch, H. Autocorrelation function of microcavity-emitting field in the linear regime. Eur. Phys. J. D 2008, 48, 139. [Google Scholar] [CrossRef]
- Eleuch, H.; Rachid, N. Autocorrelation function of microcavity-emitting field in the non-linear regime. Eur. Phys. J. D 2010, 57, 259. [Google Scholar] [CrossRef]
- Jabri, H.; Eleuch, H.; Djerad, T. Lifetimes of highly excited atomic states. Phys. Scr. 2006, 73, 397. [Google Scholar] [CrossRef]
- Carmichael, H.J. Statistical Methods in Quantum Optics 2; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Carmichael, H.J.; Brecha, R.J.; Rice, P.R. Quantum interference and collapse of the wavefunction in cavity QED. Opt. Commun. 1991, 82, 73. [Google Scholar] [CrossRef]
- Brecha, R.J.; Rice, P.R.; Xiao, M. N two-level atoms in a driven optical cavity: Quantum dynamics of forward photon scattering for weak incident fields. Phys. Rev. A 1991, 59, 2392. [Google Scholar] [CrossRef] [Green Version]
- Pati, A.K. Geometric aspects of noncyclic quantum evolutions. Phys. Rev. A 1995, 52, 2576. [Google Scholar] [CrossRef] [PubMed]
- Pati, A.K. Gauge-invariant reference section and geometric phase. J. Phys. A 1995, 28, 2087. [Google Scholar] [CrossRef]
- Mukunda, N.; Simon, R. Quantum Kinematic Approach to the Geometric Phase. I. General Formalism. Ann. Phys. 1993, 228, 205. [Google Scholar]
- Sjoqvist, E.; Pati, A.K.; Ekert, A.; Anandan, J.S.; Ericsson, M.; Oi, D.K.L.; Vedral, V. Geometric Phases for Mixed States in Interferometry. Phys. Rev. Lett. 2000, 84, 14. [Google Scholar] [CrossRef] [PubMed] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Altowyan, A.S.; Berrada, K.; Abdel-Khalek, S.; Eleuch, H. Quantum Coherence and Total Phase in Semiconductor Microcavities for Multi-Photon Excitation. Nanomaterials 2022, 12, 2671. https://doi.org/10.3390/nano12152671
Altowyan AS, Berrada K, Abdel-Khalek S, Eleuch H. Quantum Coherence and Total Phase in Semiconductor Microcavities for Multi-Photon Excitation. Nanomaterials. 2022; 12(15):2671. https://doi.org/10.3390/nano12152671
Chicago/Turabian StyleAltowyan, Abeer S., Kamal Berrada, Sayed Abdel-Khalek, and Hichem Eleuch. 2022. "Quantum Coherence and Total Phase in Semiconductor Microcavities for Multi-Photon Excitation" Nanomaterials 12, no. 15: 2671. https://doi.org/10.3390/nano12152671




