Magneto-Tactile Sensor Based on a Commercial Polyurethane Sponge
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
- (a)
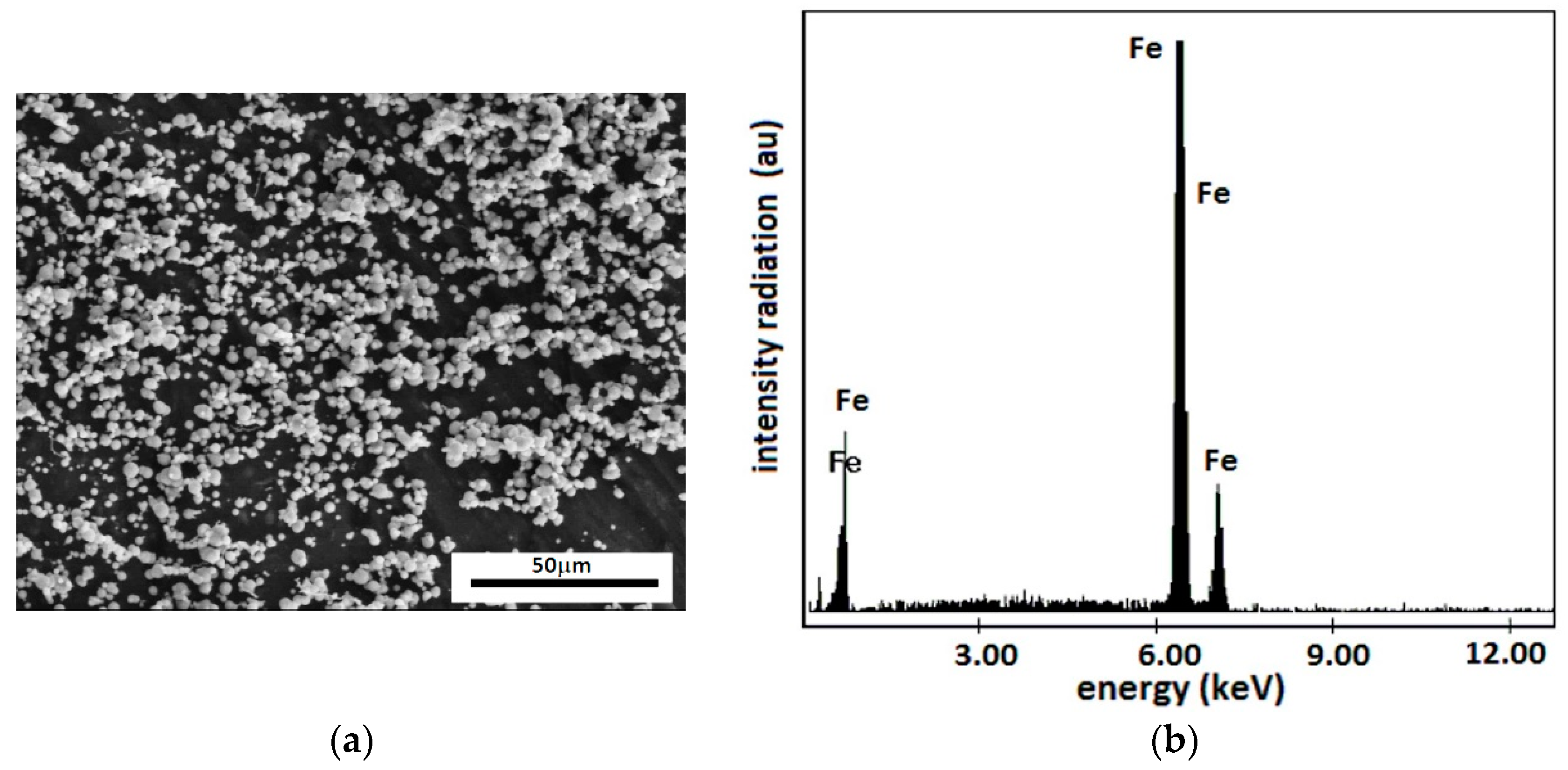
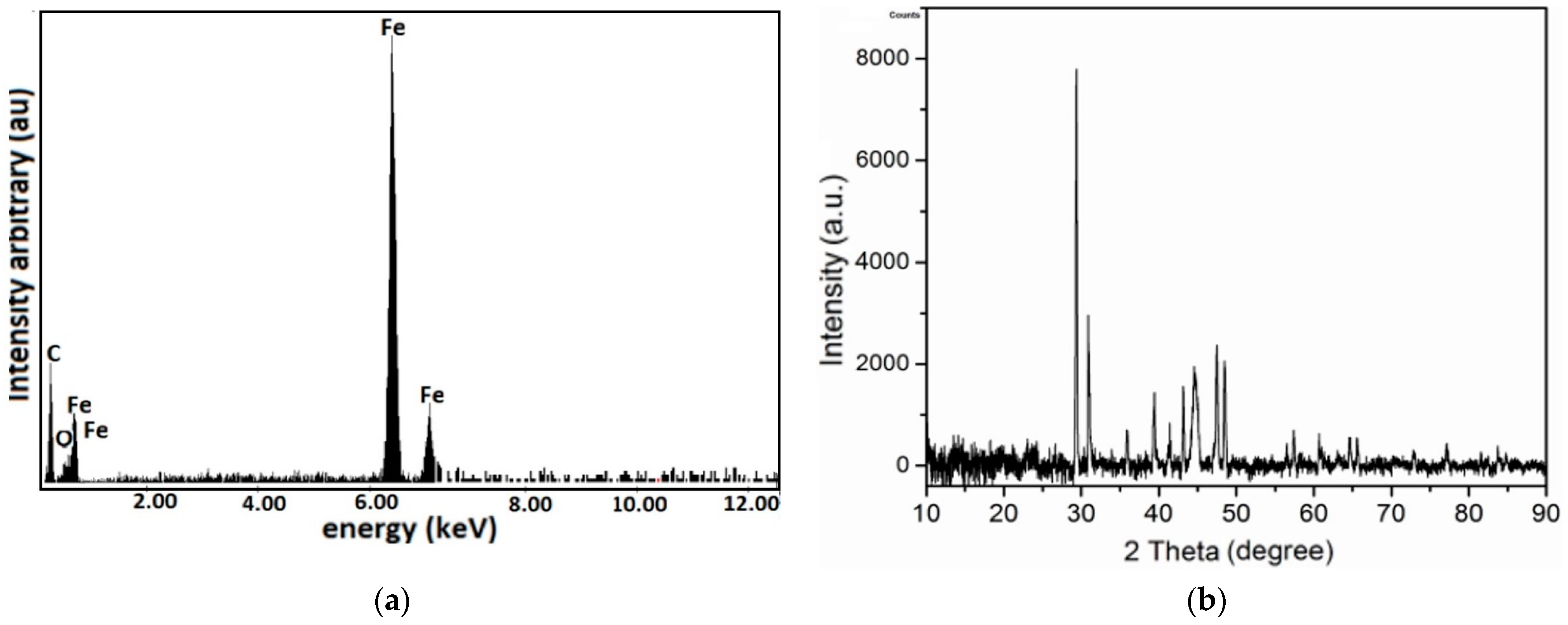
- Carbonyl iron microparticles (Sigma-Aldrich, St. Louis, MO, USA) have an average diameter of and an iron content of at least 97%. The mass density of the CI microparticles is . The particles visualized using SEM were spheres and were confirmed to have an average diameter of (Figure 1a). They have a high degree of purity, as shown in Figure 1b.
- (b)
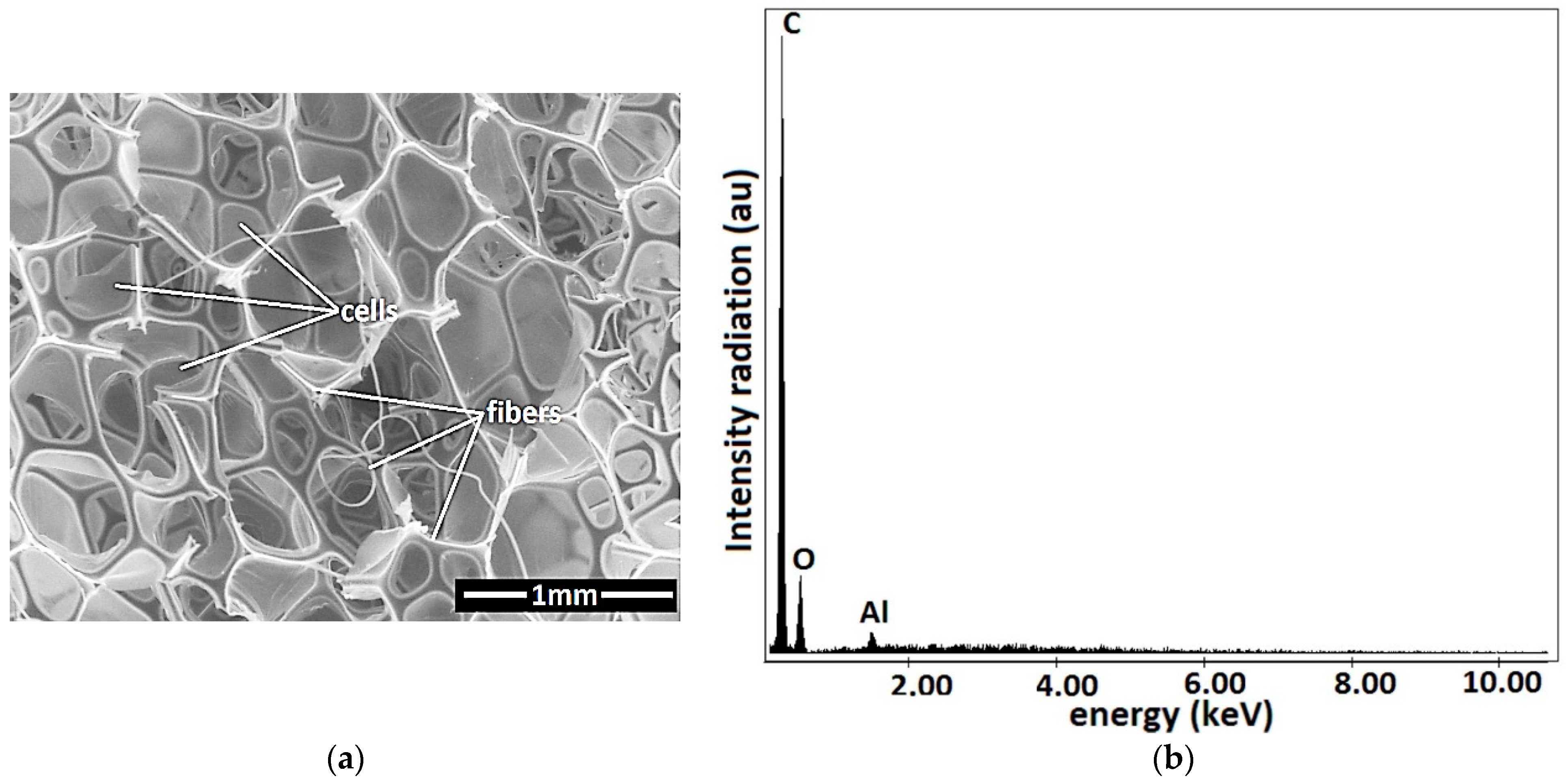
- Super absorbent cloth (AC), of the type “Scotch-Brite” (3M, Saint Paul, MN, USA) , is made in Italy and contains (see officedirect.ro) 48% viscose, 12% polyester, 25% polyurethane foam, and 15% latex. A piece with the dimensions is cut from AC (Figure 3a). By exfoliating a face, the polyurethane sponge (PS) from Figure 3b is obtained, with the dimensions .
- (c)
- Laboratory Reactive Ethyl Alcohol (EA) was purchased from MedAz.ro and has an alcohol content of 96.0%.
- (d)
- Copper foil with electroconductive adhesive (CS) (Huizhou Yunze Electronic Technology, Huizhou, China) has a length of 20 m, a width of 3 cm, and a thickness of 0.05 mm. It was acquired from Frugo (Hong Kong, China).
2.2. Procedure for Making the MPS and Designing the MTS
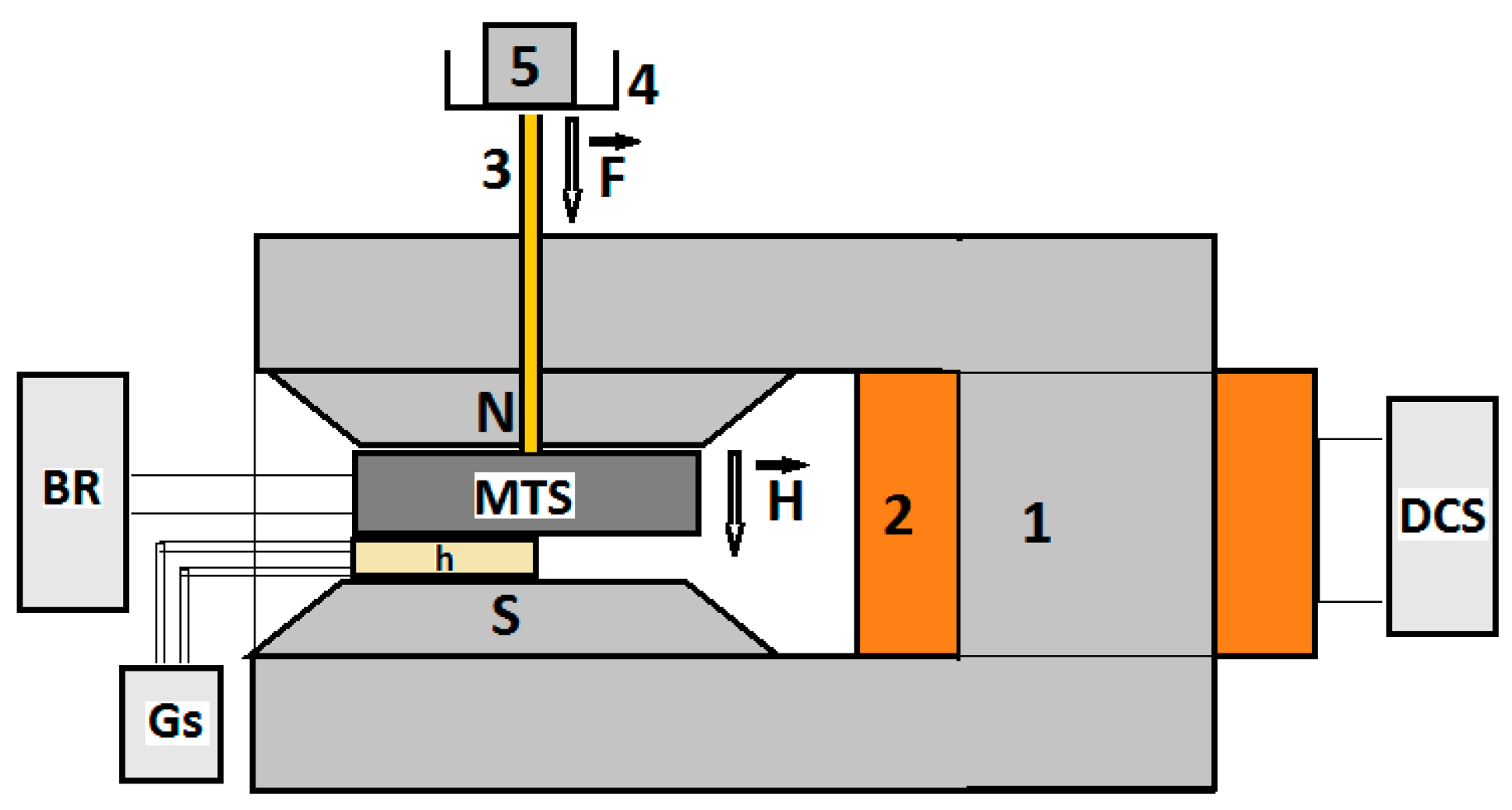
2.3. Experimental Set-Up and Measurements
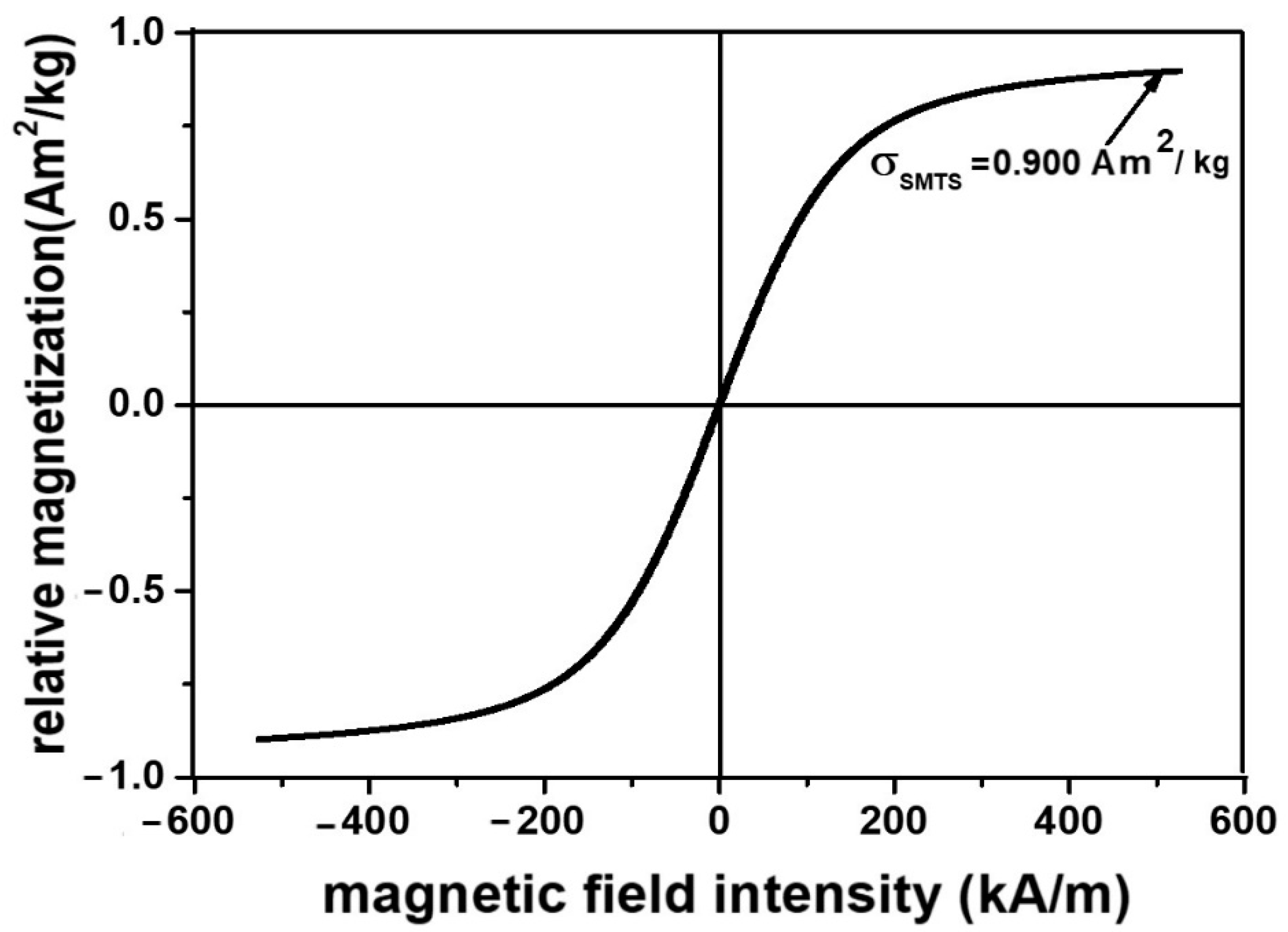
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A
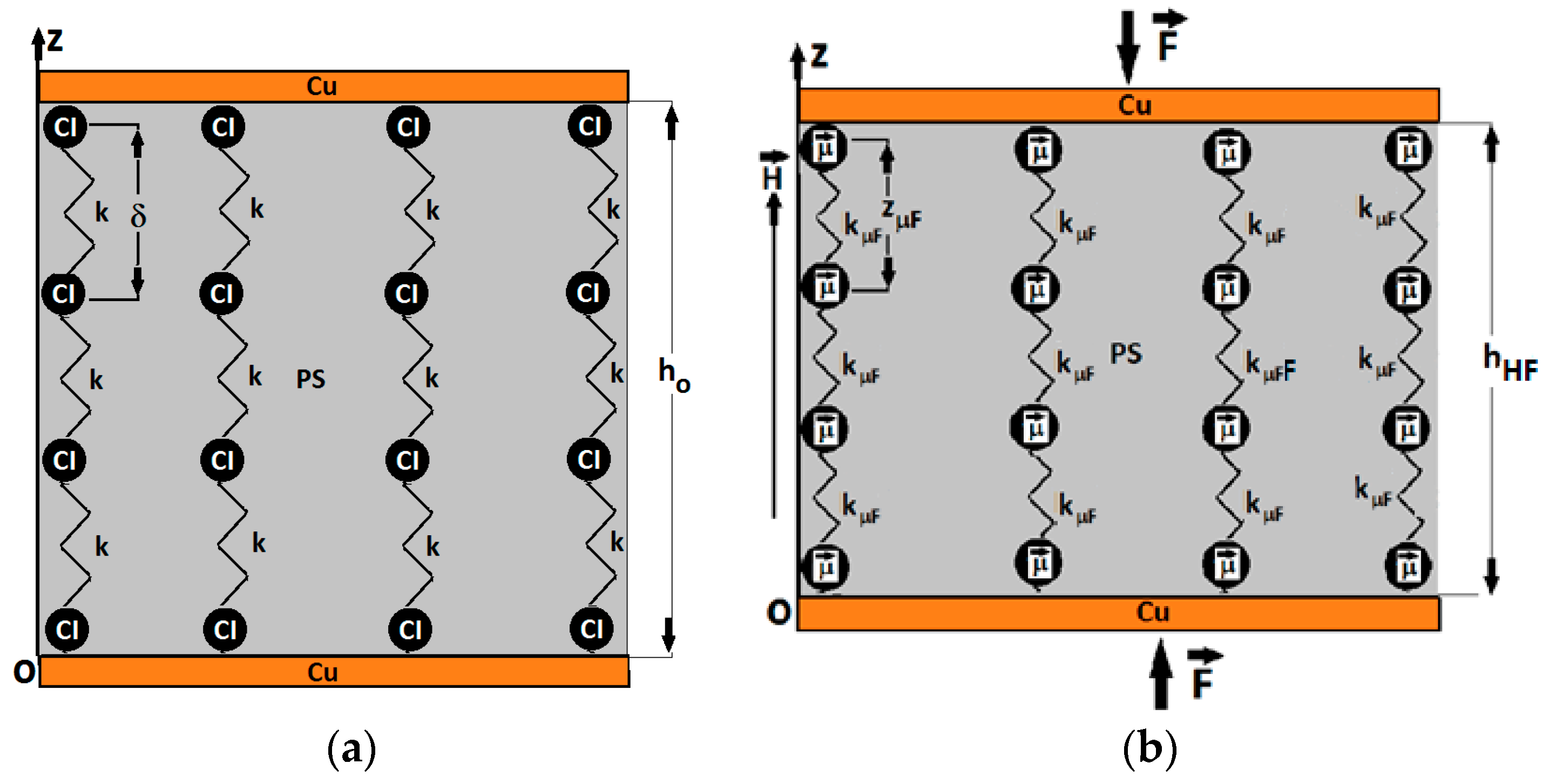
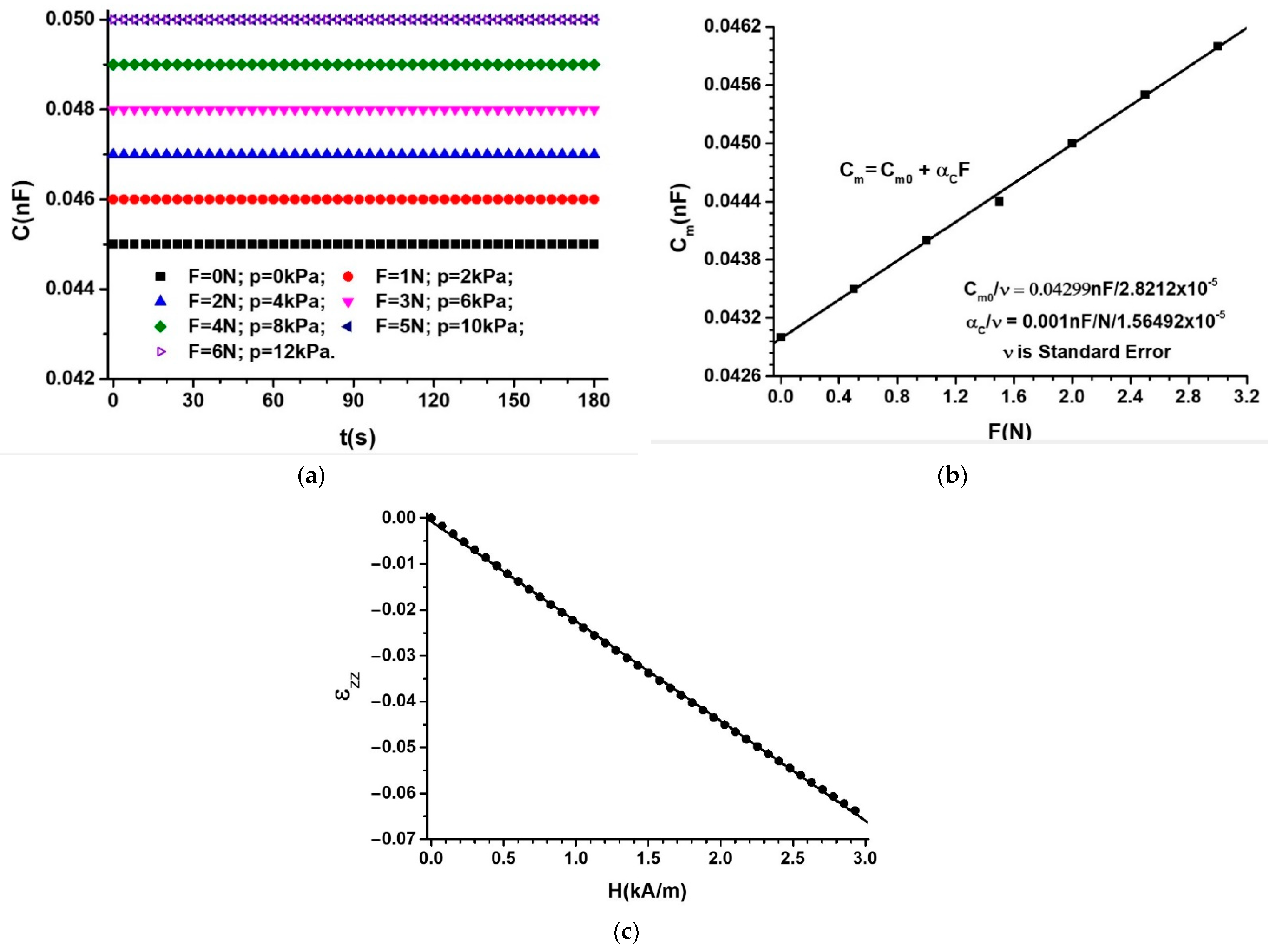
Appendix A.1. MTS Subjected to a Field of Compression Forces

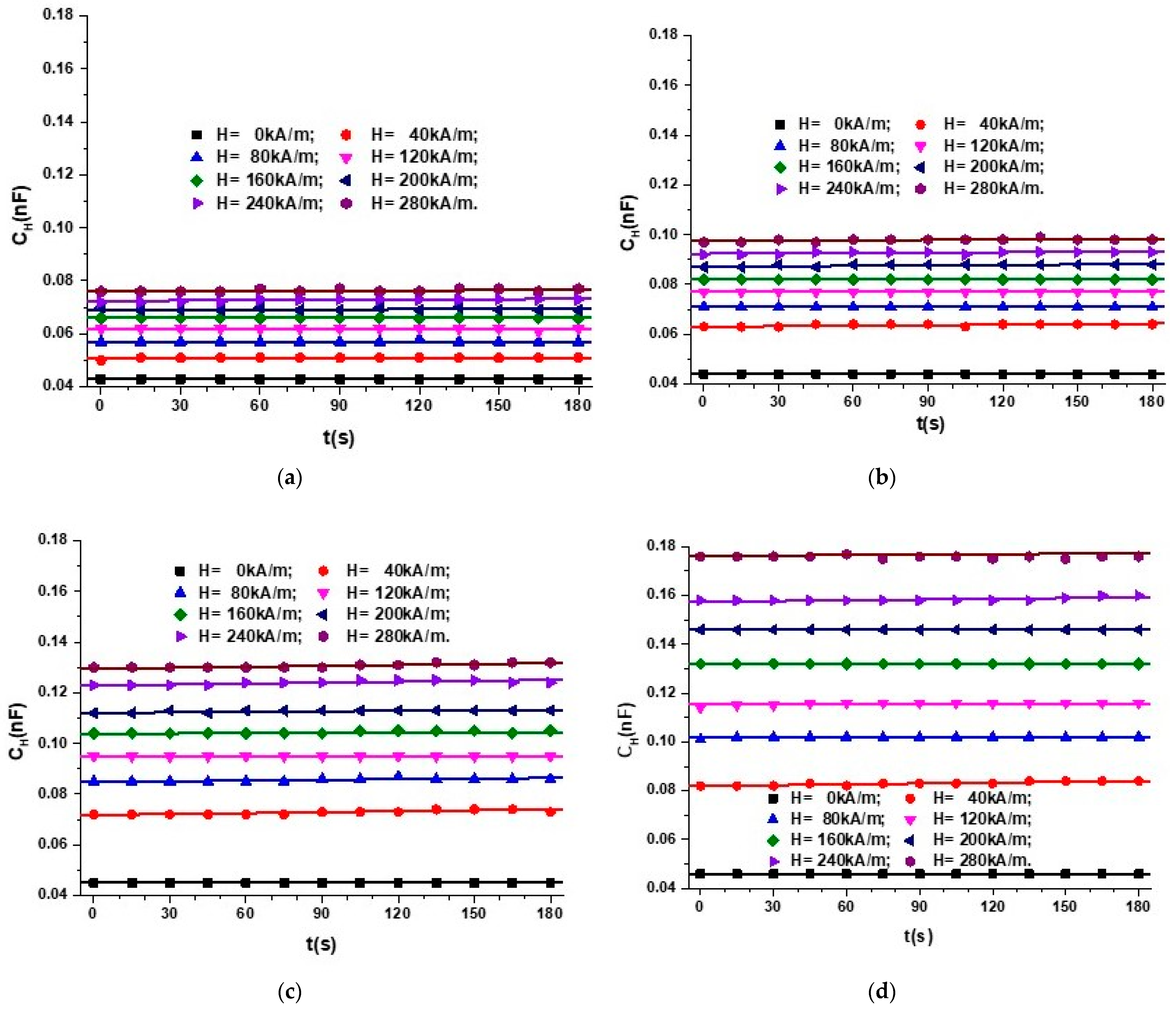
Appendix A.2. MTS Subjected to a Magnetic Field
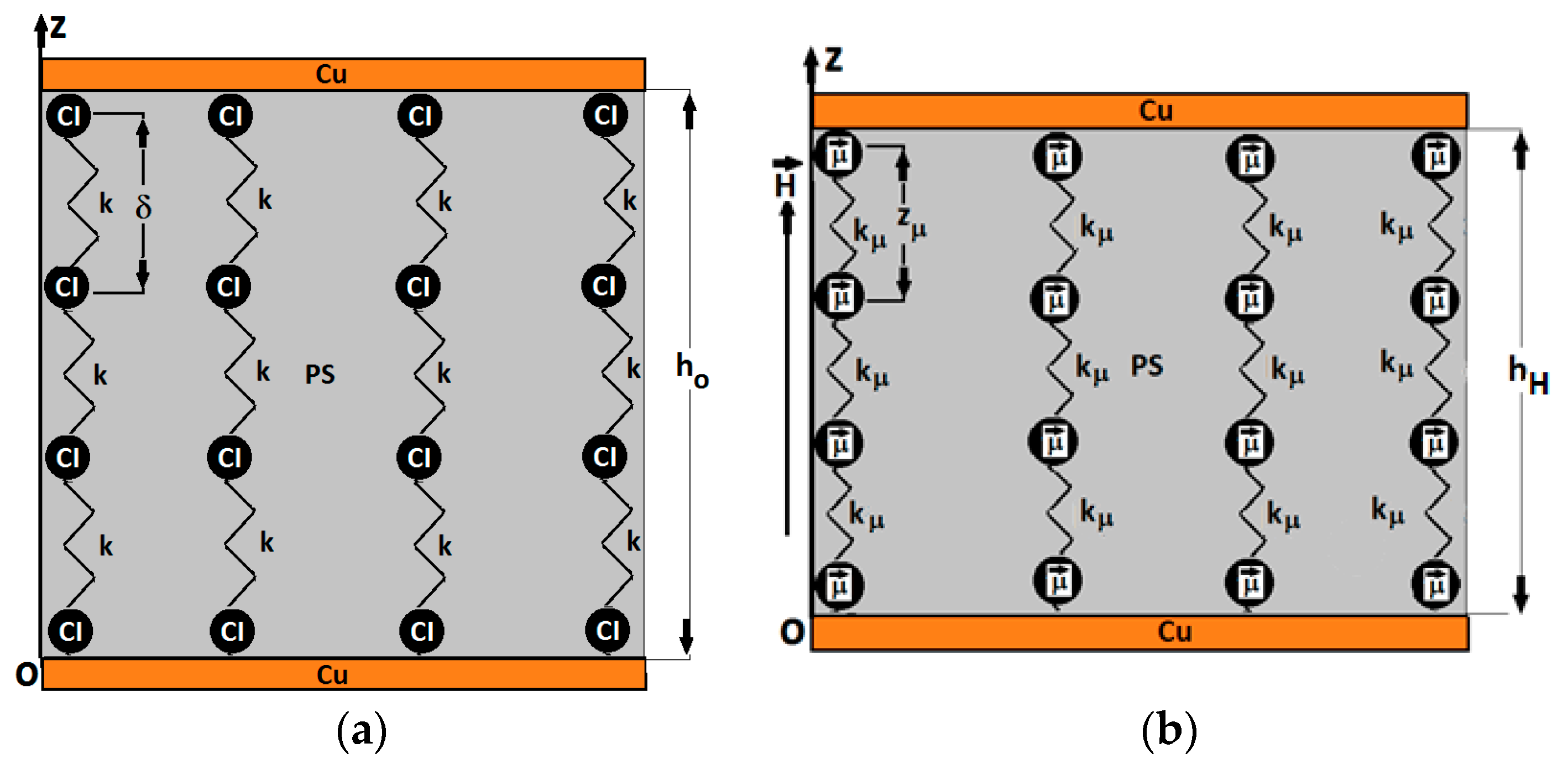
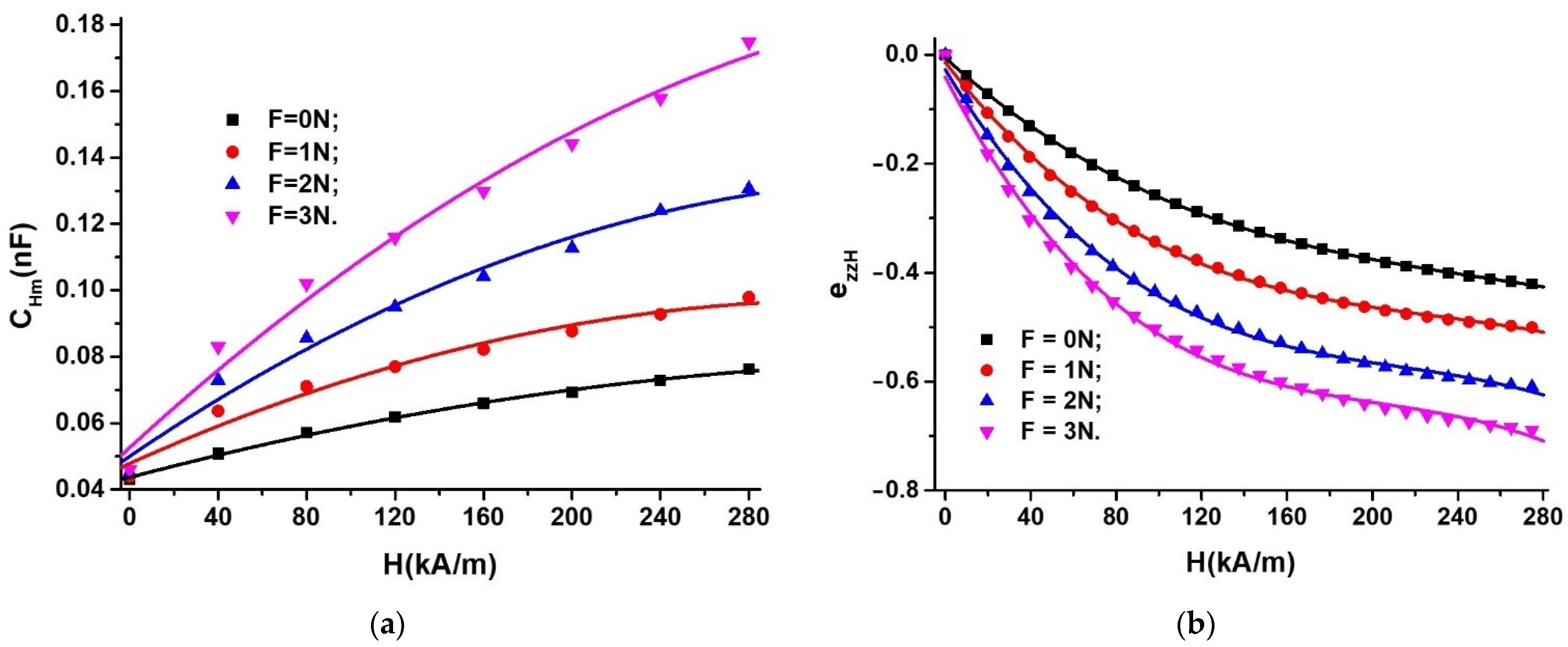
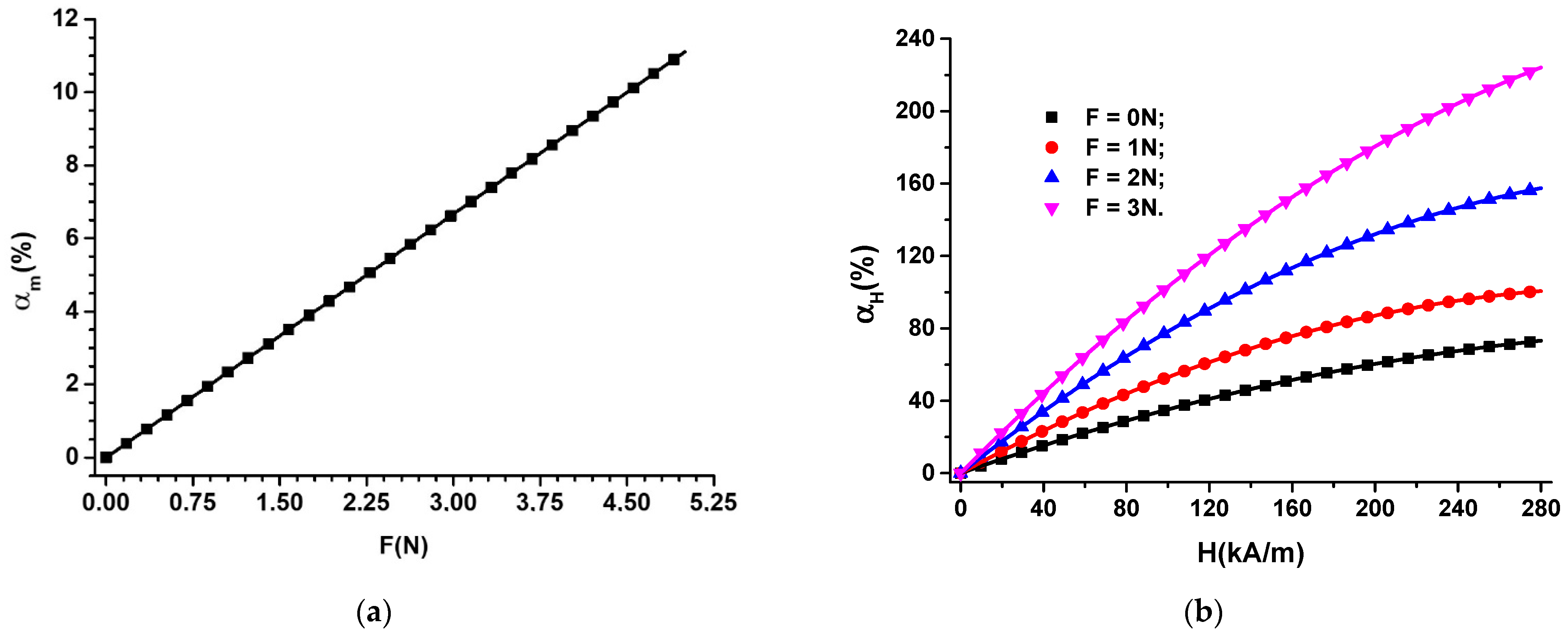
Appendix A.3. MTS Subjected to a Magnetic Field Superimposed on a Field of Compression Forces
References
- Sun, X.; Sun, J.; Li, T.; Zheng, S.; Wang, C.; Tan, W.; Zhang, J.; Liu, C.; Ma, T.; Qi, Z.; et al. Flexible Tactile Electronic Skin Sensor with 3D Force Detection Based on Porous CNTs/PDMS Nanocomposites. Nano-Micro Lett. 2019, 11, 57. [Google Scholar] [CrossRef] [PubMed]
- Chittibabu, S.K.; Chintagumpala, K.; Chandrasekhar, A. Porous dielectric materials based wearable capacitance pressure sensors for vital signs monitoring: A review. Mater. Sci. Semicond. Process. 2022, 151, 106976. [Google Scholar] [CrossRef]
- Gao, Y.; Xiao, T.; Li, Q.; Chen, Y.; Qiu, X.; Liu, J.; Bian, Y.; Xuan, F.-Z. Flexible microstructured pressure sensors: Design, fabrication and applications. Nanotechnology 2022, 33, 322002. [Google Scholar] [CrossRef] [PubMed]
- Weng, X.; Zhang, C.; Feng, C.; Jiang, H. Facile Fabrication of an Ultrasensitive All-Fabric Wearable Pressure Sensor Based on Phosphorene-Gold Nanocomposites. Adv. Mater. Interfaces 2022, 9, 2102588. [Google Scholar] [CrossRef]
- Kang, D.; Pikhitsa, P.V.; Choi, Y.W.; Lee, C.; Shin, S.S.; Piao, L.; Park, B.; Suh, K.Y.; Kim, T.I.; Choi, M. Ultrasensitive mechanical crack-based sensor inspired by the spider sensory system. Nature 2014, 516, 222–226. [Google Scholar] [CrossRef] [PubMed]
- Alfadhel, A.; Kosel, J. Magnetic Nanocomposite Cilia Tactile Sensor. Adv. Mater. 2015, 27, 7888–7892. [Google Scholar] [CrossRef]
- Wang, H.L.; Guo, Z.H.; Pu, X.; Wang, Z.L. Ultralight Iontronic Triboelectric Mechanoreceptor with High Specific Outputs for Epidermal Electronics. Nano-Micro Lett. 2022, 14, 86. [Google Scholar] [CrossRef]
- Kurup, L.A.; Arthur, J.N.; Yambem, S.D. Highly Sensitive Capacitive Low-Pressure Graphene Porous Foam Sensors. ACS Appl. Electron. Mater. 2022, 4, 3962–3972. [Google Scholar] [CrossRef]
- Wu, D.; Cheng, X.; Chen, Z.; Xu, Z.; Zhu, M.; Zhao, Y.; Zhu, R.; Lin, L. A flexible tactile sensor that uses polyimide/graphene oxide nanofiber as dielectric membrane for vertical and lateral force detection. Nanotechnology 2022, 33, 405205. [Google Scholar] [CrossRef]
- Kim, H.; Kim, G.; Kim, T.; Lee, S.; Kang, D.; Hwang, M.-S.; Chae, Y.; Kang, S.; Lee, H.; Park, H.-G.; et al. Transparent, Flexible, Conformal Capacitive Pressure Sensors with Nanoparticles. Small 2018, 14, 1703432. [Google Scholar] [CrossRef]
- Pavel, I.-A.; Lakard, S.; Lakard, B. Flexible Sensors Based on Conductive Polymers. Chemosensors 2022, 10, 97. [Google Scholar] [CrossRef]
- Xie, L.; Chen, X.; Wen, Z.; Yang, Y.; Shi, J.; Chen, C.; Peng, M.; Liu, Y.; Sun, X. Spiral Steel Wire Based Fiber-Shaped Stretchable and Tailorable Triboelectric Nanogenerator for Wearable Power Source and Active Gesture Sensor. Nano-Micro Lett. 2019, 11, 39. [Google Scholar] [CrossRef]
- Hua, Q.; Sun, J.; Liu, H.; Bao, R.; Yu, R.; Zhai, J.; Pan, C.; Wang, Z.L. Skin-inspired highly stretchable and conformable matrix networks for multifunctional sensing. Nat. Commun. 2018, 9, 244. [Google Scholar] [CrossRef]
- Lo, L.-W.; Zhao, J.; Aono, K.; Li, W.; Wen, Z.; Pizzella, S.; Wang, Y.; Chakrabartty, S.; Wang, C. Stretchable Sponge Electrodes for Long-Term and Motion-Artifact-Tolerant Recording of High-Quality Electrophysiologic Signals. ACS Nano 2022, 16, 11792–11801. [Google Scholar] [CrossRef]
- Chen, H.; Song, Y.; Guo, H.; Miao, L.; Chen, X.; Su, Z.; Zhang, H. Hybrid porous micro structured finger skin inspired self-powered electronic skin system for pressure sensing and sliding detection. Nano Energy 2018, 51, 496–503. [Google Scholar] [CrossRef]
- Wang, X.; Ling, X.; Hu, Y.; Hu, X.; Zhang, Q.; Sun, K.; Xiang, Y. Electronic skin based on PLLA/TFT/PVDF-TrFE array for Multi-Functional tactile sensing and visualized restoring. Chem. Eng. J. 2022, 434, 134735. [Google Scholar] [CrossRef]
- Tao, Z.; Huang, Y.-A.; Liu, X.; Chen, J.; Lei, W.; Wang, X.; Pan, L.; Pan, J.; Huang, Q.; Zhang, Z. High-Performance Photo-Modulated Thin-Film Transistor Based on Quantum dots/Reduced Graphene Oxide Fragment-Decorated ZnO Nanowires. Nano-Micro Lett. 2016, 8, 247–253. [Google Scholar] [CrossRef]
- Bai, S.; Zhang, S.; Zhou, W.; Ma, D.; Ma, Y.; Joshi, P.; Hu, A. Laser-Assisted Reduction of Highly Conductive Circuits Based on Copper Nitrate for Flexible Printed Sensors. Nano-Micro Lett. 2017, 9, 42. [Google Scholar] [CrossRef]
- Kim, Y.; Chortos, A.; Xu, W.; Liu, Y.; Oh, J.Y.; Son, D.; Kang, J.; Foudeh, A.M.; Zhu, C.; Lee, Y.; et al. A bioinspired flexible organic artificial afferent nerve. Science 2018, 360, 998–1003. [Google Scholar] [CrossRef]
- Nguyen, T.-D.; Lee, J.S. Recent Development of Flexible Tactile Sensors and Their Applications. Sensors 2021, 22, 50. [Google Scholar] [CrossRef]
- Jiang, C.; Liu, J.; Yang, L.; Gong, J.; Wei, H.; Xu, W. A Flexible Artificial Sensory Nerve Enabled by Nanoparticle-Assembled Synaptic Devices for Neuromorphic Tactile Recognition. Adv. Sci. 2022, 9, 2106124. [Google Scholar] [CrossRef]
- Liu, W.; Liu, N.; Yue, Y.; Rao, J.; Cheng, F.; Su, J.; Liu, Z.; Gao, Y. Piezoresistive Pressure Sensor Based on Synergistical Innerconnect Polyvinyl Alcohol Nanowires/Wrinkled Graphene Film. Small 2018, 14, e1704149. [Google Scholar] [CrossRef]
- Sun, X.; Wang, C.; Chi, C.; Xue, N.; Liu, C. A highly-sensitive flexible tactile sensor array utilizing piezoresistive carbon nanotube–polydimethylsiloxane composite. J. Micromech. Microeng. 2018, 28, 105011. [Google Scholar] [CrossRef]
- Li, T.; Luo, H.; Qin, L.; Wang, X.; Xiong, Z.; Ding, H.; Gu, Y.; Liu, Z.; Zhang, T. Flexible Capacitive Tactile Sensor Based on Micropatterned Dielectric Layer. Small 2016, 12, 5042–5048. [Google Scholar] [CrossRef]
- Choi, D.; Jang, S.; Kim, J.S.; Kim, H.-J.; Kim, D.H.; Kwon, J.-Y. A Highly Sensitive Tactile Sensor Using a Pyramid-Plug Structure for Detecting Pressure, Shear Force, and Torsion. Adv. Mater. Technol. 2018, 4, 1800284. [Google Scholar] [CrossRef]
- Shu, Y.; Tian, H.; Yang, Y.; Li, C.; Cui, Y.; Mi, W.; Li, Y.; Wang, Z.; Deng, N.; Peng, B.; et al. Surface-modified piezoresistive nanocomposite flexible pressure sensors with high sensitivity and wide linearity. Nanoscale 2015, 7, 8636–8644. [Google Scholar] [CrossRef]
- Park, C.-S.; Park, J.; Lee, D.-W. A piezoresistive tactile sensor based on carbon fibers and polymer substrates. Microelectron. Eng. 2009, 86, 1250–1253. [Google Scholar] [CrossRef]
- Pan, L.; Chortos, A.; Yu, G.; Wang, Y.; Isaacson, S.; Allen, R.; Shi, Y.; Dauskardt, R.; Bao, Z. An ultra-sensitive resistive pressure sensor based on hollow-sphere microstructure induced elasticity in conducting polymer film. Nat. Commun. 2014, 5, 3002. [Google Scholar] [CrossRef]
- Tang, Z.; Jia, S.; Shi, S.; Wang, F.; Li, B. Coaxial carbon nanotube/polymer fibers as wearable piezoresistive sensors. Sens. Actuators A Phys. 2018, 284, 85–95. [Google Scholar] [CrossRef]
- A Dobrzynska, J.; Gijs, M.A.M. Polymer-based flexible capacitive sensor for three-axial force measurements. J. Micromech. Microeng. 2013, 23, 015009. [Google Scholar] [CrossRef]
- Kim, M.-S.; Ahn, H.-R.; Lee, S.; Kim, C.; Kim, Y.-J. A dome-shaped piezoelectric tactile sensor arrays fabricated by an air inflation technique. Sens. Actuators A Phys. 2014, 212, 151–158. [Google Scholar] [CrossRef]
- Chiappim, W.; Fraga, M.A.; Furlan, H.; Ardiles, D.C.; Pessoa, R.S. The status and perspectives of nanostructured materials and fabrication processes for wearable piezoresistive sensors. Microsyst. Technol. 2022, 28, 1561–1580. [Google Scholar] [CrossRef] [PubMed]
- Ahmadi, R.; Packirisamy, M.; Dargahi, J.; Cecere, R. Discretely Loaded Beam-Type Optical Fiber Tactile Sensor for Tissue Manipulation and Palpation in Minimally Invasive Robotic Surgery. IEEE Sens. J. 2012, 12, 22–32. [Google Scholar] [CrossRef]
- Li, X.; Huang, W.; Yao, G.; Gao, M.; Wei, X.; Liu, Z.; Zhang, H.; Gong, T.; Yu, B. Highly sensitive flexible tactile sensors based on microstructured multiwall carbon nanotube arrays. Scr. Mater. 2017, 129, 61–64. [Google Scholar] [CrossRef]
- Hasan, S.A.U.; Jung, Y.; Kim, S.; Jung, C.-L.; Oh, S.; Kim, J.; Lim, H. A Sensitivity Enhanced MWCNT/PDMS Tactile Sensor Using Micropillars and Low Energy Ar+ Ion Beam Treatment. Sensors 2016, 16, 93. [Google Scholar] [CrossRef]
- Wang, J.J.; Lu, C.E.; Huang, J.L.; Chen, R.; Fang, W. Nano-composite rubber elastomer with piezoresistive detectionfor flexible tactile sense application. In Proceedings of the 2017 IEEE 30th International Conference on Micro Electro Mechanical Systems (MEMS), Las Vegas, NV, USA, 22–26 January 2017; pp. 720–723. [Google Scholar] [CrossRef]
- Chun, S.; Hong, A.; Choi, Y.; Ha, C.; Park, W. A tactile sensor using a conductive graphene-sponge composite. Nanoscale 2016, 8, 9185–9192. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, L.J.; Zhang, H.M.; Zhao, Z.X.; Dong, S.L.; Wei, S.; Zhao, J.; Wang, Z.L.; Guo, B.; Hu, P.A. Highly sensitive flexible three-axis tactile sensors based on the interface contact resistance of microstructured graphene. Nanoscale 2018, 10, 7387–7395. [Google Scholar] [CrossRef]
- Pei, Z.; Hu, H.; Liang, G.; Ye, C. Carbon-Based Flexible and All-Solid-State Micro-supercapacitors Fabricated by Inkjet Printing with Enhanced Performance. Nano-Micro Lett. 2017, 9, 19. [Google Scholar] [CrossRef]
- Wang, J.; Jiu, J.; Araki, T.; Nogi, M.; Sugahara, T.; Nagao, S.; Koga, H.; He, P.; Suganuma, K. Silver Nanowire Electrodes: Conductivity Improvement Without Post-treatment and Application in Capacitive Pressure Sensors. Nano-Micro Lett. 2015, 7, 51–58. [Google Scholar] [CrossRef] [Green Version]
- Weng, L.; Xie, G.; Zhang, B.; Huang, W.; Wang, B.; Deng, Z. Magnetostrictive tactile sensor array for force and stiffness detection. J. Magn. Magn. Mater. 2020, 513, 167068. [Google Scholar] [CrossRef]
- Bica, I.; Anitas, E.M. Electrical devices based on hybrid membranes with mechanically and magnetically controllable, resistive, capacitive and piezoelectric properties. Smart Mater. Struct. 2022, 31, 045001. [Google Scholar] [CrossRef]
- Pascu, G.; Bunoiu, O.M.; Bica, I. Magnetic Field Effects Induced in Electrical Devices Based on Cotton Fiber Composites, Carbonyl Iron Microparticles and Barium Titanate Nanoparticles. Nanomaterials 2022, 12, 888. [Google Scholar] [CrossRef]
- Bica, I.; Bǎlǎșoiu, M.; Sfirloaga, P. Effects of electric and magnetic fields on dielectric and elastic properties of membranes composed of cotton fabric and carbonyl iron microparticles. Results Phys. 2022, 35, 105332. [Google Scholar] [CrossRef]
- Bica, I.; Iacobescu, G.-E. Magneto-Dielectric Effects in Polyurethane Sponge Modified with Carbonyl Iron for Applications in Low-Cost Magnetic Sensors. Polymers 2022, 14, 2062. [Google Scholar] [CrossRef]
- Ercuta, A. Sensitive AC Hysteresigraph of Extended Driving Field Capability. IEEE Trans. Instrum. Meas. 2020, 69, 1643–1651. [Google Scholar] [CrossRef]
- Japka, J.E. Microstructure and Properties of Carbonyl Iron Powder. JOM 1988, 40, 18–21. [Google Scholar] [CrossRef]
- Atkins, A.J.; Bauer, M.; Jacob, C.R. High-resolution X-ray absorption spectroscopy of iron carbonyl complexes. Phys. Chem. Chem. Phys. 2015, 17, 13937–13948. [Google Scholar] [CrossRef]
- König, R.; Müller, S.; Dinnebier, R.E.; Hinrichsen, B.; Müller, P.; Ribbens, A.; Hwang, J.; Liebscher, R.; Etter, M.; Pistidda, C. The crystal structures of carbonyl iron powder—revised using in situ synchrotron XRPD. Z. Krist. Cryst. Mater. 2017, 232, 835–842. [Google Scholar] [CrossRef]
- Huang, C.; Niu, H.; Wu, J.; Ke, Q.; Mo, X.; Lin, T. Needleless Electrospinning of Polystyrene Fibers with an Oriented Surface Line Texture. J. Nanomater. 2012, 2012, 473872. [Google Scholar] [CrossRef] [Green Version]
- Bica, I.; Anitas, E.M.; Choi, H.J.; Sfirloaga, P. Microwave-assisted synthesis and characterization of iron oxide microfibers. J. Mater. Chem. C 2020, 8, 6159–6167. [Google Scholar] [CrossRef]
- Bica, I.; Anitas, E. Magnetic flux density effect on electrical properties and visco-elastic state of magnetoactive tissues. Compos. Part B Eng. 2019, 15, 13–19. [Google Scholar] [CrossRef]
- Genç, S. Synthesis and Properties of Magnethoreological (MR) Fluids. Ph.D. Thesis, University of Pitsburgh, Pittsburgh, PA, USA, 2002. [Google Scholar]
- Bica, I.; Anitas, E.M.; Chirigiu, L. Hybrid Magnetorheological Composites for Electric and Magnetic Field Sensors and Transducers. Nanomaterials 2020, 10, 2060. [Google Scholar] [CrossRef]
- Terman, F.E. Radio Engineers’ Handbook; McGraw-Hill: New York, NY, USA, 1943. [Google Scholar]
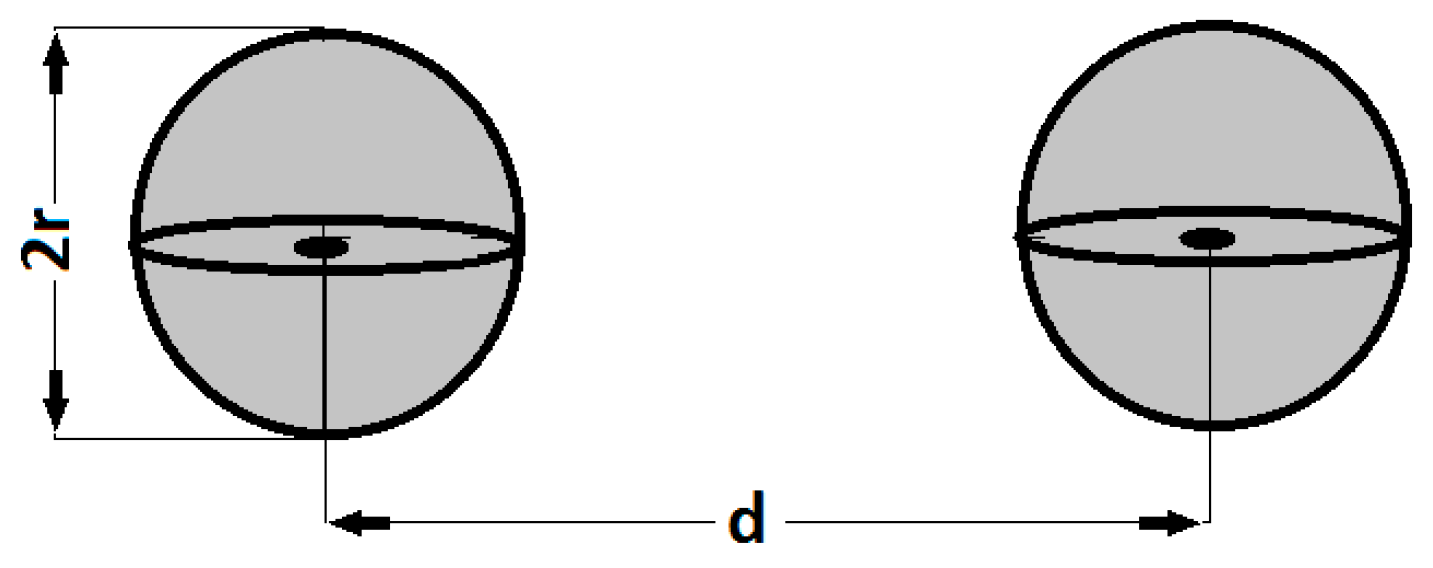
- Rawlins, A. Note on the Capacitance of Two Closely Separated Spheres. IMA J. Appl. Math. 1985, 34, 119–120. [Google Scholar] [CrossRef]







| 59 | 40 | 1 | 0.46 | 92.3 | 7.24 |
| 0 | |||
| 1 | |||
| 2 | |||
| 3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bica, I.; Iacobescu, G.-E.; Chirigiu, L.-M.-E. Magneto-Tactile Sensor Based on a Commercial Polyurethane Sponge. Nanomaterials 2022, 12, 3231. https://doi.org/10.3390/nano12183231
Bica I, Iacobescu G-E, Chirigiu L-M-E. Magneto-Tactile Sensor Based on a Commercial Polyurethane Sponge. Nanomaterials. 2022; 12(18):3231. https://doi.org/10.3390/nano12183231
Chicago/Turabian StyleBica, Ioan, Gabriela-Eugenia Iacobescu, and Larisa-Marina-Elisabeth Chirigiu. 2022. "Magneto-Tactile Sensor Based on a Commercial Polyurethane Sponge" Nanomaterials 12, no. 18: 3231. https://doi.org/10.3390/nano12183231
APA StyleBica, I., Iacobescu, G.-E., & Chirigiu, L.-M.-E. (2022). Magneto-Tactile Sensor Based on a Commercial Polyurethane Sponge. Nanomaterials, 12(18), 3231. https://doi.org/10.3390/nano12183231