Thermal Transport Properties of Diamond Phonons by Electric Field
Abstract
:1. Introduction
2. Methods and Models
2.1. Computational Details
2.2. Electron−Phonon Matrix Elements
3. Results
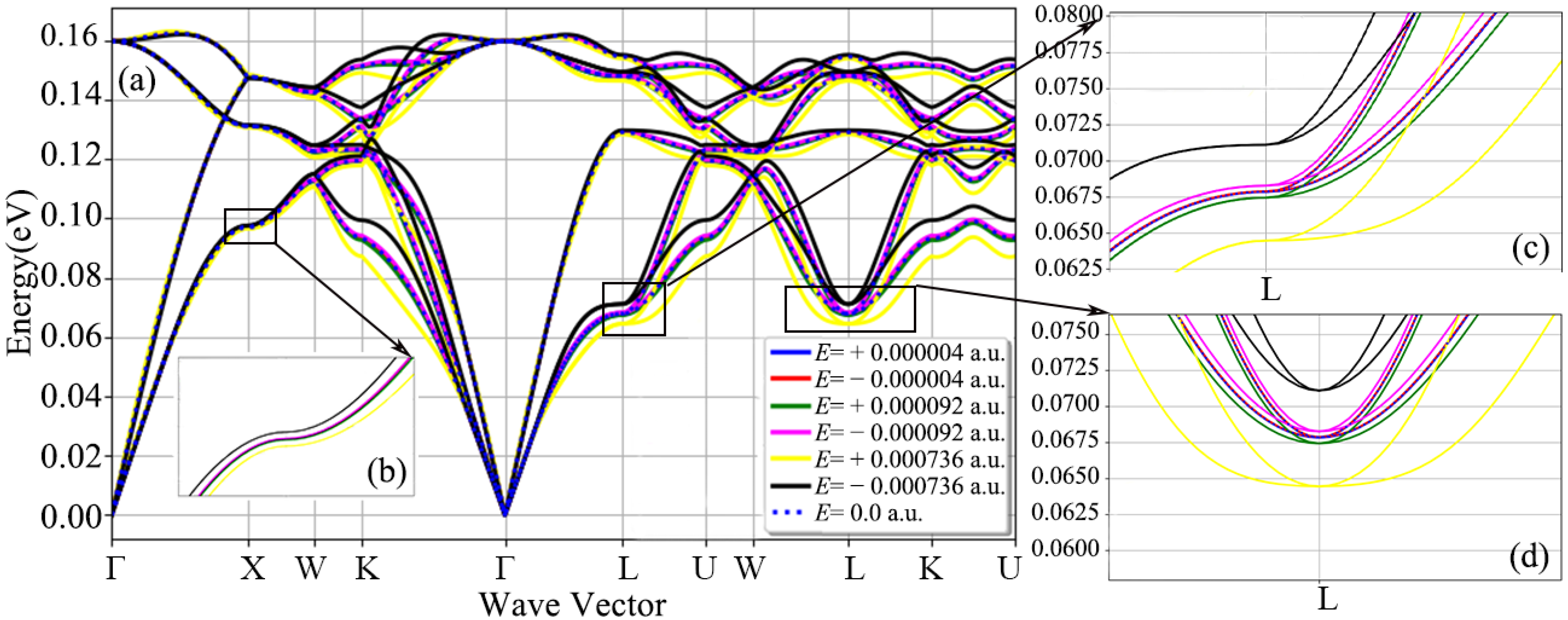
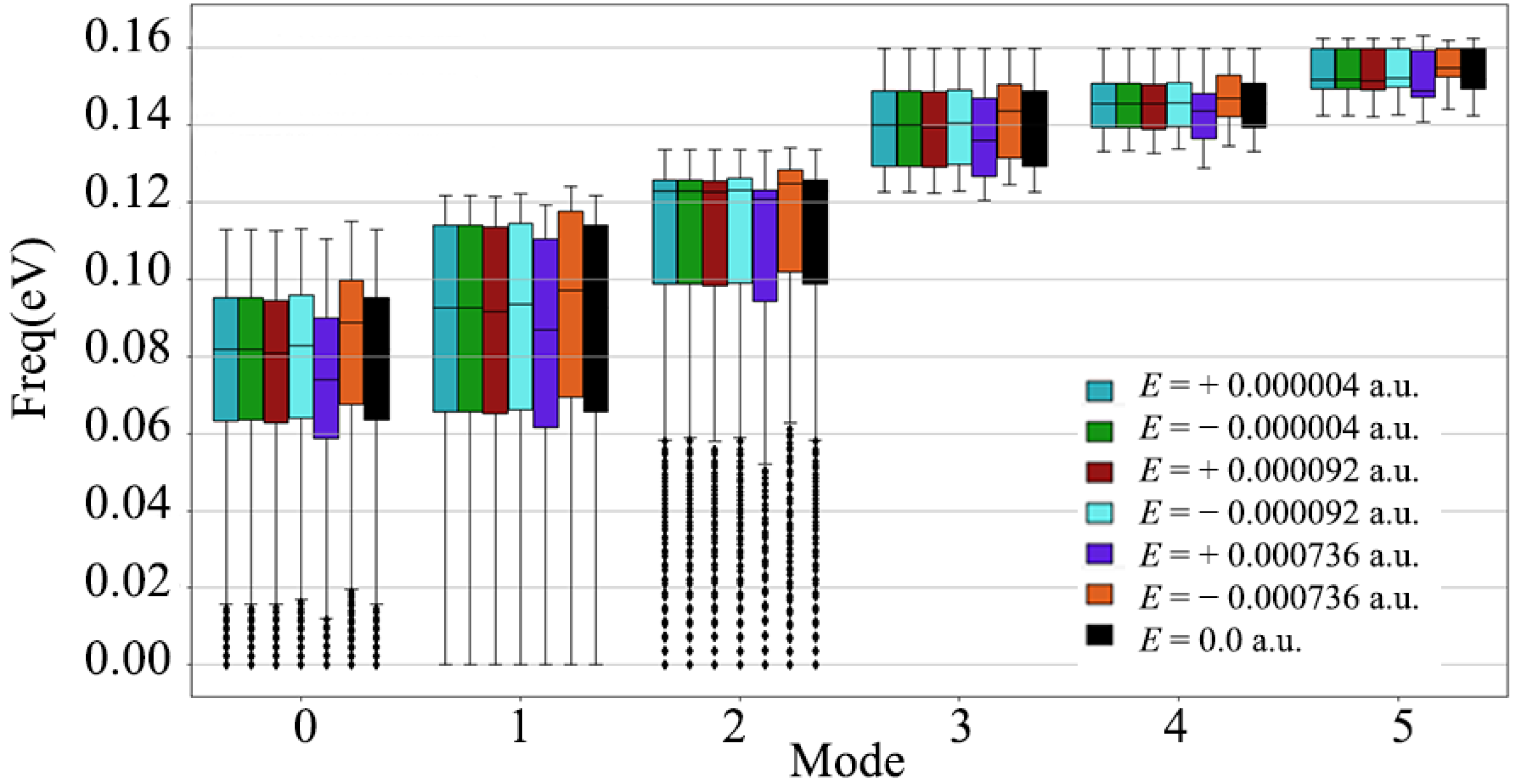
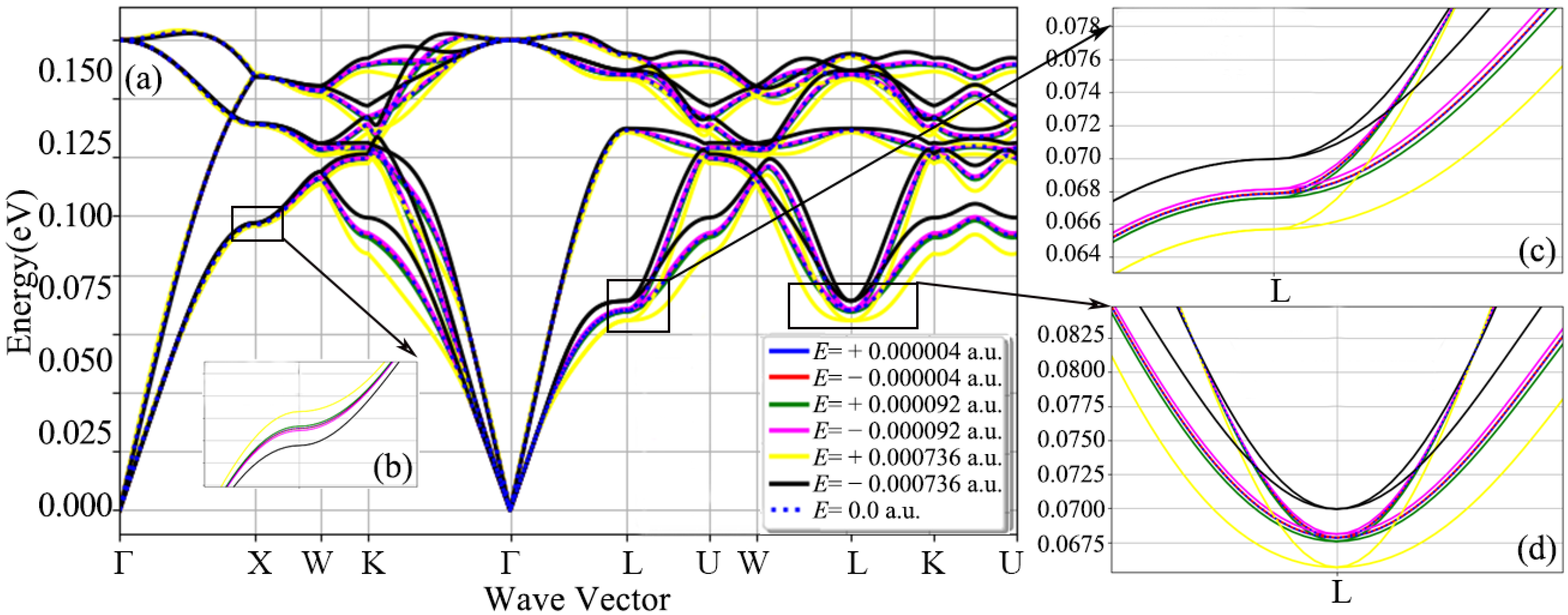
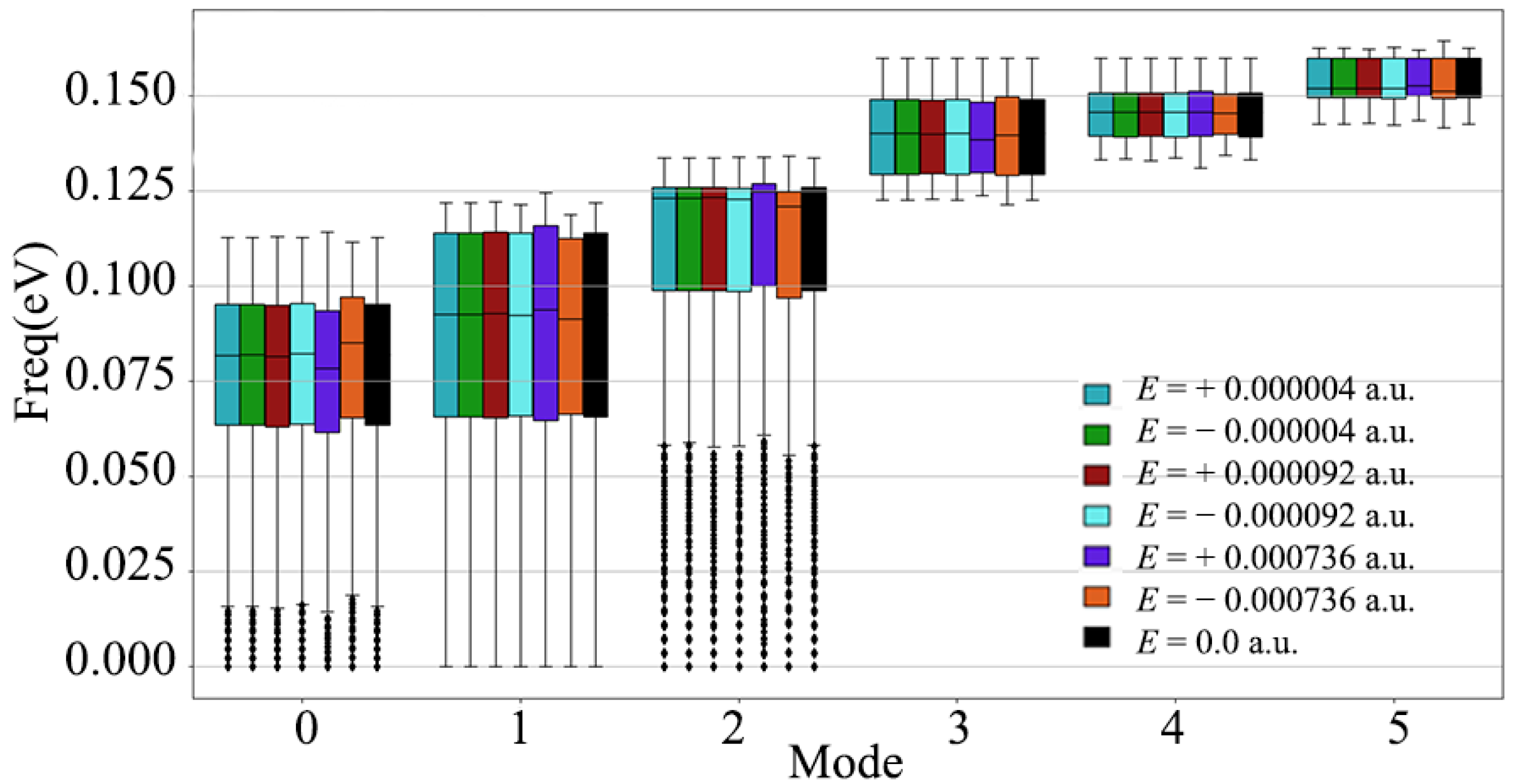
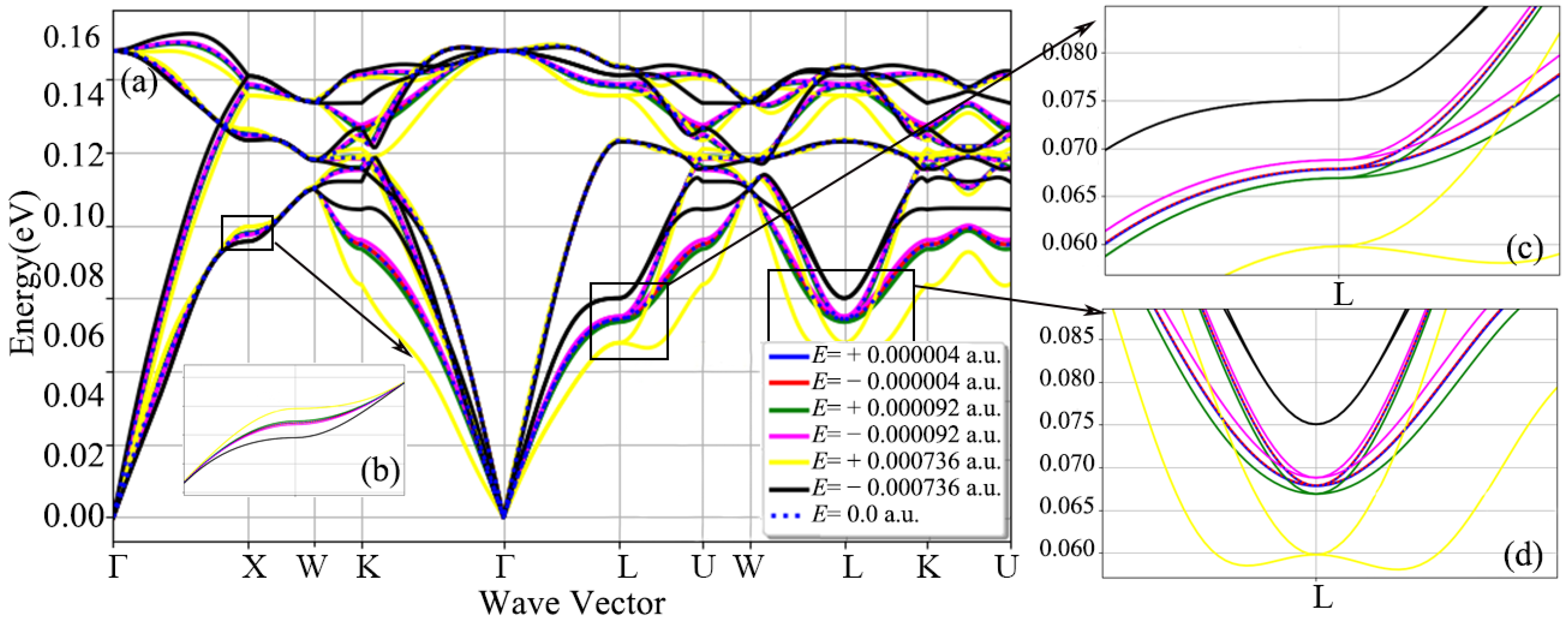
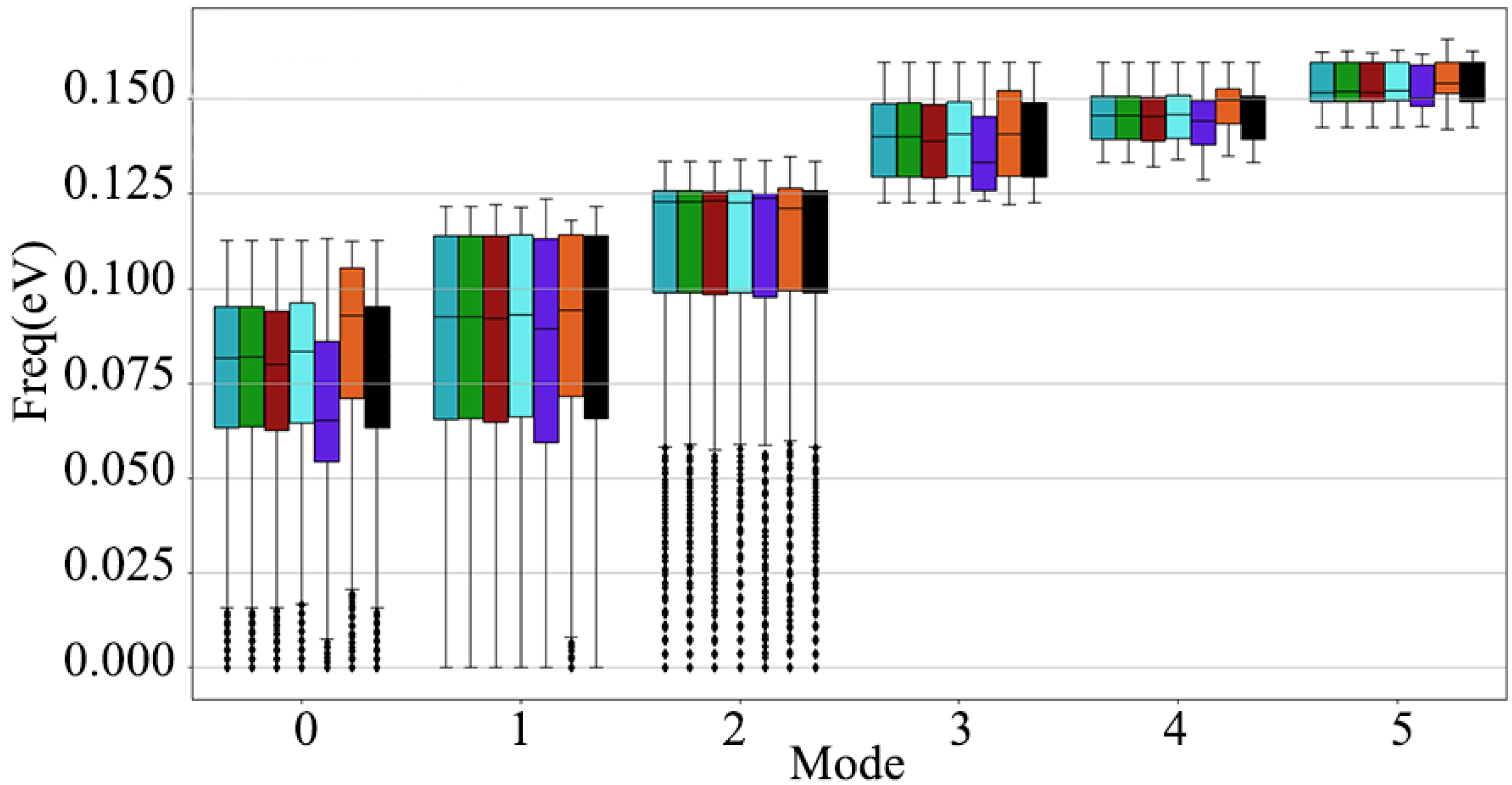
3.1. Phonon Dispersion Relation of Diamond under Electric Field
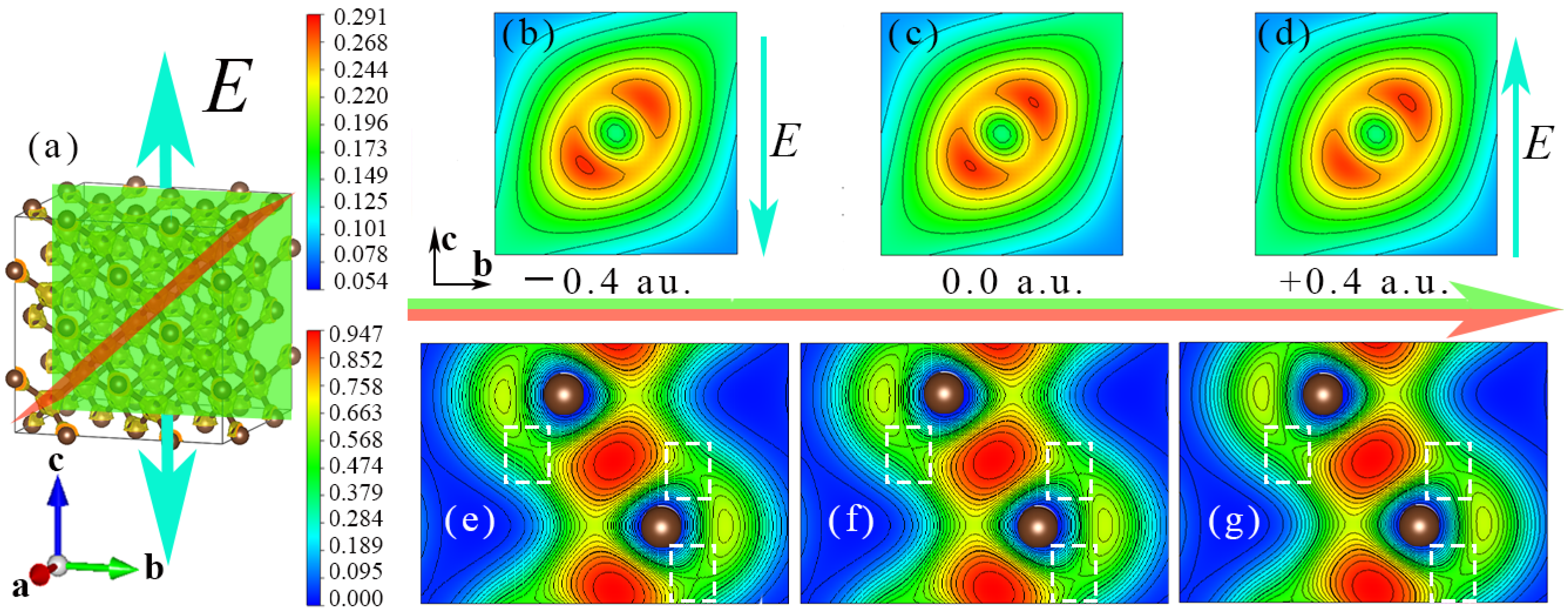
3.2. Charge Density Characteristics of Diamond under the Action of External Electric Field
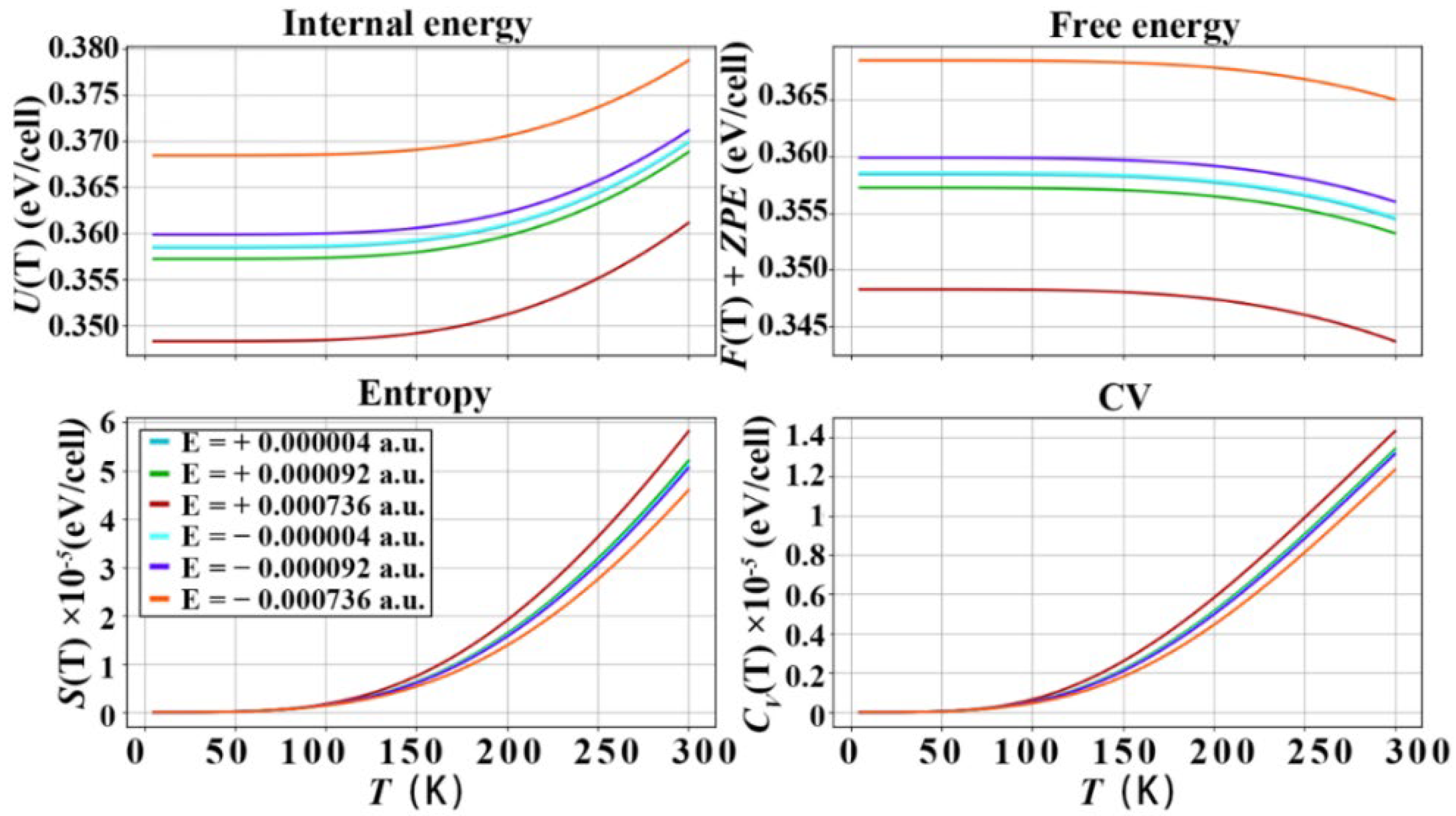
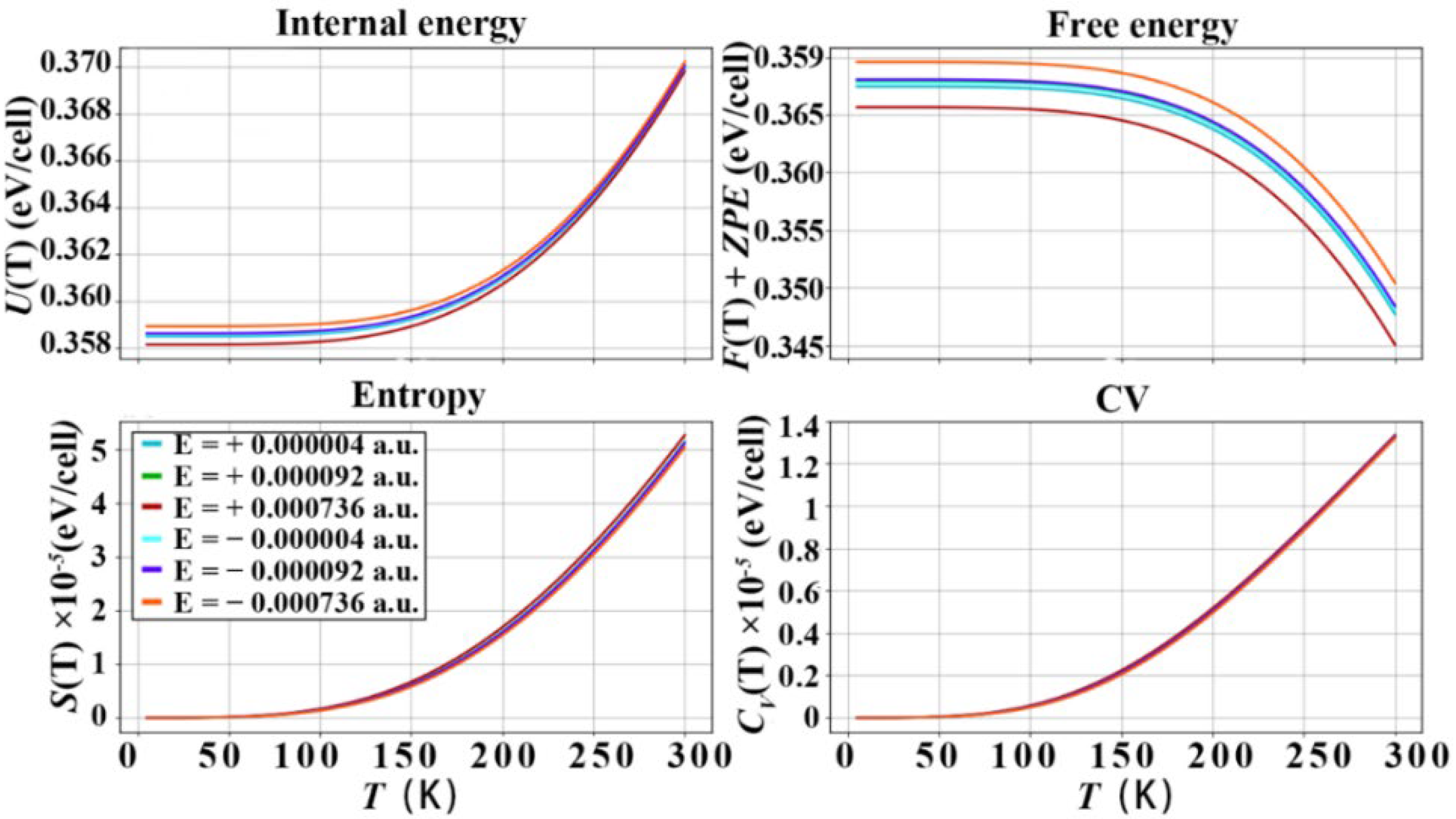
3.3. Thermodynamic Properties of Diamond under the Action of Electric Field
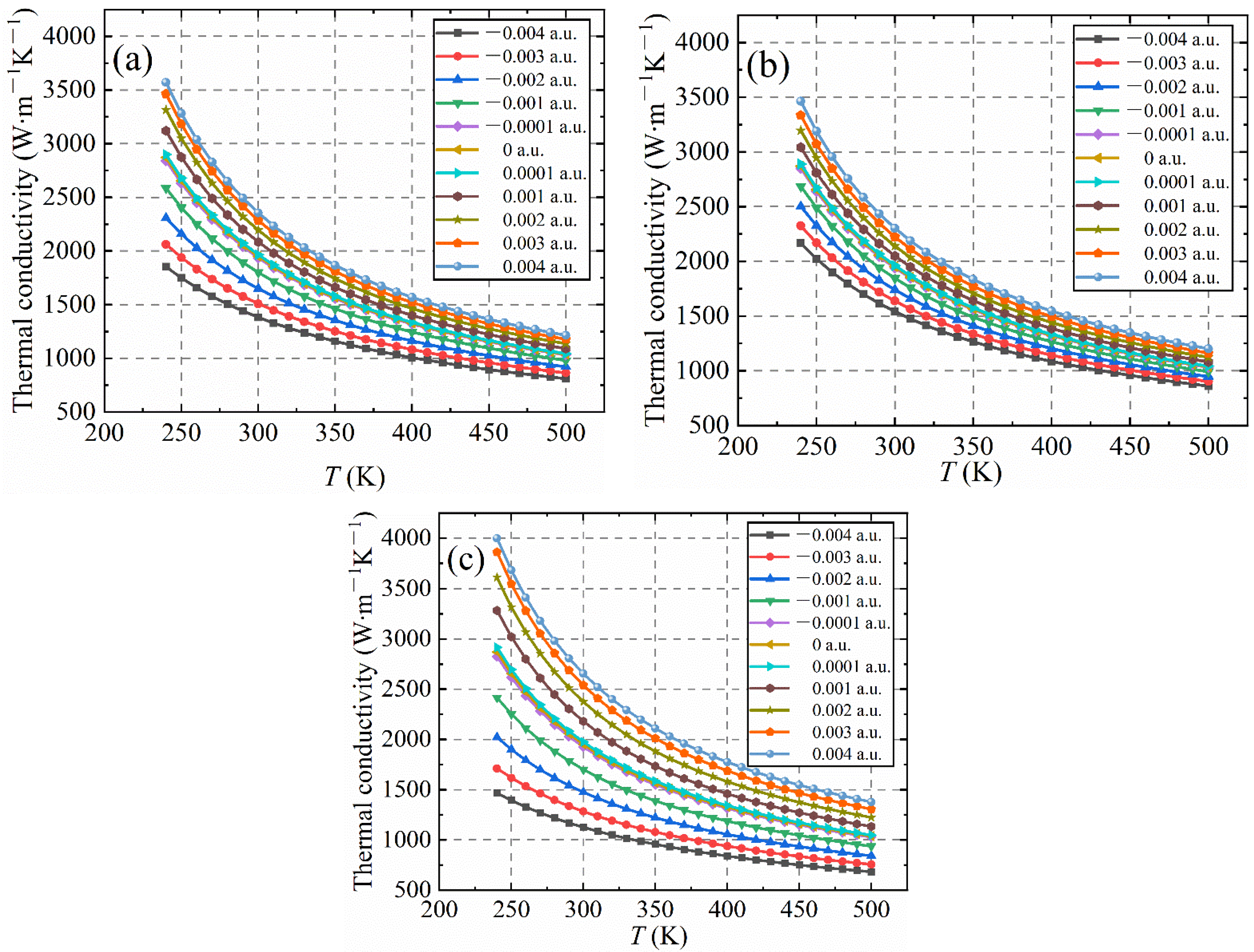
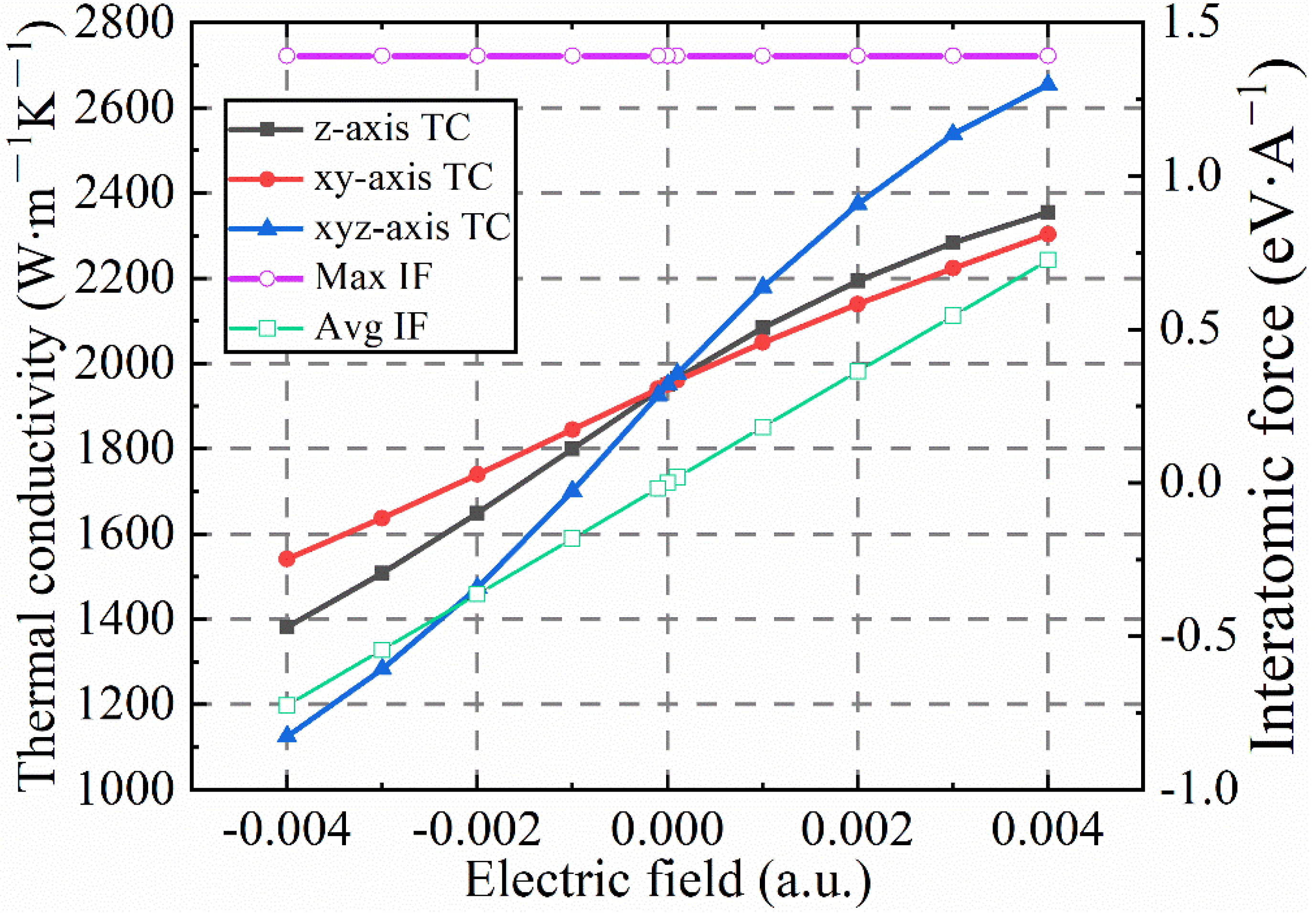
3.4. Variation in Lattice Thermal Conductivity of Diamond under Electric Field
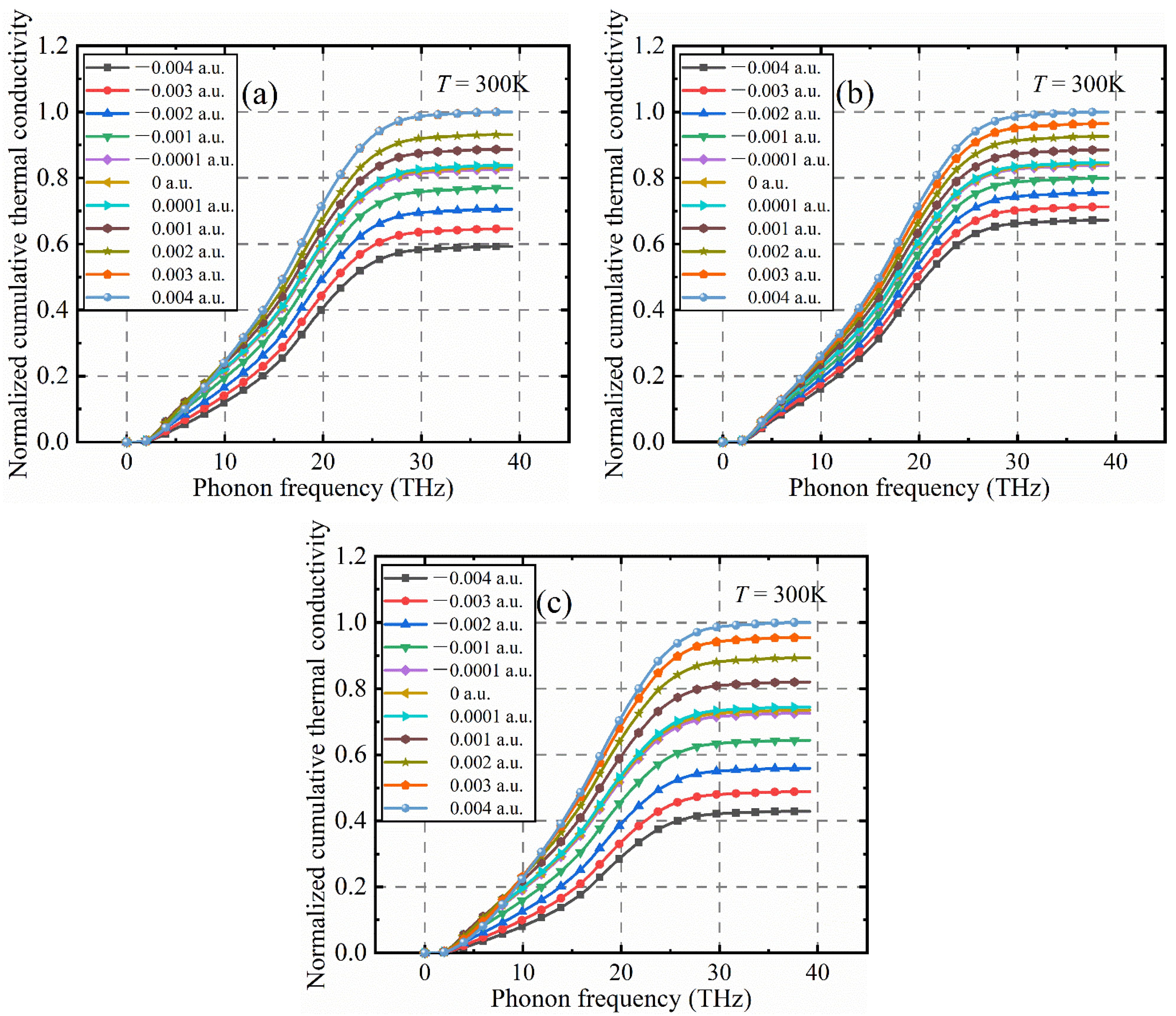
3.5. Phonon Thermal Transport Properties of Diamond under Electric Field
4. Conclusions
- (1)
- The response of diamond to the external electric field has anisotropy in three crystallographic directions. Moreover, the damage of positive and negative electric fields to the diamond phonon dispersion relationship is different. The three low-frequency acoustic branches are more sensitive to the electric field than the three high-frequency optical branches. The low-frequency lattice vibration of the diamond is more sensitive to the electric field.
- (2)
- In the case of considering the electro-acoustic coupling, it is found by calculating the thermodynamic properties of a diamond under the electric field. The electric field will change the internal energy, free energy, entropy and specific heat capacity of the diamond. The [001] and [111] orientations of diamond are more sensitive to electric field than the [110] orientation. In the [111] crystallographic orientation, when the electric field strength is ±0.000736 a.u., the constant volume specific heat capacities are 1.45 × 10−4 eV/cell and 1.22 × 10−4 eV/cell, which are increased and decreased by 9.8% and −7.6%, respectively. The electric field causes changes in the extranuclear electron potential and kinetic energy of the C atoms in diamond, and the electroacoustic coupling causes the electrons to transfer part of the energy of the electric field to the phonons.
- (3)
- The electric field will lead to a change in the thermal conductivity of the diamond lattice. Under the positive electric field, the thermal conductivity of the diamond lattice will increase, and conversely, the thermal conductivity of the diamond lattice will decrease under the negative electric field. When an electric field of ±0.004 a.u. is applied in the diamond [111] crystallographic direction and the temperature is 300 K, the thermal conductivity is 2654 and 1283 . The corresponding percentages are 36.1% and −34%, respectively. The electric field will cause changes in the electron density distribution in diamond, destroying diamond lattice symmetry and leading to a change in the interatomic force constant. The average interatomic force increases linearly with the increase in the electric field strength.
- (4)
- By calculating and analyzing the thermal transport properties of diamond phonons under the electric field, it is found that the electric field does not significantly change the phonon group velocity of the diamond. The response of diamond phonon thermal transport characteristics to electric field mainly focuses on the change of phonon mean free path, phonon–phonon interaction strength and phonon lifetime. Under a positive electric field, the increase in the mean free path of phonons, the enhancement of phonon–phonon interaction strength, and the prolongation of phonon lifetime all significantly promote the thermal conductivity of diamond lattice. On the contrary, under the negative electric field, the decrease in the phonon mean free path, the decrease in phonon–phonon interaction strength and the shortening of phonon lifetime significantly reduce the thermal conductivity of the diamond lattice. The response of the diamond phonon’s thermal transport to an electric field is mainly concentrated in the phonon part with a frequency of less than 30 THz.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Larsson, K. The Combined Influence of Dopant Species and Surface Termination on the Electronic Properties of Diamond Surfaces. C–J. Carbon Res. 2020, 6, 22. [Google Scholar] [CrossRef]
- Silvestri, L.; Cervenka, J.; Prawer, S.; Ladouceur, F. First Principle Study of Valence-Band Offsets at AlN/Diamond Heterojunctions. Diam. Relat. Mater. 2013, 31, 25–29. [Google Scholar] [CrossRef]
- Rao, L.; Liu, H.; Shao, W.; Hu, T.; Xing, X.; Ren, X.; Zhou, Y.; Yang, Q. Investigation on the Interface Characteristic between TiN and Diamond by First-Principles Calculation. Diam. Relat. Mater. 2020, 109, 108023. [Google Scholar] [CrossRef]
- Wei, L.; Kuo, P.K.; Thomas, R.L.; Anthony, T.R.; Banholzer, W.F. Thermal Conductivity of Isotopically Modified Single Crystal Diamond. Phys. Rev. Lett. 1993, 70, 3764–3767. [Google Scholar] [CrossRef]
- Twitchen, D.J.; Pickles, C.S.J.; Coe, S.E.; Sussmann, R.S.; Hall, C.E. Thermal Conductivity Measurements on CVD Diamond. Diam. Relat. Mater. 2001, 10, 731–735. [Google Scholar] [CrossRef]
- Hartmann, J.; Voigt, P.; Reichling, M. Measuring Local Thermal Conductivity in Polycrystalline Diamond with a High Resolution Photothermal Microscope. J. Appl. Phys. 1997, 81, 2966–2972. [Google Scholar] [CrossRef]
- Chakraborty, P.; Xiong, G.; Cao, L.; Wang, Y. Lattice Thermal Transport in Superhard Hexagonal Diamond and Wurtzite Boron Nitride: A Comparative Study with Cubic Diamond and Cubic Boron Nitride. Carbon 2018, 139, 85–93. [Google Scholar] [CrossRef]
- Ciupiński, Ł.; Kruszewski, M.J.; Grzonka, J.; Chmielewski, M.; Zielińsk, R.; Moszczyńska, D.; Michalski, A. Design of Interfacial Cr3C2 Carbide Layer via Optimization of Sintering Parameters Used to Fabricate Copper/Diamond Composites for Thermal Management Applications. Mater. Des. 2017, 120, 170–185. [Google Scholar] [CrossRef]
- Bai, G.; Zhang, Y.; Dai, J.; Wang, L.; Wang, X.; Wang, J.; Kim, M.J.; Chen, X.; Zhang, H. Tunable Coef Fi Cient of Thermal Expansion of Cu-B/Diamond Composites Prepared by Gas Pressure in Fi Ltration. J. Alloys Compd. 2019, 794, 473–481. [Google Scholar] [CrossRef]
- Arai, S.; Ueda, M. Fabrication of High Thermal Conductivity Copper/Diamond Composites by Electrodeposition under Potentiostatic Conditions. J. Appl. Electrochem. 2020, 50, 631–638. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Zheng, S.; Lu, Z.; Pu, J.; Zhang, G. Adhesive Transfer at Copper/Diamond Interface and Adhesion Reduction Mechanism with Fluorine Passivation: A First-Principles Study. Carbon 2018, 127, 548–556. [Google Scholar] [CrossRef]
- Ren, S.; Shen, X.; Guo, C.; Liu, N.; Zang, J.; He, X.; Qu, X. Effect of Coating on the Microstructure and Thermal Conductivities of Diamond-Cu Composites Prepared by Powder Metallurgy. Compos. Sci. Technol. 2011, 71, 1550–1555. [Google Scholar] [CrossRef]
- Mortazavi, B.; Shojaei, F.; Zhuang, X.; Pereira, L.F.C. First-Principles Investigation of Electronic, Optical, Mechanical and Heat Transport Properties of Pentadiamond: A Comparison with Diamond. Carbon Trends 2021, 3, 100036. [Google Scholar] [CrossRef]
- Barman, S.; Srivastava, G.P. Quantitative Estimate of Phonon Scattering Rates in Different Forms of Diamond. Phys. Rev. B 2006, 73, 073301. [Google Scholar] [CrossRef]
- Vasil’ev, N.S.; Gorelik, V.S. Properties of Optical and Acoustic Phonons in Diamond Crystals. Bull. Lebedev. Phys. Inst. 2011, 38, 255–262. [Google Scholar] [CrossRef]
- Lu, T.; Chen, Q. Ultrastrong Regulation Effect of the Electric Field on the All-Carboatomic Ring Cyclo [18]Carbon**. ChemPhysChem 2021, 22, 386–395. [Google Scholar] [CrossRef]
- Ran, Z.; Du, B.; Li, J.; Liang, H.; Kong, X.; Jiang, J.; Wang, M. Electric Field Regulation of Insulator Interface by FGM With Conductivity for Superconducting-GIL. IEEE Trans. Appl. Supercond. 2019, 29, 1–5. [Google Scholar] [CrossRef]
- Duan, Y.-J.; Zhao, Y.; Cheng, S.-B.; Wei, Q. On the Precise and Continuous Regulation of the Superatomic and Spectroscopic Behaviors of the Quasi-Cubic W4C4 Cluster by the Oriented External Electric Field. J. Phys. Chem. A 2022, 126, 29–35. [Google Scholar] [CrossRef]
- Souza, I.; Íñiguez, J.; Vanderbilt, D. First-Principles Approach to Insulators in Finite Electric Fields. Phys. Rev. Lett. 2002, 89, 117602. [Google Scholar] [CrossRef]
- Kim, K.; Ju, H.; Kim, J. Filler Orientation of Boron Nitride Composite via External Electric Field for Thermal Conductivity Enhancement. Ceram. Int. 2016, 42, 8657–8663. [Google Scholar] [CrossRef]
- Huber, W.H.; Hernandez, L.M.; Goldman, A.M. Electric Field Dependence of the Thermal Conductivity of Quantum Paraelectrics. Phys. Rev. B 2000, 62, 8588–8591. [Google Scholar] [CrossRef]
- Aikawa, Y.; Baba, K.; Shohata, N.; Yoneda, H.; Ueda, K. Photoconductive Properties of Polycrystalline Diamond under High Electric Field Strength. Diam. Relat. Mater. 1996, 5, 737–740. [Google Scholar] [CrossRef]
- Sankara Reddy, K.S.; Satyam, M. Structural Ordering of Diamond like Carbon Films by Applied Electric Field. Solid State Commun. 1995, 93, 797–799. [Google Scholar] [CrossRef]
- Gao, Y.; Okada, S. Electronic Properties of Diamond Nanowires under an External Electric Field. Diam. Relat. Mater. 2022, 125, 109029. [Google Scholar] [CrossRef]
- Lambert, N.; Taylor, A.; Hubík, P.; Bulíř, J.; More-Chevalier, J.; Karaca, H.; Fleury, C.; Voves, J.; Šobáň, Z.; Pogany, D.; et al. Modeling Current Transport in Boron-Doped Diamond at High Electric Fields Including Self-Heating Effect. Diam. Relat. Mater. 2020, 109, 108003. [Google Scholar] [CrossRef]
- Gonze, X.; Amadon, B.; Antonius, G.; Arnardi, F.; Baguet, L.; Beuken, J.-M.; Bieder, J.; Bottin, F.; Bouchet, J.; Bousquet, E.; et al. The Abinitproject: Impact, Environment and Recent Developments. Comput. Phys. Commun. 2020, 248, 107042. [Google Scholar] [CrossRef]
- Romero, A.H.; Allan, D.C.; Amadon, B.; Antonius, G.; Applencourt, T.; Baguet, L.; Bieder, J.; Bottin, F.; Bouchet, J.; Bousquet, E.; et al. ABINIT: Overview and Focus on Selected Capabilities. J. Chem. Phys. 2020, 152, 124102. [Google Scholar] [CrossRef]
- Gonze, X.; Jollet, F.; Abreu Araujo, F.; Adams, D.; Amadon, B.; Applencourt, T.; Audouze, C.; Beuken, J.-M.; Bieder, J.; Bokhanchuk, A.; et al. Recent Developments in the ABINIT Software Package. Comput. Phys. Commun. 2016, 205, 106–131. [Google Scholar] [CrossRef]
- Gonze, X.; Amadon, B.; Anglade, P.-M.; Beuken, J.-M.; Bottin, F.; Boulanger, P.; Bruneval, F.; Caliste, D.; Caracas, R.; Côté, M.; et al. ABINIT: First-Principles Approach to Material and Nanosystem Properties. Comput. Phys. Commun. 2009, 180, 2582–2615. [Google Scholar] [CrossRef]
- Torrent, M.; Jollet, F.; Bottin, F.; Zérah, G.; Gonze, X. Implementation of the Projector Augmented-Wave Method in the ABINIT Code: Application to the Study of Iron under Pressure. Comput. Mater. Sci. 2008, 42, 337–351. [Google Scholar] [CrossRef]
- Togo, A.; Chaput, L.; Tanaka, I. Distributions of Phonon Lifetimes in Brillouin Zones. Phys. Rev. B 2015, 91, 094306. [Google Scholar] [CrossRef]
- Chaput, L. Direct Solution to the Linearized Phonon Boltzmann Equation. Phys. Rev. Lett. 2013, 110, 265506. [Google Scholar] [CrossRef] [PubMed]
- Momma, K.; Izumi, F. VESTA 3 for Three-Dimensional Visualization of Crystal, Volumetric and Morphology Data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Petretto, G.; Gonze, X.; Hautier, G.; Rignanese, G.-M. Convergence and Pitfalls of Density Functional Perturbation Theory Phonons Calculations from a High-Throughput Perspective. Comput. Mater. Sci. 2018, 144, 331–337. [Google Scholar] [CrossRef]
- Brunin, G.; Miranda, H.P.C.; Giantomassi, M.; Royo, M.; Stengel, M.; Verstraete, M.J.; Gonze, X.; Rignanese, G.-M.; Hautier, G. Phonon-Limited Electron Mobility in Si, GaAs, and GaP with Exact Treatment of Dynamical Quadrupoles. Phys. Rev. B 2020, 102, 094308. [Google Scholar] [CrossRef]
- Zhao, Y.; Yan, F.; An, Y. Formation and Performance of Diamond (111)/Cu Interface from First-Principles Calculation. Coatings 2022, 12, 619. [Google Scholar] [CrossRef]
- Park, M.; Choi, W.B.; Schlesser, R.; Sowers, A.T.; Bergman, L.; Nemanich, R.J.; Sitar, Z.; Hren, J.J.; Cuomo, J.J. The Effect of Substitutional Nitrogen Incorporation on Electron Emission from CVD Diamond. In Proceedings of the Eleventh International Vacuum Microelectronics Conference, IVMC’98 (Cat. No. 98TH8382), Asheville, NC, USA, 19–24 July 1998; IEEE: Piscataway, NJ, USA, 1998; pp. 269–270. [Google Scholar]
- Irie, M.; Endo, S.; Wang, C.L.; Ito, T. Fabrication and Properties of Lateral P-i-p Structures Using Single-Crystalline CVD Diamond Layers for High Electric Field Applications. Diam. Relat. Mater. 2003, 12, 1563–1568. [Google Scholar] [CrossRef]
- Giustino, F. Electron-Phonon Interactions from First Principles. Rev. Mod. Phys. 2017, 89, 015003. [Google Scholar] [CrossRef]
- Abrikosov, A.A.; Gorkov, L.P.; Dzyaloshinskii, E. Methods of Quantum Field Theory in Statistical Physics; Dover Publications: Dover, NY, USA, 1975. [Google Scholar]
- Poncé, S.; Li, W.; Reichardt, S.; Giustino, F. First-Principles Calculations of Charge Carrier Mobility and Conductivity in Bulk Semiconductors and Two-Dimensional Materials. Reports Prog. Phys. 2020, 83, 036501. [Google Scholar] [CrossRef]
- Madsen, G.K.H.; Carrete, J.; Verstraete, M.J. BoltzTraP2, a Program for Interpolating Band Structures and Calculating Semi-Classical Transport Coefficients. Comput. Phys. Commun. 2018, 231, 140–145. [Google Scholar] [CrossRef] [Green Version]
- Nunes, R.W.; Gonze, X. Berry-Phase Treatment of the Homogeneous Electric Field Perturbation in Insulators. Phys. Rev. B 2001, 63, 155107. [Google Scholar] [CrossRef]
- Resta, R. Macroscopic Polarization in Crystalline Dielectrics: The Geometric Phase Approach. Rev. Mod. Phys. 1994, 66, 899–915. [Google Scholar] [CrossRef]
- Tang, D.S.; Cao, B.Y. Phonon Thermal Transport Properties of GaN with Symmetry-Breaking and Lattice Deformation Induced by the Electric Field. Int. J. Heat Mass Transf. 2021, 179, 121659. [Google Scholar] [CrossRef]
- Qi, R.; Li, N.; Du, J.; Shi, R.; Huang, Y.; Yang, X.; Liu, L.; Xu, Z.; Dai, Q.; Yu, D.; et al. Four-Dimensional Vibrational Spectroscopy for Nanoscale Mapping of Phonon Dispersion in BN Nanotubes. Nat. Commun. 2021, 12, 1179. [Google Scholar] [CrossRef]
- De Leonardis, F.; Soref, R.A.; Passaro, V.M.N. Dispersion of Nonresonant Third-Order Nonlinearities in Silicon Carbide. Sci. Rep. 2017, 7, 40924. [Google Scholar] [CrossRef]
- Calzolari, A.; Nardelli, M.B. Dielectric Properties and Raman Spectra of ZnO from a First Principles Finite-Differences/Finite-Fields Approach. Sci. Rep. 2013, 3, 2999. [Google Scholar] [CrossRef]
- Chen, L.; Chen, S.; Hou, Y. Understanding the Thermal Conductivity of Diamond/Copper Composite by First-Principles Calculations. Carbon 2019, 148, 249–257. [Google Scholar] [CrossRef]
- Kim, H.; Vogelgesang, R.; Ramdas, A.; Rodriguez, S.; Grimsditch, M. Electronic Raman and Infrared Spectra of Acceptors in Isotopically Controlled Diamonds. Phys. Rev. B-Condens. Matter Mater. Phys. 1998, 57, 15315–15327. [Google Scholar] [CrossRef]
- Sparavigna, A. Influence of Isotope Scattering on the Thermal Conductivity of Diamond. Phys. Rev. B-Condens. Matter Mater. Phys. 2002, 65, 1–5. [Google Scholar] [CrossRef]
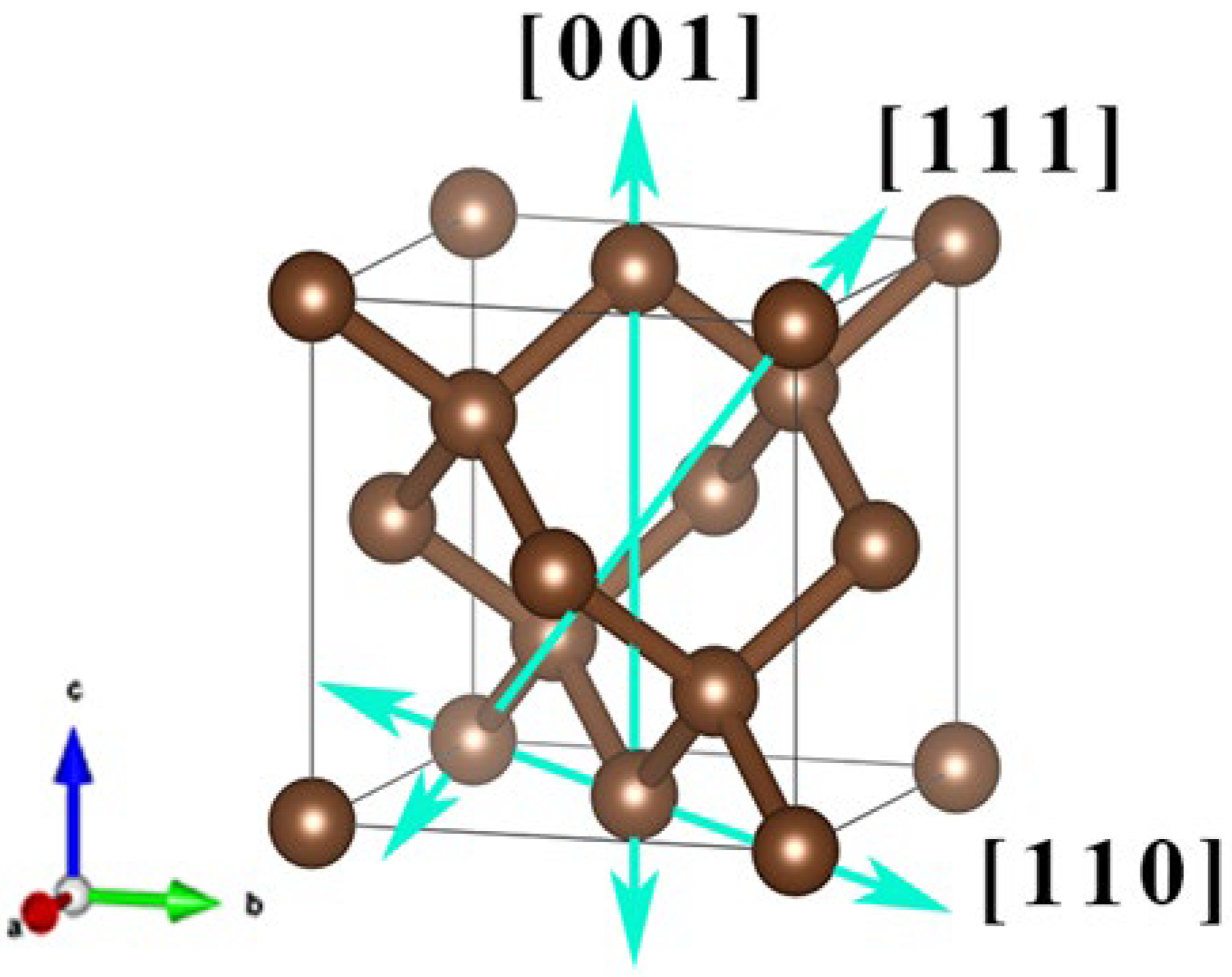




| Primitive Cell Base Vector | Electric Field Strength (Macroscopic Electric Field Unit: V∙cm−1, Microscopic Electric Field Unit: a.u.) | |||
|---|---|---|---|---|
| ±2.06 × 105 | ±9.78 × 106 | ±4.73 × 107 | ±3.78 × 108 | |
| ±4 × 10−6 | ±1.9 × 10−5 | ±9.2 × 10−5 | ±7.36 × 10−4 | |
| Crystal Orientation | Electric Field Strength (Macroscopic Electric Field Unit: V∙cm−1, Microscopic Electric Field Unit: a.u.) | ||||
|---|---|---|---|---|---|
| ±5.14 × 107 | ±5.14 × 108 | ±1.03 × 109 | ±1.54 × 109 | ±2.06 × 109 | |
| ±1 × 104 | ±1 × 103 | ±2 × 103 | ±3 × 103 | ±4 × 103 | |
| Crystal Orientation | ||||||||
|---|---|---|---|---|---|---|---|---|
| [001] | −125.808 | −140.295 | −151.474 | −150.824 | 132.951 | 109.738 | 89.784 | 71.913 |
| [110] | −95.855 | −102.547 | −105.554 | −105.337 | 98.76 | 90.083 | 84.159 | 79.801 |
| [111] | −157.797 | −190.544 | −226.948 | −249.92 | 228.873 | 194.761 | 163.914 | 115.839 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Yan, F.; Liu, X.; Ma, H.; Zhang, Z.; Jiao, A. Thermal Transport Properties of Diamond Phonons by Electric Field. Nanomaterials 2022, 12, 3399. https://doi.org/10.3390/nano12193399
Zhao Y, Yan F, Liu X, Ma H, Zhang Z, Jiao A. Thermal Transport Properties of Diamond Phonons by Electric Field. Nanomaterials. 2022; 12(19):3399. https://doi.org/10.3390/nano12193399
Chicago/Turabian StyleZhao, Yongsheng, Fengyun Yan, Xue Liu, Hongfeng Ma, Zhenyu Zhang, and Aisheng Jiao. 2022. "Thermal Transport Properties of Diamond Phonons by Electric Field" Nanomaterials 12, no. 19: 3399. https://doi.org/10.3390/nano12193399
APA StyleZhao, Y., Yan, F., Liu, X., Ma, H., Zhang, Z., & Jiao, A. (2022). Thermal Transport Properties of Diamond Phonons by Electric Field. Nanomaterials, 12(19), 3399. https://doi.org/10.3390/nano12193399





