A New Approach to Modeling Ultrashort Channel Ballistic Nanowire GAA MOSFETs
Abstract
:1. Introduction
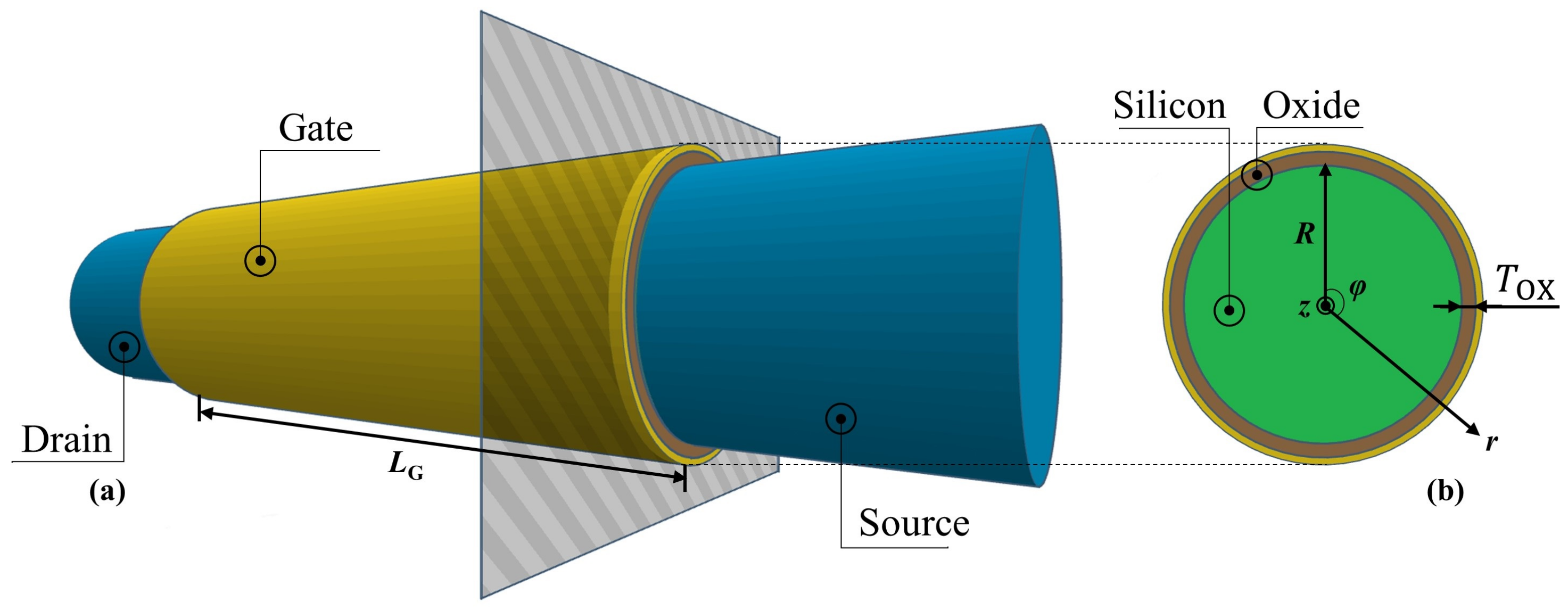
2. Device Structure and Model Formulas
2.1. Model Structure
2.2. Potential Profile
2.3. Landauer Formula
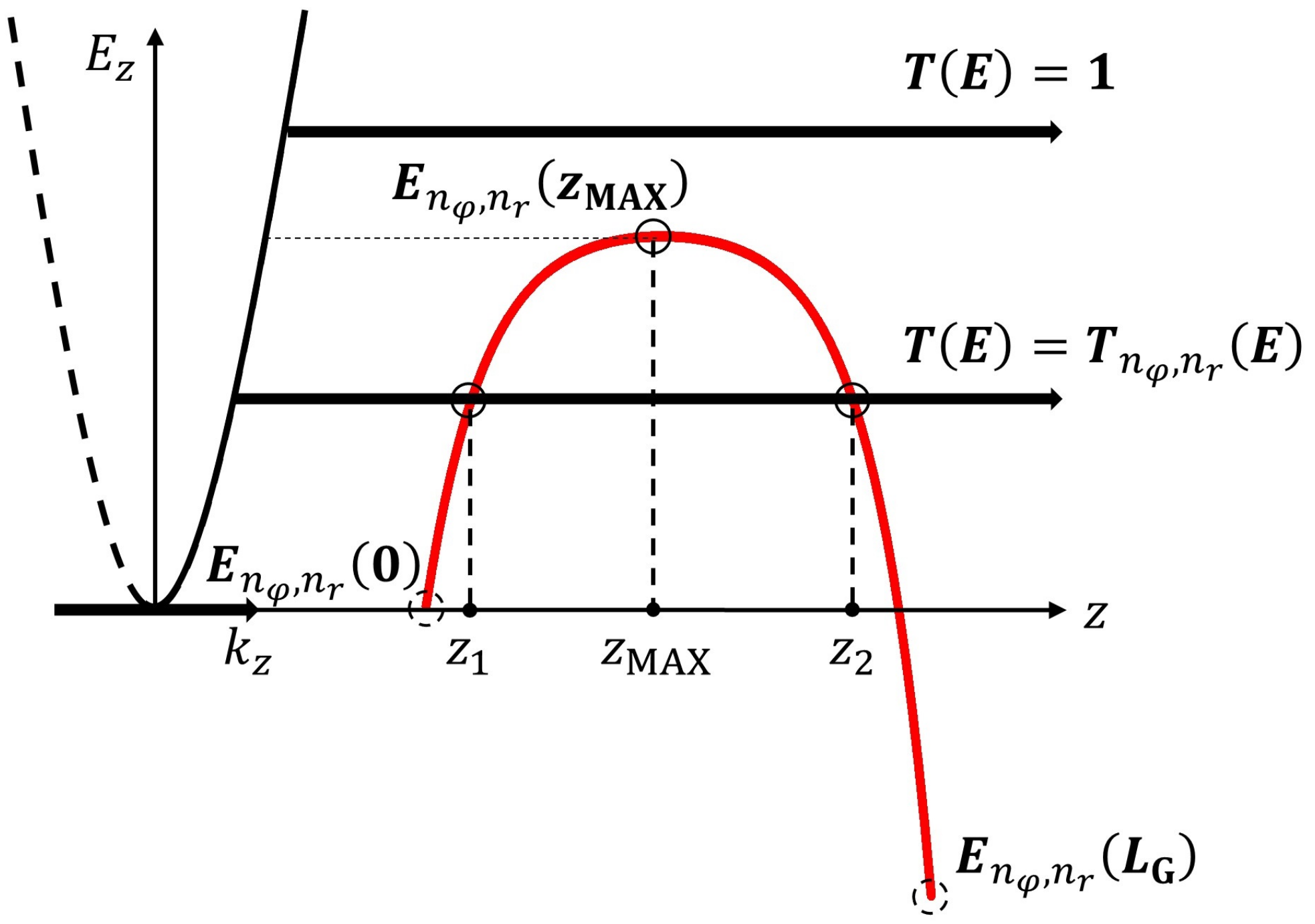
3. Calculation Method
3.1. Parabolic Energy Level Approximation
3.2. Unknown Parameter for All Operating Regions
3.3. Potential Barrier Top for All Operating Regions
3.4. Transmission Coefficient for All Operating Regions
3.5. Drain Current for All Operating Regions
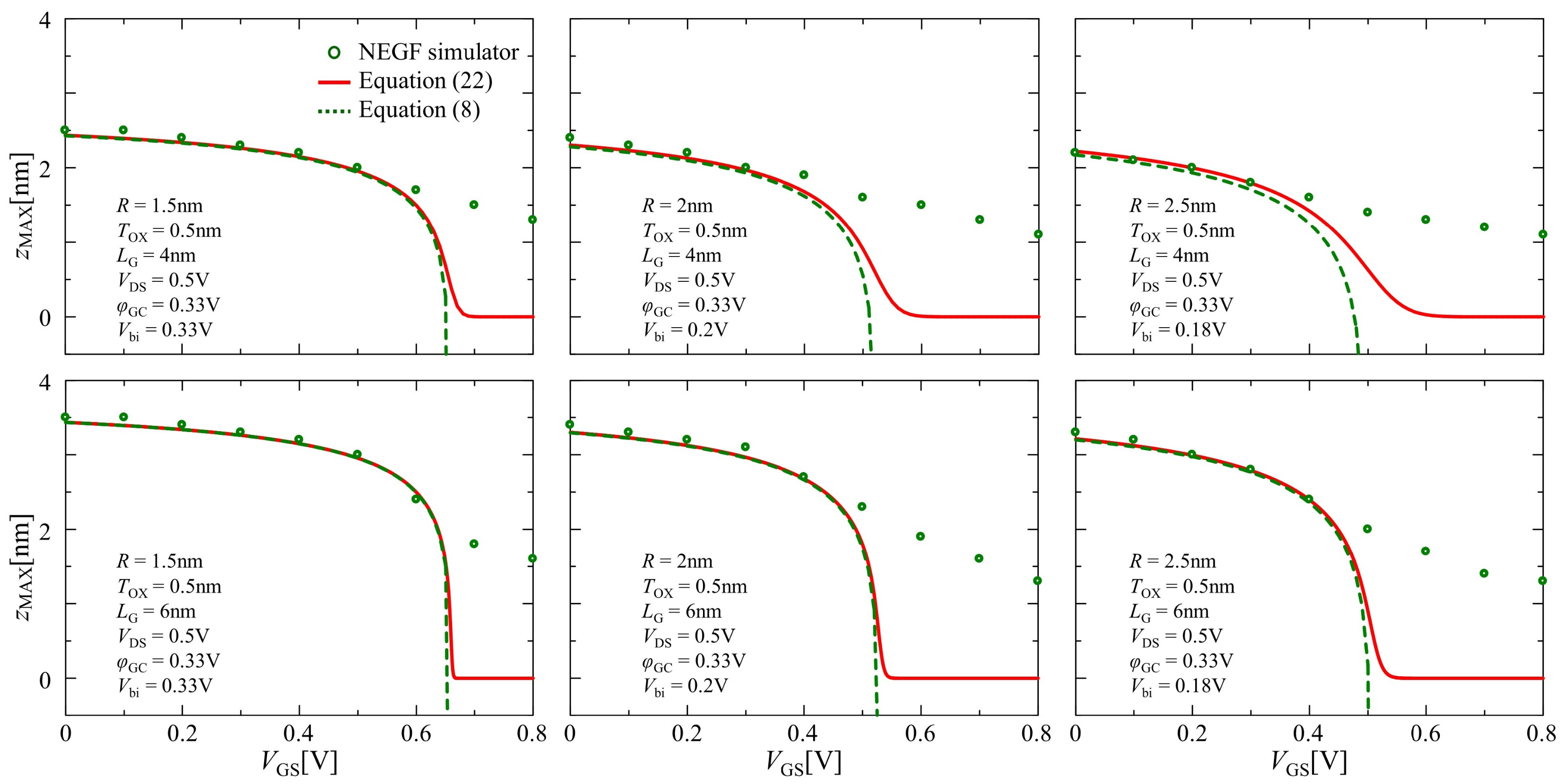
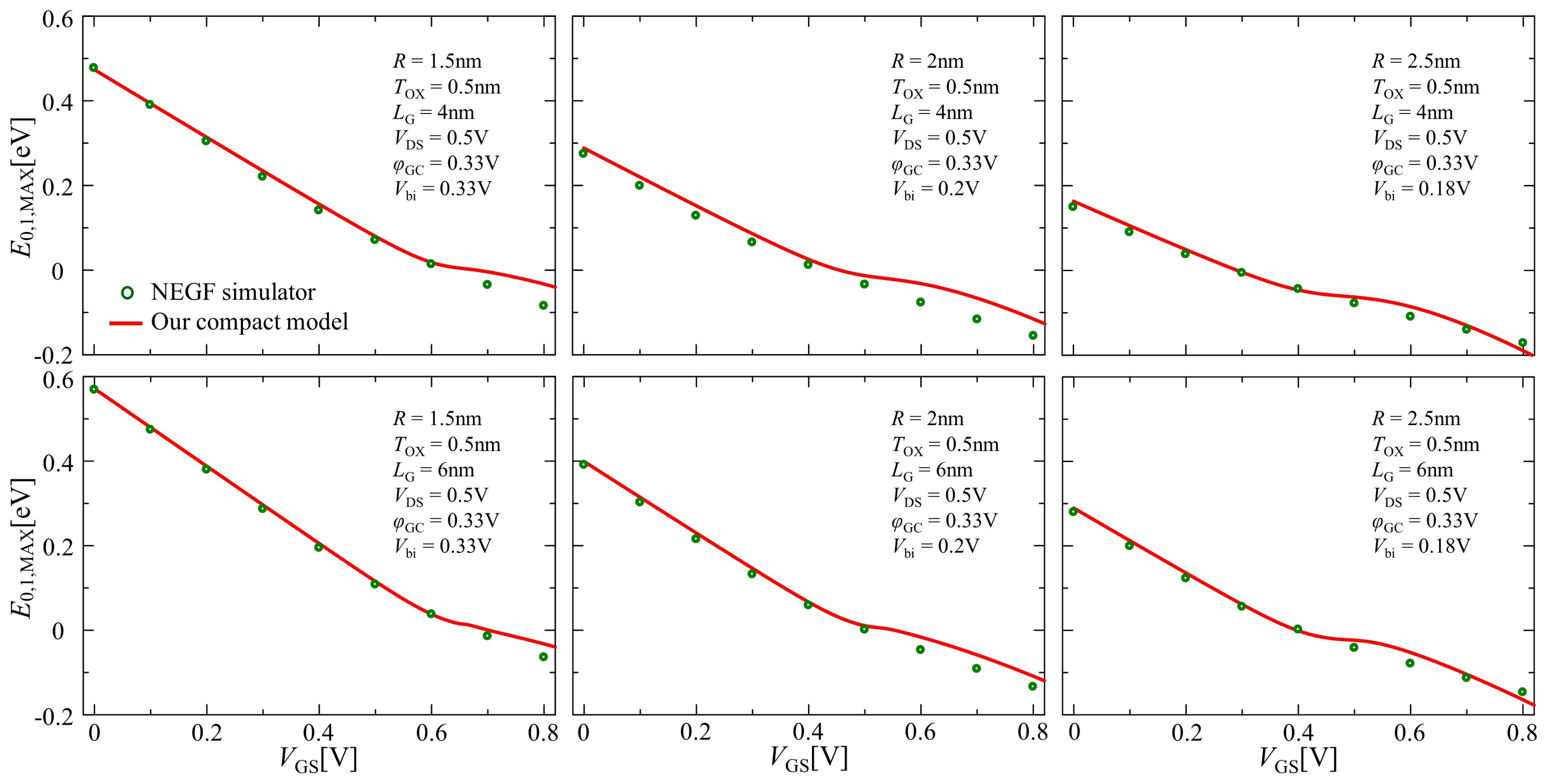
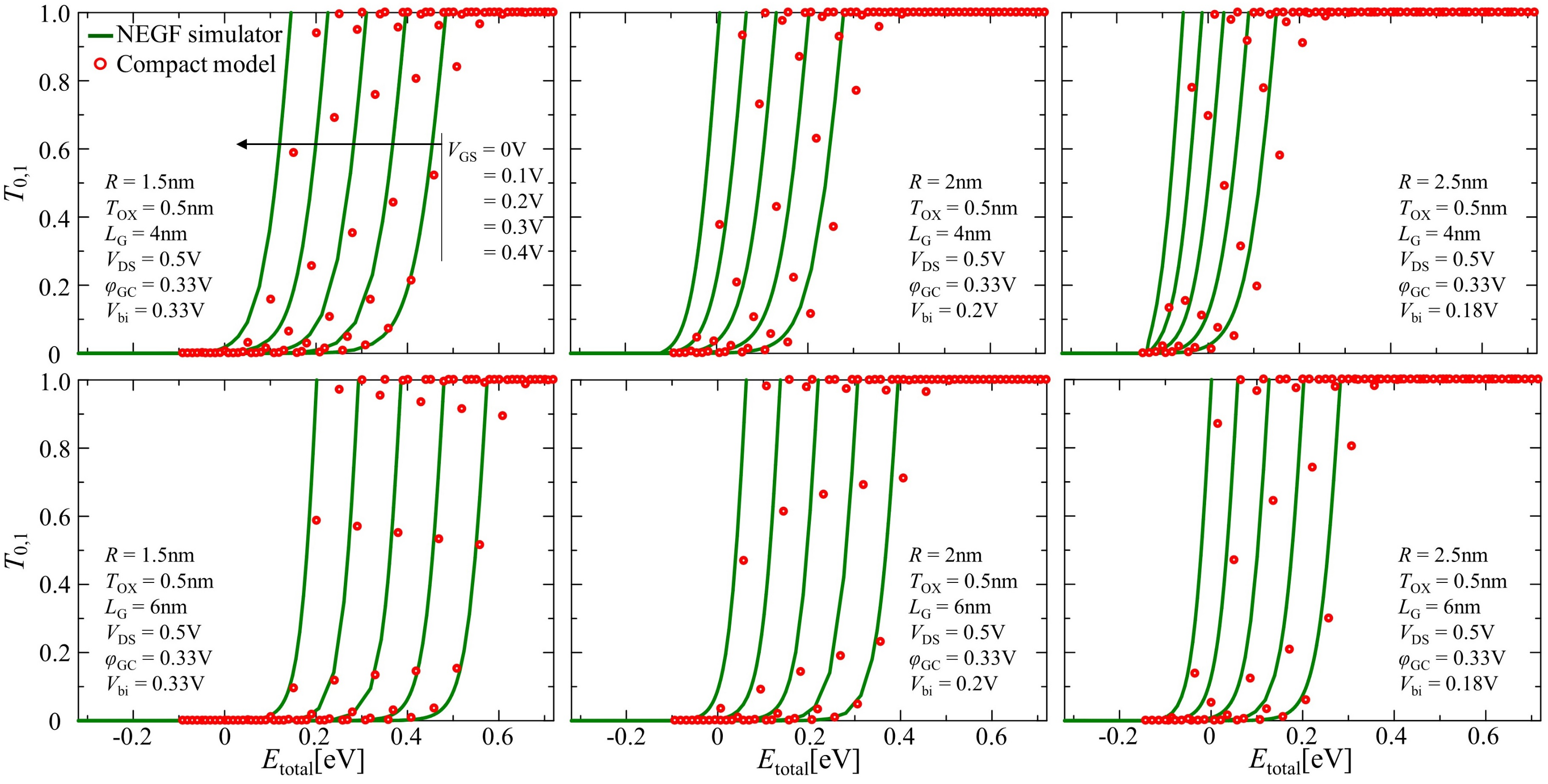
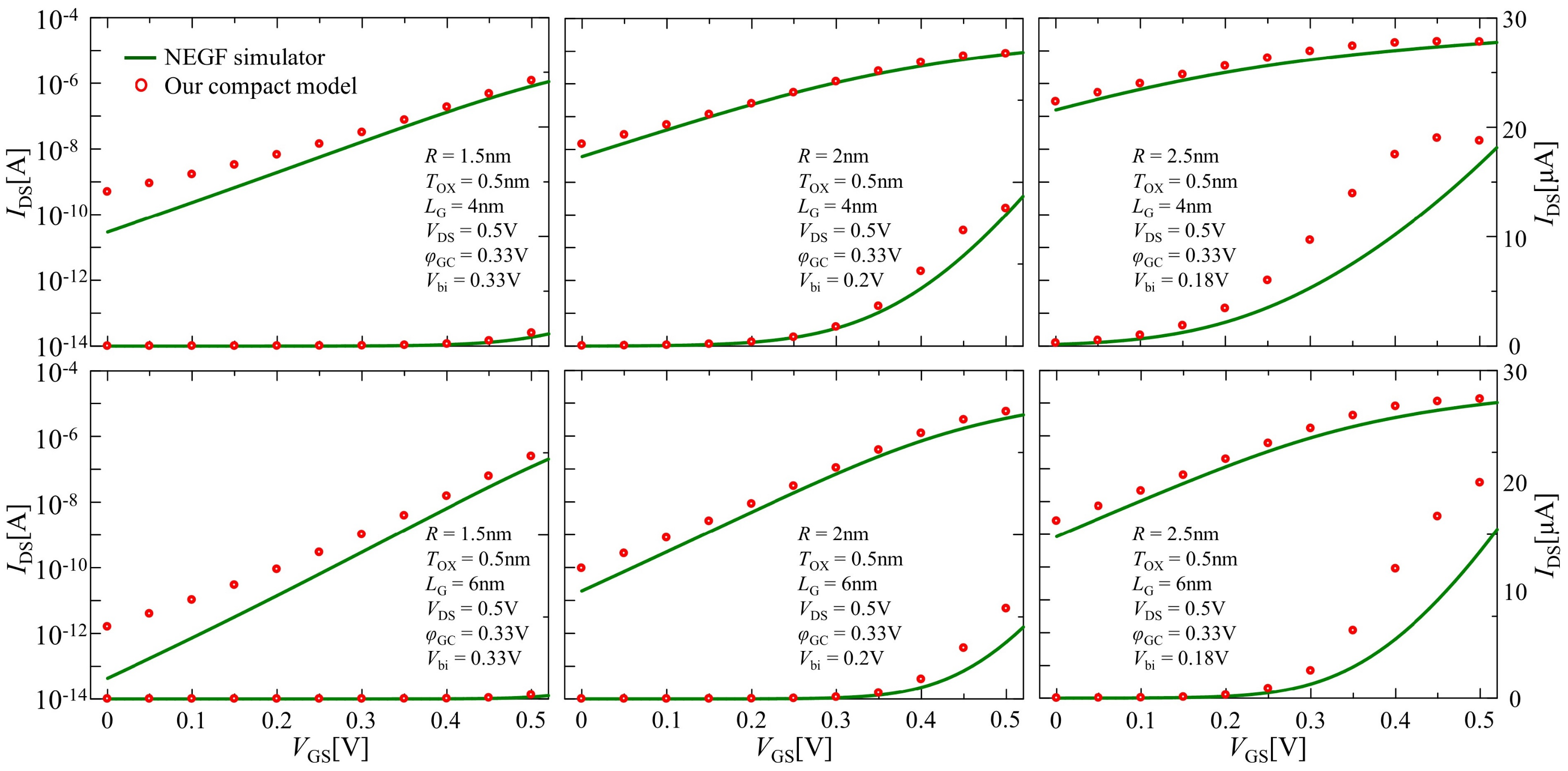
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rathee, D.S.; Yadav, R.; Ahuja, K. Reduction of drain induced barrier lowering by optimization Trimetal-GAA -Si -NW MOSFET in multimedia tools. Multimed. Tools Appl. 2022, 81, 19849–19862. [Google Scholar] [CrossRef]
- Bhol, K.; Nanda, U. Nanowire Array-based MOSFET for Future CMOS Technology to Attain the Ultimate Scaling Limit. Silicon 2021, 14, 1169–1177. [Google Scholar] [CrossRef]
- Kumar, R.; Bala, S.; Kumar, A. Study and Analysis of Advanced 3D Multi-Gate Junctionless Transistors. Silicon 2021, 14, 1053–1067. [Google Scholar] [CrossRef]
- Lee, Y.; Park, G.-H.; Choi, B.; Yoon, J.; Kim, H.-J.; Kim, D.H.; Kim, D.M.; Kang, M.-H.; Choi, S.-J. Design study of the gate-all-around silicon nanosheet MOSFETs. Semicond. Sci. Technol. 2020, 35, 03LT01. [Google Scholar] [CrossRef]
- Yilmaz, K.; Darbandy, G.; Reimbold, G.; Iniguez, B.; Lime, F.; Kloes, A. Equivalent DG Dimensions Concept for Compact Modeling of Short-Channel and Thin Body GAA MOSFETs Including Quantum Confinement. IEEE Trans. Electron Devices 2020, 67, 5381–5387. [Google Scholar] [CrossRef]
- Cheng, H.; Uno, S.; Nakazato, K. Analytic compact model of ballistic and quasi-ballistic transport for cylindrical gate-all-around MOSFET including drain-induced barrier lowering effect. J. Comput. Electron 2014, 14, 321–328. [Google Scholar] [CrossRef]
- Naveh, Y.; Likharev, K.K. Modeling of 10-nm-Scale Ballistic MOSFET’s. IEEE Electron Device Lett. 2000, 21, 5. [Google Scholar] [CrossRef]
- Abdi, M.A.; Djeffal, F.; Arar, D.; Hafiane, M.L. Numerical analysis of double gate and gate all around MOSFETs with bulk trap states. J. Mater. Sci. Mater. Electron. 2008, 19, 248–253. [Google Scholar] [CrossRef]
- Hosseini, R.; Fathipour, M.; Faez, R. Quantum simulation study of gate-all-around (GAA) silicon nanowire transistor and double gate metal oxide semiconductor field effect transistor (DG MOSFET). Int. J. Phys. Sci. 2012, 7, 5054–5061. [Google Scholar] [CrossRef]
- Vashishtha, V.; Clark, L.T. Comparing bulk-Si FinFET and gate-all-around FETs for the 5 nm technology node. Microelectron. J. 2021, 107, 104942. [Google Scholar] [CrossRef]
- Yilmaz, K.; Iniguez, B.; Lime, F.; Kloes, A. Quasi-Compact Model of Direct Source-to-Drain Tunneling Current in Ultrashort-Channel Nanosheet MOSFETs by Wavelet Transform. IEEE Trans. Electron. Devices 2022, 69, 1. [Google Scholar] [CrossRef]
- Zhang, Y.N.; Han, K.; Li, J.W. A Simulation Study of a Gate-All-Around Nanowire Transistor with a Core–Insulator. Micromachines 2020, 11, 223. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.H.; Li, X.J.; Sun, Y.B.; Shi, Y.L. A Vertical Combo Spacer to Optimize Electrothermal Characteristics of 7-nm Nanosheet Gate-All-Around Transistor. IEEE Trans. Electron Devices 2020, 67, 1–6. [Google Scholar] [CrossRef]
- Ganapati, R.; Samoju, V.R.; Jammu, B.R. Analytical Modeling of Threshold Voltage for Dual-Metal Double-Gate Gate-All-Around (DM-DG-GAA) MOSFET. Silicon 2021, 13, 2869–2880. [Google Scholar] [CrossRef]
- Das, U.K.; Bhattacharyya, T.K. Opportunities in Device Scaling for 3-nm Node and Beyond: FinFET versus GAA-FET Versus UFET. IEEE Trans. Electron Devices 2020, 67, 2633–2638. [Google Scholar] [CrossRef]
- Jang, D.; Yakimets, D.; Eneman, G.; Schuddinck, P.; Bardon, M.G.; Raghavan, P.; Spessot, A.; Verkest, D.; Mocuta, A. Device Exploration of NanoSheet Transistors for Sub-7-nm Technology Node. IEEE Trans. Electron Devices 2017, 64, 2707–2713. [Google Scholar] [CrossRef]
- Ajayan, J.; Nirmal, D.; Tayal, S.; Bhattacharya, S.; Arivazhagan, L.; Augustine Fletcher, A.A.S.; Murugapandiyan, P.; Ajitha, D. Nanosheet field effect transistors—A next generation device to keep Moore’s law alive: An intensive study. Microelectron. J. 2021, 114, 105141. [Google Scholar] [CrossRef]
- Natori, K. Ballistic/quasi-ballistic transport in nanoscale transistor. Appl. Surf. Sci. 2008, 254, 6194–6198. [Google Scholar] [CrossRef]
- Gu, J.; Zhang, Q.; Wu, Z.; Yao, J.; Zhang, Z.; Zhu, X.; Wang, G.; Li, J.; Zhang, Y.; Cai, Y. Cryogenic Transport Characteristics of P-Type Gate-All-Around Silicon Nanowire MOSFETs. Nanomaterials 2021, 11, 309. [Google Scholar] [CrossRef]
- Chatterjee, A.K.; Kushwaha, M.; Prasad, B. Analytical Model for Drain Current of a Ballistic MOSFET. Silicon 2021, 13, 1777–1785. [Google Scholar] [CrossRef]
- Aguirre, P.; Schenk, A. Ballistic Mobility Model for QDD Simulation of Ultra-short Transistors. In Proceedings of the 2018 IEEE 2nd Electron Devices Technology and Manufacturing Conference (EDTM), Kobe, Japan, 13–16 March 2018; pp. 77–79. [Google Scholar] [CrossRef]
- Cheng, H.; Zhang, C.; Liu, T.F.; Xie, C.; Yang, Z.J.; Zhang, Z.P. A Charge Density Model of Silicon-nanowire GAA MOSFET Incoroperating the Source-drian Tunneling Effect for IC Design. In Proceedings of the 2021 International Symposium on Computer Technology and Information Science (ISCTIS), Guilin, China, 4–6 June 2021; pp. 351–355. [Google Scholar] [CrossRef]
- Cousin, B.; Reyboz, M.; Rozeau, O.; Jaud, M.A.; Ernst, T.; Jomaah, J. A unified short-channel compact model for cylindrical surrounding-gate MOSFET. Solid-State Electron. 2011, 56, 40–46. [Google Scholar] [CrossRef]
- Cheng, H.; Uno, S.; Numata, T.; Nakazato, K. Analytic Compact Model of Ballistic and Quasi-Ballistic Cylindrical Gate-All-Around Metal-Oxide-Semiconductor Field Effect Transistors Including Two Subbands. Jpn. J. Appl. Phys. 2013, 52, 04CN03. [Google Scholar] [CrossRef]
- Cheng, H.; Zhang, Z.; Yang, Z.; Liu, Z. Compact model of short-channel cylindrical ballistic gate-all-around mosfet including the source-to-drain tunneling. J. Phys. Conf. Ser. 2018, 1026, 012011. [Google Scholar] [CrossRef]
- Mohan, C.; Choudhary, S.; Prasad, B. Gate All Around FET: AnAlternative of FinFET for Future Technology Nodes. In Proceedings of the International Conference on Emerging Trends in Engineering, Technology, Science and Management ICETETSM-2017, New Delhi, India, 11 June 2017; pp. 561–569. [Google Scholar]
- Yoon, J.S.; Jeong, J.; Lee, S.; Lee, J.; Baek, R.H. Gate-all-around FETs–nanosheet structure. In Nanowires–Recent Progress; IntechOpen: Rijeka, Croatia, 2020; Chapter 9. [Google Scholar] [CrossRef]
- Darbandy, G.; Mothes, S.; Schröter, M.; Kloes, A.; Claus, M. Performance analysis of parallel array of nanowires and a nanosheet in SG, DG and GAA FETs. Solid-State Electron. 2019, 162, 107641. [Google Scholar] [CrossRef]
- Kim, S.; Lee, K.; Kim, S.; Kim, M.; Lee, J.H.; Kim, S.; Park, B.G. Investigation of Device Performance for Fin Angle Optimization in FinFET and Gate-All-Around FETs for 3 nm-Node and Beyond. IEEE Trans. Electron Devices 2022, 69, 2088–2093. [Google Scholar] [CrossRef]
- Mil’nikov, G.; Mori, N.; Kamakura, Y.; Ezaki, T. R-matrix theory of quantum transport and recursive propagation method for device simulations. J. Appl. Phys. 2008, 104, 044506. [Google Scholar] [CrossRef]
- Khan, T.; Iztihad, H.M.; Sufian, A.; Alam, M.N.K.; Mollah, M.N.; Islam, M.R. Gate length scaling of Si nanowire FET: A NEGF study. In Proceedings of the 2015 International Conference on Electrical Engineering and Information Communication Technology (ICEEICT), Savar, Bangladesh, 21–23 May 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Zeng, J.W.; Deng, W.L.; Zhou, C.J.; Peng, J.; Huang, J.K. A Compact Model of MoS2 Field-Effect Transistors From Drift-Diffusion to Ballistic Carrier Transport Regimes. IEEE J. Electron Dev. 2020, 8, 285–290. [Google Scholar] [CrossRef]
- Vimala, P.; Kumar, N.R.N. Analytical Quantum Model for Germanium Channel Gate-All-Around (GAA) MOSFET. J. Nano Res. 2019, 59, 137–148. [Google Scholar] [CrossRef]
- Kim, S.; Kim, J.; Jang, D.; Ritzenthaler, R.; Lee, J.W. Comparison of temperature dependent carrier transport in finfet and gate-all-around nanowire fet. Appl. Sci. 2020, 10, 2979. [Google Scholar] [CrossRef]
- Bhol, K.; Jena, B.; Nanda, U. Journey of MOSFET from Planar to Gate All Around: A Review. Recent Pat. Nanotechnol. 2022, 16, 326–332. [Google Scholar] [CrossRef]
- Natori, K.; Kimura, Y.; Shimizu, T. Characteristics of a carbon nanotube field-effect transistor analyzed as a ballistic nanowire field-effect transistor. J. Appl. Phys. 2005, 97, 034306. [Google Scholar] [CrossRef]
- Hamid, H.A.E.; Iñíguez, B.; Guitart, J.R. Analytical model of the threshold voltage and subthreshold swing of undoped cylindrical gate-all-around-based MOSFETs. IEEE Trans. Electron Devices 2007, 54, 572–579. [Google Scholar] [CrossRef]
- Ragi, R.; Tayette da Nobrega, R.V.; Duarte, U.R.; Romero, M.A. An explicit quantum-mechanical compact model for the I–Vcharacteristics of cylindrical nanowire MOSFETs. IEEE Trans. Nanotechnol. 2016, 15, 627–634. [Google Scholar] [CrossRef]
- Seon, Y.; Kim, J.; Kim, S.; Jeon, J. Analytical Current-Voltage Model for Gate-All-Around Transistor with Poly-Crystalline Silicon Channel. Electronics 2019, 8, 988. [Google Scholar] [CrossRef]
- Numata, T.; Uno, S.; Hattori, J.; Mil’Nikov, G.; Kamakura, Y.; Mori, N.; Nakazato, K. A Self-Consistent Compact Model of Ballistic Nanowire MOSFET with Rectangular Cross Section. IEEE Trans. Electron. Devices 2013, 60, 856–862. [Google Scholar] [CrossRef]
- Lin, Y.K.; Duarte, J.P.; Kushwaha, P.; Agarwal, H.; Chang, H.L.; Sachid, A.; Salahuddin, S.; Hu, C.M. Compact Modeling Source-to-Drain Tunneling in Sub-10-nm GAA FinFET With Industry Standard Model. IEEE Trans. Electron Devices 2017, 64, 3576–3581. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Lam, K.T.; Low, K.L.; Yeo, Y.C.; Liang, G.C. Nanoscale FETs Simulation Based on Full-Complex-Band Structure and Self-Consistently Solved Atomic Potential. IEEE Trans. Electron Devices 2017, 64, 58–65. [Google Scholar] [CrossRef]
- Wong, H. Compact Modeling and Short-Channel Effects of Nanowire MOS Transistors. In Proceedings of the 2018 IEEE International Conference on Integrated Circuits, Technologies and Applications (ICTA), Beijing, China, 21–23 November 2018; pp. 7–10. [Google Scholar] [CrossRef]
- Lee, K.H.; Erlebach, A.; Penzin, O.; Smith, L. Quasi-Ballistic Drift-Diffusion Simulation of SiGe Nanowire MOSFETs Using the Kinetic Velocity Model. J. Electron Devices Soc. 2021, 9, 387–392. [Google Scholar] [CrossRef]
- Dasgupta, A.; Parihar, S.S.; Kushwaha, P.; Agarwal, H.; Kao, M.Y.; Salahuddin, S.; Chauhan, Y.S.; Hu, C.M. BSIM Compact Model of Quantum Confinement in Advanced Nanosheet FETs. IEEE Trans. Electron Devices 2020, 67, 730–737. [Google Scholar] [CrossRef]
- Bae, M.S.; Park, C.; Yun, H. Compact Drain Current Model of Nanoscale FinFET Considering Short Channel Effect in Ballistic Transport Regime. In Proceedings of the 2018 15th International Conference on Synthesis, Modeling, Analysis and Simulation Methods and Applications to Circuit Design (SMACD), Prague, Czech Republic, 2–5 July 2018; pp. 109–112. [Google Scholar] [CrossRef]
- Cheng, H.; Liu, T.F.; Zhang, C.; Liu, Z.F.; Yang, Z.J.; Nakazato, K.; Zhang, Z.P. Nanowire gate-all-around MOSFETs modeling: Ballistic transport incorporating the source-to-drain tunneling. Jpn. J. Appl. Phys. 2020, 59, 074002. [Google Scholar] [CrossRef]
- Numata, T.; Uno, S.; Kamakura, Y.; Mori, N.; Nakazato, K. Analytic Circuit Model of Ballistic Nanowire Metal–Oxide–Semiconductor Field-Effect Transistor for Transient Analysis. Jpn. J. Appl. Phys. 2013, 52, 04CN01. [Google Scholar] [CrossRef]
- Atlas User’s Manual DEVICE SIMULATION SOFTWARE, Charpter 14, Quantum Effect Simulation. Silvaco, Inc.: Santa Clara, CA, USA, 2016; pp. 771–815. Available online: https://dynamic.silvaco.com/dynamicweb/silen/ (accessed on 25 September 2022).
- More Moore. International Roadmap for Devices and Systems: 2017 Edition. IEEE Advancing Technology for Humanity. 2017. Available online: https://irds.ieee.org/editions/2017 (accessed on 25 September 2022).



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, H.; Yang, Z.; Zhang, C.; Xie, C.; Liu, T.; Wang, J.; Zhang, Z. A New Approach to Modeling Ultrashort Channel Ballistic Nanowire GAA MOSFETs. Nanomaterials 2022, 12, 3401. https://doi.org/10.3390/nano12193401
Cheng H, Yang Z, Zhang C, Xie C, Liu T, Wang J, Zhang Z. A New Approach to Modeling Ultrashort Channel Ballistic Nanowire GAA MOSFETs. Nanomaterials. 2022; 12(19):3401. https://doi.org/10.3390/nano12193401
Chicago/Turabian StyleCheng, He, Zhijia Yang, Chao Zhang, Chuang Xie, Tiefeng Liu, Jian Wang, and Zhipeng Zhang. 2022. "A New Approach to Modeling Ultrashort Channel Ballistic Nanowire GAA MOSFETs" Nanomaterials 12, no. 19: 3401. https://doi.org/10.3390/nano12193401
APA StyleCheng, H., Yang, Z., Zhang, C., Xie, C., Liu, T., Wang, J., & Zhang, Z. (2022). A New Approach to Modeling Ultrashort Channel Ballistic Nanowire GAA MOSFETs. Nanomaterials, 12(19), 3401. https://doi.org/10.3390/nano12193401





