Metal–Dielectric Polarization-Preserving Anisotropic Mirror for Chiral Optical Tamm State
Abstract
:1. Introduction
2. Description of the Model
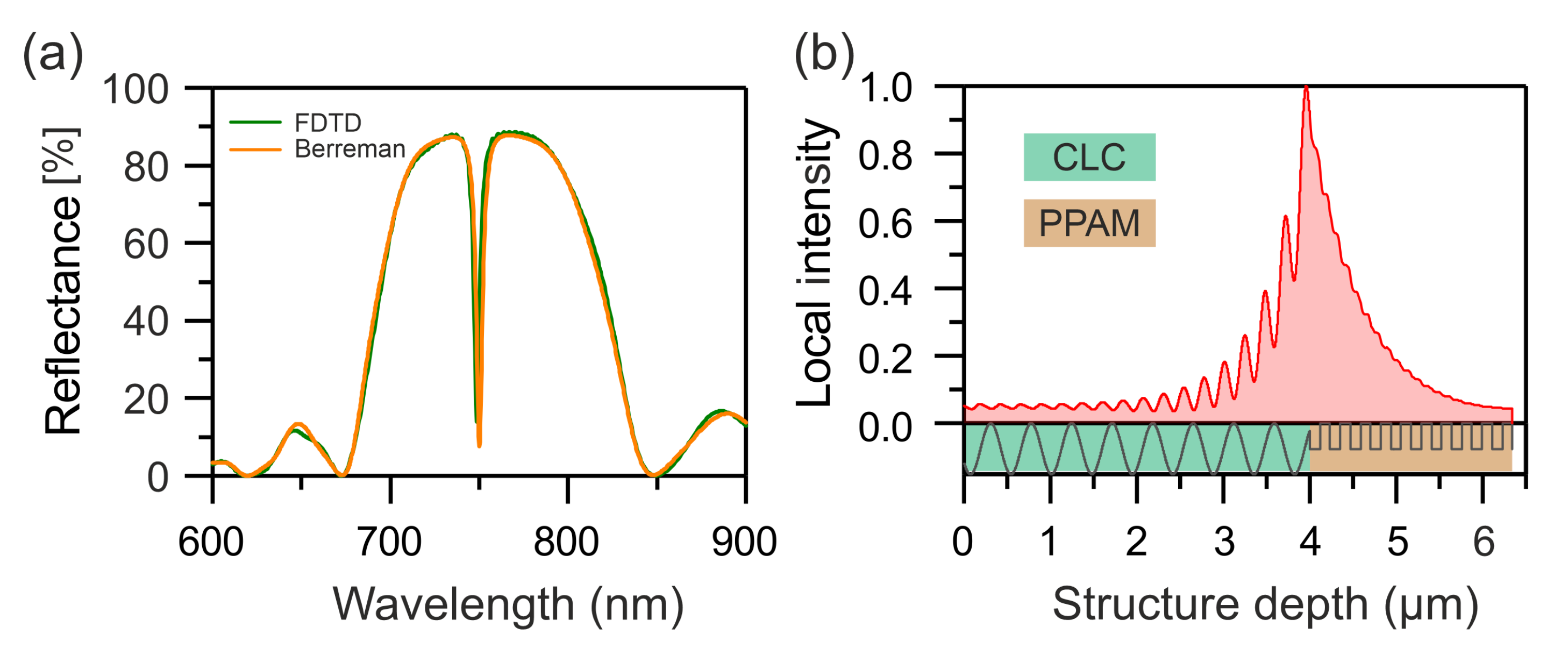
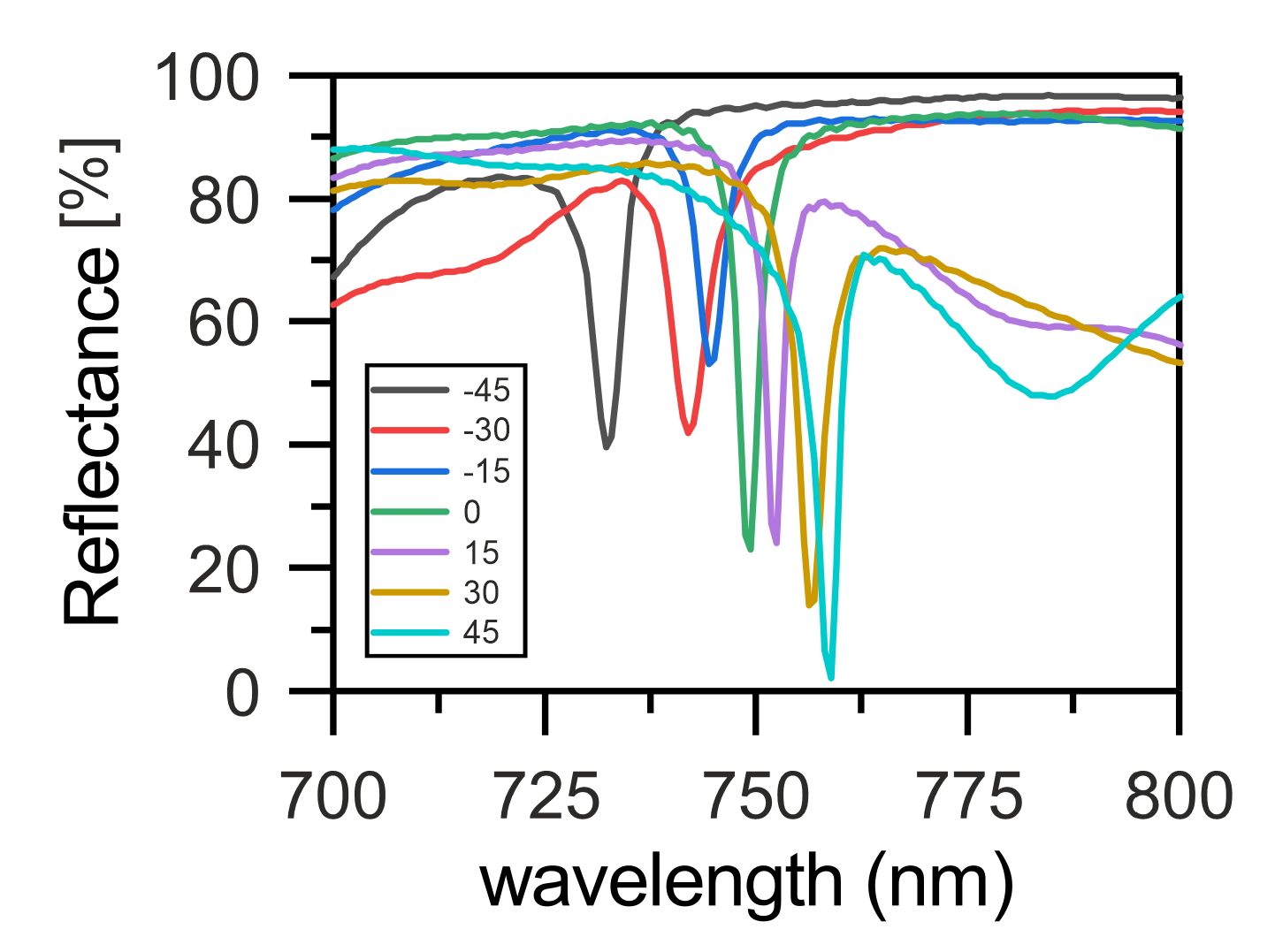
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kavokin, A.V.; Shelykh, I.A.; Malpuech, G. Lossless interface modes at the boundary between two periodic dielectric structures. Phys. Rev. B 2005, 72, 233102. [Google Scholar] [CrossRef] [Green Version]
- Vinogradov, A.P.; Dorofeenko, A.V.; Merzlikin, A.M.; Lisyansky, A.A. Surface states in photonic crystals. Phys.-Uspekhi 2010, 53, 243–256. [Google Scholar] [CrossRef]
- Kaliteevski, M.; Iorsh, I.; Brand, S.; Abram, R.A.; Chamberlain, J.M.; Kavokin, A.V.; Shelykh, I.A. Tamm plasmon-polaritons: Possible electromagnetic states at the interface of a metal and a dielectric Bragg mirror. Phys. Rev. B 2007, 76, 165415. [Google Scholar] [CrossRef] [Green Version]
- Tamm, I. On the possible bound states of electrons on a crystal surface. Phys. Z. Sowiet Union 1932, 1, 733. [Google Scholar]
- Sasin, M.E.; Seisyan, R.P.; Kalitteevski, M.A.; Brand, S.; Abram, R.A.; Chamberlain, J.M.; Egorov, A.Y.; Vasil’ev, A.P.; Mikhrin, V.S.; Kavokin, A.V. Tamm plasmon polaritons: Slow and spatially compact light. Appl. Phys. Lett. 2008, 92, 251112. [Google Scholar] [CrossRef] [Green Version]
- Goto, T.; Dorofeenko, A.V.; Merzlikin, A.M.; Baryshev, A.V.; Vinogradov, A.P.; Inoue, M.; Lisyansky, A.A.; Granovsky, A.B. Optical Tamm States in One-Dimensional Magnetophotonic Structures. Phys. Rev. Lett. 2008, 101. [Google Scholar] [CrossRef]
- Huang, S.G.; Chen, K.P.; Jeng, S.C. Phase sensitive sensor on Tamm plasmon devices. Opt. Mater. Express 2017, 7, 1267. [Google Scholar] [CrossRef]
- Buchnev, O.; Belosludtsev, A.; Reshetnyak, V.; Evans, D.R.; Fedotov, V.A. Observing and controlling a Tamm plasmon at the interface with a metasurface. Nanophotonics 2020, 9, 897–903. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Zhang, Q.; Peng, C.; Tang, C.; Shen, X.; Deng, L.; Park, G.S. Optical Cavity-Enhanced Localized Surface Plasmon Resonance for High-Quality Sensing. IEEE Photonics Technol. Lett. 2018, 30, 728–731. [Google Scholar] [CrossRef]
- Thompson, R.J.; Siday, T.; Glass, S.; Luk, T.S.; Reno, J.L.; Brener, I.; Mitrofanov, O. Optically thin hybrid cavity for terahertz photo-conductive detectors. Appl. Phys. Lett. 2017, 110, 041105. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.L.; Wang, F.; Rao, Y.J.; Jiang, Y. Novel sensing concept based on optical Tamm plasmon. Opt. Express 2014, 22, 14524–14529. [Google Scholar] [CrossRef]
- Jeng, S.C. Applications of Tamm plasmon-liquid crystal devices. Liq. Cryst. 2020, 47, 1223–1231. [Google Scholar] [CrossRef]
- Zhou, W.; Dridi, M.; Suh, J.Y.; Kim, C.H.; Co, D.T.; Wasielewski, M.R.; Schatz, G.C.; Odom, T.W. Lasing action in strongly coupled plasmonic nanocavity arrays. Nat. Nanotechnol. 2013, 8, 506. [Google Scholar] [CrossRef]
- Kavokin, A.; Shelykh, I.; Malpuech, G. Optical Tamm states for the fabrication of polariton lasers. Appl. Phys. Lett. 2005, 87, 261105. [Google Scholar] [CrossRef]
- Symonds, C.; Lheureux, G.; Hugonin, J.P.; Greffet, J.J.; Laverdant, J.; Brucoli, G.; Lemaitre, A.; Senellart, P.; Bellessa, J. Confined Tamm Plasmon Lasers. Nano Lett. 2013, 13, 3179–3184. [Google Scholar] [CrossRef]
- Fang, M.; Shi, F.; Chen, Y. Unidirectional All-Optical Absorption Switch Based on Optical Tamm State in Nonlinear Plasmonic Waveguide. Plasmonic 2016, 11, 197. [Google Scholar] [CrossRef]
- Bikbaev, R.; Vetrov, S.; Timofeev, I. Epsilon-Near-Zero Absorber by Tamm Plasmon Polariton. Photonics 2019, 6, 28. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Cai, W.; Bie, M.; Zhang, X.; Xu, J. Zak phase and topological plasmonic Tamm states in one-dimensional plasmonic crystals. Opt. Express 2018, 26, 28963. [Google Scholar] [CrossRef]
- Lakhtakia, A.; McCall, M. Sculptured thin films as ultranarrow-bandpass circular-polarization filters. Opt. Commun. 1999, 168, 457–465. [Google Scholar] [CrossRef]
- Zhou, H.; Yang, G.; Wang, K.; Long, H.; Lu, P. Multiple optical Tamm states at a metal–dielectric mirror interface. Opt. Lett. 2010, 35, 4112–4114. [Google Scholar] [CrossRef]
- Zhang, X.L.; Song, J.F.; Li, X.B.; Feng, J.; Sun, H.B. Optical Tamm states enhanced broad-band absorption of organic solar cells. Appl. Phys. Lett. 2012, 101, 243901. [Google Scholar] [CrossRef] [Green Version]
- Bikbaev, R.G.; Vetrov, S.Y.; Timofeev, I.V.; Shabanov, V.F. Photosensitivity and reflectivity of the active layer in a Tamm-plasmon-polariton-based organic solar cell. Appl. Opt. 2021, 60, 3338. [Google Scholar] [CrossRef]
- Timofeev, I.V.; Vetrov, S.Y. Chiral optical Tamm states at the boundary of the medium with helical symmetry of the dielectric tensor. JETP Lett. 2016, 104, 380–383. [Google Scholar] [CrossRef] [Green Version]
- Belyakov, V.A.; Sonin, A.S. Optics of Choltsteric Liquid Crystals; Nauka Publ.: Moscow, Russia, 1982; p. 360. [Google Scholar]
- Belyakov, V.A. Diffraction Optics of Complex-Structured Periodic Media: Localized Optical Modes of Spiral Media; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; p. 253. [Google Scholar] [CrossRef]
- Timofeev, I.V.; Arkhipkin, V.G.; Vetrov, S.Y.; Zyryanov, V.Y.; Lee, W. Enhanced light absorption with a cholesteric liquid crystal layer. Opt. Mater. Express 2013, 3, 496–501. [Google Scholar] [CrossRef]
- Vetrov, S.Y.; Pyatnov, M.V.; Timofeev, I.V. Surface modes in “photonic cholesteric liquid crystal–phase plate–metal” structure. Opt. Lett. 2014, 39, 2743. [Google Scholar] [CrossRef]
- Lin, M.Y.; Xu, W.H.; Bikbaev, R.G.; Yang, J.H.; Li, C.R.; Timofeev, I.V.; Lee, W.; Chen, K.P. Chiral-Selective Tamm Plasmon Polaritons. Materials 2021, 14, 2788. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, Y.; Pu, M.; Zhao, Z.; Wu, X.; Ma, X.; Wang, C.; Yan, L.; Luo, X. Dispersion management of anisotropic metamirror for super-octave bandwidth polarization conversion. Sci. Rep. 2015, 5, 8434. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Jia, H.; Yao, K.; Cai, W.; Chen, H.; Liu, Y. Circular Dichroism Metamirrors with Near-Perfect Extinction. ACS Photonics 2016, 3, 2096–2101. [Google Scholar] [CrossRef]
- Wen, X.M.; Bi, Y.G.; Yi, F.S.; Zhang, X.L.; Liu, Y.F.; Wang, W.Q.; Feng, J.; Sun, H.B. Tunable surface plasmon-polariton resonance in organic light-emitting devices based on corrugated alloy electrodes. Opto-Electron. Adv. 2021, 4, 200024-1–200024-7. [Google Scholar] [CrossRef]
- Rudakova, N.V.; Timofeev, I.V.; Vetrov, S.Y.; Lee, W. All-dielectric polarization-preserving anisotropic mirror. OSA Contin. 2018, 1, 682. [Google Scholar] [CrossRef]
- Rudakova, N.V.; Timofeev, I.V.; Bikbaev, R.G.; Pyatnov, M.V.; Vetrov, S.Y.; Lee, W. Chiral Optical Tamm States at the Interface between an All-Dielectric Polarization-Preserving Anisotropic Mirror and a Cholesteric Liquid Crystal. Crystals 2019, 9, 502. [Google Scholar] [CrossRef] [Green Version]
- Berreman, D.W. Optics in Stratified and Anisotropic Media: 4x4-Matrix Formulation. J. Opt. Soc. Am. 1972, 62, 502. [Google Scholar] [CrossRef]
- Johnson, P.; Christy, R.W. Optical constants of the noble metals. Phys. Rev. B 1972, 6, 4370–4379. [Google Scholar] [CrossRef]
- Fan, S.; Suh, W.; Joannopoulos, J.D. Temporal coupled-mode theory for the Fano resonance in optical resonators. J. Opt. Soc. Am. A 2003, 20, 569. [Google Scholar] [CrossRef] [Green Version]
- Timofeev, I.V.; Pankin, P.S.; Vetrov, S.Y.; Arkhipkin, V.G.; Lee, W.; Zyryanov, V.Y. Chiral Optical Tamm States: Temporal Coupled-Mode Theory. Crystals 2017, 7, 113. [Google Scholar] [CrossRef] [Green Version]
- Haus, H.A. Waves and Fields in Optoelectronics; Prentice Hall: Hoboken, NJ, USA, 1983; p. 402. [Google Scholar]
- Auguié, B.; Bruchhausen, A.; Fainstein, A. Critical coupling to Tamm plasmons. J. Opt. 2015, 17, 035003. [Google Scholar] [CrossRef] [Green Version]
- Pyatnov, M.V.; Bikbaev, R.G.; Timofeev, I.V.; Vetrov, S.Y. Model of a tunable hybrid Tamm mode–liquid crystal device. Appl. Opt. 2020, 59, 6347. [Google Scholar] [CrossRef]
- Symonds, C.; Lemaître, A.; Senellart, P.; Jomaa, M.H.; Aberra Guebrou, S.; Homeyer, E.; Brucoli, G.; Bellessa, J. Lasing in a hybrid GaAs/silver Tamm structure. Appl. Phys. Lett. 2012, 100, 121122. [Google Scholar] [CrossRef]
- Belyakov, V.A.; Semenov, S.V. Optical edge modes in photonic liquid crystals. J. Exp. Theor. Phys. 2009, 109, 687–699. [Google Scholar] [CrossRef]
- Belyakov, V.; Semenov, S. Optical Defect Modes in Photonic Chiral Liquid Crystals. Mol. Cryst. Liq. Cryst. 2011, 543, 123–135. [Google Scholar] [CrossRef]
- Kopp, V.I.; Zhang, Z.Q.; Genack, A.Z. Lasing in chiral photonic structures. Prog. Quantum Electron. 2003, 27, 369–416. [Google Scholar] [CrossRef]
- Huang, J.C.; Hsiao, Y.C.; Lin, Y.T.; Lee, C.R.; Lee, W. Electrically switchable organo–inorganic hybrid for a white-light laser source. Sci. Rep. 2016, 6, 28363. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Huang, Z.T.; Maksimov, D.N.; Pankin, P.S.; Timofeev, I.V.; Hong, K.B.; Li, H.; Chen, J.W.; Hsu, C.Y.; Liu, Y.; et al. Low–Threshold Bound State in the Continuum Lasers in Hybrid Lattice Resonance Metasurfaces. Laser Photonics Rev. 2021, 15, 2100118. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rudakova, N.V.; Bikbaev, R.G.; Pankin, P.S.; Vetrov, S.Y.; Timofeev, I.V.; Chen, K.-P.; Lee, W. Metal–Dielectric Polarization-Preserving Anisotropic Mirror for Chiral Optical Tamm State. Nanomaterials 2022, 12, 234. https://doi.org/10.3390/nano12020234
Rudakova NV, Bikbaev RG, Pankin PS, Vetrov SY, Timofeev IV, Chen K-P, Lee W. Metal–Dielectric Polarization-Preserving Anisotropic Mirror for Chiral Optical Tamm State. Nanomaterials. 2022; 12(2):234. https://doi.org/10.3390/nano12020234
Chicago/Turabian StyleRudakova, Natalya V., Rashid G. Bikbaev, Pavel S. Pankin, Stepan Ya. Vetrov, Ivan V. Timofeev, Kuo-Ping Chen, and Wei Lee. 2022. "Metal–Dielectric Polarization-Preserving Anisotropic Mirror for Chiral Optical Tamm State" Nanomaterials 12, no. 2: 234. https://doi.org/10.3390/nano12020234
APA StyleRudakova, N. V., Bikbaev, R. G., Pankin, P. S., Vetrov, S. Y., Timofeev, I. V., Chen, K.-P., & Lee, W. (2022). Metal–Dielectric Polarization-Preserving Anisotropic Mirror for Chiral Optical Tamm State. Nanomaterials, 12(2), 234. https://doi.org/10.3390/nano12020234








