Complex Phase-Fluctuation Effects Correlated with Granularity in Superconducting NbN Nanofilms
Abstract
:1. Introduction
2. Materials And Methods
2.1. Deposition
2.2. Fabrication of the Hall Bar
2.3. Electrical Characterization
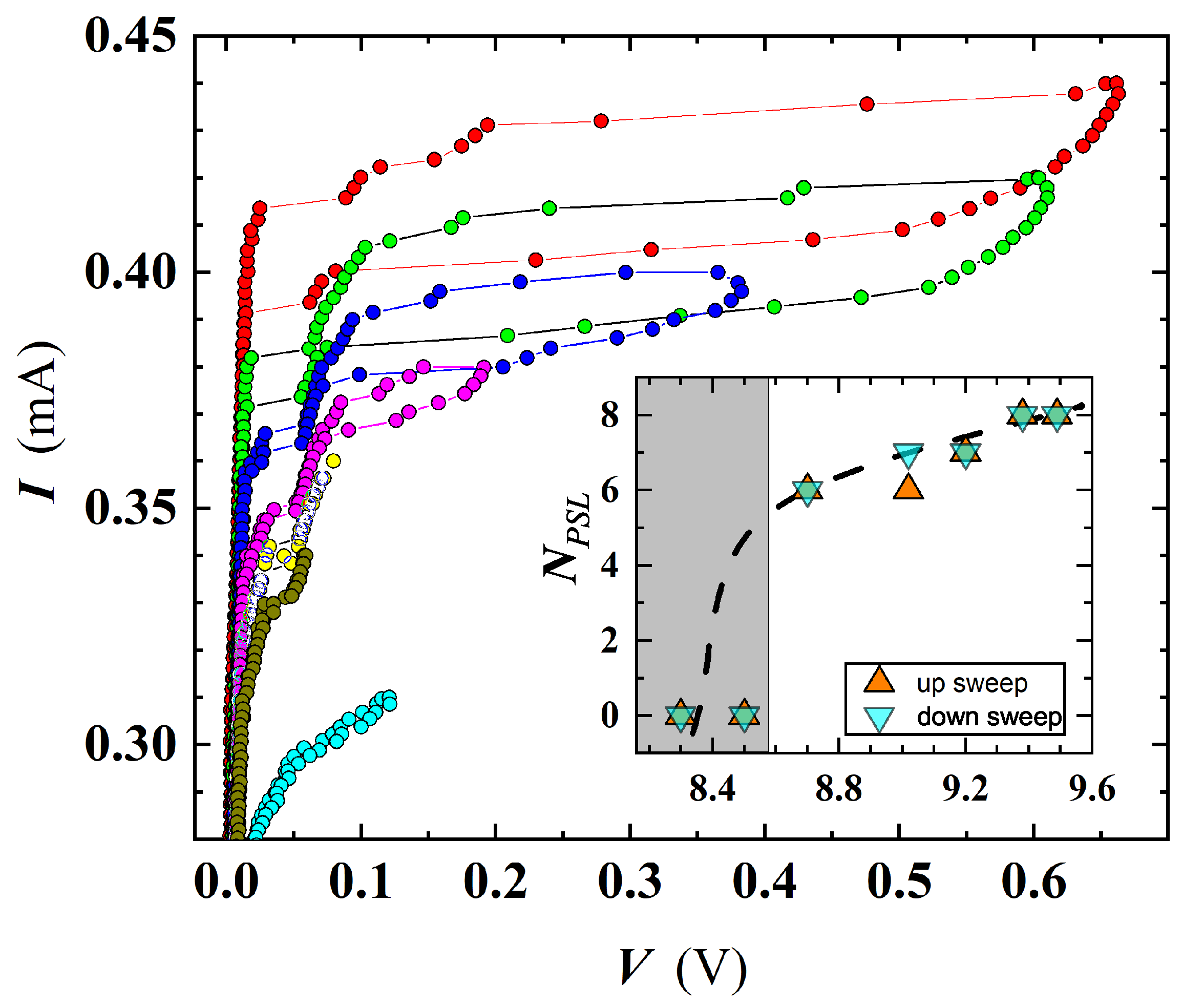
3. Results
3.1. Superconducting State Properties
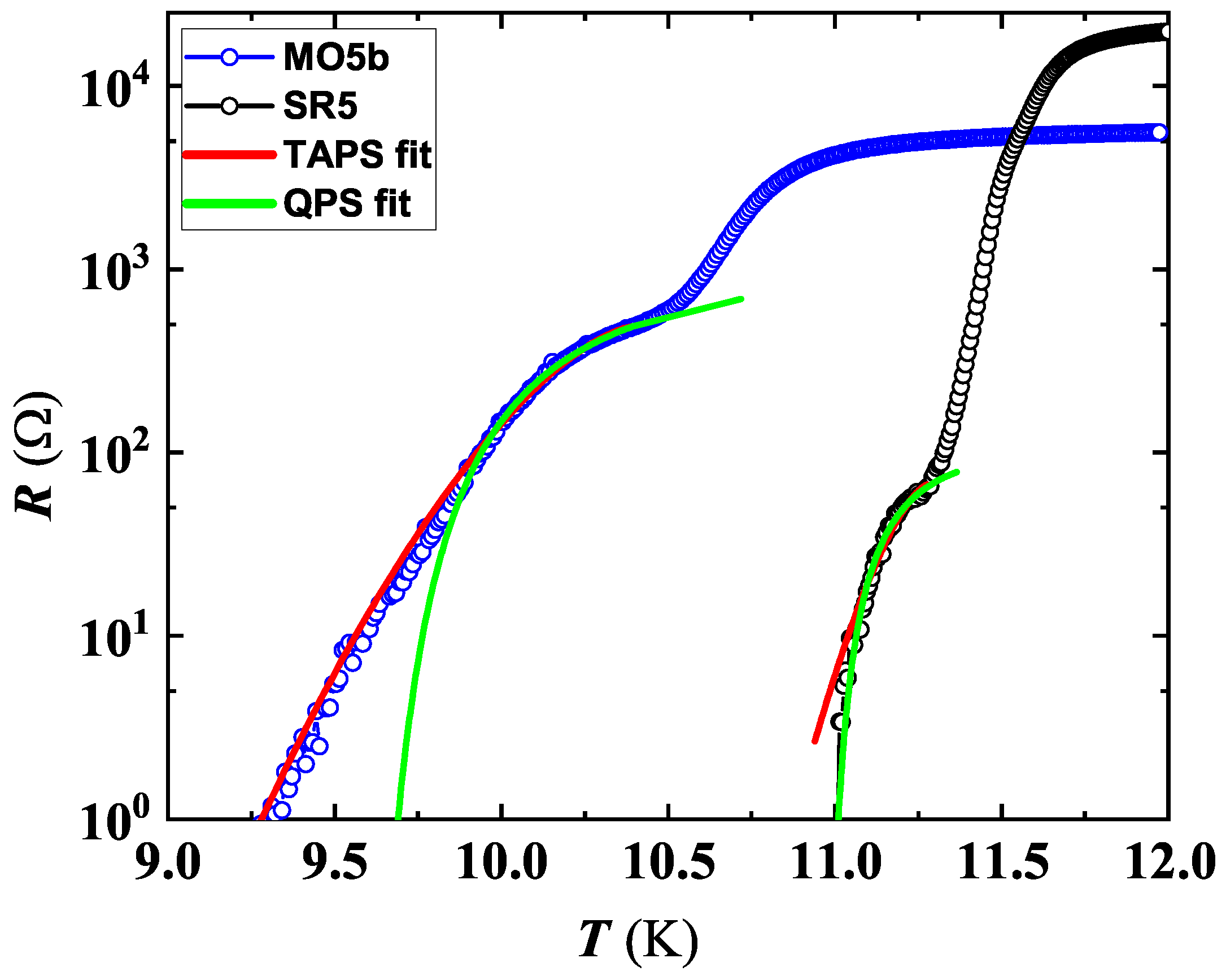
3.2. Berezinskii–Kosterlitz–Thouless Transition
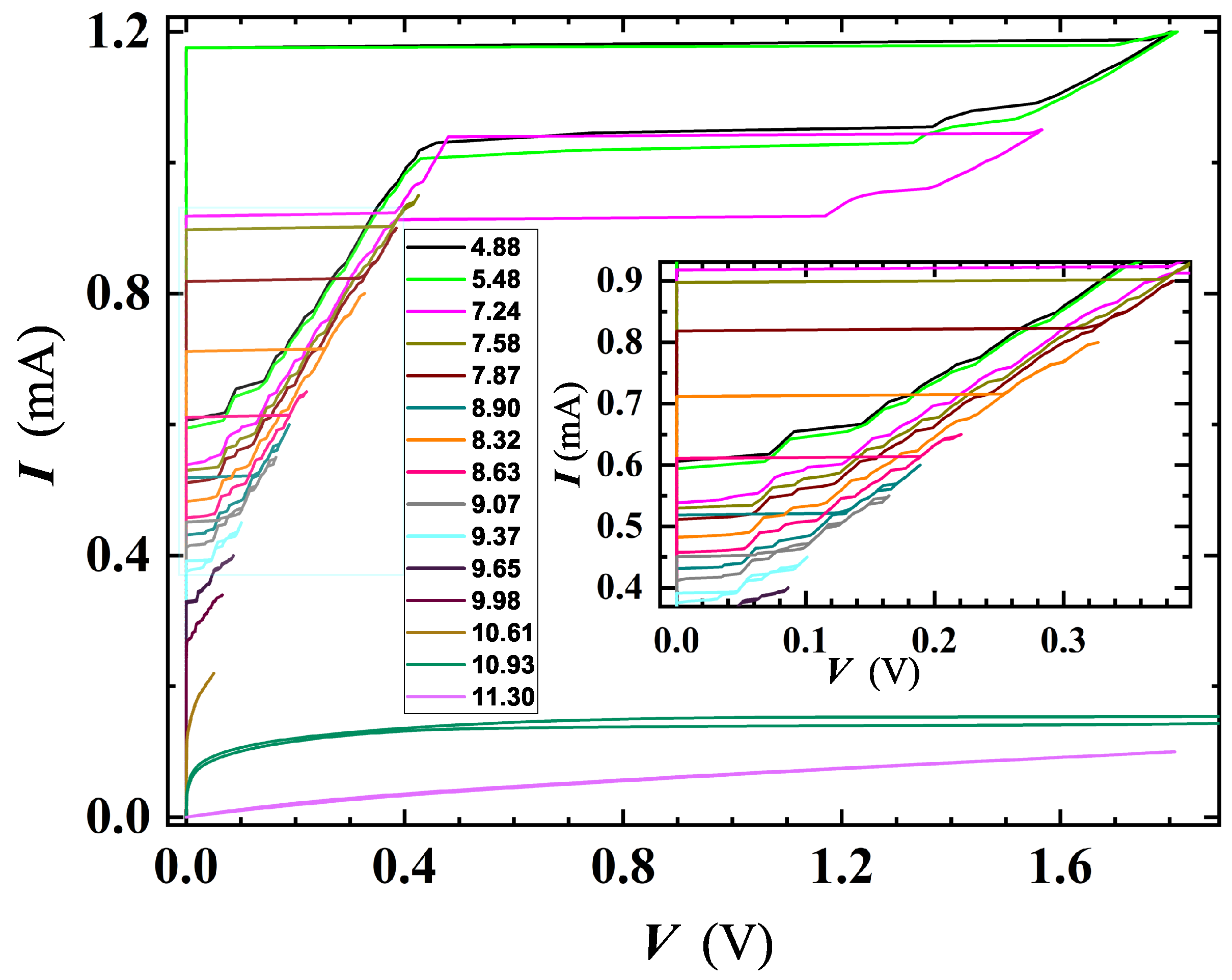
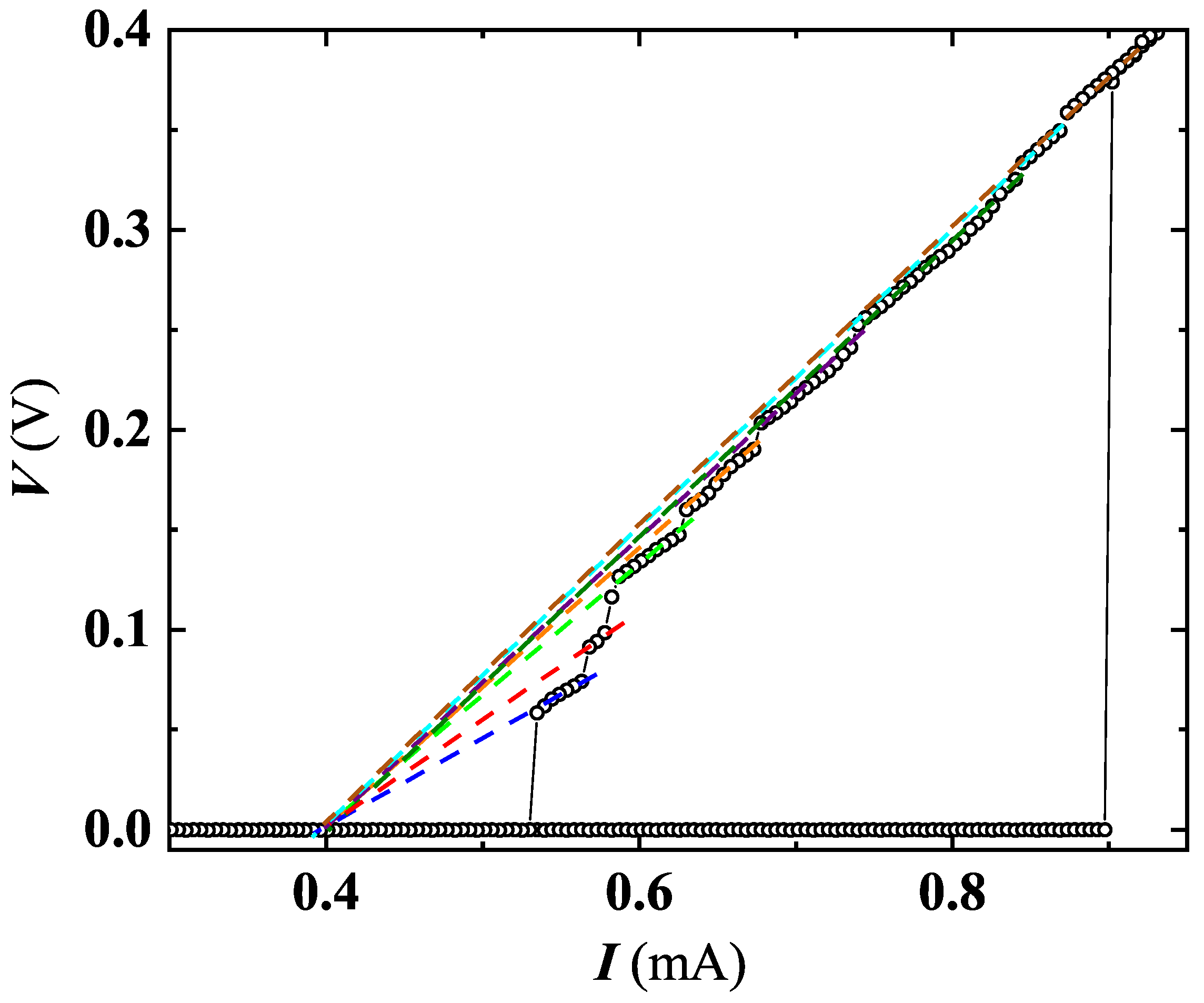
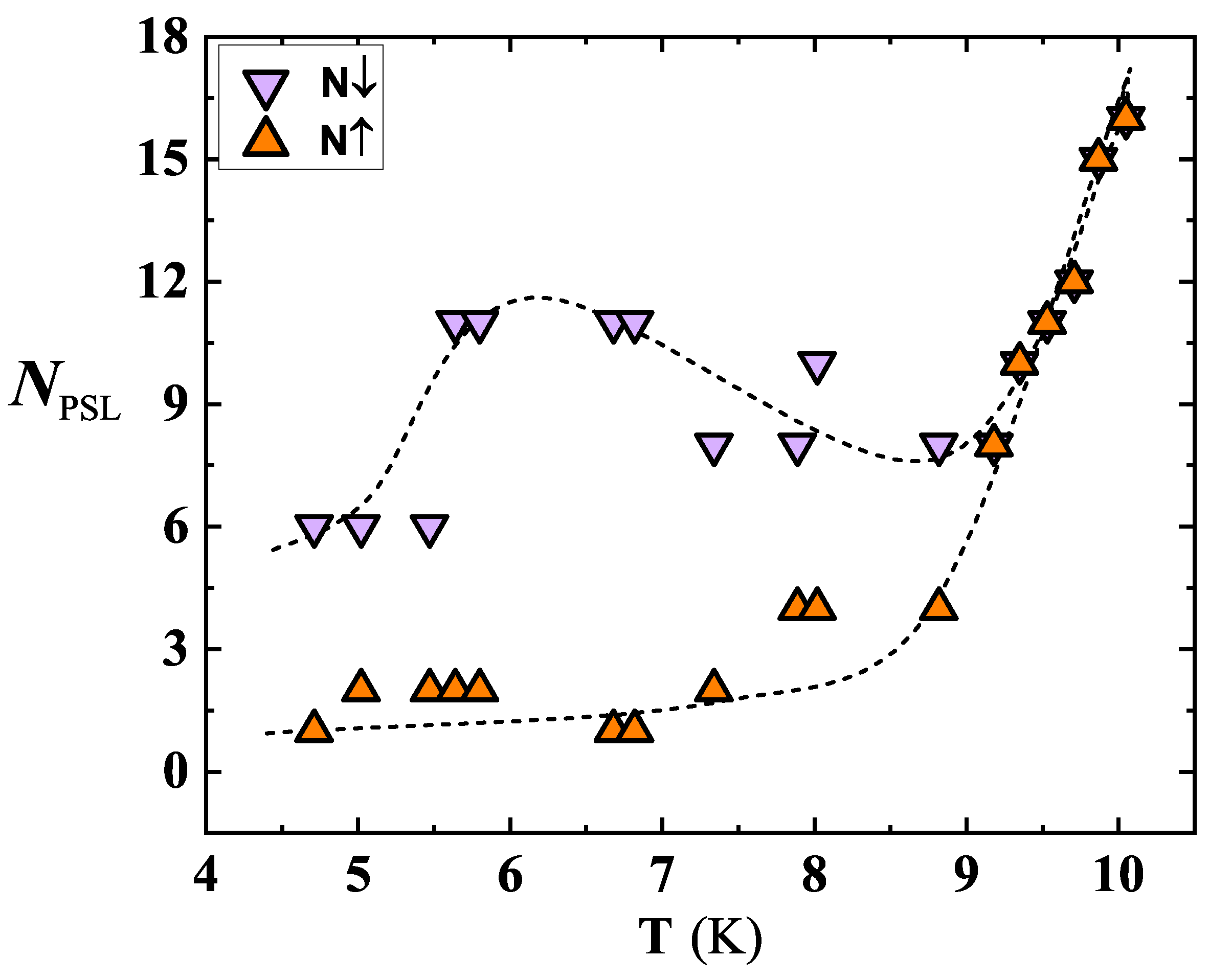
3.3. Phase Slips
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SC | Superconducting |
| BKT | Berezinskii–Kosterlitz–Thouless |
| PS | Phase slip |
| TAPS | Thermally activated phase slips |
| QPS | Quantum phase slips |
| NCP | Nano-conducting path |
References
- Bezryadin, A.; Lau, C.N.; Tinkham, M. Quantum suppression of superconductivity in ultrathin nanowires. Nature 2000, 404, 971. [Google Scholar] [CrossRef] [Green Version]
- Bezryadin, A. Quantum suppression of superconductivity in nanowires. J. Phys. Cond. Mat. 2008, 20, 043202. [Google Scholar] [CrossRef] [Green Version]
- Zhao, W.; Liu, X.; Chan, M. Quantum Phase Slips in 6 mm Long Niobium Nanowire. Nano Lett. 2016, 16, 1173–1178. [Google Scholar] [CrossRef]
- Lehtinen, J.S.; Sajavaara, T.; Arutyunov, K.Y.; Presnjakov, M.Y.; Vasiliev, A.L. Evidence of quantum phase slip effect in titanium nanowires. Phys. Rev. B 2012, 85, 094508. [Google Scholar] [CrossRef] [Green Version]
- Baumans, X.; Adami, D.C.O.; Zharinov, V.S.; Verellen, N.; Papari, G.; Scheerder, J.E.; Zhang, G.; Moshchalkov, V.V.; Silhanek, A.V.; de Vondel, J.V. Thermal and quantum depletion of superconductivity in narrow junctions created by controlled electromigration. Nat. Commun. 2016, 7, 10560. [Google Scholar] [CrossRef]
- Kim, H.; Gay, F.; Maestro, A.D.; Sacépé, B.; Rogachev, A. Pair-breaking quantum phase transition in superconducting nanowires. Nat. Phys. 2018, 14, 912–917. [Google Scholar] [CrossRef] [Green Version]
- Carbillet, C.; Caprara, S.; Grilli, M.; Brun, C.; Cren, T.; Debontridder, F.; Vignolle, B.; Tabis, W.; Demaille, D.; Largeau, L.; et al. Confinement of superconducting fluctuations due to emergent electronic inhomogeneities. Phys. Rev. B 2016, 93, 144509. [Google Scholar] [CrossRef] [Green Version]
- Mason, N.; Kapitulnik, A. Dissipation Effects on the Superconductor-Insulator Transition in 2D Superconductors. Phys. Rev. Lett. 1999, 82, 5341–5344. [Google Scholar] [CrossRef] [Green Version]
- Breznay, N.; Tendulkar, M.; Zhang, L.; Lee, S.C.; Kapitulnik, A. Superconductor to weak-insulator transitions in disordered tantalum nitride films. Phys. Rev. B 2017, 96, 134522. [Google Scholar] [CrossRef] [Green Version]
- Bell, M.; Sergeev, A.; Mitin, V.; Bird, J.; Verevkin, A.; Gol’tsman, G. One-dimensional resistive states in quasi-two-dimensional superconductors: Experiment and theory. Phys. Rev. B 2007, 76, 094521. [Google Scholar] [CrossRef]
- Gajar, B.; Yadav, S.; Sawle, D.; Maurya, K.K.; Gupta, A.; Aloysius, R.P.; Sahoo, S. Substrate mediated nitridation of niobium into superconducting Nb2N thin films for phase slip study. Sci. Rep. 2019, 9, 8811. [Google Scholar] [CrossRef] [Green Version]
- Kamiński, M.; Schrefler, B. Probabilistic effective characteristics of cables for superconducting coils. Comp. Meth. Appl. Mechan. Eng. 2000, 188, 1–16. [Google Scholar] [CrossRef]
- Bartolf, H.; Engel, A.; Schilling, A.; Il’in, K.; Siegel, M.; Hübers, H.W.; Semenov, A. Current-assisted thermally activated flux liberation in ultrathin nanopatterned NbN superconducting meander structures. Phys. Rev. B 2010, 81, 024502. [Google Scholar] [CrossRef] [Green Version]
- Sidorova, M.; Semenov, A.; Hubers, H.W.; Ilin, K.; Siegel, M.; Charaev, I.; Moshkova, M.; Kaurova, N.; Goltsman, G.N.; Zhang, X.; et al. Electron energy relaxation in disordered superconducting NbN films. Phys. Rev. B 2020, 102, 054501. [Google Scholar] [CrossRef]
- Koushik, R.; Kumar, S.; Amin, K.R.; Mondal, M.; Jesudasan, J.; Bid, A.; Raychaudhuri, P.; Ghosh, A. Correlated Conductance Fluctuations Close to the Berezinskii-Kosterlitz-Thouless Transition in Ultrathin NbN Films. Phys. Rev. Lett. 2013, 111, 197001. [Google Scholar] [CrossRef] [Green Version]
- Venditti, G.; Biscaras, J.; Hurand, S.; Bergeal, N.; Lesueur, J.; Dogra, A.; Budhani, R.C.; Mondal, M.; Jesudasan, J.; Raychaudhuri, P.; et al. Nonlinear I-V characteristics of two-dimensional superconductors: Berezinskii-Kosterlitz-Thouless physics versus inhomogeneity. Phys. Rev. B 2019, 100, 064506. [Google Scholar] [CrossRef] [Green Version]
- Berezinskii, V.L. Destruction of Long-range Order in One-dimensional and Two-dimensional Systems having a Continuous Symmetry Group I. Classical Systems. Sov. Phys. JETP 1971, 32, 493–500. [Google Scholar]
- Berezinskii, V.L. Destruction of Long-range Order in One-dimensional and Two-dimensional Systems Possessing a Continuous Symmetry Group. II. Quantum Systems. Sov. Phys. JETP 1972, 34, 610–616. [Google Scholar]
- Kosterlitz, J.M.; Thouless, D.J. Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C Sol. State Phys. 1973, 6, 1181–1203. [Google Scholar] [CrossRef]
- Kosterlitz, J.M. The critical properties of the two-dimensional xy model. J. Phys. C Sol. State Phys. 1974, 7, 1046–1060. [Google Scholar] [CrossRef]
- Yong, J.; Lemberger, T.; Benfatto, L.; Ilin, K.; Siegel, M. Robustness of the Berezinskii-Kosterlitz-Thouless transition in ultrathin NbN films near the superconductor-insulator transition. Phys. Rev. B 2013, 87, 184505. [Google Scholar] [CrossRef] [Green Version]
- Giachetti, G.; Defenu, N.; Ruffo, S.; Trombettoni, A. Berezinskii-Kosterlitz-Thouless phase transitions with long-range couplings. Phys. Rev. Lett. 2021, 127, 156801. [Google Scholar] [CrossRef]
- Beasley, M.R.; Mooij, J.E.; Orlando, T.P. Possibility of Vortex-Antivortex Pair Dissociation in Two-Dimensional Superconductors. Phys. Rev. Lett. 1979, 42, 1165–1168. [Google Scholar] [CrossRef]
- Chu, S.L.; Bollinger, A.T.; Bezryadin, A. Phase slips in superconducting films with constrictions. Phys. Rev. B 2004, 70, 214506. [Google Scholar] [CrossRef] [Green Version]
- Benfatto, L.; Perali, A.; Castellani, C.; Grilli, M. Kosterlitz-Thouless vs. Ginzburg-Landau description of 2D superconducting fluctuations. Eur. Phys. J. B Cond. Mat. Compl. Syst. 2000, 13, 609–612. [Google Scholar] [CrossRef] [Green Version]
- Mondal, M.; Kumar, S.; Chand, M.; Kamlapure, A.; Saraswat, G.; Seibold, G.; Benfatto, L.; Raychaudhuri, P. Role of the vortex-core energy on the Berezinskii-Kosterlitz-Thouless transition in thin films of NbN. Phys. Rev. Lett. 2011, 107, 217003. [Google Scholar] [CrossRef] [Green Version]
- Paradiso, N.; Nguyen, A.T.; Kloss, K.E.; Strunk, C. Phase slip lines in superconducting few-layer NbSe2 crystals. 2D Mater. 2019, 6, 025039. [Google Scholar] [CrossRef]
- Rezaev, R.; Smirnova, E.; Schmidt, O.; Fomin, V. Topological transitions in superconductor nanomembranes under a strong transport current. Commun. Phys. 2020, 3, 1–8. [Google Scholar] [CrossRef]
- Alfonso, J.; Buitrago, J.; Torres, J.; Marco, J.; Santos, B. Influence of fabrication parameters on crystallization, microstructure, and surface composition of NbN thin films deposited by rf magnetron sputtering. J. Mat. Sci. 2010, 45, 5528–5533. [Google Scholar] [CrossRef]
- Delacour, C.; Pannetier, B.; Villegier, J.C.; Bouchiat, V. Quantum and thermal phase slips in superconducting niobium nitride (NbN) ultrathin crystalline nanowire: Application to single photon detection. Nano Lett. 2012, 12, 3501–3506. [Google Scholar] [CrossRef]
- Pinto, N.; Rezvani, S.J.; Perali, A.; Flammia, L.; Milošević, M.V.; Fretto, M.; Cassiago, C.; De Leo, N. Dimensional crossover and incipient quantum size effects in superconducting niobium nanofilms. Sci. Rep. 2018, 8, 4710. [Google Scholar] [CrossRef] [Green Version]
- Rezvani, S.; Perali, A.; Fretto, M.; De Leo, N.; Flammia, L.; Milošević, M.; Nannarone, S.; Pinto, N. Substrate-Induced Proximity Effect in Superconducting Niobium Nanofilms. Cond. Matter 2019, 4, 4. [Google Scholar] [CrossRef]
- Daire, A. An improved method for differential conductance measurements. Keithley White Pap. 2005. Available online: https://www.tek.com/en/documents/whitepaper/improved-method-differential-conductance-measurements (accessed on 1 November 2022).
- Keithley Instruments, Inc. Achieving Accurate and Reliable Resistance Measurements in Low Power and Low Voltage Applications; Keithley Instruments, Inc.: Cleveland, OH, USA, 2004. [Google Scholar]
- Joshi, L.M.; Verma, A.; Gupta, A.; Rout, P.; Husale, S.; Budhani, R. Superconducting properties of NbN film, bridge and meanders. AIP Adv. 2018, 8, 055305. [Google Scholar] [CrossRef]
- Hazra, D.; Tsavdaris, N.; Jebari, S.; Grimm, A.; Blanchet, F.; Mercier, F.; Blanquet, E.; Chapelier, C.; Hofheinz, M. Superconducting properties of very high quality NbN thin films grown by high temperature chemical vapor deposition. Supercond. Sci. Technol. 2016, 29, 105011. [Google Scholar] [CrossRef] [Green Version]
- Soldatenkova, M.; Triznova, A.; Baeva, E.; Zolotov, P.; Lomakin, A.; Kardakova, A.; Goltsman, G. Normal-state transport in superconducting NbN films on r-cut sapphire. J. Phys. Confer. Ser. 2021, 2086, 012212. [Google Scholar] [CrossRef]
- Kang, L.; Jin, B.B.; Liu, X.Y.; Jia, X.Q.; Chen, J.; Ji, Z.M.; Xu, W.W.; Wu, P.H.; Mi, S.B.; Pimenov, A.; et al. Suppression of superconductivity in epitaxial NbN ultrathin films. J. Appl. Phys. 2011, 109, 033908. [Google Scholar] [CrossRef]
- Smirnov, K.; Divochiy, A.; Vakhtomin, Y.; Morozov, P.; Zolotov, P.; Antipov, A.; Seleznev, V. NbN single-photon detectors with saturated dependence of quantum efficiency. Supercond. Sci. Technol. 2018, 31, 035011. [Google Scholar] [CrossRef] [Green Version]
- Senapati, K.; Pandey, N.K.; Nagar, R.; Budhani, R.C. Normal-state transport and vortex dynamics in thin films of two structural polymorphs of superconducting NbN. Phys. Rev. B 2006, 74, 104514. [Google Scholar] [CrossRef]
- Chockalingam, S.P.; Chand, M.; Jesudasan, J.; Tripathi, V.; Raychaudhuri, P. Superconducting properties and Hall effect of epitaxial NbN thin films. Phys. Rev. B 2008, 77, 214503. [Google Scholar] [CrossRef] [Green Version]
- Il’in, K.; Siegel, M.; Semenov, A.; Engel, A.; Hübers, H.W. Critical current of Nb and NbN thin-film structures: The cross-section dependence. Phys. Stat. Sol. 2005, 2, 1680–1687. [Google Scholar] [CrossRef]
- Kamlapure, A.; Mondal, M.; Chand, M.; Mishra, A.; Jesudasan, J.; Bagwe, V.; Benfatto, L.; Tripathi, V.; Raychaudhuri, P. Measurement of magnetic penetration depth and superconducting energy gap in very thin epitaxial NbN films. App. Phys. Lett. 2010, 96, 072509. [Google Scholar] [CrossRef] [Green Version]
- Aslamasov, L.; Larkin, A. The influence of fluctuation pairing of electrons on the conductivity of normal metal. Phys. Lett. A 1968, 26, 238–239. [Google Scholar] [CrossRef]
- Maki, K. Critical Fluctuation of the Order Parameter in a Superconductor. I. Prog. Theor. Phys. 1968, 40, 193–200. [Google Scholar] [CrossRef] [Green Version]
- Thompson, R. Microwave, Flux Flow, and Fluctuation Resistance of Dirty Type-II Superconductors. Phys. Rev. B 1970, 1, 327–333. [Google Scholar] [CrossRef]
- Benfatto, L.; Castellani, C.; Giamarchi, T. Broadening of the Berezinskii-Kosterlitz-Thouless superconducting transition by inhomogeneity and finite-size effects. Phys. Rev. B 2009, 80, 214506. [Google Scholar] [CrossRef] [Green Version]
- Yamashita, T.; Miki, S.; Makise, K.; Qiu, W.; Terai, H.; Fujiwara, M.; Sasaki, M.; Wang, Z. Origin of intrinsic dark count in superconducting nanowire single-photon detectors. Appl. Phys. Lett. 2011, 99, 161105. [Google Scholar] [CrossRef] [Green Version]
- Nelson, D.R.; Kosterlitz, J. Universal jump in the superfluid density of two-dimensional superfluids. Phys. Rev. Lett. 1977, 39, 1201. [Google Scholar] [CrossRef] [Green Version]
- Saito, Y.; Itahashi, Y.M.; Nojima, T.; Iwasa, Y. Dynamical vortex phase diagram of two-dimensional superconductivity in gated Mo S 2. Phys. Rev. Mat. 2020, 4, 074003. [Google Scholar]
- McNaughton, B.; Pinto, N.; Perali, A.; Milošević, M. Causes and Consequences of Ordering and Dynamic Phases of Confined Vortex Rows in Superconducting Nanostripes. Nanomaterials 2022, 12, 4043. [Google Scholar] [CrossRef]
- Giordano, N. Superconductivity and dissipation in small-diameter Pb-In wires. Phys. Rev. B 1991, 43, 160. [Google Scholar] [CrossRef]
- Joshi, L.M.; Rout, P.; Husale, S.; Gupta, A. Dissipation processes in superconducting NbN nanostructures. AIP Adv. 2020, 10, 115116. [Google Scholar] [CrossRef]
- Sivakov, A.G.; Glukhov, A.M.; Omelyanchouk, A.N.; Koval, Y.; Müller, P.; Ustinov, A.V. Josephson Behavior of Phase-Slip Lines in Wide Superconducting Strips. Phys. Rev. Lett. 2003, 91, 267001. [Google Scholar] [CrossRef] [Green Version]
- Kumar, A.; Husale, S.; Pandey, H.; Yadav, M.G.; Yousuf, M.; Papanai, G.S.; Gupta, A.; Aloysius, R. On the switching current and the re-trapping current of tungsten nanowires fabricated by Focussed Ion Beam (FIB) technique. Eng. Res. Express 2021, 3, 025017. [Google Scholar] [CrossRef]
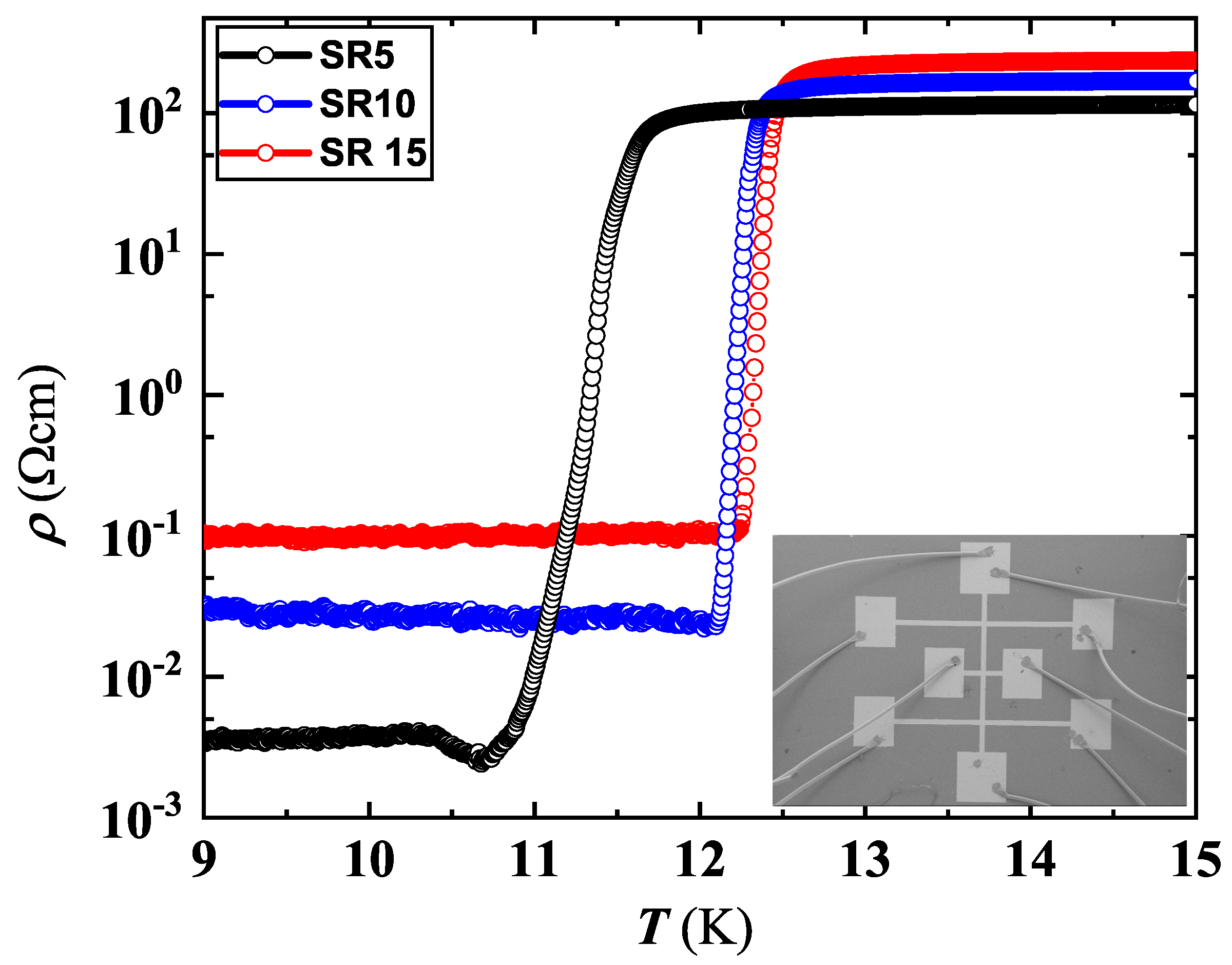
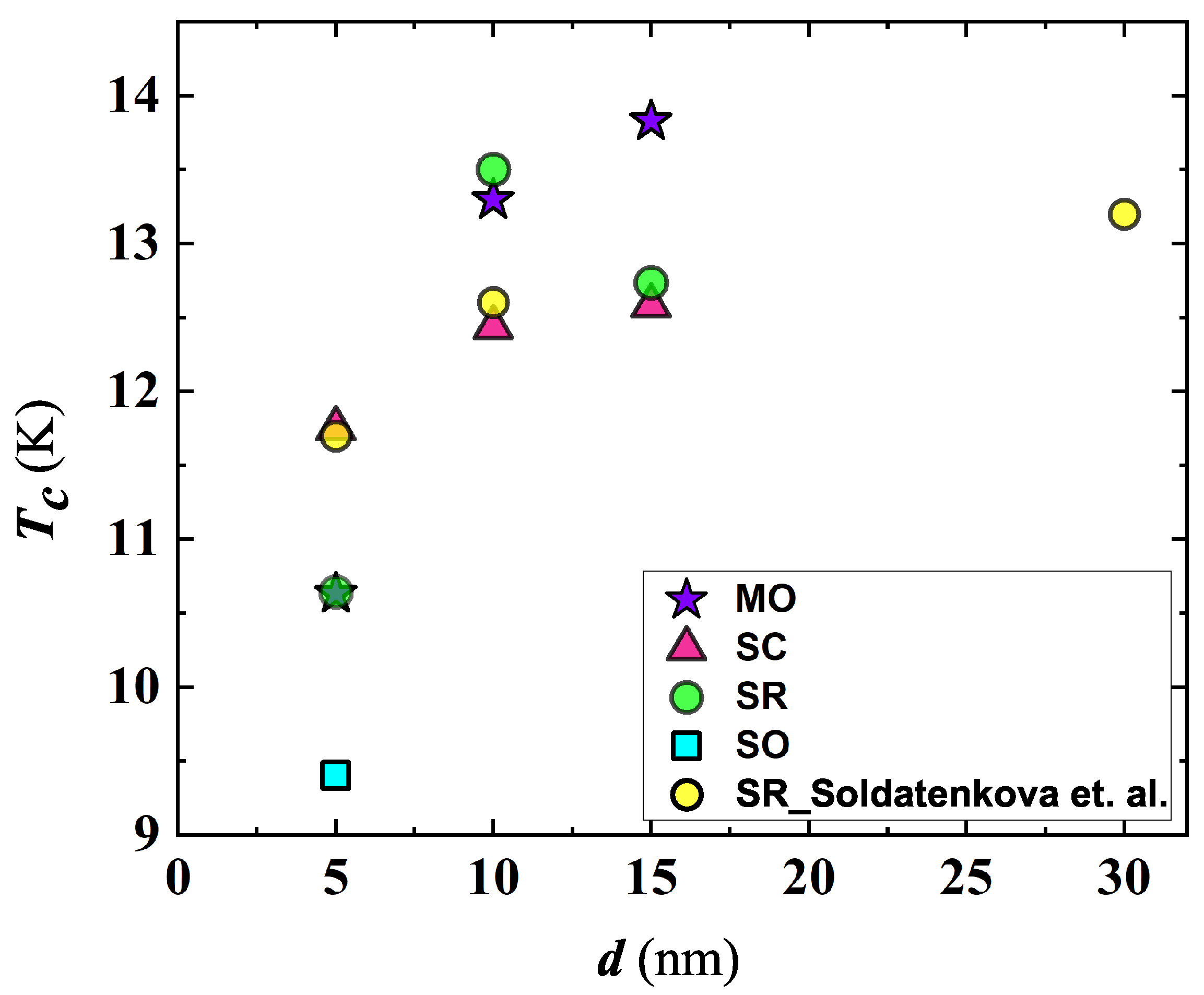
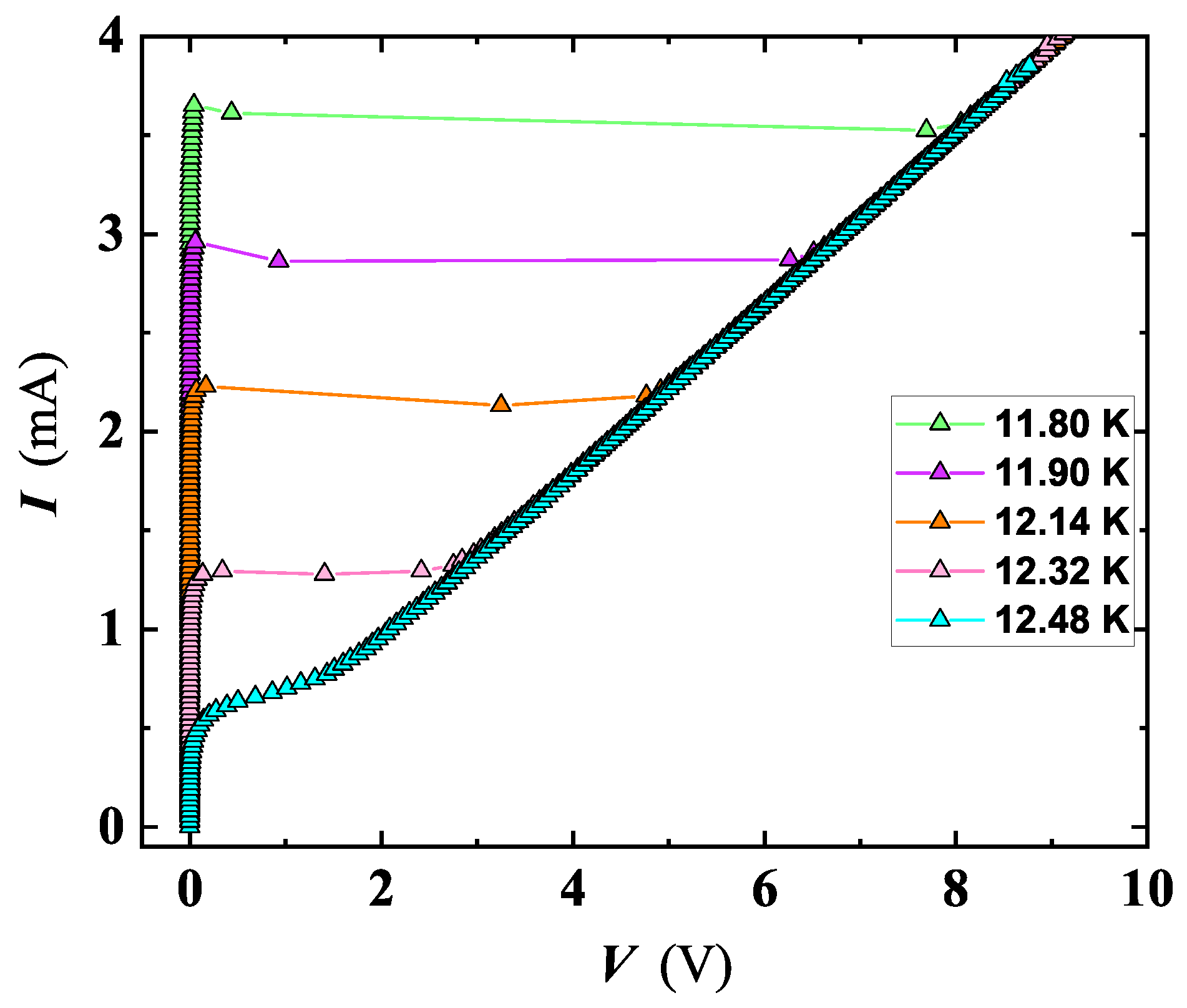
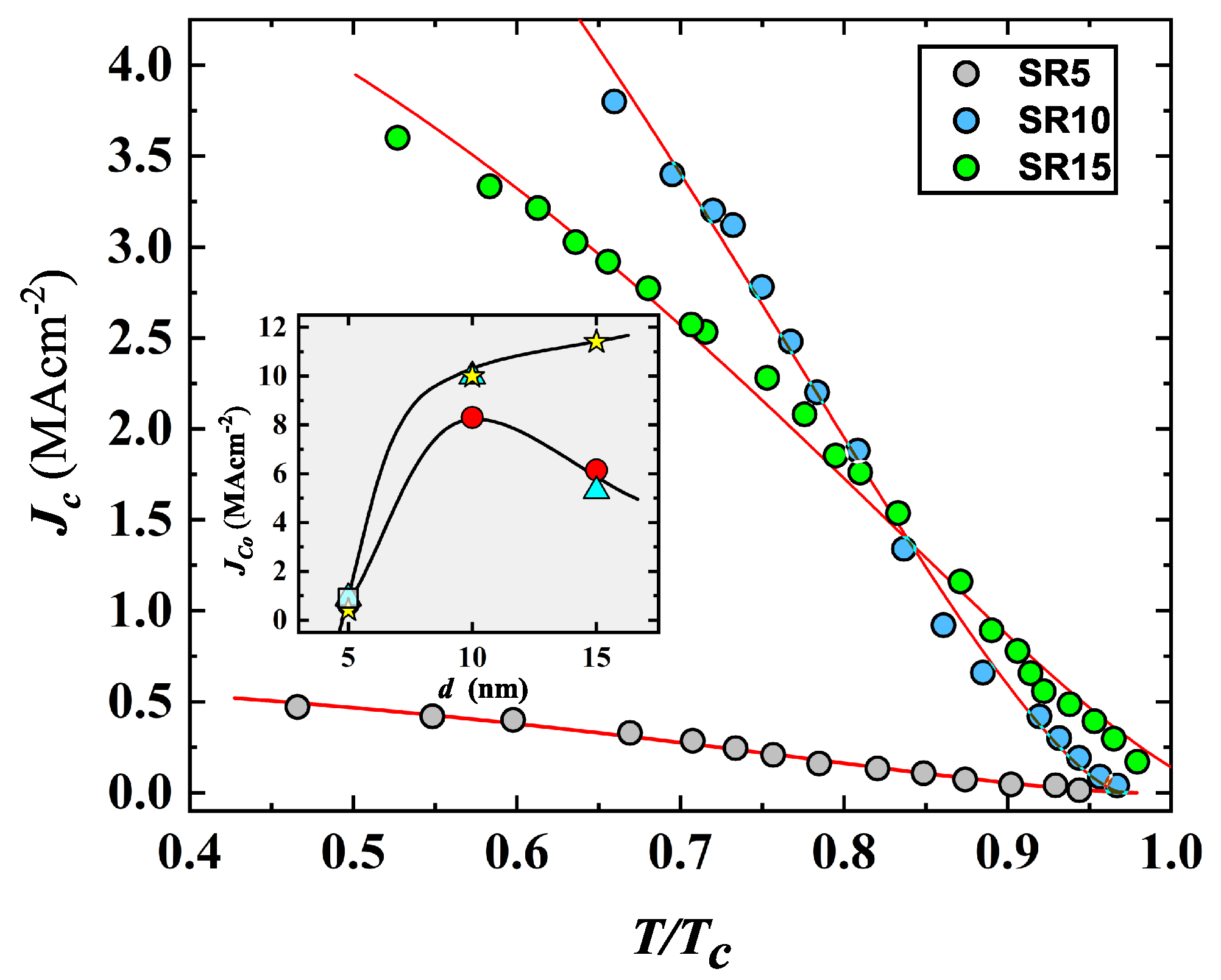
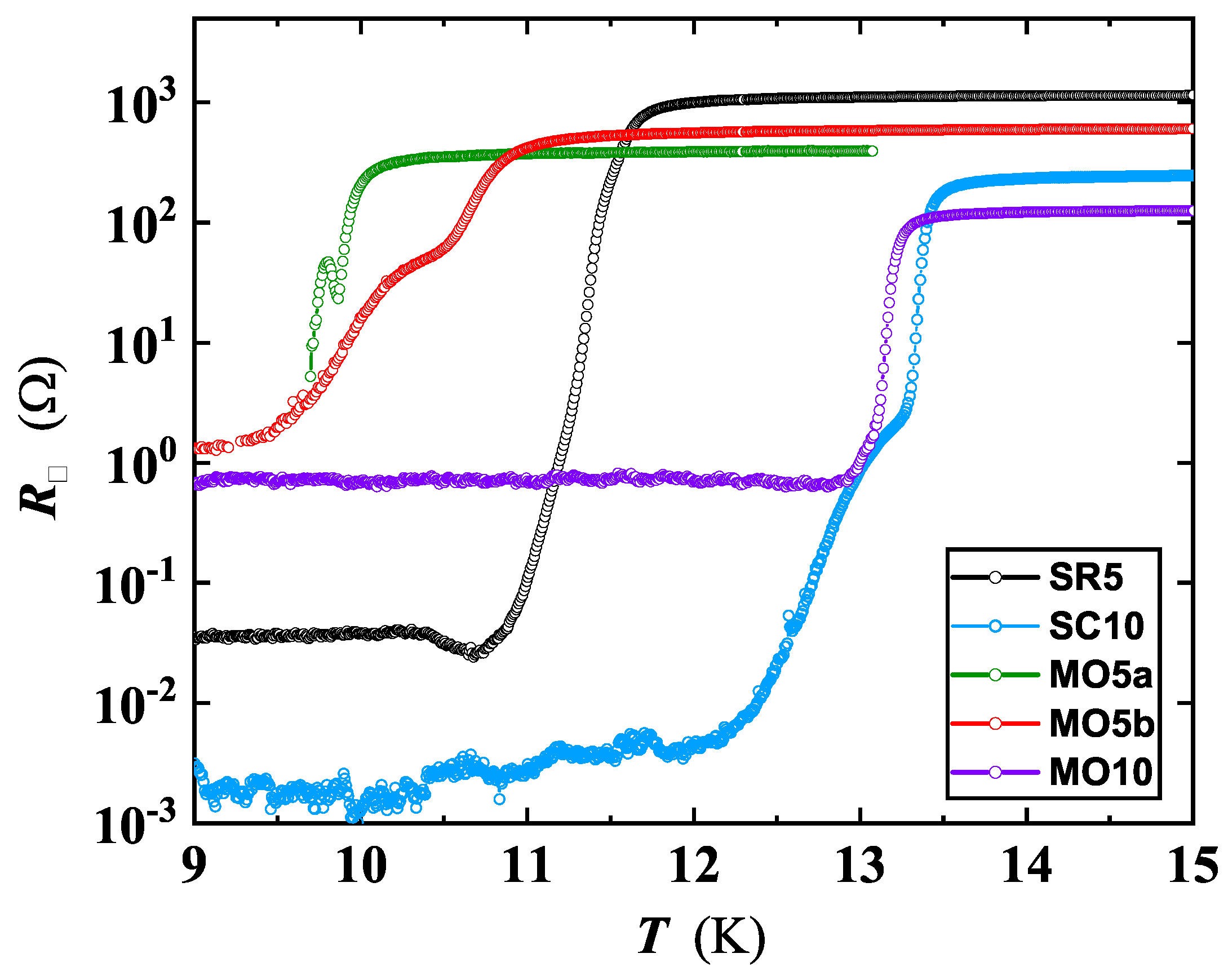
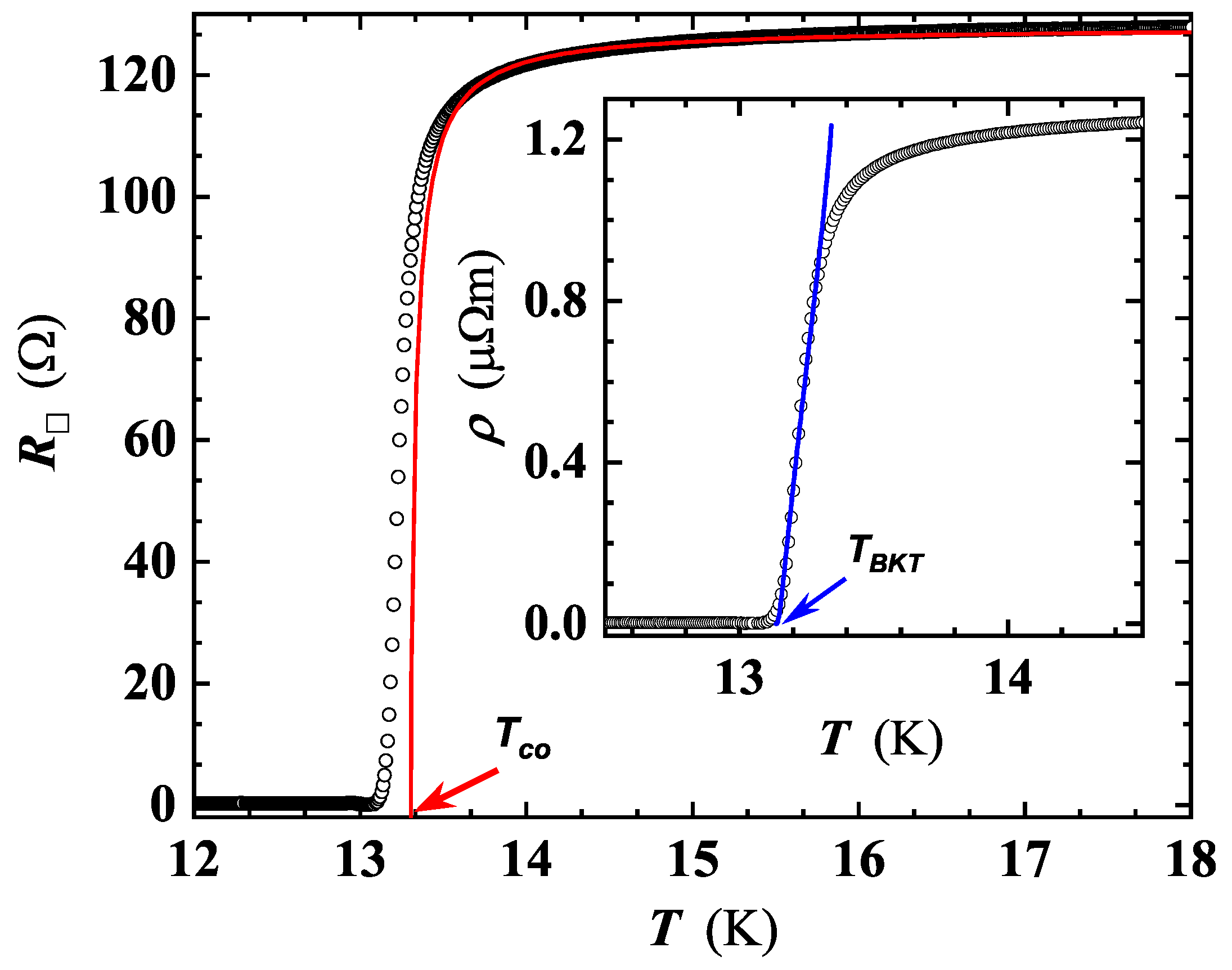
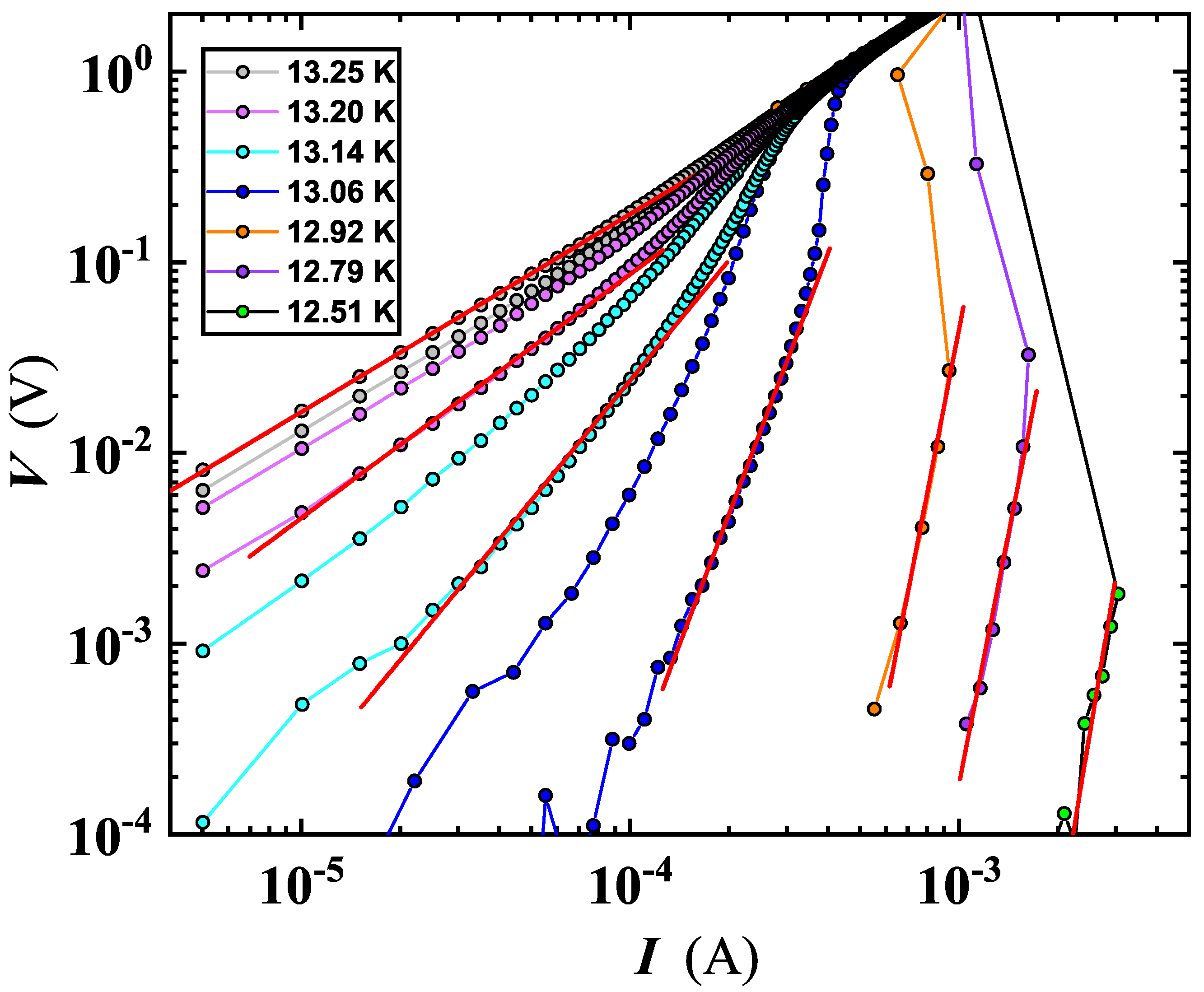
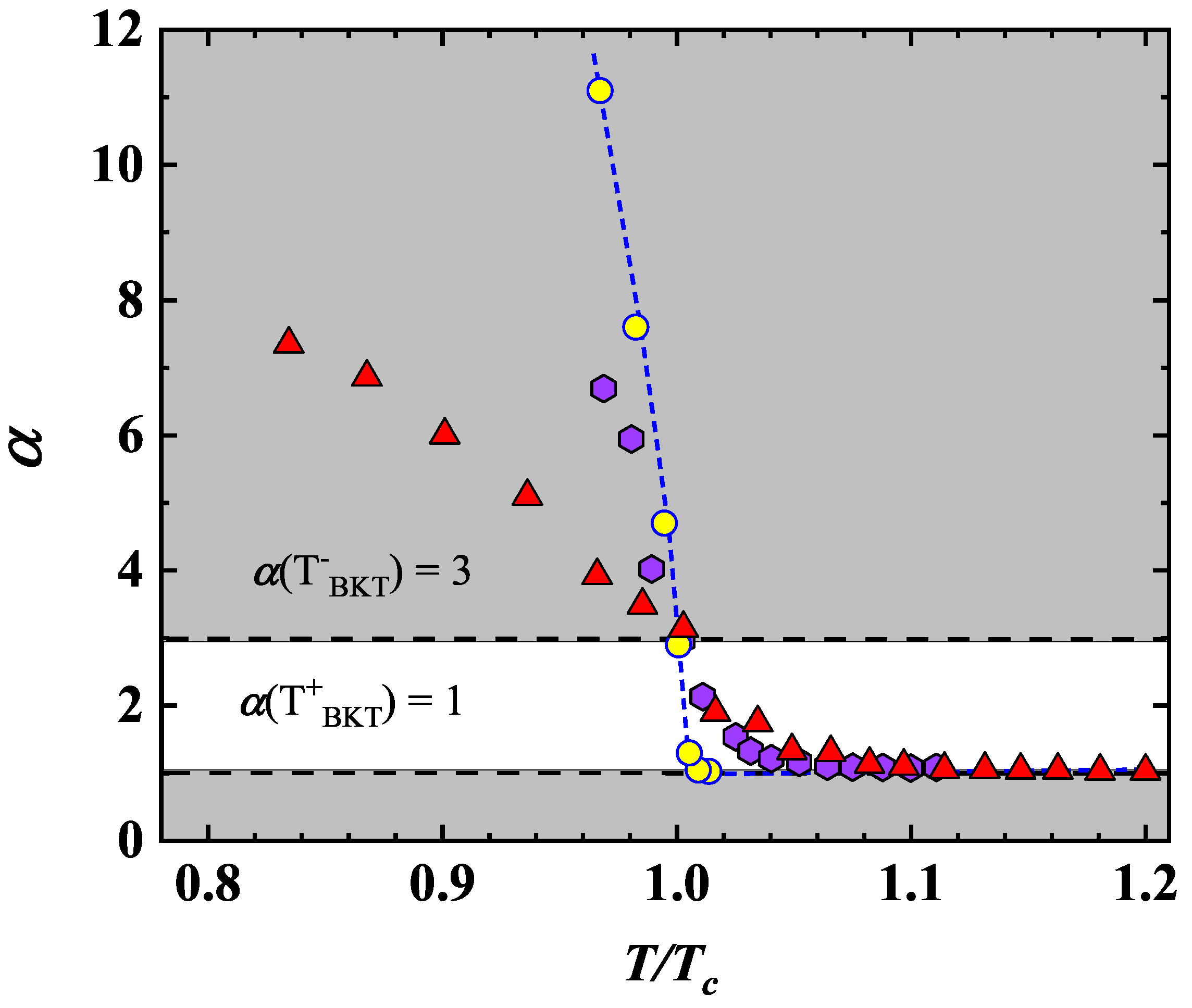

| Sample | ( cm) | (K) | (K) | (MA/cm) |
|---|---|---|---|---|
| MO5a * | 8.0 × | 10.072 | 0.08 | 0.40 ± 0.014 |
| MO5b ** | 5.8 × | 11.02 | 0.79 | 2.24 ± 0.013 |
| MO10 | 1.2 × | 13.29 | 0.27 | 9.98 ± 0.15 |
| MO15 | 2.4 × | 13.83 | 0.23 | 11.40 ± 0.016 |
| SC5 | 8.0 × | 10.64 | 0.43 | 0.90 ± 0.010 |
| SC10 | 2.4 × | 13.50 | 0.40 | 10 ± 0.028 |
| SC15 | 1.7 × | 12.73 | 0.24 | 5.29 ± 0.08 |
| SR5 ** | 1.1 × | 11.76 | 0.68 | 0.63 ± 0.013 |
| SR10 | 1.7 × | 12.43 | 0.30 | 8.3 ± 0.18 |
| SR15 | 2.3 × | 12.58 | 0.38 | 6.14 ± 0.13 |
| SO5 | 9.3 × | 9.40 | 0.46 | 0.89 ± 0.024 |
| Sample | (K) | (K) ** | () | ||
|---|---|---|---|---|---|
| MO5a | 9.70 ± 0.03 | 9.90 | 502.30 ± 0.01 | 0.970 ± 0.002 | 10.28 ± 0.030 |
| MO5b | 10.30 ± 0.02 | 10.60 | 620 ± 1.06 | 1.500 ± 0.005 | 11.49 ± 0.022 |
| MO10 | 13.060 ± 0.008 | 13.31 | 129.8 ± 0.60 | 1.56 ± 0.09 | 25.5 ± 0.11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharma, M.; Singh, M.; Rakshit, R.K.; Singh, S.P.; Fretto, M.; De Leo, N.; Perali, A.; Pinto, N. Complex Phase-Fluctuation Effects Correlated with Granularity in Superconducting NbN Nanofilms. Nanomaterials 2022, 12, 4109. https://doi.org/10.3390/nano12234109
Sharma M, Singh M, Rakshit RK, Singh SP, Fretto M, De Leo N, Perali A, Pinto N. Complex Phase-Fluctuation Effects Correlated with Granularity in Superconducting NbN Nanofilms. Nanomaterials. 2022; 12(23):4109. https://doi.org/10.3390/nano12234109
Chicago/Turabian StyleSharma, Meenakshi, Manju Singh, Rajib K. Rakshit, Surinder P. Singh, Matteo Fretto, Natascia De Leo, Andrea Perali, and Nicola Pinto. 2022. "Complex Phase-Fluctuation Effects Correlated with Granularity in Superconducting NbN Nanofilms" Nanomaterials 12, no. 23: 4109. https://doi.org/10.3390/nano12234109
APA StyleSharma, M., Singh, M., Rakshit, R. K., Singh, S. P., Fretto, M., De Leo, N., Perali, A., & Pinto, N. (2022). Complex Phase-Fluctuation Effects Correlated with Granularity in Superconducting NbN Nanofilms. Nanomaterials, 12(23), 4109. https://doi.org/10.3390/nano12234109







