A Scenario for the Critical Fluctuations near the Transition of Few-Bilayer Films of High-Temperature Cuprate Superconductors
Abstract
:1. Introduction

| (K) | (K) | Gi | / | |||||
|---|---|---|---|---|---|---|---|---|
| 1 | 17.5 | 51.2 | 2.5 | 0.065 | 7.8 | 0.55 | — | 0.40 |
| 2 | 46.9 | 65.4 | 2 | 0.035 | 4.1 | 0.45 | 30 | 0.35 |
| 3 | 58.1 | 71.8 | 2 | 0.02 | 4.5 | 0.30 | 30 | 0.35 |
| 4 | 74.3 | 82.2 | 1.5 | 0.01 | 5.6 | 0.60 | 30 | 0.25 |
2. Calculation of the Fluctuation Electrical Conductivity of a HTSC Composed of -Bilayers in the Gaussian–Ginzburg–Landau GGL and Kosterlitz–Thouless KT-like Regimes
2.1. Spectrum of Fluctuations above the Mean-Field Critical Temperature for Few-Bilayers Superconductors in a Gaussian–Ginzburg–Landau (GGL) Approximation
2.2. Gaussian-Ginzburg-Landau Paraconductivity
2.3. Crossover from the Gaussian–Ginzburg–Landau GGL Regime to the Kosterlitz–Thouless KT-like Regime: Ginzburg Number for Few-Bilayers Superconductors
2.4. Kosterlitz–Thouless Paraconductivity
2.5. Effective Medium Approximation for the Effects of Inhomogenities
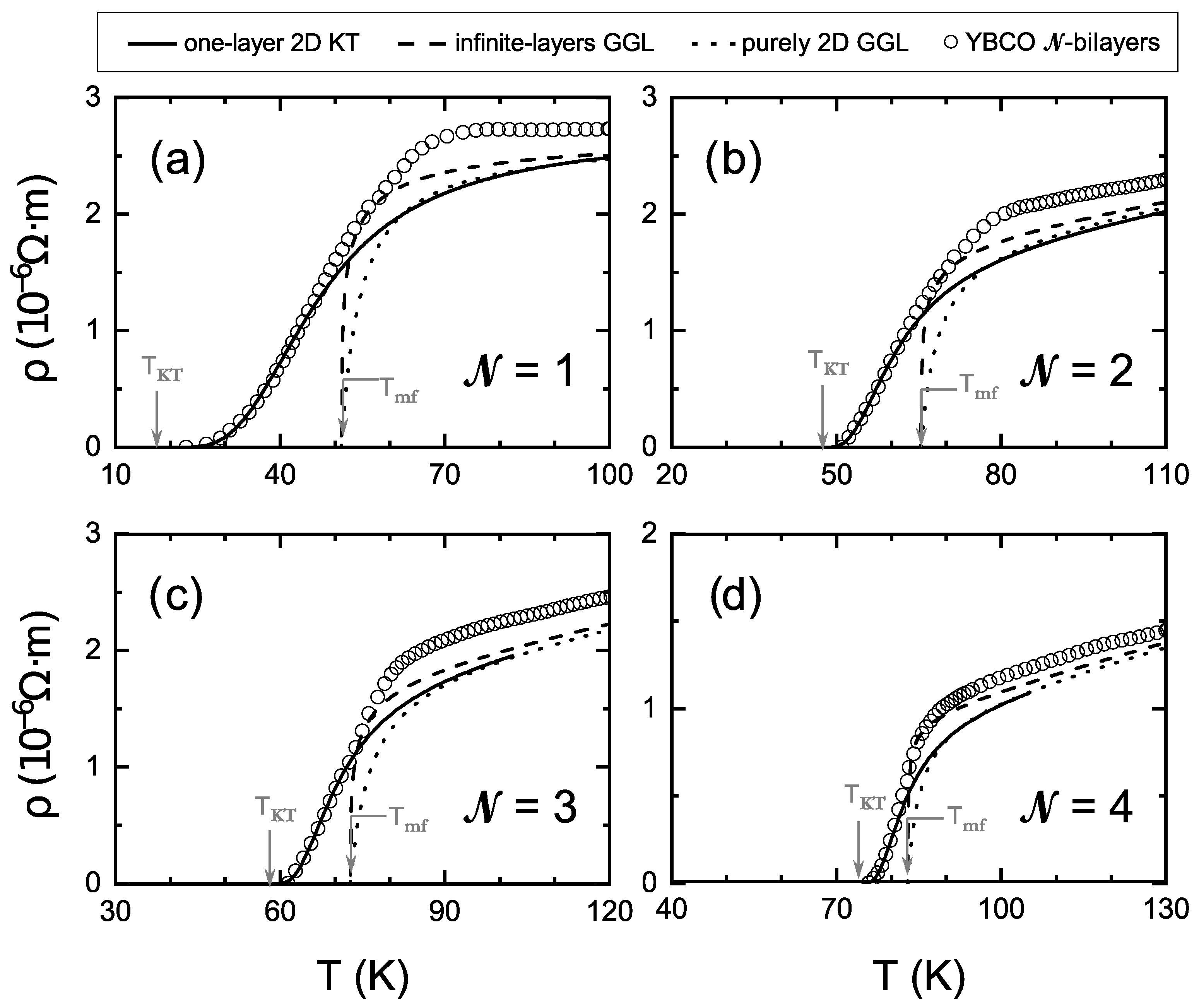
3. Analysis of Experimental Data
4. Conclusions: Some Implications and Open Aspects
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| 2D | two-dimensional |
| BCS | Bardeen–Cooper–Schieffer |
| GGL | Gaussian–Ginzburg–Landau |
| GL | Ginzburg–Landau |
| HN | Halperin–Nelson |
| HTSC | high-temperature superconducting cuprates |
| KT | Kosterlitz–Thouless |
| LD | Lawrence–Doniach |
| PBCO | |
| YBCO | |
| BSCCO |
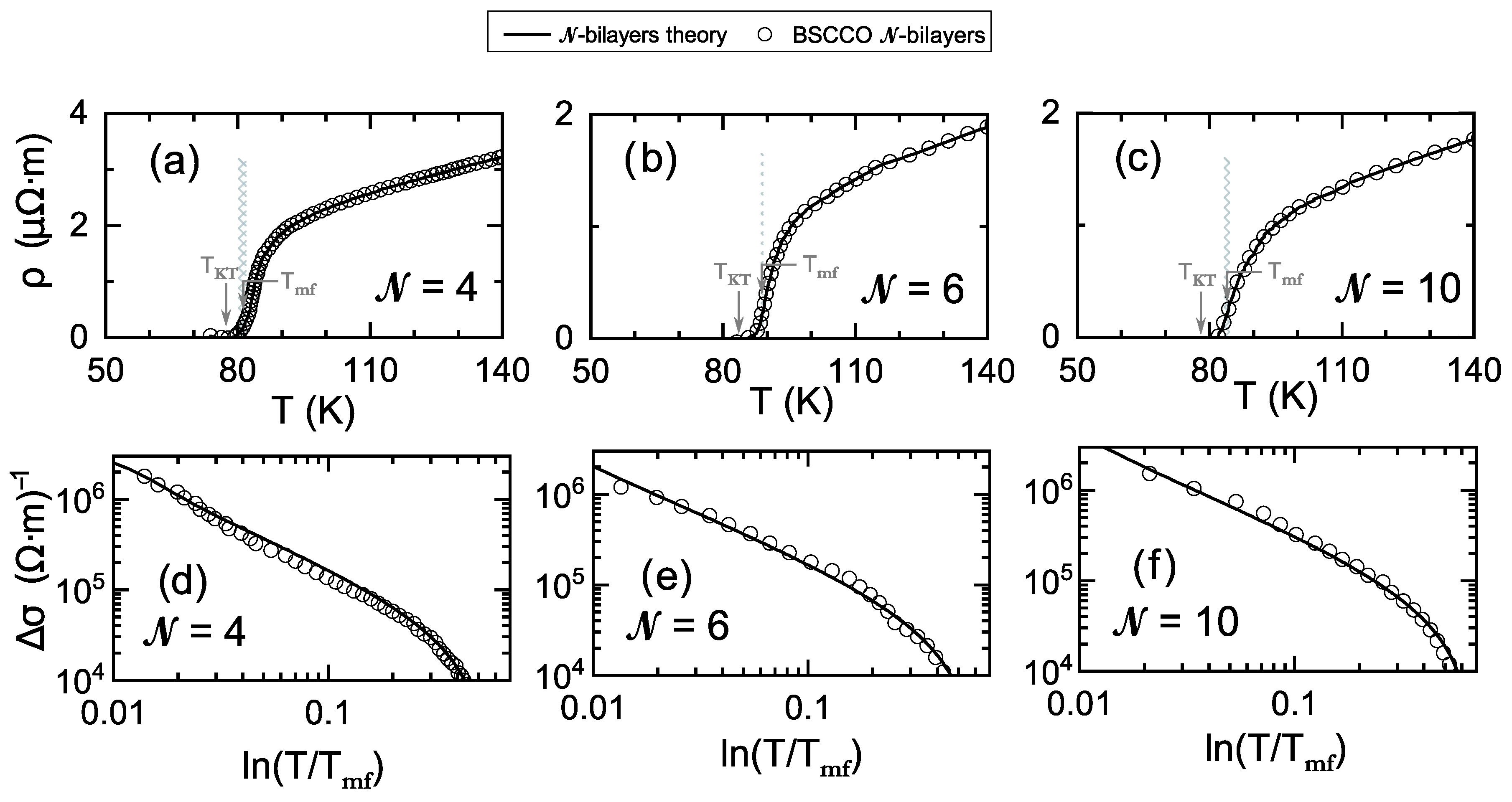
Appendix A. Comparison with Few-Bilayer Bi2Sr2CaCu2O8+x Ultra-Thin Films
References
- Emery, V.J.; Kivelson, S.A. Importance of phase fluctuations in superconductors with small superfluid density. Nature 1995, 374, 434–437. [Google Scholar] [CrossRef]
- Franz, M. Superconductivity: Importance of fluctuations. Nat. Phys. 2007, 3, 686–687. [Google Scholar] [CrossRef]
- Li, L.; Wang, Y.; Komiya, S.; Ono, S.; Ando, Y.; Gu, G.D.; Ong, N.P. Diamagnetism and Cooper pairing above Tc in cuprates. Phys. Rev. B 2010, 81, 054510. [Google Scholar] [CrossRef] [Green Version]
- Rey, R.I.; Ramos-Álvarez, A.; Mosqueira, J.; Ramallo, M.V.; Vidal, F. Comment on “Diamagnetism and Cooper pairing above in cuprates”. Phys. Rev. B 2013, 87, 056501. [Google Scholar] [CrossRef] [Green Version]
- Rullier-Albenque, F.; Alloul, H.; Tourbot, R. Influence of pair breaking and phase fluctuations on disordered high-Tc cuprate superconductors. Phys. Rev. Lett. 2003, 91, 047001. [Google Scholar] [CrossRef] [Green Version]
- Varma, C.M. Quantum-critical fluctuations in 2D metals: Strange metals and superconductivity in antiferromagnets and in cuprates. Rep. Prog. Phys. 2016, 79, 082501. [Google Scholar] [CrossRef] [Green Version]
- Auvray, N.; Loret, B.; Benhabib, S.; Cazayous, M.; Zhong, R.D.; Schneeloch, J.; Gu, G.D.; Forget, A.; Colson, D.; Paul, I.; et al. Nematic fluctuations in the cuprate superconductor Bi2Sr2CaCu2O8+δ. Nat. Commun. 2019, 10, 5209. [Google Scholar] [CrossRef] [Green Version]
- Michon, B.; Girod, C.; Badoux, S.; Kačmarčík, J.; Ma, Q.; Dragomir, M.; Dabkowska, H.A.; Gaulin, B.D.; Zhou, J.-S.; Pyon, S.; et al. Thermodynamic signatures of quantum criticality in cuprate superconductors. Nature 2019, 567, 218–222. [Google Scholar] [CrossRef] [Green Version]
- Baraduc, C.; Buzdin, A.I. Fluctuations in layered superconductors—Different inter-plane coupling and effect on the London penetration depth. Phys. Lett. A 1992, 171, 408–414. [Google Scholar] [CrossRef]
- Klemm, R.A. Phenomenological model of the copper oxide superconductors. Phys. Rev. B 1990, 41, 2073. [Google Scholar] [CrossRef]
- Ramallo, M.V.; Pomar, A.; Vidal, F. In-plane paraconductivity and fluctuation-induced magnetoconductivity in biperiodic layered superconductors: Application to YBa2Cu3O7−δ. Phys. Rev. B 1996, 54, 4341. [Google Scholar] [CrossRef]
- Viña, J.; Campá, J.A.; Carballeira, C.; Currás, S.R.; Maignan, A.; Ramallo, M.V.; Rasines, I.; Veira, J.A.; Wagner, P.; Vidal, F. Universal behavior of the in-plane paraconductivity of cuprate superconductors in the short-wavelength fluctuation regime. Phys. Rev. B 2002, 65, 212509. [Google Scholar] [CrossRef]
- Puica, I.; Lang, W. Critical fluctuation conductivity in layered superconductors in a strong electric field. Phys. Rev. B 2003, 68, 054517. [Google Scholar] [CrossRef] [Green Version]
- Terashima, T.; Shimura, K.; Bando, Y.; Matsuda, Y.; Fujiyama, A.; Komiyama, S. Superconductivity of one-unit-cell thick YBa2Cu3O7−δ thin film. Phys. Rev. Lett. 1991, 67, 1362. [Google Scholar] [CrossRef]
- Matsuda, Y.; Komiyama, S.; Terashima, T.; Shimura, K.; Bando, Y. Disappearance of Hall resistance in one-unit-cell-thick YBa2Cu3O7−δ: Evidence of free vortex-antivortex excitation. Phys. Rev. Lett. 1992, 69, 3228. [Google Scholar] [CrossRef]
- Fischer, Ø.; Brunner, O.; Antognazza, L.; Triscone, J.-M.; Miéville, L.; Karkut, M.G.; van der Linden, P.; Perenboom, J.A.A.J. Anisotropic magnetotransport in high temperature superconductor multilayers. Phys. B 1992, 177, 87–93. [Google Scholar] [CrossRef] [Green Version]
- Fischer, Ø.; Brunner, O.; Antognazza, L.; Miéville, L.; Triscone, J.-M. Investigation of superlattices and ultrathin layers made from HTS cuprates. Phys. Scr. 1992, 1992, 46. [Google Scholar] [CrossRef] [Green Version]
- Cieplak, M.Z.; Guha, S.; Vadlamannati, S.; Giebultowicz, T.; Lindenfeld, P. Origin of the Tc depression and the role of charge transfer and dimensionality in ultrathin Y1Ba2Cu3O7−δ. Phys. Rev. B 1994, 50, 12876. [Google Scholar] [CrossRef]
- Triscone, J.-M.; Frauchiger, L.; Decroux, M.; Miéville, L.; Fischer, Ø. Growth and structural properties of epitaxial Pb(ZrxTi1−x)O3 films and Pb(ZrxTi1−x)O3-cuprate heterostructures. J. Appl. Phys. 1996, 79, 4298–4305. [Google Scholar] [CrossRef]
- Prieto, P.; Vivas, P.; Campillo, G.; Baca, E.; Castro, L.F.; Varela, M.; Ballesteros, C.; Villegas, J.E.; Arias, D.; Leon, C.; et al. Magnetism and superconductivity in La0.7Ca0.3MnO3/YBa2Cu3O7−δ superlattices. J. Appl. Phys. 2001, 89, 8026–8029. [Google Scholar] [CrossRef]
- Przyslupski, P.; Komissarov, I.; Paszkowicz, W.; Dluzewski, P.; Minikayev, R.; Sawicki, M. Magnetic properties of La0.67Sr0.33MnO3/YBa2Cu3O7 superlattices. Phys. Rev. B 2004, 69, 134428. [Google Scholar] [CrossRef]
- Bollinger, A.T.; Dubuis, G.; Yoon, J.; Pavuna, D.; Misewich, J.; Božović, I. Superconductor–insulator transition in La2−xSrxCuO4 at the pair quantum resistance. Nature 2011, 472, 458–460. [Google Scholar] [CrossRef]
- Sen, K.; Marsik, P.; Das, S.; Perret, E.; de Andrés Prada, R.; Alberca, A.; Biškup, N.; Varela, M.; Bernhard, C. Superconductivity and charge-carrier localization in ultrathin La1.85Sr0.15CuO4/La2CuO4 bilayers. Phys. Rev. B 2017, 95, 214506. [Google Scholar] [CrossRef] [Green Version]
- Brun, C.; Cren, T.; Roditchev, D. Review of 2D superconductivity: The ultimate case of epitaxial monolayers. Supercond. Sci. Technol. 2017, 30, 013003. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Pan, Y.H.; Yang, R.; Bao, L.H.; Meng, L.; Luo, H.L.; Cai, Y.Q.; Liu, G.D.; Zhao, W.J.; Zhou, Z.; et al. Universal mechanical exfoliation of large-area 2D crystals. Nat. Commun. 2020, 11, 2453. [Google Scholar] [CrossRef]
- Berezinskii, V.L. Destruction of long-range order in one-dimensional and two-dimensional systems having a continuous symmetry group I. Classical systems. Sov. Phys. JETP 1971, 32, 493–500. [Google Scholar]
- Berezinskii, V.L. Destruction of Long-range Order in One-dimensional and Two-dimensional Systems Possessing a Continuous Symmetry Group. II. Quantum Systems. Sov. Phys. JETP 1972, 34, 610–616. [Google Scholar]
- Kosterlitz, J.M.; Thouless, D. Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C Solid State Phys. 1973, 6, 1181. [Google Scholar] [CrossRef]
- Doniach, S.; Huberman, B.A. Topological Excitations in Two-Dimensional Superconductors. Phys. Rev. Lett. 1979, 42, 1169. [Google Scholar] [CrossRef]
- Halperin, B.I.; Nelson, D.R. Resistive Transition in Superconducting Films. J. Low Temp. Phys. 1979, 36, 599–616. [Google Scholar] [CrossRef]
- Leggett, A.J. What DO we know about high Tc? Nat. Phys. 2006, 2, 134–136. [Google Scholar] [CrossRef]
- Fischer, K.H. Kosterlitz-Thouless transition in layered high-Tc superconductors. Phys. C 1993, 210, 179–187. [Google Scholar] [CrossRef]
- Lawrence, W.E.; Doniach, S. Theory of layer structure, superconductors. In Proceedings of the 12th International Conference on Low Temperature Physics, Kyoto, Japan, 4–10 September 1971; p. 361. [Google Scholar]
- Aslamazov, L.G.; Larkin, A.I. The influence of fluctuation pairing of electrons on the conductivity of normal metal. Phys. Lett. A 1968, 26, 238–239. [Google Scholar] [CrossRef]
- Hikami, S.; Larkin, A.I. Magnetoresistance of high temperature superconductors. Mod. Phys. Lett. B 1988, 2, 693–698. [Google Scholar] [CrossRef]
- Maki, K. The critical fluctuation of the order parameter in type-II superconductors. Prog. Theor. Phys. 1968, 39, 897–906. [Google Scholar] [CrossRef] [Green Version]
- Thompson, R.S. Microwave, flux flow, and fluctuation resistance of dirty type-II superconductors. Phys. Rev. B 1970, 1, 327. [Google Scholar] [CrossRef]
- Yip, S.K. Fluctuations in an impure unconventional superconductor. Phys. Rev. B 1990, 41, 2612. [Google Scholar] [CrossRef]
- Viz, A.S.; Botana, M.M.; Verde, J.C.; Ramallo, M.V. Dimensional crossovers in the Gaussian critical fluctuations above Tc of two-layer and three-layer superconductors. SN Appl. Sci. 2022, 4, 175. [Google Scholar] [CrossRef]
- Zhao, S.Y.F.; Poccia, N.; Panetta, M.G.; Yu, C.; Johnson, J.W.; Yoo, H.; Zhong, R.; Gu, G.D.; Watanabe, K.; Taniguchi, T.; et al. Sign-reversing Hall effect in atomically thin high-temperature Bi2.1Sr1.9CaCu2.0O8+δ superconductors. Phys. Rev. Lett. 2019, 122, 247001. [Google Scholar] [CrossRef] [Green Version]
- Mosqueira, J.; Ramallo, M.V.; Currás, S.R.; Torrón, C.; Vidal, F. Fluctuation-induced diamagnetism above the superconducting transition in MgB2. Phys. Rev. B 2002, 65, 174522. [Google Scholar] [CrossRef]
- Loram, J.W.; Cooper, J.R.; Wheatley, J.M.; Mirza, K.A.; Liu, R.S. Critical and Gaussian fluctuation effects in the specific heat and conductivity of high-Tc superconductors. Philos. Mag. B 1992, 65, 1405–1417. [Google Scholar] [CrossRef]
- Carballeira, C.; Mosqueira, J.; Ramallo, M.V.; Veira, J.A.; Vidal, F. Fluctuation-induced diamagnetism in bulk isotropic superconductors at high reduced temperatures. J. Phys. Condens. Matter 2001, 13, 9271. [Google Scholar] [CrossRef]
- Ramallo, M.V.; Vidal, F. On the width of the full-critical region for thermal fluctuations around the superconducting transition in layered superconductors. Europhys. Lett. 1997, 39, 177. [Google Scholar] [CrossRef]
- Barišić, N.; Chan, M.C.; Li, Y.; Yu, G.; Zhao, X.; Dressel, M.; Smontara, A.; Greven, M. Universal sheet resistance and revised phase diagram of the cuprate high-temperature superconductors. Proc. Natl. Acad. Sci. USA 2013, 110, 12235. [Google Scholar] [CrossRef] [Green Version]
- Caprara, S.; Grilli, M.; Benfatto, L.; Castellani, C. Effective medium theory for superconducting layers: A systematic analysis including space correlation effects. Phys. Rev. B 2011, 84, 014514. [Google Scholar] [CrossRef] [Green Version]
- Baity, P.G.; Shi, X.; Shi, Z.; Benfatto, L.; Popović, D. Effective two-dimensional thickness for the Berezinskii-Kosterlitz-Thouless-like transition in a highly underdoped La2−xSrxCuO4. Phys. Rev. B 2016, 93, 024519. [Google Scholar] [CrossRef] [Green Version]
- Pomar, A.; Ramallo, M.V.; Maza, J.; Vidal, F. Measurements of the fluctuation-induced magnetoconductivity in the a-direction of an untwinned Y1Ba2Cu3O7−δ single-crystal in the weak magnetic-field limit. Phys. C 1994, 225, 287–293. [Google Scholar] [CrossRef]
- Maza, J.; Vidal, F. Critical-temperature inhomogeneities and resistivity rounding in copper oxide superconductors. Phys. Rev. B 1991, 43, 10560. [Google Scholar] [CrossRef]
- Anderson, P.W. c-axis electrodynamics as evidence for the interlayer theory of high-temperature superconductivity. Science 1998, 279, 1196–1198. [Google Scholar] [CrossRef]
- Leggett, A.J. Cuprate superconductivity: Dependence of Tc on the c-axis layering structure. Phys. Rev. Lett. 1999, 83, 392. [Google Scholar] [CrossRef]
- Ramallo, M.V. On the energy saved by interlayer interactions in the superconducting state of cuprates. EPL 2004, 65, 249. [Google Scholar] [CrossRef] [Green Version]
- Uemura, Y.J.; Luke, G.M.; Sternlieb, B.J.; Brewer, J.H.; Carolan, J.F.; Hardy, W.; Kadono, R.; Kempton, J.R.; Kiefl, R.F.; Kreitzman, S.R.; et al. Universal correlations between Tc and ns/m* (carrier density over effective mass) in high-Tc cuprate superconductors. Phys. Rev. Lett. 1989, 62, 2317–2320. [Google Scholar] [CrossRef] [PubMed]
- Cotón, N.; Mercey, B.; Mosqueira, J.; Ramallo, M.V.; Vidal, F. Synthesis from separate oxide targets of high quality La2−xSrxCuO4 thin films and dependence with doping of their superconducting transition width. Supercond. Sci. Technol. 2013, 26, 075011. [Google Scholar] [CrossRef]
- Lee, S.; Tarantini, C.; Gao, P.; Jiang, J.; Weiss, J.D.; Kametani, F.; Folkman, C.M.; Zhang, Y.; Pan, X.Q.; Hellstrom, E.E.; et al. Artificially engineered superlattices of pnictide superconductors. Nat. Mater. 2013, 12, 392–396. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Deng, L.Z.; Lv, Z.; Wu, Z.; Xue, Y.Y.; Zhang, W.H.; Li, F.S.; Wang, L.L.; Ma, X.C.; Xue, Q.K.; Chu, C.W. Meissner and mesoscopic superconducting states in 1–4 unit-cell FeSe films. Phys. Rev. B 2014, 90, 214513. [Google Scholar] [CrossRef]
- Haindl, S.; Kidszum, M.; Kauffman, A.; Nenkov, K.; Kozlova, N.; Freudenberger, J.; Thersleff, T.; Hänisch, J.; Werner, J.; Reich, E.; et al. High Upper Critical Fields and Evidence of Weak-Link Behavior in Superconducting LaFeAsO1−xFx Thin Films. Phys. Rev. Lett. 2010, 104, 077001. [Google Scholar] [CrossRef]
- Matsumoto, J.; Hanzawa, K.; Sasase, M.; Haindl, S.; Katase, T.; Hiramatsu, H.; Hosono, H. Superconductivity at 48 K of heavily hydrogen-doped SmFeAsO epitaxial films grown by topotactic chemical reaction using CaH2. Phys. Rev. Mater. 2019, 3, 103401. [Google Scholar] [CrossRef] [Green Version]
- Katase, T. High-critical temperature iron-based superconductor epitaxial films for expanding the potential applications. Supercond. Sci. Technol. 2022, 35, 120502. [Google Scholar] [CrossRef]
- Ricci, A.; Poccia, N.; Ciasca, G.; Fratini, M.; Bianconi, A. The Microstrain-Doping Phase Diagram of the Iron Pnictides: Heterostructures at Atomic Limit. J. Supercond. Nov. Magn. 2009, 22, 589–593. [Google Scholar] [CrossRef]
- Laad, M.S.; Craco, L. Theory of Multiband Superconductivity in Iron Pnictides. Phys. Rev. Lett. 2009, 103, 017002. [Google Scholar] [CrossRef] [Green Version]
- Stanev, V.; Kang, J.; Tesanovic, Z. Spin fluctuation dynamics and multiband superconductivity in iron pnictides. Phys. Rev. B 2008, 78, 184509. [Google Scholar] [CrossRef] [Green Version]
- He, Q.L.; Liu, H.; He, M.; Lai, Y.H.; He, H.; Wang, G.; Law, K.T.; Lortz, R.; Wang, J.; Sou, I.K. Two-dimensional superconductivity at the interface of a Bi2Te3/FeTe heterostructure. Nat. Commun. 2014, 5, 4247. [Google Scholar] [CrossRef] [Green Version]
- Qiu, W.; Ma, Q.; Ma, Z.; Tang, J.; Sang, L.; Cai, C.; Shahriar, M.; Hossain, A.; Cheng, Z.; Wang, X.; et al. Enhanced superconductivity induced by several-unit-cells diffusion in an FeTe/FeSe bilayer heterostructure. Phys. Rev. B 2019, 99, 064502. [Google Scholar] [CrossRef] [Green Version]
- Saito, K.; Kaise, M. Superconductivity and structure of a few-unit-cells-thick Bi-Sr-Ca-Cu-O ultrathin films. Phys. Rev. B 1998, 57, 11786. [Google Scholar] [CrossRef]
- Jiang, D.; Hi, T.; You, L.; Li, Q.; Li, A.; Wang, H.; Mu, G.; Chen, Z.; Zhang, H.; Yu, G.; et al. High-Tc superconductivity in ultrathin Bi2Sr2CaCu2O8+δ down to half-unit-cell thickness by protection with graphene. Nat. Commun. 2014, 5, 5708. [Google Scholar] [CrossRef] [Green Version]
- Yu, Y.; Ma, L.; Cai, P.; Zhong, R.; Ye, C.; Shen, J.; Gu, G.D. High-temperature superconductivity in monolayer Bi2Sr2CaCu2O8+δ. Nature 2019, 575, 156–163. [Google Scholar] [CrossRef]
- Poccia, N.; Zhao, S.Y.F.; Yoo, H.; Xiaojing, H.; Hanfei, Y.; Yong, S.C.; Ruidan, Z.; Gu, G.D.; Mazzoli, C.; Watanabe, K.; et al. Spatially correlated incommensurate lattice modulations in an atomically thin high-temperature Bi2.1Sr1.9CaCu2.0O8+δ superconductor. Phys. Rev. Mater. 2020, 4, 114007. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Botana, M.M.; Ramallo, M.V. A Scenario for the Critical Fluctuations near the Transition of Few-Bilayer Films of High-Temperature Cuprate Superconductors. Nanomaterials 2022, 12, 4368. https://doi.org/10.3390/nano12244368
Botana MM, Ramallo MV. A Scenario for the Critical Fluctuations near the Transition of Few-Bilayer Films of High-Temperature Cuprate Superconductors. Nanomaterials. 2022; 12(24):4368. https://doi.org/10.3390/nano12244368
Chicago/Turabian StyleBotana, Martín M., and Manuel V. Ramallo. 2022. "A Scenario for the Critical Fluctuations near the Transition of Few-Bilayer Films of High-Temperature Cuprate Superconductors" Nanomaterials 12, no. 24: 4368. https://doi.org/10.3390/nano12244368





