ZnO Electrodeposition Model for Morphology Control
Abstract
:1. Introduction
2. Materials and Methods
2.1. ZnO Electrodeposition Model Development
2.2. Experimental Determination of ZnO Electrodeposition and Simulation Model
2.3. ZnO Electrodeposition
- A period of constant current (−4 mA).
- A period for concentration homogenization (no current applied).
- Then, the electrodepositions were carried out in two phases.
- The first phase of 70 s with cycles of 1.5 s of constant current and 0.5 s without current.
- The second phase of 730 s with cycles of 1 s of constant current and 1 s without current.
2.4. ZnO Characterization
3. Results and Discussion
3.1. ZnO Electrodeposition Model
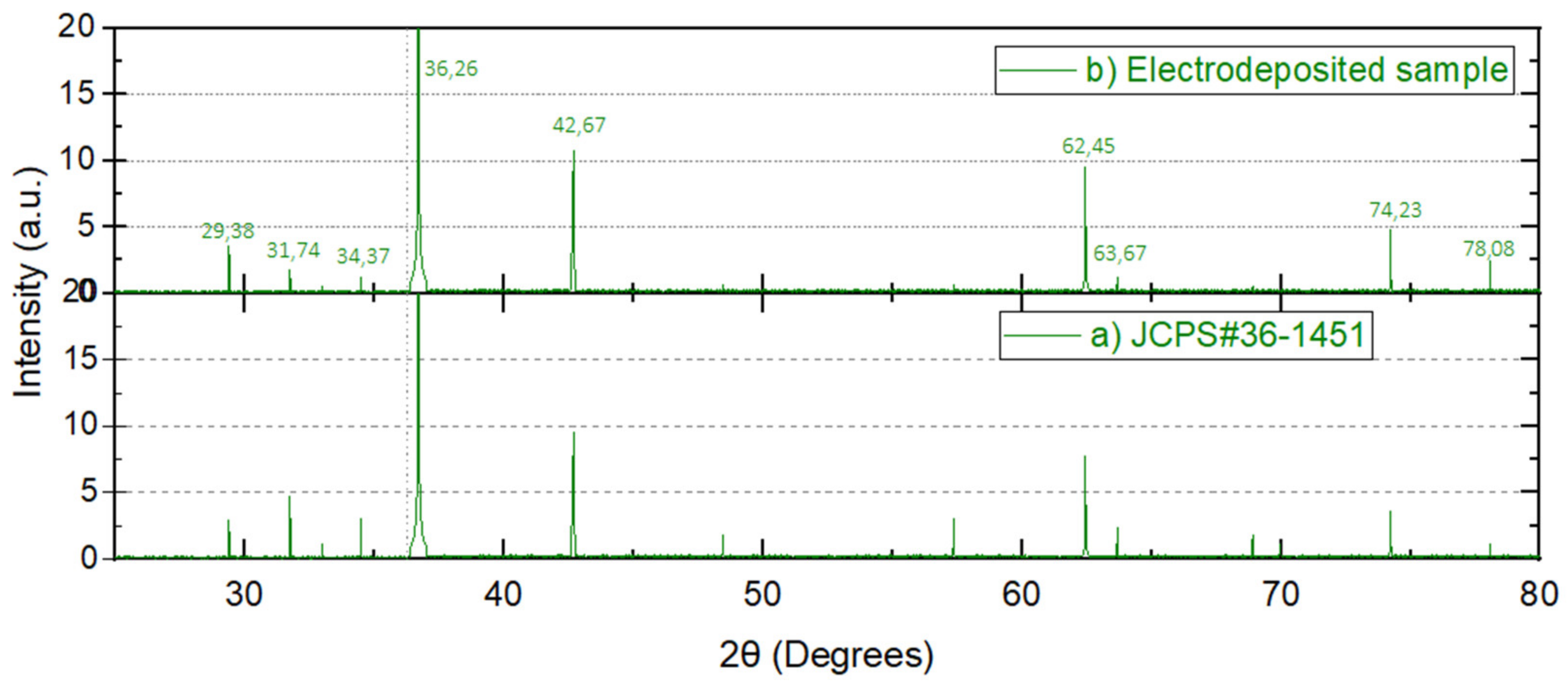
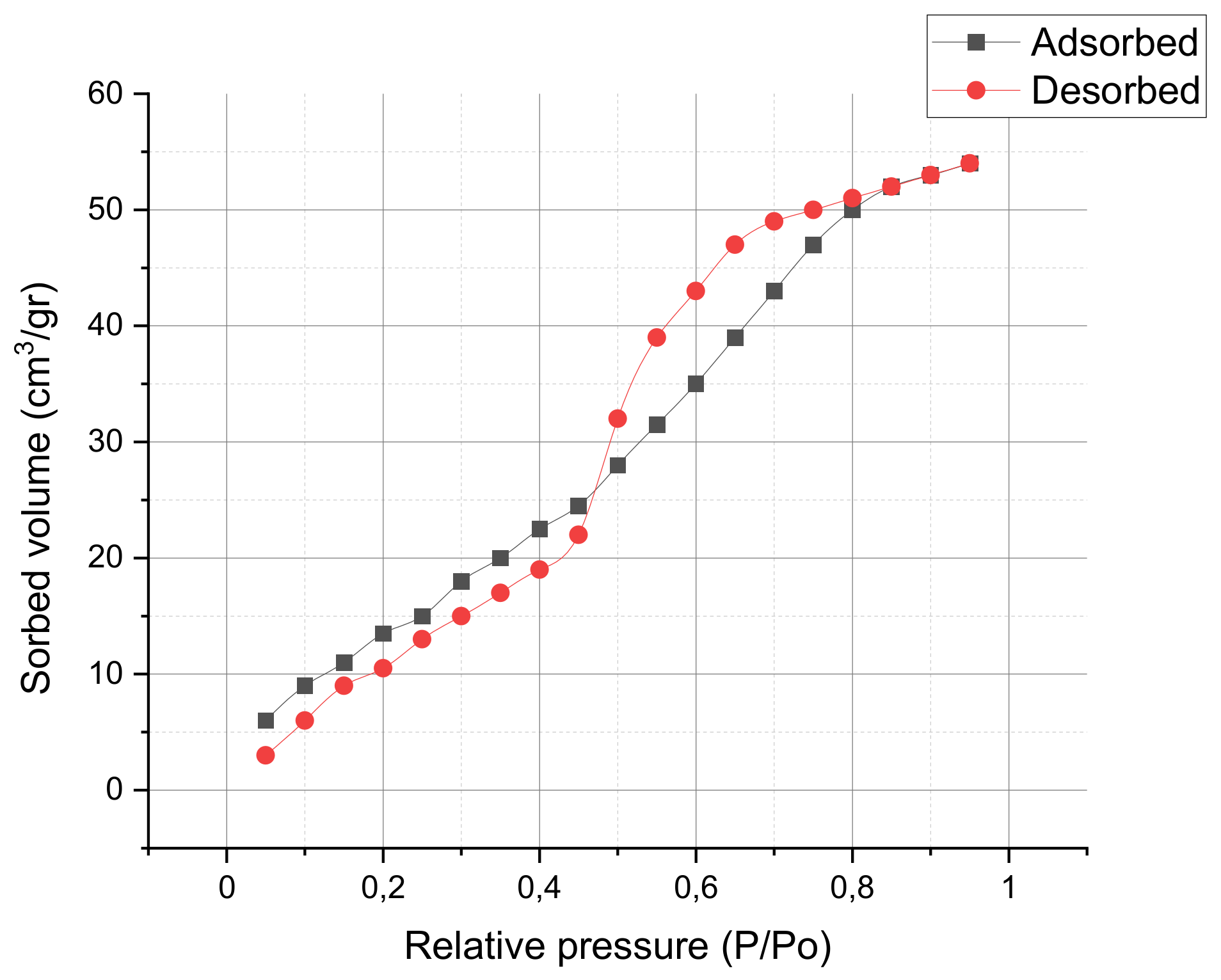
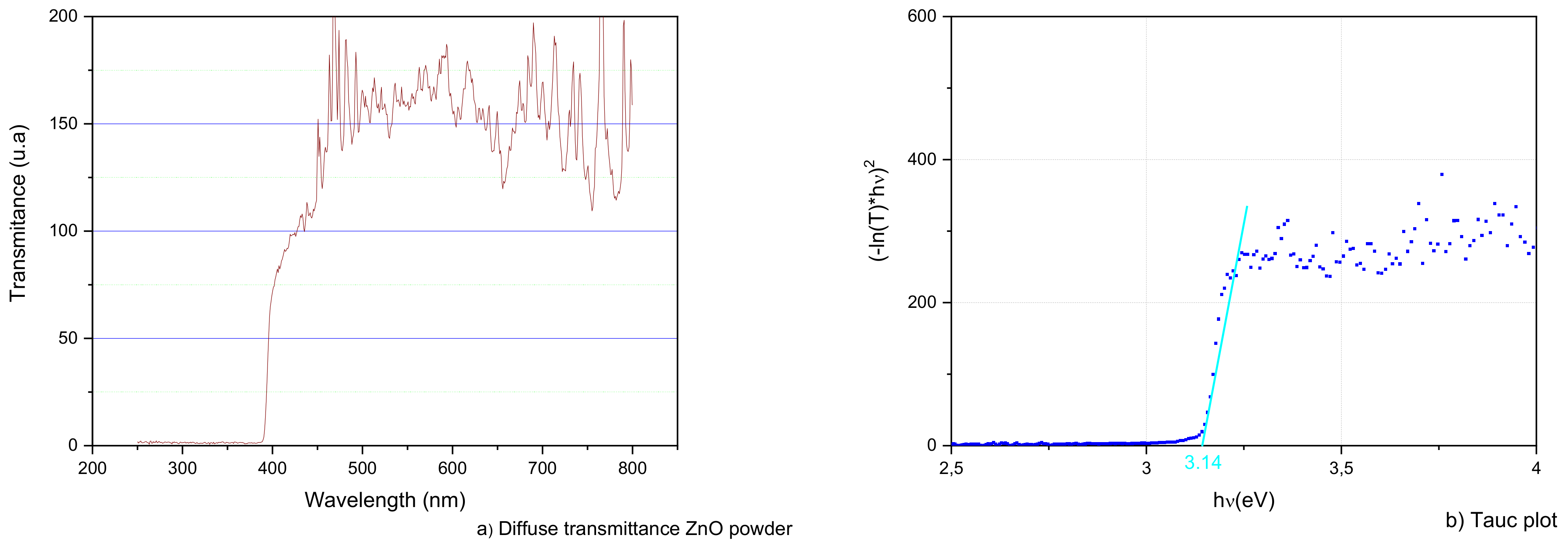
3.2. ZnO Characterization
- (a)
- Random microstructure for amorphous Zn(OH)2 with corresponding irregular diffraction pattern below.
- (b)
- Small ZnO wurtzite monocrystalline nuclei with high quality XR diffraction pattern below showing main crystal directions (1,1,0), (0,0,1), (0,0,2).
- (c)
- Average quality crystalline microstructure for a ZnO wurtzite column showing the lattice spacing (0.26 nm). Below the expected average quality diffraction pattern (with main crystal directions (1,1,0), (0,0,1), (0,0,2)).
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Johar, M.A.; Afzal, R.A.; Alazba, A.A.; Manzoor, U. Photocatalysis and Bandgap Engineering Using ZnO Nanocomposites. Adv. Mater. Sci. Eng. 2015, 2015, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Saravanan, S.; Dubey, R. An experimental investigation of ZnO nanostructures on various substrates using electrodeposition method. Mater. Today Proc. 2021, 49, 2862–2866. [Google Scholar] [CrossRef]
- Lin, H.-P.; Lin, P.-Y.; Perng, D.-C. Fast-Response and Self-Powered Cu2O/ZnO Nanorods Heterojunction UV-Visible (570 nm) Photodetectors. J. Electrochem. Soc. 2020, 167, 067507. [Google Scholar] [CrossRef]
- Manzano, C.V.; Serrano, A.; Muñoz-Noval, A.; Fernandez, J.F.; Martín-González, M. Crystal defects and optical emissions of pulse electrodeposited ZnO. Electrochim. Acta 2020, 357, 136662. [Google Scholar] [CrossRef]
- Yang, S.; Sha, S.; Lu, H.; Wu, J.; Ma, J.; Wang, D.; Sheng, Z. Electrodeposition of hierarchical zinc oxide nanostructures on metal meshes as photoanodes for flexible dye-sensitized solar cells. Colloids Surfaces A Physicochem. Eng. Asp. 2020, 594, 124665. [Google Scholar] [CrossRef]
- Tolosa, M.D.R.; Orozco-Messana, J.; Damonte, L.C.; Hernandez-Fenollosa, M.A. ZnO Nanoestructured Layers Processing with Morphology Control by Pulsed Electrodeposition. J. Electrochem. Soc. 2011, 158, D452–D455. [Google Scholar] [CrossRef]
- Choi, C.-H.; Su, Y.-W.; Chang, C.-H. Effects of fluid flow on the growth and assembly of ZnO nanocrystals in a continuous flow microreactor. CrystEngComm 2013, 15, 3326–3333. [Google Scholar] [CrossRef]
- Alatawi, N.; Ben Saad, L.; Soltane, L.; Moulahi, A.; Mjejri, I.; Sediri, F. Enhanced solar photocatalytic performance of Cu-doped nanosized ZnO. Polyhedron 2021, 197, 115022. [Google Scholar] [CrossRef]
- Kim, Y.E.; Chae, Y.; Moon, J.; Lee, J.Y.; Baek, U.C.; Park, J.T. Tailored ZnO Nanostructure Based Quasi-Solid-State Electrolyte and Mesoporous Carbon Electrocatalyst for Solar Energy Conversion. ECS J. Solid State Sci. Technol. 2021, 10, 085005. [Google Scholar] [CrossRef]
- Hu, R.; Su, X.; Liu, H.; Liu, Y.; Huo, M.-M.; Zhang, W. Recycled indium tin oxide transparent conductive electrode for polymer solar cells. J. Mater. Sci. 2020, 55, 11403–11410. [Google Scholar] [CrossRef]
- Txintxurreta, J.; G-Berasategui, E.; Ortiz, R.; Hernández, O.; Mendizábal, L.; Barriga, J. Indium Tin Oxide Thin Film Deposition by Magnetron Sputtering at Room Temperature for the Manufacturing of Efficient Transparent Heaters. Coatings 2021, 11, 92. [Google Scholar] [CrossRef]
- Calvo, G.; Valero, A. Strategic mineral resources: Availability and future estimations for the renewable energy sector. Environ. Dev. 2021, 100640, in press. [Google Scholar] [CrossRef]
- Giuliano, G.; Bonasera, A.; Arrabito, G.; Pignataro, B. Semitransparent Perovskite Solar Cells for Building Integration and Tandem Photovoltaics: Design Strategies and Challenges. Sol. RRL 2021, 5, 2100702. [Google Scholar] [CrossRef]
- Qu, S.; Yu, J.; Cao, J.; Liu, X.; Wang, H.; Guang, S.; Tang, W. Highly efficient organic solar cells enabled by a porous ZnO/PEIE electron transport layer with enhanced light trapping. Sci. China Mater. 2020, 64, 808–819. [Google Scholar] [CrossRef]
- Prochowicz, D.; Tavakoli, M.M.; Wolska-Pietkiewicz, M.; Jędrzejewska, M.; Trivedi, S.; Kumar, M.; Zakeeruddin, S.M.; Lewiński, J.; Graetzel, M.; Yadav, P. Suppressing recombination in perovskite solar cells via surface engineering of TiO2 ETL. Sol. Energy 2020, 197, 50–57. [Google Scholar] [CrossRef]
- Magne, C.; Moehl, T.; Urien, M.; Grätzel, M.; Pauporté, T. Effects of ZnO film growth route and nanostructure on electron transport and recombination in dye-sensitized solar cells. J. Mater. Chem. A 2012, 1, 2079–2088. [Google Scholar] [CrossRef]
- Zirino, A.; Yamamoto, S. A pH-Dependent Model for the Chemical Speciation of Copper, Zinc, Cadmium, and Lead in Seawater. Limnol. Oceanogr. 1972, 17, 661–671. [Google Scholar] [CrossRef]
- Tonelli, D.; Scavetta, E.; Gualandi, I. Electrochemical Deposition of Nanomaterials for Electrochemical Sensing. Sensors 2019, 19, 1186. [Google Scholar] [CrossRef] [Green Version]
- Ansys CFX. Available online: https://www.ansys.com/products/fluids/ansys-cfx#tab1-1 (accessed on 30 January 2022).
- Lincot, D. Electrodeposition of semiconductors. Thin Solid Films 2005, 487, 40–48. [Google Scholar] [CrossRef]
- El Belghiti, H.; Pauporté, T.; Lincot, D. Mechanistic study of ZnO nanorod array electrodeposition. Phys. Status Solidi (A) 2008, 205, 2360–2364. [Google Scholar] [CrossRef]
- Sedlak, J.; Kuritka, I.; Masar, M.; Machovsky, M.; Urbanek, P.; Bazant, P.; Janota, P.; Dvorackova, M. Contributions of morphological and structural parameters at different hierarchical morphology levels to photocatalytic activity of mesoporous nanostructured ZnO. Appl. Surf. Sci. 2020, 513, 145773. [Google Scholar] [CrossRef]
- Yadav, M.S.; Singh, N.; Bobade, S.M. Zinc oxide nanoparticles and activated charcoal-based nanocomposite electrode for supercapacitor application. Ionics 2018, 24, 3611–3630. [Google Scholar] [CrossRef]
- Lakshmi, B.; Thomas, B.J.; Gopinath, P. Accurate band gap determination of chemically synthesized cobalt ferrite nanoparticles using diffuse reflectance spectroscopy. Adv. Powder Technol. 2021, 32, 3706–3716. [Google Scholar] [CrossRef]
- Coulter, J.B.; Birnie, D.P. Assessing Tauc Plot Slope Quantification: ZnO Thin Films as a Model System. Phys. Status Solidi (B) 2017, 255, 1700393. [Google Scholar] [CrossRef]
- Bihar, E.; Corzo, D.; Hidalgo, T.C.; Rosas-Villalva, D.; Salama, K.N.; Inal, S.; Baran, D. Fully Inkjet-Printed, Ultrathin and Conformable Organic Photovoltaics as Power Source Based on Cross-Linked PEDOT:PSS Electrodes. Adv. Mater. Technol. 2020, 5, 2000226. [Google Scholar] [CrossRef]
- Karunakaran, S.K.; Arumugam, G.M.; Yang, W.; Ge, S.; Khan, S.N.; Lin, X.; Yang, G. Recent progress in inkjet-printed solar cells. J. Mater. Chem. A 2019, 7, 13873–13902. [Google Scholar] [CrossRef]


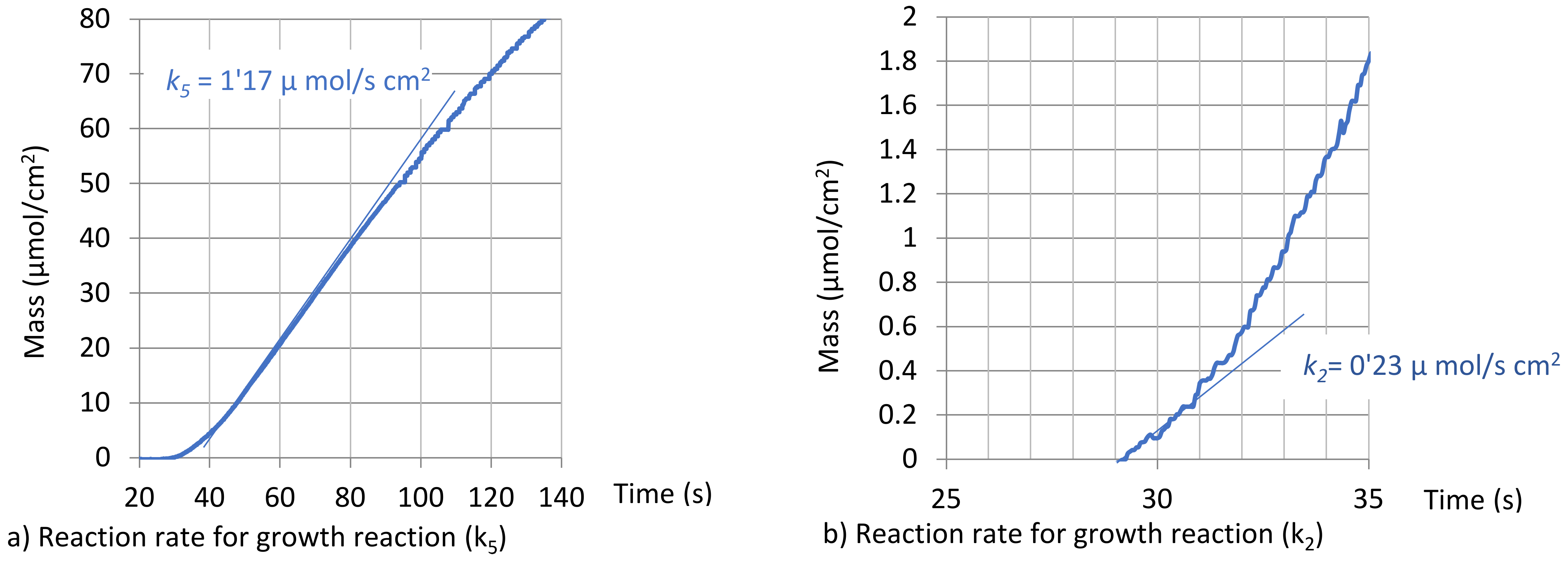



| x | Reaction | kx | nxi (i = 1.2) | Deposition Reaction Rate | |
|---|---|---|---|---|---|
| 1 | 1.1 | 0.4 | |||
| 2 | 0.6 | 0.5 | |||
| 3 | 0.9 | 0.8 | |||
| 4 | 1.9 | 0.4 | |||
| 5 | 1.0 | – | |||
| Time (s) | ZnOH+ (mN/L) | Zn(OH)2 (µm/cm2) | ZnO (µm/cm2) |
|---|---|---|---|
| 0 | 5.83 × 10−6 | 0.000 | 0.000 |
| 20 | 8.46 × 10−6 | 0.182 | 0.000 |
| 40 | 4.60 × 10−6 | 0.381 | 0.000 |
| 60 | 8.28 × 10−6 | 0.598 | 0.000 |
| 80 | 1.24 × 10−6 | 0.702 | 0.014 |
| 100 | 1.64 × 10−6 | 0.702 | 0.015 |
| 120 | 2.31 × 10−6 | 0.702 | 0.032 |
| 140 | 2.61 × 10−6 | 0.702 | 0.054 |
| – | – | – | – |
| 680 | 5.83 × 10−6 | 0.702 | 7.091 |
| 700 | 5.83 × 10−6 | 0.702 | 7.114 |
| 720 | 5.83 × 10−6 | 0.702 | 7.133 |
| 740 | 5.83 × 10−5 | 0.702 | 7.156 |
| 760 | 5.83 × 10−5 | 0.702 | 7.176 |
| 780 | 5.83 × 10−5 | 0.702 | 7.195 |
| 800 | 5.83 × 10−6 | 0.702 | 7.210 |
| Property | ZnO |
|---|---|
| Crystallite size (nm) | 10.2 |
| Surface area (m2/g) | 20.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Orozco-Messana, J.; Camaratta, R. ZnO Electrodeposition Model for Morphology Control. Nanomaterials 2022, 12, 720. https://doi.org/10.3390/nano12040720
Orozco-Messana J, Camaratta R. ZnO Electrodeposition Model for Morphology Control. Nanomaterials. 2022; 12(4):720. https://doi.org/10.3390/nano12040720
Chicago/Turabian StyleOrozco-Messana, Javier, and Rubens Camaratta. 2022. "ZnO Electrodeposition Model for Morphology Control" Nanomaterials 12, no. 4: 720. https://doi.org/10.3390/nano12040720
APA StyleOrozco-Messana, J., & Camaratta, R. (2022). ZnO Electrodeposition Model for Morphology Control. Nanomaterials, 12(4), 720. https://doi.org/10.3390/nano12040720







