Effect of Vacancy Defects on the Vibration Frequency of Graphene Nanoribbons
Abstract
:1. Introduction
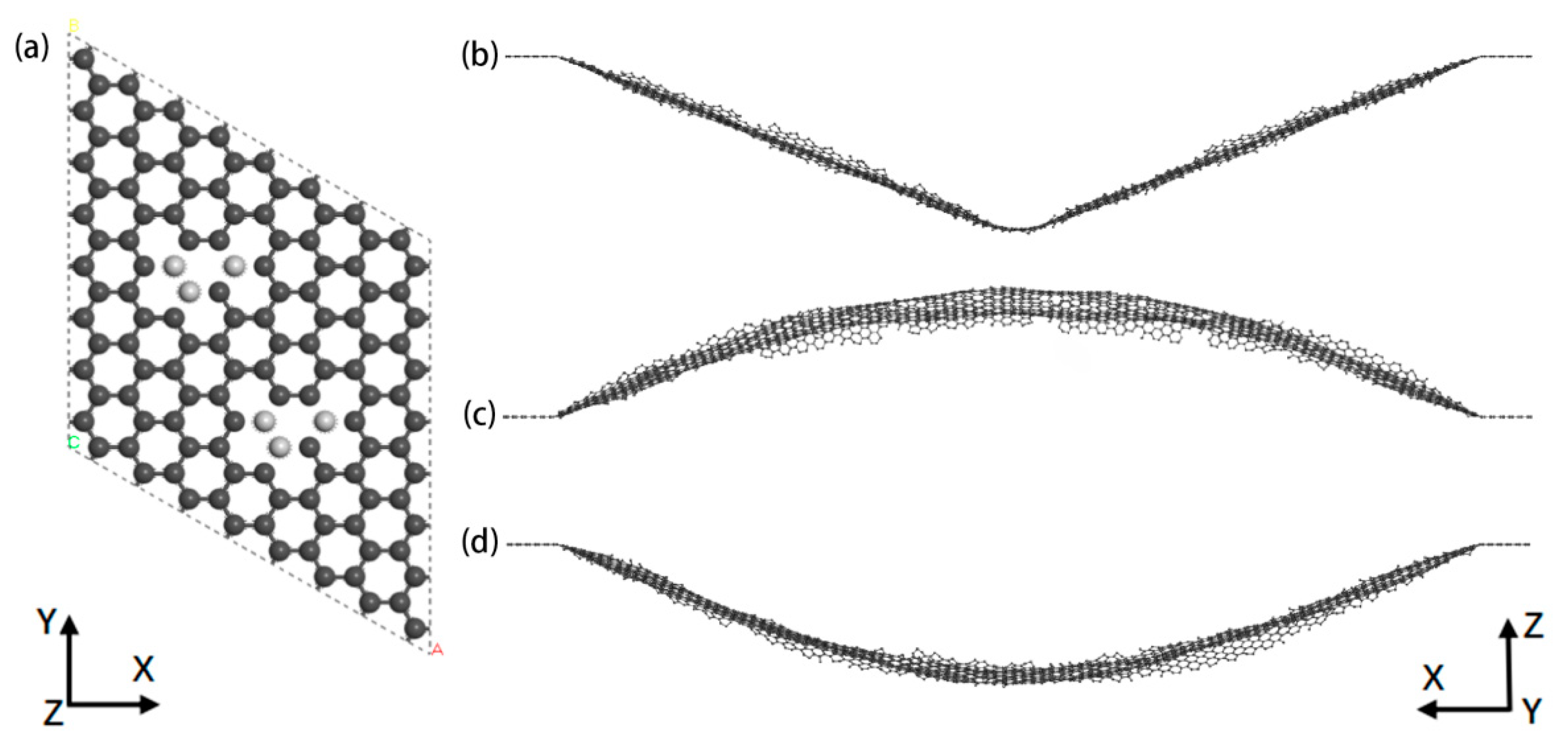
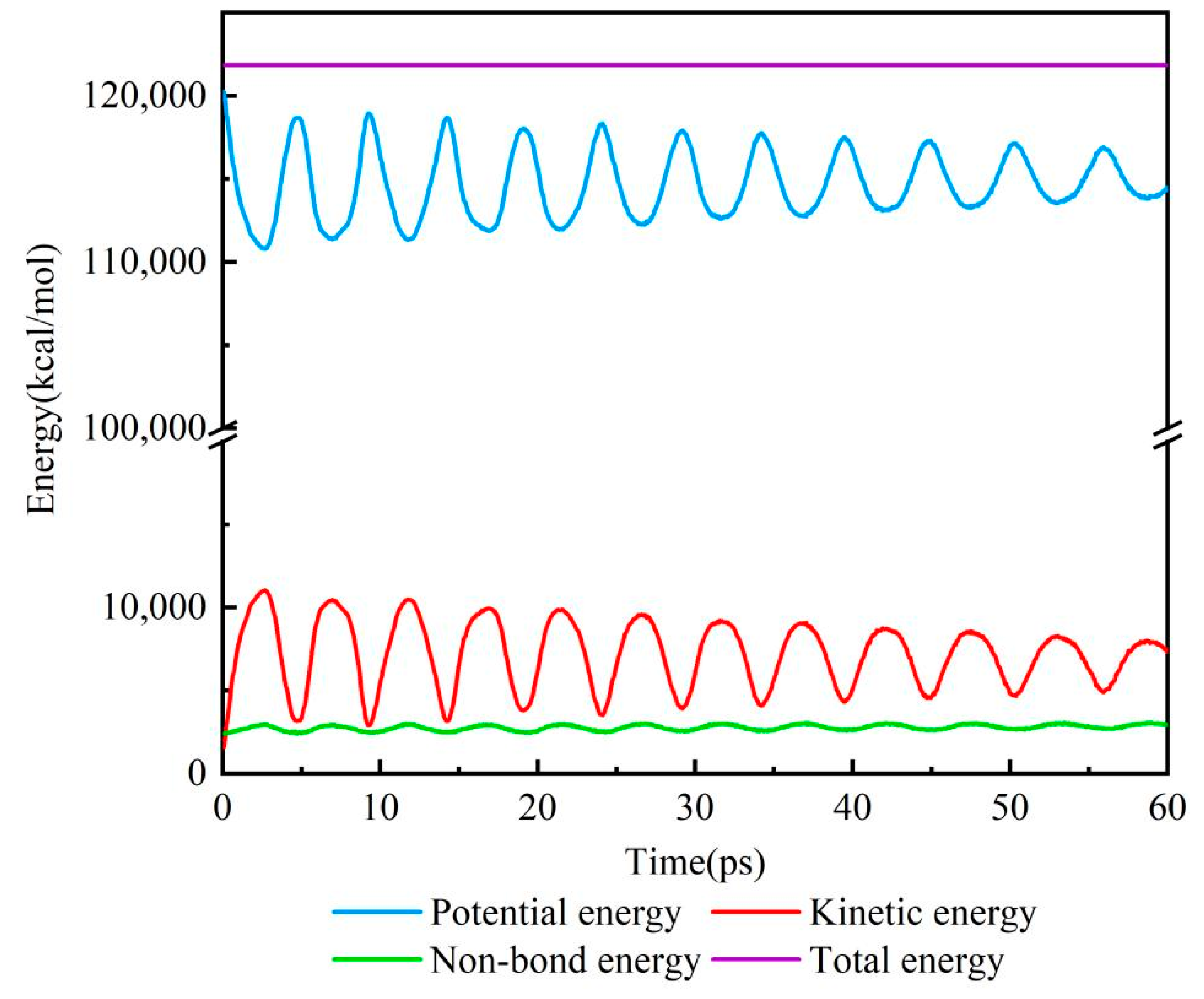
2. Physical Model and Simulation Method
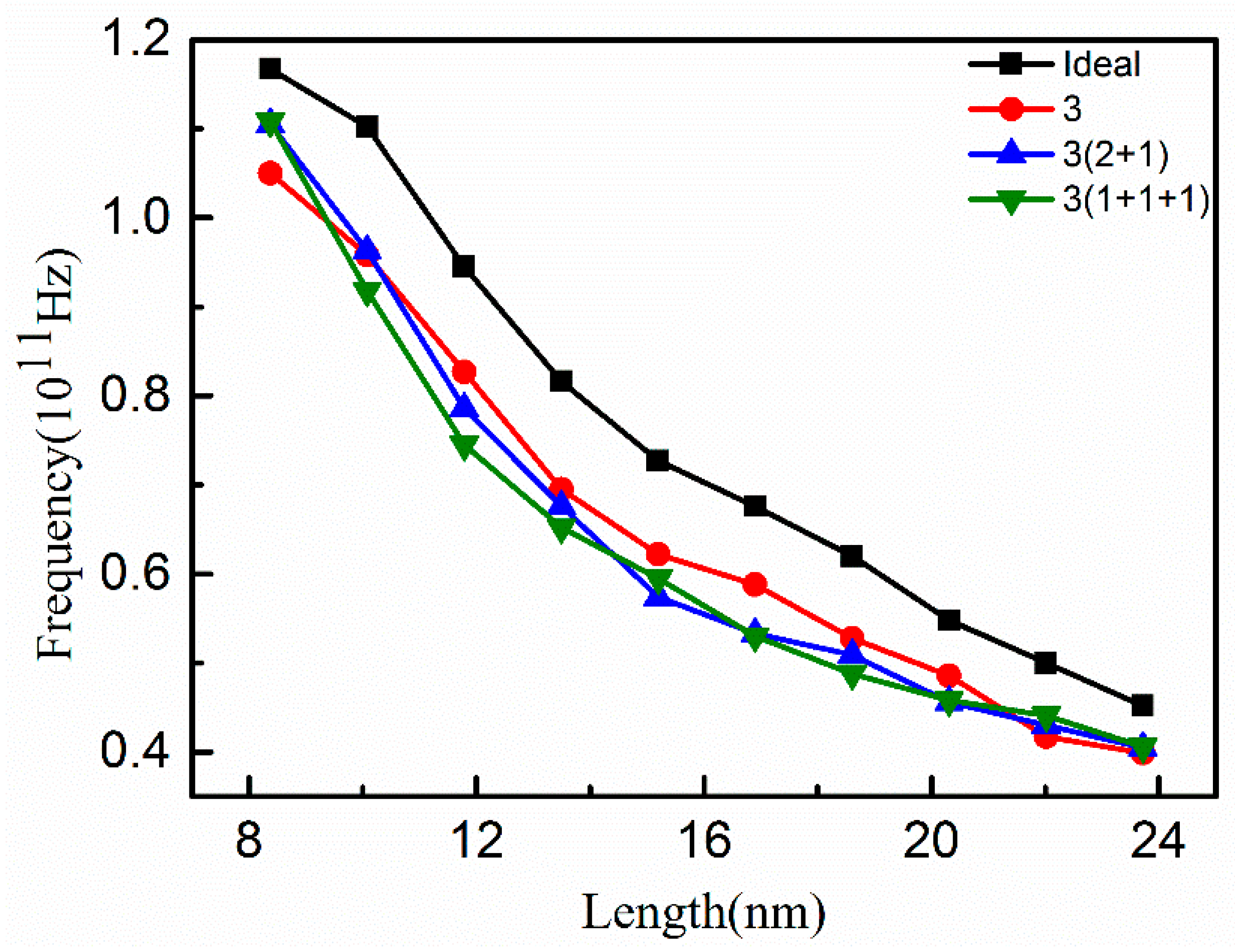
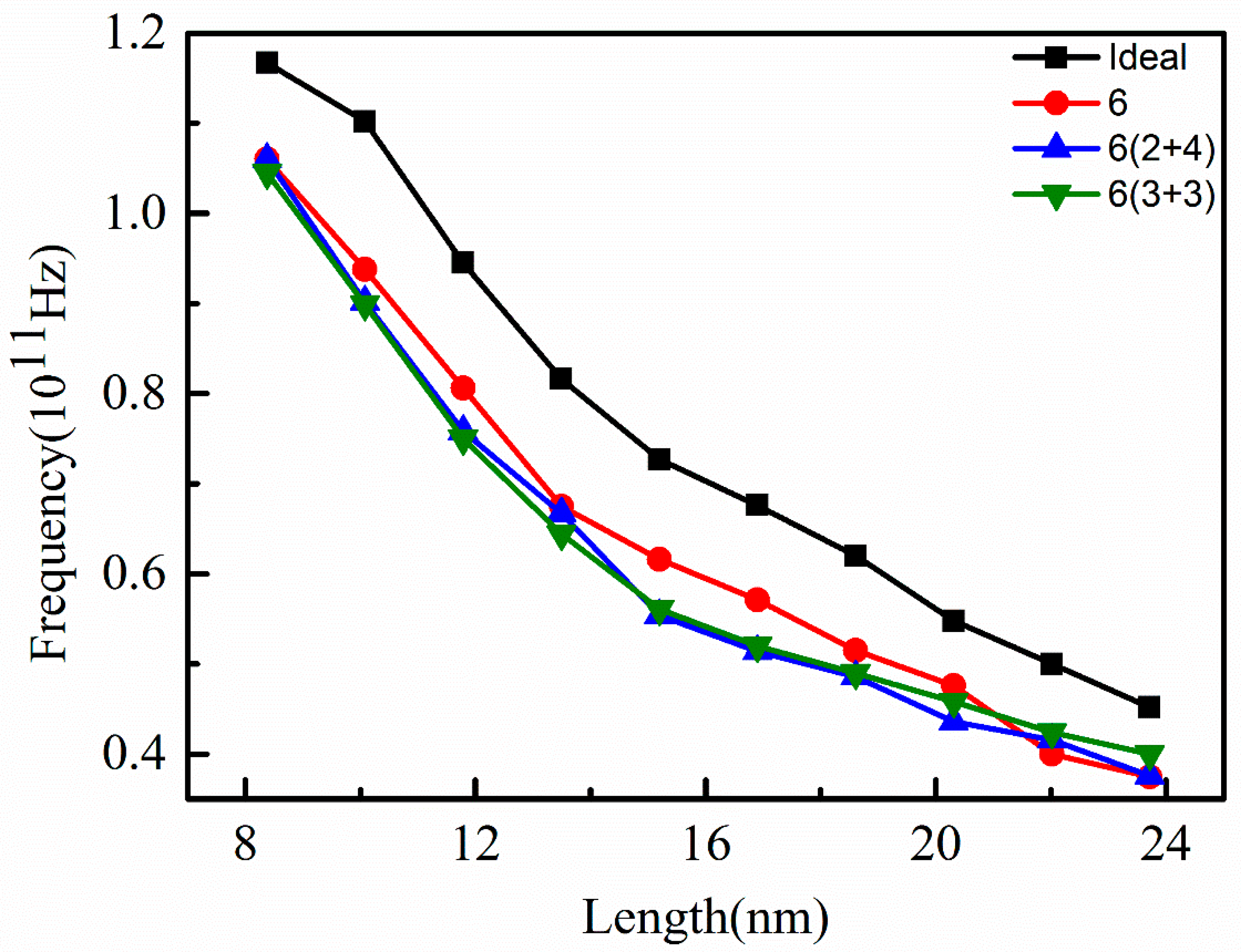
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bhadra, S.; Khastgir, D.; Singha, N.K.; Hee-Lee, J. Progress in polymer science. Polym. Int. 2010, 35, 1275–1350. [Google Scholar]
- Das, T.K.; Prusty, S. Graphene-based polymer composites and their applications. Polym. -Plast. Technol. Eng. 2013, 52, 319–331. [Google Scholar] [CrossRef]
- Jing, N.; Xue, Q.; Ling, C.; Shan, M.; Zhang, T.; Zhou, X.; Jiao, Z. Effect of defects on Young’s modulus of graphene sheets: A molecular dynamics simulation. Rsc Adv. 2012, 2, 9124–9129. [Google Scholar] [CrossRef]
- Verdejo, R.; Bernal, M.M.; Romasanta, L.J.; Lopez-Manchado, M.A. Graphene filled polymer nanocomposites. J. Mater. Chem. 2011, 21, 3301–3310. [Google Scholar] [CrossRef] [Green Version]
- Xiao, J.R.; Staniszewski, J.W., Jr. Tensile behaviors of graphene sheets and carbon nanotubes with multiple Stone–Wales defects. Mater. Sci. Eng. A 2010, 527, 715–723. [Google Scholar] [CrossRef]
- Pei, Q.X.; Zhang, Y.W.; Shenoy, V.B. A molecular dynamics study of the mechanical properties of hydrogen functionalized graphene. Carbon 2010, 48, 898–904. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, Q.; Chen, D.; Lu, P. Enhanced mechanical properties of graphene-based poly(vinyl alcohol) composites. Macromolecules 2010, 43, 2357–2363. [Google Scholar] [CrossRef]
- Lee, E.; Zhi, L.; Burghard, M.; Muellen, K.; Kern, K. Electrical properties and photoconductivity of stacked-graphene carbon nanotubes. Adv. Mater. 2010, 22, 1854–1857. [Google Scholar] [CrossRef]
- Park, S.; Ji, W.S.; An, J.; Oh, J.; Lee, S.; Lee, W.; Potts, J.R.; Byun, J.H.; Ruoff, R.S. The effect of concentration of graphene nanoplatelets on mechanical and electrical properties of reduced graphene oxide papers. Carbon 2012, 50, 4573–4578. [Google Scholar] [CrossRef]
- Obata, S.; Tanaka, H.; Saiki, K. Electrical and spectroscopic investigations on the reduction mechanism of graphene oxide. Carbon 2013, 55, 126–132. [Google Scholar] [CrossRef]
- Sankeshwar, A. Electronic thermal conductivity and thermopower of armchair graphene nanoribbons. Carbon 2013, 52, 201–208. [Google Scholar]
- Tang, G.P.; Zhou, J.C.; Zhang, Z.H.; Deng, X.Q.; Fan, Z.Q. A theoretical investigation on the possible improvement of spin-filter effects by an electric field for a zigzag graphene nanoribbon with a line defect. Carbon 2013, 60, 94–101. [Google Scholar] [CrossRef]
- Joh, H.I.; Lee, S.; Kim, T.W.; Hwang, S.Y.; Hahn, J.R. Synthesis and properties of an atomically thin carbon nanosheet similar to graphene and its promising use as an organic thin film transistor. Carbon 2013, 55, 299–304. [Google Scholar] [CrossRef]
- Qureshi, A.; Kang, W.P.; Davidson, J.L.; Gurbuz, Y. Review on carbon-derived, solid-state, micro and nano sensors for electrochemical sensing applications. Diam. Relat. Mater. 2009, 18, 1401–1420. [Google Scholar] [CrossRef] [Green Version]
- Sorkin, V.; Yong, W.Z. Graphene-based pressure nano-sensors. J. Mol. Modeling 2011, 17, 2825–2830. [Google Scholar] [CrossRef] [PubMed]
- Yao, J.; Shen, X.; Wang, B.; Liu, H.; Wang, G. In situ chemical synthesis of SnO2-graphene nanocomposite as anode materials for lithiumion batteries. Electrochem. Commun. 2009, 11, 1849–1852. [Google Scholar] [CrossRef]
- Sun, X.; Zhuang, L.; Welsher, K.; Robinson, J.T.; Goodwin, A.; Zaric, S.; Dai, H. Nano-graphene oxide for cellular imaging and drug delivery. Nano Res. 2008, 1, 203–212. [Google Scholar] [CrossRef] [Green Version]
- Cai, D.; Wang, S.; Lian, P.; Zhu, X.; Li, D.; Yang, W.; Wang, H. Superhigh capacity and rate capability of high-level nitrogen-doped graphene sheets as anode materials for lithium-ion batteries. Electrochim. Acta 2013, 90, 492–497. [Google Scholar] [CrossRef]
- Choi, H.J.; Jung, S.M.; Seo, J.M.; Chang, D.W.; Dai, L.; Baek, J.B. Graphene for energy conversion and storage in fuel cells and supercapacitors. Nano Energy 2012, 1, 534–551. [Google Scholar] [CrossRef]
- Hong, B.H. Large-scale pattern growth of graphene films for stretchable transparent electrodes. Nature 2009, 457, 706–710. [Google Scholar]
- Hu, J.M.; Yang, T.; Wang, J.; Huang, H.; Nan, C.W. Purely electric-field-driven perpendicular magnetization reversal. Nano Lett. 2015, 15, 616–622. [Google Scholar] [CrossRef] [PubMed]
- Peng, Z.; Ma, L.; Fan, F.; Zhi, Z.; Cheng, P.; Loya, P.E.; Zheng, L.; Gong, Y.; Zhang, J.; Zhang, X. Fracture toughness of graphene. Nat. Commun. 2014, 5, 3782. [Google Scholar]
- Rajasekaran, G.; Narayanan, P.; Parashar, A. Effect of point and line defects on mechanical and thermal properties of graphene: A review. Crit. Rev. Solid State Mater. Sci. 2016, 4, 47–71. [Google Scholar] [CrossRef]
- Gass, M.H.; Bangert, U.; Bleloch, A.L.; Wang, P.; Nair, R.R.; Geim, A.K. Free-standing graphene at atomic resolution. Nat. Nanotechnol. 2008, 3, 676–681. [Google Scholar] [CrossRef] [PubMed]
- Yazyev, O.V.; Louie, S.G. Topological defects in graphene: Dislocations and grain boundaries. Phys. Rev. B Condens. Matter 2010, 81, 195420. [Google Scholar] [CrossRef] [Green Version]
- Lehtinen, P.O.; Foster, A.S.; Ayuela, A.; Krasheninnikov, A.; Nordlund, K.; Nieminen, R.M. Magnetic properties and diffusion of adatoms on a graphene sheet. Phys. Rev. Lett. 2003, 91, 17202. [Google Scholar] [CrossRef] [Green Version]
- Yadav, S.; Zhu, Z.; Singh, C.V. Defect engineering of graphene for effective hydrogen storage. Int. J. Hydrogen Energy 2014, 39, 4981–4995. [Google Scholar] [CrossRef]
- Wang, M.C.; Yan, C.; Ma, L.; Hu, N.; Chen, M.W. Effect of defects on fracture strength of graphene sheets. Comput. Mater. Sci. 2012, 54, 236–239. [Google Scholar] [CrossRef] [Green Version]
- Rahmandoust, M. Computational evaluation of the mechanical properties of synthesized graphene quantum dots under consideration of defects. Carbon Lett. 2021, 31, 427–440. [Google Scholar] [CrossRef]
- Park, Y.; Hyun, S. Size effect of defects on the mechanical properties of graphene. J. Korean Phys. Soc. 2018, 72, 681–686. [Google Scholar] [CrossRef]
- Motamedi, M.; Esfandiarpour, A. Effect of center crack on mechanical properties of graphene. J. Nano Res. 2018, 55, 22–31. [Google Scholar] [CrossRef]
- Lopez-Polin, G.; Gomez-Navarro, C.; Parente, V.; Guinea, F.; Gomez-Herrero, J. Increasing the elastic modulus of graphene by controlled defect creation. Nat. Phys. 2015, 11, 26–31. [Google Scholar] [CrossRef]
- Ng, T.Y.; Yeo, J.J.; Liu, Z.S. A molecular dynamics study of the thermal conductivity of graphene nanoribbons containing dispersed Stone–Thrower–Wales defects. Carbon 2012, 50, 4887–4893. [Google Scholar] [CrossRef]
- Teng, Y.N.; Yeo, J.; Liu, Z. Molecular dynamics simulation of the thermal conductivity of shorts strips of graphene and silicene: A comparative study. Int. J. Mech. Mater. Des. 2013, 9, 105–114. [Google Scholar]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef]
- Georgakaki, D.; Ziogos, O.G.; Polatoglou, H.M. Vibrational and mechanical properties of Si/Ge nanowires as resonators: A molecular dynamics study. Phys. Status Solidi 2014, 211, 267–276. [Google Scholar] [CrossRef]
- Zhan, H.F.; Gu, Y.T. A fundamental numerical and theoretical study for the vibrational properties of nanowires. J. Appl. Phys. 2012, 111, 124303. [Google Scholar] [CrossRef] [Green Version]
- Sun, H.; Jin, Z.; Yang, C.; Akkermans, R.L.; Robertson, S.H.; Spenley, N.A.; Miller, S.; Todd, S.M. COMPASS II: Extended coverage for polymer and drug-like molecule databases. J. Mol. Modeling 2016, 22, 47. [Google Scholar] [CrossRef]
- Pykal, M.; Jureka, P.; Karlick, F.; Otyepka, M. Modelling of graphene functionalization. Phys. Chem. Chem. Phys. 2015, 18, 6351–6372. [Google Scholar] [CrossRef] [Green Version]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, H.; Wang, J. Effect of Vacancy Defects on the Vibration Frequency of Graphene Nanoribbons. Nanomaterials 2022, 12, 764. https://doi.org/10.3390/nano12050764
Guo H, Wang J. Effect of Vacancy Defects on the Vibration Frequency of Graphene Nanoribbons. Nanomaterials. 2022; 12(5):764. https://doi.org/10.3390/nano12050764
Chicago/Turabian StyleGuo, Hong, and Jing Wang. 2022. "Effect of Vacancy Defects on the Vibration Frequency of Graphene Nanoribbons" Nanomaterials 12, no. 5: 764. https://doi.org/10.3390/nano12050764
APA StyleGuo, H., & Wang, J. (2022). Effect of Vacancy Defects on the Vibration Frequency of Graphene Nanoribbons. Nanomaterials, 12(5), 764. https://doi.org/10.3390/nano12050764





