Near-Interface Defects in Graphene/H-BN In-Plane Heterostructures: Insights into the Interfacial Thermal Transport
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
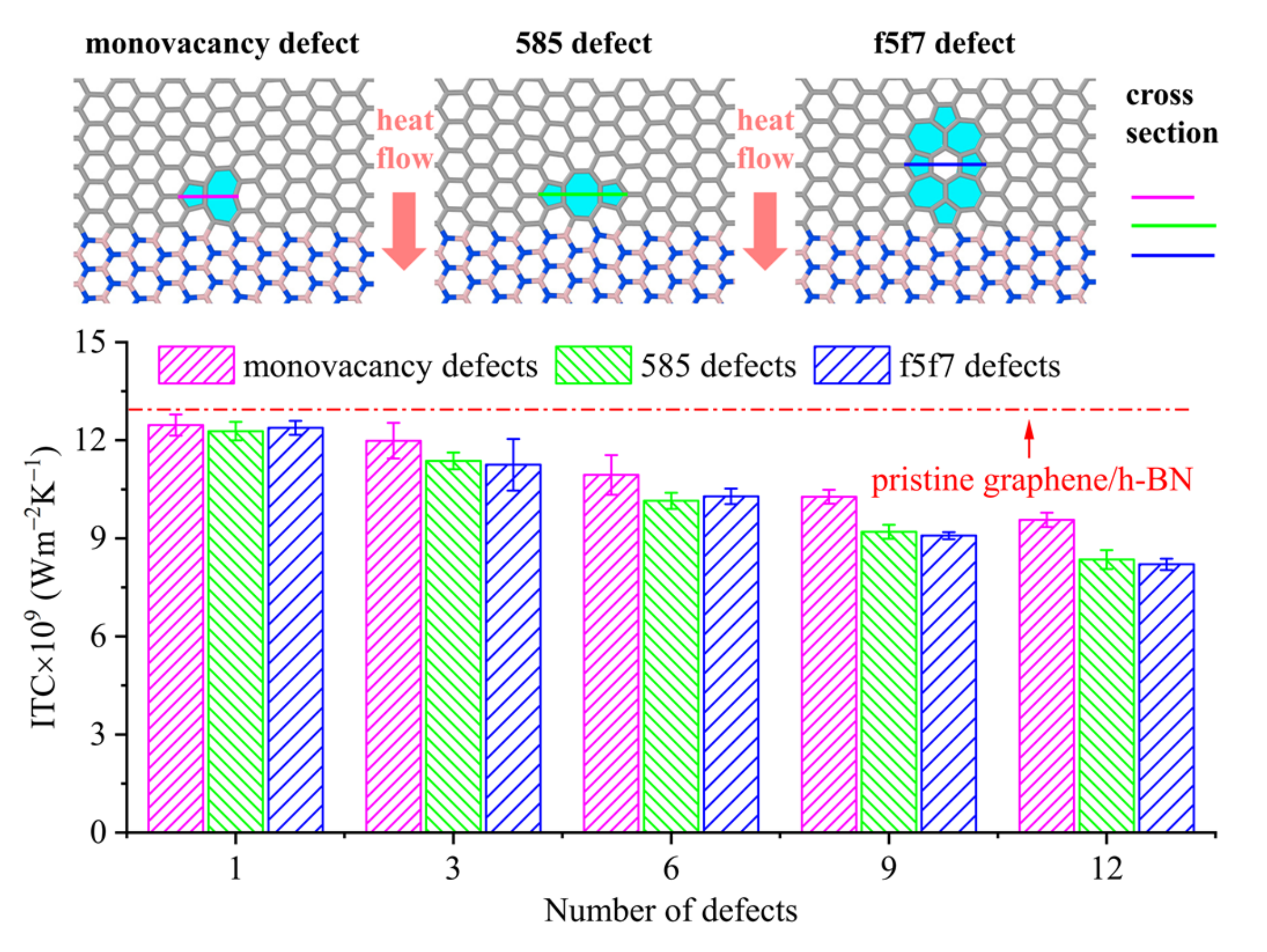
3.1. The ITC Results of Pristine Graphene/h-BN and Graphene/h-BN with Near-Interface Defects
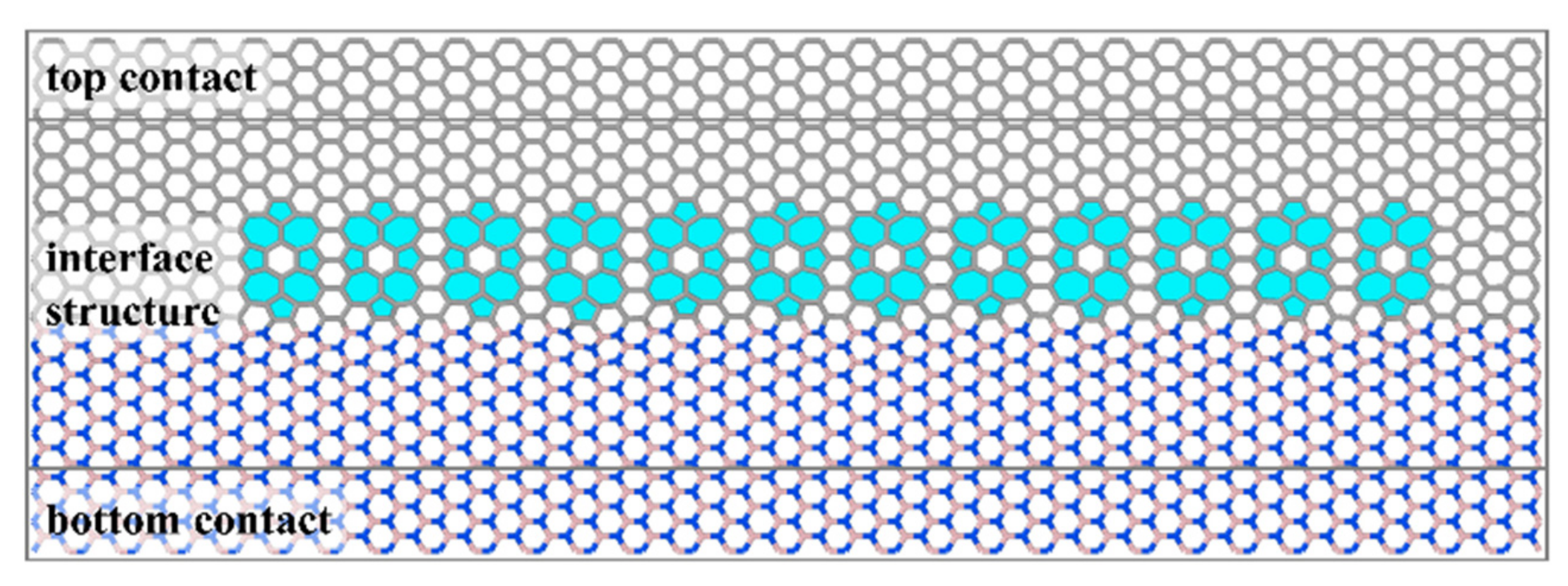
3.2. Near-Interface Defects and Induced Wrinkles
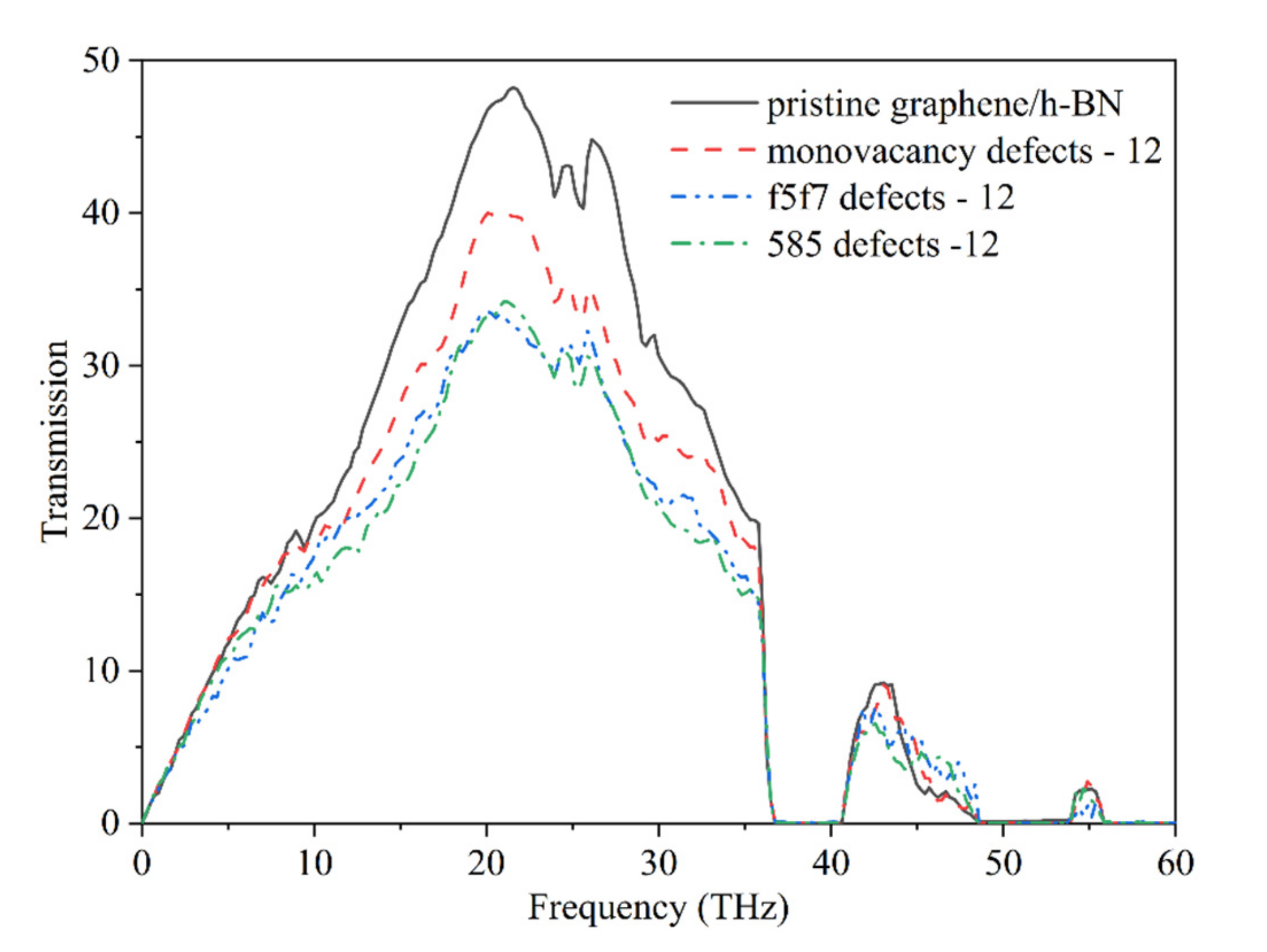
3.3. Phonon Transmission
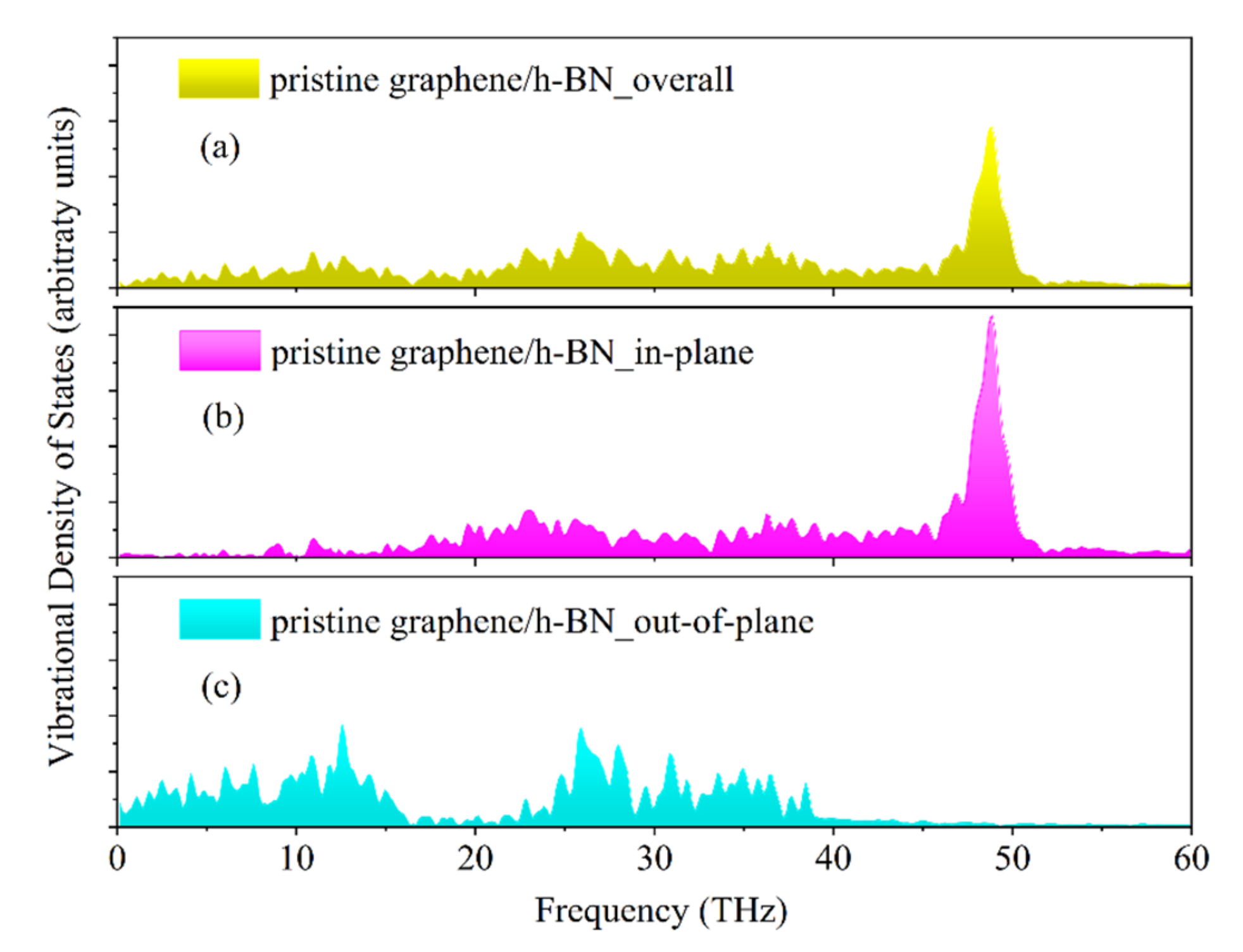
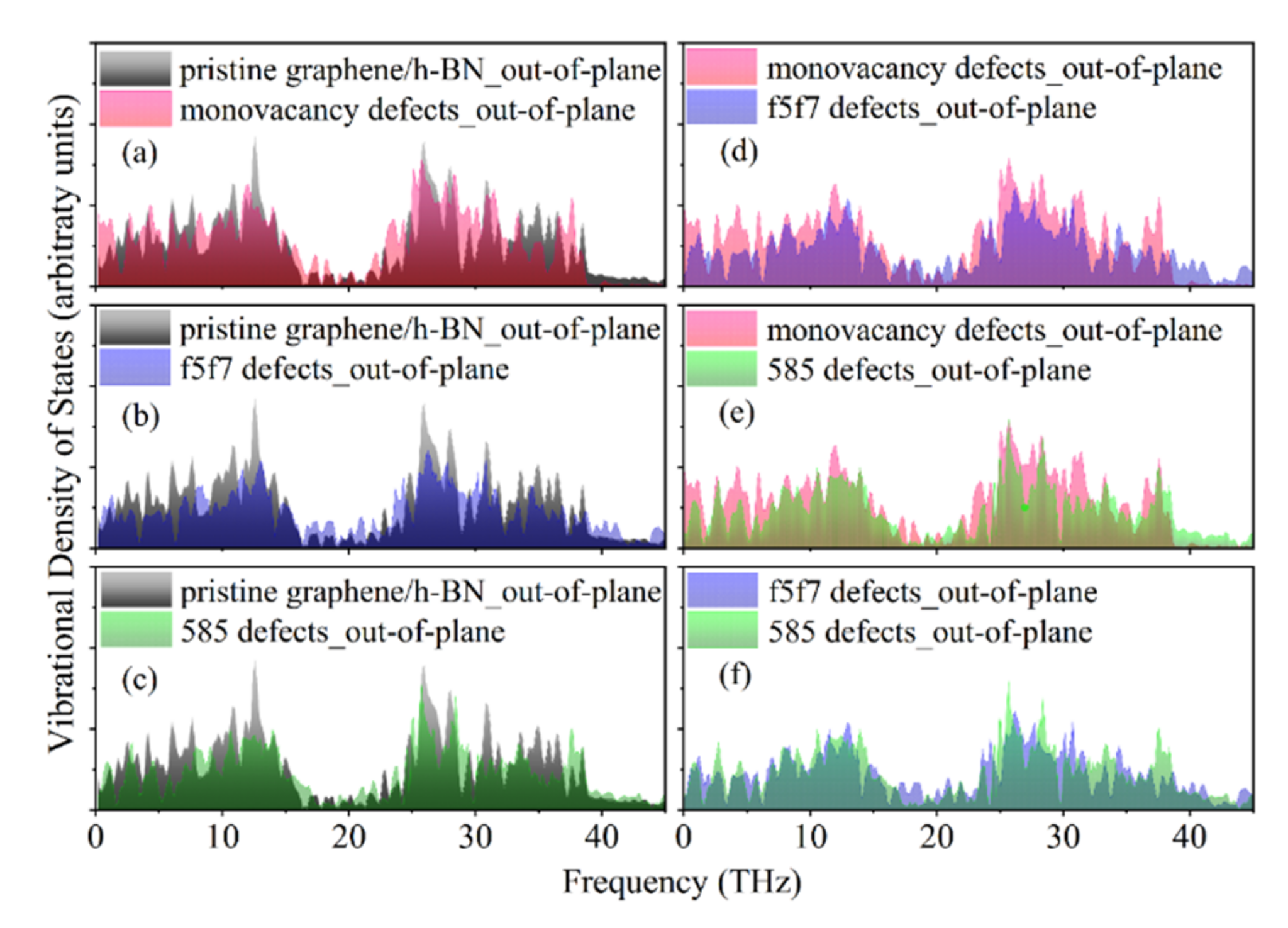
3.4. Vibrational Density of States
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Geng, D.; Abdelwahab, I.; Xiao, X.; Cernescu, A.; Fu, W.; Giannini, V.; Maier, S.A.; Li, L.; Hu, W.; Loh, K.P.; et al. One-pot confined epitaxial growth of 2D heterostructure arrays. ACS Mater. Lett. 2021, 3, 217–223. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, P.; Bian, X.; Huang, J.; Li, W.; Chen, G.; Yang, Y. Adlayer-substrate interactions in controlled growth of graphene/h-BN heterostructure on Ni (111) and Cu (111) surfaces. Appl. Surf. Sci. 2019, 480, 154–161. [Google Scholar] [CrossRef]
- Bradford, J.; Shafiei, M.; MacLeod, J.; Motta, N. Transfer-free synthesis of lateral graphene–hexagonal boron nitride heterostructures from chemically converted epitaxial graphene. Adv. Mater. Interfaces 2019, 6, 1900419. [Google Scholar] [CrossRef]
- Sharma, S.; Kalita, G.; Vishwakarma, R.; Zulkifli, Z.; Tanemura, M. Opening of triangular hole in triangular-shaped chemical vapor deposited hexagonal boron nitride crystal. Sci. Rep. 2015, 5, 10426. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Zhang, Z.; Luo, Z.; Lv, B.; Ding, Z. Tunable electronic properties of graphene/g-AlN heterostructure: The effect of vacancy and strain engineering. Nanomaterials 2019, 9, 1674. [Google Scholar] [CrossRef] [Green Version]
- Ci, L.; Song, L.; Jin, C.; Jariwala, D.; Wu, D.; Li, Y.; Srivastava, A.; Wang, Z.F.; Storr, K.; Balicas, L.; et al. Atomic layers of hybridized boron nitride and graphene domains. Nat. Mater. 2010, 9, 430–435. [Google Scholar] [CrossRef]
- Kim, G.; Lim, H.; Ma, K.Y.; Jang, A.; Ryu, G.H.; Jung, M.; Shin, H.; Lee, Z.; Shin, H.S. Catalytic conversion of hexagonal boron nitride to graphene for in-plane heterostructures. Nano Lett. 2015, 15, 4769–4775. [Google Scholar] [CrossRef]
- Fan, L.; Yao, W. Reduction of interfacial thermal transport of bilayer in-plane graphene/hexagonal boron nitride heterostructures via interlayer sp3 bonds, defects and stacking angle. Diam. Relat. Mater. 2021, 118, 108521. [Google Scholar] [CrossRef]
- Lu, G.; Wu, T.; Yang, P.; Yang, Y.; Jin, Z.; Chen, W.; Jia, S.; Wang, H.; Zhang, G.; Sun, J.; et al. Synthesis of high-quality graphene and hexagonal boron nitride monolayer In-plane heterostructure on Cu-Ni alloy. Adv. Sci. 2017, 4, 1700076. [Google Scholar] [CrossRef] [Green Version]
- Wu, Q.; Wongwiriyapan, W.; Park, J.; Park, S.; Jung, S.J.; Jeong, T.; Lee, S.; Lee, Y.H.; Song, Y.J. In situ chemical vapor deposition of graphene and hexagonal boron nitride heterostructures. Curr. Appl. Phys. 2016, 16, 1175–1191. [Google Scholar] [CrossRef]
- Liu, L.; Park, J.; Siegel, D.A.; McCarty, K.F.; Clark, K.W.; Deng, W.; Basile, L.; Idrobo, J.C.; Li, A.P.; Gu, G. Heteroepitaxial growth of two-dimensional hexagonal boron nitride templated by graphene edges. Science 2014, 343, 163–167. [Google Scholar] [CrossRef]
- Zhang, S.; Li, J.; Wu, H.; Li, X.; Guo, W. Direct synthesizing in-plane heterostructures of graphene and hexagonal boron nitride in designed pattern. Adv. Mater. Interfaces 2018, 5, 1800208. [Google Scholar] [CrossRef]
- Vahedi, A.; Lahidjani, M.H.S. Tunable thermal conductivity along graphene/hexagonal boron-nitride polycrystalline heterostructures. Eur. Phys. J. Plus 2017, 132, 420. [Google Scholar] [CrossRef]
- Jiang, P.; Tao, X.; Kang, L.; Hao, H.; Song, L.; Lan, J.; Zheng, X.; Zhang, L.; Zeng, Z. Spin current generation by thermal gradient in graphene/h-BN/graphene lateral heterojunctions. J. Phys. D 2018, 52, 015303. [Google Scholar] [CrossRef]
- Li, Q.; Liu, M.; Zhang, Y.; Liu, Z. Hexagonal boron nitride–graphene heterostructures: Synthesis and interfacial properties. Small 2016, 12, 32–50. [Google Scholar] [CrossRef]
- Zhao, J.; Cheng, K.; Han, N.; Zhang, J. Growth control, interface behavior, band alignment, and potential device applications of 2D lateral heterostructures. Science 2018, 8, e1353. [Google Scholar] [CrossRef]
- Seoi, G.; Jing, G. Bandgap opening in boron nitride confined armchair graphene nanoribbon. Appl. Phys. Lett. 2011, 98, 666. [Google Scholar]
- An, Y.; Zhang, M.; Wu, D.; Wang, T.; Jiao, Z.; Xia, C.; Fu, Z.; Wang, K. The rectifying and negative differential resistance effects in graphene/h-BN nanoribbon heterojunctions. Phys. Chem. Chem. Phys. 2016, 18, 27976–27980. [Google Scholar] [CrossRef]
- Balandin, A.A. Phononics of graphene and related materials. ACS Nano 2020, 14, 5170–5178. [Google Scholar] [CrossRef]
- Fu, Y.; Hansson, J.; Liu, Y.; Chen, S.; Zehri, A.; Samani, M.K.; Wang, N.; Ni, Y.; Zhang, Y.; Zhang, Z.-B.; et al. Graphene related materials for thermal management. 2D Mater. 2020, 7, 012001. [Google Scholar] [CrossRef]
- Chen, X.K.; Xie, Z.X.; Zhou, W.X.; Tang, L.M.; Chen, K.Q. Thermal rectification and negative differential thermal resistance behaviors in graphene/hexagonal boron nitride heterojunction. Carbon 2016, 100, 492–500. [Google Scholar] [CrossRef]
- Liang, T.; Zhou, M.; Zhang, P.; Yuan, P.; Yang, D. Multilayer in-plane graphene/hexagonal boron nitride heterostructures: Insights into the interfacial thermal transport properties. Int. J. Heat Mass Tran. 2010, 151, 119395. [Google Scholar] [CrossRef]
- Li, M.; Zheng, M.; Duan, K.; Zhang, Y.; Huang, Z.; Zhou, H. Effect of defects on the thermal transport across the graphene/hexagonal boron nitride interface. J. Phys. Chem. C 2018, 122, 14945–14953. [Google Scholar] [CrossRef]
- Wu, X.; Han, Q. Semidefective graphene/h-BN in-plane heterostructures: Enhancing interface thermal conductance by topological defects. J. Phys. Chem. C 2021, 125, 2748–2760. [Google Scholar] [CrossRef]
- Liu, X.J.; Gang, Z.; Zhang, Y.W. Topological defects at the graphene/h-BN interface abnormally enhance its thermal conductance. Nano Lett. 2016, 16, 4954–4959. [Google Scholar] [CrossRef]
- Liu, F.; Zou, R.; Hu, N.; Ning, H.; Yan, C.; Liu, Y.; Wu, L.; Mo, F.; Fu, S. Enhancement of thermal energy transport across the graphene/h-BN heterostructure interface. Nanoscale 2019, 11, 4067–4072. [Google Scholar] [CrossRef]
- Chanana, A.; Sengupta, A.; Mahapatra, S. Performance analysis of boron nitride embedded armchair graphene nanoribbon metal–oxide–semiconductor field effect transistor with Stone-Wales defects. J. Appl. Phys. 2014, 115, 034501. [Google Scholar] [CrossRef] [Green Version]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Tersoff, J. New empirical approach for the structure and energy of covalent systems. Phys. Rev. B 1998, 37, 6991–7000. [Google Scholar] [CrossRef]
- Tersoff, J. Modeling solid-state chemistry: Interatomic potentials for multicomponent systems. Phys. Rev. B 1989, 39, 5566. [Google Scholar] [CrossRef]
- Kinaci, A.; Haskins, J.B.; Sevik, C.; Çağın, T. Thermal conductivity of BN-C nanostructures. Phys. Rev. B 2012, 86, 115410. [Google Scholar] [CrossRef] [Green Version]
- Dong, H.; Hirvonen, P.; Fan, Z.; Qian, P.; Su, Y.; Ala-Nissila, T. Heat transport across graphene/hexagonal-BN tilted grain boundaries from phase-field crystal model and molecular dynamics simulations. J. Appl. Phys. 2021, 130, 235102. [Google Scholar] [CrossRef]
- Schneider, T.; Stoll, E. Molecular-dynamics study of a three-dimensional one-component model for distortive phase transitions. Phys. Rev. B 1978, 17, 1302. [Google Scholar] [CrossRef]
- Saiz-Bretín, M.; Malyshev, A.V.; Domínguez-Adame, F.; Quigley, D.; Romer, R.A. Lattice thermal conductivity of graphene nanostructures. Carbon 2018, 127, 64–69. [Google Scholar] [CrossRef] [Green Version]
- Farzadian, O.; Spitas, C.; Kostas, K.V. Graphene-carbon nitride interface-geometry effects on thermal rectification: A molecular dynamics simulation. Nanotechnology 2021, 32, 215403. [Google Scholar] [CrossRef]
- Kakanakova-Georgieva, A.; Gueorguiev, G.K.; Sangiovanni, D.G.; Suwannaharn, N.; Ivanov, I.G.; Cora, I.; Pecz, B.; Nicotra, G.; Giannazzo, F. Nanoscale phenomena ruling deposition and intercalation of AlN at the graphene/SiC interface. Nanoscale 2020, 12, 19470–19476. [Google Scholar] [CrossRef]
- Kakanakova-Georgieva, A.; Giannazzo, F.; Nicotra, G.; Cora, I.; Gueorguiev, G.K.; Persson, P.O.Å.; Pécz, B. Material proposal for 2D indium oxide. Appl. Surf. Sci. 2021, 548, 149275. [Google Scholar] [CrossRef]
- Banhart, F.; Kotakoski, J.; Krasheninnikov, A.V. Structural defects in graphene. ACS Nano 2011, 5, 26–41. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.; Qing, M.; Wang, Y.; Chen, S. Defects in graphene: Generation, healing, and their effects on the properties of graphene: A Review. J. Mater Sci. Technol. 2015, 31, 599–606. [Google Scholar] [CrossRef]
- Luo, M.; Li, B.L.; Li, D. Effects of divacancy and extended line defects on the thermal transport properties of graphene nanoribbons. Nanomaterials 2019, 9, 160. [Google Scholar] [CrossRef] [Green Version]
- Jahn, H.A.; Teller, E. Stability of polyatomic molecules in degenerate electronic states-I-Orbital degeneracy. Proc. R. Soc. Lond. Ser. A-Math. Phys. Sci. 1937, 161, 220–235. [Google Scholar]
- Ugeda, M.M.; Brihuega, I.; Guinea, F.; Gómez-Rodríguez, J.M. Missing atom as a source of carbon magnetism. Phys. Rev. Lett. 2010, 104, 096804. [Google Scholar] [CrossRef] [PubMed]
- Jin, C.; Lin, F.; Suenaga, K.; Iijima, S. Fabrication of a freestanding boron nitride single layer and its defect assignments. Phys. Rev. Lett. 2009, 102, 195505. [Google Scholar] [CrossRef] [Green Version]
- Sun, Z.H.; Huang, Q.; Zhang, Y.; Huang, P.R.; Zhi, H.Y.; Zou, Y.; Xu, F.; Sun, L.X. First-principle calculation study of (CN)3VB defect in hexagonal boron nitride monolayer. Acta Phys. Sin. 2021, 70, 033102. [Google Scholar]
- Wang, M.; Zhang, G.; Peng, H.; Yan, C. Energetic and thermal properties of tilt grain boundaries in graphene/hexagonal boron nitride heterostructures. Funct. Mater. Lett. 2015, 8, 1550038. [Google Scholar] [CrossRef] [Green Version]
- Renteria, J.D.; Ramirez, S.; Malekpour, H.; Alonso, B.; Centeno, A.; Zurutuza, A.; Cocemasov, A.I.; Nika, D.L.; Balandin, A.A. Strongly anisotropic thermal conductivity of free-standing reduced graphene oxide films annealed at high temperature. Adv. Funct. Mater. 2015, 25, 4664–4672. [Google Scholar] [CrossRef]
- Malekpour, H.; Ramnani, P.; Srinivasan, S.; Balasubramanian, G.; Nika, D.L.; Mulchandani, A.; Lake, R.K.; Balandin, A.A. Thermal conductivity of graphene with defects induced by electron beam irradiation. Nanoscale 2016, 8, 14608–14616. [Google Scholar] [CrossRef] [Green Version]
- Stevenson, D.P. The strengths of chemical bonds. J. Am. Chem. Soc. 1955, 77, 2350. [Google Scholar] [CrossRef]
- Cui, L.; Du, X.; Wei, G.; Feng, Y. Thermal conductivity of graphene wrinkles: A molecular dynamics simulation. J. Phys. Chem. C 2016, 120, 23807–23812. [Google Scholar] [CrossRef]
- Wan, X.; Ma, D.; Pan, D.; Yang, L.; Yang, N. Optimizing thermal transport in graphene nanoribbon based on phonon resonance hybridization. Mater. Today Phys. 2021, 20, 100445. [Google Scholar] [CrossRef]
- Wang, J.S.; Wang, J.; Zeng, N. Nonequilibrium Green’s function approach to mesoscopic thermal transport. Phys. Rev. B 2006, 74, 033408. [Google Scholar] [CrossRef] [Green Version]
- Wang, T.Y.; Tsai, J.L. Investigating thermal conductivities of functionalized graphene and graphene/epoxy nanocomposites. Comput. Mater. Sci. 2016, 122, 272–280. [Google Scholar] [CrossRef]
- Grest, G.S.; Nagel, S.R.; Rahman, A.; Witten, T.A. Density of states and the velocity autocorrelation function derived from quench studies. J. Chem. Phys. 1981, 74, 3532–3534. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, N.; Zhou, B.; Li, D.; Qi, D.; Wu, Y.; Zheng, H.; Yang, B. Near-Interface Defects in Graphene/H-BN In-Plane Heterostructures: Insights into the Interfacial Thermal Transport. Nanomaterials 2022, 12, 1044. https://doi.org/10.3390/nano12071044
Zhang N, Zhou B, Li D, Qi D, Wu Y, Zheng H, Yang B. Near-Interface Defects in Graphene/H-BN In-Plane Heterostructures: Insights into the Interfacial Thermal Transport. Nanomaterials. 2022; 12(7):1044. https://doi.org/10.3390/nano12071044
Chicago/Turabian StyleZhang, Nana, Baoming Zhou, Dongbo Li, Dongfeng Qi, Yongling Wu, Hongyu Zheng, and Bing Yang. 2022. "Near-Interface Defects in Graphene/H-BN In-Plane Heterostructures: Insights into the Interfacial Thermal Transport" Nanomaterials 12, no. 7: 1044. https://doi.org/10.3390/nano12071044
APA StyleZhang, N., Zhou, B., Li, D., Qi, D., Wu, Y., Zheng, H., & Yang, B. (2022). Near-Interface Defects in Graphene/H-BN In-Plane Heterostructures: Insights into the Interfacial Thermal Transport. Nanomaterials, 12(7), 1044. https://doi.org/10.3390/nano12071044








