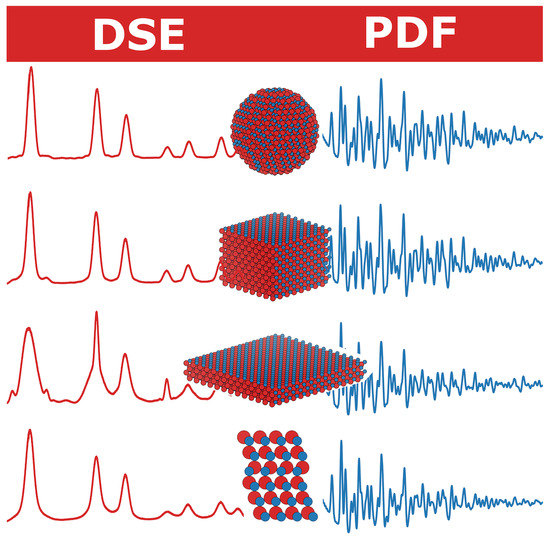
Effects of Structural and Microstructural Features on the Total Scattering Pattern of Nanocrystalline Materials
Abstract
:1. Introduction
2. Methods
2.1. The Debye Scattering Equation (DSE) Approach
2.1.1. The Instrumental Profile
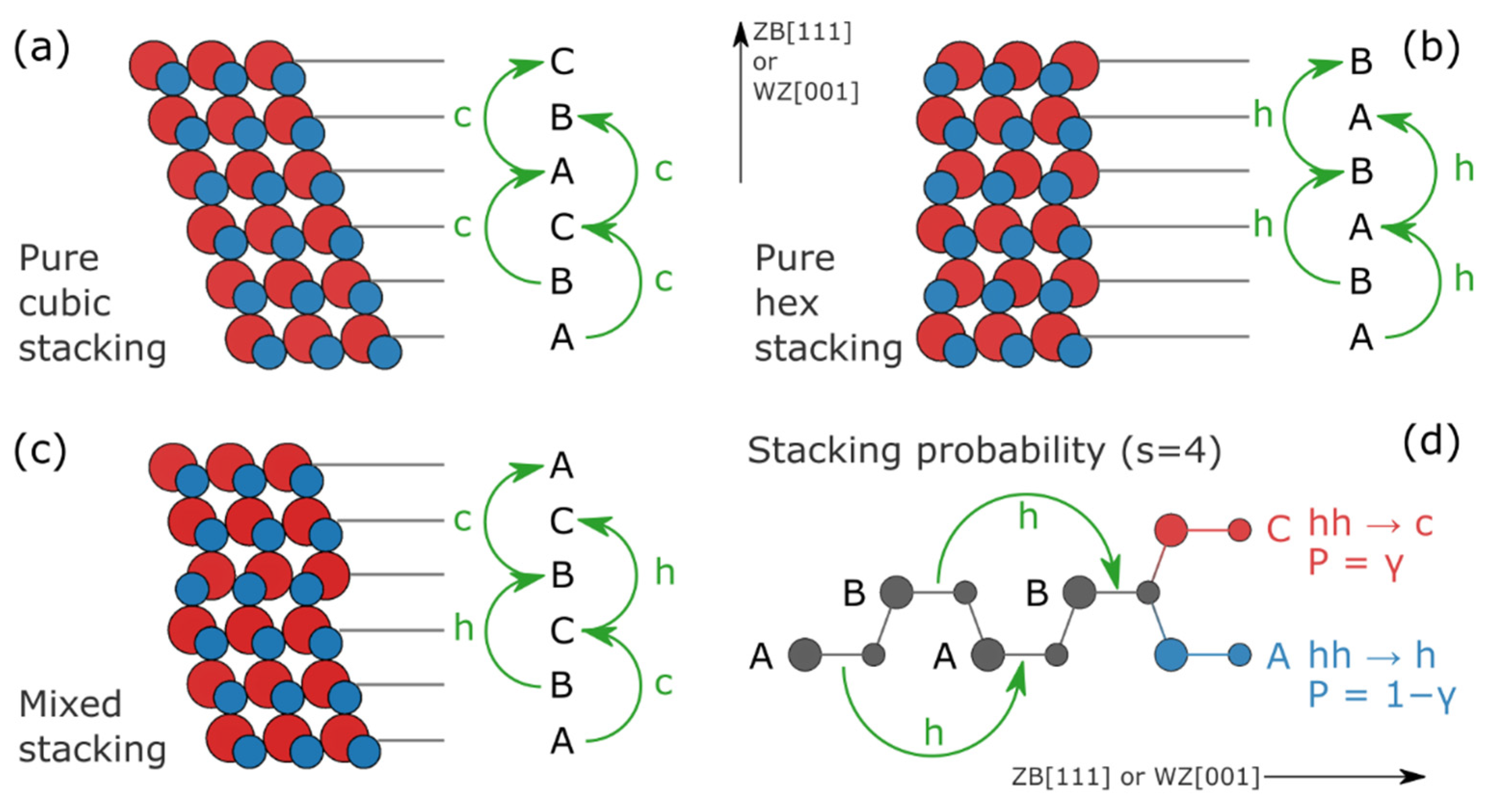
2.1.2. Stacking Disorder in CdSe ZB QDs
2.2. The Atomic Pair Distribution Function (PDF) Method
3. Results and Discussion
3.1. On the Instrumental Resolution Function
3.2. Influence of Nanocrystals Size and Size Distribution on Total Scattering Patterns
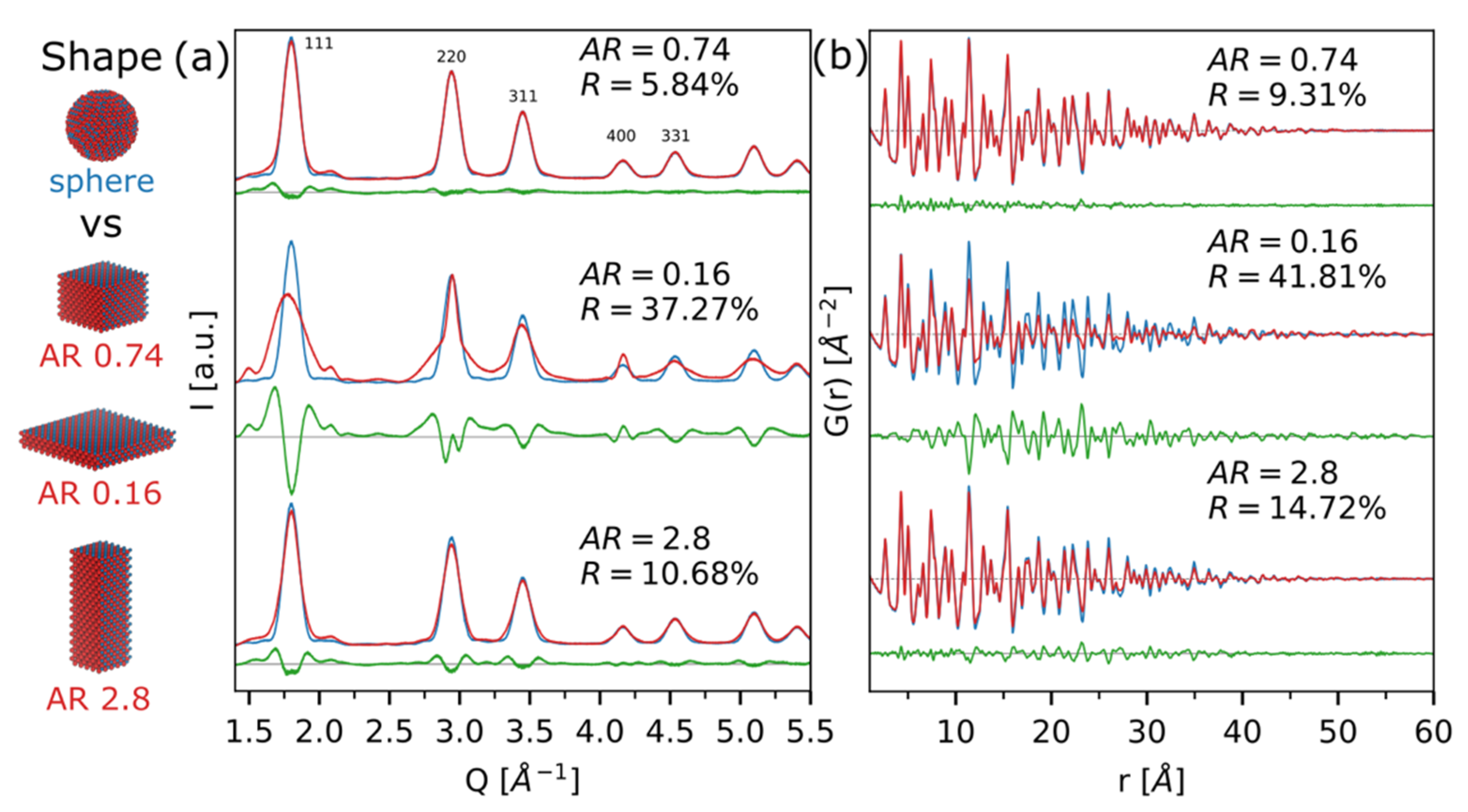
3.3. Extracting Morphological Features from Wide-Angle X-ray Total Scattering
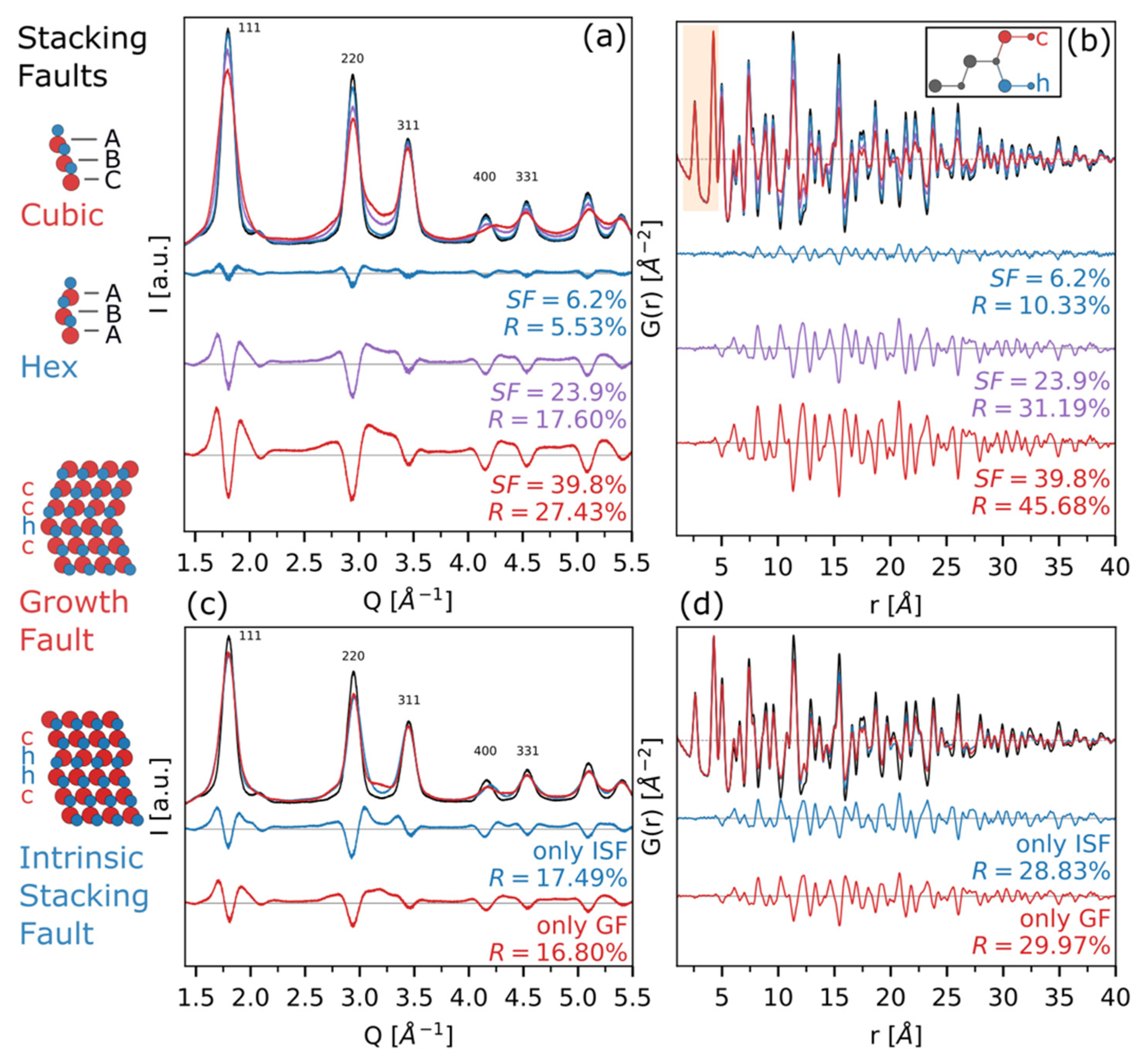
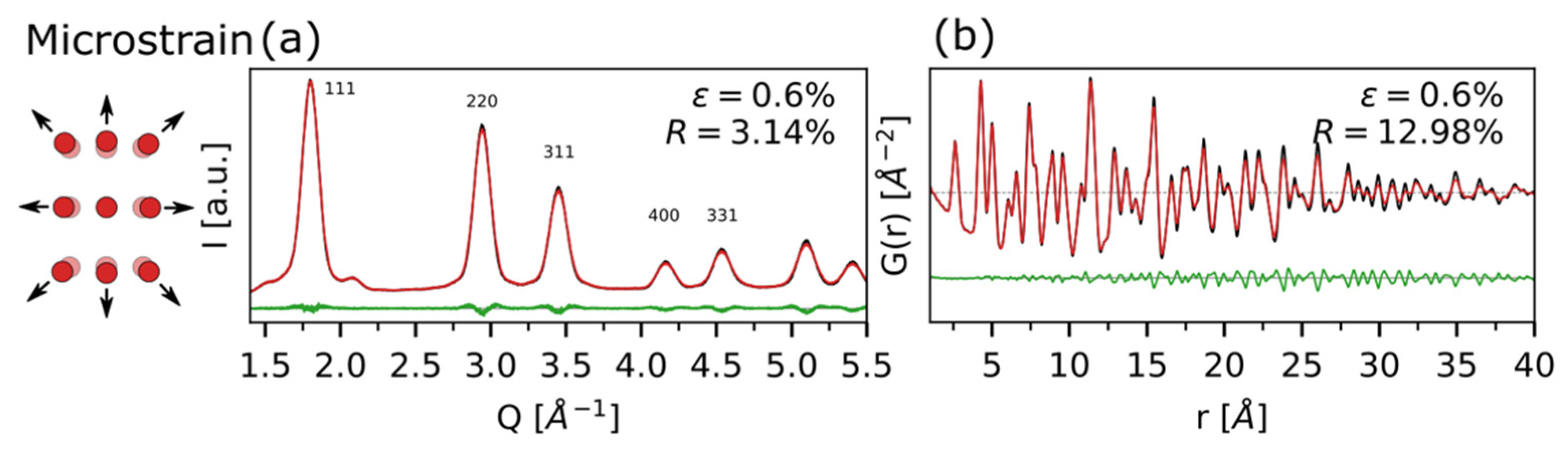
3.4. Structural Defectiveness in Real and Reciprocal Spaces
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Code Availability
References
- Kovalenko, M.V.; Manna, L.; Cabot, A.; Hens, Z.; Talapin, D.V.; Kagan, C.R.; Klimov, V.I.; Rogach, A.L.; Reiss, P.; Milliron, D.J.; et al. Prospects of nanoscience with nanocrystals. ACS Nano 2015, 9, 1012–1057. [Google Scholar] [CrossRef] [PubMed]
- Bourzac, K. Quantum dots go on display. Nat. News 2013, 493, 283. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Choi, M.K.; Yang, U.J.; Kim, S.Y.; Kim, Y.S.; Kim, J.H.; Kim, D.-H.; Hyeon, T. Toward full-color electroluminescent quantum dot displays. Nano Lett. 2021, 21, 26–33. [Google Scholar] [CrossRef] [PubMed]
- Huang, F.; Zhang, L.; Zhang, Q.; Hou, J.; Wang, H.; Wang, H.; Peng, S.; Liu, J.; Cao, G. High efficiency CdS/CdSe quantum dot sensitized solar cells with two ZnSe layers. ACS Appl. Mater. Interfaces 2016, 8, 34482–34489. [Google Scholar] [CrossRef] [PubMed]
- Rahman, M.M.; Karim, M.R.; Alharbi, H.F.; Aldokhayel, B.; Uzzaman, T.; Zahir, H. Cadmium selenide quantum dots for solar cell applications: A review. Chem.-Asian J. 2021, 16, 902–921. [Google Scholar] [CrossRef] [PubMed]
- Murray, C.B.; Norris, D.J.; Bawendi, M.G. Synthesis and characterization of nearly monodisperse CdE (E = Sulfur, Selenium, Tellurium) semiconductor nanocrystallites. J. Am. Chem. Soc. 1993, 115, 8706–8715. [Google Scholar] [CrossRef]
- Owen, J.; Brus, L. Chemical synthesis and luminescence applications of colloidal semiconductor quantum dots. J. Am. Chem. Soc. 2017, 139, 10939–10943. [Google Scholar] [CrossRef]
- Gottschalk, H.; Patzer, G.; Alexander, H. Stacking fault energy and ionicity of cubic III–V compounds. Phys. Status Solidi A 1978, 45, 207–217. [Google Scholar] [CrossRef]
- Takeuchi, S.; Suzuki, K. Stacking fault energies of tetrahedrally coordinated crystals. Phys. Stutus Solidi C 1999, 171, 99–103. [Google Scholar] [CrossRef]
- Soni, U.; Arora, V.; Sapra, S. Wurtzite or zinc blende? Surface decides the crystal structure of nanocrystals. Cryst. Eng. Comm. 2013, 15, 5458–5463. [Google Scholar] [CrossRef]
- Gao, Y.; Peng, X. Crystal structure control of CdSe nanocrystals in growth and nucleation: Dominating effects of surface versus interior structure. J. Am. Chem. Soc. 2014, 136, 6724–6732. [Google Scholar] [CrossRef] [PubMed]
- Bawendi, M.G.; Kortan, A.R.; Steigerwald, M.L.; Brus, L.E. X-ray structural characterization of larger CdSe semiconductor clusters. J. Chem. Phys. 1989, 91, 7282–7290. [Google Scholar] [CrossRef]
- Moscheni, D.; Bertolotti, F.; Piveteau, L.; Protesescu, L.; Dirin, D.N.; Kovalenko, M.V.; Cervellino, A.; Pedersen, J.S.; Masciocchi, N.; Guagliardi, A. Size-dependent fault-driven relaxation and faceting in zincblende CdSe colloidal quantum dots. ACS Nano 2018, 12, 12558–12570. [Google Scholar] [CrossRef] [PubMed]
- Bertolotti, F.; Tǎbǎcaru, A.; Muşat, V.; Ţigǎu, N.; Cervellino, A.; Masciocchi, N.; Guagliardi, A. Band gap narrowing in silane-grafted ZnO nanocrystals. A comprehensive study by wide-angle X-ray total scattering methods. J. Phys. Chem. C 2021, 125, 4806–4819. [Google Scholar] [CrossRef]
- Jang, E.; Kim, Y.; Won, Y.-H.; Jang, H.; Choi, S.-M. Environmentally friendly InP-based quantum dots for efficient wide color gamut displays. ACS Energy Lett. 2020, 5, 1316–1327. [Google Scholar] [CrossRef] [Green Version]
- Pietryga, J.M.; Park, Y.S.; Lim, J.; Fidler, A.F.; Bae, W.K.; Brovelli, S.; Klimov, V.I. Spectroscopic and device aspects of nanocrystal quantum dots. Chem. Rev. 2016, 116, 10513–10622. [Google Scholar] [CrossRef] [PubMed]
- Sercel, P.C.; Shabaev, A.; Efros, A.L. Photoluminescence enhancement through symmetry breaking induced by defects in nanocrystals. Nano Lett. 2017, 17, 4820–4830. [Google Scholar] [CrossRef] [Green Version]
- Smith, A.M.; Mohs, A.M.; Nie, S. Tuning the optical and electronic properties of colloidal nanocrystals by lattice strain. Nat. Nanotechnol. 2008, 4, 56–63. [Google Scholar] [CrossRef] [Green Version]
- Cui, J.; Beyler, A.P.; Coropceanu, I.; Cleary, L.; Avila, T.R.; Chen, Y.; Cordero, J.M.; Heathcote, S.L.; Harris, D.K.; Chen, O.; et al. Evolution of the single-nanocrystal photoluminescence linewidth with size and shell: Implications for exciton-phonon coupling and the optimization of spectral linewidths. Nano Lett. 2016, 16, 289–296. [Google Scholar] [CrossRef]
- Jasieniak, J.; Smith, L.; van Embden, J.; Mulvaney, P.; Califano, M. Re-examination of the size-dependent absorption properties of CdSe quantum dots. J. Phys. Chem. C 2009, 113, 19468–19474. [Google Scholar] [CrossRef]
- Ithurria, S.; Tessier, M.D.; Mahler, B.; Lobo, R.P.S.M.; Dubertret, B.; Efros, A.L. Colloidal nanoplatelets with two-dimensional electronic structure. Nat. Mater. 2011, 10, 936–941. [Google Scholar] [CrossRef] [PubMed]
- Ithurria, S.; Bousquet, G.; Dubertret, B. Continuous transition from 3D to 1D confinement observed during the formation of CdSe nanoplatelets. J. Am. Chem. Soc. 2011, 133, 3070–3077. [Google Scholar] [CrossRef] [PubMed]
- De Mello Donega, C. Synthesis and properties of colloidal heteronanocrystals. Chem. Soc. Rev. 2011, 40, 1512–1546. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, J.; Olds, D.; Peng, R.; Yu, L.; Foo, G.S.; Qian, S.; Keum, J.; Guiton, B.S.; Wu, Z.; Page, K. Quantitative analysis of the morphology of {101} and {001} faceted anatase TiO2 nanocrystals and its implication on photocatalytic activity. Chem. Mater. 2017, 29, 5591–5604. [Google Scholar] [CrossRef]
- Maes, J.; Castro, N.; de Nolf, K.; Walravens, W.; Abécassis, B.; Hens, Z. Size and concentration determination of colloidal nanocrystals by small-angle X-ray scattering. Chem. Mater. 2018, 30, 3952–3962. [Google Scholar] [CrossRef]
- Scardi, P.; Leoni, M.; Beyerlein, K.R. On the modelling of the powder pattern from a nanocrystalline material. Z. Krist. 2011, 226, 924–933. [Google Scholar] [CrossRef]
- Bertolotti, F.; Moscheni, D.; Guagliardi, A.; Masciocchi, N. When crystals go nano—The role of advanced X-ray total scattering methods in nanotechnology. Eur. J. Inorg. Chem. 2018, 2018, 3789–3803. [Google Scholar] [CrossRef]
- Egami, T.; Billinge, S.J.L. Underneath the Bragg Peaks. Structural Analysis of Complex Materials; Cahn, R.W., Ed.; Pergamon Materials Series; Kidlington: Oxford, UK, 2003. [Google Scholar]
- Cervellino, A.; Frison, R.; Bertolotti, F.; Guagliardi, A. DEBUSSY 2.0: The new release of a debye user system for nanocrystalline and/or disordered materials. J. Appl. Cryst. 2015, 48, 2026–2032. [Google Scholar] [CrossRef] [Green Version]
- Cervellino, A.; Giannini, C.; Guagliardi, A. On the efficient evaluation of fourier patterns for nanoparticles and clusters. J. Comput. Chem. 2006, 27, 995–1008. [Google Scholar] [CrossRef]
- Bertolotti, F.; Dirin, D.N.; Ibáñez, M.; Krumeich, F.; Cervellino, A.; Frison, R.; Voznyy, O.; Sargent, E.H.; Kovalenko, M.V.; Guagliardi, A.; et al. Crystal symmetry breaking and vacancies in colloidal lead chalcogenide quantum dots. Nat. Mater. 2016, 15, 987–994. [Google Scholar] [CrossRef]
- Bertolotti, F.; Carmona, F.J.; dal Sasso, G.; Ramírez-Rodríguez, G.B.; Delgado-López, J.M.; Pedersen, J.S.; Ferri, F.; Masciocchi, N.; Guagliardi, A. On the amorphous layer in bone mineral and biomimetic apatite: A combined small- and wide-angle X-Ray scattering analysis. Acta Biomater. 2021, 120, 167–180. [Google Scholar] [CrossRef] [PubMed]
- Bertolotti, F.; Vivani, A.; Moscheni, D.; Ferri, F.; Cervellino, A.; Masciocchi, N.; Guagliardi, A. Structure, morphology, and faceting of TiO2 photocatalysts by the Debye scattering equation method. The P25 and P90 cases of study. Nanomaterials 2020, 10, 743. [Google Scholar] [CrossRef] [PubMed]
- Bertolotti, F.; Moscheni, D.; Migliori, A.; Zacchini, S.; Cervellino, A.; Guagliardi, A.; Masciocchi, N. A total scattering debye function analysis study of faulted pt nanocrystals embedded in a porous matrix. Acta Crystallogr. A 2016, 72, 632–644. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peterson, P.F.; Olds, D.; McDonnell, M.T.; Page, K. Illustrated formalisms for total scattering data: A guide for new practitioners. J. Appl. Cryst. 2021, 54, 317–332. [Google Scholar] [CrossRef] [PubMed]
- Farrow, C.L.; Juhas, P.; Liu, J.W.; Bryndin, D.; Božin, E.S.; Bloch, J.; Proffen, T.; Billinge, S.J.L. PDFfit2 and PDFgui: Computer programs for studying nanostructure in crystals. J. Phys. Condens. Mat. 2007, 19, 335219. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Usher, T.-M.; Olds, D.; Liu, J.; Page, K. A numerical method for deriving shape functions of nanoparticles for pair distribution function refinements. Acta Cryst. A 2018, 74, 322–331. [Google Scholar] [CrossRef]
- Masadeh, A.S.; Božin, E.S.; Farrow, C.L.; Paglia, G.; Juhas, P.; Billinge, S.J.L.; Karkamkar, A.; Kanatzidis, M.G. Quantitative size-dependent structure and strain determination of cdse nanoparticles using atomic pair distribution function analysis. Phys. Rev. B 2007, 76, 115413. [Google Scholar] [CrossRef] [Green Version]
- Debye, P. Zerstreuung von Röntgenstrahlen. Ann. Phys. 1915, 351, 809–823. [Google Scholar] [CrossRef] [Green Version]
- Olds, D.; Saunders, C.N.; Peters, M.; Proffen, T.; Neuefeind, J.; Page, K. Precise Implications for real-space pair distribution function modeling of effects intrinsic to modern time-of-flight neutron diffractometers. Acta Cryst. A 2018, 74, 293–307. [Google Scholar] [CrossRef] [Green Version]
- Metz, P.C.; Huegle, T.; Olds, D.; Page, K. Simulating and benchmarking neutron total scattering instrumentation from inception of events to reduced and fitted data. J. Appl. Cryst. 2021, 54, 1047–1056. [Google Scholar] [CrossRef]
- Cheary, R.W.; Coelho, A. A fundamental parameters approach to X-ray line-profile fitting. J. Appl. Crystallogr. 1992, 25, 109–121. [Google Scholar] [CrossRef]
- Topas-R, V3.0; Bruker AXS: Karlsruhe, Germany, 2005.
- Bertero, M.; Boccacci, P.; Desiderà, G.; Vicidomini, G. Image deblurring with poisson data: From cells to galaxies. Inverse Probl. 2009, 25, 123006. [Google Scholar] [CrossRef]
- Kakinoki, J. Diffraction by a one-dimensionally disordered crystal. II. Close-packed structures. Acta Cryst. 1967, 23, 875–885. [Google Scholar] [CrossRef]
- Jagodziniski, H. Polytypism in SiC crystals. Acta Cryst. 1954, 7, 300. [Google Scholar] [CrossRef]
- Silva, D.S. Elementary Scattering Theory—For X-ray and Neutron Users; Oxford University Press Inc.: New York, NY, USA, 2011. [Google Scholar]
- Farrow, C.L.; Billinge, S.J.L. Relationship between the atomic pair distribution function and small-angle scattering: Implications for modeling of nanoparticles. Acta Cryst. A 2009, 65, 232–239. [Google Scholar] [CrossRef] [Green Version]
- Farrow, C.L.; Shaw, M.; Kim, H.; Juhás, P.; Billinge, S.J.L. Nyquist-shannon sampling theorem applied to refinements of the atomic pair distribution function. Phys. Rev. B 2011, 84, 134105. [Google Scholar] [CrossRef] [Green Version]
- Chupas, P.J.; Qiu, X.; Hanson, J.C.; Lee, P.L.; Greya, C.P.; Billinge, S.J.L. Rapid-acquisition pair distribution function (RA-PDF) analysis. J. Appl. Cryst. 2003, 36, 1342–1347. [Google Scholar] [CrossRef] [Green Version]
- Cervellino, A.; Frison, R.; Masciocchi, N.; Guagliardi, A. X-ray and Neutron Techniques for Nanomaterials Characterization; Kumar, C.S.S.R., Ed.; Springer: Berlin, Germany, 2016; pp. 545–608. ISBN 978-3-662-48606-1. [Google Scholar]
- Toby, B.H.; Egami, T. Accuracy of pair distribution function analysis applied to crystalline and non-crystalline materials. Acta Cryst. A 1992, 48, 336–346. [Google Scholar] [CrossRef]
- Terban, M.W.; Billinge, S.J.L. Structural analysis of molecular materials using the pair distribution function. Chem. Rev. 2021, 1, 1208–1272. [Google Scholar] [CrossRef]
- Bergamaschi, A.; Cervellino, A.; Dinapoli, R.; Gozzo, F.; Henrich, B.; Johnson, I.; Kraft, P.; Mozzanica, A.; Schmitt, B.; Shi, X. The MYTHEN detector for X-ray powder diffraction experiments at the swiss light source. J. Synchrotron Radiat. 2010, 17, 653–668. [Google Scholar] [CrossRef] [Green Version]
- Mittemeijer, E.J.; Welzel, U. The “state of the art” of the diffraction analysis of crystallite size and lattice strain. Z. Kristallogr. 2008, 223, 552–560. [Google Scholar] [CrossRef]
- Gilbert, B. Finite size effects on the real-space pair distribution function of nanoparticles. J. Appl. Cryst. 2008, 41, 554–562. [Google Scholar] [CrossRef]
- Bertolotti, F.; Protesescu, L.; Kovalenko, M.V.; Yakunin, S.; Cervellino, A.; Billinge, S.J.L.; Terban, M.W.; Pedersen, J.S.; Masciocchi, N.; Guagliardi, A. Coherent nanotwins and dynamic disorder in cesium lead halide perovskite nanocrystals. ACS Nano 2017, 11, 3819–3831. [Google Scholar] [CrossRef] [PubMed]
- Warner, J.H.; Rümmeli, M.H.; Bachmatiuk, A.; Büchner, B. Atomic resolution imaging and topography of boron nitride sheets produced by chemical exfoliation. ACS Nano 2010, 4, 1299–1304. [Google Scholar] [CrossRef]
- Warner, J.H.; Rümmeli, M.H.; Gemming, T.; Büchner, B.; Briggs, G.A.D. Direct imaging of rotational stacking faults in few layer graphene. Nano Lett. 2009, 9, 102–106. [Google Scholar] [CrossRef]
- Iijama, S.; Buseck, P.R. Experimental study of disordered mica structures by high-resolution electron microscopy. Acta Cryst. A 1978, 34, 709–719. [Google Scholar] [CrossRef]
- Metz, P.C.; Koch, R.; Misture, S.T. Differential evolution and markov chain monte carlo analyses of layer disorder in nanosheet ensembles using total scattering. J. Appl. Cryst. 2018, 51, 1437–1444. [Google Scholar] [CrossRef]
- Beyerlein, K.R.; Snyder, R.L.; Scardi, P. Faulting in finite face-centered-cubic crystallites. Acta Crystallogr. A 2011, 67, 252–263. [Google Scholar] [CrossRef]
- Longo, A.; Sciortino, L.; Giannici, F.; Martorana, A. Crossing the boundary between face-centred cubic and hexagonal close packed: The structure of nanosized cobalt is unraveled by a model accounting for shape, size distribution and stacking faults, allowing simulation of XRD, XANES and EXAFS. J. Appl. Crystallogr. 2014, 47, 1562–1568. [Google Scholar] [CrossRef]
- Longo, A.; Giannici, F.; Sciortino, L.; Martorana, A. A real-space approach to the analysis of stacking faults in close-packed metals: G(r) modelling and Q-space feedback. Acta Cryst. A 2020, 76, 84–91. [Google Scholar] [CrossRef]
- Smallman, R.E.; Westmacott, K.H. Stacking faults in face-centred cubic metals and alloys. Philos. Mag. 1957, 2, 669–683. [Google Scholar] [CrossRef]
- Yoo, S.-H.; Butler, K.T.; Soon, A.; Abbas, A.; Walls, J.M.; Walsh, A. Identification of critical stacking faults in thin-film CdTe solar cells. Appl. Phys. Lett. 2014, 105, 062104. [Google Scholar] [CrossRef]
- Izumi, S.; Tsuchida, H.; Kamata, I.; Tawara, T. Structural analysis and reduction of in-grown stacking faults in 4H–SiC epilayers. Appl. Phys. Lett. 2005, 86, 202108. [Google Scholar] [CrossRef]
- Demortière, A.; Leonard, D.N.; Petkov, V.; Chapman, K.; Chattopadhyay, S.; She, C.; Cullen, D.A.; Shibata, T.; Pelton, M.; Shevchenko, E.V. Strain-driven stacking faults in CdSe/CdS Core/shell nanorods. J. Phys. Chem. Lett. 2018, 9, 1900–1906. [Google Scholar] [CrossRef] [PubMed]
- Dovidenko, K.; Oktyabrsky, S.; Narayan, J. Characteristics of stacking faults in AlN thin films. J. Appl. Phys. 1997, 82, 4296–4299. [Google Scholar] [CrossRef]
- Lähnemann, J.; Jahn, U.; Brandt, O.; Flissikowski, T.; Dogan, P.; Grahn, H.T. Luminescence associated with stacking faults in GaN. J. Phys. D Appl. Phys. 2014, 47, 423001. [Google Scholar] [CrossRef] [Green Version]
- Hughes, S.M.; Alivisatos, A.P. Anisotropic formation and distribution of stacking faults in II–VI semiconductor nanorods. Nano Lett. 2013, 13, 106–110. [Google Scholar] [CrossRef] [Green Version]
- Jagodzinski, H. Eindimensionale Fehlordnung in Kristallen Und Ihr Einfluss Auf Die Röntgeninterferenzen. III. Vergleich Der Berechnungen Mit Experimentellen Ergebnissen. Acta Crystallogr. 1949, 2, 298–304. [Google Scholar] [CrossRef]
- Yang, X.; Masadeh, A.S.; McBride, J.R.; Bozin, E.S.; Rosenthal, S.J.; Billinge, S.J. Confirmation of disordered structure of ultrasmall CdSe nanoparticles from X-Ray atomic pair distribution function analysis. Phys. Chem. 2013, 15, 8480–8486. [Google Scholar] [CrossRef]
- Kumpf, C.; Neder, R.B.; Niederdraenk, F.; Luczak, P.; Stahl, A.; Scheuermann, M.; Joshi, S.; Kulkarni, S.K.; Barglik-Chory, C.; Heske, C.; et al. Structure determination of CdS and ZnS nanoparticles: Direct modeling of synchrotron-radiation diffraction data. J. Chem. Phys. 2005, 123, 224707. [Google Scholar] [CrossRef]
- Niederdraenk, F.; Seufert, K.; Luczak, P.; Kulkarni, S.K.; Chory, C.; Neder, R.B.; Kumpf, C. Structure of small II-VI semiconductor nanoparticles: A new approach based on powder diffraction. Phys. Status Solidi C 2007, 4, 3234–3243. [Google Scholar] [CrossRef]
- Neder, R.B.; Korsunskiy, V.I.; Chory, C.; Müller, G.; Hofmann, A.; Dembski, S.; Graf, C.; Rühl, E. Structural characterization of II-VI semiconductor nanoparticles. Phys. Status Solidi C 2007, 4, 3221–3233. [Google Scholar] [CrossRef]
- Guinier, A.; Bokij, G.B.; Boll-Dornberger, K.; Cowley, J.M.; Ďurovič, S.; Jagodzinski, H.; Krishna, P.; de Wolff, P.M.; Zvyagin, B.B.; Cox, D.E.; et al. Nomenclature of polytype structures. report of the international union of crystallography it ad hoc committee on the nomenclature of disordered, modulated and polytype structures. Acta Crystallogr. A 1984, 40, 399–404. [Google Scholar] [CrossRef] [Green Version]
- Gagin, A.; Allen, A.J.; Levin, I. Combined fitting of small- and Wide-Angle X-ray total scattering data from nanoparticles: Benefits and issues. J. Appl. Cryst. 2014, 47, 619–629. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dengo, N.; Masciocchi, N.; Cervellino, A.; Guagliardi, A.; Bertolotti, F. Effects of Structural and Microstructural Features on the Total Scattering Pattern of Nanocrystalline Materials. Nanomaterials 2022, 12, 1252. https://doi.org/10.3390/nano12081252
Dengo N, Masciocchi N, Cervellino A, Guagliardi A, Bertolotti F. Effects of Structural and Microstructural Features on the Total Scattering Pattern of Nanocrystalline Materials. Nanomaterials. 2022; 12(8):1252. https://doi.org/10.3390/nano12081252
Chicago/Turabian StyleDengo, Nicola, Norberto Masciocchi, Antonio Cervellino, Antonietta Guagliardi, and Federica Bertolotti. 2022. "Effects of Structural and Microstructural Features on the Total Scattering Pattern of Nanocrystalline Materials" Nanomaterials 12, no. 8: 1252. https://doi.org/10.3390/nano12081252
APA StyleDengo, N., Masciocchi, N., Cervellino, A., Guagliardi, A., & Bertolotti, F. (2022). Effects of Structural and Microstructural Features on the Total Scattering Pattern of Nanocrystalline Materials. Nanomaterials, 12(8), 1252. https://doi.org/10.3390/nano12081252