Hydrothermal and Entropy Investigation of Nanofluid Natural Convection in a Lid-Driven Cavity Concentric with an Elliptical Cavity with a Wavy Boundary Heated from Below
Abstract
:1. Introduction
2. Physical Model
The Governing Equations
3. Numerical Method and Validation
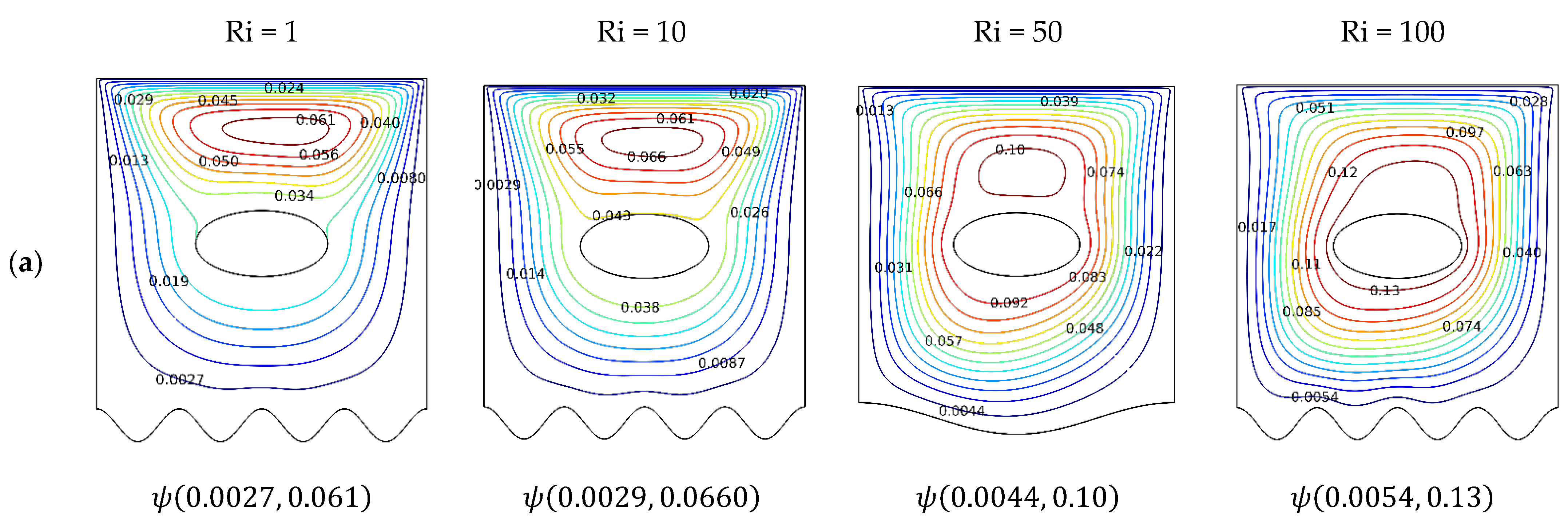
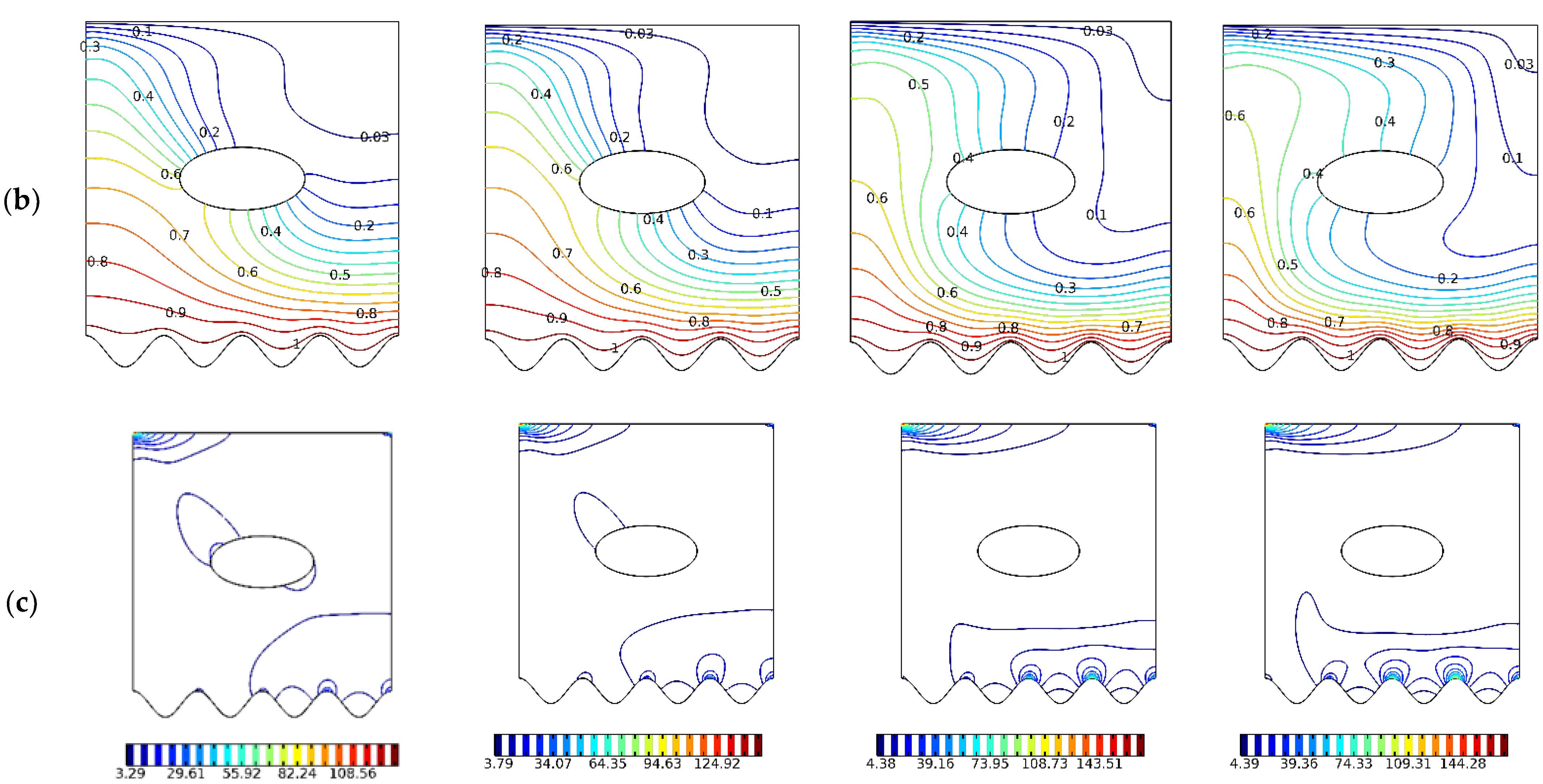
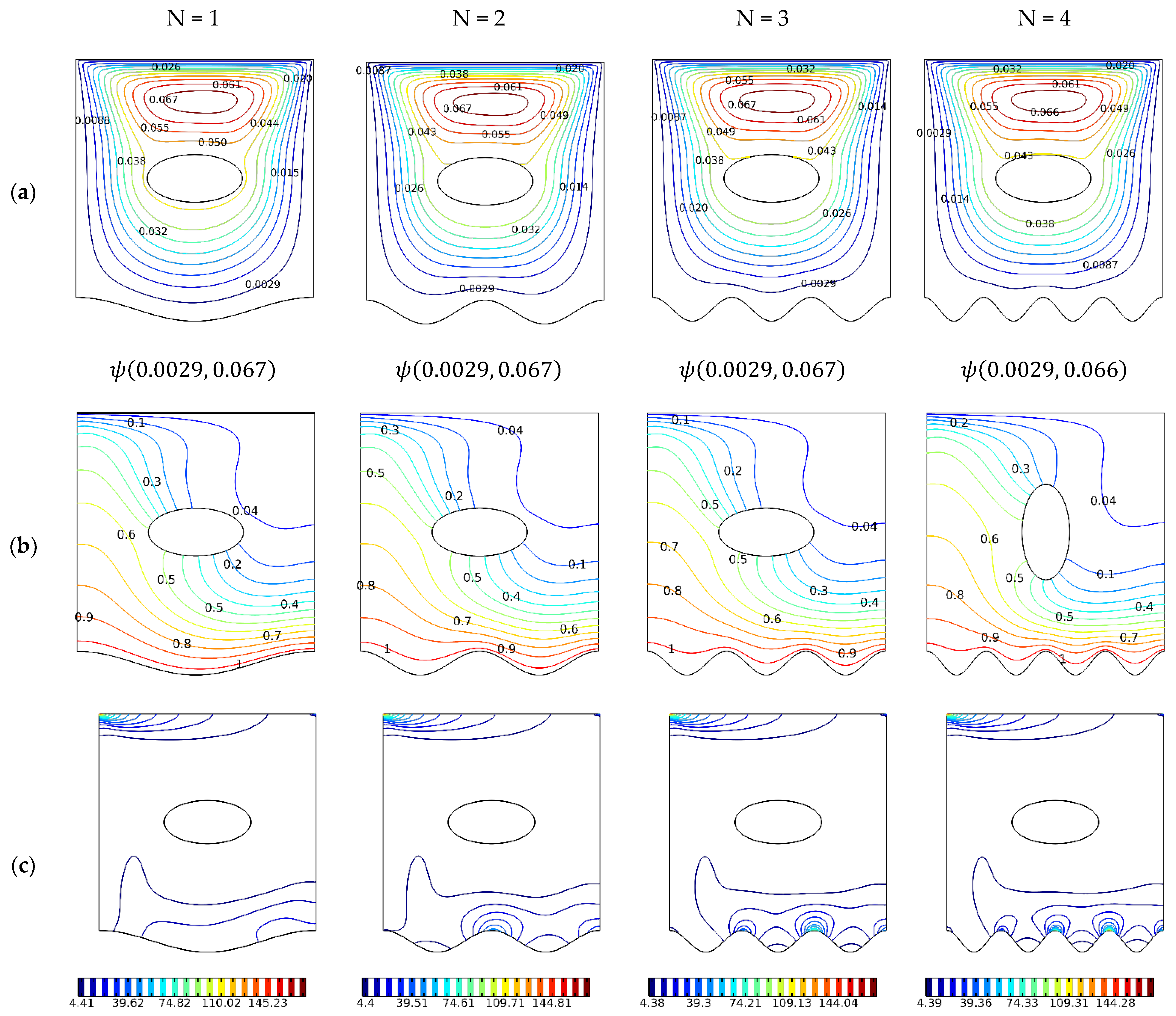
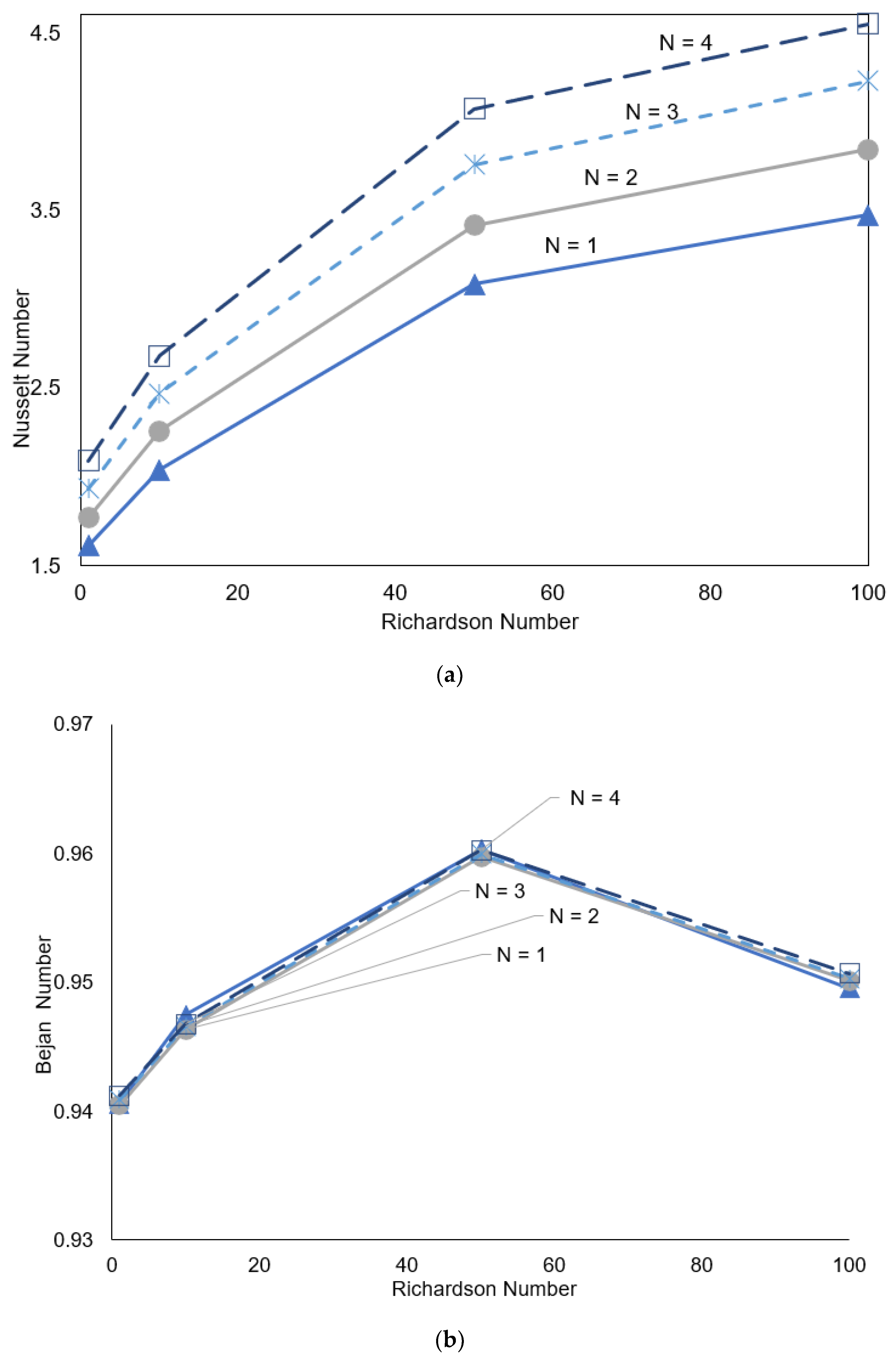
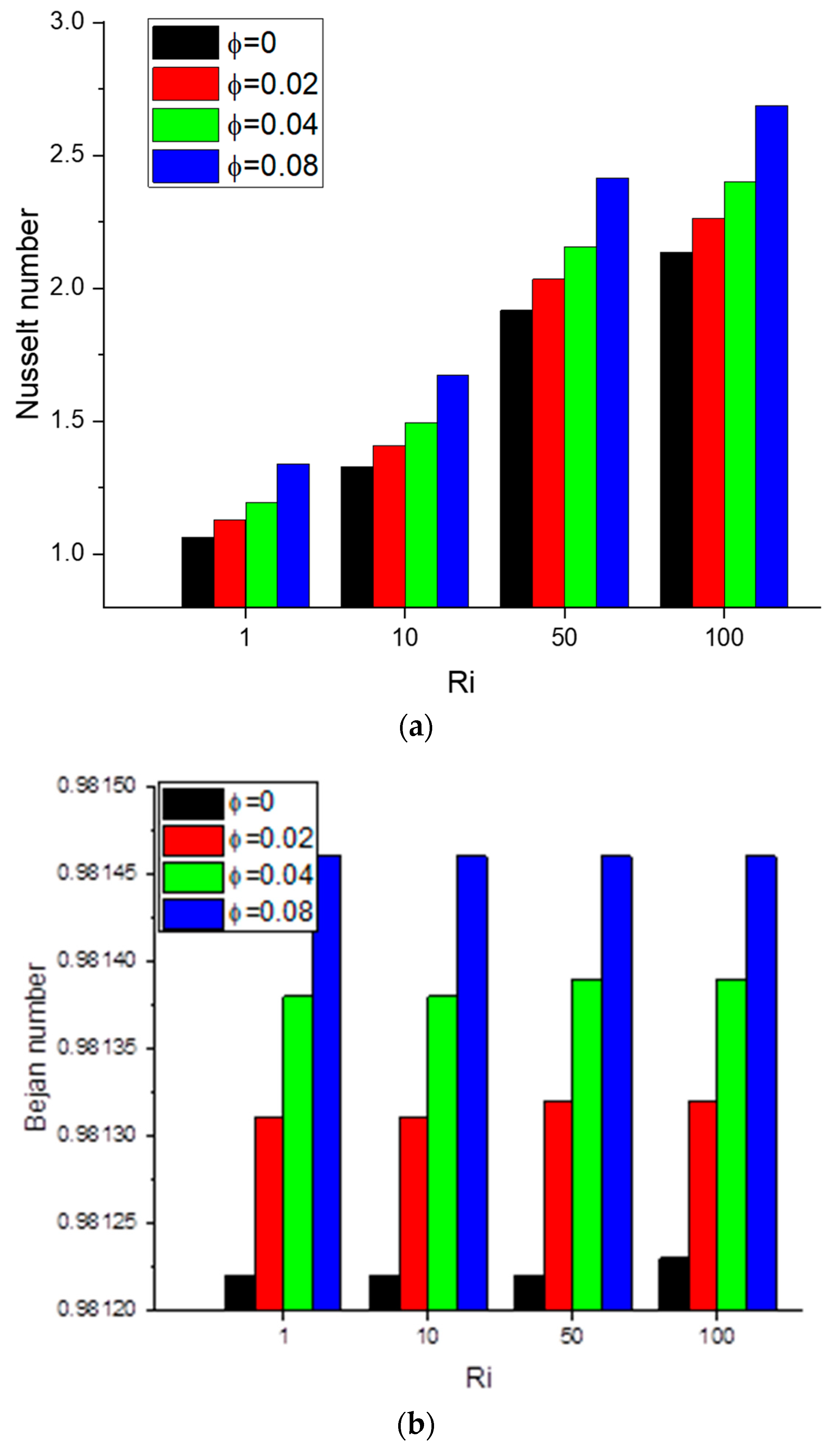
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | amplitude [m] |
| B0 | magnetic induction (Wb/m2) |
| Be | Bejan number |
| Cp | specific heat at constant pressure [J/kg·K] |
| g | gravity [m2/s] |
| Gr | Grashof number |
| Ha | Hartman number |
| k | thermal conductivity of air [W/m·K] |
| L | dimension of the cavity [m] |
| N | undulation |
| Nu | average Nusselt number |
| p | pressure [Pa] |
| P | non-dimensional pressure |
| Pr | Prandtl number |
| Re | Reynolds number |
| Ri | Richardson number |
| S | entropy [J/K] |
| T | temperature [K] |
| To | microchannel wall temperature [K] |
| Uo | moving lid velocity [m/s] |
| u,v | velocity components [m/s] |
| U,V | non-dimensional velocity components |
| x,y | coordinates [m] |
| X,Y | non-dimensional coordinate |
| Greek Symbols | |
| α | thermal diffusivity [m2/s] |
| β | thermal expansion coefficient [1/K] |
| γ | rotation angle [deg] |
| φ | nanoparticles volume fraction |
| μ | dynamic viscosity [kg·m/s] |
| θ | dimensionless temperature |
| ρ | density of fluid [kg/m3] |
| σ | fluid electrical conductivity [S/m] |
| ψ | irreversibly |
| Subscripts | |
| Gen | generation |
| nb | base fluid |
| nf | nanofluid |
| av | average |
| c | cold |
| h | hot |
| s | surface |
References
- Choi, S. Nanofluid Technology: Current Status and Future Research; Argonne National Laboratory, Energy Technology Division: Argonne, IL, USA, 1999; pp. 604–639.
- Azizul, F.; Alsabery, A.I.; Hashim, I. Heatlines visualisation of mixed convection flow in a wavy heated cavity filled with nanofluids and having an inner solid block. Int. J. Mech. Sci. 2020, 175, 105529. [Google Scholar] [CrossRef]
- Alsabery, A.I.; Ghalambaz, M.; Armaghani, T.; Chamkha, A.; Hashim, I.; Pour, M.S. Role of Rotating Cylinder toward Mixed Convection inside a Wavy Heated Cavity via Two-Phase Nanofluid Concept. Nanomaterials 2020, 10, 1138. [Google Scholar] [CrossRef] [PubMed]
- Bendrer, B.; Abderrahmane, A.; Ahmed, S.E.; Raizah, Z.A. 3D magnetic buoyancy-driven flow of hybrid nanofluids confined wavy cubic enclosures including multi-layers and heated obstacle. Int. Commun. Heat Mass Transf. 2021, 126, 105431. [Google Scholar] [CrossRef]
- Azizul, F.M.; Alsabery, A.I.; Hashim, I.; Chamkha, A.J. Heatline visualization of mixed convection inside double lid-driven cavity having heated wavy wall. J. Therm. Anal. 2020, 145, 3159–3176. [Google Scholar] [CrossRef]
- Alshare, A.; Al-Kouz, W.; Khan, W. Cu-Al2O3 water hybrid nanofluid transport in a periodic structure. Processes 2020, 8, 285. [Google Scholar] [CrossRef] [Green Version]
- Asad, F.-A.; Hossain, M.A.; Sarker, M.M.A. Numerical investigation of MHD mixed convection heat transfer having vertical fin in a lid-driven square cavity. In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2019. [Google Scholar] [CrossRef]
- Hussain, S.; Ahmed, S.E. Unsteady MHD forced convection over a backward facing step including a rotating cylinder utilizing Fe3O4-water ferrofluid. J. Magn. Magn. Mater. 2019, 484, 356–366. [Google Scholar] [CrossRef]
- Mansour, M.A.; Ahmed, S.E. Mixed convection flows in a square lid-driven cavity with heat source at the bottom utilising nanofluid. Can. J. Chem. Eng. 2012, 90, 100–110. [Google Scholar] [CrossRef]
- Louaraychi, A.; Lamsaadi, M.; Namimi, M.; Harf, H.; Kaddiri, M.; Raji, A.; Hasnaoui, M. Mixed convection heat transfer cor-relations in shallow rectangular cavities with single and double-lid driven boundaries. Int. J. Heat Mass Transf. 2019, 132, 394–406. [Google Scholar] [CrossRef]
- Gangawane, K.M.; Gupta, S. Mixed convection characteristics in rectangular enclosure containing heated elliptical block: Effect of direction of moving wall. Int. J. Therm. Sci. 2018, 130, 100–115. [Google Scholar] [CrossRef]
- Fayz-Al-Asad, M.; Sarker, M.M.A.; Munshi, M.J.H. Munshi, Numerical investigation of natural convection flow in a hexagonal enclosure having vertical fin. J. Sci. Res. 2019, 11, 173–183. [Google Scholar] [CrossRef] [Green Version]
- Nasrin, R.; Alim, M.A.; Chamkha, A.J. Combined convection flow in triangular wavy chamber filled with water-CuO nanofluid: Effect of viscosity models. Int. Commun. Heat Mass Transf. 2012, 139, 226–1236. [Google Scholar] [CrossRef]
- Radouane, F.; Abderrahmane, A.; Mebarek-Oudina, F.; Ahmed, W.; Rashad, A.; Sahnoun, M.; Ali, H.M. Magneto-Free Convectiveof Hybrid Nanofluid inside Non-Darcy Porous Enclosure Containing an Adiabatic Rotating Cylinder. Energy Sources Part A Recover. Util. Environ. Eff. 2020, 1–16. [Google Scholar] [CrossRef]
- Srinivasacharya, D.; Kumar, P.V. Mixed Convection over an Inclined Wavy Surface in a Nanofluid Saturated Non-Darcy Porous Medium with Radiation Effect. Int. J. Chem. Eng. 2015, 2015, 927508. [Google Scholar] [CrossRef] [Green Version]
- Fares, R.; Naim, H.; Abderrahmane, A.; Bouadi, A. Mixed convection of a nanofluid flow in a vented cavity under the influence of magnetic field. J. Mater. Struct. 2020, 4, 1–11. [Google Scholar]
- Ahmed, S.E.; Aly, A. Mixed convection in a nanofluid-filled sloshing porous cavity including inner heated rose. J. Therm. Anal. 2020, 143, 275–291. [Google Scholar] [CrossRef]
- Slimani, R.; Aissa, A.; Mebarek-Oudina, F.; Khan, U.; Sahnoun, M.; Chamkha, A.J.; Medebber, M.A. Natural convection analysis flow of Al2O3-Cu/water hybrid nanofluid in a porous conical enclosure subjected to the magnetic field. Eur. Phys. J. Appl. Phys. 2020, 92, 10904. [Google Scholar] [CrossRef]
- Abu-Nada, E.; Chamkha, A.J. Mixed convection of a nanofluid in a lid-driven cavity with wavy wall. Int. Commun. Heat Mass Transf. 2014, 57, 36–47. [Google Scholar] [CrossRef]
- Misirlioglu, A.; Baytas, A.C.; Pop, I. Natural Convection Inside an Inclined Wavy Enclosure Filled with a Porous Medium. Transp. Porous Media 2006, 64, 229–246. [Google Scholar] [CrossRef]
- Mushate, K.S. CFD prediction of natural convection in a wavy cavity filled with porous medium. Glob. J. Res. Eng. 2011, 11, 29–45. [Google Scholar]
- Sheremet, M.A.; Pop, I. Natural Convection in a Wavy Porous Cavity with Sinusoidal Temperature Distributions on Both Side Walls Filled with a Nanofluid: Buongiorno’s Mathematical Model. J. Heat Transf. 2015, 137, 072601. [Google Scholar] [CrossRef]
- Shenoy, A.; Sheremet, M.; Pop, I. Convective Flow and Heat Transfer from Wavy Surfaces: Viscous Fluids, Porous Media, and Nanofluids; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Cheong, H.T.; Sivasankaran, S.; Bhuvaneswari, M. Natural convection in a wavy porous cavity with sinusoidal heating and internal heat generation. Int. J. Numer. Methods Heat Fluid Flow 2017, 27, 287–309. [Google Scholar] [CrossRef]
- Al-Asad, F.; Alam, N.; Tunç, C.; Sarker, M.M.A. Heat Transport Exploration of Free Convection Flow inside Enclosure Having Vertical Wavy Walls. J. Appl. Comput. Mech. 2020, 7, 520–527. [Google Scholar] [CrossRef]
- Zahan, I.; Nasrin, R.; Alim, M.A. MHD effect on conjugate heat transfer in a nanofluid rectangular enclosure. Int. J. Petro-Chem. Seci. Eng. 2018, 3, 114–123. [Google Scholar] [CrossRef] [Green Version]
- Öztop, H.F.; Sakhrieh, A.; Abu-Nada, E.; Al-Salem, K. Mixed convection of MHD flow in nanofluid filled and partially heated wavy walled lid-driven enclosure. Int. Commun. Heat Mass Transf. 2017, 86, 42–51. [Google Scholar] [CrossRef]
- Ashorynejad, H.R.; Shahriari, A. MHD natural convection of hybrid nanofluid in an open wavy cavity. Results Phys. 2018, 9, 440–455. [Google Scholar] [CrossRef]
- Cho, C.-C. Mixed convection heat transfer and entropy generation of Cu-water nanofluid in wavy-wall lid-driven cavity in presence of inclined magnetic field. Int. J. Mech. Sci. 2018, 151, 703–714. [Google Scholar] [CrossRef]
- Alsabery, A.I.; Tayebi, T.; Kadhim, H.T.; Ghalambaz, M.; Hashim, I.; Chamkha, A.J. Impact of two-phase hybrid nanofluid approach on mixed convection inside wavy lid-driven cavity having localized solid block. J. Adv. Res. 2020, 30, 63–74. [Google Scholar] [CrossRef]
- Ahmed, S.E.; Mansour, M.A.; Rashad, A.M.; Morsy, Z. MHD free convection and sinusoidal heating in a wavy cavity filled with a heat-generating porous medium using cu-water nanofluids. Comput. Therm. Sci. Int. J. 2020, 12, 217–232. [Google Scholar] [CrossRef]
- Sun, C.; Yu, B.; Oztop, H.F.; Wang, Y.; Wei, J. Control of mixed convection in lid-driven enclosures using conductive triangular fins. Int. J. Heat Mass Transf. 2011, 54, 894–909. [Google Scholar] [CrossRef]
- Elatar, A.; Teamah, M.A.; Hassab, M.A. Numerical study of laminar natural convection inside square enclosure with single horizontal fin. Int. J. Therm. Sci. 2016, 99, 41–51. [Google Scholar] [CrossRef]
- Palaniappan, G.; Murugan, M.; Al-Mdallal, Q.M.; Abdalla, B.; Doh, D.-H. Numerical Investigation of Open Cavities with Parallel Insulated Baffles. Int. J. Heat Technol. 2020, 38, 611–621. [Google Scholar] [CrossRef]
- Al-Kouz, W.; Al-Muhtady, A.; Owhaib, W.; Al-Dahidi, S.; Hader, M.; Abu-Alghanam, R. Entropy Generation Optimization for Rarified Nanofluid Flows in a Square Cavity with Two Fins at the Hot Wall. Entropy 2019, 21, 103. [Google Scholar] [CrossRef] [Green Version]
- Shulepova, E.V.; Sheremet, M.A.; Oztop, H.F.; Abu-Hamdeh, N. Mixed convection of Al2O3–H2O nanoliquid in a square chamber with complicated fin. Int. J. Mech. Sci. 2019, 165, 105192. [Google Scholar] [CrossRef]
- Hussain, S.; Jamal, M.; Geridonmez, B.P. Impact of fins and inclined magnetic field in double lid-driven cavity with Cu–water nanofluid. Int. J. Therm. Sci. 2020, 161, 106707. [Google Scholar] [CrossRef]
- Al-Kouz, W.G.; Kiwan, S.; Alkhalidi, A.; Sari, M.E.; Alshare, A. Numerical study of heat transfer enhancement for low-pressure flows in a square cavity with two fins attached to the hot wall using Al2O3-air nanofluid. Stroj. Vestn.-J. Mech. Eng. 2018, 64, 26–36. [Google Scholar]
- Al-Kouz, W.; Saleem, K.B.; Chamkha, A. Numerical investigation of rarefied gaseous flows in an oblique wavy sided walls square cavity. Int. Commun. Heat Mass Transf. 2020, 116, 104719. [Google Scholar] [CrossRef]
- Alkhalidi, A.; Kiwan, S.; Al-Kouz, W.; Alshare, A. Conjugate heat transfer in rarefied gas in enclosed cavities. Vacuum 2016, 130, 137–145. [Google Scholar] [CrossRef]
- Mourad, A.; Aissa, A.; Mebarek-Oudina, F.; Al-Kouz, W.; Sahnoun, M. Natural convection of nanoliquid from elliptic cylinder in wavy enclosure under the effect of uniform magnetic field: Numerical investigation. Eur. Phys. J. Plus 2021, 136, 429. [Google Scholar] [CrossRef]
- Al-Kouz, W.; Bendrer, B.A.-I.; Aissa, A.; Almuhtady, A.; Jamshed, W.; Nisar, K.S.; Mourad, A.; Alshehri, N.A.; Zakarya, M. Galerkin finite element analysis of magneto two-phase nanofluid flowing in double wavy enclosure comprehending an adiabatic rotating cylinder. Sci. Rep. 2021, 11, 16494. [Google Scholar] [CrossRef]
- Al-Kouz, W.; Aissa, A.; Koulali, A.; Jamshed, W.; Moria, H.; Nisar, K.S.; Mourad, A.; Abdel-Aty, A.H.; Khashan, M.M.; Yahia, I.S. MHD darcy-forchheimer nanofluid flow and entropy optimization in an odd-shaped enclosure filled with a (MWCNT-Fe3O4/water) using galerkin finite element analysis. Sci. Rep. 2021, 11, 22635. [Google Scholar] [CrossRef]
- Shamshuddin, M.D.; Abderrahmane, A.; Koulali, A.; Eid, M.R.; Shahzad, F.; Jamshed, W. Thermal and solutal performance of Cu/CuO nanoparticles on a non-linear radially stretching surface with heat source/sink and varying chemical reaction effects. Int. Commun. Heat Mass Transf. 2021, 29, 105710. [Google Scholar] [CrossRef]
- Jamshed, W.; Eid, M.R.; Aissa, A.; Mourad, A.; Nisar, K.S.; Shahzad, F.; Saleel, C.A.; Vijayakumar, V. Partial velocity slip effect on working magneto non-Newtonian nanofluids flow in solar collectors subject to change viscosity and thermal conductivity with temperature. PLoS ONE 2021, 16, e0259881. [Google Scholar] [CrossRef] [PubMed]
- Riaz, A.; Bobescu, E.; Ramesh, K.; Ellahi, R. Entropy Analysis for Cilia-Generated Motion of Cu-Blood Flow of Nanofluid in an Annulus. Symmetry 2021, 13, 2358. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Sadri, M.; Sheremet, M.A. Numerical Simulation of Hybrid Nanofluid Mixed Convection in a Lid-Driven Square Cavity with Magnetic Field Using High-Order Compact Scheme. Nanomaterials 2021, 11, 2250. [Google Scholar] [CrossRef]
- Nazari, S.; Ellahi, R.; Sarafraz, M.; Safaei, M.R.; Asgari, A.; Akbari, O.A. Numerical study on mixed convection of a non-Newtonian nanofluid with porous media in a two lid-driven square cavity. J. Therm. Anal. 2019, 140, 1121–1145. [Google Scholar] [CrossRef]
- Imran, M.; Yasmin, S.; Waqas, H.; Khan, S.A.; Muhammad, T.; Alshammari, N.; Hamadneh, N.N.; Khan, I. Computational Analysis of Nanoparticle Shapes on Hybrid Nanofluid Flow Due to Flat Horizontal Plate via Solar Collector. Nanomaterials 2022, 12, 663. [Google Scholar] [CrossRef] [PubMed]
- Jani, S.; Mahmoodi, M.; Amini, M. Magnetohydrodynamic free convection in a square cavity heated from below and cooled from other walls. Int. J. Mech. Aerosp. Ind. Mechatron. Eng. 2013, 7, 331–336. [Google Scholar]
- Selimefendigil, F.; Öztop, H.F. Numerical study of MHD mixed convection in a nanofluid filled lid driven square enclosure with a rotating cylinder. Int. J. Heat Mass Transf. 2014, 78, 741–754. [Google Scholar] [CrossRef]
- Albojamal, A.; Vafai, K. Analysis of single phase discrete and mixture models in predicting nanofluid transport. Int. J. Heat Mass Transf. 2017, 114, 225–237. [Google Scholar] [CrossRef]
- Taylor, C.; Hood, P. A numerical solution of the Navier-Stokes equations using the finite element technique. Comput. Fluids 1973, 1, 73–100. [Google Scholar] [CrossRef]
- Dechaumphai, P. Finite Element Method in Engineering, 2nd ed.; Chulalongkorn University Press: Bangkok, Thailand, 1999. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L. The Finite Element Method for Solid and Structural Mechanics, 6th ed.; Butterworth-Heinemann: Oxford, UK, 2005. [Google Scholar]
- Iwatsu, R.; Hyun, J.M.; Kuwahara, K. Mixed convection in a driven cavity with a stable vertical temperature gradient. Int. J. Heat Mass Transf. 1993, 36, 1601–1608. [Google Scholar] [CrossRef]





| Material | [W/m·k] | [S/m] | ||||
|---|---|---|---|---|---|---|
| Alumina (Al2O3) | 3970 | 765 | - | 0.85 | 25 | 10−10 |
| Water | 997.1 | 4179 | 695 | 21 | 0.613 | 0.05 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshare, A.; Abderrahmane, A.; Guedri, K.; Younis, O.; Fayz-Al-Asad, M.; Ali, H.M.; Al-Kouz, W. Hydrothermal and Entropy Investigation of Nanofluid Natural Convection in a Lid-Driven Cavity Concentric with an Elliptical Cavity with a Wavy Boundary Heated from Below. Nanomaterials 2022, 12, 1392. https://doi.org/10.3390/nano12091392
Alshare A, Abderrahmane A, Guedri K, Younis O, Fayz-Al-Asad M, Ali HM, Al-Kouz W. Hydrothermal and Entropy Investigation of Nanofluid Natural Convection in a Lid-Driven Cavity Concentric with an Elliptical Cavity with a Wavy Boundary Heated from Below. Nanomaterials. 2022; 12(9):1392. https://doi.org/10.3390/nano12091392
Chicago/Turabian StyleAlshare, Aiman, Aissa Abderrahmane, Kamel Guedri, Obai Younis, Muhammed Fayz-Al-Asad, Hafiz Muhammed Ali, and Wael Al-Kouz. 2022. "Hydrothermal and Entropy Investigation of Nanofluid Natural Convection in a Lid-Driven Cavity Concentric with an Elliptical Cavity with a Wavy Boundary Heated from Below" Nanomaterials 12, no. 9: 1392. https://doi.org/10.3390/nano12091392
APA StyleAlshare, A., Abderrahmane, A., Guedri, K., Younis, O., Fayz-Al-Asad, M., Ali, H. M., & Al-Kouz, W. (2022). Hydrothermal and Entropy Investigation of Nanofluid Natural Convection in a Lid-Driven Cavity Concentric with an Elliptical Cavity with a Wavy Boundary Heated from Below. Nanomaterials, 12(9), 1392. https://doi.org/10.3390/nano12091392









