Abstract
A valley-Hall-like photonic insulator based on Kagome split-ring is proposed. Theoretical analysis and numerical calculations illustrate that symmetry can be broken not only by global rotation but also individual rotation of the split rings, providing topological phase transitions. Furthermore, refraction of the edge state from the interface into the background space at Zigzag termination is explored. It is shown that positive/negative refraction of the outgoing beam depends on the type of valley (K or ), from which the edge state is projected. These results provide a new way to manipulate terahertz wave propagation and facilitate the potential applications in directional collimation, beam splitting, negative refraction image, etc.
1. Introduction
Photonic topological insulators support some of the most fascinating properties for signal transport and show excellent potential applications in modern optical devices [1,2,3,4,5,6,7], such as reflectionless waveguides, topological quantum interfaces, splitters, robust delay lines, etc.
The key to topological phase transition lies in opening an energy gap in the band structure at certain degenerate points by breaking either the time-reversal symmetry (TRS) or inversion symmetry, which can be realized in classical wave systems mimicking the quantum Hall effect (QHE) [8,9,10,11,12,13,14], the quantum spin Hall effect (QSHE) [15,16,17,18,19,20,21,22,23], or the quantum valley Hall effect (QVHE) [24,25,26,27,28,29,30,31,32,33]. In analogues of the QHE system, breaking of TRS can be achieved by applying a magnetic field or an effective ‘magnetic’ field from circulating fluid flows [10,11,12] or gyroscopes [13,14]. However, this strategy remains challenging due to the structural complexity. In mimicking QSHE or QVHE systems, breaking the symmetry does not require any external fields. Generally, analogues of QSHE can be provided by constructing the system to have two pseudospins, either integrating the different wave polarization degree of freedom or folding the band structure to form a double Dirac cone [15,16,17,18,19,20,21,22,23,30]. For emulating QVHE, such as symmetry photonic crystals composed of triangular rods [6,24,34], square lattices containing square inclusions [35], the new class of valley-Hall-like topological insulators can be designed by breaking the inversion symmetry of the systems [36,37,38].
So far, varieties of topological insulators have been demonstrated. However, most of the current studies focus on the robust wave propagation along the topological interfaces [10,11,12,13,14,31,32,39,40,41]. Further exploration for applicable topological devices, including outcoupling effects or wave manipulations, need to be taken into consideration. More recently, topological positive/negative, near-zero refraction and wave splitting have been reported in valley crystal [25,29,30,31], Weyl [42], and QSHE inspired systems [43,44], which may have potential applications in directional collimation [45], beam splitting [46,47,48], and others.
In this work, a new kind of valley-Hall-like photonic insulator based on two-dimensional (2D) Kagome split-ring is proposed. Theoretical analysis and numerical calculations by COMSOL Multiphysics illustrate that symmetry can be broken not only by global rotation but also by individual rotation of the split rings, providing topological phase transitions. Further, topological positive/negative refraction of the edge states from the interface into background space at Zigzag termination is explored. The results show that refraction of the outgoing beam depends on the type of valley (K or ) from which the edge state is projected.
2. Model and Calculation Method
2.1. Model
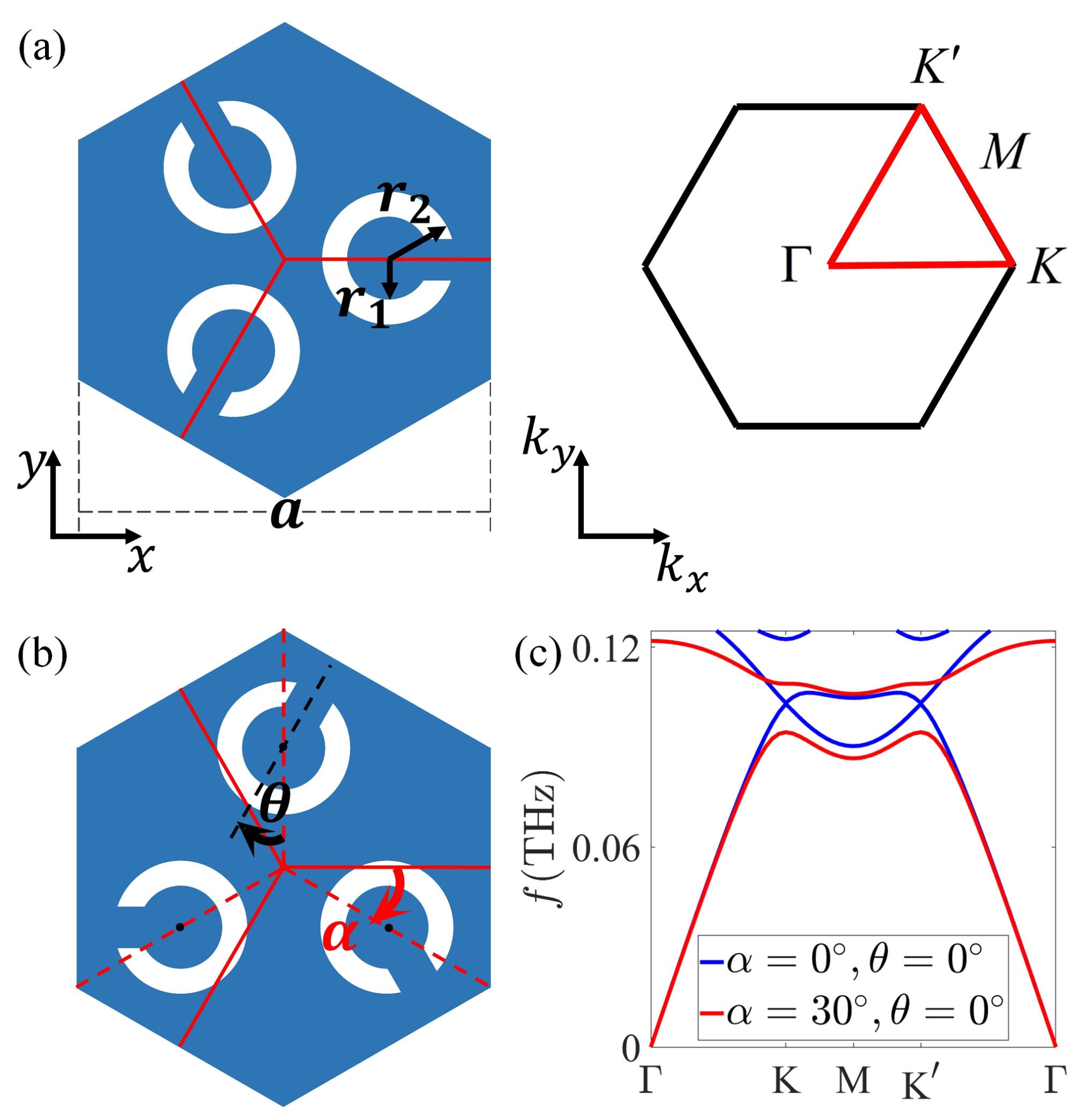
The 2D unit cell of Kagome split-ring photonic insulator (SRPI) is shown in Figure 1a, where the lattice constant, and the inner and outer diameters of each split ring are a, , and , respectively. The background material is silicon (Si) with permittivity , and the split ring is set as a perfect electric conductor. The proposed symmetry-broken unit cell to provide non-trivial valley-Hall-like topological states is demonstrated in Figure 1b, in which and are the global and individual rotation of the split rings. As m, , , the photonic bands ( modes with magnetic field along z axis) for , , and , are shown in Figure 1c with blue and red curves, respectively. The existing bandgap closes for and opens for .
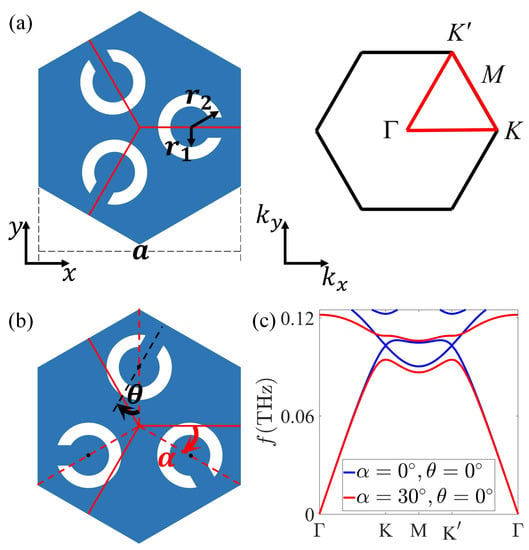
Figure 1.
(a) The 2D unit cell and first Brillouin zone of Kagome SRPI. The geometric parameters are taken as m, , . (b) symmetry-broken unit cell, and are the global and individual rotation of the split rings. (c) Photonic bands of the SRPI for , (blue solid curves) and , (red solid curves).
2.2. Valley Chern Number
In SRPI, the Dirac cone near the K point can be approximately regarded as a two-band model, and its effective Hamiltonian has the following form through the perturbation method [24,49,50]:
where is the group velocity at the degenerate Dirac cone, represents the momentum deviation from the K point, is Pauli matrix, , and separately represent the two frequencies at the boundaries of bandgap after the Dirac point lifted. The Berry curvature can be obtained through effective Hamiltonian [49,51]:
The valley Chern number can be obtained by the numerical integration of Berry curvature around the K valley:
Equation (3) shows that the valley Chern number only depends on the sign of the Dirac mass m ( for and for ). The band inversion means the reversal of and , and consequently the signs of valley Chern number .
3. Results
3.1. Band Inversion of Topological Valley-Hall-like States
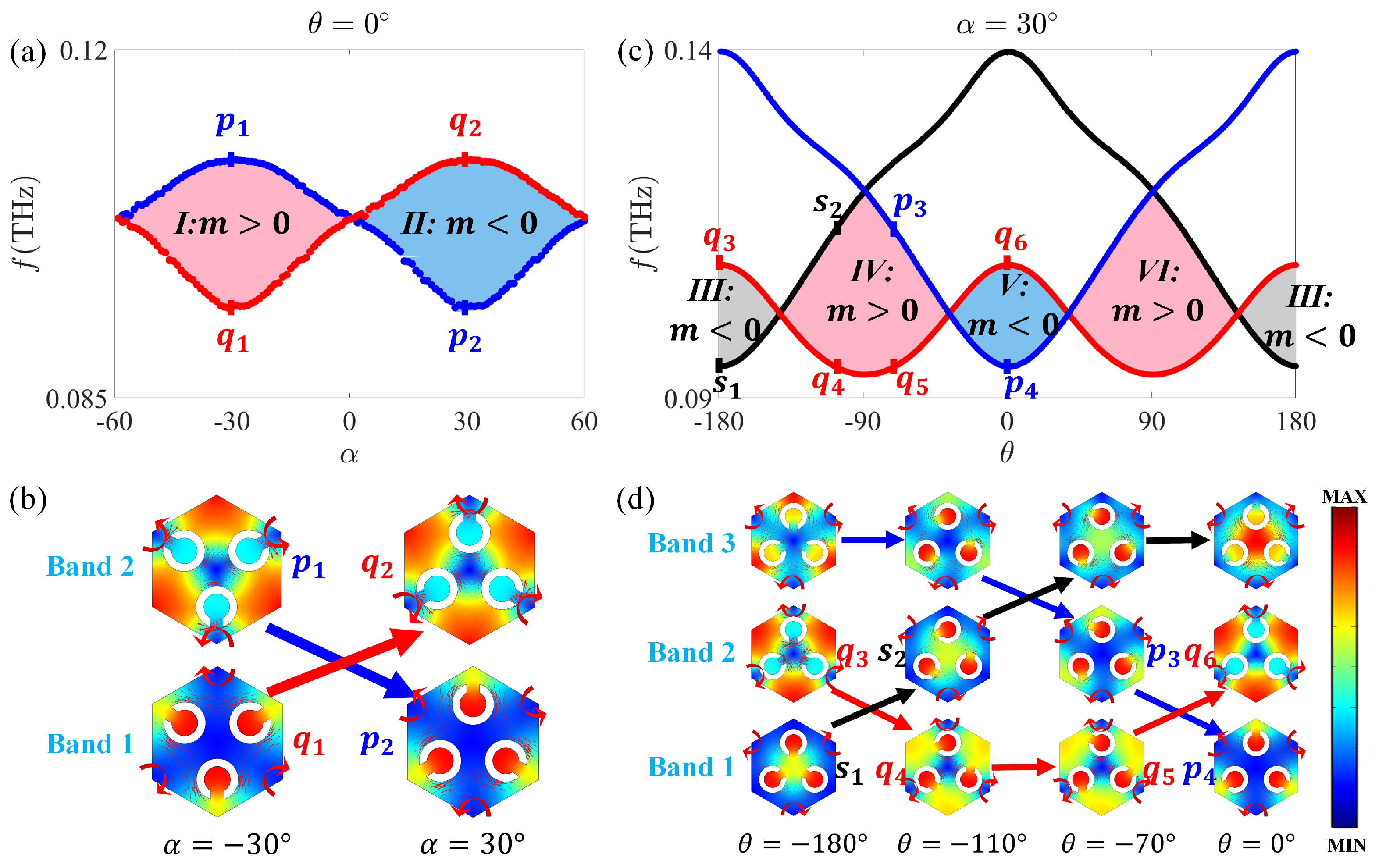
Typically, the process of band inversion can make the bandgap open then close and then reopen, resulting in the topological phase transition at the K (or ) point [52]. For our proposed Kagome split-ring photonic insulator shown in Figure 1b, the topological phase transition depending on both global and individual rotation is illustrated in Appendix A. Specifically, for , the topological phase varying with global is shown in Figure 2a, in which the original symmetry at is reduced to the symmetry. Accordingly, the twofold Dirac degeneracy at the K (or ) point is lifted. The field distributions of the two eigenstates at the K point (denoted as p and q) for and , respectively, are illustrated in Figure 2b. When the degeneracy is lifted, the frequency order of the p and q states flips, indicating a typical band inversion and topological phase transition. According to Equation (3), the signs of Dirac mass m () for bandgap I and in Figure 2a are opposite, and the difference of valley Chern number I and II is , which implies that valley-Hall-like topological edge states can exist at the interface of system composed of SRPIs with distinct valley-Hall-like phases (Section 3.2).
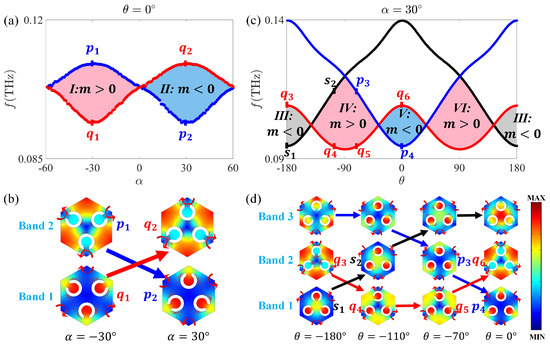
Figure 2.
(a) Dependence of topological phase transition on global as at the K point; the region I and represent bandgaps with and , respectively. (b) The field distribution of the two eigenstates at the K point (denoted as p and q) for and . (c) Dependence of topological phase transition on individual as at the K point; the region , () and V represent bandgaps with , , and , respectively. (d) The field distribution of three eigenstates at the K point (denoted as s, p, and q) for , , , and . The Poynting vectors are represented by red arrows.
As , the topological phase varying with global is shown in Figure 2c. The field profiles of the eigenstates at the K point for , , , and are shown in Figure 2d. Similar to Figure 2b, the frequency order of the eigenstates flips for different . With two different bands in Figure 2b involved in the topological phase transition, three bands are involved in Figure 2c, where two different kinds of band inversions (one is between () and (), and the other is between () and V (V)) exist. In regions () and (), the signs of Dirac mass m () are opposite, and the difference of their valley Chern numbers is , which guarantees the existence of topological edge states (Appendix B). Similarly, for () and V (V), opposite signs of Dirac mass m () and different valley Chern numbers () are obtained, providing topological edge states (Appendix B).
3.2. Valley Topological Refraction
It is known that the direction of the outgoing beam of the topological edge state depends on the type of valley (K or ), from which the edge state is projected [45]. Hence, a wave launched from left to right along positive-type and negative-type interfaces will be projected from the K and valley, respectively. To illustrate the refraction of the radiated beam, a topological insulator in Figure 3a is designed, and refractions of edge states from the interface into the background space at Zigzag termination are explored.
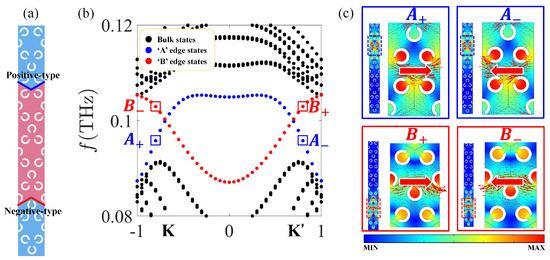
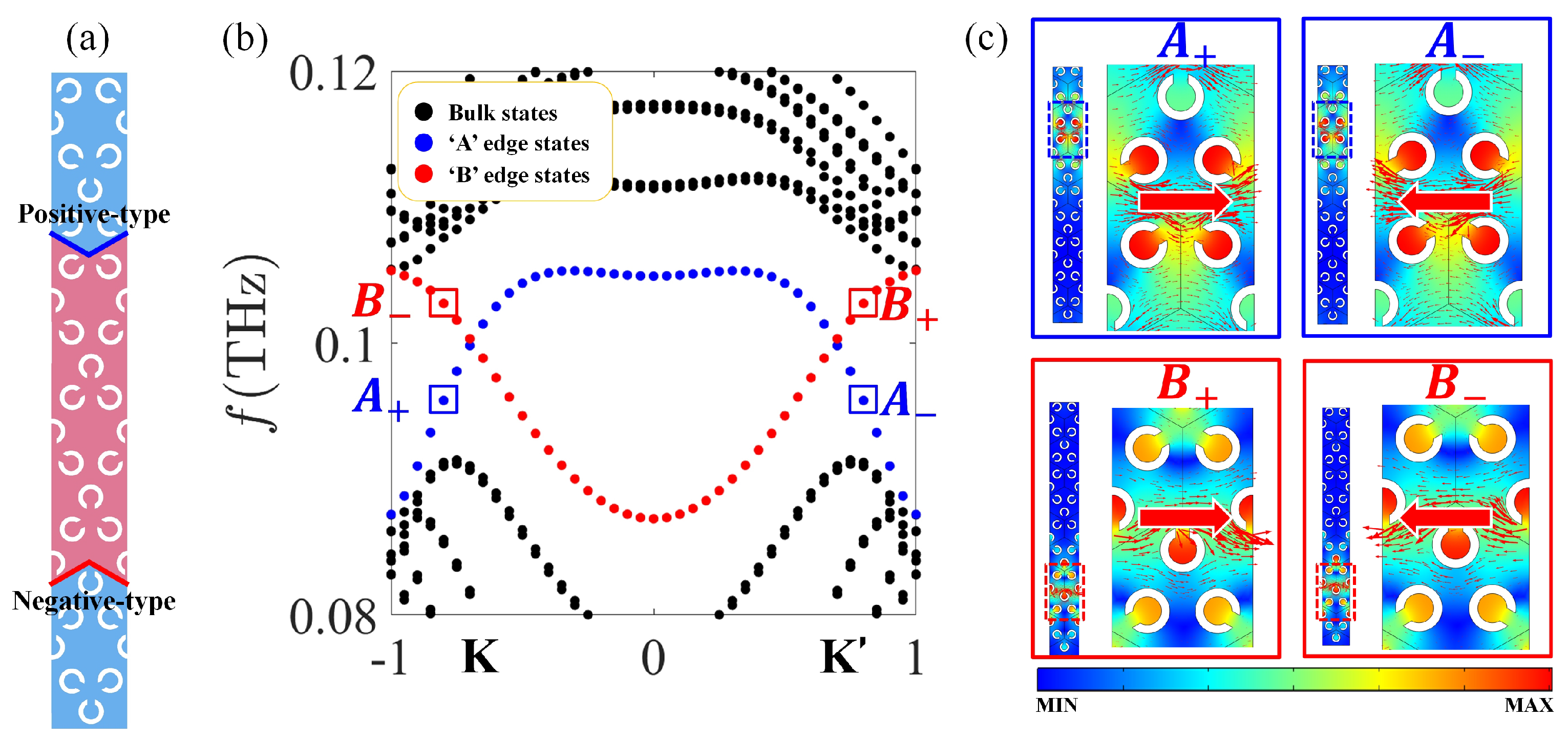
Figure 3.
(a) Supercell and (b) bands of topological insulator with (light red) and (light blue). In (b), dashed black curves represent the bulk modes and the dashed red/blue curves represent the negative-type/positive-type interfaces edge states. (c) The distribution of field for , , , in (b), and the Poynting vectors are represented by red arrows.
Figure 3b shows the dispersion relation of the topological insulator containing different interfaces. Dashed black curves represent the bulk modes, and the dashed red/blue curves represent the negative-type/positive-type interfaces edge states. For different points at the interfaces edge states, the distributions of fields and Poynting vectors (represented by arrows) are shown in Figure 3c.
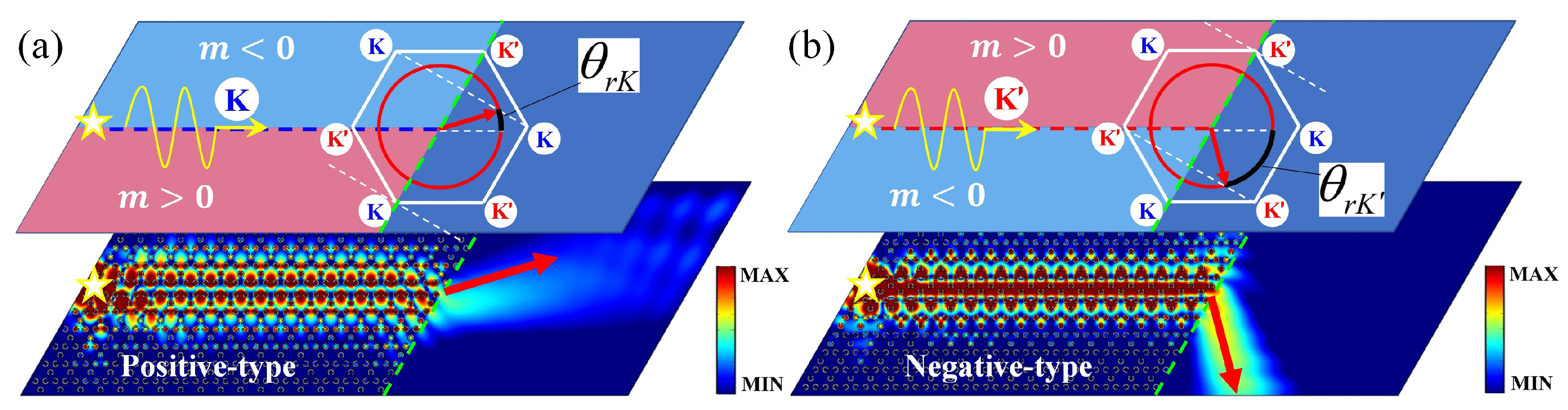
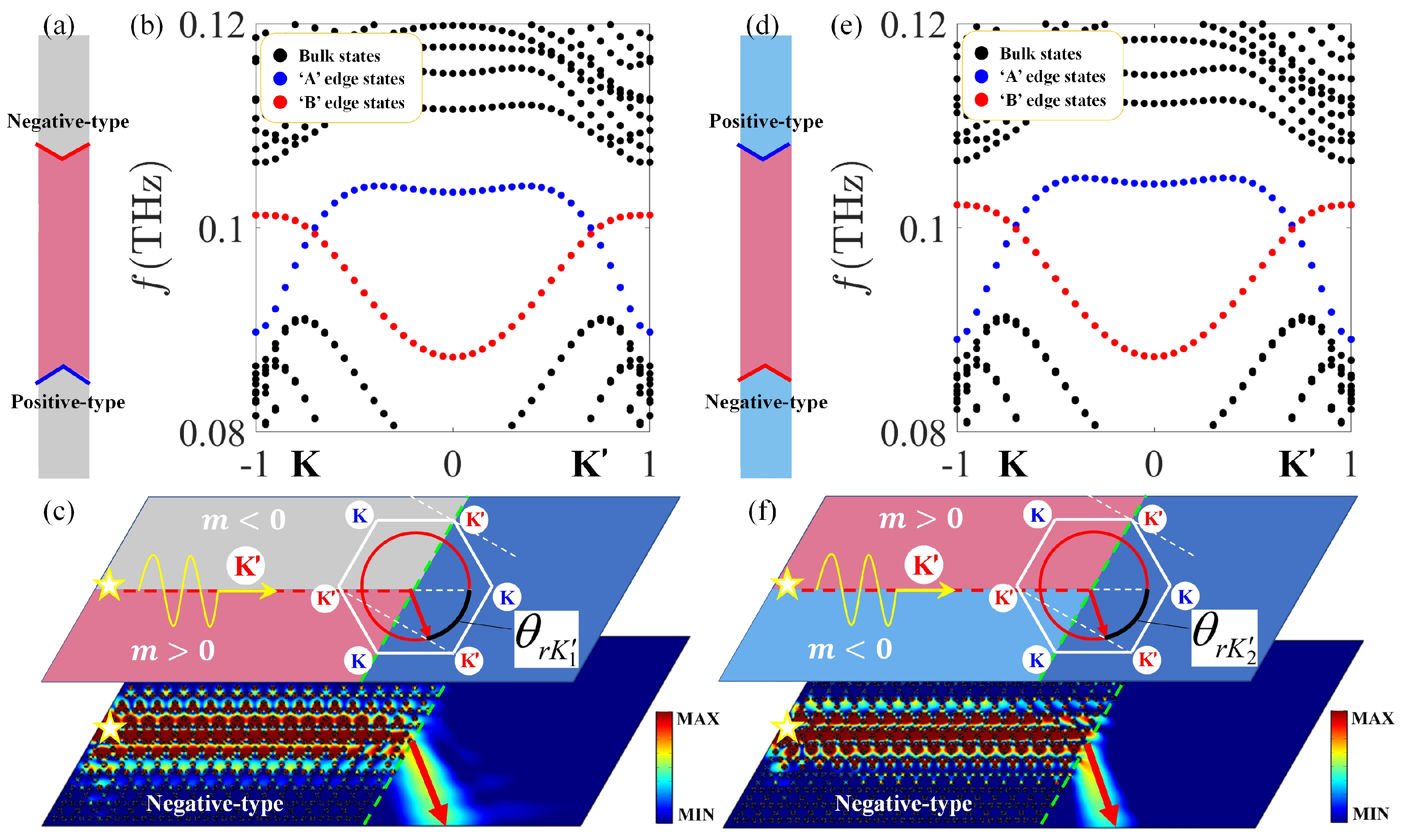
The k-space analysis on out-coupling of K projected edge states along the positive-type (Zigzag) interface is demonstrated in Figure 4a. The white solid hexagon represents the first Brillouin zone, and red solid circles show the dispersion in background material Si, in which the incident wavevector K will be matched with the equifrequency curve of Si to determine the propagation direction of the radiated beam. The simulated distribution of fields at frequency THz is illustrated in the bottom panel. For out-coupling of projected edge state along the negative-type (Zigzag) interface, the corresponding analyses are shown in Figure 4b. Obviously, the direction of the outgoing beam in Figure 4a is different with that in Figure 4b due to the different type of valley (K or ) from which the edge state is projected. Further, the theoretical refraction angle can be quantitatively determined by the phase-matching condition at the terminal (parallel to ), which is and , for positive-type and negative-type interfaces, respectively. Here, the equifrequency curves k of background Si can be determined by , where f represents the incident frequency, c is light speed in air, and is the refractive index of Si. Consequently, and are obtained in Figure 4a,b. We note that the topological refraction and transmission in our SRPI can maintain strong robustness (Appendix C).
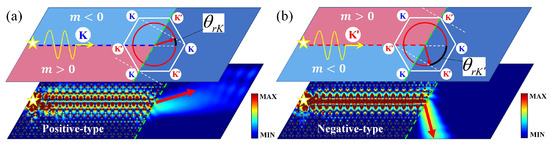
Figure 4.
(a) The k-space analysis on out-coupling of K valley projected edge states along the positive-type (Zigzag) interface. (b) The k-space analysis on the out-coupling of valley projected edge states along the negative-type (Zigzag) interface. The white solid hexagon represents the first Brillouin zone, and the red solid circles show the dispersion in background material Si. The simulated distribution of fields at the frequency THz (in bandgap) are separately illustrated in the bottom panels. The light-red and light-blue regions represent and , respectively.
4. Conclusions
A valley-Hall-like photonic insulator based on Kagome split-ring is proposed. Theoretical analysis and numerical calculations illustrate that symmetry can be broken by either the global rotation or individual rotation of split rings, providing topological phase transitions. Additionally, refractions of the outgoing beam from the interface into the background space at Zigzag termination are explored. We show that positive/negative refraction can be obtained, which is determined by the type of valley (K or ). These results provide a new way to manipulate THz wave propagation and facilitate the potential applications in directional collimation, beam splitting, and negative refraction image.
Author Contributions
Y.S. and X.D. supervised this project. H.L. provided the original idea and did the calculations. H.L., C.L., T.Z., J.X., X.Z. and Y.S. analyzed the data and discussed the results. H.L. and Y.S. wrote the paper. All authors have read and agreed to the published version of the manuscript.
Funding
The authors are grateful for the support from the National Natural Science Foundation of China (Grant numbers 61865009, 61927813).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
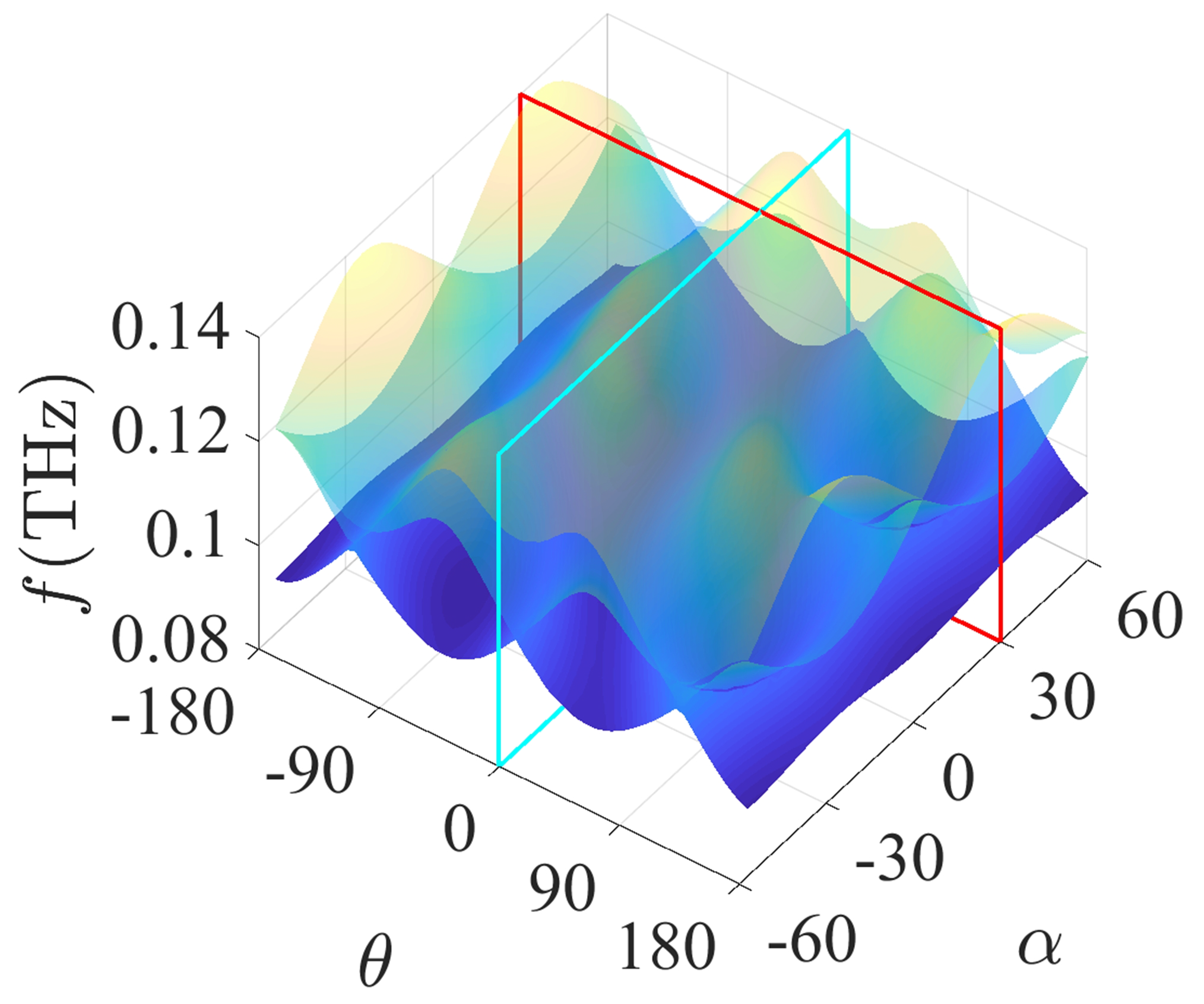
Topological phase transition at the K point depending on global and individual rotation is illustrated in Figure A1.
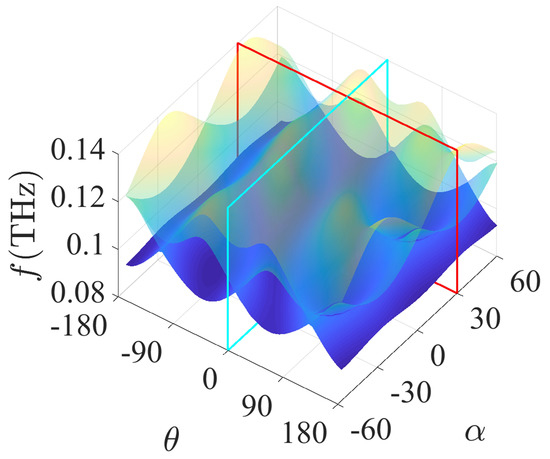
Figure A1.
Dependence of topological phase transition at K point on global and individual rotations. Specifically, the cross sections formed by the cyan frame and the red frame are shown in Figure 2a,c.
Figure A1.
Dependence of topological phase transition at K point on global and individual rotations. Specifically, the cross sections formed by the cyan frame and the red frame are shown in Figure 2a,c.
Appendix B
For the band inversion between bandgap and , the corresponding supercell, bands, and k-space analysis are shown in Figure A2a–c, respectively. Nonzero supports the existence of negative-type/positive-type topological edge states. Specifically, for negative refraction, is obtained.
For and V, supercell, bands, and k-space analysis are separately shown in Figure A2d–f. Likewise, nonzero supports the existence of negative-type/positive-type topological edge states, and the corresponding negative refraction angle is .
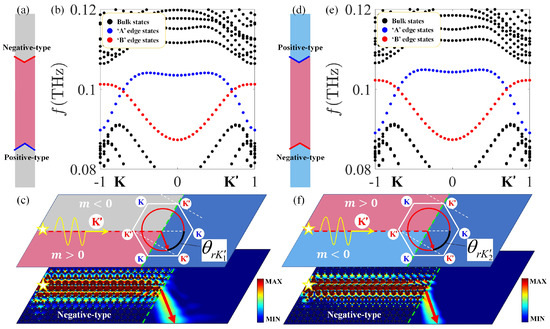
Figure A2.
(a) Supercell and (b) bands of topological insulator with (gray) and (light red). (c) The k-space analysis on the out-coupling of valley and projected edge states along negative-type (Zigzag) interface. (d) Supercell and (e) bands of topological insulator with (light red) and (light blue). (f) The k-space analysis on the out-coupling of valley and projected edge states along negative-type (Zigzag) interface. In (b,e), dashed black curves represent the bulk modes. The dashed red/blue curves represent the negative-type/positive-type interfaces edge states. In (c,f), the white solid hexagon represents the first Brillouin zone. The red solid circle shows the dispersion in background material Si. Simulated distribution of fields at frequency THz and THz are separately illustrated in the bottom panels.
Figure A2.
(a) Supercell and (b) bands of topological insulator with (gray) and (light red). (c) The k-space analysis on the out-coupling of valley and projected edge states along negative-type (Zigzag) interface. (d) Supercell and (e) bands of topological insulator with (light red) and (light blue). (f) The k-space analysis on the out-coupling of valley and projected edge states along negative-type (Zigzag) interface. In (b,e), dashed black curves represent the bulk modes. The dashed red/blue curves represent the negative-type/positive-type interfaces edge states. In (c,f), the white solid hexagon represents the first Brillouin zone. The red solid circle shows the dispersion in background material Si. Simulated distribution of fields at frequency THz and THz are separately illustrated in the bottom panels.
Appendix C
By adding impurity and defect, topological refraction and transmission can maintain strong robustness, as shown in Figure A3.
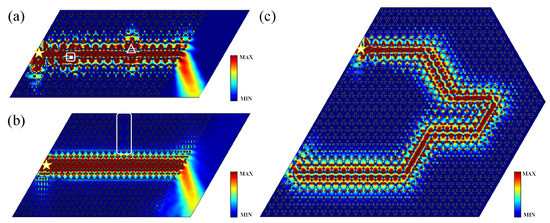
Figure A3.
Simulated propagation of a light beam through the Zigzag interface with THz. In (a), the tentagram, square, and triangle represent source, impurity, and defect, respectively. In (b), the tentagram and rectangle represent source and defect, respectively. In (c), the tentagram represents source.
Figure A3.
Simulated propagation of a light beam through the Zigzag interface with THz. In (a), the tentagram, square, and triangle represent source, impurity, and defect, respectively. In (b), the tentagram and rectangle represent source and defect, respectively. In (c), the tentagram represents source.
References
- Rycerz, A.; Tworzydło, J.; Beenakker, C.W.J. Valley filter and valley valve in graphene. Nat. Phys. 2007, 3, 172–175. [Google Scholar] [CrossRef] [Green Version]
- Xiao, D.; Yao, W.; Niu, Q. Valley-contrasting physics in graphene: Magnetic moment and topological transport. Phys. Rev. Lett. 2007, 99, 236809. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Garcia-Pomar, J.L.; Cortijo, A.; Nieto-Vesperinas, M. Fully valley-polarized electron beams in graphene. Phys. Rev. Lett. 2008, 100, 236801. [Google Scholar] [CrossRef] [PubMed]
- Hafezi, M.; Demler, E.A.; Lukin, M.D.; Taylor, J.M. Robust optical delay lines with topological protection. Nat. Phys. 2011, 7, 907–912. [Google Scholar] [CrossRef]
- Lai, K.; Ma, T.; Bo, X.; Anlage, S.; Shvets, G. Experimental realization of a reflections-free compact delay line based on a photonic topological insulator. Sci. Rep. 2016, 6, 28453. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.W.; Tian, Y.; Cheng, Y.; Wei, Q.; Liu, X.J.; Christensen, J. Topological acoustic delay line. Phys. Rev. Appl. 2018, 9, 034032. [Google Scholar] [CrossRef] [Green Version]
- Kang, Y.H.; Ni, X.; Cheng, X.J.; Khanikaev, A.B.; Genack, A.Z. Pseudo-spin–valley coupled edge states in a photonic topological insulator. Nat. Commun. 2018, 9, 3029. [Google Scholar] [CrossRef] [Green Version]
- Haldane, F.D.M.; Raghu, S. Possible realization of directional optical waveguides in photonic crystals with broken time-reversal symmetry. Phys. Rev. Lett. 2008, 100, 013904. [Google Scholar] [CrossRef] [Green Version]
- Lu, L.; Joannopoulos, J.D.; Soljačić, M. Topological photonics. Nat. Photonics 2014, 8, 821–829. [Google Scholar] [CrossRef] [Green Version]
- Khanikaev, A.B.; Fleury, R.; Mousavi, S.H.; Alu, A. Topologically robust sound propagation in an angular-momentum-biased graphene-like resonator lattice. Nat. Commun. 2015, 6, 8260. [Google Scholar] [CrossRef]
- Wang, P.; Lu, L.; Bertoldi, K. Topological phononic crystals with one-way elastic edge waves. Phys. Rev. Lett. 2015, 115, 104302. [Google Scholar] [CrossRef] [PubMed]
- Nash, L.M.; Kleckner, D.; Read, A.; Vitelli, V.; Turner, A.M.; Irvine, W.T.M. Topological mechanics of gyroscopic metamaterials. Proc. Natl. Acad. Sci. USA 2015, 112, 14495. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, Z.; Gao, F.; Shi, X.; Lin, X.; Gao, Z.; Chong, Y.; Zhang, B. Topological Acoustics. Phys. Rev. Lett. 2015, 114, 114301. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Peng, Y.; Zhu, Y.; Fan, X.; Yang, J.; Liang, B.; Zhu, X.; Wan, X.; Cheng, J. Experimental demonstration of acoustic chern insulators. Phys. Rev. Lett. 2019, 122, 014302. [Google Scholar] [CrossRef] [PubMed]
- Mousavi, S.H.; Khanikaev, A.B.; Wang, Z. Topologically protected elastic waves in phononic metamaterials. Nat. Commun. 2015, 6, 8682. [Google Scholar] [CrossRef]
- Mei, J.; Chen, Z.; Wu, Y. Pseudo-time-reversal symmetry and topological edge states in two-dimensional acoustic crystals. Sci. Rep. 2016, 6, 32752. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- He, C.; Ni, X.; Ge, H.; Sun, X.C.; Chen, Y.B.; Lu, M.H.; Liu, X.P.; Chen, Y.F. Acoustic topological insulator and robust one-way sound transport. Nat. Phys. 2016, 12, 1124–1129. [Google Scholar] [CrossRef]
- Xia, B.Z.; Liu, T.T.; Huang, G.L.; Dai, H.Q.; Jiao, J.R.; Zang, X.G.; Yu, D.J.; Zheng, S.J.; Liu, J. Topological phononic insulator with robust pseudospin-dependent transport. Phys. Rev. B 2017, 96, 094106. [Google Scholar] [CrossRef] [Green Version]
- Yves, S.; Fleury, R.; Lemoult, F.; Fink, M.; Lerosey, G. Topological acoustic polaritons: Robust sound manipulation at the subwavelength scale. New J. Phys. 2017, 19, 075003. [Google Scholar] [CrossRef]
- Miniaci, M.; Pal, R.K.; Morvan, B.; Ruzzene, M. Experimental Observation of Topologically Protected Helical Edge Modes in Patterned Elastic Plates. Phys. Rev. X 2018, 8, 031074. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Yu, K.; Wu, Y.; Zhao, R.; Liu, S. Topological spin-hall edge states of flexural wave in perforated metamaterial plates. J. Phys. D 2018, 51, 325302. [Google Scholar] [CrossRef] [Green Version]
- Yu, S.Y.; He, C.; Wang, Z.; Liu, F.K.; Sun, X.C.; Li, Z.; Lu, H.Z.; Lu, M.H.; Liu, X.P.; Chen, Y.F. Elastic pseudospin transport for integratable topological phononic circuits. Nat. Commun. 2018, 9, 3072. [Google Scholar] [CrossRef] [PubMed]
- Chaunsali, R.; Chen, C.W.; Yang, J. Subwavelength and directional control of flexural waves in zone-folding induced topological plates. Phys. Rev. B 2018, 97, 054307. [Google Scholar] [CrossRef] [Green Version]
- Lu, J.; Qiu, C.; Ye, L.; Fan, X.; Ke, M.; Zhang, F.; Liu, Z. Observation of topological valley transport of sound in sonic crystals. Nat. Phys. 2017, 13, 369–374. [Google Scholar] [CrossRef] [Green Version]
- Gao, F.; Xue, H.; Yang, Z.; Lai, K.; Yu, Y.; Lin, X.; Chong, Y.; Shvets, G.; Zhang, B. Topologically protected refraction of robust kink states in valley photonic crystals. Nat. Phys. 2018, 14, 140–144. [Google Scholar] [CrossRef]
- Makwana, M.P.; Craster, R.V. Geometrically navigating topological plate modes around gentle and sharp bends. Phys. Rev. B 2018, 98, 184105. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Chaunsali, R.; Yasuda, H.; Yu, K.; Yang, J. Dial-in topological metamaterials based on bistable stewart platform. Sci. Rep. 2018, 8, 112. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Bonello, B.; Djafari-Rouhani, B.; Pennec, Y. Topological valley, pseudospin, and pseudospin-valley protected edge states in symmetric pillared phononic crystals. Phys. Rev. B 2019, 100, 140101(R). [Google Scholar] [CrossRef] [Green Version]
- Zhu, Z.; Huang, X.; Lu, J.; Yan, M.; Li, F.; Deng, W.; Liu, Z. Negative refraction and partition in acoustic valley materials of a square lattice. Phys. Rev. Appl. 2019, 12, 024007. [Google Scholar] [CrossRef]
- Xie, B.; Liu, H.; Cheng, H.; Liu, Z.; Chen, S.; Tian, J. Acoustic topological transport and refraction in a kekulé lattice. Phys. Rev. Appl. 2019, 11, 044086. [Google Scholar] [CrossRef]
- Wang, W.; Bonello, B.; Djafari-Rouhani, B.; Pennec, Y. Polarization-dependent and valley-protected Lamb waves in asymmetric pillared phononic crystals. J. Phys. D 2019, 52, 505302. [Google Scholar] [CrossRef] [Green Version]
- Zheng, L.Y.; Achilleos, V.; Chen, Z.G.; Richoux, O.; Theocharis, G.; Wu, Y.; Mei, J.; Felix, S.; Tournat, V.; Pagneux, V. Acoustic graphene network loaded with helmholtz resonators: A first-principle modeling, dirac cones, edge and interface waves. New J. Phys. 2020, 22, 013029. [Google Scholar] [CrossRef]
- Zhang, Q.; Chen, Y.; Zhang, K.; Hu, G. Dirac degeneracy and elastic topological valley modes induced by local resonant states. Phys. Rev. B 2020, 101, 014101. [Google Scholar] [CrossRef]
- Lu, J.; Qiu, C.; Deng, W.; Huang, X.; Li, F.; Zhang, F.; Chen, S.; Liu, Z. Valley topological phases in bilayer sonic crystals. Phys. Rev. Lett. 2018, 120, 116802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xia, B.Z.; Zheng, S.J.; Liu, T.T.; Jiao, J.R.; Chen, N.; Dai, H.Q.; Yu, D.J.; Liu, J. Observation of valleylike edge states of sound at a momentum away from the high-symmetry points. Phys. Rev. B 2018, 97, 155124. [Google Scholar] [CrossRef] [Green Version]
- Lu, J.; Qiu, C.; Ke, M.; Liu, Z. Valley vortex states in sonic crystals. Phys. Rev. Lett. 2016, 116, 093901. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.; Meng, Y.; Tian, J.; Huang, Y.; Xiang, H.; Han, D.; Wen, W. Direct observation of valley-polarized topological edge states in designer surface plasmon crystals. Nat. Commun. 2017, 8, 1304. [Google Scholar] [CrossRef]
- Raj, K.P.; Massimo, R. Edge waves in plates with resonators: An elastic analogue of the quantum valley Hall effect. New J. Phys. 2017, 19, 025001. [Google Scholar]
- Miniaci, M.; Pal, R.K.; Manna, R.; Ruzzene, M. Valley-based splitting of topologically protected helical waves in elastic plates. Phys. Rev. B 2019, 100, 024304. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Jin, Y.; Wang, W.; Bonello, B.; Djafari-Rouhani, B.; Fleury, R. Robust Fano resonance in a topological mechanical beam. Phys. Rev. B 2020, 101, 024101. [Google Scholar] [CrossRef]
- Zheng, L.Y.; Christensen, J. Topological radiation engineering in hyperbolic sonic semimetals. Phys. Rev. B 2021, 103, 064307. [Google Scholar] [CrossRef]
- He, H.; Qiu, C.; Ye, L.; Cai, X.; Fan, X.; Ke, M.; Zhang, F.; Liu, Z. Topological negative refraction of surface acoustic waves in a Weyl phononic crystal. Nat. (London) 2018, 560, 61–64. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Z.; Tian, Y.; Cheng, Y.; Liu, X.; Christensen, J. Experimental verification of acoustic pseudospin multipoles in a symmetry-broken snowflakelike topological insulator. Phys. Rev. B 2017, 96, 241306(R). [Google Scholar] [CrossRef] [Green Version]
- Huang, H.; Tan, Z.; Huo, S.; Feng, L.; Chen, J.; Han, X. Topologically protected zero refraction of elastic waves in pseudospin-hall phononic crystals. Commun. Phys. 2020, 3, 46. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Tian, Y.; Wang, Y.; Gao, S.; Cheng, Y.; Liu, X.; Christensen, J. Directional acoustic antennas based on valley-hall topological insulators. Adv. Mater. 2018, 30, 1803229. [Google Scholar] [CrossRef] [Green Version]
- Ju, L.; Shi, Z.; Nair, N.; Lv, Y.; Jin, C.; Velasco, J.; Ojeda-Aristizabal, J.C.; Bechtel, H.A.; Martin, M.C.; Zettl, A.; et al. Topological valley transport at bilayer graphene. Nature 2015, 520, 650–655. [Google Scholar] [CrossRef]
- Li, J.; Wang, K.; McFaul, K.J.; Zern, Z.; Ren, Y.; Watanabe, K.; Taniguchi, T.; Qiao, Z.; Zhu, J. Gate-controlled topological conducting channels in bilayer graphene. Nat. Nanotech. 2016, 11, 1060–1065. [Google Scholar] [CrossRef]
- Li, J.; Zhang, R.X.; Yin, Z.; Zhang, J.; Watanabe, K.; Taniguchi, T.; Liu, C.; Zhu, J. A valley valve and electron beam splitter. Science 2018, 362, 1149–1152. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.Y.; Yang, Y.Z.; Li, H.Y.; Jia, H.; Luo, J.L.; Huang, J.; Wang, Z.N.; Jiang, B.; Yang, N.J.; Jin, G.J.; et al. Multichannel Topological Transport in an Acoustic Valley Hall Insulator. Phys. Rev. Appl. 2021, 15, 024019. [Google Scholar] [CrossRef]
- Chen, Y.; He, X.T.; Cheng, Y.J.; Qiu, H.Y.; Feng, L.T.; Zhang, M.; Dai, D.X.; Guo, G.C.; Dong, J.W.; Ren, X.F. Topologically Protected Valley-Dependent Quantum Photonic Circuits. Phys. Rev. Lett. 2021, 126, 230503. [Google Scholar] [CrossRef]
- Jia, D.; Ge, Y.; Xue, H.R.; Yuan, S.Q.; Sun, H.X.; Yang, Y.H.; Liu, X.J.; Zhang, B.L. Topological refraction in dual-band valley sonic crystals. Phys. Rev. B 2021, 103, 144309. [Google Scholar] [CrossRef]
- Zhang, X.J.; Liu, L.; Lu, M.H.; Chen, Y.F. Valley-Selective Topological Corner States in Sonic Crystals. Phys. Rev. Lett. 2021, 126, 156401. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).