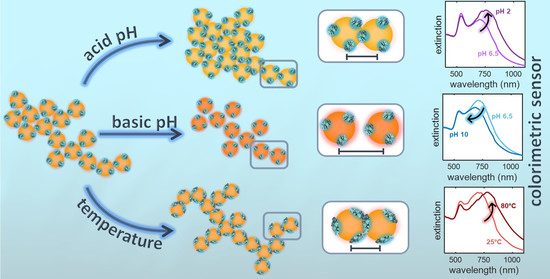
Responsivity of Fractal Nanoparticle Assemblies to Multiple Stimuli: Structural Insights on the Modulation of the Optical Properties
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Sample Preparation
2.3. Dynamic Light Scattering
2.4. Extinction Spectroscopy
2.5. Scanning Electron Microscopy
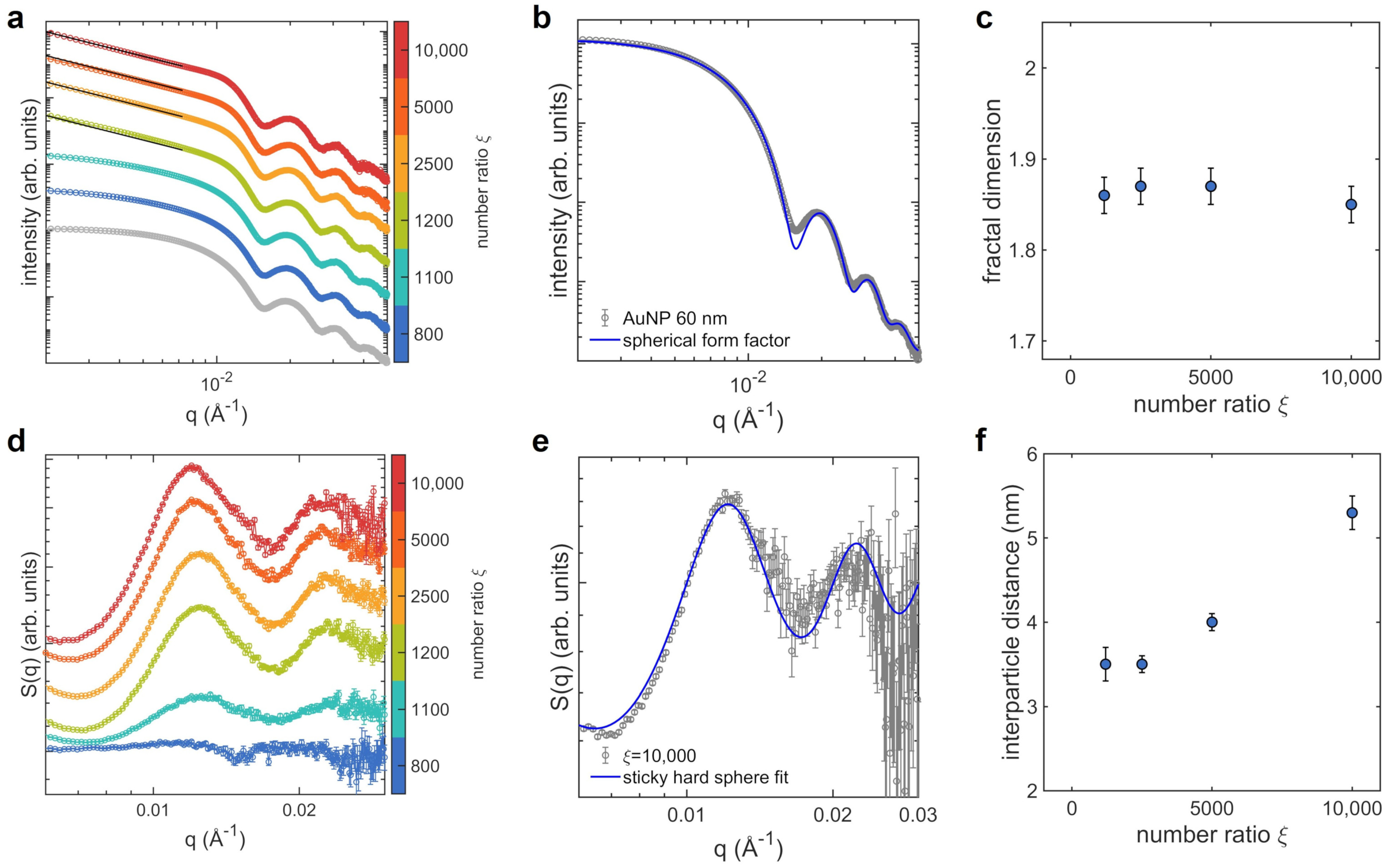
2.6. Small Angle X-ray Scattering
3. Results
3.1. Aggregates at Different Protein Concentrations
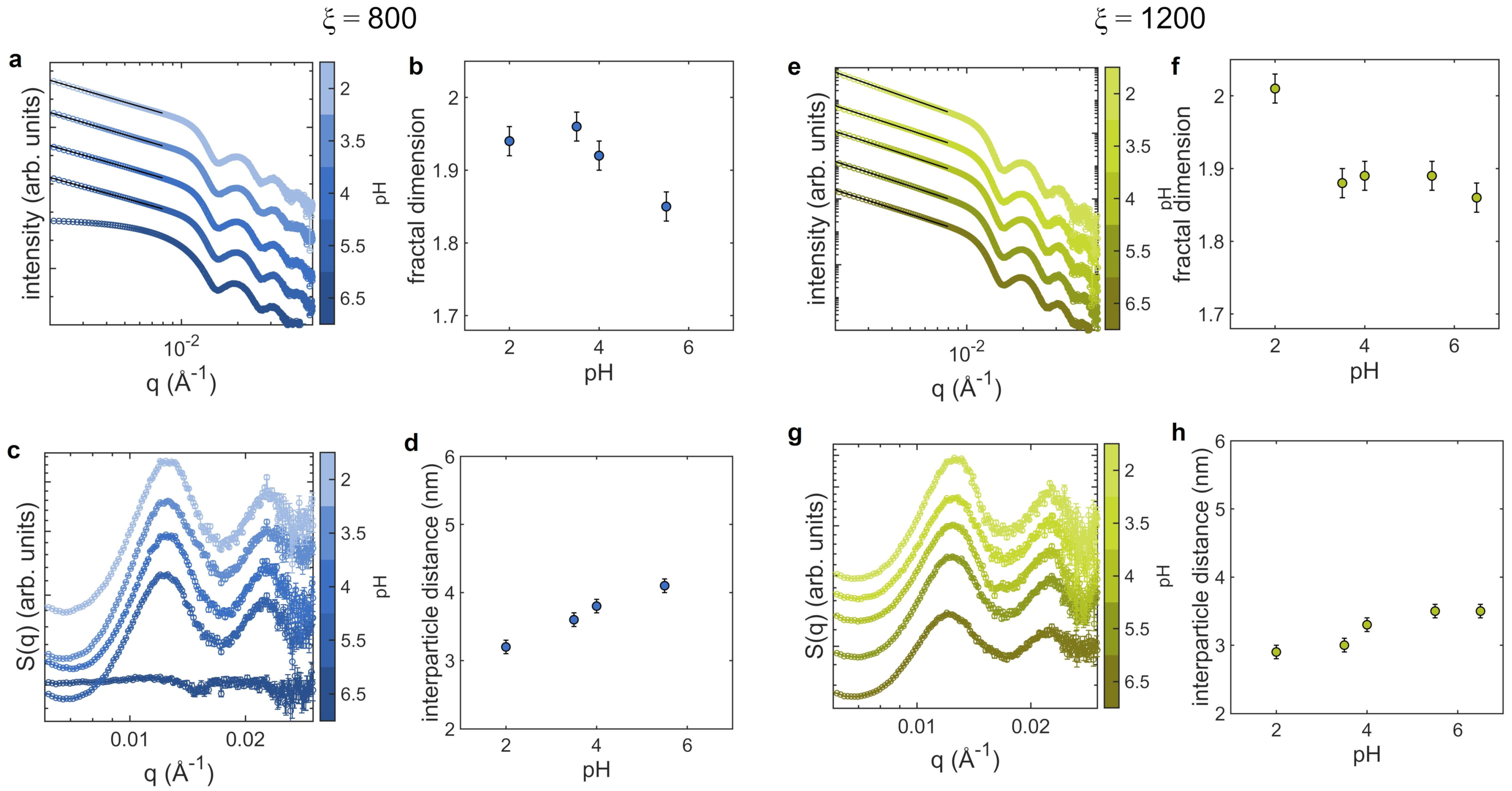
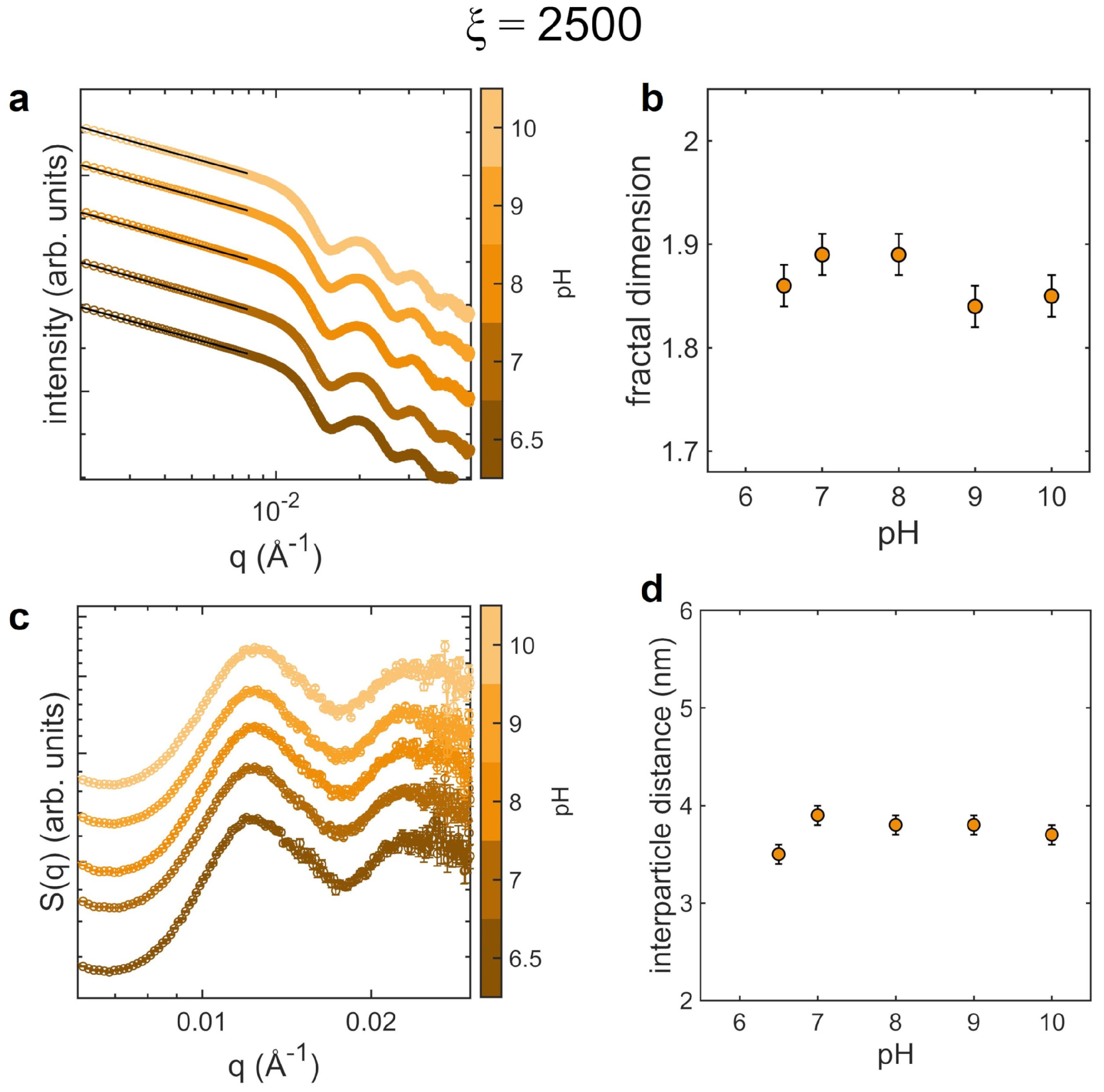
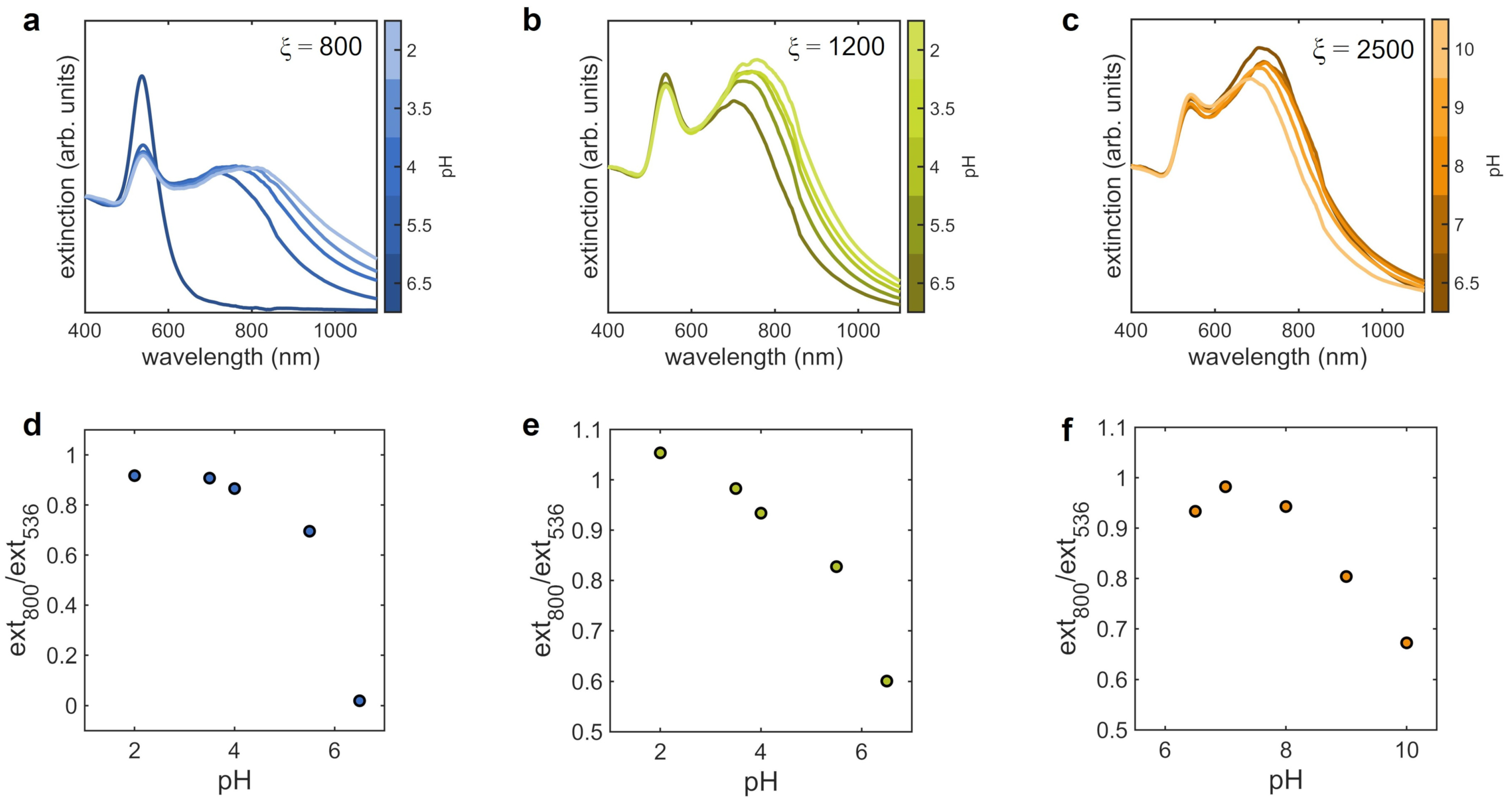
3.2. Aggregates at Different pH
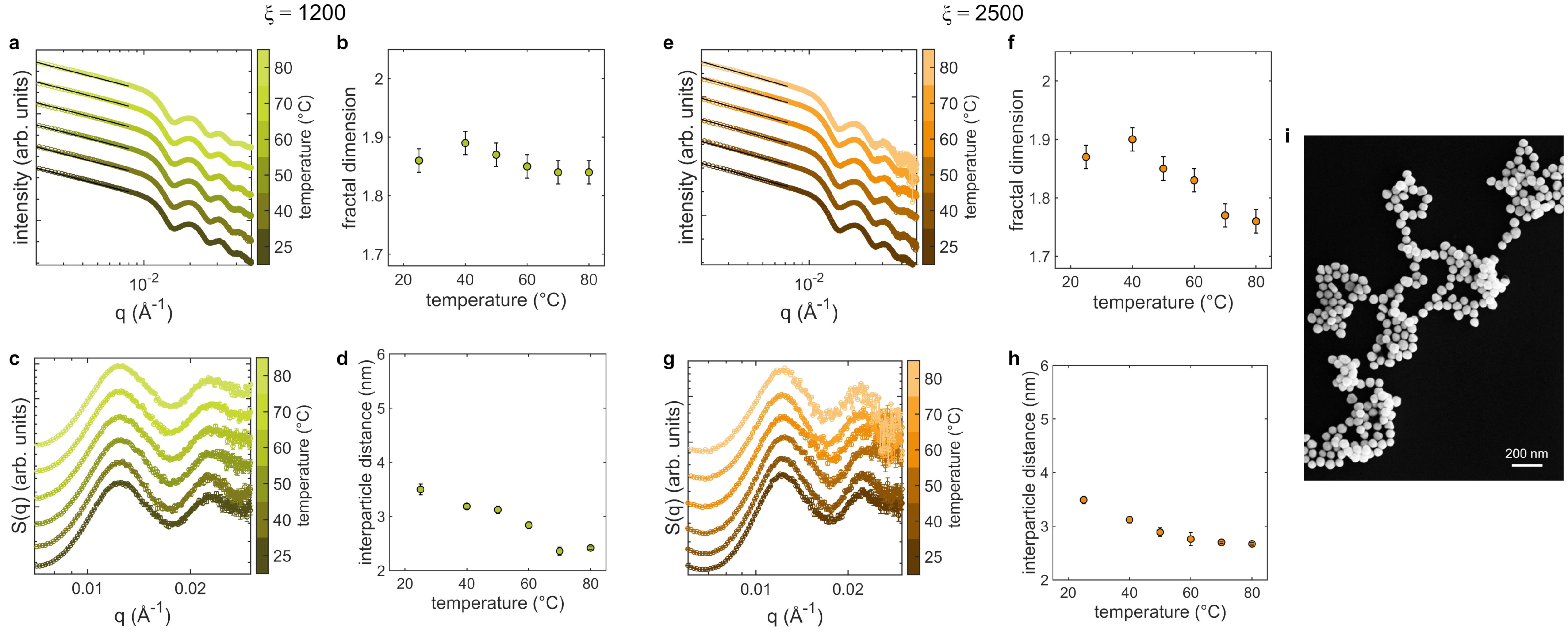
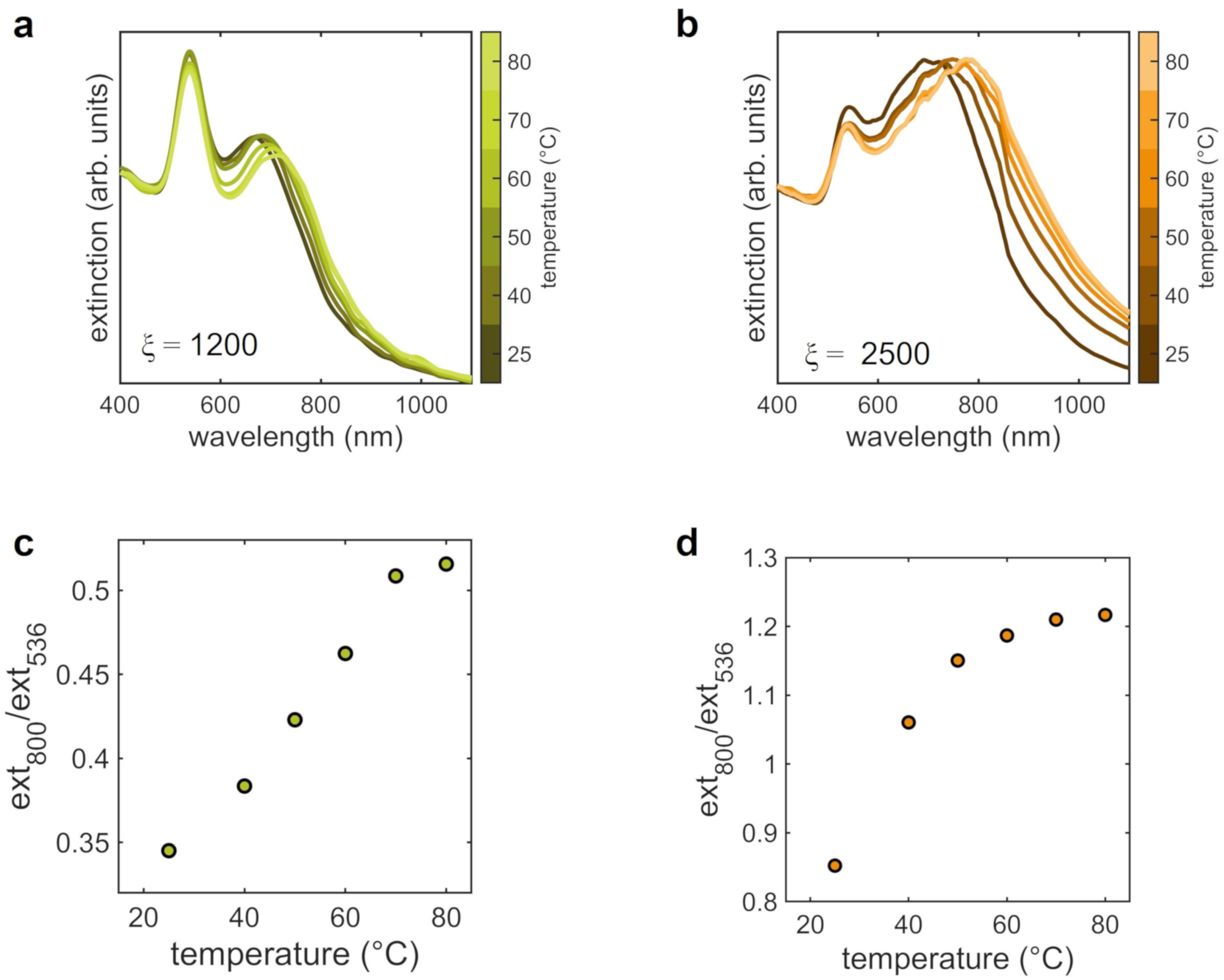
3.3. Aggregates at Different Temperatures
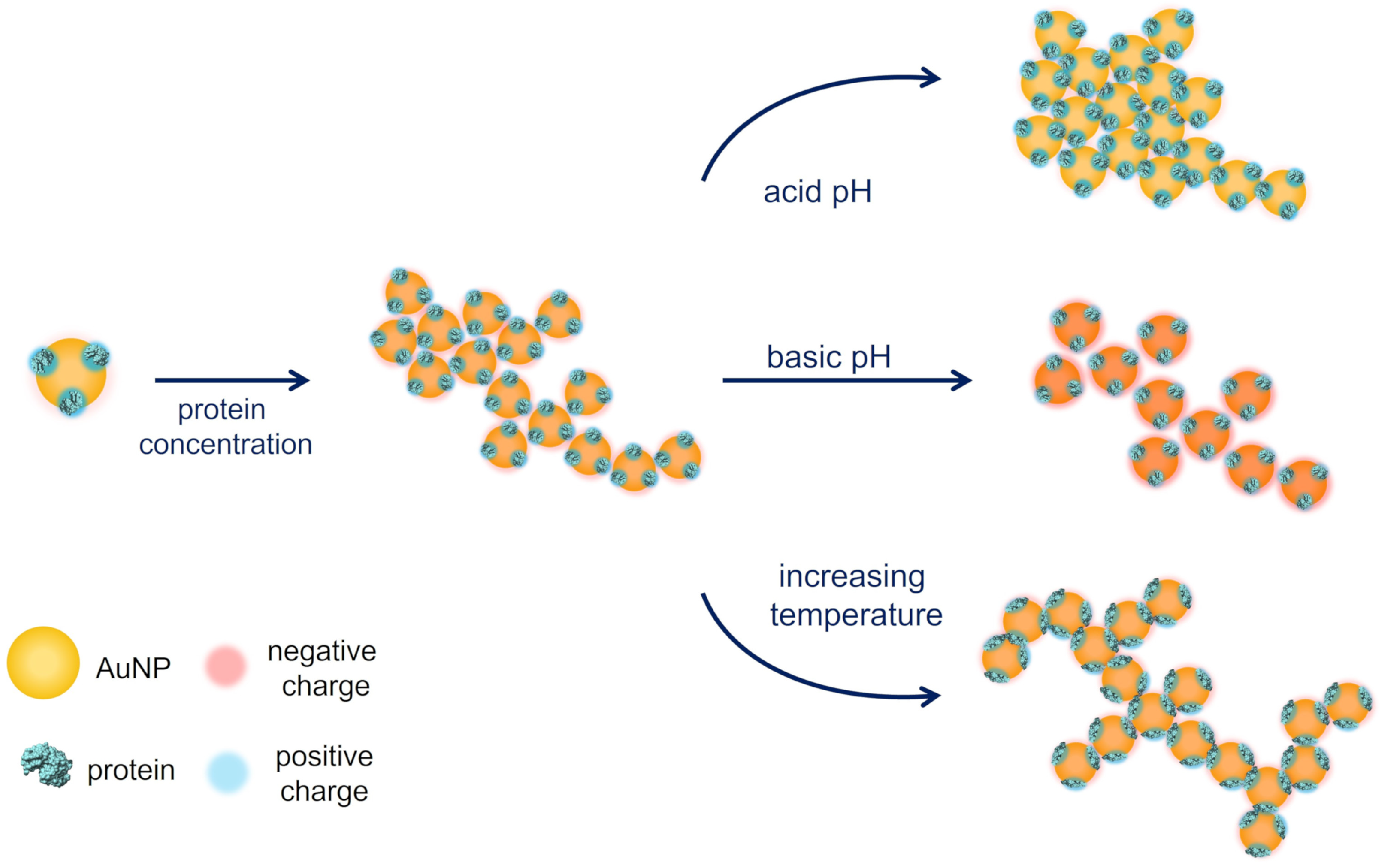
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stockman, M.I.; Kneipp, K.; Bozhevolnyi, S.I.; Saha, S.; Dutta, A.; Ndukaife, J.; Kinsey, N.; Reddy, H.; Guler, U.; Shalaev, V.M.; et al. Roadmap on plasmonics. J. Opt. 2018, 20, 43001. [Google Scholar] [CrossRef] [Green Version]
- Eustis, S.; El-Sayed, M.A. Why gold nanoparticles are more precious than pretty gold: Noble metal surface plasmon resonance and its enhancement of the radiative and nonradiative properties of nanocrystals of different shapes. Chem. Soc. Rev. 2006, 35, 209–217. [Google Scholar] [CrossRef] [PubMed]
- Kelly, K.L.; Coronado, E.; Zhao, L.L.; Schatz, G.C. The optical properties of metal nanoparticles: The influence of size, shape, and dielectric environment. J. Phys. Chem. B 2003, 107, 668–677. [Google Scholar] [CrossRef]
- Jiang, Y.; Shi, M.; Liu, Y.; Wan, S.; Cui, C.; Zhang, L.; Tan, W. Aptamer/AuNP biosensor for colorimetric profiling of exosomal proteins. Angew. Chem. Int. Ed. 2017, 56, 11916–11920. [Google Scholar] [CrossRef] [PubMed]
- Halas, N.J.; Lal, S.; Chang, W.S.; Link, S.; Nordlander, P. Plasmons in strongly coupled metallic nanostructures. Chem. Rev. 2011, 111, 3913–3961. [Google Scholar] [CrossRef]
- Oliverio, M.; Perotto, S.; Messina, G.C.; Lovato, L.; De Angelis, F. Chemical functionalization of plasmonic surface biosensors: A tutorial review on issues, strategies, and costs. ACS Appl. Mater. Interfaces 2017, 9, 29394–29411. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Wang, W.; Yin, Y. Colloidal assembly and active tuning of coupled plasmonic nanospheres. Trends Chem. 2020, 2, 593–608. [Google Scholar] [CrossRef]
- Spedalieri, C.; Szekeres, G.P.; Werner, S.; Guttmann, P.; Kneipp, J. Probing the Intracellular Bio-Nano Interface in Different Cell Lines with Gold Nanostars. Nanomaterials 2021, 11, 1183. [Google Scholar] [CrossRef]
- Domenici, F.; Fasolato, C.; Mazzi, E.; De Angelis, L.; Brasili, F.; Mura, F.; Postorino, P.; Bordi, F. Engineering microscale two-dimensional gold nanoparticle cluster arrays for advanced Raman sensing: An AFM study. Colloids Surf. A Physicochem. Eng. Asp. 2016, 498, 168–175. [Google Scholar] [CrossRef]
- Hou, S.; Zhang, A.; Su, M. Nanomaterials for biosensing applications. Nanomaterials 2016, 6, 58. [Google Scholar] [CrossRef] [Green Version]
- Gerosa, C.; Crisponi, G.; Nurchi, V.M.; Saba, L.; Cappai, R.; Cau, F.; Faa, G.; Van Eyken, P.; Scartozzi, M.; Floris, G.; et al. Gold nanoparticles: A new golden era in oncology? Pharmaceuticals 2020, 13, 192. [Google Scholar] [CrossRef] [PubMed]
- Domenici, F.; Capocefalo, A.; Brasili, F.; Bedini, A.; Giliberti, C.; Palomba, R.; Silvestri, I.; Scarpa, S.; Morrone, S.; Paradossi, G.; et al. Ultrasound delivery of Surface Enhanced InfraRed Absorption active gold-nanoprobes into fibroblast cells: A biological study via Synchrotron-based InfraRed microanalysis at single cell level. Sci. Rep. 2019, 9, 1–13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gerber, A.; Bundschuh, M.; Klingelhofer, D.; Groneberg, D.A. Gold nanoparticles: Recent aspects for human toxicology. J. Occup. Med. Toxicol. 2013, 8, 1–6. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lasagna-Reeves, C.; Gonzalez-Romero, D.; Barria, M.; Olmedo, I.; Clos, A.; Ramanujam, V.S.; Urayama, A.; Vergara, L.; Kogan, M.J.; Soto, C. Bioaccumulation and toxicity of gold nanoparticles after repeated administration in mice. Biochem. Biophys. Res. Commun. 2010, 393, 649–655. [Google Scholar] [CrossRef]
- Capocefalo, A.; Deckert-Gaudig, T.; Brasili, F.; Postorino, P.; Deckert, V. Unveiling the interaction of protein fibrils with gold nanoparticles by plasmon enhanced nano-spectroscopy. Nanoscale 2021, 13, 14469–14479. [Google Scholar] [CrossRef]
- Chen, Y.S.; Hung, Y.C.; Liau, I.; Huang, G.S. Assessment of the in vivo toxicity of gold nanoparticles. Nanoscale Res. Lett. 2009, 4, 858–864. [Google Scholar] [CrossRef] [Green Version]
- Johnson, L.; Gray, D.M.; Niezabitowska, E.; McDonald, T.O. Multi-stimuli-responsive aggregation of nanoparticles driven by the manipulation of colloidal stability. Nanoscale 2021, 13, 7879–7896. [Google Scholar] [CrossRef]
- Caprara, D.; Ripanti, F.; Capocefalo, A.; Sarra, A.; Brasili, F.; Petrillo, C.; Fasolato, C.; Postorino, P. DNA-functionalized gold nanoparticle assemblies for Surface Enhanced Raman Scattering. Colloids Surf. A Physicochem. Eng. Asp. 2020, 589, 124399. [Google Scholar] [CrossRef] [Green Version]
- Brasili, F.; Capocefalo, A.; Palmieri, D.; Capitani, F.; Chiessi, E.; Paradossi, G.; Bordi, F.; Domenici, F. Assembling patchy plasmonic nanoparticles with aggregation-dependent antibacterial activity. J. Colloid Interface Sci. 2020, 580, 419–428. [Google Scholar] [CrossRef]
- Ofir, Y.; Samanta, B.; Rotello, V.M. Polymer and biopolymer mediated self-assembly of gold nanoparticles. Chem. Soc. Rev. 2008, 37, 1814–1825. [Google Scholar] [CrossRef] [Green Version]
- Zeng, S.; Yong, K.T.; Roy, I.; Dinh, X.Q.; Yu, X.; Luan, F. A review on functionalized gold nanoparticles for biosensing applications. Plasmonics 2011, 6, 491–506. [Google Scholar] [CrossRef]
- Graczyk, A.; Pawlowska, R.; Jedrzejczyk, D.; Chworos, A. Gold nanoparticles in conjunction with nucleic acids as a modern molecular system for cellular delivery. Molecules 2020, 25, 204. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kaefer, K.; Krüger, K.; Schlapp, F.; Uzun, H.; Celiksoy, S.; Flietel, B.; Heimann, A.; Schroeder, T.; Kempski, O.; Sönnichsen, C. Implantable sensors based on gold nanoparticles for continuous long-term concentration monitoring in the body. Nano Lett. 2021, 21, 3325–3330. [Google Scholar] [CrossRef] [PubMed]
- Xing, S.; Xu, X.; Fu, P.; Xu, M.; Gao, T.; Zhang, X.; Zhao, C. Colorimetric detection of single base-pair mismatches based on the interactions of PNA and PNA/DNA complexes with unmodified gold nanoparticles. Colloids Surf. B Biointerfaces 2019, 181, 333–340. [Google Scholar] [CrossRef]
- Ma, X.; Kou, X.; Xu, Y.; Yang, D.; Miao, P. Colorimetric sensing strategy for heparin assay based on PDDA-induced aggregation of gold nanoparticles. Nanoscale Adv. 2019, 1, 486–489. [Google Scholar] [CrossRef] [Green Version]
- Höller, R.P.; Dulle, M.; Thomä, S.; Mayer, M.; Steiner, A.M.; Foörster, S.; Fery, A.; Kuttner, C.; Chanana, M. Protein-assisted assembly of modular 3D plasmonic raspberry-like core/satellite nanoclusters: Correlation of structure and optical properties. ACS Nano 2016, 10, 5740–5750. [Google Scholar] [CrossRef]
- Guinier, A.; Fournet, G.; Yudowitch, K.L. Small-Angle Scattering of X-rays; John Wiley & Sons: New York, NY, USA, 1955. [Google Scholar]
- Menon, S.; Manohar, C.; Rao, K.S. A new interpretation of the sticky hard sphere model. J. Chem. Phys. 1991, 95, 9186–9190. [Google Scholar] [CrossRef]
- Baxter, R. Percus–Yevick equation for hard spheres with surface adhesion. J. Chem. Phys. 1968, 49, 2770–2774. [Google Scholar] [CrossRef]
- Aili, D.; Gryko, P.; Sepulveda, B.; Dick, J.A.; Kirby, N.; Heenan, R.; Baltzer, L.; Liedberg, B.; Ryan, M.P.; Stevens, M.M. Polypeptide folding-mediated tuning of the optical and structural properties of gold nanoparticle assemblies. Nano Lett. 2011, 11, 5564–5573. [Google Scholar] [CrossRef]
- Doucet, M.; Cho, J.H.; Alina, G.; Attala, Z.; Bakker, J.; Bouwman, W.; Butler, P.; Campbell, K.; Cooper-Benun, T.; Durniak, C.; et al. SasView, version 5.0.4; Zenodo: Genève, Switzerland, 2021. [Google Scholar] [CrossRef]
- Loumaigne, M.; Midelet, C.; Doussineau, T.; Dugourd, P.; Antoine, R.; Stamboul, M.; Débarre, A.; Werts, M.H. Optical extinction and scattering cross sections of plasmonic nanoparticle dimers in aqueous suspension. Nanoscale 2016, 8, 6555–6570. [Google Scholar] [CrossRef]
- Esteban, R.; Taylor, R.W.; Baumberg, J.J.; Aizpurua, J. How chain plasmons govern the optical response in strongly interacting self-assembled metallic clusters of nanoparticles. Langmuir 2012, 28, 8881–8890. [Google Scholar] [CrossRef] [PubMed]
- Herrmann, L.O.; Valev, V.K.; Aizpurua, J.; Baumberg, J.J. Self-sifting of chain plasmons: The complex optics of Au nanoparticle clusters. Opt. Express 2013, 21, 32377–32385. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Japaridze, A.; Vobornik, D.; Lipiec, E.; Cerreta, A.; Szczerbinski, J.; Zenobi, R.; Dietler, G. Toward an effective control of DNA’s submolecular conformation on a surface. Macromolecules 2016, 49, 643–652. [Google Scholar] [CrossRef]
- Bushell, G.; Yan, Y.; Woodfield, D.; Raper, J.; Amal, R. On techniques for the measurement of the mass fractal dimension of aggregates. Adv. Colloid Interface Sci. 2002, 95, 1–50. [Google Scholar] [CrossRef]
- Lattuada, M.; Wu, H.; Morbidelli, M. Hydrodynamic radius of fractal clusters. J. Colloid Interface Sci. 2003, 268, 96–105. [Google Scholar] [CrossRef] [PubMed]
- Balfourier, A.; Mulens-Arias, V.; Gazeau, F.; Carn, F. Rational Design of Fractal Gold Nanosphere Assemblies with Optimized Photothermal Conversion Using a Quantitative Structure Property Relationship (QSPR) Approach. J. Phys. Chem. C 2020, 124, 8938–8948. [Google Scholar] [CrossRef]
- Wallace, G.Q.; Lagugné-Labarthet, F. Advancements in fractal plasmonics: Structures, optical properties, and applications. Analyst 2019, 144, 13–30. [Google Scholar] [CrossRef]
- Fusco, Z.; Tran-Phu, T.; Cembran, A.; Kiy, A.; Kluth, P.; Nisbet, D.; Tricoli, A. Engineering Fractal Photonic Metamaterials by Stochastic Self-Assembly of Nanoparticles. Adv. Photon. Res. 2021, 2, 2100020. [Google Scholar] [CrossRef]
- Teixeira, J. Small-angle scattering by fractal systems. J. Appl. Crystallogr. 1988, 21, 781–785. [Google Scholar] [CrossRef] [Green Version]
- Verma, A.; Srivastava, S.; Rotello, V.M. Modulation of the interparticle spacing and optical behavior of nanoparticle ensembles using a single protein spacer. Chem. Mater. 2005, 17, 6317–6322. [Google Scholar] [CrossRef]
- Piccinini, E.; Pallarola, D.; Battaglini, F.; Azzaroni, O. Self-limited self-assembly of nanoparticles into supraparticles: Towards supramolecular colloidal materials by design. Mol. Syst. Des. Eng. 2016, 1, 155–162. [Google Scholar] [CrossRef]
- Sennato, S.; Chauveau, E.; Casciardi, S.; Bordi, F.; Truzzolillo, D. The double-faced electrostatic behavior of PNIPAm microgels. Polymers 2021, 13, 1153. [Google Scholar] [CrossRef] [PubMed]
- Truzzolillo, D.; Sennato, S.; Sarti, S.; Casciardi, S.; Bazzoni, C.; Bordi, F. Overcharging and reentrant condensation of thermoresponsive ionic microgels. Soft Matter 2018, 14, 4110–4125. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hierrezuelo, J.; Sadeghpour, A.; Szilagyi, I.; Vaccaro, A.; Borkovec, M. Electrostatic stabilization of charged colloidal particles with adsorbed polyelectrolytes of opposite charge. Langmuir 2010, 26, 15109–15111. [Google Scholar] [CrossRef] [PubMed]
- Bordi, F.; Sennato, S.; Truzzolillo, D. Polyelectrolyte-induced aggregation of liposomes: A new cluster phase with interesting applications. J. Phys. Condens. Matter 2009, 21, 203102. [Google Scholar] [CrossRef]
- Velegol, D.; Thwar, P.K. Analytical model for the effect of surface charge nonuniformity on colloidal interactions. Langmuir 2001, 17, 7687–7693. [Google Scholar] [CrossRef]
- Lin, M.; Lindsay, H.; Weitz, D.; Ball, R.; Klein, R.; Meakin, P. Universality in colloid aggregation. Nature 1989, 339, 360–362. [Google Scholar] [CrossRef]
- Jungblut, S.; Joswig, J.O.; Eychmüller, A. Diffusion-and reaction-limited cluster aggregation revisited. Phys. Chem. Chem. Phys. 2019, 21, 5723–5729. [Google Scholar] [CrossRef] [Green Version]
- Papagianni, M. Advances in citric acid fermentation by Aspergillus niger: Biochemical aspects, membrane transport and modeling. Biotechnol. Adv. 2007, 25, 244–263. [Google Scholar] [CrossRef]
- Kubiak-Ossowska, K.; Cwieka, M.; Kaczynska, A.; Jachimska, B.; Mulheran, P.A. Lysozyme adsorption at a silica surface using simulation and experiment: Effects of pH on protein layer structure. Phys. Chem. Chem. Phys. 2015, 17, 24070–24077. [Google Scholar] [CrossRef] [Green Version]
- Komorek, P.; Wałek, M.; Jachimska, B. Mechanism of lysozyme adsorption onto gold surface determined by quartz crystal microbalance and surface plasmon resonance. Bioelectrochemistry 2020, 135, 107582. [Google Scholar] [CrossRef] [PubMed]
- Komorek, P.; Jachimska, B.; Brand, I. Adsorption of lysozyme on gold surfaces in the presence of an external electric potential. Bioelectrochemistry 2021, 142, 107946. [Google Scholar] [CrossRef] [PubMed]
- Tang, P.; Colflesh, D.E.; Chu, B. Temperature effect on fractal structure of silica aggregates. J. Colloid Interface Sci. 1988, 126, 304–313. [Google Scholar] [CrossRef]
- Sennato, S.; Truzzolillo, D.; Bordi, F.; Cametti, C. Effect of Temperature on the Reentrant Condensation in Polyelectrolyte- Liposome Complexation. Langmuir 2008, 24, 12181–12188. [Google Scholar] [CrossRef] [Green Version]
- Czeslik, C.; Winter, R. Effect of temperature on the conformation of lysozyme adsorbed to silica particles. Phys. Chem. Chem. Phys. 2001, 3, 235–239. [Google Scholar] [CrossRef]
- Bordi, F.; Cametti, C.; Sennato, S.; Diociaiuti, M. Direct evidence of multicompartment aggregates in polyelectrolyte-charged liposome complexes. Biophys. J. 2006, 91, 1513–1520. [Google Scholar] [CrossRef] [Green Version]
- Sciortino, F.; Mossa, S.; Zaccarelli, E.; Tartaglia, P. Equilibrium cluster phases and low-density arrested disordered states: The role of short-range attraction and long-range repulsion. Phys. Rev. Lett. 2004, 93, 055701. [Google Scholar] [CrossRef] [Green Version]
- Sciortino, F.; Tartaglia, P.; Zaccarelli, E. One-dimensional cluster growth and branching gels in colloidal systems with short-range depletion attraction and screened electrostatic repulsion. J. Phys. Chem. B 2005, 109, 21942–21953. [Google Scholar] [CrossRef] [Green Version]
- Retout, M.; Mantri, Y.; Jin, Z.; Zhou, J.; Noël, G.; Donovan, B.; Yim, W.; Jokerst, J.V. Peptide-Induced Fractal Assembly of Silver Nanoparticles for Visual Detection of Disease Biomarkers. ACS Nano 2022, 16, 6165–6175. [Google Scholar] [CrossRef]
- Siddiqui, S.; Shawuti, S.; Sirajuddin; Niazi, J.H.; Qureshi, A. l-Cysteine-Mediated Self-Assembled Ag–Au Nanoparticles As Fractal Patterns with Bowling-Alley-like Hollow Arrays for Electrochemical Sensing of Dopamine. Ind. Eng. Chem. Res. 2019, 58, 8035–8043. [Google Scholar] [CrossRef]
- Liu, G.; Lu, M.; Huang, X.; Li, T.; Xu, D. Application of gold-nanoparticle colorimetric sensing to rapid food safety screening. Sensors 2018, 18, 4166. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mohseni, N.; Bahram, M.; Baheri, T. Chemical nose for discrimination of opioids based on unmodified gold nanoparticles. Sens. Actuators B Chem. 2017, 250, 509–517. [Google Scholar] [CrossRef]
- Choe, A.; Yeom, J.; Shanker, R.; Kim, M.P.; Kang, S.; Ko, H. Stretchable and wearable colorimetric patches based on thermoresponsive plasmonic microgels embedded in a hydrogel film. NPG Asia Mater. 2018, 10, 912–922. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Capocefalo, A.; Bizien, T.; Sennato, S.; Ghofraniha, N.; Bordi, F.; Brasili, F. Responsivity of Fractal Nanoparticle Assemblies to Multiple Stimuli: Structural Insights on the Modulation of the Optical Properties. Nanomaterials 2022, 12, 1529. https://doi.org/10.3390/nano12091529
Capocefalo A, Bizien T, Sennato S, Ghofraniha N, Bordi F, Brasili F. Responsivity of Fractal Nanoparticle Assemblies to Multiple Stimuli: Structural Insights on the Modulation of the Optical Properties. Nanomaterials. 2022; 12(9):1529. https://doi.org/10.3390/nano12091529
Chicago/Turabian StyleCapocefalo, Angela, Thomas Bizien, Simona Sennato, Neda Ghofraniha, Federico Bordi, and Francesco Brasili. 2022. "Responsivity of Fractal Nanoparticle Assemblies to Multiple Stimuli: Structural Insights on the Modulation of the Optical Properties" Nanomaterials 12, no. 9: 1529. https://doi.org/10.3390/nano12091529
APA StyleCapocefalo, A., Bizien, T., Sennato, S., Ghofraniha, N., Bordi, F., & Brasili, F. (2022). Responsivity of Fractal Nanoparticle Assemblies to Multiple Stimuli: Structural Insights on the Modulation of the Optical Properties. Nanomaterials, 12(9), 1529. https://doi.org/10.3390/nano12091529