Contact and Tribological Study of Micro/Nano Groove Texture on the Surface of Gas Bearing Materials Based on Nanoscale
Abstract
:1. Introduction
2. Contact Analysis
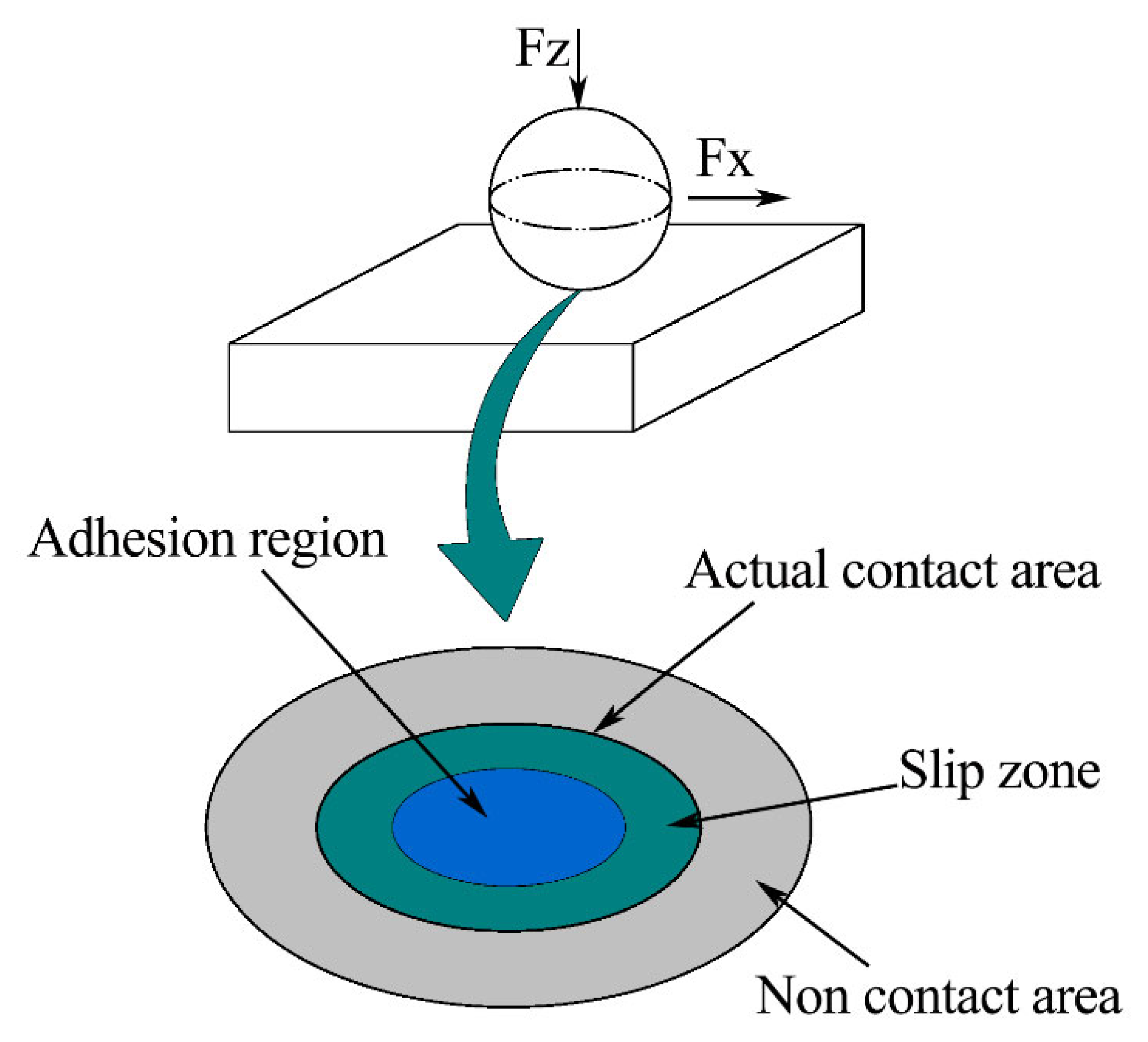
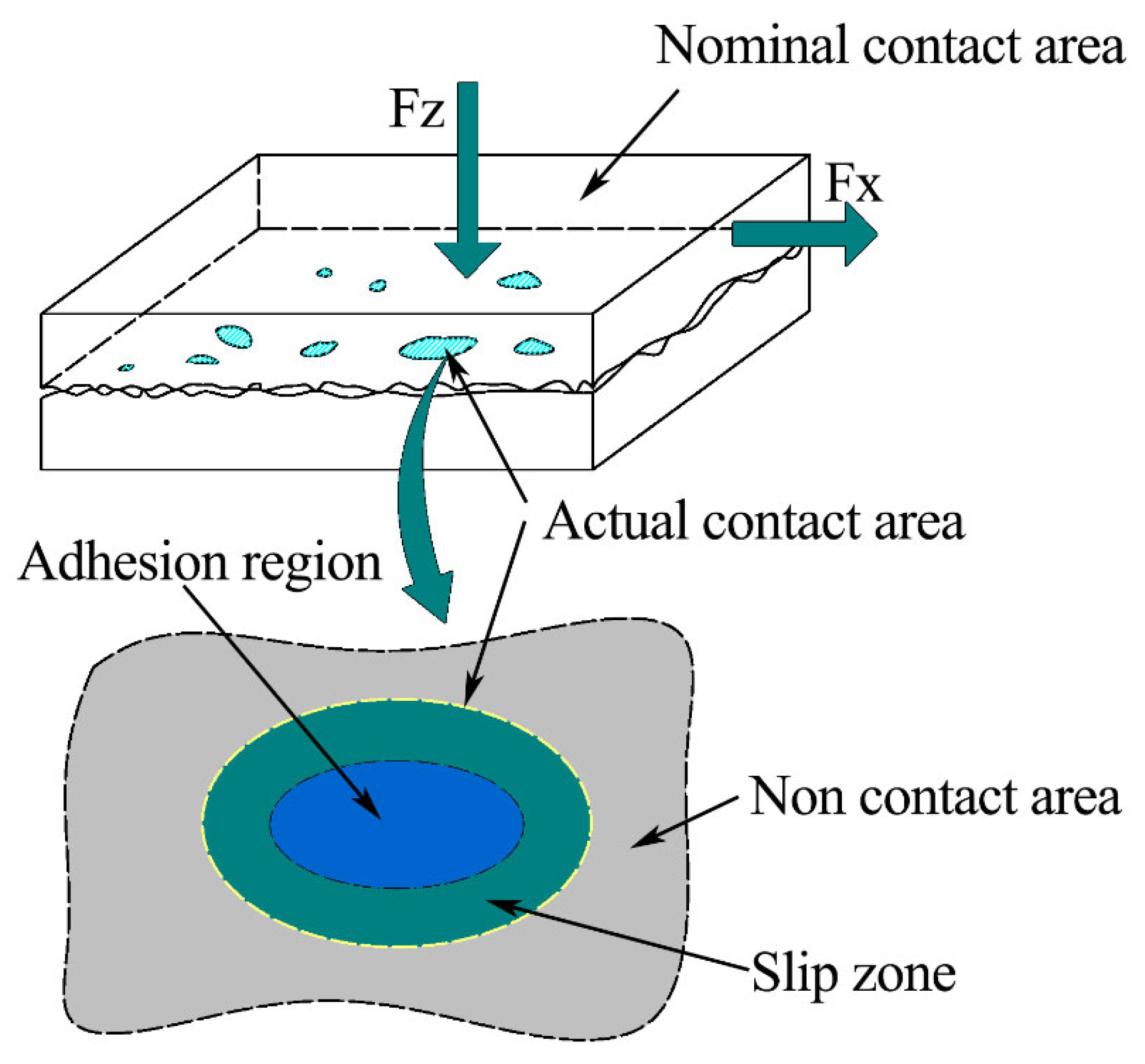
2.1. Macro Contact of Friction Pair
2.2. Micro Contact of Friction Pair
2.2.1. Micro-Convex Body Contact
2.2.2. Fractal Contact at Nanoscale
3. Materials and Methods
3.1. Micromachining Plate
3.2. Friction and Wear Test Material
3.3. Friction and Wear Calculation
4. Results and Discussion
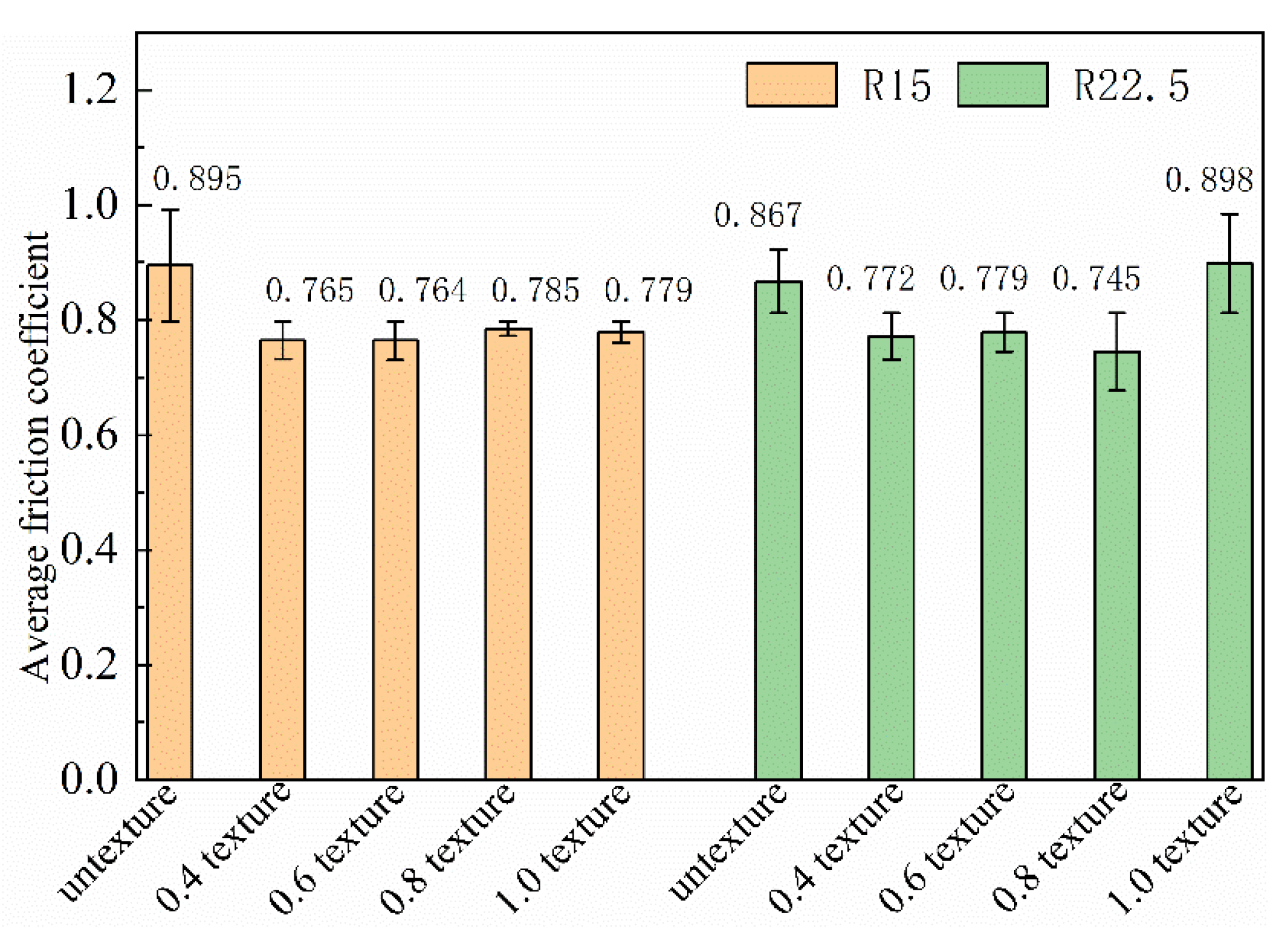
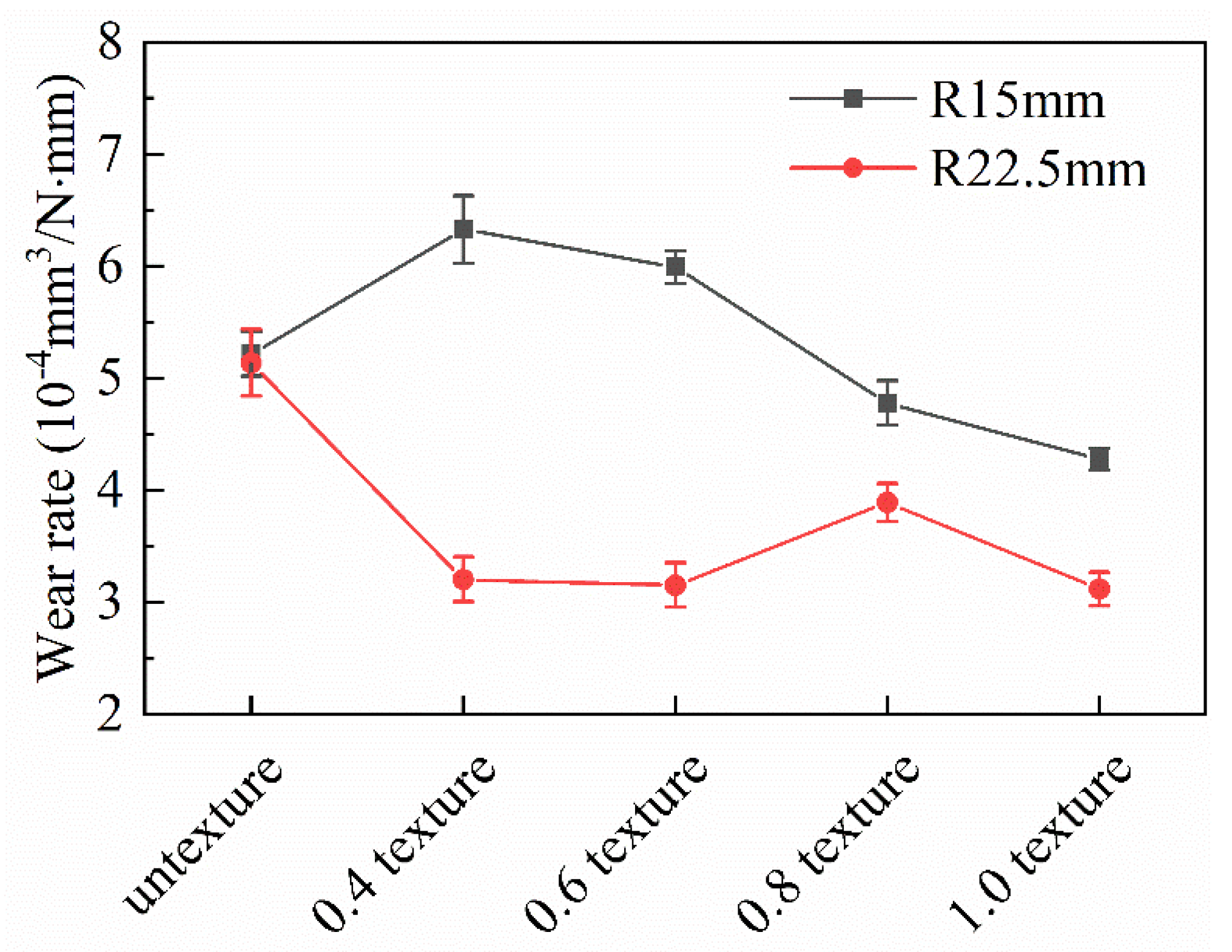
4.1. Friction Coefficient and Wear Rate
4.2. Analysis of Wear Morphology
4.3. Electron Microscope and Energy Dispersive Spectrum (EDS) Analysis of Worn Surface
5. Conclusions
- Calculating and analyzing friction and wear with the aid of artificial intelligence technology;
- Promoting surface texture technology to other widely used materials;
- Comprehensively analyzing the influence of multi-factor coupling such as speed, load and friction heat on friction reduction;
- The team will also conduct in-depth research on friction and wear prediction of material surfaces in the future.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kumar, M.; Kim, D. Static Performance of Hydrostatic Air Bump Foil Bearing. Tribol. Int. 2010, 43, 752–758. [Google Scholar] [CrossRef]
- Zhou, Q.; Hou, Y.; Chen, C. Dynamic stability experiments of compliant foil thrust bearing with viscoelastic support. Tribol. Int. 2009, 42, 662–665. [Google Scholar] [CrossRef]
- Valizadeh, Y.Y.; Ahmadi, N.; Abbaspour-sani, E. A thermal-calorimetric gas flow meter with improved isolating feature. Microsyst. Technol. 2017, 23, 1927–1936. [Google Scholar] [CrossRef]
- Choudhury, R.; Das, U.J.; Ceruti, A.; Piancastelli, L.; Frizziero, L.; Zanuccoli, G.; Daidzic, N.E.; Rocchi, I.; Casano, G.; Piva, S.; et al. Visco-elastic effects on the three dimensional hydrodynamic flow past a vertical porous plate. Int. Inf. Eng. Technol. Assoc. 2013, 31, 1–8. [Google Scholar]
- Guo, J.; Peng, R.; Du, H.; Shen, Y.; Li, Y.; Li, J.; Dong, G. The Application of Nano-MoS2 Quantum Dots as Liquid Lubricant Additive for Tribological Behavior Improvement. Nanomaterials 2020, 10, 200. [Google Scholar] [CrossRef] [Green Version]
- Zhao, J.; He, Y.; Wang, Y.; Wang, W.; Yan, L.; Luo, J. An investigation on the tribological properties of multilayer graphene and MoS 2 nanosheets as additives used in hydraulic applications. Tribol. Int. 2016, 97, 14–20. [Google Scholar] [CrossRef]
- Zhang, X.; Luster, B.; Church, A.; Muratore, C.; Voevodin, A.A.; Kohli, P.; Aouadi, S.; Talapatra, S. Carbon nanotube—MoS2 composites as solid lubricants. ACS Appl. Mater. Interfaces 2009, 1, 735–739. [Google Scholar] [CrossRef]
- Rabaso, P.; Ville, F.; Dassenoy, F.; Diaby, M.; Afanasiev, P.; Cavoret, J.; Vacher, B.; Le Mogne, T. Boundary lubrication: Influence of the size and structure of inorganic fullerene-like MoS 2 nanoparticles on friction and wear reduction. Wear 2014, 320, 161–178. [Google Scholar] [CrossRef]
- Pershin, V.; Ovchinnikov, K.; Alsilo, A.; Stolyarov, R.; Memetov, N. Development of Environmentally Safe Lubricants Modified by Grapheme. Nanotechnol. Russ. 2018, 13, 344–348. [Google Scholar] [CrossRef]
- Nagarajan, T.; Khalid, M.; Sridewi, N.; Jagadish, P.; Walvekar, R. Microwave Synthesis of Molybdenum Disulfide Nanoparticles Using Response Surface Methodology for Tribological Application. Nanomaterials 2022, 12, 3369. [Google Scholar] [CrossRef]
- Kumar, V.G.B.; Pramod, R.; Reddy, H.K.R.; Ramu, P.; Kumar, K.B.; Madhukar, P.; Chavali, M.; Mohammad, F.; Khiste, S.K. Investigation of the Tribological Characteristics of Aluminum 6061-Reinforced Titanium Carbide Metal Matrix Composites. Nanomaterials 2021, 11, 3039. [Google Scholar] [CrossRef]
- Lu, C.; Shi, P.; Yang, J.; Jia, J.; Xie, E.; Sun, Y. Effects of surface texturing on the tribological behaviors of PEO/PTFE coating on aluminum alloy for heavy-load and long-performance applications. J. Mater. Res. Technol. 2020, 9, 12149–12156. [Google Scholar] [CrossRef]
- Arenas, M.A.; Ahuir-Torres, J.I.; García, I.; Carvajal, H. Tribological behaviour of laser textured Ti6Al4V alloy coated with MoS2 and graphene. Tribol. Int. 2018, 128, 240–247. [Google Scholar] [CrossRef]
- Xiong, D.S.; Qin, Y.K.; Li, J.L.; Wan, Y.; Tyagi, R. Tribological properties of PTFE/laser surface textured stainless steel under starved oil lubrication. Tribol. Int. 2015, 82, 305–310. [Google Scholar] [CrossRef]
- Li, J.; Liu, S.; Yu, A.; Xiang, S. Effect of laser surface texture on CuSn6 bronze sliding against PTFE material under dry friction. Tribol. Int. 2018, 118, 37–45. [Google Scholar] [CrossRef]
- Saeidi, F.; Meylan, B.; Hoffmann, P.; Wasmer, K. Effect of surface texturing on cast iron reciprocating against steel under starved lubrication conditions: A parametric study. Wear 2016, 348, 17–26. [Google Scholar] [CrossRef] [Green Version]
- Cunha, A.; Elie, A.-M.; Plawinski, L.; Serro, A.P.; Botelho, R.; Almeida, A.; Urdaci, M.; Durrieu, M.; Vilar, R. Femtosecond laser surface texturing of titanium as a method to reduce the adhesion of Staphylococcus aureus and biofilm formation. Appl. Surf. Sci. 2016, 360, 485–493. [Google Scholar] [CrossRef]
- Basset, S.; Heisbourg, G.; Pascale, A.; Benayoun, S.; Valette, S. Effect of Texturing Environment on Wetting of Biomimetic Superhydrophobic Surfaces Designed by Femtosecond Laser Texturing. Nanomaterials 2022, 12, 3099. [Google Scholar] [CrossRef] [PubMed]
- Wood, M.J.; Servio, P.; Kietzig, A.-M. The Tuning of LIPSS Wettability during Laser Machining and through Post-Processing. Nanomaterials 2021, 11, 973. [Google Scholar] [CrossRef]
- Yu, H.; Huang, W.; Wang, X. Dimple patterns design for different circumstances. Lubr. Sci. 2013, 25, 67–78. [Google Scholar] [CrossRef]
- Tang, W.; Zhou, Y.; Zhu, H.; Yang, H. The effect of surface texturing on reducing the friction and wear of steel under lubricated sliding contact. Appl. Surf. Sci. 2013, 273, 199–204. [Google Scholar] [CrossRef]
- Yang, L.; Ma, W.; Gao, F.; Xi, S. Effect of Groove Width on Micromachine Groove Texture Tribology Characteristics of 0Cr17Ni7Al. Coatings 2022, 12, 1221. [Google Scholar] [CrossRef]
- Huang, W.; Wang, X. Biomimetic design of elastomer surface pattern for friction control under wet conditions. Bioinspir. Biomim. 2013, 8, 046001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Etsion, I. State of the art in laser surface texturing. J. Tribol. Trans. ASME 2005, 127, 248–253. [Google Scholar] [CrossRef]
- SUN, J.; Huo, D.; LI, B.; Xing, K.; Wang, W.; Yang, Z. Wear performance of electric pruning scissors based on bionic Micro-structure. J. Agric. Mach. 2020, 51, 10. [Google Scholar] [CrossRef]
- Chen, S.; Qian, G.; Yang, L. Precise control of surface texture on carbon film by ion etching through filter: Optimization of texture size for improving tribological behavior. Surf. Coat. Technol. 2019, 362, 105–112. [Google Scholar] [CrossRef]
- Ahn, S.; Park, H.; Cho, J.; Park, C.; Park, J.; Lee, H.; Hong, K.; Bong, S.; Yi, J. Reactive-ion-etched glass surface with 2D periodic surface texture for application in solar cells. Optik 2021, 229, 166304. [Google Scholar] [CrossRef]
- Natsu, W.; Ikeda, T.; Kunieda, M. Generating complicated surface with electrolyte jet machining. Precis. Eng. 2007, 31, 33–39. [Google Scholar] [CrossRef]
- Kern, P.; Veh, J.; Michler, J. New developments in through-mask electrochemical micromachining of titanium. J. Micromech. Microeng. 2007, 17, 1168. [Google Scholar] [CrossRef]
- Zhang, P.; Jia, R.; Tao, K.; Jiang, S.; Dai, X.; Sun, H.; Jin, Z.; Ji, Z.; Liu, X.; Zhao, C.; et al. The influence of Ag-ion concentration on the performance of mc-Si silicon solar cells textured by metal assisted chemical etching (MACE) method. Sol. Energy Mater. Sol. Cells 2019, 200, 109983. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, Y.; Chen, W.; Wu, J.; Chen, Q.; Tang, H.; Wang, Y.; Du, X. Regulation of surface texturization through copper-assisted chemical etching for silicon solar cells. Sol. Energy 2020, 201, 461–468. [Google Scholar] [CrossRef]
- Yang, J.; Shen, H.; Jiang, Y.; Sun, L. Controllable fabrication and mechanism study of textured ultra-thin silicon wafers via one-step Cu-assisted chemical etching. Mat. Sci. Semicond. Proc. 2019, 100, 79–86. [Google Scholar] [CrossRef]
- Yang, L.; Ma, W.; Gao, F.; Xi, S. Effect of EDM and Femtosecond-Laser Groove-Texture Collision Frequency on Tribological Properties of 0Cr17Ni7Al Stainless Steel. Coatings 2022, 12, 611. [Google Scholar] [CrossRef]
- Han, J.; Zhang, F.; Van, M.B.; Vleugels, J.; Braem, A.; Castagne, S. Laser surface texturing of zirconia-based ceramics for dental applications: A review. Mater. Sci. Eng. C Mater. Biol. Appl. 2021, 123, 112034. [Google Scholar] [CrossRef]
- Meng, R.; Deng, J.; Duan, R.; Liu, Y.; Zhang, G. Modifying tribological performances of AISI 316 stainless steel surfaces by laser surface texturing and various solid lubricants. Opt. Laser Technol. 2019, 109, 401–411. [Google Scholar] [CrossRef]
- Yang, L.; Ma, W.; Gao, F.; Xi, S. Effect of Different Laser Groove Texture Collation Frequency on Tribological Properties of 0Cr17Ni7Al Stainless Steel. Materials 2022, 15, 4419. [Google Scholar] [CrossRef]
- Ping, G.; Ehmann, K.F. An Analysis of the Surface Generation Mechanics of the Elliptical Vibration Texturing Process. Int. J. Mach. Tools Manuf. 2013, 64, 85–95. [Google Scholar] [CrossRef]
- Yang, L.; Ma, W.; Gao, F.; Li, J.; Deng, M.; Liu, Z.; Ma, L.; Meng, H. Study on Tribological Properties of groove texture in surface micromachining. Tool Technol. 2021, 55, 73–76. [Google Scholar] [CrossRef]
- Muller, V.M.; Yushchenko, V.S.; Derjaguin, B.V. On the influence of molecular forces on the deformation of an elastic sphere and its sticking to a rigid plane. J. Colloid Interface Sci. 1980, 77, 91–101. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Williamson, J.B.P. Contact of nominally flat surfaces. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1966, 295, 300–319. [Google Scholar] [CrossRef]
- McCool, J.I. Predicting Microfracture in Ceramics Via a Microcontact Model. J. Tribol. 1986, 108, 380–385. [Google Scholar] [CrossRef]
- Chang, L.; Jeng, Y.R. Effects of negative skewness of surface roughness on the contact and lubrication of nominally flat metallic surfaces. Proc. Inst. Mech. Eng. 2012, 227, 559–569. [Google Scholar] [CrossRef]
- Pogačnik, A.; Kalin, M. How to determine the number of asperity peaks, their radii and their heights for engineering surfaces: A critical appraisal. Wear 2013, 300, 143–154. [Google Scholar] [CrossRef]
- Majumdar, A.; Bhushan, B. Role of Fractal Geometry in Roughness Characterization and Contact Mechanics of Surfaces. J. Tribol. 1990, 112, 205–216. [Google Scholar] [CrossRef]









| Material | Hardness | Surface Roughness | Number ofGrooves (pcs.) | Groove Width (mm) | Groove Depth (mm) | Groove Length (mm) | |
|---|---|---|---|---|---|---|---|
| Ball | 9Cr18 | 64HRC | 0.014 µm | 0 | 0 | 0 | 0 |
| untextured | 0Cr17Ni7Al | 42HRC | 0.05 µm | 0 | 0 | 0 | 0 |
| 0.4 mm texture | 0Cr17Ni7Al | 42HRC | 0.05 µm | 60 | 0.4 | 0.15 | 12 |
| 0.6 mm texture | 0Cr17Ni7Al | 42HRC | 0.05 µm | 40 | 0.6 | 0.15 | 12 |
| 0.8 mm texture | 0Cr17Ni7Al | 42HRC | 0.05 µm | 30 | 0.8 | 0.15 | 12 |
| 1.0 mm texture | 0Cr17Ni7Al | 42HRC | 0.05 µm | 24 | 1.0 | 0.15 | 12 |
| Value | Unit | |
|---|---|---|
| Spindle speed | 13000 | r/m (s) |
| Feed speed | 1000 | mm/m (F) |
| Slotting speed | 100 | % |
| Cutting speed | 100 | % |
| Cutting angle Maximum depth of each layer | 0.02 0.009 | mm mm |
| Material | S | P | Al | C | Mn | Si | Ni | Cr | |
|---|---|---|---|---|---|---|---|---|---|
| Plate | 0Cr17Ni7Al | 0.03 | 0.04 | 0.75~1.5 | 0.09 | 1.0 | 1.0 | 6.5~7.75 | 16~18 |
| Ball | 9Cr18 | 0.03 | 0.04 | - | 0.9~1.0 | 0.8 | 0.8 | 0.06 | 17~19 |
| Test Radius (mm) | Rotation Speed (r/min) | Load (N) | Time (min) | Average Friction Coefficient | Wear Rate | |
|---|---|---|---|---|---|---|
| Untextured | 15 | 60 | 10 | 20 | 0.895 | 5.219 |
| 22.5 | 40 | 10 | 20 | 0.867 | 5.140 | |
| 0.4 mm texture | 15 22.5 | 60 40 | 10 10 | 20 20 | 0.765 0.772 | 6.330 3.208 |
| 0.6 mm texture | 15 22.5 | 60 40 | 10 10 | 20 20 | 0.764 0.779 | 5.993 3.155 |
| 0.8 mm texture | 15 22.5 | 60 40 | 10 10 | 20 20 | 0.785 0.745 | 4.778 3.894 |
| 1.0 mm texture | 15 | 60 | 10 | 20 | 0.779 | 4.279 |
| 22.5 | 40 | 10 | 20 | 0.898 | 3.118 |
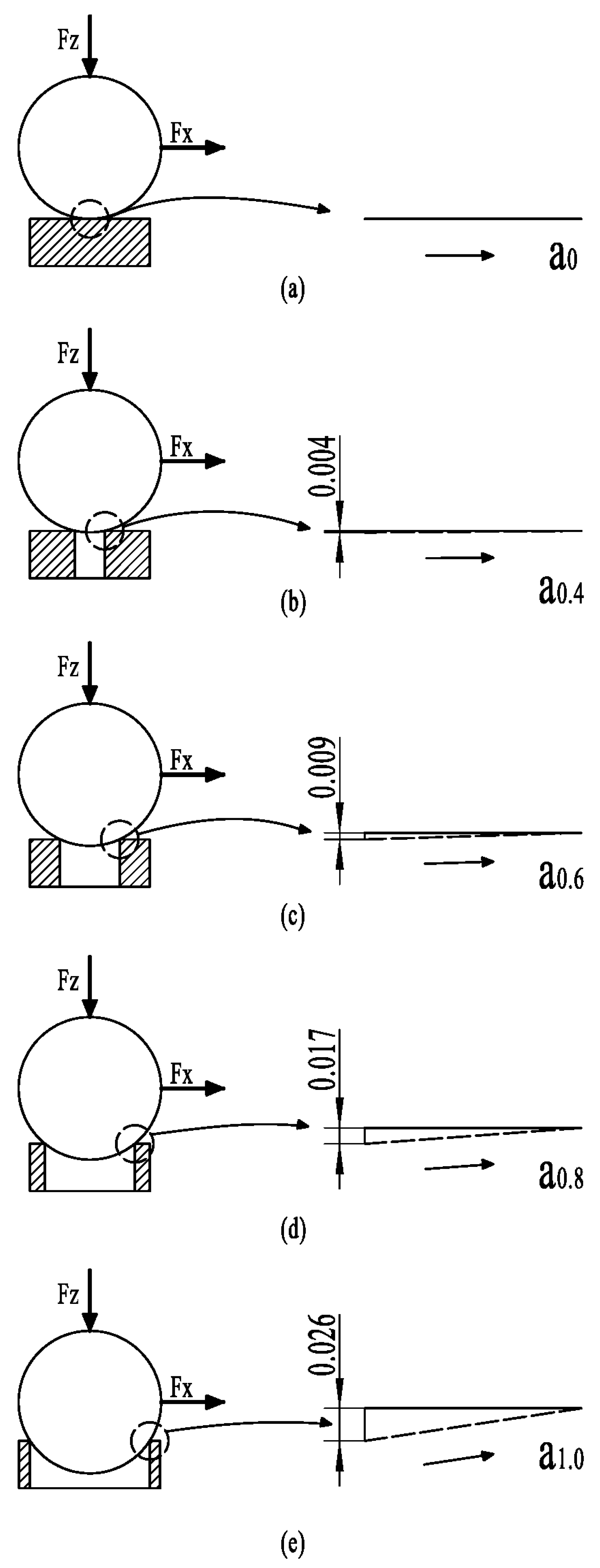
| Number of Grooves (PCs.) | Test Radius (mm) | Climbing Height per Circle (mm) | Total Friction Turns | Total Climbing Height (mm) | Total Number of Collisions (times) | |
|---|---|---|---|---|---|---|
| Untextured | 0 | 15 | 0.000 | 1200 | 0 | 0 |
| 0 | 22.5 | 0.000 | 800 | 0 | 0 | |
| 0.4 mm texture | 60 60 | 15 22.5 | 0.004 0.004 | 1200 800 | 288 192 | 72,000 48,000 |
| 0.6 mm texture | 40 40 | 15 22.5 | 0.009 0.009 | 1200 800 | 432 288 | 48,000 32,000 |
| 0.8 mm texture | 30 30 | 15 22.5 | 0.017 0.017 | 1200 800 | 612 408 | 36,000 24,000 |
| 1.0 mm texture | 24 | 15 | 0.026 | 1200 | 748.8 | 28,800 |
| 24 | 22.5 | 0.026 | 800 | 499.2 | 19,200 |
| Untextured | 0.4 mm Texture | 0.6 mm Texture | 0.8 mm Texture | 1.0 mm Texture |
|---|---|---|---|---|
| 20 μm | 34 μm | 24 μm | 19 μm | 21 μm |
| Untextured | 0.4 mm Texture | 0.6 mm Texture | 0.8 mm Texture | 1.0 mm Texture |
|---|---|---|---|---|
| 28 μm | 19 μm | 19 μm | 25 μm | 18 μm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Ma, W.; Gao, F.; Xi, S.; Ma, Z.; Ma, Z. Contact and Tribological Study of Micro/Nano Groove Texture on the Surface of Gas Bearing Materials Based on Nanoscale. Nanomaterials 2023, 13, 152. https://doi.org/10.3390/nano13010152
Yang L, Ma W, Gao F, Xi S, Ma Z, Ma Z. Contact and Tribological Study of Micro/Nano Groove Texture on the Surface of Gas Bearing Materials Based on Nanoscale. Nanomaterials. 2023; 13(1):152. https://doi.org/10.3390/nano13010152
Chicago/Turabian StyleYang, Liguang, Wensuo Ma, Fei Gao, Shiping Xi, Zhenyu Ma, and Zhenhao Ma. 2023. "Contact and Tribological Study of Micro/Nano Groove Texture on the Surface of Gas Bearing Materials Based on Nanoscale" Nanomaterials 13, no. 1: 152. https://doi.org/10.3390/nano13010152
APA StyleYang, L., Ma, W., Gao, F., Xi, S., Ma, Z., & Ma, Z. (2023). Contact and Tribological Study of Micro/Nano Groove Texture on the Surface of Gas Bearing Materials Based on Nanoscale. Nanomaterials, 13(1), 152. https://doi.org/10.3390/nano13010152







