A Topological Multichannel Add-Drop Filter Based on Gyromagnetic Photonic Crystals
Abstract
:1. Introduction
2. Materials and Methods
3. Results
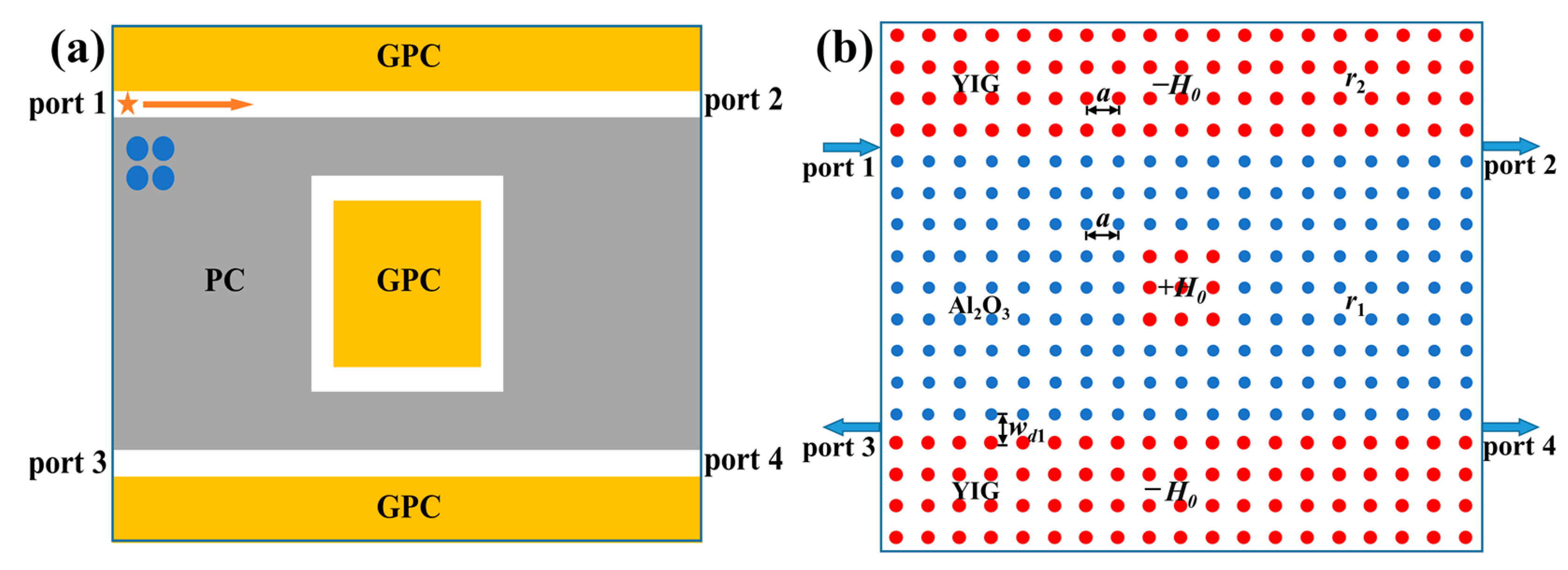
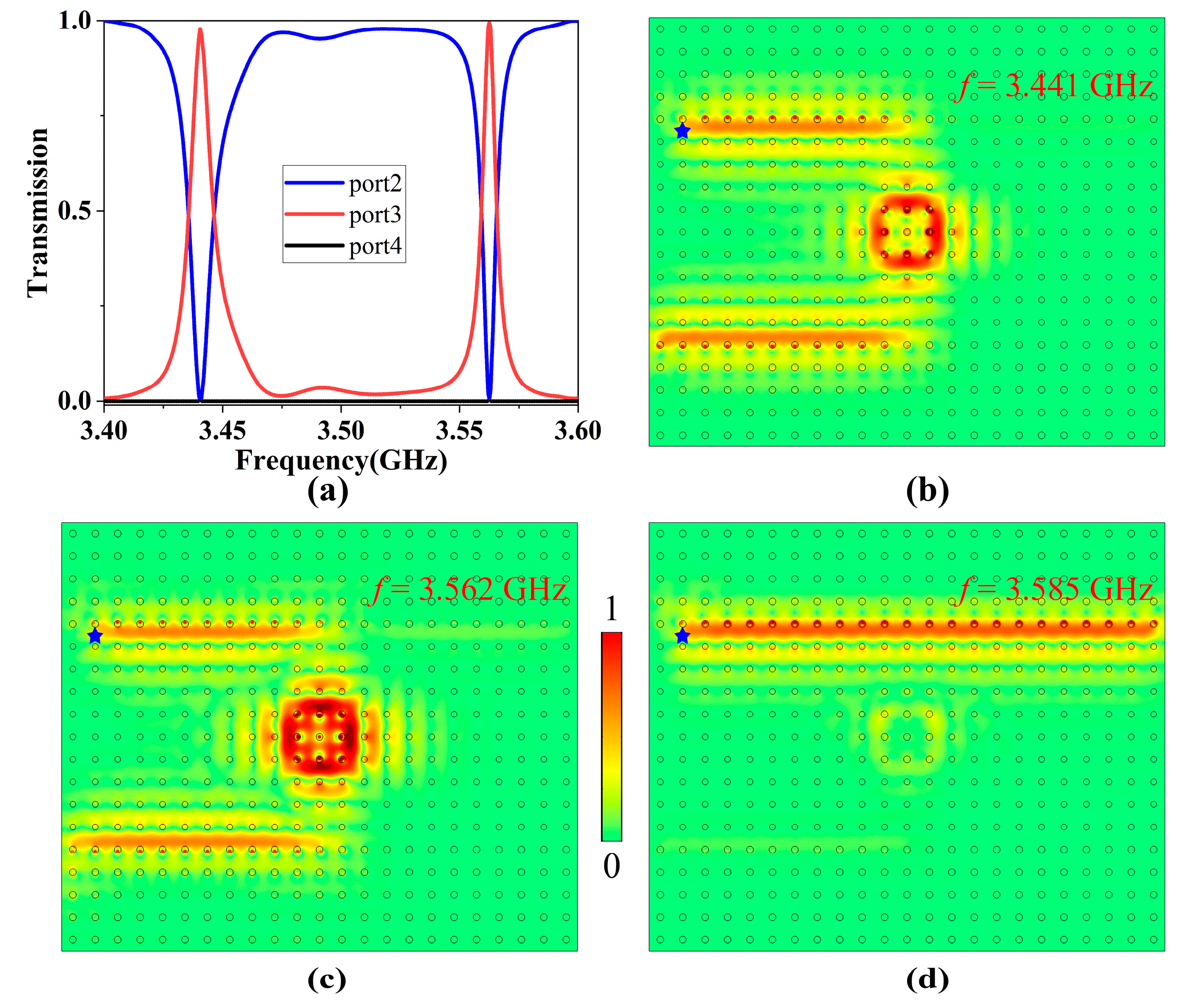
3.1. Topological Four-Port ADF
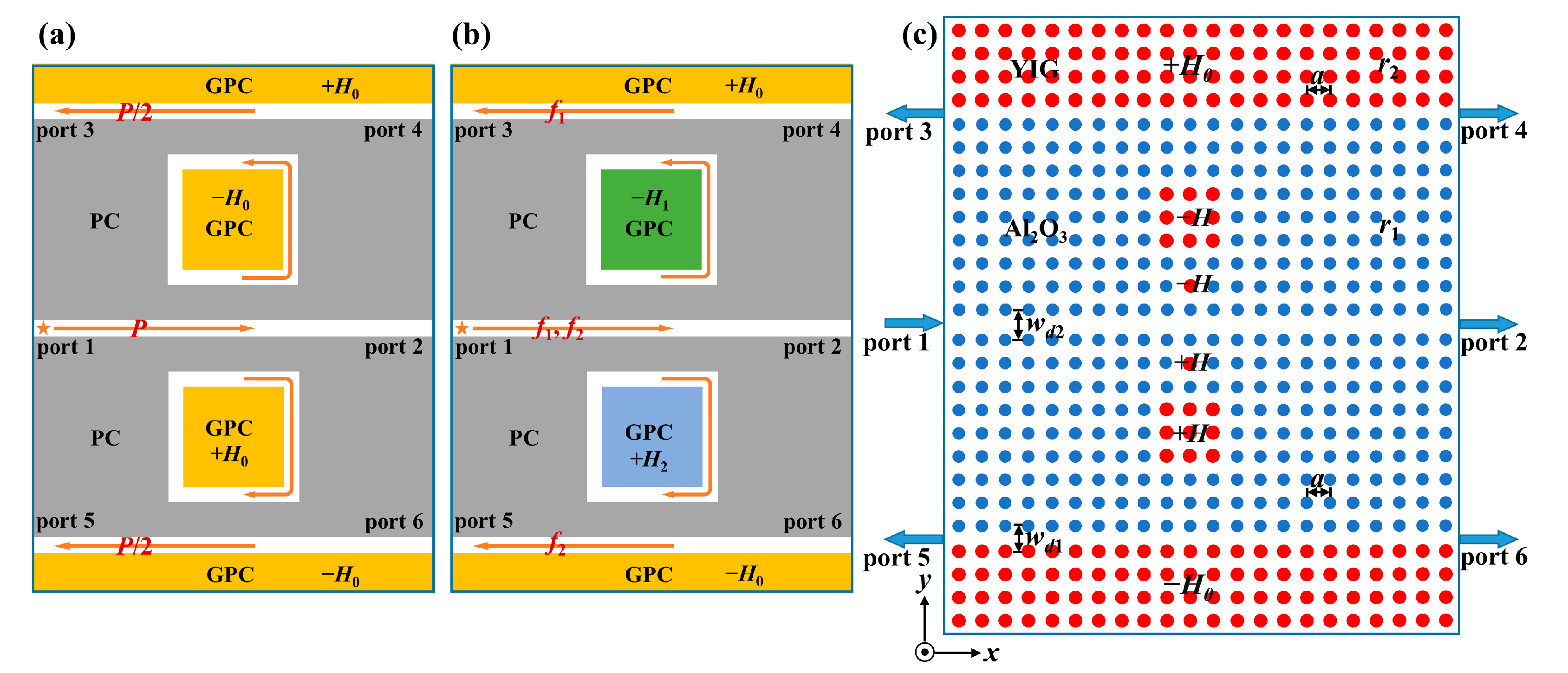
3.2. Topological Multichannel ADF
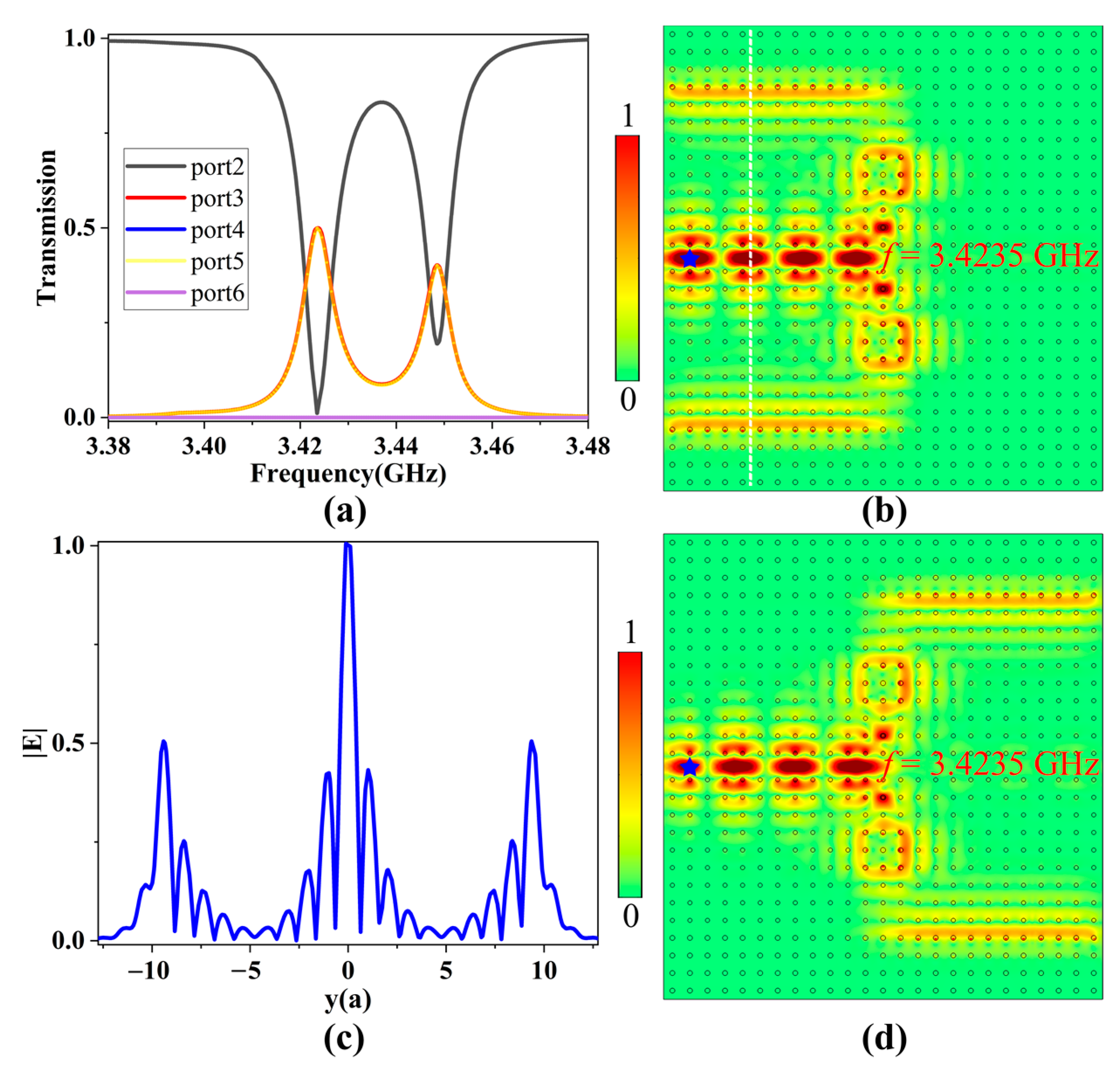
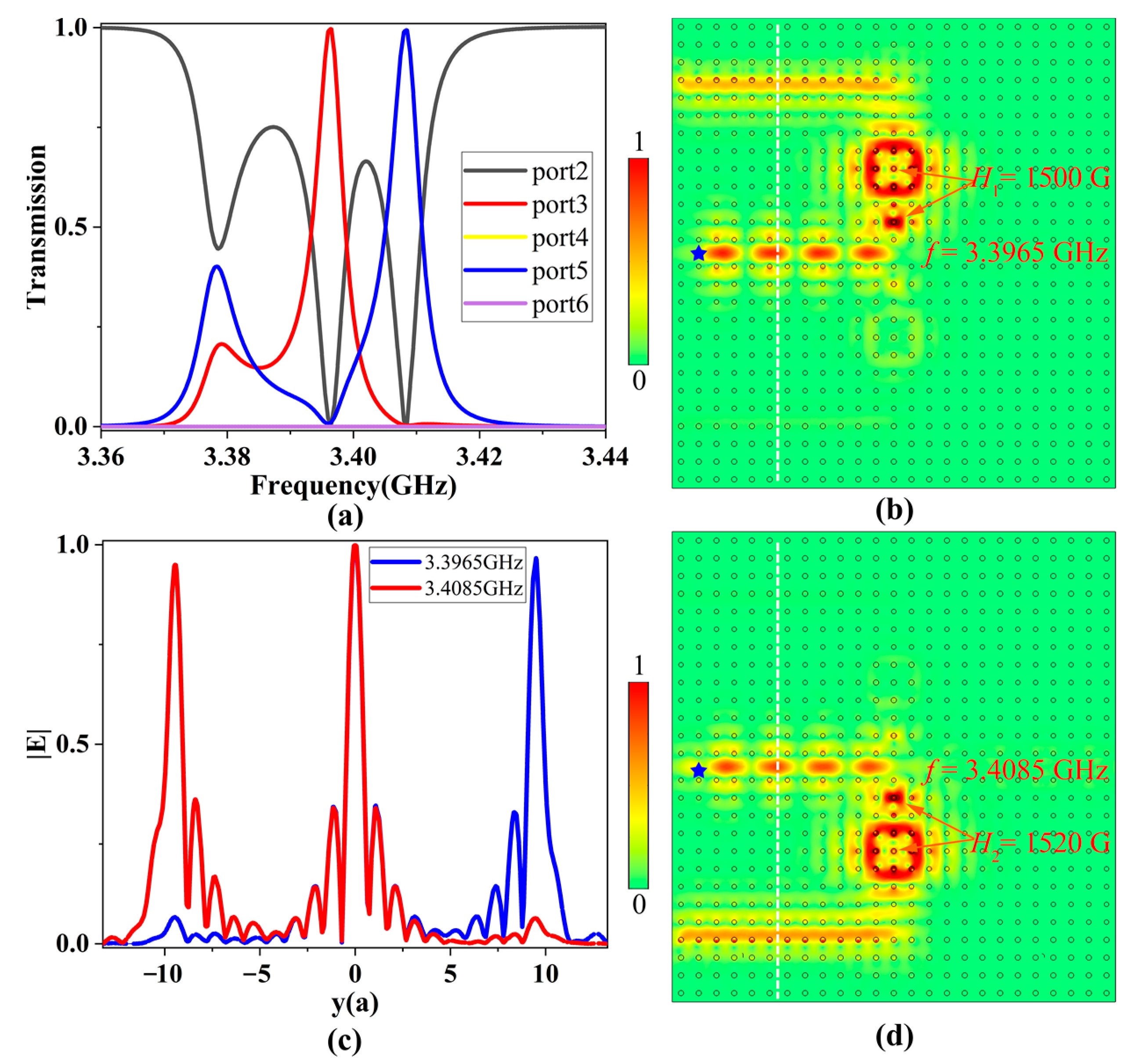
3.2.1. Power Splitting Mode
3.2.2. Frequency Separating Mode
3.2.3. Robustness Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Khanikaev, A.B.; Shvets, G. Two-dimensional topological photonics. Nat. Photonics 2017, 11, 763–773. [Google Scholar] [CrossRef]
- Wu, Y.; Li, C.; Hu, X.Y.; Ao, Y.T.; Zhao, Y.F.; Gong, Q.H. Applications of Topological Photonics in Integrated Photonic Devices. Adv. Opt. Mater. 2017, 5, 1700357. [Google Scholar] [CrossRef]
- Xie, B.Y.; Wang, H.F.; Zhu, X.Y.; Lu, M.H.; Wang, Z.D.; Chen, Y.F. Photonics meets topology. Opt. Express 2018, 26, 24531–24550. [Google Scholar] [CrossRef]
- Ozawa, T.; Price, H.M.; Amo, A.; Goldman, N.; Hafezi, M.; Lu, L.; Rechtsman, M.C.; Schuster, D.; Simon, J.; Zilberberg, O.; et al. Topological photonics. Rev. Mod. Phys. 2019, 91, 015006. [Google Scholar] [CrossRef]
- Rider, M.S.; Palmer, S.J.; Pocock, S.R.; Xiao, X.F.; Huidobro, P.A.; Giannini, V. A perspective on topological nanophotonics: Current status and future challenges. J. Appl. Phys. 2019, 125, 120901. [Google Scholar] [CrossRef]
- Tang, G.J.; He, X.T.; Shi, F.L.; Liu, J.W.; Chen, X.D.; Dong, J.W. Topological photonic crystals: Physics, designs, and applications. Laser Photonics Rev. 2022, 16, 2100300. [Google Scholar] [CrossRef]
- Iwamoto, S.; Ota, Y.; Arakawa, Y. Recent progress in topological waveguides and nanocavities in a semiconductor photonic crystal platform Invited. Opt. Mater. Express 2021, 11, 319–337. [Google Scholar] [CrossRef]
- Jiang, P.; Ma, N.; Qiao, X.Z.; Zhang, H. Recent Progress in Chiral Topological Quantum Interface. Front. Phys. 2022, 10, 845579. [Google Scholar] [CrossRef]
- Lu, Y.X.; Liu, Q.S.; Chen, Y.H.; Chen, Z.F.; Zhang, D.W.; Deng, H.Y.; Zhu, S.L.; Han, P.; Shen, N.H.; Koschny, T.; et al. Topological Transition Enabled by Surface Modification of Photonic Crystals. ACS Photonics 2021, 8, 1385–1392. [Google Scholar] [CrossRef]
- He, C.; Sun, X.C.; Liu, X.P.; Lu, M.H.; Chen, Y.; Feng, L.; Chen, Y.F. Photonic topological insulator with broken time-reversal symmetry. Proc. Natl. Acad. Sci. USA 2016, 113, 4924–4928. [Google Scholar] [CrossRef]
- Rechtsman, M.C.; Zeuner, J.M.; Plotnik, Y.; Lumer, Y.; Podolsky, D.; Dreisow, F.; Nolte, S.; Segev, M.; Szameit, A. Photonic Floquet topological insulators. Nature 2013, 496, 196–200. [Google Scholar] [CrossRef]
- He, L.; Addison, Z.; Jin, J.C.; Mele, E.J.; Johnson, S.G.; Zhen, B. Floquet Chern insulators of light. Nat. Commun. 2019, 10, 4194. [Google Scholar] [CrossRef]
- Yu, T.; Luo, R.; Wang, T.B.A.; Zhang, D.J.; Liu, W.X.; Yu, T.B.; Liao, Q.H. Enhancement of Casimir Friction between Graphene-Covered Topological Insulator. Nanomaterials 2022, 12, 1148. [Google Scholar] [CrossRef]
- Chen, J.; Liang, W.; Li, Z.-Y. Progress of topological photonic state in magneto-optical photonic crystal. Acta Opt. Sin. 2021, 41, 0823015. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, W.; Zhang, H.; Elshahat, S.; Lu, C. Magnetic-optic effect-based topological state: Realization and application. Front. Mater. 2022, 8, 816877. [Google Scholar] [CrossRef]
- Raghu, S.; Haldane, F.D.M. Analogs of quantum-Hall-effect edge states in photonic crystals. Phys. Rev. A 2008, 78, 033834. [Google Scholar] [CrossRef]
- Haldane, F.D.M.; Raghu, S. Possible realization of directional optical waveguides in photonic crystals with broken time-reversal symmetry. Phys. Rev. Lett. 2008, 100, 013904. [Google Scholar] [CrossRef]
- Wang, Z.; Chong, Y.D.; Joannopoulos, J.D.; Soljacic, M. Observation of unidirectional backscattering-immune topological electromagnetic states. Nature 2009, 461, 772–775. [Google Scholar] [CrossRef]
- Fu, J.X.; Liu, R.J.; Li, Z.Y. Robust one-way modes in gyromagnetic photonic crystal waveguides with different interfaces. Appl. Phys. Lett. 2010, 97, 041112. [Google Scholar] [CrossRef]
- Poo, Y.; Wu, R.X.; Lin, Z.F.; Yang, Y.; Chan, C.T. Experimental Realization of Self-Guiding Unidirectional Electromagnetic Edge States. Phys. Rev. Lett. 2011, 106, 093903. [Google Scholar] [CrossRef]
- Li, Z.; Wu, R.X.; Li, Q.B.; Poo, Y. Realization of self-guided unidirectional waveguides by a chain of gyromagnetic rods. Appl. Opt. 2015, 54, 1267–1272. [Google Scholar] [CrossRef]
- Li, Q.B.; Ma, H.; Wu, R.X. Achieving self-guiding unidirectional electromagnetic bulk states by breaking time-mirror symmetry. Appl. Phys. Lett. 2019, 115, 111902. [Google Scholar] [CrossRef]
- Mansha, S.; Chong, Y.D. Robust edge states in amorphous gyromagnetic photonic lattices. Phys. Rev. B 2017, 96, 121405. [Google Scholar] [CrossRef]
- Yang, B.; Zhang, H.F.; Wu, T.; Dong, R.X.; Yan, X.L.; Zhang, X.D. Topological states in amorphous magnetic photonic lattices. Phys. Rev. B 2019, 99, 45307. [Google Scholar] [CrossRef]
- Skirlo, S.A.; Lu, L.; Soljacic, M. Multimode One-Way Waveguides of Large Chern Numbers. Phys. Rev. Lett. 2014, 113, 113904. [Google Scholar] [CrossRef]
- Skirlo, S.A.; Lu, L.; Igarashi, Y.C.; Yan, Q.H.; Joannopoulos, J.; Soljacic, M. Experimental Observation of Large Chern Numbers in Photonic Crystals. Phys. Rev. Lett. 2015, 115, 253901. [Google Scholar] [CrossRef]
- He, C.; Chen, X.L.; Lu, M.H.; Li, X.F.; Wan, W.W.; Qian, X.S.; Yin, R.C.; Chen, Y.F. Tunable one-way cross-waveguide splitter based on gyromagnetic photonic crystal. Appl. Phys. Lett. 2010, 96, 111111. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Shen, L.F.; Yu, Z.H.; Zhang, X.M.; Zheng, X.D. Highly efficient photonic-crystal splitters based on one-way waveguiding. J. Opt. Soc. Am. B 2013, 30, 173–176. [Google Scholar] [CrossRef]
- Chen, J.F.; Liang, W.Y.; Li, Z.-Y. Strong coupling of topological edge states enabling group-dispersionless slow light in magneto-optical photonic crystals. Phys. Rev. B 2019, 99, 014103. [Google Scholar] [CrossRef]
- Chen, J.F.; Liang, W.Y.; Li, Z.-Y. Switchable slow light rainbow trapping and releasing in strongly coupling topological photonic systems. Photonics Res. 2019, 7, 1075–1080. [Google Scholar] [CrossRef]
- Chen, J.F.; Liang, W.Y.; Li, Z.-Y. Broadband group dispersionless topological slow-light states. Opt. Lett. 2020, 45, 4964–4967. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.T.; Xue, H.R.; Zhang, B.L. Topological slow light via coupling chiral edge modes with flatbands. Appl. Phys. Lett. 2021, 118, 071102. [Google Scholar] [CrossRef]
- Wang, Q.; Ouyang, Z.B.; Lin, M.; Liu, Q. Compact photonic crystal circulator with flat-top transmission band created by cascading magneto-optical resonance cavities. Appl. Opt. 2015, 54, 9741–9746. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhang, D.G.; Xu, S.X.; Ouyang, Z.B.; Li, J.Z. Low-loss Y-junction two-dimensional magneto-photonic crystals circulator using a ferrite cylinder. Opt. Commun. 2016, 369, 1–6. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Shen, L.F.; Zhang, X.M.; Wang, Y.G.; Yu, Z.H.; Zheng, X.D. Photonic crystal cavity with one-way rotating state and its coupling with photonic crystal waveguide. J. Appl. Phys. 2011, 110, 043106. [Google Scholar] [CrossRef]
- Fu, J.X.; Lian, J.; Liu, R.J.; Gan, L.; Li, Z.-Y. Unidirectional channel-drop filter by one-way gyromagnetic photonic crystal waveguides. Appl. Phys. Lett. 2011, 98, 211104. [Google Scholar] [CrossRef]
- Tao, K.; Xiao, J.J.; Yin, X. Nonreciprocal photonic crystal add-drop filter. Appl. Phys. Lett. 2014, 105, 211105. [Google Scholar] [CrossRef]
- Zhang, Q.; Xun, L. One-Way Rotating Photonic Crystal Ring Resonator with High Quality Factor. IEEE Photonics J. 2018, 10, 4700110. [Google Scholar] [CrossRef]
- Shi, A.Q.; Ge, R.; Liu, J.J. Side-coupled liquid sensor and its array with magneto-optical photonic crystal. J. Opt. Soc. Am. A 2020, 37, 1244–1248. [Google Scholar] [CrossRef]
- Gu, L.P.; Yuan, Q.C.; Zhao, Q.; Ji, Y.F.; Liu, Z.Y.; Fang, L.; Gan, X.T.; Zhao, J.L. A Topological Photonic Ring-Resonator for On-Chip Channel Filters. J. Light. Technol. 2021, 39, 5069–5073. [Google Scholar] [CrossRef]
- Jin, M.C.; Gao, Y.F.; Huang, G.Y.; He, Y.H.; Sun, J.P.; Song, H. Manipulation of coupling between waveguide and ring resonator in topological photonic crystals. Phys. E 2022, 136, 115013. [Google Scholar] [CrossRef]
- Seifouri, M.; Fallahi, V.; Olyaee, S. Ultra-high-Q optical filter based on photonic crystal ring resonator. Photonic Netw. Commun. 2018, 35, 225–230. [Google Scholar] [CrossRef]
- Fallahi, V.; Seifouri, M.; Mohammadi, M. A new design of optical add/drop filters and multi-channel filters based on hexagonal PhCRR for WDM systems. Photonic Netw. Commun. 2019, 37, 100–109. [Google Scholar] [CrossRef]
- Masilamani, S.; Punniakodi, S. Optical Channel Drop Filter Design Based on PCRR and Micro Cavity Resonator. Plasmonics 2021, 16, 1253–1259. [Google Scholar] [CrossRef]
- Bahari, B.; Tellez-Limon, R.; Kante, B. Topological terahertz circuits using semiconductors. Appl. Phys. Lett. 2016, 109, 143501. [Google Scholar] [CrossRef]
- Dinh, M.Q.; Le, M.T. Non-reciprocal diplexer and power combiner/divider from topological cavities with both splitting and combining functions. AIP Adv. 2022, 12, 045112. [Google Scholar] [CrossRef]
- Tang, G.C.; Huang, Y.H.; Chen, J.F.; Li, Z.-Y.; Liang, W.Y. Controllable one-way add-drop filter based on magneto-optical photonic crystal with ring resonator and microcavities. Opt. Express 2022, 30, 28762–28773. [Google Scholar] [CrossRef]
- Li, Q.; Wang, T.; Su, Y.K.; Yan, M.; Qiu, M. Coupled mode theory analysis of mode-splitting in coupled cavity system. Opt. Express 2010, 18, 8367–8382. [Google Scholar] [CrossRef]
- Kristensen, P.T.; Lasson, J.R.; Heuck, M.; Gregersen, N.; Mork, J. On the Theory of Coupled Modes in Optical Cavity-Waveguide Structures. J. Light. Technol. 2017, 35, 4247–4259. [Google Scholar] [CrossRef]
- Zhao, R.; Xie, G.D.; Chen, M.L.N.; Lan, Z.H.; Huang, Z.X.; Sha, W.E.I. First-principle calculation of Chern number in gyrotropic photonic crystals. Opt. Express 2020, 28, 4638–4649. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, H.; Yuan, H.; Zhong, J.; Lu, C. Universal numerical calculation method for the Berry curvature and Chern numbers of typical topological photonic crystals. Front. Optoelectron. 2020, 13, 73–88. [Google Scholar] [CrossRef]
- Tian, Y.; Shen, Q.; You, Y.; Shen, L.F. Robust one-way modes in photonic crystals without an external magnetic field. Opt. Mater. Express 2021, 11, 3896–3907. [Google Scholar] [CrossRef]
- Goudarzi, K.; Maragheh, H.G.; Lee, M. Calculation of the Berry curvature and Chern number of topological photonic crystals. J. Korean Phy. Soc. 2022, 81, 386–390. [Google Scholar] [CrossRef]
- Wang, H.-X.; Guo, G.-Y.; Jiang, J.-H. Band topology in classical waves: Wilson-loop approach to topological numbers and fragile topology. New J. Phys. 2019, 21, 093029. [Google Scholar] [CrossRef]
- Chen, J.F.; Qin, Q.M.; Peng, C.Q.; Li, Z.-Y. Robust topological one-way edge states in radius-fluctuated photonic Chern topological insulators. Opt. Express 2022, 30, 21621–21633. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, G.; Huang, Y.; Chen, J.; Li, Z.-Y.; Liang, W. A Topological Multichannel Add-Drop Filter Based on Gyromagnetic Photonic Crystals. Nanomaterials 2023, 13, 1711. https://doi.org/10.3390/nano13111711
Tang G, Huang Y, Chen J, Li Z-Y, Liang W. A Topological Multichannel Add-Drop Filter Based on Gyromagnetic Photonic Crystals. Nanomaterials. 2023; 13(11):1711. https://doi.org/10.3390/nano13111711
Chicago/Turabian StyleTang, Gangchao, Yuhao Huang, Jianfeng Chen, Zhi-Yuan Li, and Wenyao Liang. 2023. "A Topological Multichannel Add-Drop Filter Based on Gyromagnetic Photonic Crystals" Nanomaterials 13, no. 11: 1711. https://doi.org/10.3390/nano13111711




