Exchange Coupling Effects on the Magnetotransport Properties of Ni-Nanoparticle-Decorated Graphene
Abstract
1. Introduction
2. Materials and Methods
2.1. Electrode Patterning
2.2. Graphene Growth
2.3. Film Transfer
2.4. Photolithography and Annealing
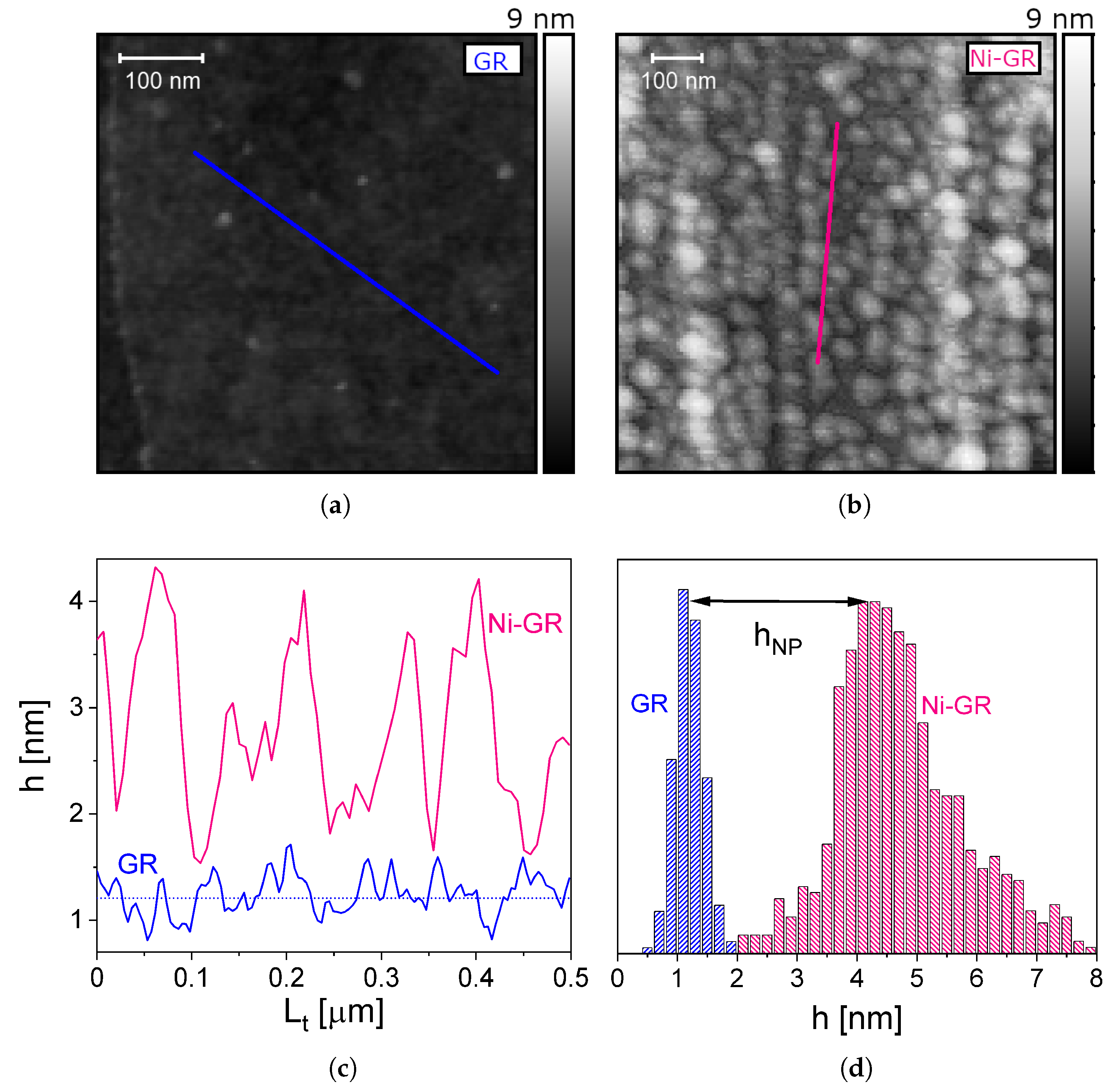
2.5. Sample Characterization
3. Theoretical Background
4. Results
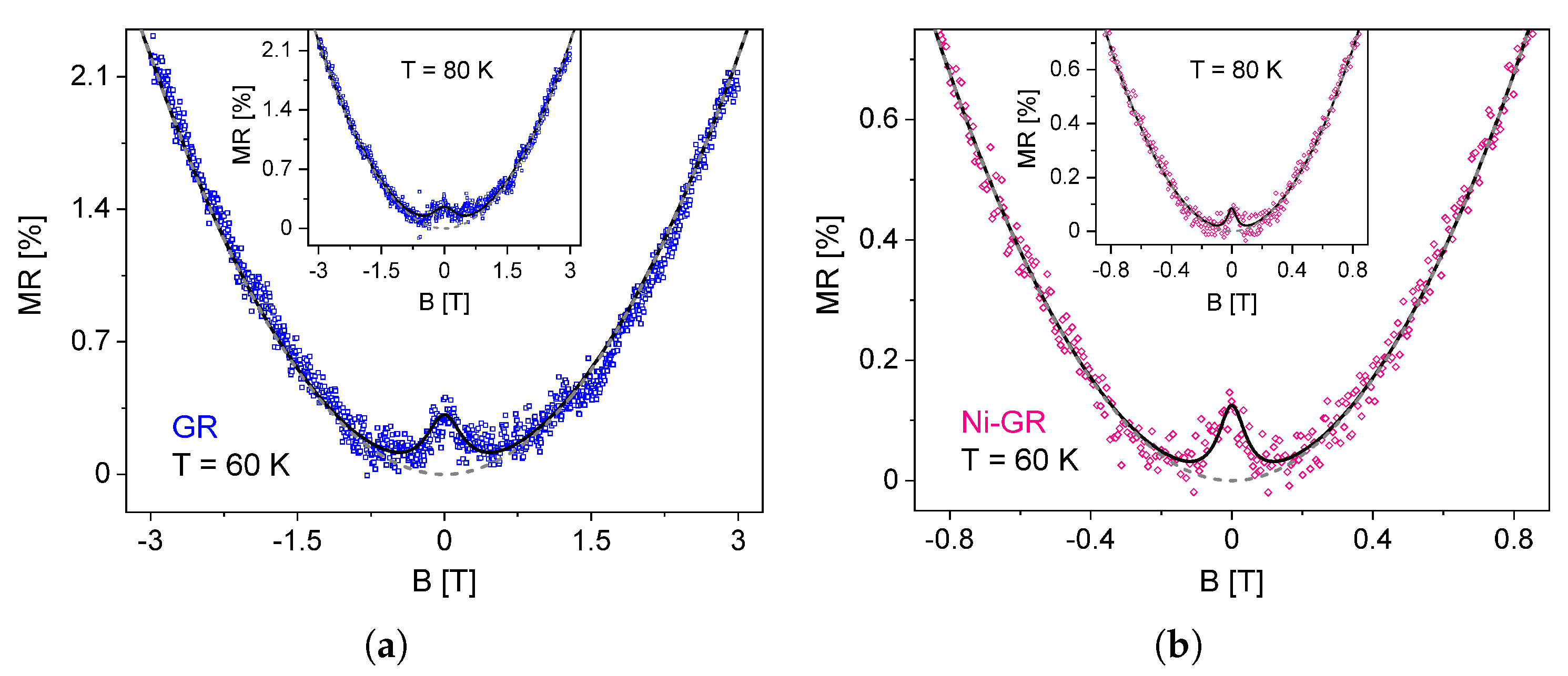
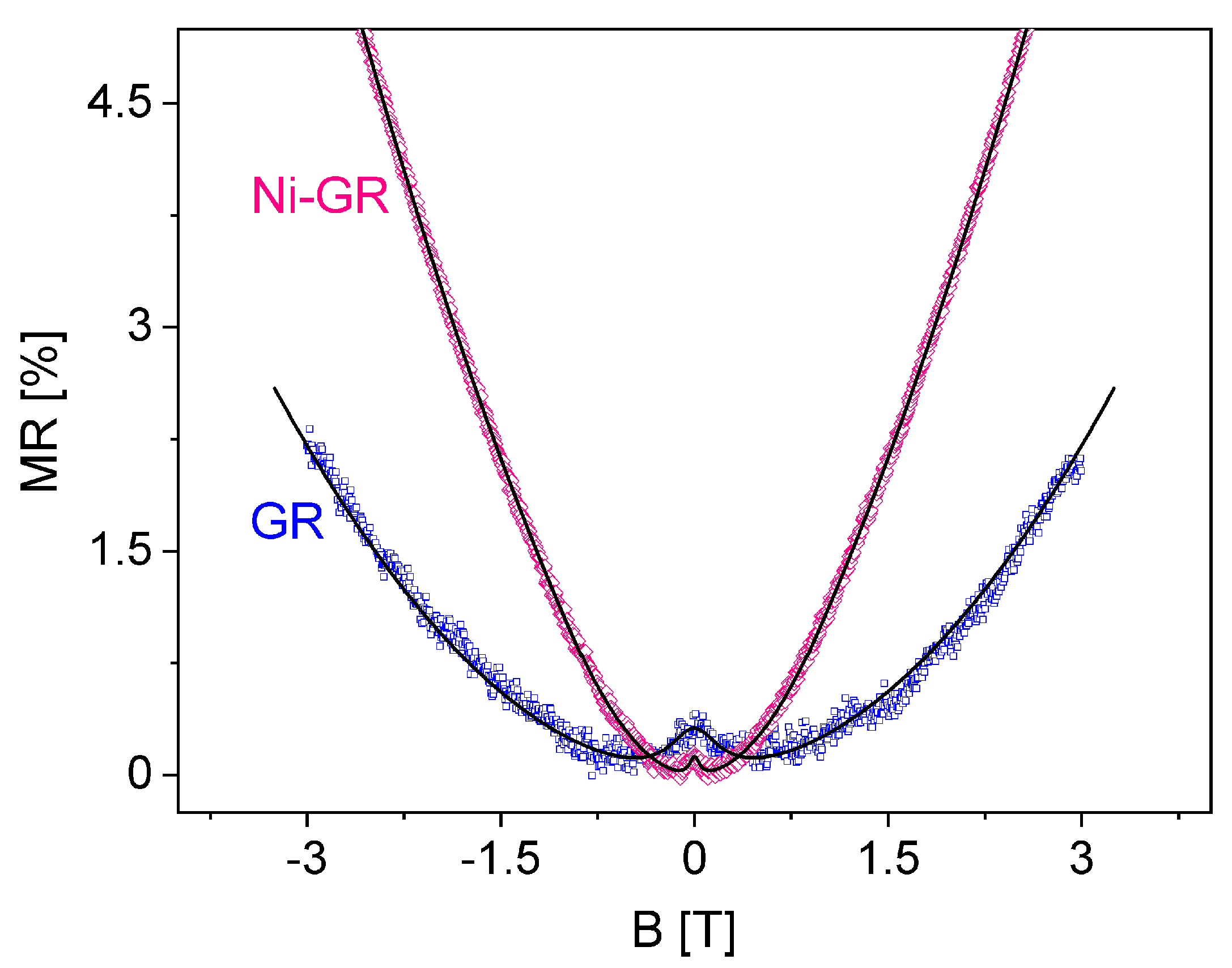
4.1. Low Fields: Weak Localization
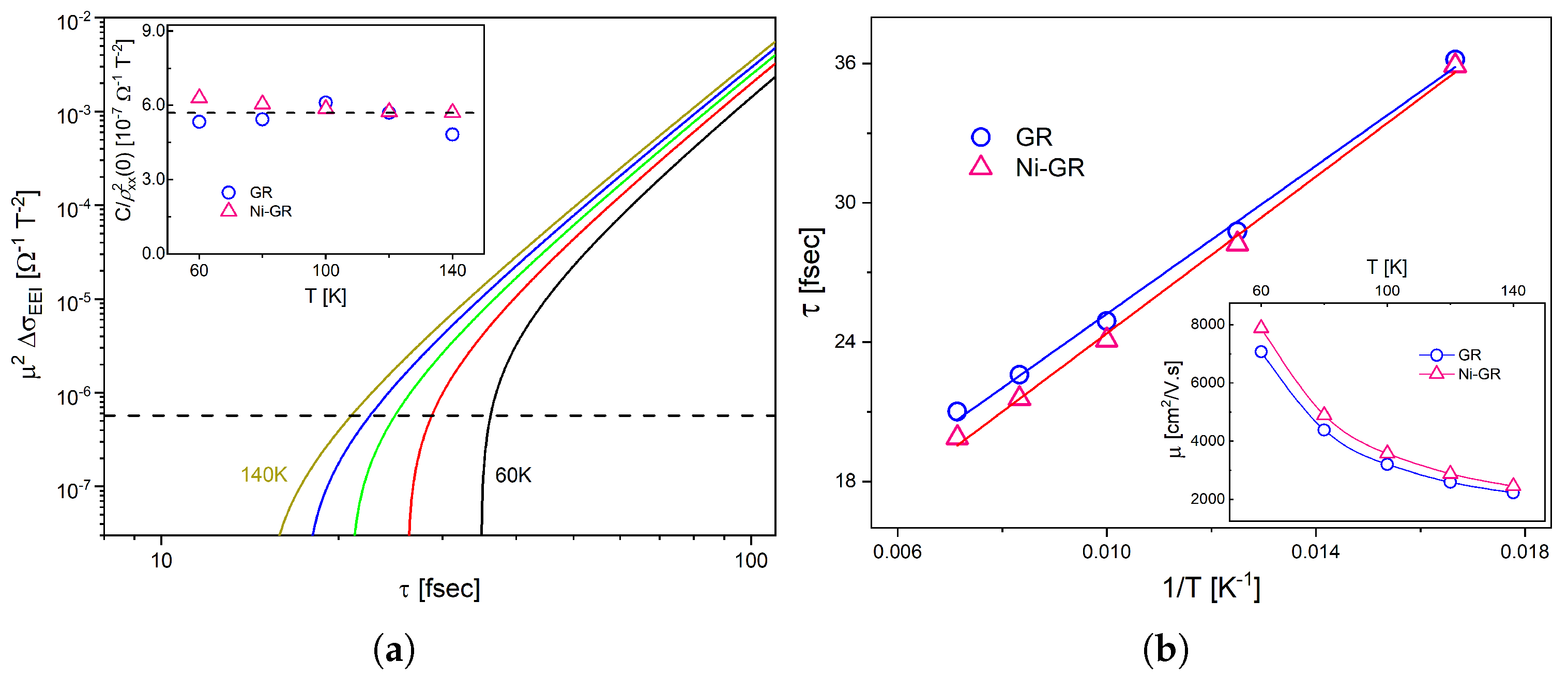
4.2. High Fields: Electron–Electron Interaction
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, J.H.; Jang, C.; Xiao, S.; Ishigami, M.; Fuhrer, M.S. Intrinsic and extrinsic performance limits of graphene devices on SiO2. Nat. Nanotechnol. 2008, 3, 206–209. [Google Scholar] [CrossRef] [PubMed]
- Morozov, S.V.; Novoselov, K.S.; Katsnelson, M.I.; Schedin, F.; Elias, D.C.; Jaszczak, J.A.; Geim, A.K. Giant Intrinsic Carrier Mobilities in Graphene and Its Bilayer. Phys. Rev. Lett. 2008, 100, 16602. [Google Scholar] [CrossRef]
- Murali, R.; Yang, Y.; Brenner, K.; Beck, T.; Meindl, J.D. Breakdown current density of graphene nanoribbons. Appl. Phys. Lett. 2009, 94, 243114. [Google Scholar] [CrossRef]
- Lee, K.J.; Chandrakasan, A.P.; Kong, J. Breakdown Current Density of CVD-Grown Multilayer Graphene Interconnects. IEEE Electron. Device Lett. 2011, 32, 557–559. [Google Scholar] [CrossRef]
- Balandin, A.A.; Ghosh, S.; Bao, W.; Calizo, I.; Teweldebrhan, D.; Miao, F.; Lau, C.N. Superior Thermal Conductivity of Single-Layer Graphene. Nano Lett. 2008, 8, 902–907. [Google Scholar] [CrossRef]
- Cai, W.; Moore, A.L.; Zhu, Y.; Li, X.; Chen, S.; Shi, L.; Ruoff, R.S. Thermal Transport in Suspended and Supported Monolayer Graphene Grown by Chemical Vapor Deposition. Nano Lett. 2010, 10, 1645–1651. [Google Scholar] [CrossRef] [PubMed]
- Bunch, J.S.; Verbridge, S.S.; Alden, J.S.; van der Zande, A.M.; Parpia, J.M.; Craighead, H.G.; McEuen, P.L. Impermeable Atomic Membranes from Graphene Sheets. Nano Lett. 2008, 8, 2458–2462. [Google Scholar] [CrossRef]
- Sun, P.Z.; Yang, Q.; Kuang, W.J.; Stebunov, Y.V.; Xiong, W.Q.; Yu, J.; Nair, R.R.; Katsnelson, M.I.; Yuan, S.J.; Grigorieva, I.V.; et al. Limits on gas impermeability of graphene. Nature 2020, 579, 229–232. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Jiang, Z.; Zhang, Y.; Morozov, S.V.; Stormer, H.L.; Zeitler, U.; Maan, J.C.; Boebinger, G.S.; Kim, P.; Geim, A.K. Room-temperature quantum Hall effect in graphene. Science 2007, 315, 1379. [Google Scholar] [CrossRef]
- Bolotin, K.I.; Ghahari, F.; Shulman, M.D.; Stormer, H.L.; Kim, P. Observation of the fractional quantum Hall effect in graphene. Nature 2009, 462, 196–199. [Google Scholar] [CrossRef]
- Zhang, Y.; Tan, Y.W.; Stormer, H.L.; Kim, P. Experimental observation of the quantum Hall effect and Berry’s phase in graphene. Nature 2005, 438, 201–204. [Google Scholar] [CrossRef]
- Zhu, Y.; Ji, H.; Cheng, H.M.; Ruoff, R.S. Mass production and industrial applications of graphene materials. Natl. Sci. Rev. 2018, 5, 90–101. [Google Scholar] [CrossRef]
- Drummond, T.G.; Hill, M.G.; Barton, J.K. Electrochemical DNA sensors. Nat. Biotechnol. 2003, 21, 1192–1199. [Google Scholar] [CrossRef]
- Priyadarsini, S.; Mohanty, S.; Mukherjee, S.; Basu, S.; Mishra, M. Graphene and graphene oxide as nanomaterials for medicine and biology application. J. Nanostruct. Chem. 2018, 8, 123–137. [Google Scholar] [CrossRef]
- Stoller, M.D.; Park, S.; Zhu, Y.; An, J.; Ruoff, R.S. Graphene-Based Ultracapacitors. Nano Lett. 2008, 8, 3498–3502. [Google Scholar] [CrossRef]
- Pandolfo, A.G.; Hollenkamp, A.F. Carbon properties and their role in supercapacitors. J. Power Sources 2006, 157, 11–27. [Google Scholar] [CrossRef]
- Dikin, D.A.; Stankovich, S.; Zimney, E.J.; Piner, R.D.; Dommett, G.H.B.; Evmenenko, G.; Nguyen, S.T.; Ruoff, R.S. Preparation and characterization of graphene oxide paper. Nature 2007, 448, 457–460. [Google Scholar] [CrossRef]
- Fan, Y.; Shen, N.H.; Zhang, F.; Zhao, Q.; Wu, H.; Fu, Q.; Wei, Z.; Li, H.; Soukoulis, C.M. Graphene plasmonics: A platform for 2D optics. Adv. Opt. Mater. 2019, 7, 1800537. [Google Scholar] [CrossRef]
- Liu, M.H.; Gorini, C.; Richter, K. Creating and steering highly directional electron beams in graphene. Phys. Rev. Lett. 2017, 118, 66801. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Yi, Y.; Yang, H.; Cheng, S.; Yang, W.; Zhang, H.; Yi, Z.; Yi, Y.; Li, H. Active tunable terahertz bandwidth absorber based on single layer graphene. Commun. Theor. Phys. 2023, 75, 045503. [Google Scholar] [CrossRef]
- Ye, Z.; Wu, P.; Wang, H.; Jiang, S.; Huang, M.; Lei, D.; Wu, F. Multimode tunable terahertz absorber based on a quarter graphene disk structure. Results Phys. 2023, 48, 106420. [Google Scholar] [CrossRef]
- Lai, R.; Shi, P.; Yi, Z.; Li, H.; Yi, Y. Triple-Band Surface Plasmon Resonance Metamaterial Absorber Based on Open-Ended Prohibited Sign Type Monolayer Graphene. Micromachines 2023, 14, 953. [Google Scholar] [CrossRef] [PubMed]
- Tang, B.; Guo, Z.; Jin, G.; Jin, G. Polarization-controlled and symmetry-dependent multiple plasmon-induced transparency in graphene-based metasurfaces. Opt. Express 2022, 30, 35554. [Google Scholar] [CrossRef]
- Lafont, F.; Ribeiro-Palau, R.; Kazazis, D.; Michon, A.; Couturaud, O.; Consejo, C.; Chassagne, T.; Zielinski, M.; Portail, M.; Jouault, B.; et al. Quantum Hall resistance standards from graphene grown by chemical vapour deposition on silicon carbide. Nat. Commun. 2015, 6, 6806. [Google Scholar] [CrossRef] [PubMed]
- Dedkov, Y.S.; Fonin, M.; Rüdiger, U.; Laubschat, C. Rashba effect in the graphene/Ni(111) system. Phys. Rev. Lett. 2008, 100, 107602. [Google Scholar] [CrossRef]
- Rader, O.; Varykhalov, A.; Sánchez-Barriga, J.; Marchenko, D.; Rybkin, A.; Shikin, A.M. Is there a Rashba effect in graphene on 3d ferromagnets? Phys. Rev. Lett. 2009, 102, 057602. [Google Scholar] [CrossRef] [PubMed]
- Rashba, E.I. Graphene with structure-induced spin–orbit coupling: Spin-polarized states, spin zero modes, and quantum Hall effect. Phys. Rev. B-Condens. Matter Mater. Phys. 2009, 79, 161409. [Google Scholar] [CrossRef]
- Varykhalov, A.; Sánchez-Barriga, J.; Shikin, A.M.; Biswas, C.; Vescovo, E.; Rybkin, A.; Marchenko, D.; Rader, O. Electronic and magnetic properties of quasifreestanding graphene on Ni. Phys. Rev. Lett. 2008, 101, 157601. [Google Scholar] [CrossRef]
- Varykhalov, A.; Rader, O. Graphene grown on Co(0001) films and islands: Electronic structure and its precise magnetization dependence. Phys. Rev. B-Condens. Matter Mater. Phys. 2009, 80, 035437. [Google Scholar] [CrossRef]
- Marchenko, D.; Varykhalov, A.; Sánchez-Barriga, J.; Rader, O.; Carbone, C.; Bihlmayer, G. Highly spin-polarized Dirac fermions at the graphene/Co interface. Phys. Rev. B-Condens. Matter Mater. Phys. 2015, 91, 235431. [Google Scholar] [CrossRef]
- Haugen, H.; Huertas-Hernando, D.; Brataas, A. Spin transport in proximity-induced ferromagnetic graphene. Phys. Rev. B-Condens. Matter Mater. Phys. 2008, 77, 115406. [Google Scholar] [CrossRef]
- Wei, P.; Lee, S.; Lemaitre, F.; Pinel, L.; Cutaia, D.; Cha, W.; Katmis, F.; Zhu, Y.; Heiman, D.; Hone, J.; et al. Strong interfacial exchange field in the graphene/EuS heterostructure. Nat. Mater. 2016, 15, 711–716. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.F.; Liu, N.H.; Wu, Q.P. Magnetoresistance and shot noise in graphene-based nanostructure with effective exchange field. J. Appl. Phys. 2012, 112, 123719. [Google Scholar] [CrossRef]
- Tang, C.; Zhang, Z.; Lai, S.; Tan, Q.; Gao, W.B. Magnetic Proximity Effect in Graphene/CrBr3 van der Waals Heterostructures. Adv. Mater. 2020, 32, 1908498. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Cui, Q.; Zhu, M.; Liu, X.; Wang, Y.; Zhang, J.; Zheng, X.; Shen, J.; Cui, P.; Yang, H.; et al. Magnetic Exchange Field Modulation of Quantum Hall Ferromagnetism in 2D van der Waals CrCl3/Graphene Heterostructures. Acs Appl. Mater. Interfaces 2021, 13, 10656–10663. [Google Scholar] [CrossRef] [PubMed]
- Abrikosov, A.A. Quantum magnetoresistance. Phys. Rev. B 1998, 58, 2788–2794. [Google Scholar] [CrossRef]
- Zhou, Y.B.; Wu, H.C.; Yu, D.P.; Liao, Z.M. Magnetoresistance in graphene under quantum limit regime. Appl. Phys. Lett. 2013, 102, 093116. [Google Scholar] [CrossRef]
- Gao, Z.; Xia, H.; Zauberman, J.; Tomaiuolo, M.; Ping, J.; Zhang, Q.; Ducos, P.; Ye, H.; Wang, S.; Yang, X.; et al. Detection of Sub-fM DNA with Target Recycling and Self-Assembly Amplification on Graphene Field-Effect Biosensors. Nano Lett. 2018, 18, 3509–3515. [Google Scholar] [CrossRef] [PubMed]
- Vishnubhotla, R.; Ping, J.; Gao, Z.; Lee, A.; Saouaf, O.; Vrudhula, A.; Johnson, A.T.C. Scalable graphene aptasensors for drug quantification. Aip Adv. 2017, 7, 115111. [Google Scholar] [CrossRef]
- Ping, J.; Pulsipher, K.; Vishnubhotla, R.; Villegas, J.A.; Hicks, T.L.; Honig, S.; Saven, J.G.; Dmochowski, I.J.; Johnson, A.T.C. Structural-functional analysis of engineered protein-nanoparticle assemblies using graphene microelectrodes. Chem. Sci. 2017, 8, 5329–5334. [Google Scholar] [CrossRef]
- Rajesh; Gao, Z.; Charlie Johnson, A.T.; Puri, N.; Mulchandani, A.; Aswal, D.K. Scalable chemical vapor deposited graphene field-effect transistors for bio/chemical assay. Appl. Phys. Rev. 2021, 8, 011311. [Google Scholar] [CrossRef]
- Gao, Z.; Ducos, P.; Ye, H.; Zauberman, J.; Sriram, A.; Yang, X.; Wang, Z.; Mitchell, M.W.; Lekkas, D.; Brisson, D.; et al. Graphene transistor arrays functionalized with genetically engineered antibody fragments for Lyme disease diagnosis. 2D Mater. 2020, 7, 024001. [Google Scholar] [CrossRef]
- Ping, J.; Vishnubhotla, R.; Xi, J.; Ducos, P.; Saven, J.; Liu, R.; Johnson, A. All-Electronic Quantification of Neuropeptide-Receptor Interaction Using a Bias-Free Functionalized Graphene Microelectrode. Acs Nano 2018, 12, 4218–4223. [Google Scholar] [CrossRef] [PubMed]
- Rajesh; Gao, Z.; Vishnubhotla, R.; Ducos, P.; Serrano, M.; Ping, J.; Robinson, M.; Johnson, A. Genetically Engineered Antibody Functionalized Platinum Nanoparticles Modified CVD-Graphene Nanohybrid Transistor for the Detection of Breast Cancer Biomarker, HER3. Adv. Mater. Interfaces 2016, 3, 1600124. [Google Scholar] [CrossRef]
- Gao, Z.; Kang, H.; Naylor, C.; Streller, F.; Ducos, P.; Serrano, M.; Ping, J.; Zauberman, J.; Rajesh; Carpick, R.; et al. Scalable Production of Sensor Arrays Based on High-Mobility Hybrid Graphene Field Effect Transistors. Acs Appl. Mater. Interfaces 2016, 8, 27546–27552. [Google Scholar] [CrossRef]
- Altshuler, B.; Aronov, A. Chapter 1—Electron-Electron Interaction in Disordered Conductors. In Electron-Electron Interactions in Disordered Systems; Efros, A.L., Pollak, M., Eds.; Elsevier: Amsterdam, The Netherlands, 1985; Volume 10, pp. 1–153. [Google Scholar] [CrossRef]
- Narozhny, B.; Zala, G.; Aleiner, I. A theory of metallic conductivity of the two-dimensional electron gas. Phys. E Low-Dimens. Syst. Nanostructures 2003, 18, 270–271. [Google Scholar] [CrossRef]
- Kozikov, A.A.; Savchenko, A.K.; Narozhny, B.N.; Shytov, A.V. Electron-electron interactions in the conductivity of graphene. Phys. Rev. B 2010, 82, 075424. [Google Scholar] [CrossRef]
- Zala, G.; Narozhny, B.N.; Aleiner, I.L. Interaction corrections at intermediate temperatures: Longitudinal conductivity and kinetic equation. Phys. Rev. B 2001, 64, 214204. [Google Scholar] [CrossRef]
- Jouault, B.; Jabakhanji, B.; Camara, N.; Desrat, W.; Consejo, C.; Camassel, J. Interplay between interferences and electron-electron interactions in epitaxial graphene. Phys. Rev. B 2011, 83, 195417. [Google Scholar] [CrossRef]
- Kliman, A. Weak Localization in Graphene. Ph.D. Thesis, Technische Universität Wien, Vienna, Austria, 2011. [Google Scholar] [CrossRef]
- Fal’ko, V.I.; Kechedzhi, K.; McCann, E.; Altshuler, B.L.; Suzuura, H.; Ando, T. Weak localization in graphene. Solid State Commun. 2007, 143, 33–38. [Google Scholar] [CrossRef]
- McCann, E.; Kechedzhi, K.; Fal’ko, V.I.; Suzuura, H.; Ando, T.; Altshuler, B.L. Weak-Localization Magnetoresistance and Valley Symmetry in Graphene. Phys. Rev. Lett. 2006, 97, 146805. [Google Scholar] [CrossRef] [PubMed]
- McCann, E.; Fal’ko, V.I. z-z Symmetry of Spin-Orbit Coupling and Weak Localization in Graphene. Phys. Rev. Lett. 2012, 108, 166606. [Google Scholar] [CrossRef] [PubMed]
- Mikitik, G.; Sharlai, Y. The Berry phase in graphene and graphite multilayers. Low Temp. Phys. 2008, 34, 794–800. [Google Scholar] [CrossRef]
- McClelland, G.M.; Erlandsson, R.; Chiang, S. Atomic Force Microscopy: General Principles and a New Implementation. In Review of Progress in Quantitative Nondestructive Evaluation; Thompson, D.O., Chimenti, D.E., Eds.; Springer: Boston, MA, USA, 1987; pp. 1307–1314. [Google Scholar]
- Weckenmann, A.; Tan, O.; Hoffmann, J.; Sun, Z. Practice-oriented evaluation of lateral resolution for micro- and nanometre measurement techniques. Meas. Sci. Technol. 2009, 20, 065103. [Google Scholar] [CrossRef]
- Russell, P.; Batchelor, D.; Thornton, J. SEM and AFM: Complementary techniques for high resolution surface investigations. Veeco Instruments 2001, 1, 2004. [Google Scholar]
- Nguyen, C.V.; Chao, K.J.; Stevens, R.M.D.; Delzeit, L.; Cassell, A.; Han, J.; Meyyappan, M. Carbon nanotube tip probes: Stability and lateral resolution in scanning probe microscopy and application to surface science in semiconductors. Nanotechnology 2001, 12, 363–367. [Google Scholar] [CrossRef]
- Kirkpatrick, S. Percolation and conduction. Rev. Mod. Phys. 1973, 45, 574. [Google Scholar] [CrossRef]
- Bollobás, B.; Riordan, O. A Short Proof of the Harris–Kesten Theorem. Bull. Lond. Math. Soc. 2006, 38, 470–484. [Google Scholar] [CrossRef]
- Stauffer, D.; Aharony, A. Introduction To Percolation Theory, 2nd ed.; Taylor & Francis: Philadelphia, PA, USA, 2018. [Google Scholar] [CrossRef]
- Tikhonenko, F.V.; Kozikov, A.A.; Savchenko, A.K.; Gorbachev, R.V. Transition between Electron Localization and Antilocalization in Graphene. Phys. Rev. Lett. 2009, 103, 226801. [Google Scholar] [CrossRef]
- He, X.; Zhong, W.; Au, C.T.; Du, Y. Size dependence of the magnetic properties of Ni nanoparticles prepared by thermal decomposition method. Nanoscale Res. Lett. 2013, 8, 446. [Google Scholar] [CrossRef]
- He, X.; Shi, H. Size and shape effects on magnetic properties of Ni nanoparticles. Particuology 2012, 10, 497–502. [Google Scholar] [CrossRef]
- Knecht, M.R.; Garcia-Martinez, J.C.; Crooks, R.M. Synthesis, Characterization, and Magnetic Properties of Dendrimer-Encapsulated Nickel Nanoparticles Containing <150 Atoms. Chem. Mater. 2006, 18, 5039–5044. [Google Scholar] [CrossRef]
- Wu, Y.F.; Song, H.D.; Zhang, L.; Yang, X.; Ren, Z.; Liu, D.; Wu, H.C.; Wu, J.; Li, J.G.; Jia, Z.; et al. Magnetic proximity effect in graphene coupled to a BiFe O3 nanoplate. Phys. Rev. B 2017, 95, 195426. [Google Scholar] [CrossRef]
- Bertoni, G.; Calmels, L.; Altibelli, A.; Serin, V. First-principles calculation of the electronic structure and EELS spectra at the graphene/Ni(111) interface. Phys. Rev. B 2005, 71, 75402. [Google Scholar] [CrossRef]
- Eriksson, O.; Johansson, B.; Albers, R.C.; Boring, A.M.; Brooks, M.S.S. Orbital magnetism in Fe, Co, and Ni. Phys. Rev. B 1990, 42, 2707–2710. [Google Scholar] [CrossRef]
- Danan, H.; Herr, A.; Meyer, A.J.P. New Determinations of the Saturation Magnetization of Nickel and Iron. J. Appl. Phys. 1968, 39, 669–670. [Google Scholar] [CrossRef]
- Krutzen, B.C.H.; Springelkamp, F. Spin-polarised relativistic electronic structure calculations. J. Phys. Condens. Matter 1989, 1, 8369–8383. [Google Scholar] [CrossRef]
- Dahal, A.; Batzill, M. Graphene–nickel interfaces: A review. Nanoscale 2014, 6, 2548–2562. [Google Scholar] [CrossRef]
- Hwang, J.Y.; Kuo, C.C.; Chen, L.C.; Chen, K.H. Correlating defect density with carrier mobility in large-scaled graphene films: Raman spectral signatures for the estimation of defect density. Nanotechnology 2010, 21, 465705. [Google Scholar] [CrossRef]
- Tan, Y.W.; Zhang, Y.; Bolotin, K.; Zhao, Y.; Adam, S.; Hwang, E.H.; Das Sarma, S.; Stormer, H.L.; Kim, P. Measurement of Scattering Rate and Minimum Conductivity in Graphene. Phys. Rev. Lett. 2007, 99, 246803. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arguello Cruz, E.; Ducos, P.; Gao, Z.; Johnson, A.T.C.; Niebieskikwiat, D. Exchange Coupling Effects on the Magnetotransport Properties of Ni-Nanoparticle-Decorated Graphene. Nanomaterials 2023, 13, 1861. https://doi.org/10.3390/nano13121861
Arguello Cruz E, Ducos P, Gao Z, Johnson ATC, Niebieskikwiat D. Exchange Coupling Effects on the Magnetotransport Properties of Ni-Nanoparticle-Decorated Graphene. Nanomaterials. 2023; 13(12):1861. https://doi.org/10.3390/nano13121861
Chicago/Turabian StyleArguello Cruz, Erick, Pedro Ducos, Zhaoli Gao, Alan T. Charlie Johnson, and Dario Niebieskikwiat. 2023. "Exchange Coupling Effects on the Magnetotransport Properties of Ni-Nanoparticle-Decorated Graphene" Nanomaterials 13, no. 12: 1861. https://doi.org/10.3390/nano13121861
APA StyleArguello Cruz, E., Ducos, P., Gao, Z., Johnson, A. T. C., & Niebieskikwiat, D. (2023). Exchange Coupling Effects on the Magnetotransport Properties of Ni-Nanoparticle-Decorated Graphene. Nanomaterials, 13(12), 1861. https://doi.org/10.3390/nano13121861






