Plasmonic Bound States in the Continuum to Tailor Exciton Emission of MoTe2
Abstract
:1. Introduction
2. Methods
3. Result and Discussion
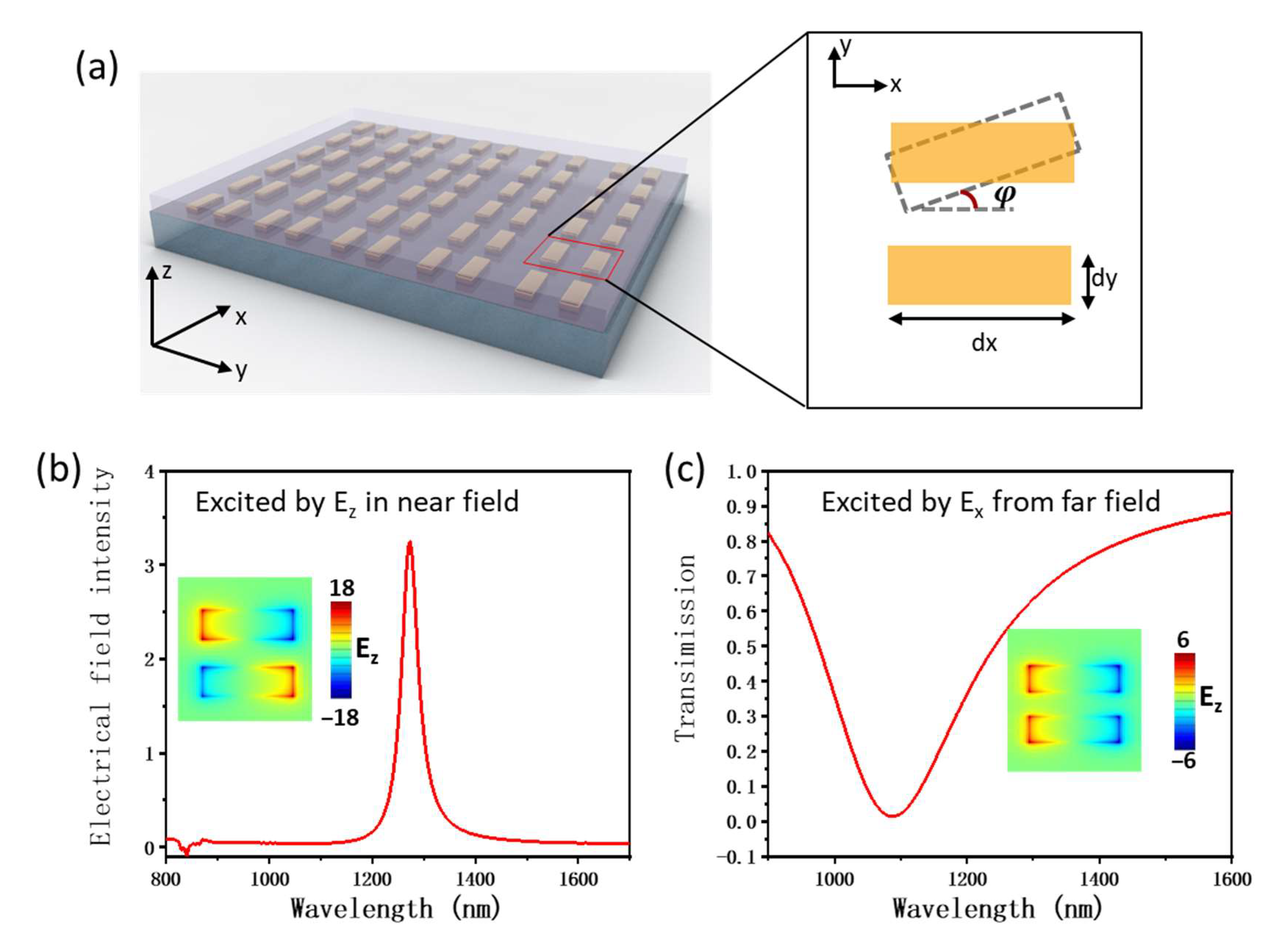
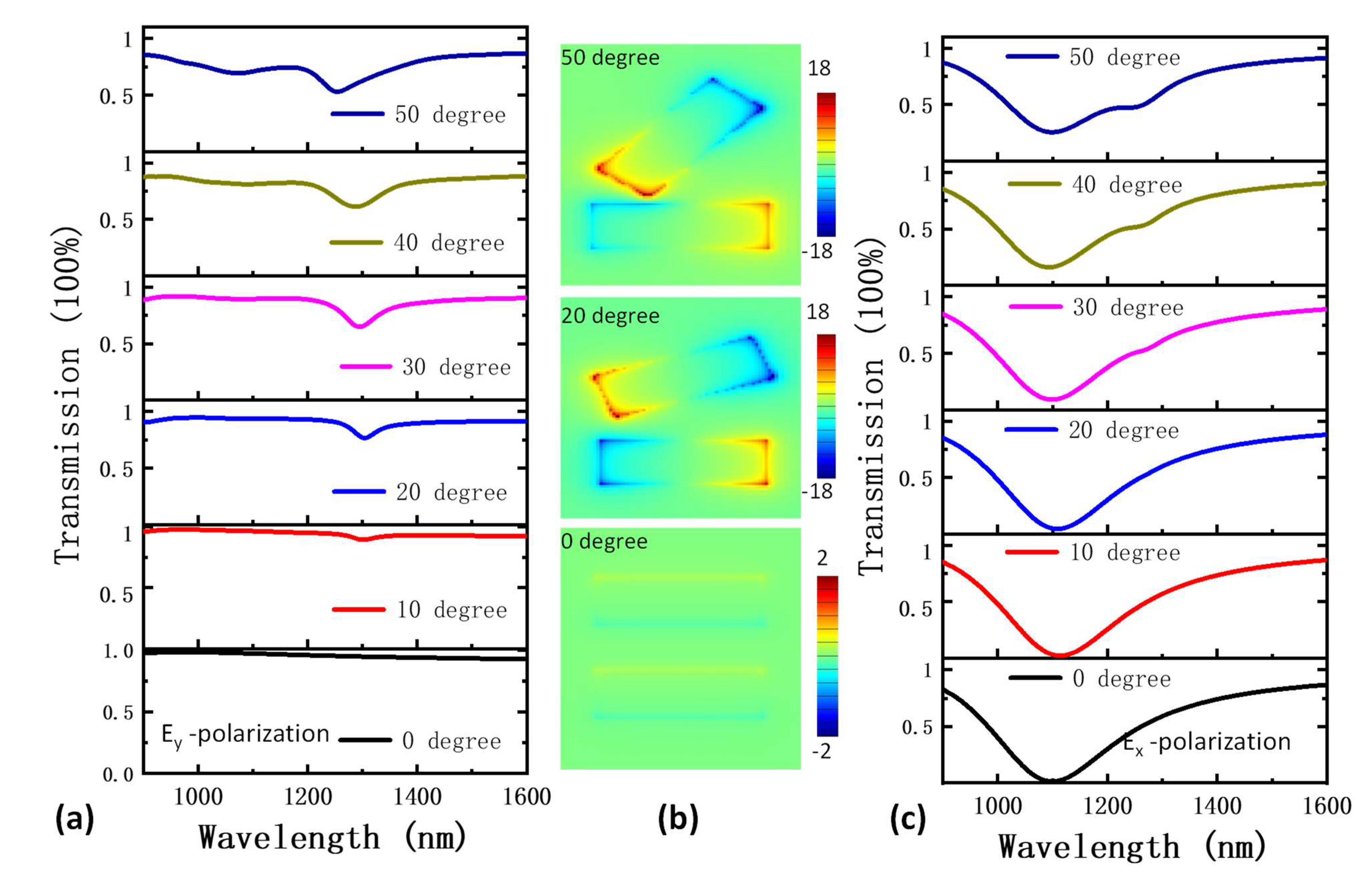
3.1. Simulation
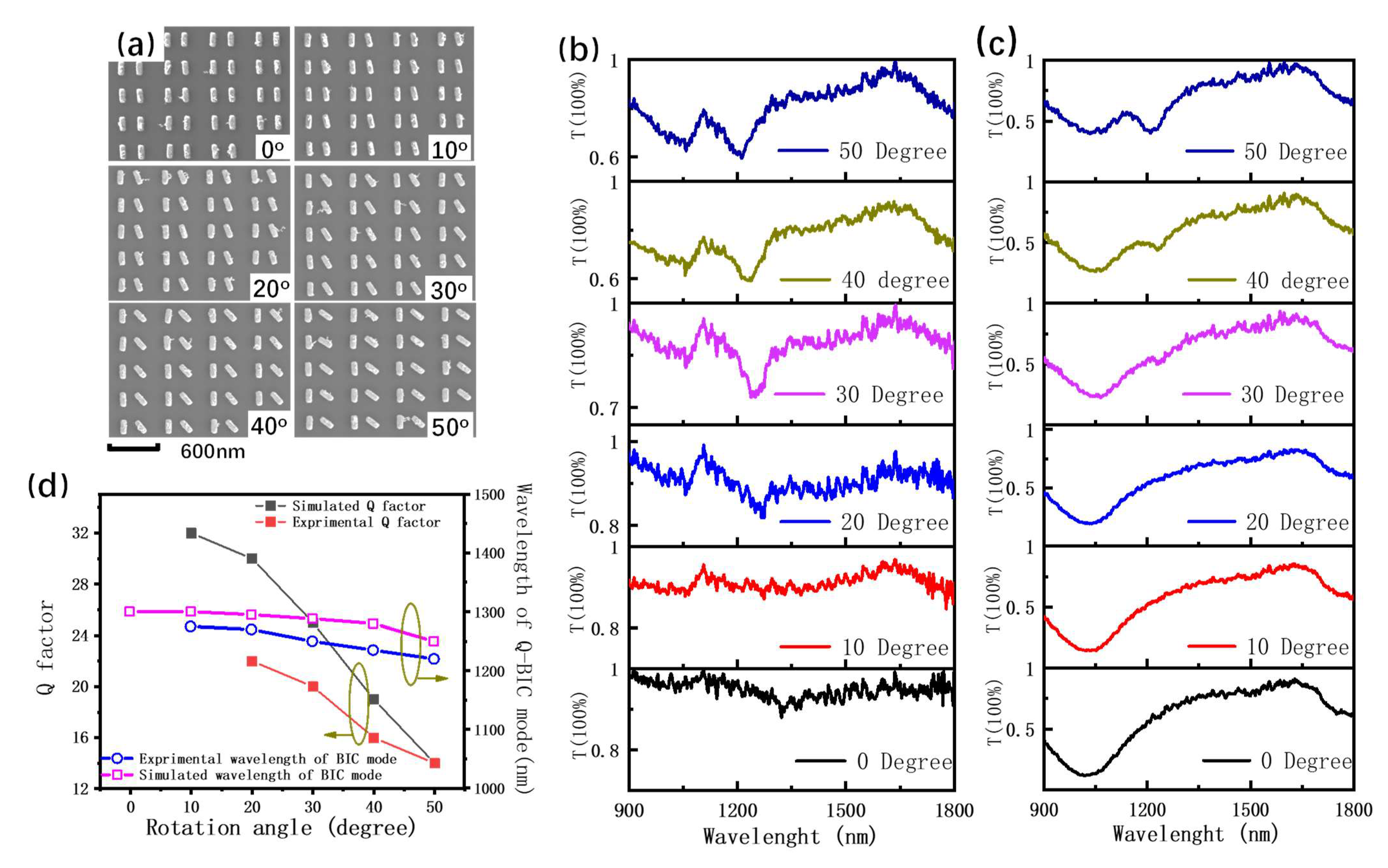
3.2. Experiment Results
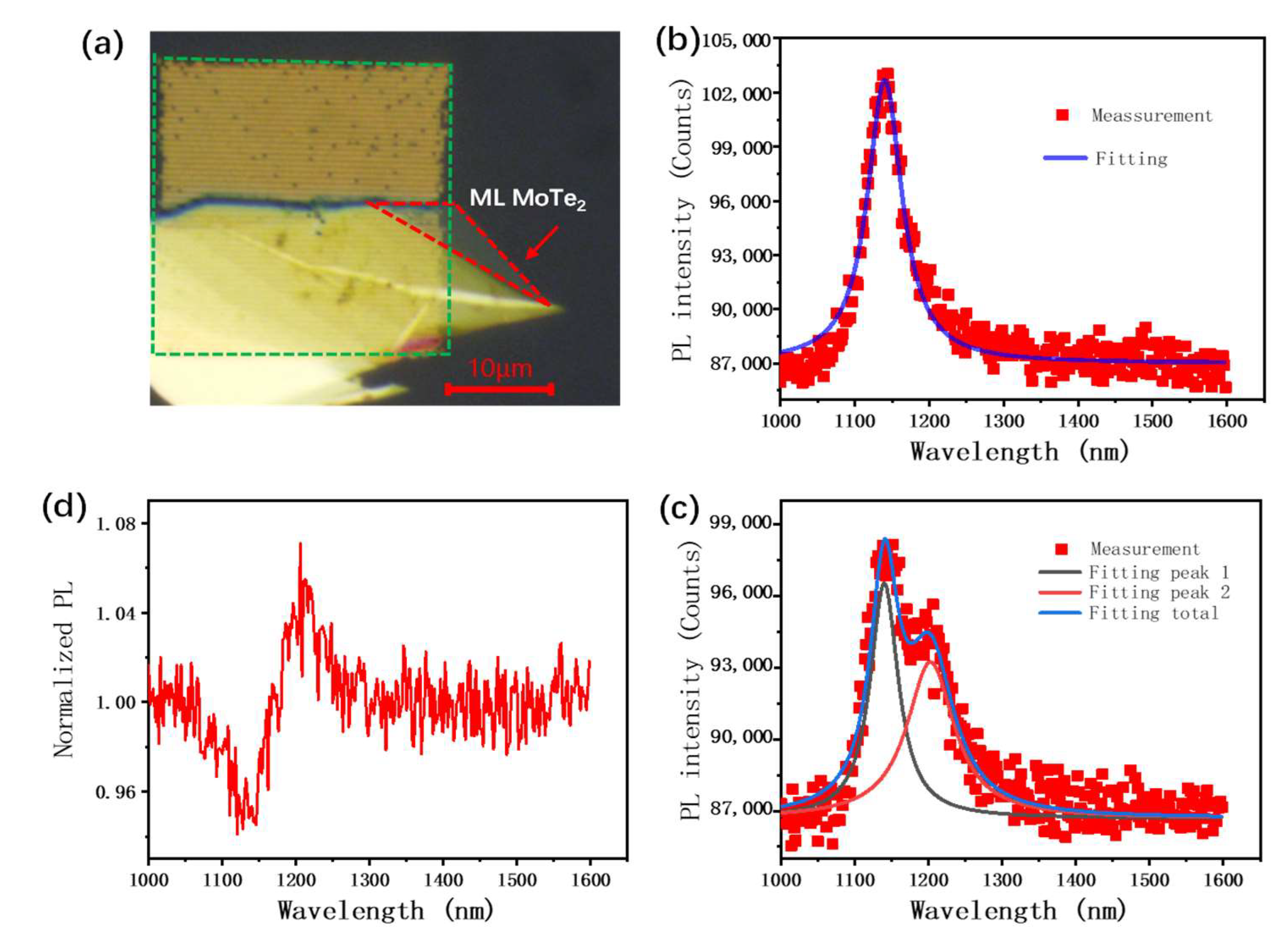
3.3. Coupling with MoTe2
4. Summary
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pala, R.A.; White, J.; Barnard, E.; Liu, J.; Brongersma, M.L. Design of plasmonic thin-film solar cells with broadband absorption enhancements. Adv. Mater. 2009, 21, 3504–3509. [Google Scholar] [CrossRef]
- Clavero, C. Plasmon-induced hot-electron generation at nanoparticle/metal-oxide interfaces for photovoltaic and photocatalytic devices. Nat. Photonics 2014, 8, 95–103. [Google Scholar] [CrossRef]
- Ding, S.Y.; Yi, J.; Li, J.F.; Ren, B.; Wu, D.Y.; Panneerselvam, R.; Tian, Z.Q. Nanostructure-based plasmon-enhanced raman spectroscopy for surface analysis of materials. Nat. Rev. Mater. 2016, 1, 16021. [Google Scholar] [CrossRef]
- Li, J.-F.; Li, C.-Y.; Aroca, R.F. Plasmon-enhanced fluorescence spectroscopy. Chem. Soc. Rev. 2017, 46, 3962–3979. [Google Scholar] [CrossRef] [PubMed]
- Kale, M.J.; Avanesian, T.; Christopher, P. Direct photocatalysis by plasmonic nanostructures. Acs Catal. 2014, 4, 116–128. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, Y.L.; Liu, R.-S.; Tsai, D.P. Plasmonic photocatalysis. Rep. Prog. Phys. 2013, 76, 046401. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Li, X.; Wang, J.; Tao, L.; Long, M.; Liang, S.-J.; Ang, L.K.; Shu, C.; Tsang, H.K.; Xu, J.-B. Synergistic effects of plasmonics and electron trapping in graphene short-wave infrared photodetectors with ultrahigh responsivity. ACS Nano 2017, 11, 430–437. [Google Scholar] [CrossRef]
- Sun, Z.; Lionel, A.; Chen, Z. Plasmonic-enhanced perovskite–graphene hybrid photodetectors. Nanoscale 2016, 8, 7377–7383. [Google Scholar] [CrossRef]
- Ho, J.; Dong, Z.; Leong, H.S.; Zhang, J.; Tjiptoharsono, F.; Daqiqeh Rezaei, S.; Goh, K.C.H.; Wu, M.; Li, S.; Chee, J.; et al. Miniaturizing color-sensitive photodetectors via hybrid nanoantennas toward submicrometer dimensions. Sci. Adv. 2022, 8, eadd3868. [Google Scholar] [CrossRef]
- Salamin, Y.; Ma, P.; Baeuerle, B.; Emboras, A.; Fedoryshyn, Y.; Heni, W.; Cheng, B.; Josten, A.; Leuthold, J. 100 GHz Plasmonic Photodetector. ACS Photonics 2018, 5, 3291–3297. [Google Scholar] [CrossRef] [Green Version]
- Stührenberg, M.; Munkhbat, B.; Baranov, D.G.; Cuadra, J.; Yankovich, A.B.; Antosiewicz, T.J.; Olsson, E.; Shegai, T. Strong light–matter coupling between plasmons in individual gold bi-pyramids and excitons in mono-and multilayer WSe2. Nano Lett. 2018, 18, 5938–5945. [Google Scholar] [CrossRef] [PubMed]
- Fernandez, H.A.; Withers, F.; Russo, S.; Barnes, W.L. Electrically tuneable exciton-polaritons through free electron doping in monolayer WS2 microcavities. Adv. Opt. Mater. 2019, 7, 1900484. [Google Scholar] [CrossRef] [Green Version]
- Han, X.; Wang, K.; Xing, X.; Wang, M.; Lu, P. Rabi splitting in a plasmonic nanocavity coupled to a WS2 monolayer at room temperature. ACS Photonics 2018, 5, 3970–3976. [Google Scholar] [CrossRef]
- Schneider, C.; Glazov, M.M.; Korn, T.; Höfling, S.; Urbaszek, B. Two-dimensional semiconductors in the regime of strong light-matter coupling. Nat. Commun. 2018, 9, 2695. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, X.; Galfsky, T.; Sun, Z.; Xia, F.; Lin, E.-C.; Lee, Y.-H.; Kéna-Cohen, S.; Menon, V.M. Strong light–matter coupling in two-dimensional atomic crystals. Nat. Photonics 2015, 9, 30–34. [Google Scholar] [CrossRef] [Green Version]
- Shen, F.; Chen, Z.; Tao, L.; Sun, B.; Xu, X.; Zheng, J.; Xu, J. Investigation on the fano-type asymmetry in atomic semiconductor coupled to the plasmonic lattice. ACS Photonics 2021, 8, 3583–3590. [Google Scholar] [CrossRef]
- Kravets, V.G.; Kabashin, A.V.; Barnes, W.L.; Grigorenko, A.N. Plasmonic surface lattice resonances: A review of properties and applications. Chem. Rev. 2018, 118, 5912–5951. [Google Scholar] [CrossRef]
- Wen, J.; Wang, H.; Wang, W.; Deng, Z.; Zhuang, C.; Zhang, Y.; Liu, F.; She, J.; Chen, J.; Chen, H.; et al. Room-temperature strong light–matter interaction with active control in single plasmonic nanorod coupled with two-dimensional atomic crystals. Nano Lett. 2017, 17, 4689–4697. [Google Scholar] [CrossRef]
- Liu, R.; Zhou, Z.-K.; Yu, Y.-C.; Zhang, T.; Wang, H.; Liu, G.; Wei, Y.; Chen, H.; Wang, X.-H. Strong light-matter interactions in single open plasmonic nanocavities at the quantum optics limit. Phys. Rev. Lett. 2017, 118, 237401. [Google Scholar] [CrossRef]
- Rodriguez, S.; Feist, J.; Verschuuren, M.; Garcia-Vidal, F.; Rivas, J.G. Thermalization and cooling of plasmon-exciton polaritons: Towards quantum condensation. Phys. Rev. Lett. 2013, 111, 166802. [Google Scholar] [CrossRef] [Green Version]
- Wersall, M.; Cuadra, J.; Antosiewicz, T.J.; Balci, S.; Shegai, T. Observation of mode splitting in photoluminescence of individual plasmonic nanoparticles strongly coupled to molecular excitons. Nano Lett. 2017, 17, 551–558. [Google Scholar] [CrossRef] [PubMed]
- Kleemann, M.-E.; Chikkaraddy, R.; Alexeev, E.M.; Kos, D.; Carnegie, C.; Deacon, W.; de Pury, A.C.; Große, C.; de Nijs, B.; Mertens, J.; et al. Strong-coupling of wse2 in ultra-compact plasmonic nanocavities at room temperature. Nat. Commun. 2017, 8, 1296. [Google Scholar] [CrossRef] [Green Version]
- Von Neumann, J.; Wigner, E. On some peculiar discrete eigenvalues. Phys. Z. 1929, 30, 465–467. [Google Scholar]
- Herrick, D.R. Construction of bound states in the continuum for epitaxial heterostructure superlattices. Phys. B+C 1976, 85, 44–50. [Google Scholar] [CrossRef]
- Joseph, S.; Pandey, S.; Sarkar, S.; Joseph, J. Bound states in the continuum in resonant nanostructures: An overview of engineered materials for tailored applications. Nanophotonics 2021, 10, 4175–4207. [Google Scholar] [CrossRef]
- Bogdanov, A.A.; Koshelev, K.L.; Kapitanova, P.V.; Rybin, M.V.; Gladyshev, S.A.; Sadrieva, Z.F.; Samusev, K.B.; Kivshar, Y.S.; Limonov, M.F. Bound states in the continuum and fano resonances in the strong mode coupling regime. Adv. Photonics 2019, 1, 016001. [Google Scholar] [CrossRef] [Green Version]
- Hsu, C.W.; Zhen, B.; Stone, A.D.; Joannopoulos, J.D.; Soljačić, M. Bound states in the continuum. Nat. Rev. Mater. 2016, 1, 16048. [Google Scholar] [CrossRef] [Green Version]
- Overvig, A.; Yu, N.; Alù, A. Chiral quasi-bound states in the continuum. Phys. Rev. Lett. 2021, 126, 073001. [Google Scholar] [CrossRef]
- Gorkunov, M.V.; Antonov, A.A.; Kivshar, Y.S. Metasurfaces with maximum chirality empowered by bound states in the continuum. Phys. Rev. Lett. 2020, 125, 093903. [Google Scholar] [CrossRef]
- Koshelev, K.; Lepeshov, S.; Liu, M.; Bogdanov, A.; Kivshar, Y. Asymmetric metasurfaces with high-q resonances governed by bound states in the continuum. Phys. Rev. Lett. 2018, 121, 193903. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liang, Y.; Koshelev, K.; Zhang, F.; Lin, H.; Lin, S.; Wu, J.; Jia, B.; Kivshar, Y. Bound States in the Continuum in Anisotropic Plasmonic Metasurfaces. Nano Lett. 2020, 20, 6351–6356. [Google Scholar] [CrossRef] [PubMed]
- Dong, Z.; Jin, L.; Rezaei, S.D.; Wang, H.; Chen, Y.; Tjiptoharsono, F.; Ho, J.; Gorelik, S.; Ng, R.J.H.; Ruan, Q.; et al. Schrödinger’s red pixel by quasi-bound-statesin-the-continuum. Sci. Adv. 2022, 8, abm4512. [Google Scholar] [CrossRef]
- Dong, Z.; Mahfoud, Z.; Paniagua-Domínguez, R.; Wang, H.; Fernández-Domínguez, A.I.; Gorelik, S.; Ha, S.T.; Tjiptoharsono, F.; Kuznetsov, A.I.; Bosman, M.; et al. Nanoscale mapping of optically inaccessible bound-states-in-the-continuum. Light Sci. Appl. 2022, 1, 20. [Google Scholar] [CrossRef]
- Koshelev, K.; Bogdanov, A.; Kivsha, Y. Meta-optics and bound states in the continuum. Sci. Bull. 2019, 12, 836–842. [Google Scholar] [CrossRef] [Green Version]
- Ruppert, C.; Aslan, B.; Heinz, T.F. Optical properties and band gap of single-and few-layer mote2 crystals. Nano Lett. 2014, 14, 6231–6236. [Google Scholar] [CrossRef] [PubMed]
- Biswas, S.; Champagne, A.; Haber, J.B.; Pokawanvit, S.; Wong, J.; Akbari, H.; Krylyuk, S.; Watanabe, K.; Taniguchi, T.; Davydov, A.V.; et al. Rydberg excitons and trions in monolayer MoTe2. ACS Nano 2023, 17, 7685–7694. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, Y.; Wu, K.; Sheng, B.; Ma, W.; Chen, Z.; Li, X. Plasmonic Bound States in the Continuum to Tailor Exciton Emission of MoTe2. Nanomaterials 2023, 13, 1987. https://doi.org/10.3390/nano13131987
Jin Y, Wu K, Sheng B, Ma W, Chen Z, Li X. Plasmonic Bound States in the Continuum to Tailor Exciton Emission of MoTe2. Nanomaterials. 2023; 13(13):1987. https://doi.org/10.3390/nano13131987
Chicago/Turabian StyleJin, Yuxuan, Kai Wu, Bining Sheng, Wentao Ma, Zefeng Chen, and Xiaofeng Li. 2023. "Plasmonic Bound States in the Continuum to Tailor Exciton Emission of MoTe2" Nanomaterials 13, no. 13: 1987. https://doi.org/10.3390/nano13131987
APA StyleJin, Y., Wu, K., Sheng, B., Ma, W., Chen, Z., & Li, X. (2023). Plasmonic Bound States in the Continuum to Tailor Exciton Emission of MoTe2. Nanomaterials, 13(13), 1987. https://doi.org/10.3390/nano13131987





