Quantum-Dot-Induced Modification of Surface Functionalization for Active Applications of Whispering Gallery Mode Resonators
Abstract
:1. Introduction
2. Materials and Methods
2.1. Fabrication of Microsphere Resonators
2.2. Characterization of Microresonators
2.3. Surface Functionalization
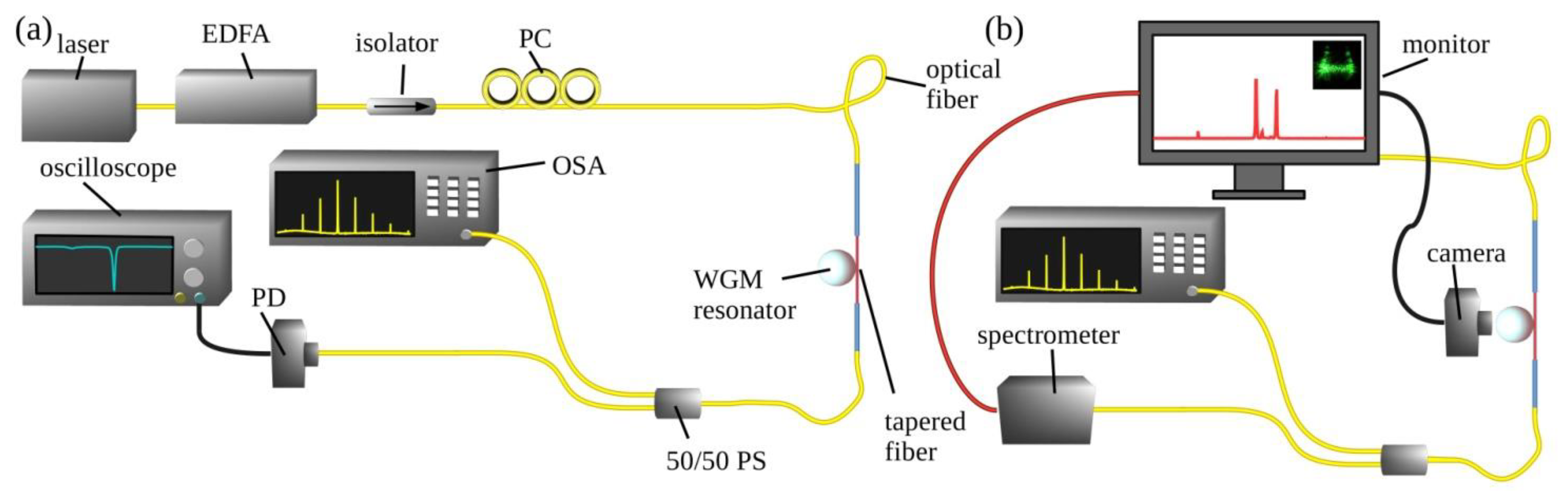
2.4. Setup of the WGMR Testing System
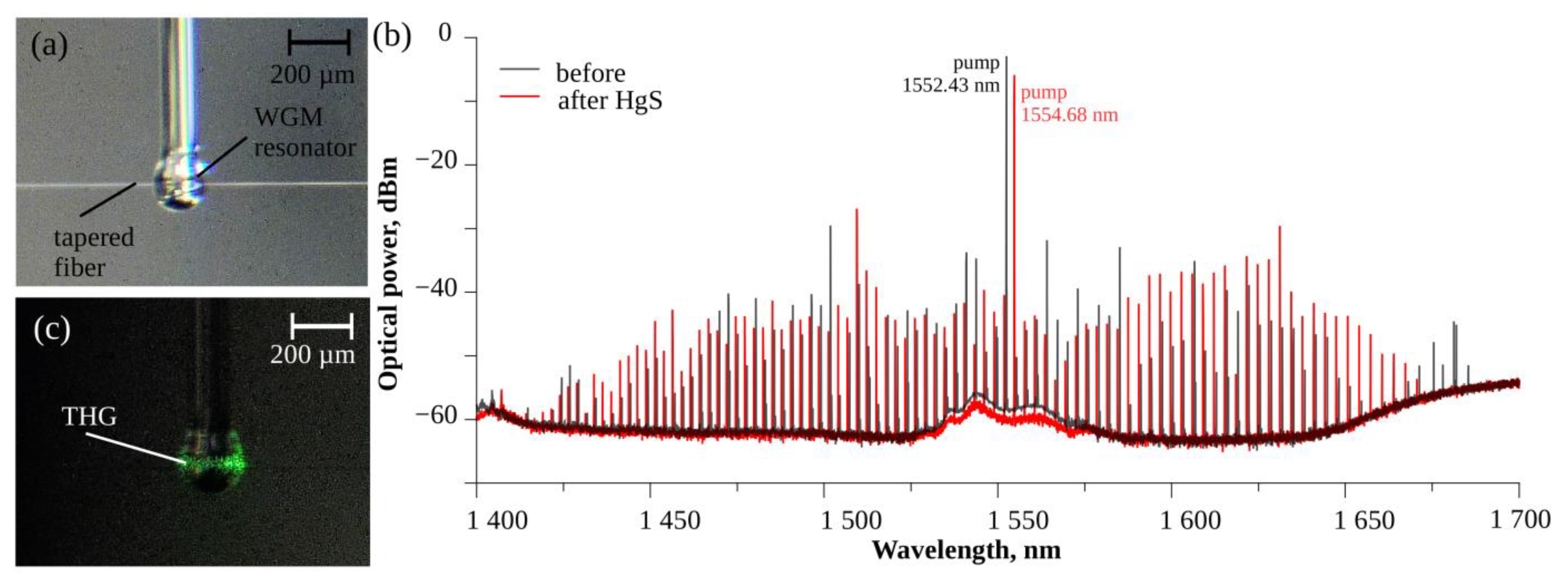
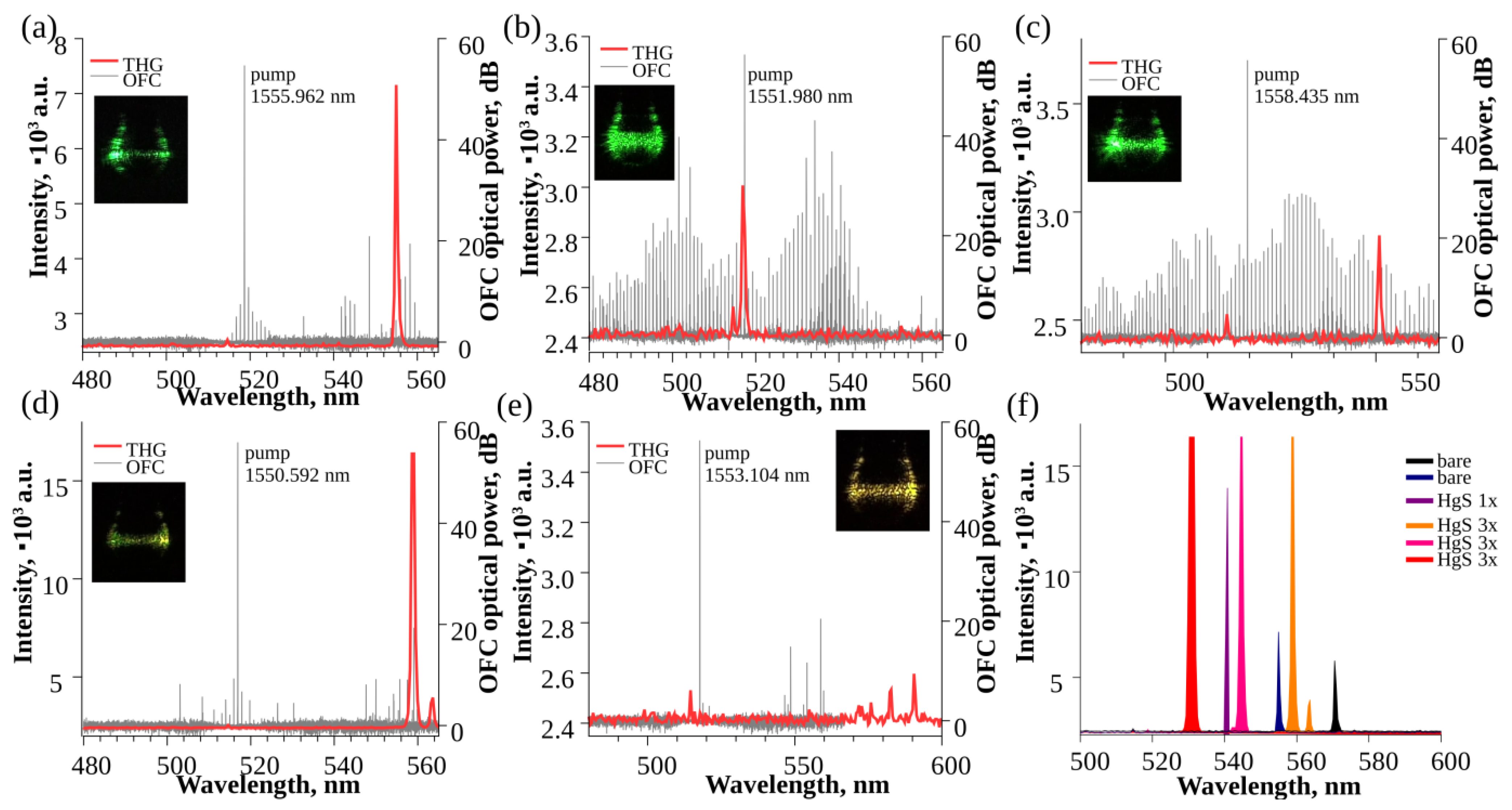
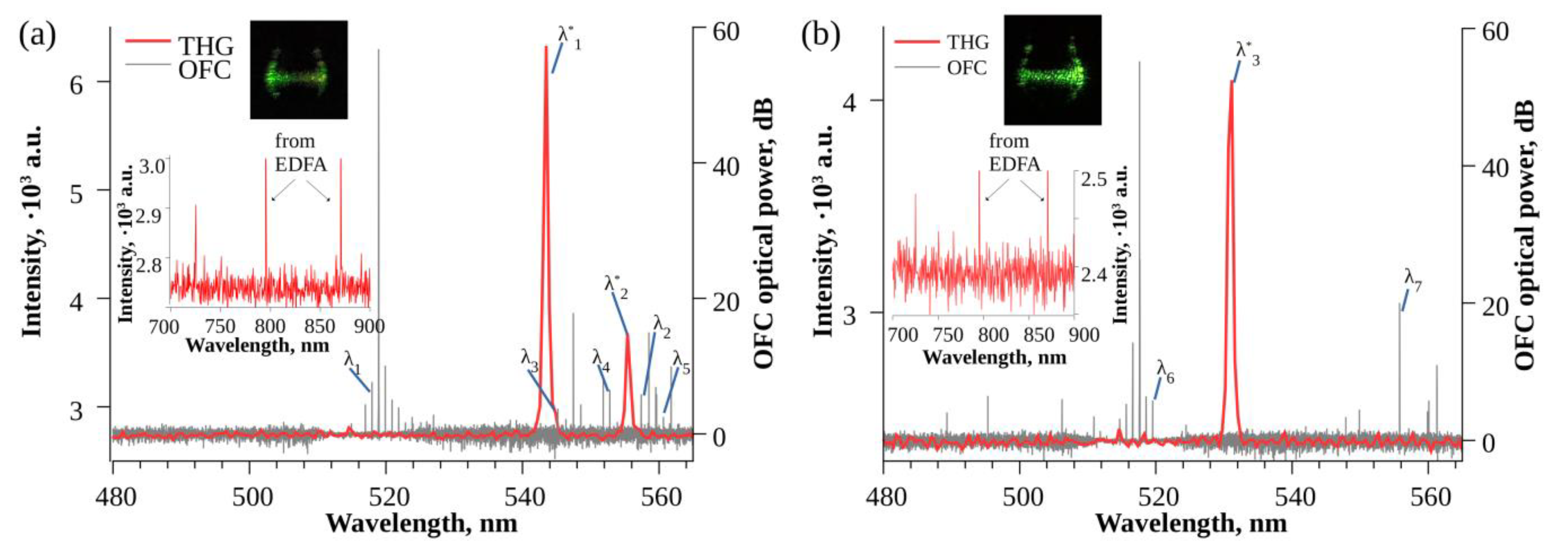
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Monifi, F.; Ozdemir, S.K.; Yang, L.; Friedlein, J. An on-chip tunable add-drop filter using a microtoroid resonator. IEEE Photonics Conf. 2012, 2012, 260–261. [Google Scholar]
- Ilchenko, V.S.; Dale, E.; Liang, W.; Byrd, J.; Eliyahu, D.; Savchenkov, A.A.; Matsko, A.B.; Seidel, D.; Maleki, L. Compact tunable kHz-linewidth semiconductor laser stabilized with a whispering-gallery mode microresonator. In Laser Resonators and Beam Control XIII; Kudryashov, A.V., Paxton, A.H., Ilchenko, V.S., Eds.; SPIE: Bellingham, WA, USA, 2011; Volume 7913, pp. 295–303. [Google Scholar]
- Petermann, A.; Hildebrandt, T.; Morgner, U.; Roth, B.; Meinhardt-Wollweber, M. Polymer based whispering gallery mode humidity sensor. Sensors 2018, 18, 2383. [Google Scholar] [CrossRef] [Green Version]
- Brice, I.; Grundsteins, K.; Atvars, A.; Alnis, J.; Viter, R.; Ramanavicius, A. Whispering gallery mode resonator and glucose oxidase based glucose biosensor. Sens. Actuators B Chem. 2020, 318, 128004. [Google Scholar] [CrossRef]
- Kalkman, J.; Polman, A.; Kippenberg, T.; Vahala, K.; Brongersma, M.L. Erbium-implanted silica microsphere laser. Nucl. Instrum. Methods Phys. Res. B 2006, 242, 182–185. [Google Scholar] [CrossRef]
- Kippenberg, T.J.; Holzwarth, R.; Diddams, S.A. Microresonator-based optical frequency combs. Science 2011, 332, 555–559. [Google Scholar] [CrossRef]
- Brice, I.; Grundsteins, K.; Atvars, A.; Alnis, J.; Viter, R. Whispering gallery mode resonators coated with Au nanoparticles. In Nanoengineering: Fabrication, Properties, Optics, Thin Films, and Devices XVI; Attias, A.-J., Panchapakesan, B., Eds.; SPIE: Bellingham, WA, USA, 2019; Volume 11089, p. 65. [Google Scholar]
- Braunfelds, J.; Murnieks, R.; Salgals, T.; Brice, I.; Sharashidze, T.; Lyashuk, I.; Ostrovskis, A.; Spolitis, S.; Alnis, J.; Porins, J.; et al. Frequency comb generation in WGM microsphere based generators for telecommunication applications. Quantum Electron. 2020, 50, 1043–1049. [Google Scholar] [CrossRef]
- Pampel, S.K.; Bae, K.; Zohrabi, M.; Grayson, M.; Horning, T.M.; Park, W.; Gopinath, J.T. Third-harmonic generation enhancement in an ITO nanoparticle-coated microresonator. Opt. Express 2020, 28, 30004. [Google Scholar] [CrossRef] [PubMed]
- Maker, A.J.; Armani, A.M. Fabrication of silica ultra high quality factor microresonators. J. Vis. Exp. 2012, 65, e4164. [Google Scholar]
- Andrianov, A.; Anashkina, E. Single-mode silica microsphere Raman laser tunable in the U-band and beyond. Res. Phys. 2020, 17, 103084. [Google Scholar] [CrossRef]
- Gorodetsky, M.L.; Savchenkov, A.A.; Ilchenko, V.S. Ultimate Q of optical microsphere resonators. Opt. Lett. 1996, 21, 453. [Google Scholar] [CrossRef] [PubMed]
- Righini, G.C.; Dumeige, Y.; Feron, P.; Ferrari, M.; Conti, G.N.; Ristic, D.; Soria, S. Whispering gallery mode microresonators: Fundamentals and applications. Riv. Nuovo C. 2011, 34, 435–488. [Google Scholar]
- Grudinin, I.S.; Ilchenko, V.S.; Maleki, L. Ultrahigh optical Q factors of crystalline resonators in the linear regime. Phys. Rev. A 2006, 74, 063806. [Google Scholar] [CrossRef]
- Righini, G.; Soria, S. Biosensing by WGM microspherical resonators. Sensors 2016, 16, 905. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rout, A.; Boltaev, G.S.; Ganeev, R.A.; Kim, V.V.; Maurya, S.K.; Mottamchety, V.; Guo, C. Nonlinear optical studies of gold nanoparticle films. Nanomaterials 2019, 9, 291. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, V.V.; Shuklov, I.A.; Mardini, A.A.; Bundulis, A.; Zvyagin, A.I.; Kholany, R.; Lizunova, A.A.; Grube, J.; Sarakovskis, A.; Ovchinnikov, O.V.; et al. Investigation of nonlinear optical processes in mercury sulfide quantum dots. Nanomaterials 2022, 12, 1264. [Google Scholar] [CrossRef]
- Ganeev, R.A.; Shuklov, I.A.; Zvyagin, A.I.; Dyomkin, D.V.; Bocharova, S.I.; Popov, V.S.; Toknova, F.; Lizunova, A.A.; Ovchinnikov, O.V.; Razumov, V.F. Low-order optical nonlinearities of PbS quantum dot liquids and films. Opt. Mater. 2021, 121, 111499. [Google Scholar] [CrossRef]
- Webb, K.E.; Erkintalo, M.; Coen, S.; Murdoch, S.G. Experimental observation of coherent cavity soliton frequency combs in silica microspheres. Opt. Lett. 2016, 41, 4613–4616. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Zou, C.-L.; Dong, C.-H.; Dai, D.-X. Optimal third-harmonic generation in an optical microcavity with χ(2) and χ(3) nonlinearities. Opt. Express 2018, 26, 27294. [Google Scholar] [CrossRef] [Green Version]
- Farnesi, D.; Barucci, A.; Righini, G.C.; Berneschi, C.; Soria, S.; Nunzi Conti, G. Optical frequency conversion in silica-whispering-gallery-mode microspherical resonators. Phys Rev. Lett. 2014, 112, 093901. [Google Scholar] [CrossRef]
- Leach, D.H.; Chang, R.K.; Acker, W.P.; Hill, S.C. Third-order sum-frequency generation in droplets: Experimental results. J. Opt. Soc. Am. B 1993, 10, 34–35. [Google Scholar] [CrossRef]
- Kasparian, J.; Krämer, B.; Dewitz, J.P.; Vajda, S.; Rairoux, P.; Vezin, B.; Boutou, V.; Leisner, T.; Hübner, W.; Wolf, J.P.; et al. Angular dependences of third harmonic generation from microdroplets. Phys. Rev. Lett. 1997, 78, 2952–2954. [Google Scholar] [CrossRef] [Green Version]
- Min, B.; Kim, S.; Okamoto, K.; Yang, L.; Scherer, A.; Atwater, H.; Vahala, K. Ultralow threshold on-chip microcavity nanocrystal quantum dot lasers. Appl. Phys. Lett. 2006, 89, 191124. [Google Scholar] [CrossRef] [Green Version]
- Carmon, T.; Vahala, K.J. Visible continuous emission from a silica microphotonic device by third-harmonic generation. Nat. Phys. 2007, 3, 430–435. [Google Scholar] [CrossRef]
- Galli, M.; Gerace, D.; Welna, K.; Krauss, T.F.; O’Faolain, L.; Guizzetti, G.; Andreani, L.C. Low-power continuous-wave generation of visible harmonics in silicon photonic crystal nanocavities. Opt. Express 2010, 18, 26613–26624. [Google Scholar] [CrossRef] [Green Version]
- Levy, J.S.; Foster, M.A.; Gaeta, A.L.; Lipson, M. Harmonic generation in silicon nitride ring resonators. Opt. Express 2011, 19, 11415–11421. [Google Scholar] [CrossRef] [Green Version]
- Ismaeel, R.; Lee, T.; Ding, M.; Broderick, N.G.R.; Brambilla, G. Nonlinear microfiber loop resonators for resonantly enhanced third harmonic generation. Opt. Lett. 2012, 37, 5121–5123. [Google Scholar] [CrossRef] [PubMed]
- Asano, M.; Komori, S.; Ikuta, R.; Imoto, N.; Özdemir, S.K.; Yamamoto, T. Visible light emission from a silica microbottle resonator by second- and third-harmonic generation. Opt. Lett. 2016, 41, 5793–5796. [Google Scholar] [CrossRef] [PubMed]
- Surya, J.B.; Guo, X.; Zou, C.L.; Tang, H.X. Efficient third-harmonic generation in composite aluminum nitride/silicon nitride microrings. Optica 2018, 5, 103–108. [Google Scholar] [CrossRef] [Green Version]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brice, I.; Kim, V.V.; Ostrovskis, A.; Sedulis, A.; Salgals, T.; Spolitis, S.; Bobrovs, V.; Alnis, J.; Ganeev, R.A. Quantum-Dot-Induced Modification of Surface Functionalization for Active Applications of Whispering Gallery Mode Resonators. Nanomaterials 2023, 13, 1997. https://doi.org/10.3390/nano13131997
Brice I, Kim VV, Ostrovskis A, Sedulis A, Salgals T, Spolitis S, Bobrovs V, Alnis J, Ganeev RA. Quantum-Dot-Induced Modification of Surface Functionalization for Active Applications of Whispering Gallery Mode Resonators. Nanomaterials. 2023; 13(13):1997. https://doi.org/10.3390/nano13131997
Chicago/Turabian StyleBrice, Inga, Vyacheslav V. Kim, Armands Ostrovskis, Arvids Sedulis, Toms Salgals, Sandis Spolitis, Vjaceslavs Bobrovs, Janis Alnis, and Rashid A. Ganeev. 2023. "Quantum-Dot-Induced Modification of Surface Functionalization for Active Applications of Whispering Gallery Mode Resonators" Nanomaterials 13, no. 13: 1997. https://doi.org/10.3390/nano13131997





