Second Harmonic Generation in Janus Transition Metal Chalcogenide Oxide Monolayers: A First-Principles Investigation
Abstract
:1. Introduction
2. Methods
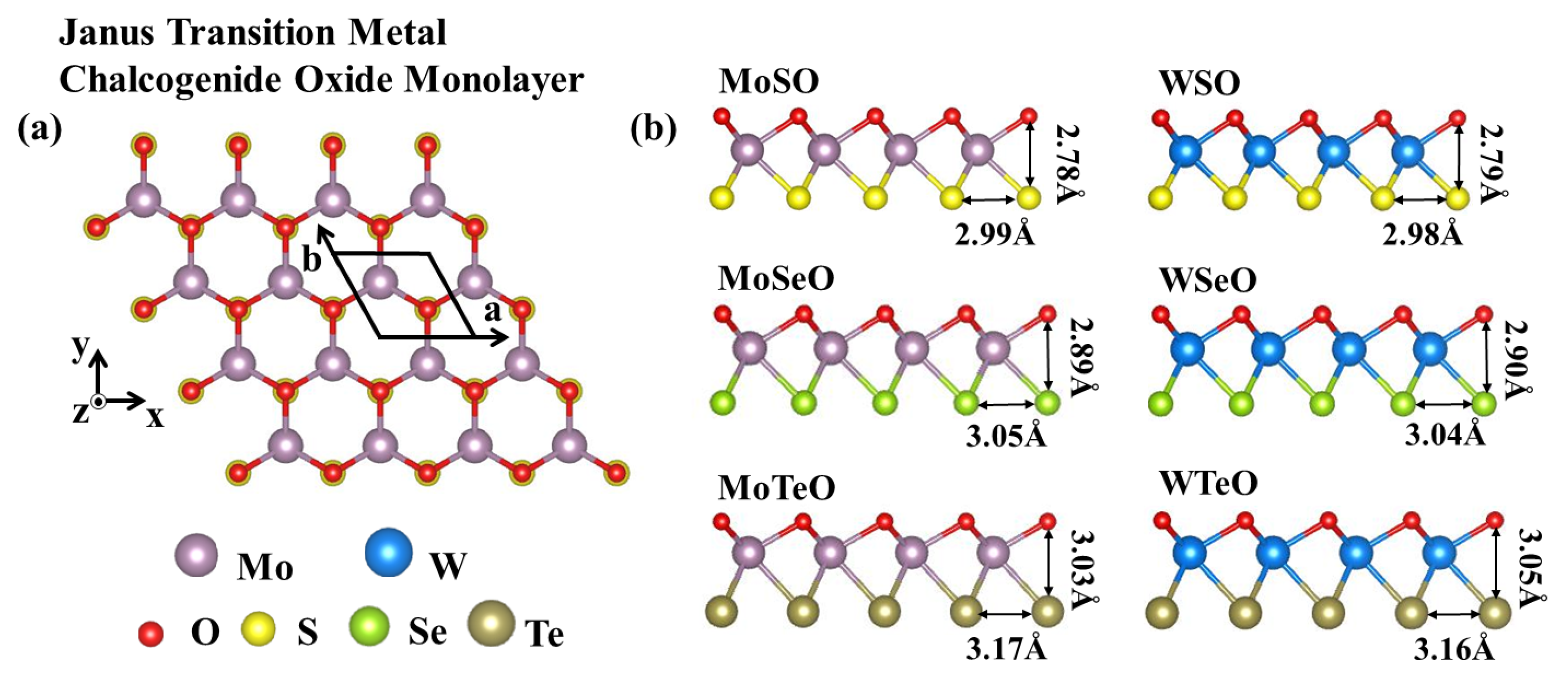
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dadap, J.I.; Karlsson, M.; Panoiu, N.C. Focus Issue Introduction: Nonlinear Optics 2013. Opt. Express 2013, 21, 31176–31178. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yelin, S.F.; Hemmer, P.R. Resonantly Enhanced Nonlinear Optics in Semiconductor Quantum Wells: An Application to Sensitive Infrared Detection. Phys. Rev. A 2002, 66, 013803. [Google Scholar] [CrossRef] [Green Version]
- Levenson, M. The Principles of Nonlinear Optics. IEEE J. Quantum Electron. 1985, 21, 400. [Google Scholar] [CrossRef]
- Manykin, E.A.; Melnichenko, E.V. Quantum Computing on Base of Technology of Nonlinear Optical Information Processing. In International Workshop on Quantum Optics 2003; Samartsev, V.V., Ed.; SPIE: Bellingham, WA, USA, 2004; pp. 130–139. [Google Scholar]
- Krijnen, G.J.M.; Popma, T.J.A.; Lambeck, P.V.; van Schoot, J.B.P.; Hoekstra, H.J.W.M.; Offrein, B.J.; Driessen, A.; Horst, F. All-Optical Integrated Optic Devices: A Hybrid Approach. IEE Proc.-Optoelectron. 1998, 145, 227–235. [Google Scholar] [CrossRef]
- Sipe, J.E.; Ghahramani, E. Nonlinear Optical Response of Semiconductors in the Independent-Particle Approximation. Phys. Rev. B 1993, 48, 11705–11722. [Google Scholar] [CrossRef]
- Cox, J.D.; Javier García de Abajo, F. Electrically Tunable Nonlinear Plasmonics in Graphene Nanoislands. Nat. Commun. 2014, 5, 5725. [Google Scholar] [CrossRef] [Green Version]
- Mikhailov, S.A. Non-Linear Electromagnetic Response of Graphene. Europhys. Lett. 2007, 79, 27002. [Google Scholar] [CrossRef] [Green Version]
- Malard, L.M.; Alencar, T.V.; Barboza, A.P.M.; Mak, K.F.; de Paula, A.M. Observation of Intense Second Harmonic Generation from MoS2 Atomic Crystals. Phys. Rev. B 2013, 87, 201401. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Rao, Y.; Mak, K.F.; You, Y.; Wang, S.; Dean, C.R.; Heinz, T.F. Probing Symmetry Properties of Few-Layer MoS2 and h-BN by Optical Second-Harmonic Generation. Nano Lett. 2013, 13, 3329–3333. [Google Scholar] [CrossRef] [PubMed]
- Lin, K.-Q.; Bange, S.; Lupton, J.M. Quantum Interference in Second-Harmonic Generation from Monolayer WSe2. Nat. Phys. 2019, 15, 242–246. [Google Scholar] [CrossRef] [Green Version]
- Wang, R.; Chien, H.-C.; Kumar, J.; Kumar, N.; Chiu, H.-Y.; Zhao, H. Third-Harmonic Generation in Ultrathin Films of MoS2. ACS Appl. Mater. Interfaces 2014, 6, 314–318. [Google Scholar] [CrossRef] [PubMed]
- Jakubczyk, T.; Delmonte, V.; Koperski, M.; Nogajewski, K.; Faugeras, C.; Langbein, W.; Potemski, M.; Kasprzak, J. Radiatively Limited Dephasing and Exciton Dynamics in MoSe2 Monolayers Revealed with Four-Wave Mixing Microscopy. Nano Lett. 2016, 16, 5333–5339. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, D.; Xiong, W.; Jiang, L.; Xiao, Z.; Rabiee Golgir, H.; Wang, M.; Huang, X.; Zhou, Y.; Lin, Z.; Song, J.; et al. Multimodal Nonlinear Optical Imaging of MoS2 and MoS2-Based van Der Waals Heterostructures. ACS Nano 2016, 10, 3766–3775. [Google Scholar] [CrossRef] [PubMed]
- Murray, W.; Lucking, M.; Kahn, E.; Zhang, T.; Fujisawa, K.; Perea-Lopez, N.; Laura Elias, A.; Terrones, H.; Terrones, M.; Liu, Z. Second Harmonic Generation in Two-Dimensional Transition Metal Dichalcogenides with Growth and Post-Synthesis Defects. 2D Mater. 2020, 7, 045020. [Google Scholar] [CrossRef]
- Zhang, J.; Jia, S.; Kholmanov, I.; Dong, L.; Er, D.; Chen, W.; Guo, H.; Jin, Z.; Shenoy, V.B.; Shi, L.; et al. Janus Monolayer Transition-Metal Dichalcogenides. ACS Nano 2017, 11, 8192–8198. [Google Scholar] [CrossRef] [Green Version]
- Zuo, X.; Chang, K.; Zhao, J.; Xie, Z.; Tang, H.; Li, B.; Chang, Z. Bubble-Template-Assisted Synthesis of Hollow Fullerene-like MoS2 Nanocages as a Lithium Ion Battery Anode Material. J. Mater. Chem. A 2016, 4, 51–58. [Google Scholar] [CrossRef]
- Sun, N.; Wang, M.; Quhe, R.; Liu, Y.; Liu, W.; Guo, Z.; Ye, H. Armchair Janus MoSSe Nanoribbon with Spontaneous Curling: A First-Principles Study. Nanomaterials 2021, 11, 3442. [Google Scholar] [CrossRef]
- Ye, H.; Zhou, J.; Er, D.; Price, C.C.; Yu, Z.; Liu, Y.; Lowengrub, J.; Lou, J.; Liu, Z.; Shenoy, V.B. Toward a Mechanistic Understanding of Vertical Growth of van Der Waals Stacked 2D Materials: A Multiscale Model and Experiments. ACS Nano 2017, 11, 12780–12788. [Google Scholar] [CrossRef]
- Ye, H.; Zhang, Y.; Wei, A.; Han, D.; Liu, Y.; Liu, W.; Yin, Y.; Wang, M. Intrinsic-Strain-Induced Curling of Free-Standing Two-Dimensional Janus MoSSe Quantum Dots. Appl. Surf. Sci. 2020, 519, 146251. [Google Scholar] [CrossRef]
- Sun, N.; Ye, H.; Quhe, R.; Liu, Y.; Wang, M. Prediction of Photogalvanic Effect Enhancement in Janus Transition Metal Dichalcogenide Monolayers Induced by Spontaneous Curling. Appl. Surf. Sci. 2023, 619, 156730. [Google Scholar] [CrossRef]
- Mocci, P.; Cardia, R.; Cappellini, G. Si-Atoms Substitutions Effects on the Electronic and Optical Properties of Coronene and Ovalene. New J. Phys. 2018, 20, 113008. [Google Scholar] [CrossRef]
- Pérez-Jiménez, Á.J.; Sancho-García, J.C. Using Circumacenes to Improve Organic Electronics and Molecular Electronics: Design Clues. Nanotechnology 2009, 20, 475201. [Google Scholar] [CrossRef] [PubMed]
- Mocci, P.; Cardia, R.; Cappellini, G. Inclusions of Si-Atoms in Graphene Nanostructures: A Computational Study on the Ground-State Electronic Properties of Coronene and Ovalene. J. Phys. Conf. Ser. 2018, 956, 012020. [Google Scholar] [CrossRef]
- Shwartz, S.; Weil, R.; Segev, M.; Lakin, E.; Zolotoyabko, E.; Menon, V.M.; Forrest, S.R.; EL-Hanany, U. Light-Induced Symmetry Breaking and Related Giant Enhancement of Nonlinear Properties in CdZnTe:V Crystals. Opt. Express 2006, 14, 9385–9390. [Google Scholar] [CrossRef] [PubMed]
- Zhao, M.; Ye, Z.; Suzuki, R.; Ye, Y.; Zhu, H.; Xiao, J.; Wang, Y.; Iwasa, Y.; Zhang, X. Atomically Phase-Matched Second-Harmonic Generation in a 2D Crystal. Light Sci. Appl. 2016, 5, e16131. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wei, Y.; Xu, X.; Wang, S.; Li, W.; Jiang, Y. Second Harmonic Generation in Janus MoSSe a Monolayer and Stacked Bulk with Vertical Asymmetry. Phys. Chem. Chem. Phys. 2019, 21, 21022–21029. [Google Scholar] [CrossRef] [PubMed]
- Strasser, A.; Wang, H.; Qian, X. Nonlinear Optical and Photocurrent Responses in Janus MoSSe Monolayer and MoS2–MoSSe van Der Waals Heterostructure. Nano Lett. 2022, 22, 4145–4152. [Google Scholar] [CrossRef] [PubMed]
- Bian, C.; Shi, J.; Liu, X.; Yang, Y.; Yang, H.; Gao, H. Optical Second-Harmonic Generation of Janus MoSSe Monolayer. Chin. Phys. B 2022, 31, 097304. [Google Scholar] [CrossRef]
- Li, X.; Chen, X.; Wei, N.; Chen, C.; Yang, Z.; Xie, H.; He, J.; Dong, N.; Dan, Y.; Wang, J. Nonlinear Absorption and Integrated Photonics Applications of MoSSe. Opt. Express 2022, 30, 32924. [Google Scholar] [CrossRef]
- Li, Y.-Q.; Wang, X.-Y.; Zhu, S.-Y.; Tang, D.-S.; He, Q.-W.; Wang, X.-C. Active Asymmetric Electron-Transfer Effect on the Enhanced Piezoelectricity in MoTO (T = S, Se, or Te) Monolayers and Bilayers. J. Phys. Chem. Lett. 2022, 13, 9654–9663. [Google Scholar] [CrossRef]
- Varjovi, M.J.; Yagmurcukardes, M.; Peeters, F.M.; Durgun, E. Janus Two-Dimensional Transition Metal Dichalcogenide Oxides: First-Principles Investigation of W X O Monolayers with X = S, Se, and Te. Phys. Rev. B 2021, 103, 195438. [Google Scholar] [CrossRef]
- Van On, V.; Nguyen, D.K.; Guerrero-Sanchez, J.; Hoat, D.M. Exploring the Electronic Band Gap of Janus MoSeO and WSeO Monolayers and Their Heterostructures. New J. Chem. 2021, 45, 20776–20786. [Google Scholar] [CrossRef]
- Nguyen, D.K.; Guerrero-Sanchez, J.; Van On, V.; Rivas-Silva, J.F.; Ponce-Pérez, R.; Cocoletzi, G.H.; Hoat, D.M. Tuning MoSO Monolayer Properties for Optoelectronic and Spintronic Applications: Effect of External Strain, Vacancies and Doping. RSC Adv. 2021, 11, 35614–35623. [Google Scholar] [CrossRef]
- Yagmurcukardes, M.; Peeters, F.M. Stable Single Layer of Janus MoSO: Strong out-of-Plane Piezoelectricity. Phys. Rev. B 2020, 101, 155205. [Google Scholar] [CrossRef]
- Xu, C.-Y.; Qin, J.-K.; Yan, H.; Li, Y.; Shao, W.-Z.; Zhen, L. Homogeneous Surface Oxidation and Triangle Patterning of Monolayer MoS2 by Hydrogen Peroxide. Appl. Surf. Sci. 2018, 452, 451–456. [Google Scholar] [CrossRef]
- Shioya, H.; Tsukagoshi, K.; Ueno, K.; Oiwa, A. Selective Oxidation of the Surface Layer of Bilayer WSe2 by Laser Heating. Jpn. J. Appl. Phys. 2019, 58, 120903. [Google Scholar] [CrossRef]
- Kang, M.; Yang, H.I.; Choi, W. Oxidation of WS2 and WSe2 Monolayers by Ultraviolet-Ozone Treatment. J. Phys. D Appl. Phys. 2019, 52, 505105. [Google Scholar] [CrossRef]
- Waheed, H.S.; Asghar, M.; Ahmad, H.S.; Abbas, T.; Ullah, H.; Ali, R.; Khan, M.J.I.; Iqbal, M.W.; Shin, Y.-H.; Khan, M.S.; et al. Janus MoSO and MoSSe Monolayers: A Promising Material for Solar Cells and Photocatalytic Applications. Phys. Status Solidi (b) 2023, 260, 2200267. [Google Scholar] [CrossRef]
- Falahati, K.; Khatibi, A.; Shokri, B. Light-Matter Interaction in Tungsten Sulfide-Based Janus Monolayers: A First-Principles Study. Appl. Surf. Sci. 2022, 599, 153967. [Google Scholar] [CrossRef]
- Pešić, J.; Vujin, J.; Tomašević-Ilić, T.; Spasenović, M.; Gajić, R. DFT Study of Optical Properties of MoS2 and WS2 Compared to Spectroscopic Results on Liquid Phase Exfoliated Nanoflakes. Opt. Quantum Electron. 2018, 50, 291. [Google Scholar] [CrossRef]
- Jia, W.; Cao, Z.; Wang, L.; Fu, J.; Chi, X.; Gao, W.; Wang, L.-W. The Analysis of a Plane Wave Pseudopotential Density Functional Theory Code on a GPU Machine. Comput. Phys. Commun. 2013, 184, 9–18. [Google Scholar] [CrossRef]
- Jia, W.; Fu, J.; Cao, Z.; Wang, L.; Chi, X.; Gao, W.; Wang, L.-W. Fast Plane Wave Density Functional Theory Molecular Dynamics Calculations on Multi-GPU Machines. J. Comput. Phys. 2013, 251, 102–115. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Hestenes, M.R.; Stiefel, E. Methods of Conjugate Gradients for Solving Linear Systems. J. Res. Natl. Bur. Stand. 1952, 49, 409–436. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid Functionals Based on a Screened Coulomb Potential. J. Chem. Phys. 2003, 118, 8207–8215. [Google Scholar] [CrossRef] [Green Version]
- Rashkeev, S.N.; Lambrecht, W.R.L.; Segall, B. Efficient Ab Initio Method for the Calculation of Frequency-Dependent Second-Order Optical Response in Semiconductors. Phys. Rev. B 1998, 57, 3905–3919. [Google Scholar] [CrossRef]
- Bernardi, M.; Palummo, M.; Grossman, J.C. Extraordinary Sunlight Absorption and One Nanometer Thick Photovoltaics Using Two-Dimensional Monolayer Materials. Nano Lett. 2013, 13, 3664–3670. [Google Scholar] [CrossRef]
- Cappellini, G.; Furthmüller, J.; Cadelano, E.; Bechstedt, F. Electronic and Optical Properties of Cadmium Fluoride: The Role of Many-Body Effects. Phys. Rev. B 2013, 87, 075203. [Google Scholar] [CrossRef] [Green Version]
- Cadelano, E.; Furthmüller, J.; Cappellini, G.; Bechstedt, F. One- and Two-Particle Effects in the Electronic and Optical Spectra of Barium Fluoride. J. Phys. Condens. Matter 2014, 26, 125501. [Google Scholar] [CrossRef]
- Sharma, S.; Ambrosch-Draxl, C. Second-Harmonic Optical Response from First Principles. Phys. Scr. 2004, T109, 128. [Google Scholar] [CrossRef] [Green Version]
- Chang, E.K.; Shirley, E.L.; Levine, Z.H. Excitonic Effects on Optical Second-Harmonic Polarizabilities of Semiconductors. Phys. Rev. B 2001, 65, 035205. [Google Scholar] [CrossRef]
- Pike, N.A.; Pachter, R. Second-Order Nonlinear Optical Properties of Monolayer Transition-Metal Dichalcogenides by Computational Analysis. J. Phys. Chem. C 2021, 125, 11075–11084. [Google Scholar] [CrossRef]
- Radziuk, D.; Möhwald, H. Ultrasonically Treated Liquid Interfaces for Progress in Cleaning and Separation Processes. Phys. Chem. Chem. Phys. 2016, 18, 21–46. [Google Scholar] [CrossRef]
- Laturia, A.; Van De Put, M.L.; Vandenberghe, W.G. Dielectric Properties of Hexagonal Boron Nitride and Transition Metal Dichalcogenides: From Monolayer to Bulk. npj 2D Mater. Appl. 2018, 2, 6. [Google Scholar] [CrossRef] [Green Version]
- Osanloo, M.R.; Van De Put, M.L.; Saadat, A.; Vandenberghe, W.G. Identification of Two-Dimensional Layered Dielectrics from First Principles. Nat. Commun. 2021, 12, 5051. [Google Scholar] [CrossRef] [PubMed]
- Fang, W.; Xiao, X.; Wei, H.; Chen, Y.; Li, M.; He, Y. The Elastic, Electron, Phonon, and Vibrational Properties of Monolayer XO2 (X = Cr, Mo, W) from First Principles Calculations. Mater. Today Commun. 2022, 30, 103183. [Google Scholar] [CrossRef]
- Yakovkin, I. Dirac Cones in Graphene, Interlayer Interaction in Layered Materials, and the Band Gap in MoS2. Crystals 2016, 6, 143. [Google Scholar] [CrossRef] [Green Version]
- Pike, N.A.; Pachter, R. Angular Dependence of the Second-Order Nonlinear Optical Response in Janus Transition Metal Dichalcogenide Monolayers. J. Phys. Chem. C 2022, 126, 16243–16252. [Google Scholar] [CrossRef]
- Taghizadeh, A.; Thygesen, K.S.; Pedersen, T.G. Two-Dimensional Materials with Giant Optical Nonlinearities near the Theoretical Upper Limit. ACS Nano 2021, 15, 7155–7167. [Google Scholar] [CrossRef]
- Lucking, M.C.; Beach, K.; Terrones, H. Large Second Harmonic Generation in Alloyed TMDs and Boron Nitride Nanostructures. Sci. Rep. 2018, 8, 10118. [Google Scholar] [CrossRef] [PubMed] [Green Version]





| This Work | Other Works | ||||||
|---|---|---|---|---|---|---|---|
| Lattice Parameter (Å) | Bandgap (eV) | Lattice Parameter (Å) | Bandgap (eV) | ||||
| a, b | PBE | HSE | a, b | PBE | HSE | Ref. | |
| MoSO | 2.987 | 1.17 | 1.73 | 3.000 | 1.09 | 1.67 | [39] |
| MoSeO | 3.050 | 0.87 | 1.14 | 3.077 | 0.82 | 1.32 | [33] |
| MoTeO | 3.172 | 0.24 | 0.71 | 3.170 | 0.25 | 0.73 | [31] |
| WSO | 2.982 | 1.62 | 2.01 | 3.050 | 1.48 | 2.06 | [60] |
| WSeO | 3.042 | 1.34 | 1.71 | 3.071 | 1.32 | 1.89 | [33] |
| WTeO | 3.16 | 0.55 | 0.96 | 3.190 | 0.52 | 0.97 | [60] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, P.; Ye, H.; Sun, N.; Liu, S.; Zhang, H. Second Harmonic Generation in Janus Transition Metal Chalcogenide Oxide Monolayers: A First-Principles Investigation. Nanomaterials 2023, 13, 2150. https://doi.org/10.3390/nano13142150
Su P, Ye H, Sun N, Liu S, Zhang H. Second Harmonic Generation in Janus Transition Metal Chalcogenide Oxide Monolayers: A First-Principles Investigation. Nanomaterials. 2023; 13(14):2150. https://doi.org/10.3390/nano13142150
Chicago/Turabian StyleSu, Peng, Han Ye, Naizhang Sun, Shining Liu, and Hu Zhang. 2023. "Second Harmonic Generation in Janus Transition Metal Chalcogenide Oxide Monolayers: A First-Principles Investigation" Nanomaterials 13, no. 14: 2150. https://doi.org/10.3390/nano13142150
APA StyleSu, P., Ye, H., Sun, N., Liu, S., & Zhang, H. (2023). Second Harmonic Generation in Janus Transition Metal Chalcogenide Oxide Monolayers: A First-Principles Investigation. Nanomaterials, 13(14), 2150. https://doi.org/10.3390/nano13142150






