Quantum Spin Hall Effect in Two-Monolayer-Thick InN/InGaN Coupled Multiple Quantum Wells
Abstract
:1. Introduction
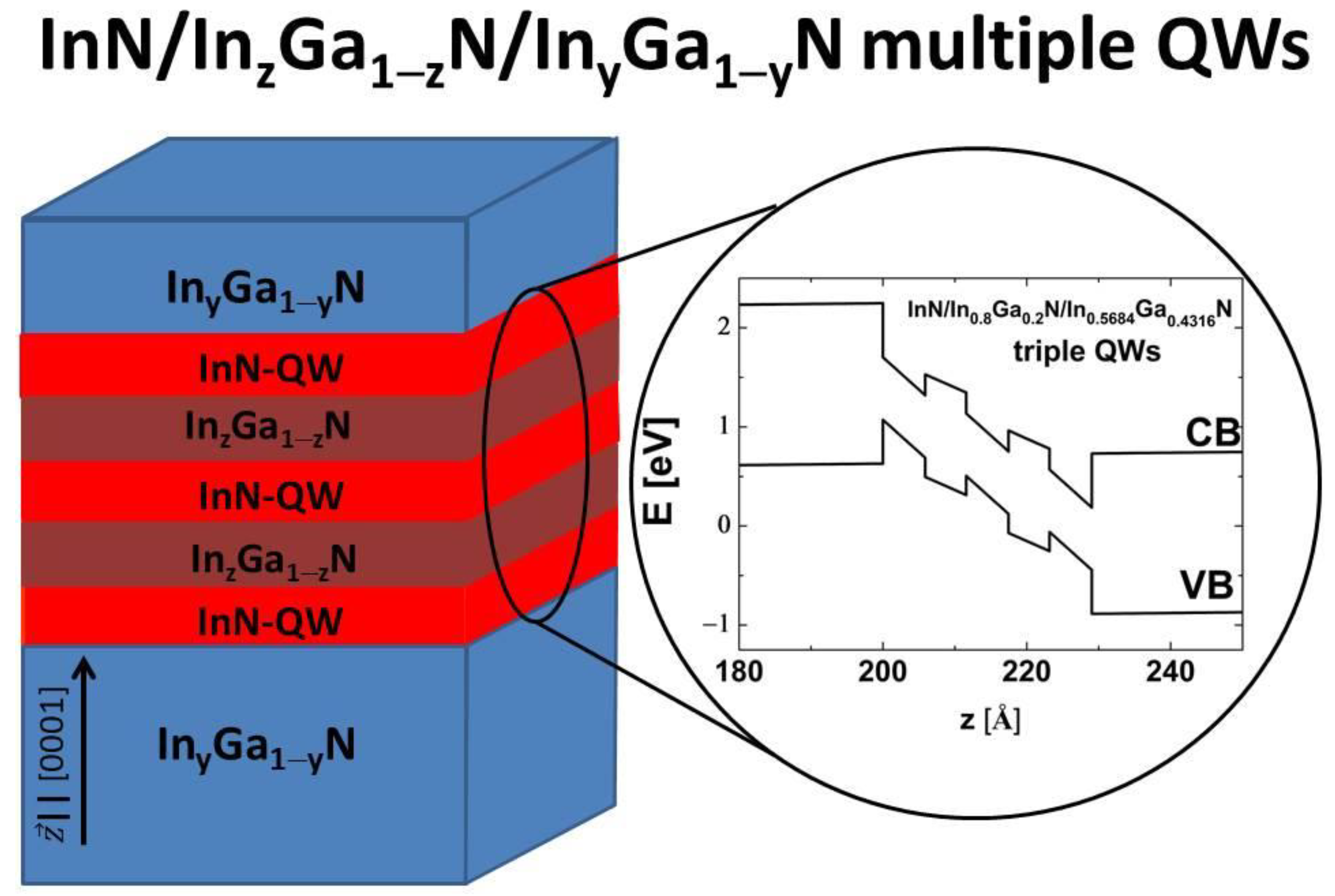
2. Theoretical Model
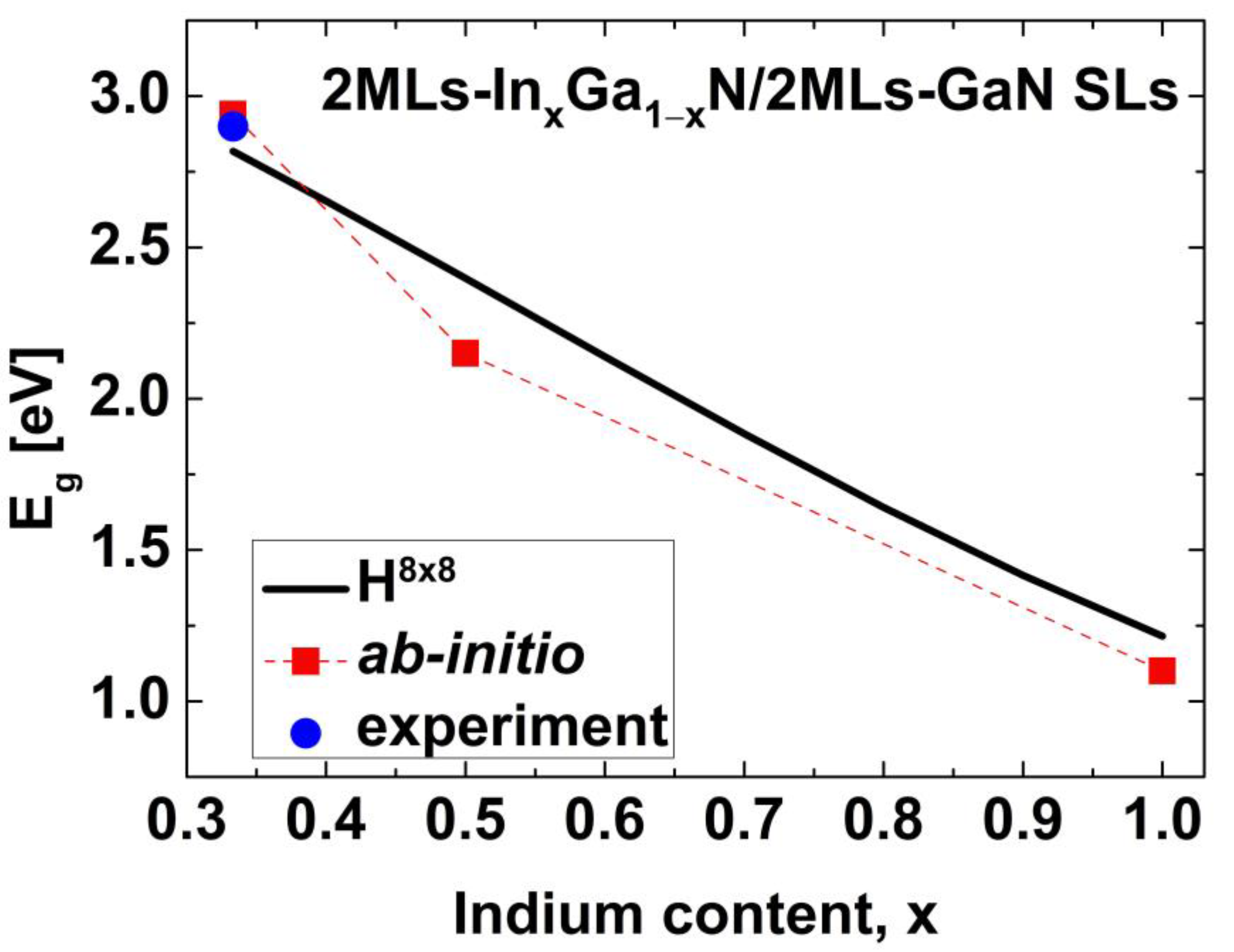
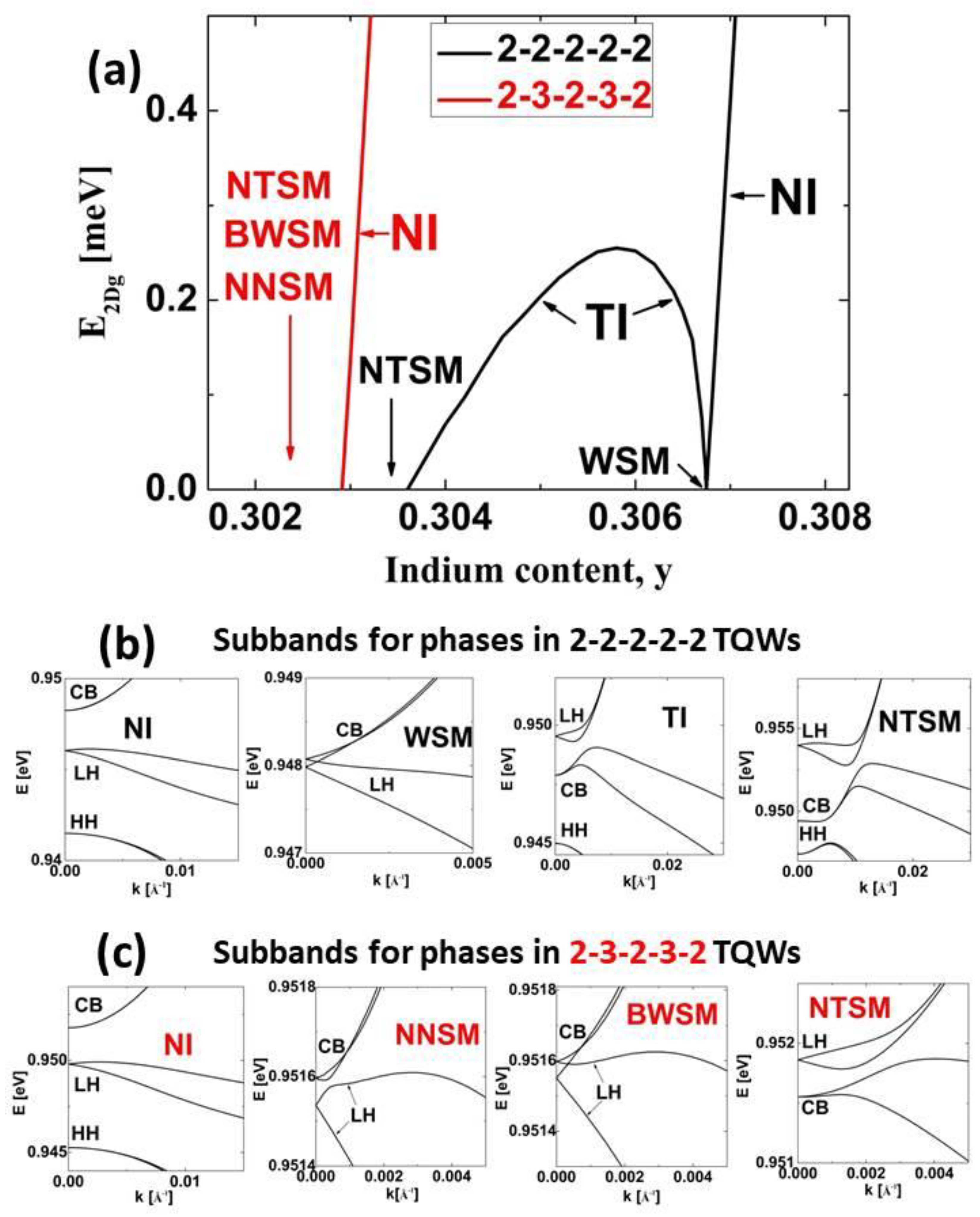
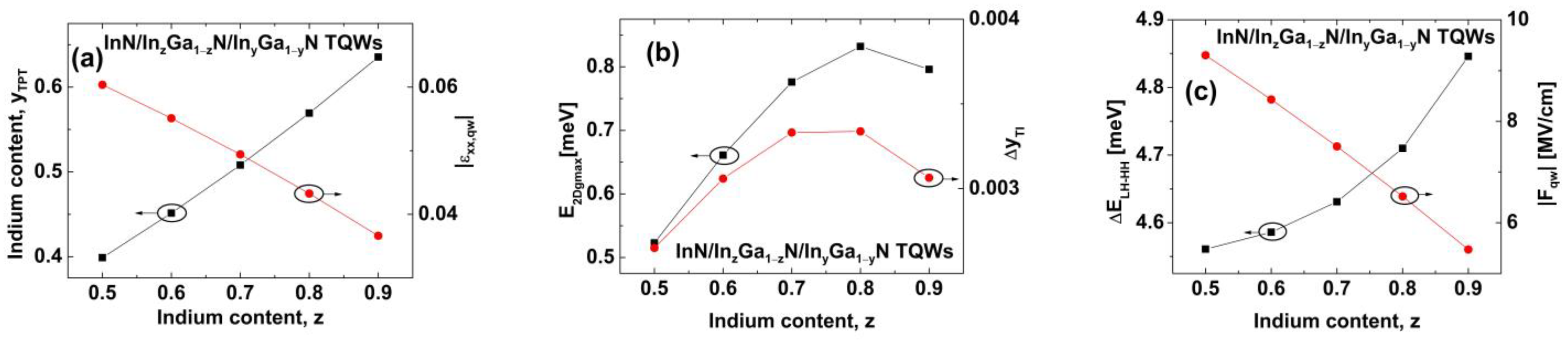
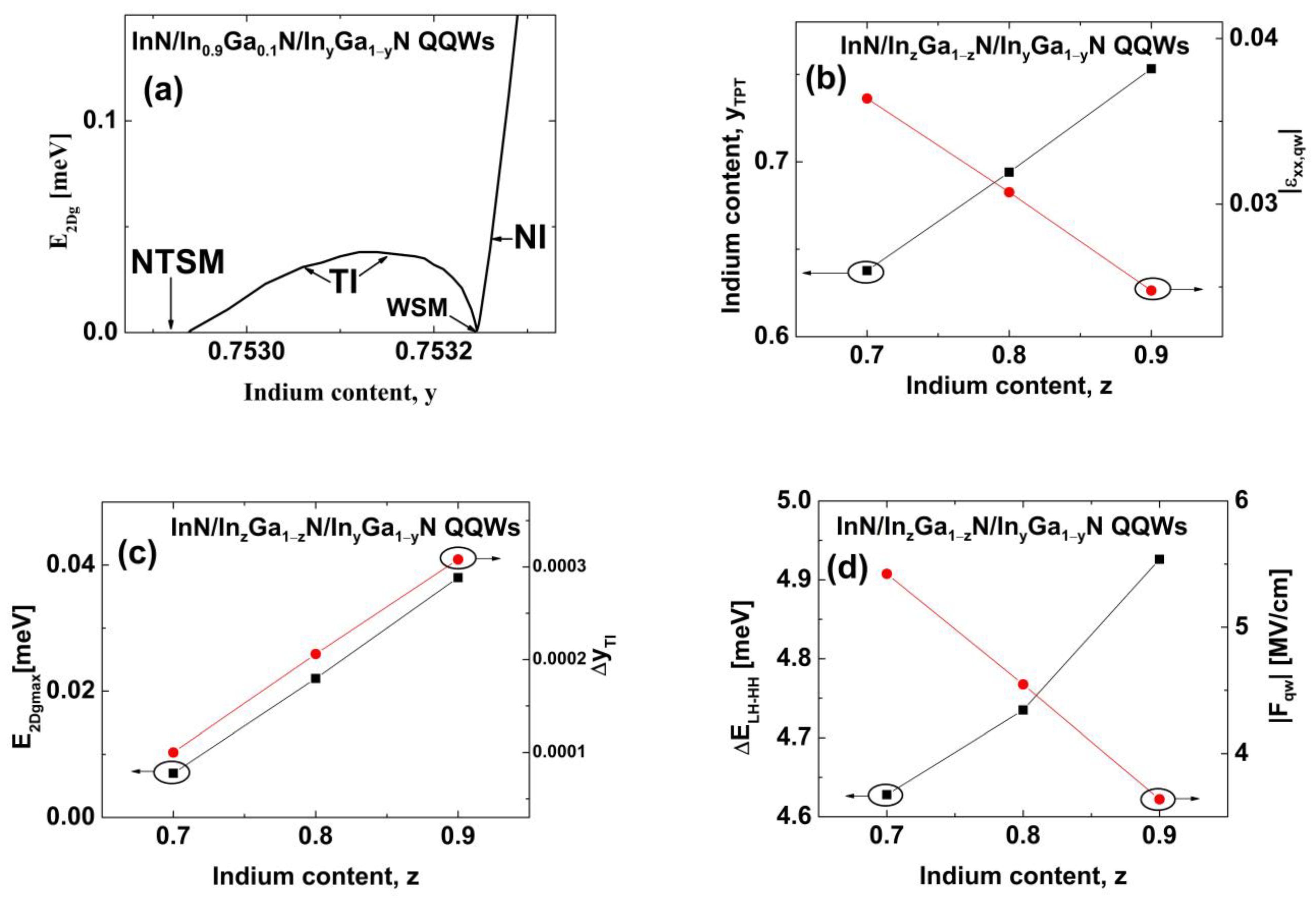
3. Results and Discussion
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045. [Google Scholar] [CrossRef] [Green Version]
- Bansil, A.; Lin, H.; Das, T. Colloquium: Topological band theory. Rev. Mod. Phys. 2016, 88, 021004. [Google Scholar] [CrossRef] [Green Version]
- Maciejko, J.; Hughes, T.L.; Zhang, S.C. The quantum spin Hall effect. Annu. Rev. Condens. Matter Phys. 2011, 2, 31–53. [Google Scholar] [CrossRef]
- Hsu, C.H.; Stano, P.; Klinovaja, J.; Loss, D. Helical liquids in semiconductors. Semicond. Sci. Technol. 2021, 36, 123003. [Google Scholar] [CrossRef]
- Yevtushenko, O.M.; Yudson, V. Protection of edge transport in quantum spin Hall samples: Spin-symmetry based general approach and examples. New J. Phys. 2022, 24, 023040. [Google Scholar] [CrossRef]
- Dietl, T. Effects of charge dopants in quantum spin Hall materials. Phys. Rev. Lett. 2023, 130, 086202. [Google Scholar] [CrossRef]
- Dietl, T. Quantitative theory of backscattering in topological HgTe and (Hg,Mn)Te quantum wells: Acceptor states, Kondo effect, precessional dephasing, and bound magnetic polaron. Phys. Rev. B 2023, 107, 085421. [Google Scholar] [CrossRef]
- Nilsson, J.; Akhmerov, A.R.; Beenakker, C.W.J. Splitting of a cooper pair by a pair of Majorana bound states. Phys. Rev. Lett. 2008, 101, 120403. [Google Scholar] [CrossRef] [Green Version]
- Elliot, S.R.; Franz, M. Colloquium: Majorana fermions in nuclear, particle, and solid-state physics. Rev. Mod. Phys. 2015, 87, 137. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Pan, W.; Bernevig, B.A.; Lutchyn, R.M. Detection of Majorana Kramers pairs using a quantum point contact. Phys. Rev. Lett. 2016, 117, 046804. [Google Scholar] [CrossRef] [Green Version]
- Aasen, D.; Hell, M.; Mishmash, R.V.; Higginbotham, A.; Danon, J.; Leijnse, M.; Jespersen, T.S.; Folk, J.A.; Marcus, C.M.; Flensberg, K.; et al. Milestones towards Majorana-based quantum computing. Phys. Rev. X 2016, 6, 031016. [Google Scholar] [CrossRef] [Green Version]
- Schrade, C.; Fu, L. Quantum computing with Majorana Kramers pairs. Phys. Rev. Lett. 2022, 129, 227002. [Google Scholar] [CrossRef] [PubMed]
- Kane, C.L.; Mele, E.J. Quantum spin Hall effect in graphene. Phys. Rev. Lett. 2005, 95, 226801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sichau, J.; Prada, M.; Anlauf, T.; Lyon, T.J.; Bosnjak, B.; Tiemann, L.; Blick, R.H. Resonance microwave measurements of an intrinsic spin-orbit coupling gap in graphene: A possible indication of a topological state. Phys. Rev. Lett. 2019, 122, 046403. [Google Scholar] [CrossRef] [Green Version]
- Bernevig, B.A.; Hughes, T.L.; Zhang, S.C. Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science 2006, 314, 1757–1761. [Google Scholar] [CrossRef] [Green Version]
- Konig, M.; Wiedmann, S.; Brune, C.; Roth, A.; Buhmann, H.; Molenkamp, L.W.; Qi, X.L.; Zhang, S.C. Quantum spin Hall effect in HgTe quantum wells. Science 2007, 318, 766–770. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Hughes, T.L.; Qi, X.L.; Wang, K.; Zhang, S.C. Quantum spin Hall effect in inverted type-II semiconductors. Phys. Rev. Lett. 2008, 100, 236601. [Google Scholar] [CrossRef]
- Knez, I.; Du, R.R.; Sullivan, G. Evidence for helical edge modes in inverted InAs/GaSb quantum wells. Phys. Rev. Lett. 2011, 107, 136603. [Google Scholar] [CrossRef] [Green Version]
- Leubner, P.; Lunczer, L.; Brüne, C.; Buhmann, H.; Molenkamp, L.W. Strain engineering of the band gap of HgTe quantum wells using superlattice virtual substrates. Phys. Rev. Lett. 2016, 117, 086403. [Google Scholar] [CrossRef] [Green Version]
- Du, L.; Li, T.; Lou, W.; Wu, X.; Liu, X.; Han, Z.; Zhang, C.; Sullivan, G.; Ikhlassi, A.; Chang, K.; et al. Tuning edge states in strained-layer InAs/GaInSb quantum spin Hall insulators. Phys. Rev. Lett. 2017, 119, 056803. [Google Scholar] [CrossRef] [Green Version]
- Ire, H.; Akiho, T.; Couëdo, F.; Suzuki, K.; Onomitsu, K.; Muraki, K. Energy gap tuning and gate-controlled topological phase transition in InAs/InxGa1−xSb composite quantum wells. Phys Rev. Mater. 2020, 4, 104201. [Google Scholar] [CrossRef]
- Avogadri, C.; Gebert, S.; Krishtopenko, S.S.; Castillo, I.; Consejo, C.; Ruffenach, S.; Roblin, C.; Bray, C.; Krupko, Y.; Juillaguet, S.; et al. Large inverted band gap in strained three-layer InAs/GaInSb quantum wells. Phys. Rev. Res. 2022, 4, L042042. [Google Scholar] [CrossRef]
- Krishtopenko, S.S.; Teppe, F. Quantum spin Hall insulator with a large bandgap, Dirac fermions, and bilayer graphene analog. Sci. Adv. 2022, 4, eaap7529. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miao, M.; Yan, Q.; Van de Walle, C.G.; Lou, W.K.; Li, L.L.; Chang, K. Polarization-driven topological insulator transition in a GaN/InN/GaN quantum well. Phys. Rev. Lett. 2012, 109, 186803. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Łepkowski, S.P.; Bardyszewski, W. Topological phase transition and evolution of edge states in In-rich InGaN/GaN quantum wells under hydrostatic pressure. J. Phys. Condens. Matter 2017, 29, 055702. [Google Scholar] [CrossRef]
- Łepkowski, S.P.; Bardyszewski, W. Topological insulator with negative spin-orbit coupling and transition between Weyl and Dirac semimetals in InGaN-based quantum wells. Sci. Rep. 2018, 8, 15403. [Google Scholar] [CrossRef] [Green Version]
- de Carvalho, I.C.; Schleife, A.; Bechstedt, F. Influence of exchange and correlation on structural and electronic properties of AlN, GaN, and InN polytypes. Phys. Rev. B 2011, 84, 195105. [Google Scholar] [CrossRef] [Green Version]
- Punya, A.; Lambrecht, W.R.L. Valence band effective-mass Hamiltonians for the group-III nitrides from quasiparticle self-consistent GW band structures. Phys. Rev. B 2012, 85, 195147. [Google Scholar] [CrossRef] [Green Version]
- Lin, K.I.; Chen, Y.J.; Cheng, Y.C.; Gwo, S. Investigation of valence-band splitting in InN by low-temperature photoreflectance spectroscopy. Jpn. J. Appl. Phys. 2015, 54, 031001. [Google Scholar] [CrossRef]
- Hiramatsu, K.; Kawaguchi, Y.; Shimizu, M.; Sawaki, N.; Zheleva, T.; Davis, R.F.; Tsuda, H.; Taki, W.; Kuwano, N.; Oki, K. The composition pulling effect in MOVPE grown InGaN on GaN and AlGaN and its TEM characterization. MRS Internet J. Nitride Semicond. 1997, 2, 6. [Google Scholar] [CrossRef]
- Pereira, S.; Correia, M.R.; Pereira, E.; O’Donnell, K.P.; Trager-Cowan, C.; Sweeney, F.; Alves, E. Compositional pulling effects in InxGa1−xN/GaN layers: A combined depth-resolved cathodoluminescence and Rutherford backscattering/channeling study. Phys. Rev. B 2001, 64, 205311. [Google Scholar] [CrossRef]
- Yoshikawa, A.; Che, S.B.; Yamaguchi, W.; Saito, H.; Wang, X.Q.; Ishitani, Y.; Hwang, E.S. Proposal and achievement of novel structure InN/GaN multiple quantum wells consisting of 1 ML and fractional monolayer InN wells inserted in GaN matrix. Appl. Phys. Lett. 2007, 90, 073101. [Google Scholar] [CrossRef]
- Zhou, L.; Dimakis, E.; Hathwar, R.; Aoki, T.; Smith, D.J.; Moustakas, T.D.; Goodnick, S.M.; McCartney, M.R. Measurement and effects of polarization fields on one-monolayer-thick InN/GaN multiple quantum wells. Phys. Rev. B 2013, 88, 125310. [Google Scholar] [CrossRef]
- Pan, W.; Dimakis, E.; Wang, G.T.; Moustakas, T.D.; Tsui, D.C. Two-dimensional electron gas in monolayer InN quantum wells. Appl. Phys. Lett. 2014, 105, 213503. [Google Scholar] [CrossRef]
- Suski, T.; Schulz, T.; Albrecht, M.; Wang, X.Q.; Gorczyca, I.; Skrobas, K.; Christensen, E.; Svane, A. The discrepancies between theory and experiment in the optical emission of monolayer In(Ga)N quantum wells revisited by transmission electron microscopy. Appl. Phys. Lett. 2014, 104, 182103. [Google Scholar] [CrossRef]
- Chèze, C.; Siekacz, M.; Isa, F.; Jenichen, B.; Feix, F.; Buller, J.; Schulz, T.; Albrecht, M.; Skierbiszewski, C.; Calarco, R.; et al. Investigation of interface abruptness and In content in (In,Ga)N/GaN superlattices. J. Appl. Phys. 2016, 120, 125307. [Google Scholar] [CrossRef]
- Chèze, C.; Feix, F.; Riechert, H.; Brandt, O.; Calarco, R.; Anikeeva, M.; Schulz, T.; Albrecht, M. In/GaN(0001)-() R30º adsorbate structure as a template for embedded (In,Ga)N/GaN monolayers and short-period superlattices. Appl. Phys. Lett. 2017, 110, 072104. [Google Scholar] [CrossRef] [Green Version]
- Dimitrakopulos, G.P.; Vasileiadis, I.G.; Smalc-Koziorowska, J.; Kret, S.; Dimakis, E.; Florini, N.; Kehagias, T.; Suski, T.; Karakostas, T.; Moustakas, T.D.; et al. Compositional and strain analysis of In(Ga)N/GaN short period superlattices. J. Appl. Phys. 2018, 123, 024304. [Google Scholar] [CrossRef]
- Lee, S.; Freysoldt, C.; Neugebauer, J. Ordering phenomena and formation of nanostructures in InxGa1-xN layers coherently grown on GaN(0001). Phys. Rev. B 2014, 90, 245301. [Google Scholar] [CrossRef]
- Lymperakis, L.; Schulz, T.; Freysoldt, C.; Anikeeva, M.; Chen, Z.; Zheng, X.; Shen, B.; Chèze, C.; Siekacz, M.; Wang, X.Q.; et al. Elastically frustrated rehybridization: Origin of chemical order and compositional limits in InGaN quantum wells. Phys. Rev. Mater. 2018, 2, 011601. [Google Scholar] [CrossRef]
- Schulz, T.; Lymperakis, L.; Anikeeva, M.; Siekacz, M.; Wolny, P.; Markurt, T.; Albrecht, M. Influence of strain on the indium incorporation in (0001) GaN. Phys. Rev. Mater. 2020, 4, 073404. [Google Scholar] [CrossRef]
- Vasileiadis, I.G.; Lymperakis, L.; Adikimenakis, A.; Gkotinakos, A.; Devulapalli, V.; Liebscher, C.H.; Androulidaki, M.; Hubner, R.; Karakostas, T.; Georgakilas, A.; et al. Substitutional synthesis of sub-nanometer InGaN/GaN quantum wells with high indium content. Sci. Rep. 2021, 11, 20606. [Google Scholar] [CrossRef] [PubMed]
- Sharma, T.K.; Towe, E. On ternary nitride substrates for visible semiconductor light-emitters. Appl. Phys. Lett. 2010, 96, 191105. [Google Scholar] [CrossRef]
- Däubler, J.; Passow, T.; Aidam, R.; Köhler, K.; Kirste, L.; Kunzer, M.; Wagner, J. Long wavelength emitting GaInN quantum wells on metamorphic GaInN buffer layers with enlarged in-plane lattice parameter. Appl. Phys. Lett. 2014, 105, 111111. [Google Scholar] [CrossRef]
- Fabien, C.A.M.; Gunning, B.P.; Doolittle, W.A.; Fischer, A.M.; Wei, Y.O.; Xie, H.; Ponce, F.A. Low-temperature growth of InGaN films over the entire composition range by MBE. J. Cryst. Growth 2015, 425, 115–118. [Google Scholar] [CrossRef] [Green Version]
- Even, A.; Laval, G.; Ledoux, O.; Ferret, P.; Sotta, D.; Guiot, E.; Levy, F.; Robin, I.C.; Dussaigne, A. Enhanced In incorporation in full InGaN heterostructure grown on relaxed InGaN pseudo-substrate. Appl. Phys. Lett. 2017, 110, 262103. [Google Scholar] [CrossRef]
- Pasayat, S.S.; Gupta, C.; Wong M., S.; Wang, Y.; Nakamura, S.; Denbaars S., P.; Keller, S.; Mishra U., K. Growth of strain-relaxed InGaN on micrometer-sized patterned compliant GaN pseudo-substrates. Appl. Phys. Lett. 2020, 116, 111101. [Google Scholar] [CrossRef]
- Grandal, J.; Pereiro, J.; Bengoechea-Encabo, A.; Fernández-Garrido, S.; Sánchez-Garcia, M.A.; Munoz, E.; Calleja, E.; Luna, E.; Trampert, A. InN/InGaN multiple quantum wells emitting at 1.5 μm grown by molecular beam epitaxy. Appl. Phys. Lett. 2011, 98, 061901. [Google Scholar] [CrossRef] [Green Version]
- Naranjo, F.B.; Kandaswamy, P.K.; Valdueza-Felip, S.; Calvo, V.; González-Herráez, M.; Martin-López, S.; Corredera, P.; Méndez, J.A.; Mutta, G.R.; Lacroix, B.; et al. Nonlinear absorption of InN/InGaN multiple-quantum well structures at optical telecommunication wavelengths. Appl. Phys. Lett. 2011, 98, 031902. [Google Scholar] [CrossRef] [Green Version]
- Valdueza-Felip, S.; Rigutti, L.; Naranjo, F.B.; Ruterana, P.; Mangeney, J.; Julien, F.H.; González-Herráez, M.; Monroy, E. Carrier localization in InN/InGaN multiple-quantum wells with high In-content. Appl. Phys. Lett. 2012, 101, 062109. [Google Scholar] [CrossRef]
- Suski, T.; Staszczak, G.; Korona, K.P.; Lefebvre, P.; Monroy, E.; Drozdz, P.A.; Muzioł, G.; Skierbiszewski, C.; Kulczykowski, M.; Matuszewski, M.; et al. Switching of exciton character in double InGaN/GaN quantum wells. Phys. Rev. B 2018, 98, 165302. [Google Scholar] [CrossRef] [Green Version]
- Łepkowski, S.P.; Anwar, A.R. Polarization-induced phase transitions in ultra-thin InGaN-based double quantum wells. Nanomaterials 2022, 12, 2418. [Google Scholar] [CrossRef]
- Zhou, B.; Lu, H.Z.; Chu, R.L.; Shen, S.Q.; Niu, Q. Finite size effects on helical edge states in a quantum spin-Hall system. Phys. Rev. Lett. 2008, 101, 246807. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhi, C.; Bin, Z. Finite size effects on helical edge states in HgTe quantum wells with the spin-orbit coupling due to bulk- and structure-inversion asymmetries. Chin. Phys. B 2014, 23, 037304. [Google Scholar] [CrossRef]
- Papaj, M.; Cywiński, Ł.; Wróbel, J.; Dietl, T. Conductance oscillations in quantum point contacts of InAs/GaSb heterostructures. Phys. Rev. B 2016, 93, 195305. [Google Scholar] [CrossRef] [Green Version]
- Vurgaftman, I.; Meyer, J.R. Band parameters for nitrogen-containing semiconductors. J. Appl. Phys. 2003, 94, 3675. [Google Scholar] [CrossRef]
- Gorczyca, I.; Łepkowski, S.P.; Suski, T.; Christensen, N.E.; Svane, A. Influence of indium clustering on the band structure of semiconducting ternary and quaternary nitride alloys. Phys. Rev. B 2009, 80, 075202. [Google Scholar] [CrossRef]
- Łepkowski, S.P.; Bardyszewski, W. Anomalous Rashba spin-orbit interaction in electrically controlled topological insulator based on InN/GaN quantum wells. J. Phys. Condens. Matter 2017, 29, 195702. [Google Scholar] [CrossRef] [PubMed]
- Łepkowski, S.P.; Bardyszewski, W. Corrigendum: Anomalous Rashba spin-orbit interaction in electrically controlled topological insulator based on InN/GaN quantum wells (2017 J. Phys.: Condens. Matter 29, 195702). J. Phys. Condens. Matter 2020, 33, 119501. [Google Scholar] [CrossRef]
- Łepkowski, S.P.; Anwar, A.R. Third-order elastic constants and biaxial relaxation coefficient in wurtzite group-III nitrides by hybrid-density functional theory calculations. J. Phys. Condens. Matter 2021, 33, 355402. [Google Scholar] [CrossRef]
- Łepkowski, S.P.; Anwar, A.R. Biaxial relaxation coefficient in group-III nitride quantum wells and thin films. Acta Phys. Pol. A 2022, 141, 130–134. [Google Scholar] [CrossRef]
- Łepkowski, S.P. Inapplicability of Martin transformation to elastic constants of zinc-blende and wurtzite group-III nitride alloys. J. Appl. Phys. 2015, 117, 105703. [Google Scholar] [CrossRef]
- Bernardini, F.; Fiorentini, V. Spontaneous versus piezoelectric polarization in III-V nitrides: Conceptual aspects and practical consequences. Phys. Stat. Sol. 1999, 216, 391–398. [Google Scholar] [CrossRef]
- Prodhomme, P.-Y.; Beya-Wakata, A.; Bester, G. Nonlinear piezoelectricity in wurtzite semiconductors. Phys. Rev. B 2013, 88, 121304. [Google Scholar] [CrossRef]
- Chuang, S.L.; Chang, C.S. k∙p method for strained wurtzite semiconductors. Phys. Rev. B 1996, 54, 2491–2504. [Google Scholar] [CrossRef]
- Łepkowski, S.P.; Gorczyca, I.; Stefańska-Skrobas, K.; Christensen, N.E.; Svane, A. Deformation potentials in AlGaN and InGaN alloys and their impact on optical polarization properties of nitride quantum wells. Phys. Rev. B 2013, 88, 081202. [Google Scholar] [CrossRef]
- Huebner, K.H.; Thornton, E.A. The Finite Element Method for Engineers; Wiley: New York, NY, USA, 1982. [Google Scholar]
- Gorczyca, I.; Suski, T.; Strak, P.; Staszczak, G.; Christensen, N.E. Band gap engineering of In(Ga)N/GaN short period superlattices. Sci. Rep. 2017, 7, 16055. [Google Scholar] [CrossRef] [Green Version]
- Gorczyca, I.; Suski, T.; Christensen, N.E.; Svane, A. Theoretical study of nitride short period superlattices. J. Phys. Condens. Matter 2018, 30. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Staszczak, G.; Gorczyca, I.; Grzanka, E.; Smalc-Koziorowska, J.; Targowski, G.; Czernecki, R.; Siekacz, M.; Grzanka, S.; Skierbiszewski, C.; Schulz, T.; et al. Bandgap behavior of InGaN/GaN short period superlattices grown by metal-organic vapor phase epitaxy. Phys. Stat. Sol. 2017, 254, 1600710. [Google Scholar] [CrossRef]
- Nakamura, K.; Shimizu, A.; Koshiba, M.; Hayata, K. Finite-element analysis of the miniband structures of semiconductor superlattices with arbitrary periodic potential profiles. IEEE J. Quantum Electron. 1991, 27, 2035–2041. [Google Scholar] [CrossRef]
- Olshanetsky, E.B.; Kvon, Z.D.; Gusev, G.M.; Levin, A.D.; Raichev, O.E.; Mikhailov, N.N.; Dvoretsky, S.A. Persistence of a two-dimensional topological insulator state in wide HgTe quantum wells. Phys. Rev. Lett. 2015, 114, 126802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dan, M.; Hu, G.; Li, I.; Zhang, Y. High performance piezotronic logic nanodevices based on GaN/InN/GaN topological insulator. Nano Energy 2018, 50, 544–551. [Google Scholar] [CrossRef] [Green Version]
- Litvinov, V.I. Quantum anomalous Hall state with Chern number C = 2 in wurtzite quantum wells. Phys. Rev. B 2021, 104, 245304. [Google Scholar] [CrossRef]
- Ferreira, G.J.; Candido, D.R.; Hernandez, F.G.G.; Gusev, G.M.; Olshanetsky, E.B.; Mikhailov, N.N.; Dvoretsky, S.A. Engineering topological phases in triple HgTe/CdTe quantum wells. Sci. Rep. 2022, 12, 2617. [Google Scholar] [CrossRef] [PubMed]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Łepkowski, S.P. Quantum Spin Hall Effect in Two-Monolayer-Thick InN/InGaN Coupled Multiple Quantum Wells. Nanomaterials 2023, 13, 2212. https://doi.org/10.3390/nano13152212
Łepkowski SP. Quantum Spin Hall Effect in Two-Monolayer-Thick InN/InGaN Coupled Multiple Quantum Wells. Nanomaterials. 2023; 13(15):2212. https://doi.org/10.3390/nano13152212
Chicago/Turabian StyleŁepkowski, Sławomir P. 2023. "Quantum Spin Hall Effect in Two-Monolayer-Thick InN/InGaN Coupled Multiple Quantum Wells" Nanomaterials 13, no. 15: 2212. https://doi.org/10.3390/nano13152212
APA StyleŁepkowski, S. P. (2023). Quantum Spin Hall Effect in Two-Monolayer-Thick InN/InGaN Coupled Multiple Quantum Wells. Nanomaterials, 13(15), 2212. https://doi.org/10.3390/nano13152212






