Ultra-Compact and Broadband Nano-Integration Optical Phased Array
Abstract
:1. Introduction
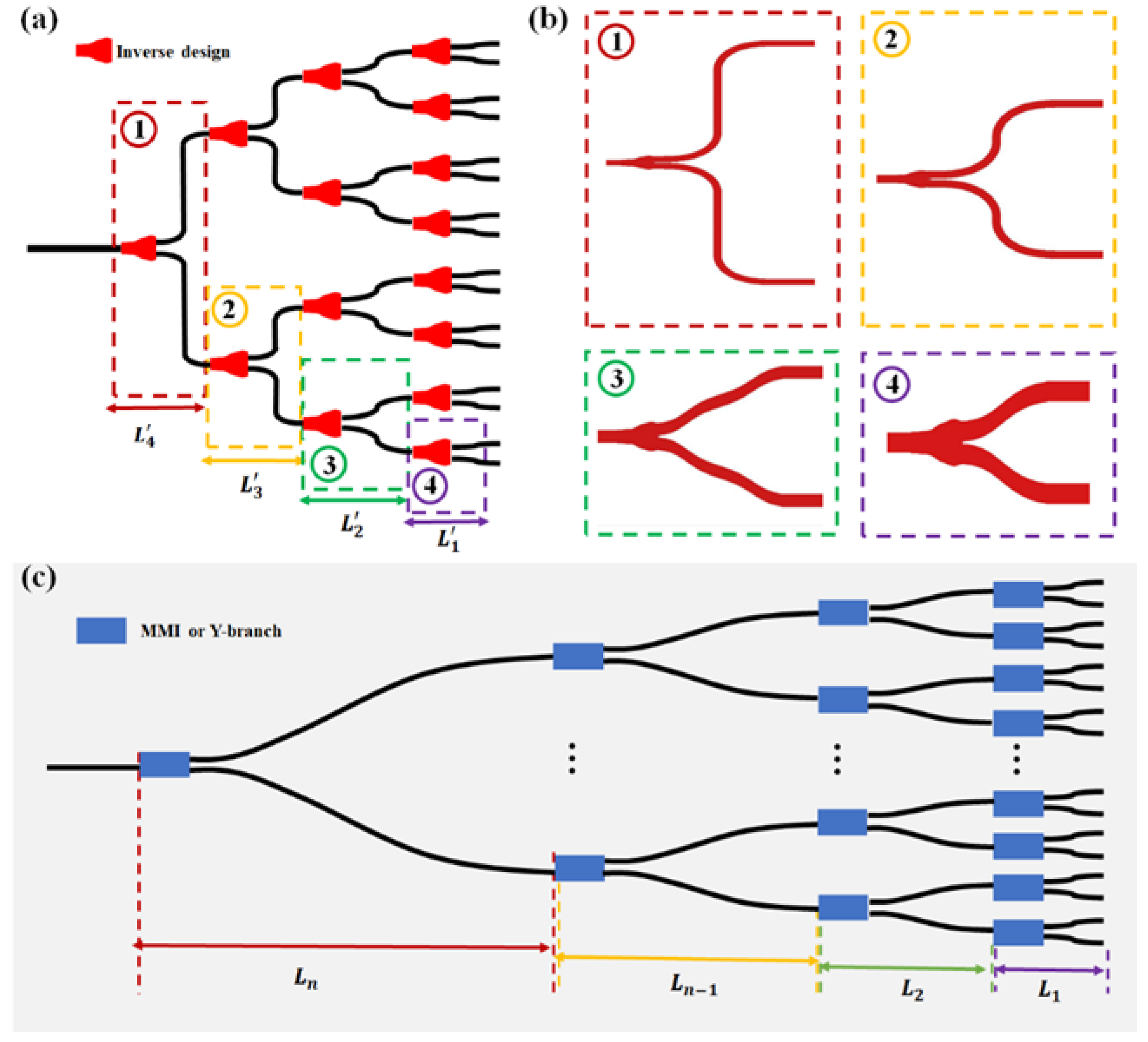
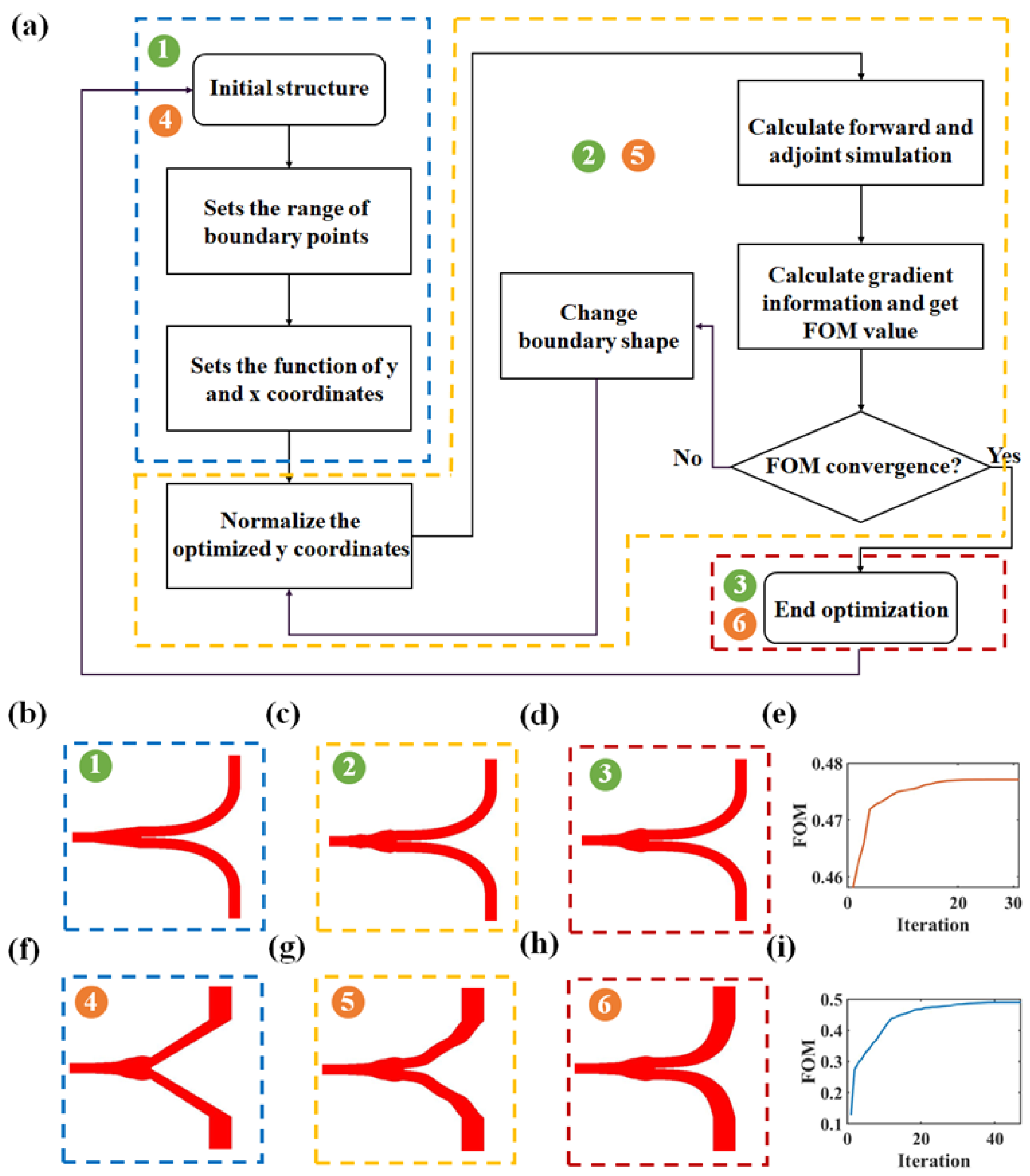
2. Design and Optimization
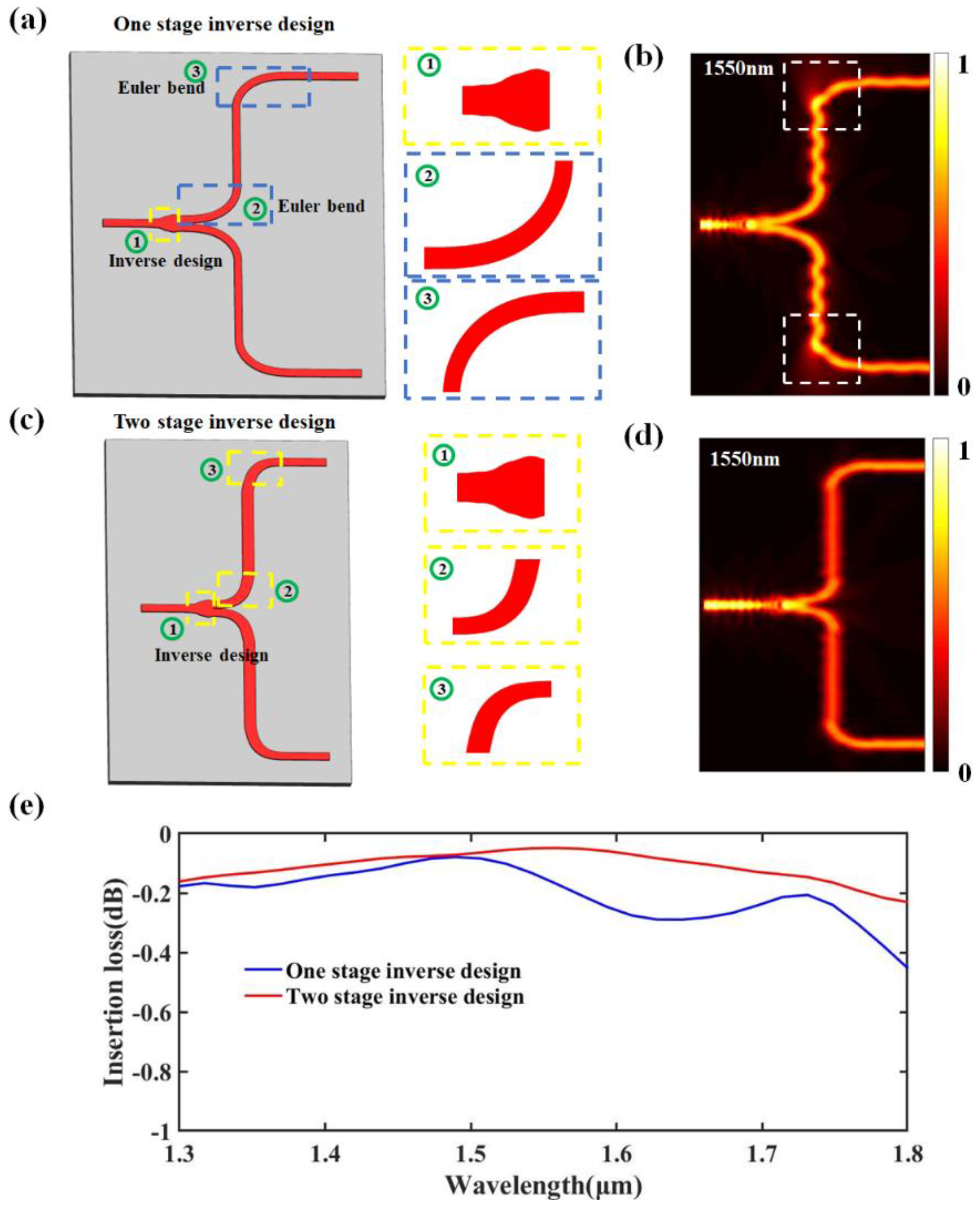
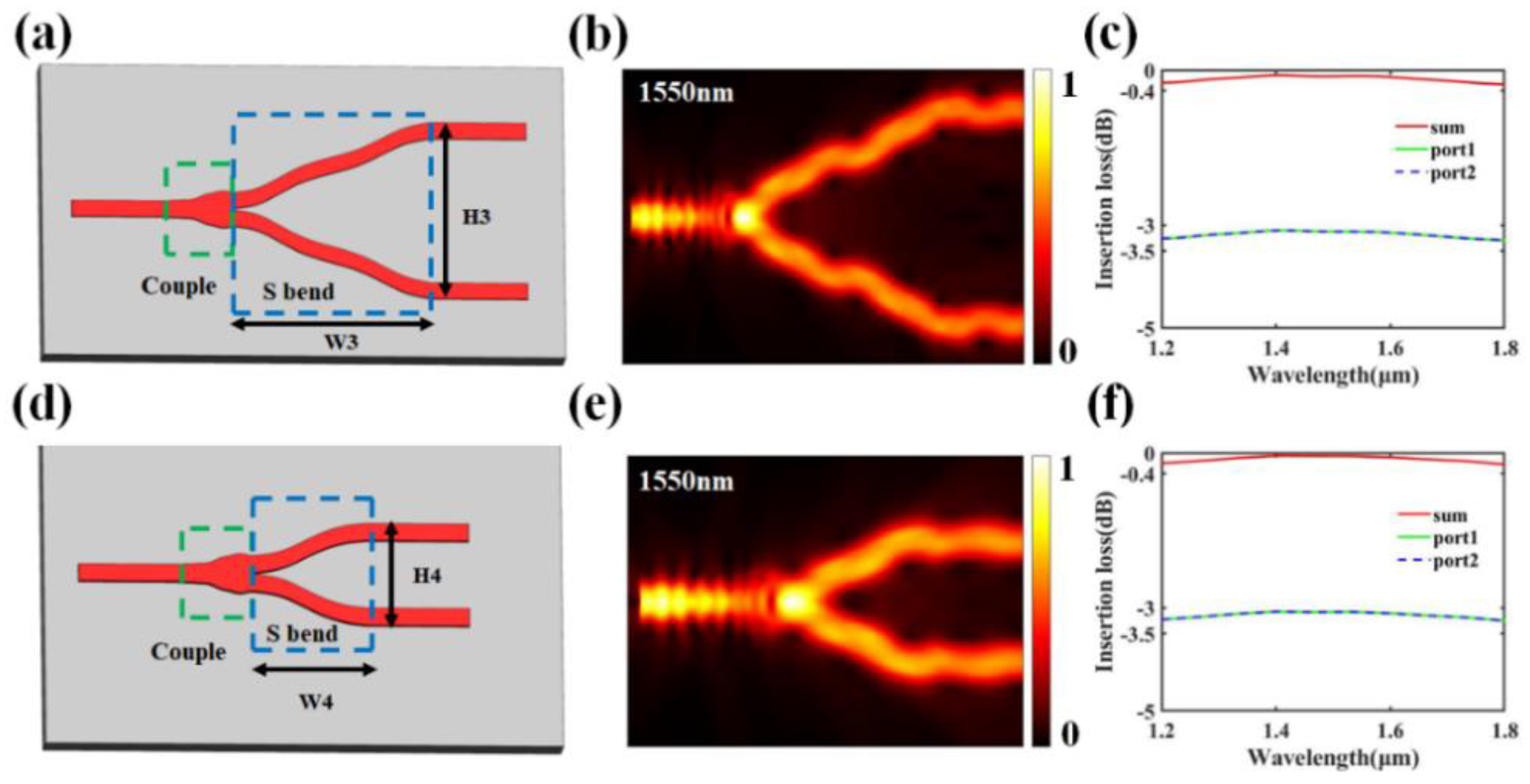
3. Simulation and Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Poulton, C.V.; Yaacobi, A.; Cole, D.B.; Byrd, M.J.; Raval, M.; Vermeulen, D.; Watts, M.R. Coherent solid-state LIDAR with silicon photonic optical phased arrays. Opt. Lett. 2017, 42, 4091–4094. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Kwon, K.; Henriksson, J.; Luo, J.; Wu, M.C. A large-scale microelectromechanical-systems-based silicon photonics LiDAR. Nature 2022, 603, 253–258. [Google Scholar] [CrossRef] [PubMed]
- Martin, A.; Dodane, D.; Leviandier, L.; Dolfi, D.; Naughton, A.; O’brien, P.; Spuessens, T.; Baets, R.; Lepage, G.; Verheyen, P. Photonic integrated circuit-based FMCW coherent LiDAR. J. Light. Technol. 2018, 36, 4640–4645. [Google Scholar] [CrossRef]
- Kohno, Y.; Komatsu, K.; Tang, R.; Ozeki, Y.; Nakano, Y.; Tanemura, T. Ghost imaging using a large-scale silicon photonic phased array chip. Opt. Express 2019, 27, 3817–3823. [Google Scholar] [CrossRef]
- Raval, M.; Yaacobi, A.; Watts, M.R. Integrated visible light phased array system for autostereoscopic image projection. Opt. Lett. 2018, 43, 3678–3681. [Google Scholar] [CrossRef]
- Aflatouni, F.; Abiri, B.; Rekhi, A.; Hajimiri, A. Nanophotonic projection system. Opt. Express 2015, 23, 21012–21022. [Google Scholar] [CrossRef]
- Rhee, H.-W.; You, J.-B.; Yoon, H.; Han, K.; Kim, M.; Lee, B.G.; Kim, S.-C.; Park, H.-H. 32 Gbps data transmission with 2D beam-steering using a silicon optical phased array. IEEE Photonics Technol. Lett. 2020, 32, 803–806. [Google Scholar] [CrossRef]
- Guan, B.; Scott, R.P.; Qin, C.; Fontaine, N.K.; Su, T.; Ferrari, C.; Cappuzzo, M.; Klemens, F.; Keller, B.; Earnshaw, M. Free-space coherent optical communication with orbital angular, momentum multiplexing/demultiplexing using a hybrid 3D photonic integrated circuit. Opt. Express 2014, 22, 145–156. [Google Scholar] [CrossRef] [PubMed]
- Rabinovich, W.S.; Goetz, P.G.; Pruessner, M.; Mahon, R.; Ferraro, M.S.; Park, D.; Fleet, E.; Deprenger, M.J. Free space optical communication link using a silicon photonic optical phased array. In Free-Space Laser Communication and Atmospheric Propagation XXVII; SPIE: Bellingham, WA, USA, 2015; Volume 9354, pp. 96–101. [Google Scholar] [CrossRef]
- Hutchison, D.N.; Sun, J.; Doylend, J.K.; Kumar, R.; Heck, J.; Kim, W.; Phare, C.T.; Feshali, A.; Rong, H. High-resolution aliasing-free optical beam steering. Optica 2016, 3, 887–890. [Google Scholar] [CrossRef]
- Tyler, N.A.; Fowler, D.; Malhouitre, S.; Garcia, S.; Grosse, P.; Rabaud, W.; Szelag, B. SiN integrated optical phased arrays for two-dimensional beam steering at a single near-infrared wavelength. Opt. Express 2019, 27, 5851–5858. [Google Scholar] [CrossRef]
- Shin, M.C.; Mohanty, A.; Watson, K.; Bhatt, G.R.; Phare, C.T.; Miller, S.A.; Zadka, M.; Lee, B.S.; Ji, X.; Datta, I. Chip-scale blue light phased array. Opt. Lett. 2020, 45, 1934–1937. [Google Scholar] [CrossRef]
- Xu, H.; Shi, Y. Diffraction engineering for silicon waveguide grating antenna by harnessing bound state in the continuum. Nanophotonics 2020, 9, 1439–1446. [Google Scholar] [CrossRef]
- Zadka, M.; Chang, Y.-C.; Mohanty, A.; Phare, C.T.; Roberts, S.P.; Lipson, M. On-chip platform for a phased array with minimal beam divergence and wide field-of-view. Opt. Express 2018, 26, 2528–2534. [Google Scholar] [CrossRef] [PubMed]
- Ginel-Moreno, P.; Pereira-Martín, D.; Hadij-Elhouati, A.; Winnie, N.Y.; Melati, D.; Xu, D.-X.; Janz, S.; Ortega-Moñux, A.; Wangüemert-Pérez, J.G.; Halir, R. Highly efficient optical antenna with small beam divergence in silicon waveguides. Opt. Lett. 2020, 45, 5668–5671. [Google Scholar] [CrossRef]
- Yaacobi, A.; Sun, J.; Moresco, M.; Leake, G.; Coolbaugh, D.; Watts, M.R. Integrated phased array for wide-angle beam steering. Opt. Lett. 2014, 39, 4575–4578. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.-X.; Li, Y.-Z.; Tao, M.; Wang, Y.-B.; Hou, Y.; Chen, B.-S.; Li, Y.-X.; Qin, L.; Gao, F.-L.; Luo, X.-S. Large-scale integrated multi-lines optical phased array chip. IEEE Photonics J. 2020, 12, 1–8. [Google Scholar] [CrossRef]
- Li, Y.; Chen, B.; Na, Q.; Xie, Q.; Tao, M.; Zhang, L.; Zhi, Z.; Li, Y.; Liu, X.; Luo, X. Wide-steering-angle high-resolution optical phased array. Photonics Res. 2021, 9, 2511–2518. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, S.; Wang, K.; Skafidas, E. Ultra-broadband and low-loss 3 dB optical power splitter based on adiabatic tapered silicon waveguides. Opt. Lett. 2016, 41, 2053–2056. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Liu, Y.; Wang, Z.; Liu, Y.; Du, J.; Song, Q.; Xu, K. Ultra-broadband 3 dB power splitter from 1.55 to 2 µm wave band. Opt. Lett. 2021, 46, 4232–4235. [Google Scholar] [CrossRef]
- Sheng, Z.; Wang, Z.; Qiu, C.; Li, L.; Pang, A.; Wu, A.; Wang, X.; Zou, S.; Gan, F. A compact and low-loss MMI coupler fabricated with CMOS technology. IEEE Photonics J. 2012, 4, 2272–2277. [Google Scholar] [CrossRef]
- Rouifed, M.-S.; Littlejohns, C.G.; Tina, G.X.; Qiu, H.; Penades, J.S.; Nedeljkovic, M.; Zhang, Z.; Liu, C.; Thomson, D.J.; Mashanovich, G.Z. Ultra-compact MMI-based beam splitter demultiplexer for the NIR/MIR wavelengths of 1.55 μm and 2 μm. Opt. Express 2017, 25, 10893–10900. [Google Scholar] [CrossRef]
- Banerji, S.; Majumder, A.; Hamrick, A.; Menon, R.; Sensale-Rodriguez, B. Machine learning enables design of on-chip integrated silicon T-junctions with footprint of 1.2 μm × 1.2 μm. Nano Commun. Netw. 2020, 25, 100312. [Google Scholar] [CrossRef]
- Shen, Y.; Sun, J.; Shen, X.; Wang, J.; Sun, L.; Han, K.; Wang, G. A compact T-branch beam splitter based on anomalous reflection in two-dimensional photonic crystals. Chin. Opt. Lett. 2008, 6, 709–712. [Google Scholar] [CrossRef]
- Ahmadivand, A.; Pala, N.; Golmohammadi, S. Electromagnetic wave propagation along T and Y-splitters composed of silicon nanorods, gold slots, and silica substrate. Opt. Commun. 2015, 343, 73–79. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, S.; Lim, A.E.-J.; Lo, G.-Q.; Galland, C.; Baehr-Jones, T.; Hochberg, M. A compact and low loss Y-junction for submicron silicon waveguide. Opt. Express 2013, 21, 1310–1316. [Google Scholar] [CrossRef]
- Molesky, S.; Lin, Z.; Piggott, A.Y.; Jin, W.; Vucković, J.; Rodriguez, A.W. Inverse design in nanophotonics. Nat. Photonics 2018, 12, 659–670. [Google Scholar] [CrossRef]
- Lu, L.; Liu, D.; Zhou, F.; Li, D.; Cheng, M.; Deng, L.; Fu, S.; Xia, J.; Zhang, M. Inverse-designed single-step-etched colorless 3 dB couplers based on RIE-lag-insensitive PhC-like subwavelength structures. Opt. Lett. 2016, 41, 5051–5054. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Yang, J.; Chen, D.; Bai, W.; Han, J.; Zhang, Z.; Zhang, J.; He, X.; Han, Y.; Liang, L. Implementation of on-chip multi-channel focusing wavelength demultiplexer with regularized digital metamaterials. Nanophotonics 2019, 9, 159–166. [Google Scholar] [CrossRef]
- Wang, K.; Ren, X.; Chang, W.; Lu, L.; Liu, D.; Zhang, M. Inverse design of digital nanophotonic devices using the adjoint method. Photonics Res. 2020, 8, 528–533. [Google Scholar] [CrossRef]
- Hughes, T.W.; Minkov, M.; Williamson, I.A.; Fan, S. Adjoint method and inverse design for nonlinear nanophotonic devices. ACS Photonics 2018, 5, 4781–4787. [Google Scholar] [CrossRef]
- Shen, B.; Wang, P.; Polson, R.; Menon, R. An integrated-nanophotonics polarization beamsplitter with 2.4 × 2.4 μm2 footprint. Nat. Photonics 2015, 9, 378–382. [Google Scholar] [CrossRef]
- Xu, J.; Liu, Y.; Guo, X.; Song, Q.; Xu, K. Inverse design of a dual-mode 3-dB optical power splitter with a 445 nm bandwidth. Opt. Express 2022, 30, 26266–26274. [Google Scholar] [CrossRef]
- Xu, K.; Liu, L.; Wen, X.; Sun, W.; Zhang, N.; Yi, N.; Sun, S.; Xiao, S.; Song, Q. Integrated photonic power divider with arbitrary power ratios. Opt. Lett. 2017, 42, 855–858. [Google Scholar] [CrossRef]
- Zheng, Z.-H.; Chen, Y.; Chen, H.-Y.; Chen, J.-H. Ultra-compact reconfigurable device for mode conversion and dual-mode DPSK demodulation via inverse design. Opt. Express 2021, 29, 17718–17725. [Google Scholar] [CrossRef] [PubMed]
- Lalau-Keraly, C.M.; Bhargava, S.; Miller, O.D.; Yablonovitch, E. Adjoint shape optimization applied to electromagnetic design. Opt. Express 2013, 21, 21693–21701. [Google Scholar] [CrossRef] [PubMed]
- Ruan, X.; Li, H.; Chu, T. Inverse-Designed Ultra-Compact Polarization Splitter–Rotator in Standard Silicon Photonic Platforms With Large Fabrication Tolerance. J. Light. Technol. 2022, 40, 7142–7149. [Google Scholar] [CrossRef]
- Piggott, A.Y.; Petykiewicz, J.; Su, L.; Vučković, J. Fabrication-constrained nanophotonic inverse design. Sci. Rep. 2017, 7, 1786. [Google Scholar] [CrossRef]
- Mckinley, S.; Levine, M. Cubic spline interpolation. Coll. Redw. 1998, 45, 1049–1060. [Google Scholar]
- Cherchi, M.; Ylinen, S.; Harjanne, M.; Kapulainen, M.; Aalto, T. Dramatic size reduction of waveguide bends on a micron-scale silicon photonic platform. Opt. Express 2013, 21, 17814–17823. [Google Scholar] [CrossRef]
- Fujisawa, T.; Makino, S.; Sato, T.; Saitoh, K. Low-loss, compact, and fabrication-tolerant Si-wire 90 waveguide bend using clothoid and normal curves for large scale photonic integrated circuits. Opt. Express 2017, 25, 9150–9159. [Google Scholar] [CrossRef]
- Jiang, X.; Wu, H.; Dai, D. Low-loss and low-crosstalk multimode waveguide bend on silicon. Opt. Express 2018, 26, 17680–17689. [Google Scholar] [CrossRef] [PubMed]
- Sakai, A.; Fukazawa, T.; Baba, T. Low loss ultra-small branches in a silicon photonic wire waveguide. IEICE Trans. Electron. 2002, 85, 1033–1038. [Google Scholar]
- Yi, D.; Zhang, Y.; Tsang, H.K. Optimal Bezier curve transition for low-loss ultra-compact S-bends. Opt. Lett. 2021, 46, 876–879. [Google Scholar] [CrossRef] [PubMed]
- Dong, Z.; Qiu, J.; Chen, Y.; Wang, L.; Guo, H.; Wu, J. Ultracompact and ultralow-loss S-bends with easy fabrication by numerical optimization. Opt. Lett. 2022, 47, 2434–2437. [Google Scholar] [CrossRef]
- Yu, Z.; Feng, A.; Xi, X.; Sun, X. Inverse-designed low-loss and wideband polarization-insensitive silicon waveguide crossing. Opt. Lett. 2019, 44, 77–80. [Google Scholar] [CrossRef]





| Reference | Bend Radius (μm) | Loss (dB) | Wave Band (nm) | Type |
|---|---|---|---|---|
| [23] | / | 0.86 | 1530–1570 | T-branch |
| [43] | 1.78 | 0.2–0.4 | 1550 | T-branch |
| [44] | 2.5 | <0.22 | 1500–1600 | S bend |
| [45] | 2.5 | <0.27 | 1400–1700 | S bend |
| This work | ~2.5 | 0.2 | 1300–1800 | T-branch |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Feng, J.; Li, H.; Zhang, Y.; Wu, Y.; Hu, Y.; Wu, J.; Yang, J. Ultra-Compact and Broadband Nano-Integration Optical Phased Array. Nanomaterials 2023, 13, 2516. https://doi.org/10.3390/nano13182516
Wang Z, Feng J, Li H, Zhang Y, Wu Y, Hu Y, Wu J, Yang J. Ultra-Compact and Broadband Nano-Integration Optical Phased Array. Nanomaterials. 2023; 13(18):2516. https://doi.org/10.3390/nano13182516
Chicago/Turabian StyleWang, Zhicheng, Junbo Feng, Haitang Li, Yuqing Zhang, Yilu Wu, Yuqi Hu, Jiagui Wu, and Junbo Yang. 2023. "Ultra-Compact and Broadband Nano-Integration Optical Phased Array" Nanomaterials 13, no. 18: 2516. https://doi.org/10.3390/nano13182516
APA StyleWang, Z., Feng, J., Li, H., Zhang, Y., Wu, Y., Hu, Y., Wu, J., & Yang, J. (2023). Ultra-Compact and Broadband Nano-Integration Optical Phased Array. Nanomaterials, 13(18), 2516. https://doi.org/10.3390/nano13182516







