1. Introduction
Due to their potential applications in a variety of industries, including the aviation, space, chemical, automotive, and biomedicine industries [
1,
2,
3,
4], polymer nanocomposites have become a hot topic of study. Conducting polymer nanocomposites are used in numerous sensor applications to achieve intelligence, informationalization, and the future networks [
5]. Performance characteristics of sensors include sensitivity, creep, repeatability, hysteresis [
6], etc. Sensitivity and creep have become the two key metrics affecting the performance of sensors, since they influence measurement accuracy and stability, respectively. However, the fabrication of materials for outstanding sensitivity and creep resistance is heavily constrained by the complexity of the sensing system.
A promising method for enhancing the sensitivity and creep resistance has been identified as properly adjusting the choice of materials and the reasonable ratio. For a piezo-resistive tactile sensor, conductive filler particles are typically chosen from materials with the same dimensions, such as Ni (zero dimensions), CNT (one dimension), MLG (two dimensions), and others. High sensitivity and creep resistance for sensors have been the focus of an intense research effort. Xu et al. [
7] produced CNT/PDMS composites to obtain great sensitivity in terms of single particle filling. The interface connection and progressive deterioration of CNT-based polymer composites were shown by Xia X et al. [
8] to be major influences on the creep, and CNT could also be employed to increase the creep resistance of composites. Sun R. et al. [
9] investigated the impact of MWCNTs and Ni on nanocomposites with regard to two-particle filling. To attain high sensitivity, a synergistic effect between two particles occurred during the experiment studying the rearrangement reaction between Ni and MWCNTs under a magnetic field. The impact of MLGs, CNTs and their combination on sensitivity was investigated by Ali A. et al. [
10]. Their findings demonstrated that composites with mixed fillings have better sensitivity than composites with single-particle filling. The impact of CNTs, MLGs, and their combination on creep resistance was investigated by Charito et al. [
11]. The outcome showed that the creep resistance can be improved by mixing CNTs and MLGs. The impact of a magnetic field on MWCNT/Ni composites blended in various ratios was investigated by Lu C. et al. [
12]. The outcome of their study demonstrated that a stronger magnetic field can improve homogeneity, which further raises a composites’ conductivity. Chen Y. et al. [
13] developed a sensor based on CNT/Ni/PMXene composites for three-particle filling. They demonstrated how three materials interacting create a one- and two-dimensional integrated conductive network, greatly enhancing the sensitivity of composites.
Table 1 displays past efforts to enhance a sensor’s performance. It can be shown that the majority of the extant literature, particularly for single-particle filling and two-particle filling, has extensively evaluated the influence of filling particles on sensitivity or creep alone. There is not much research that has examined how particle selection affects creep and sensitivity. According to the available research, the combination of filler particles with various shapes and characteristics does improve sensitivity and creep resistance. The combination of Ni and CNT can increase the sensitivity of sensors [
9,
12,
13], the mixture of CNT and MLG can increase sensitivity and creep resistance [
10,
11], and the magnetic field can somewhat improve the performance of composites by increasing uniformity [
9,
12]. The combination of the aforementioned materials is, in theory, favorable to both sensitivity and creep. To our knowledge, no performance analysis of a combination of Ni, CNT, and MLG has been published. Therefore, it is worthwhile to conduct research on both sensitivities and creep using the above materials in combination.
The additive proportion of these materials is still difficult to determine because of the complexity of the synergistic effect and reaction mechanism among filling particles. Due to several factors, it is a time-consuming and expensive operation to estimate the manufacturing conditions without a mathematical model. In the area of material synthesis and process optimization, analysis and optimization of traditional experimental synthesis methods have been significant subjects of research. One of the most used statistical analysis models, RSM, was developed by Box and Wilson in 1951 [
14], and is used to evaluate and forecast many experimental conditions. RSM, which is widely used in the food and chemical fields [
15], creates prediction models to assess the single factor or interaction of each factor based on a small number of trials. However, due to the complex nonlinear situation, the RSM quadratic polynomial occasionally fails to provide the required forecast accuracy. In comparison to RSM, the SVR model has a good prediction of non-linear and unconnected data as a nonlinear regression model, which improves the speed of operation by transforming the objective function, improving the conditions of the equations, and lowering the complexity of the computation [
16]. It has been widely used in many engineering fields. Considering the high accuracy of SVR, it may overcome the disadvantages of RSM. Although RSM and SVR models have been utilized for process prediction in the food and chemical fields, few studies have used RSM or SVR models in the sensor field to estimate and analyze performance. Thus, such a technique deserves study.
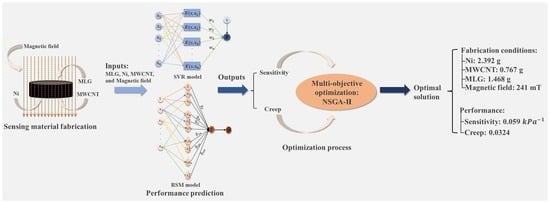
This study represents the first attempt to model and optimize the sensitivity and creep resistance of multi-component conductive nanocomposites with a magnetic field, i.e., Ni, MWCNT, and MLG, under experimental conditions. RSM and SVR algorithms were used to forecast the experimental input conditions and the output performances, respectively. The NSGA-II method was used to determine the Pareto-optimal fronts for the experimental settings, and decision-making was used to choose the best option. This work illustrated the applicability of the suggested approach for performance prediction and optimization in the realm of intelligent sensing.