Dynamics and Processes on Laser-Irradiated Surfaces
Abstract
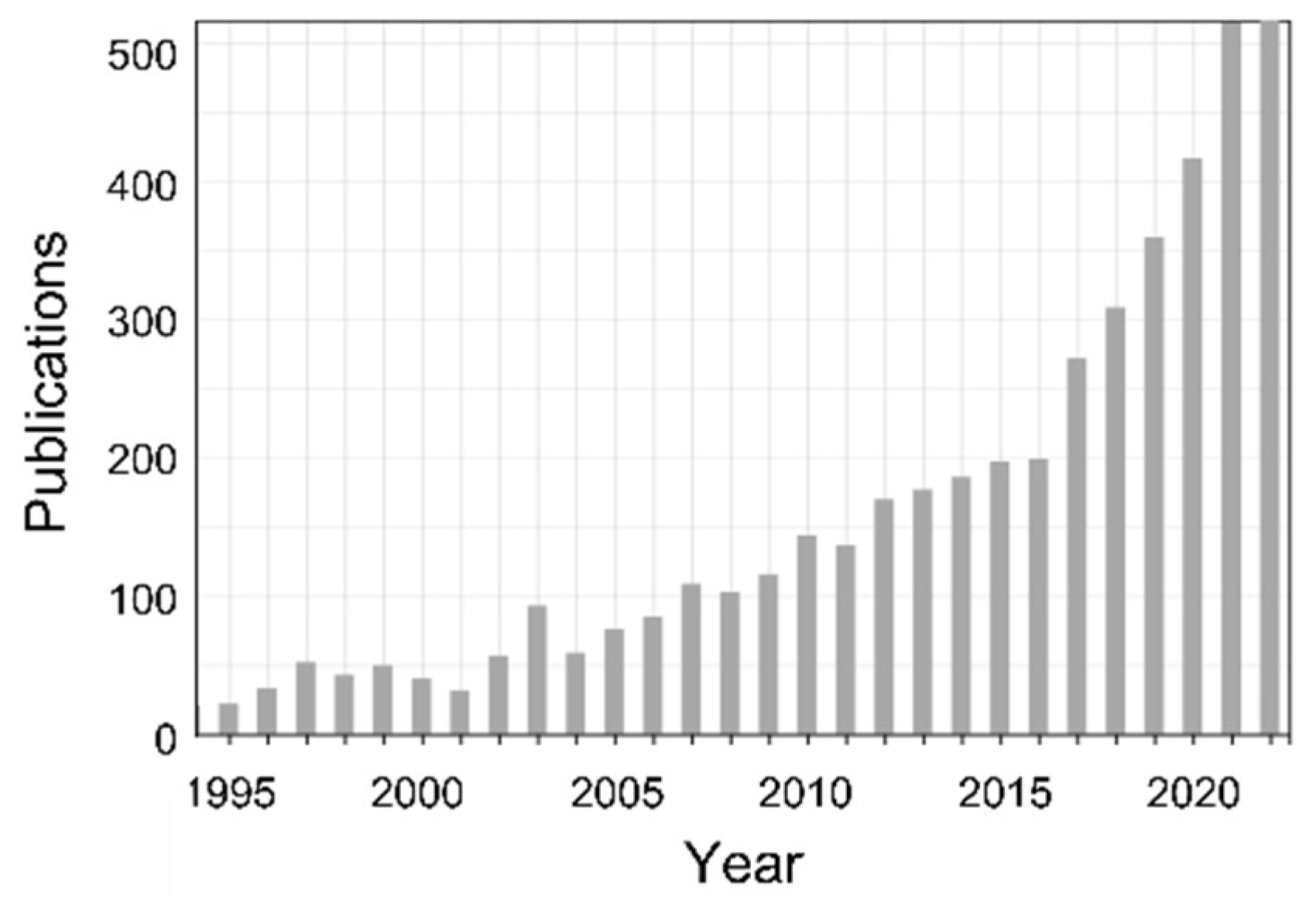
1. Introduction
2. Transient Modification of the Electronic System
- (1)
- Electrons can gain sufficient energy to escape from the material via ionization and (surface) charging;
- (2)
- The atomic binding can be softened;
- (3)
- The electron energy can be transferred to the phonon bath.
3. Permanent Material Modification
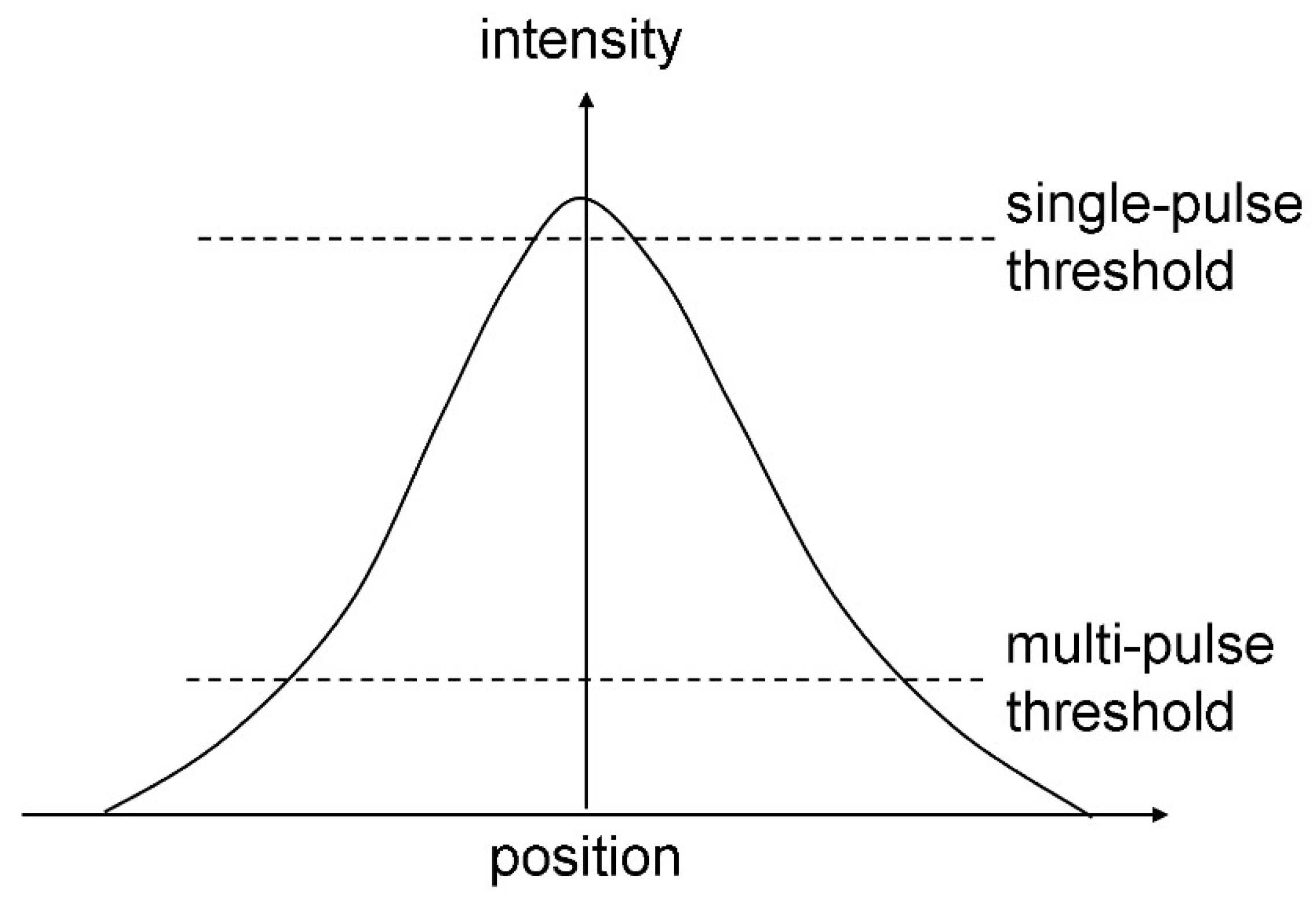
3.1. Subthreshold Interaction
3.1.1. Instantaneous Effects: Ionization and (Surface) Charging
3.1.2. Local Defects and Incubation
3.2. Near-Threshold Interaction
3.2.1. Hot Electron Excitation and Energy Dissipation
3.2.2. Rapid Heating and Melting
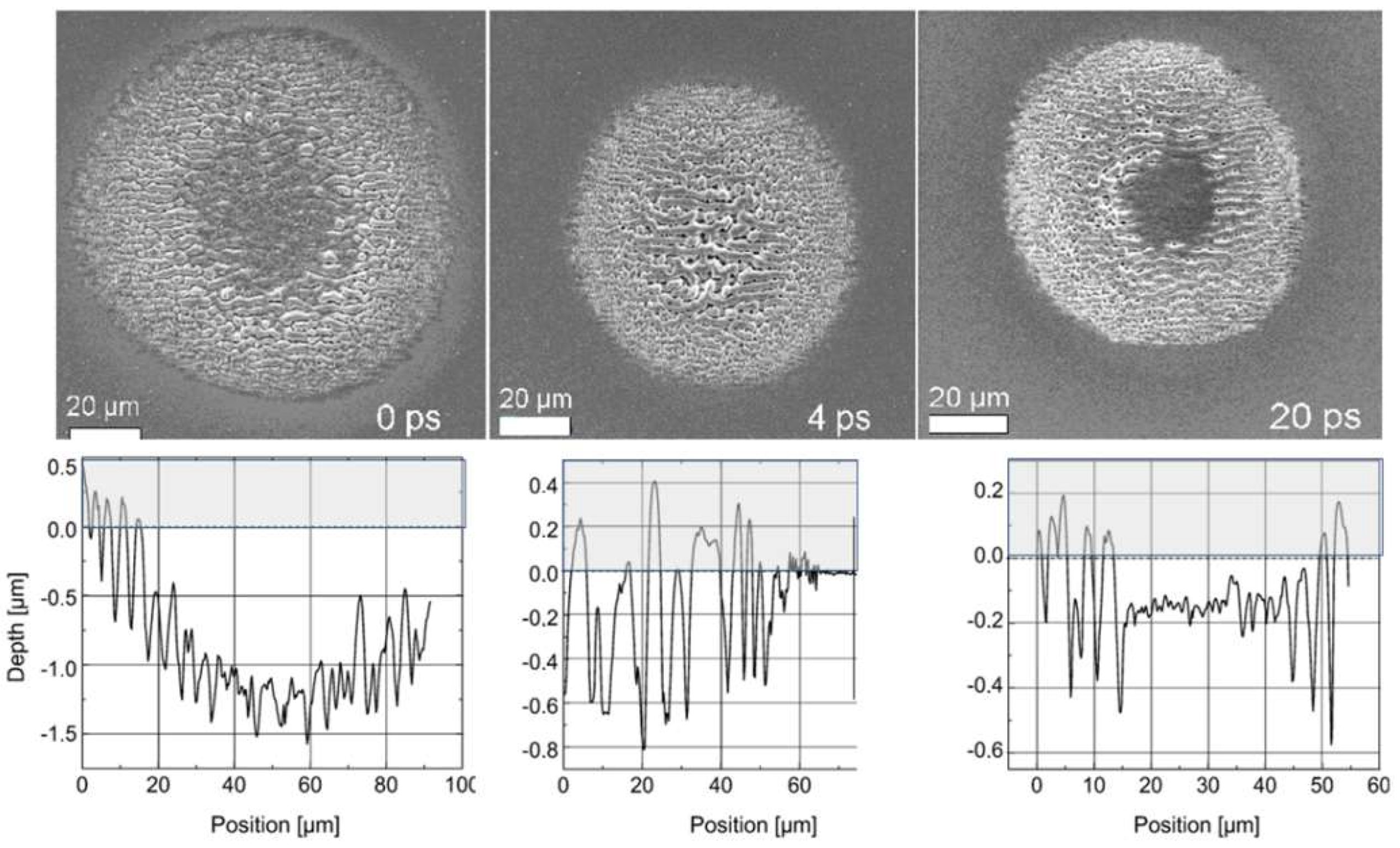
4. Modification of Surface Morphology
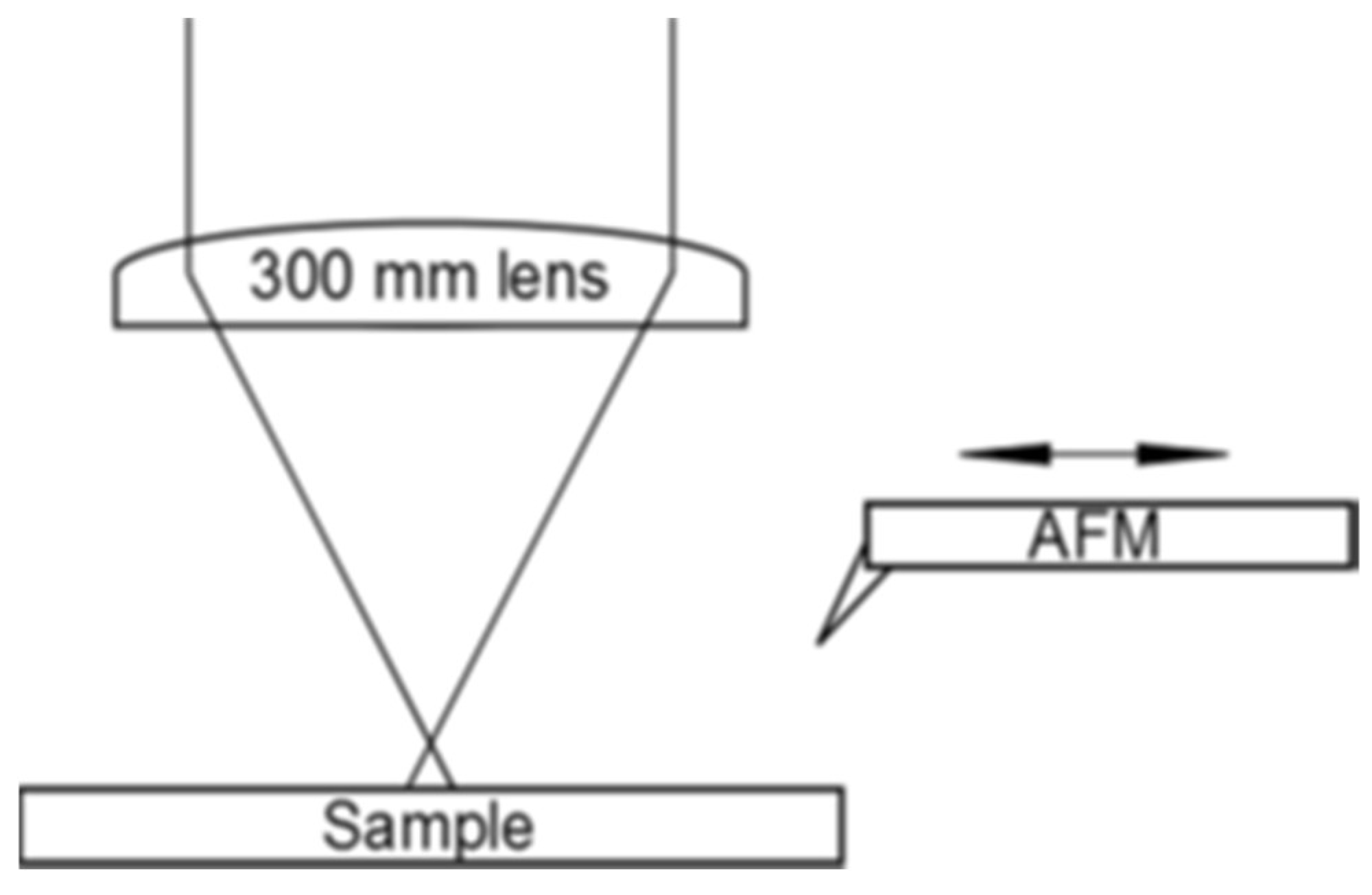
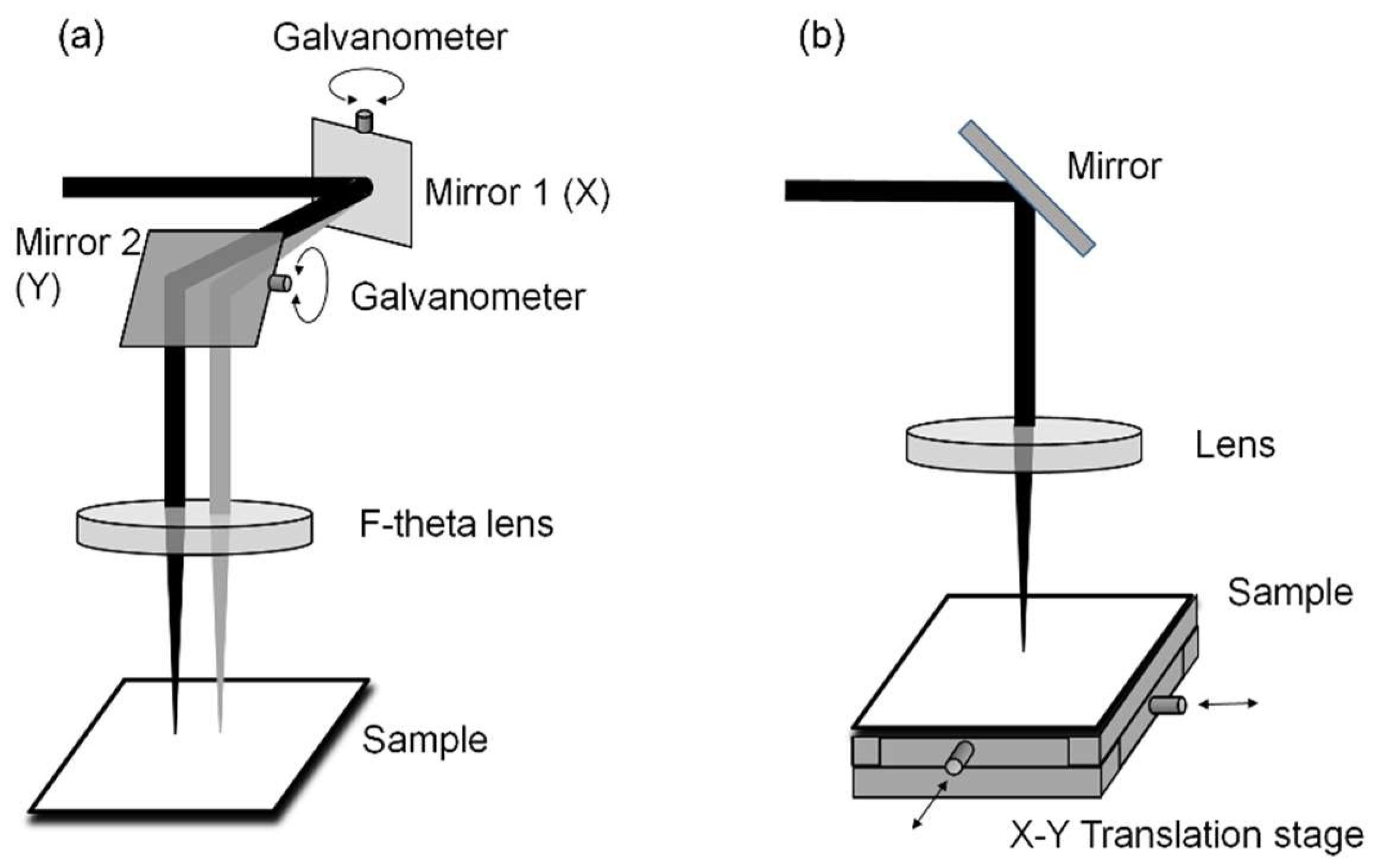
4.1. Experimental Structural Formation Results
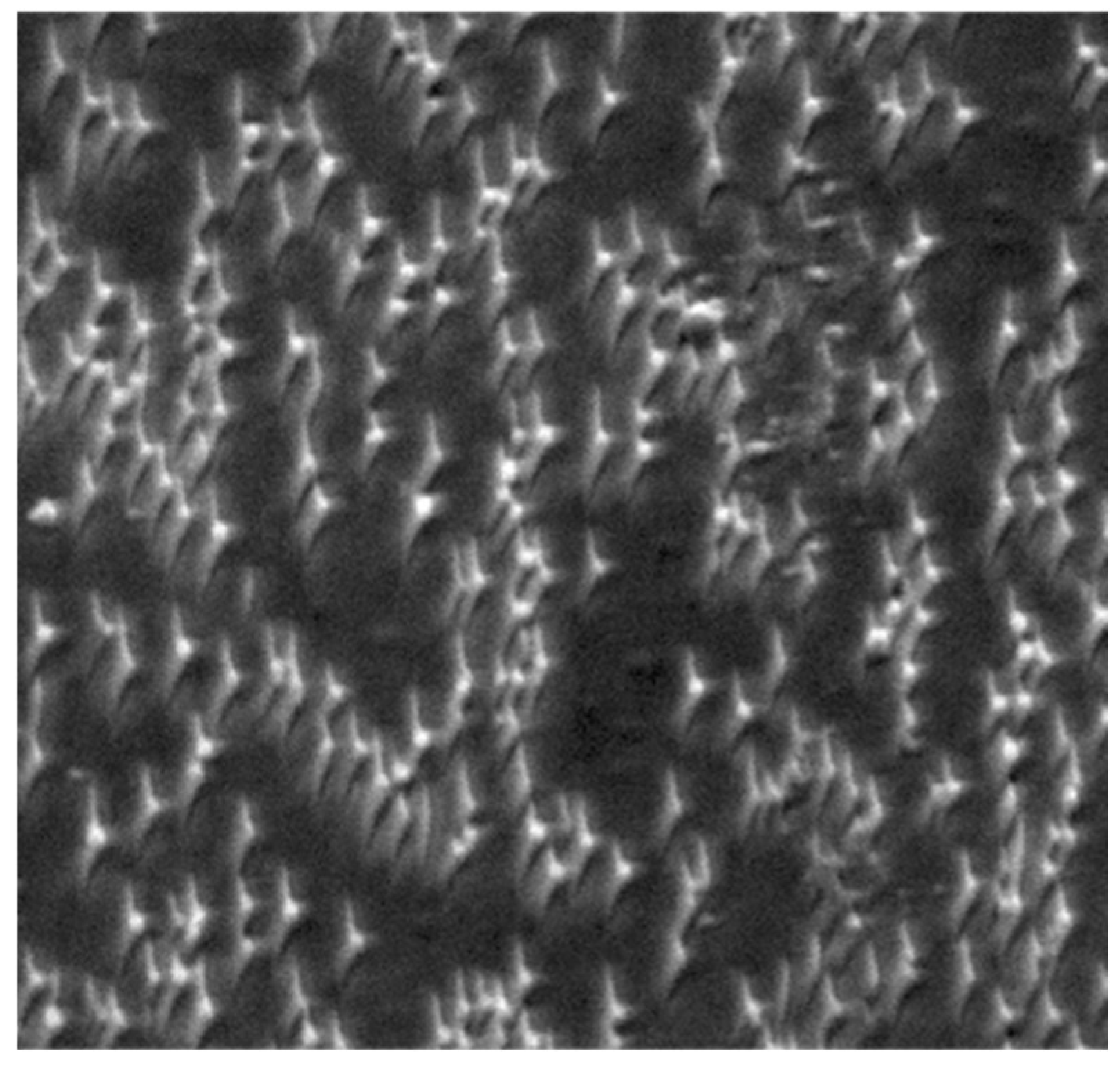
4.1.1. Laser Impact (LIPSS)
Texture of Near-Surface Volume
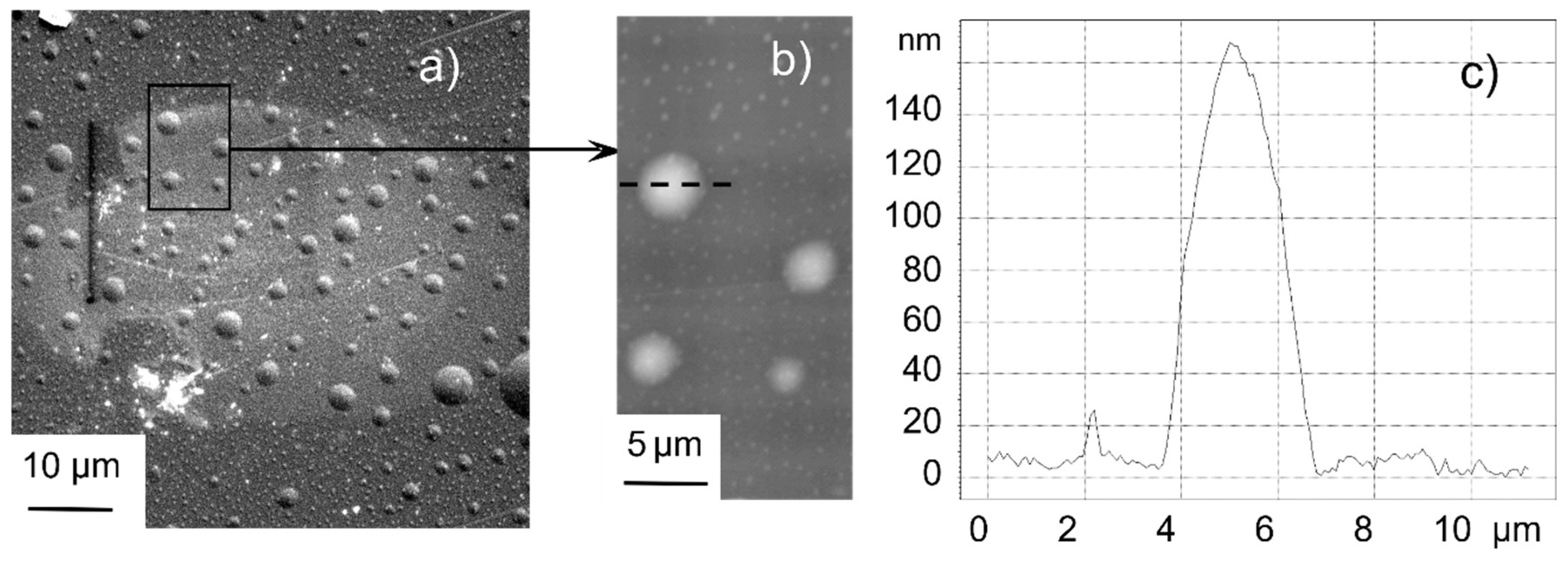
4.1.2. Ion Beam Impact
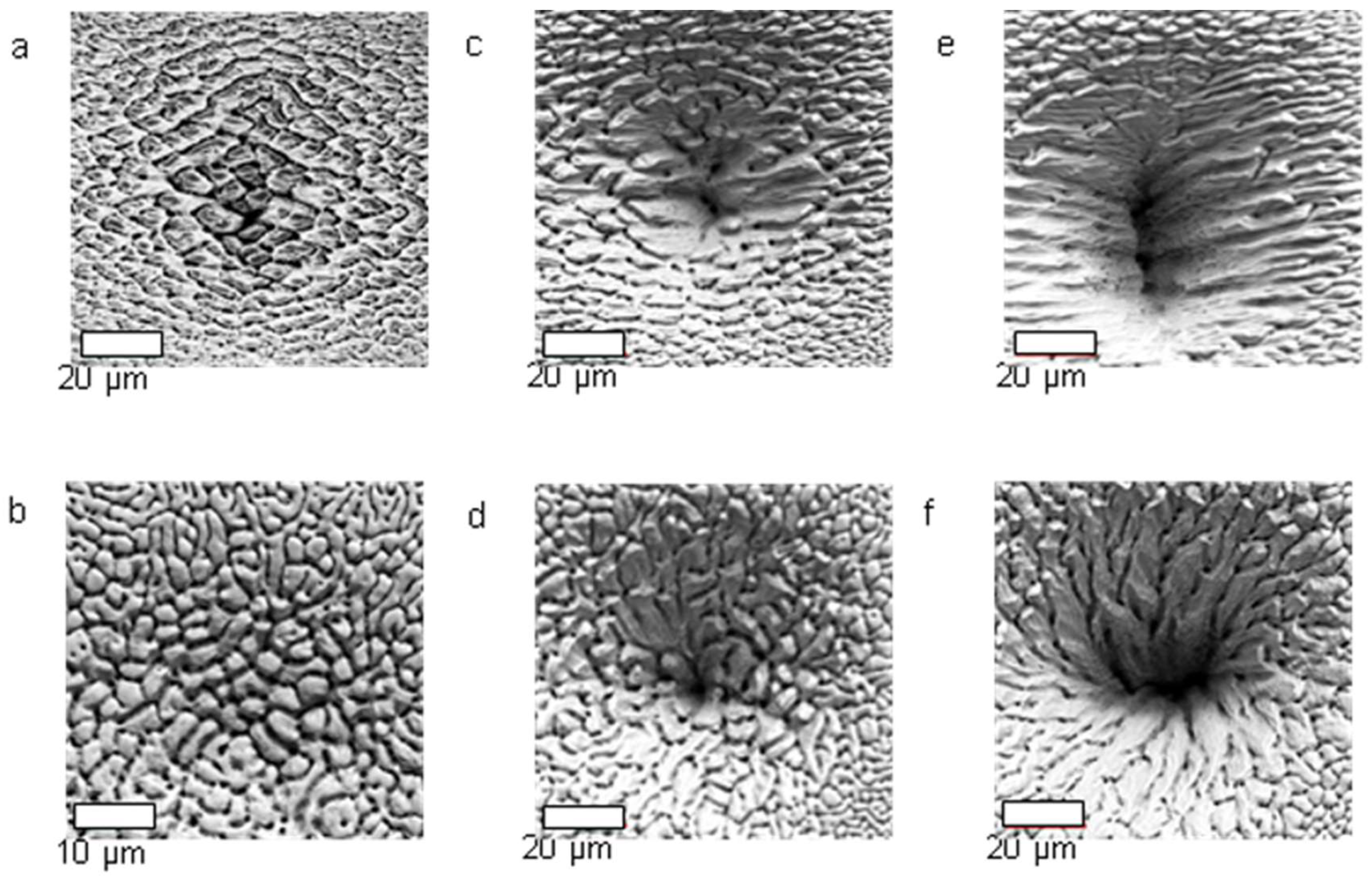
4.2. Dynamics of LIPSS Formation (Feedback)
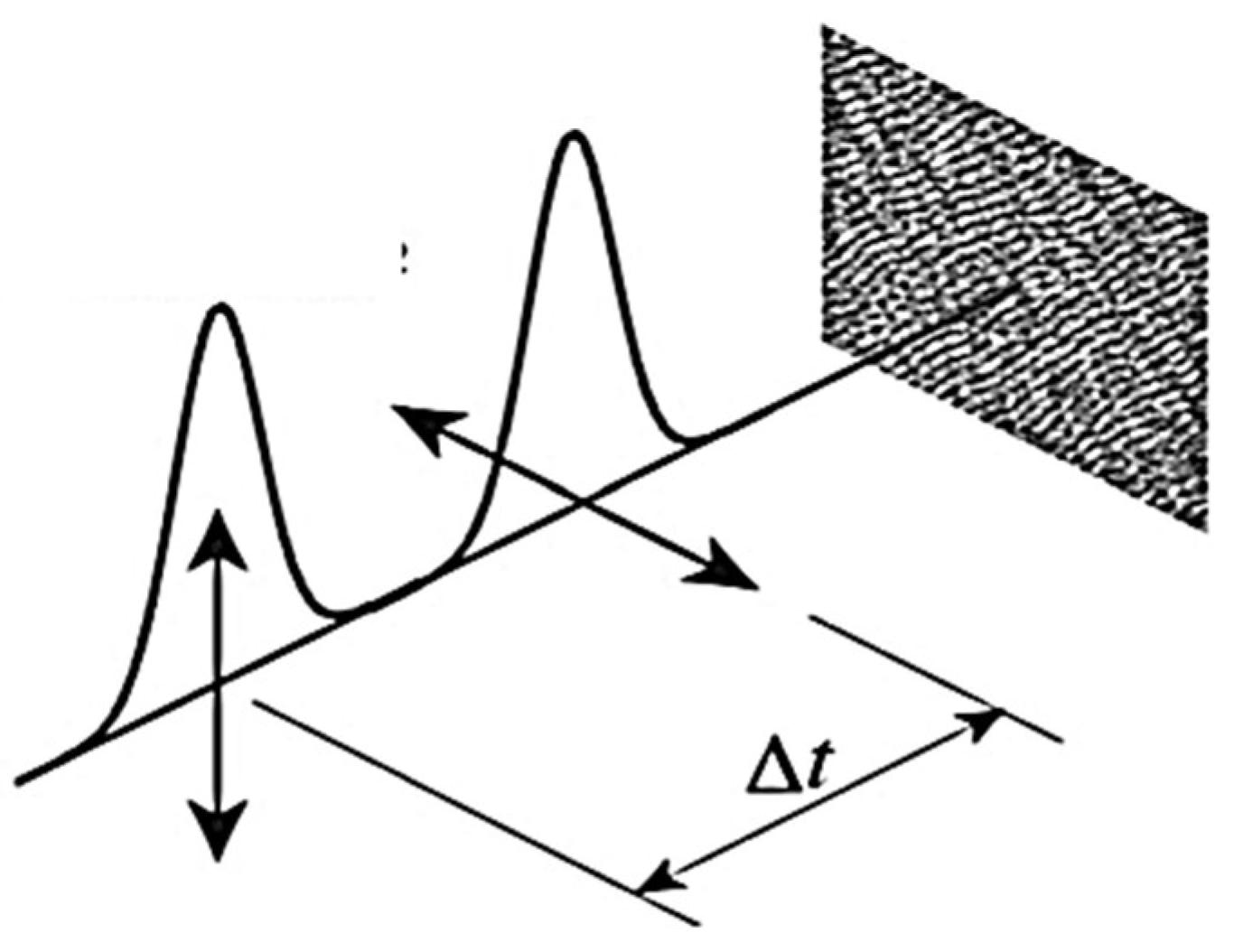
4.2.1. Double- or Multiple-Pulse Exposure
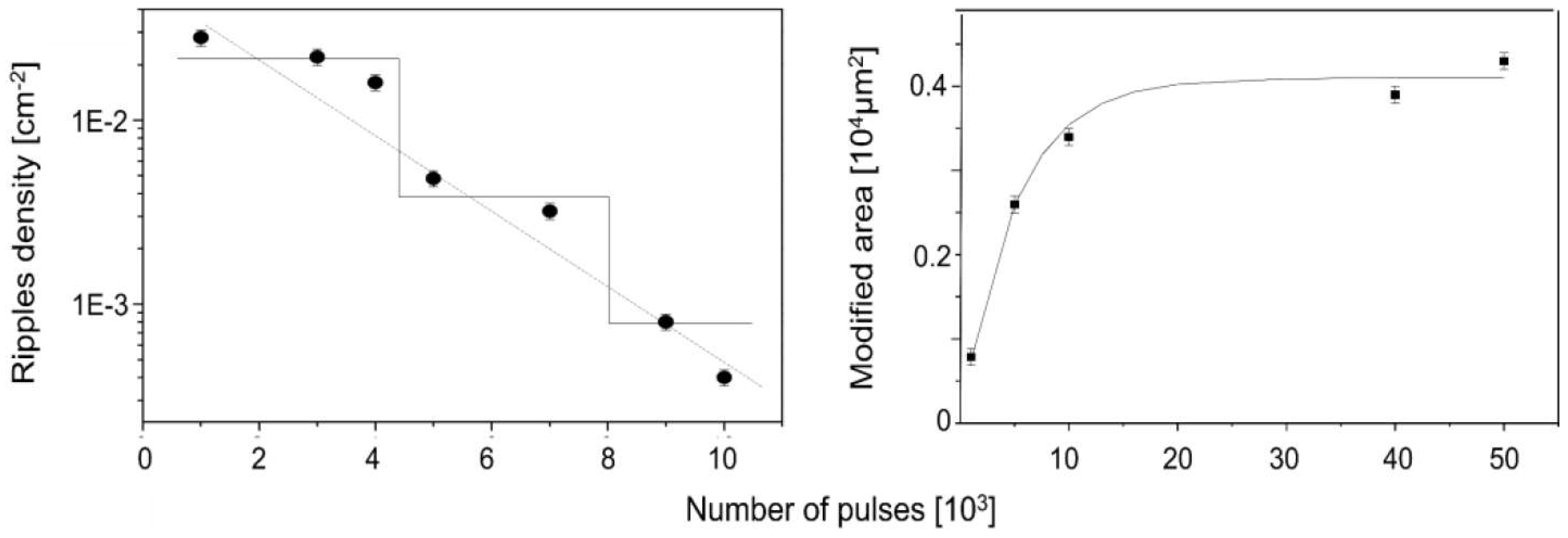
4.2.2. Pattern Evolution
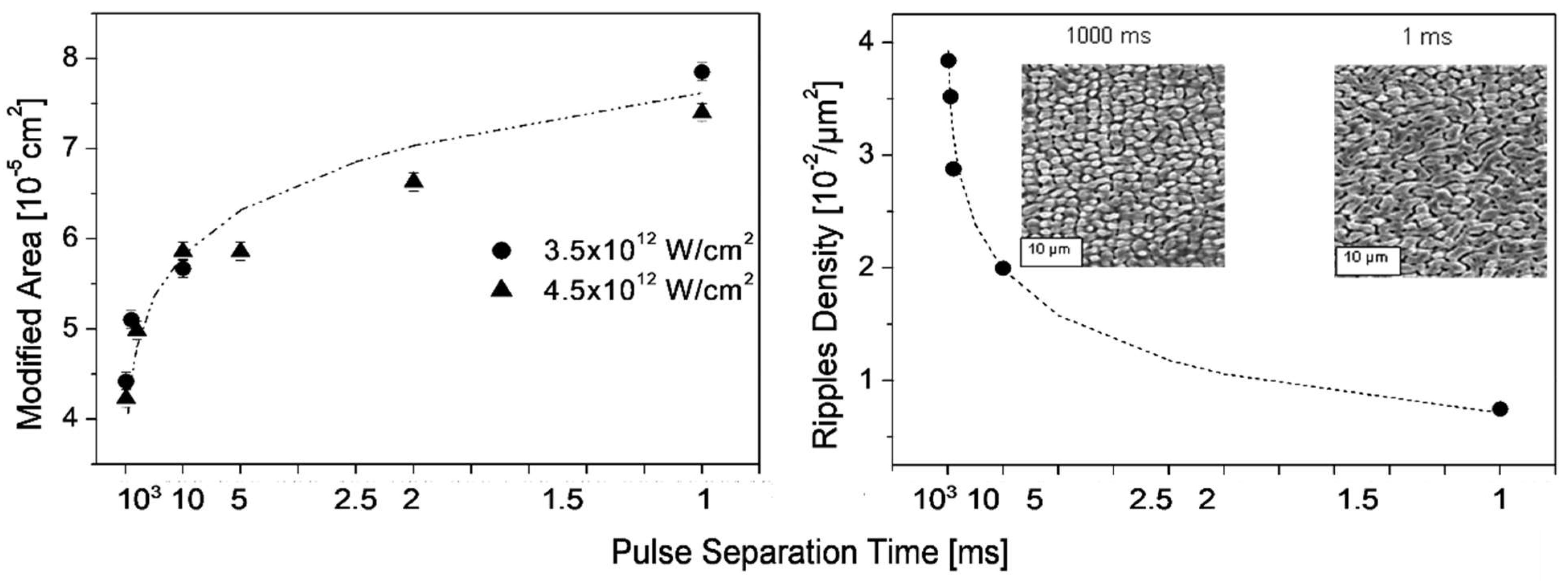
Irradiation Dose Dependence
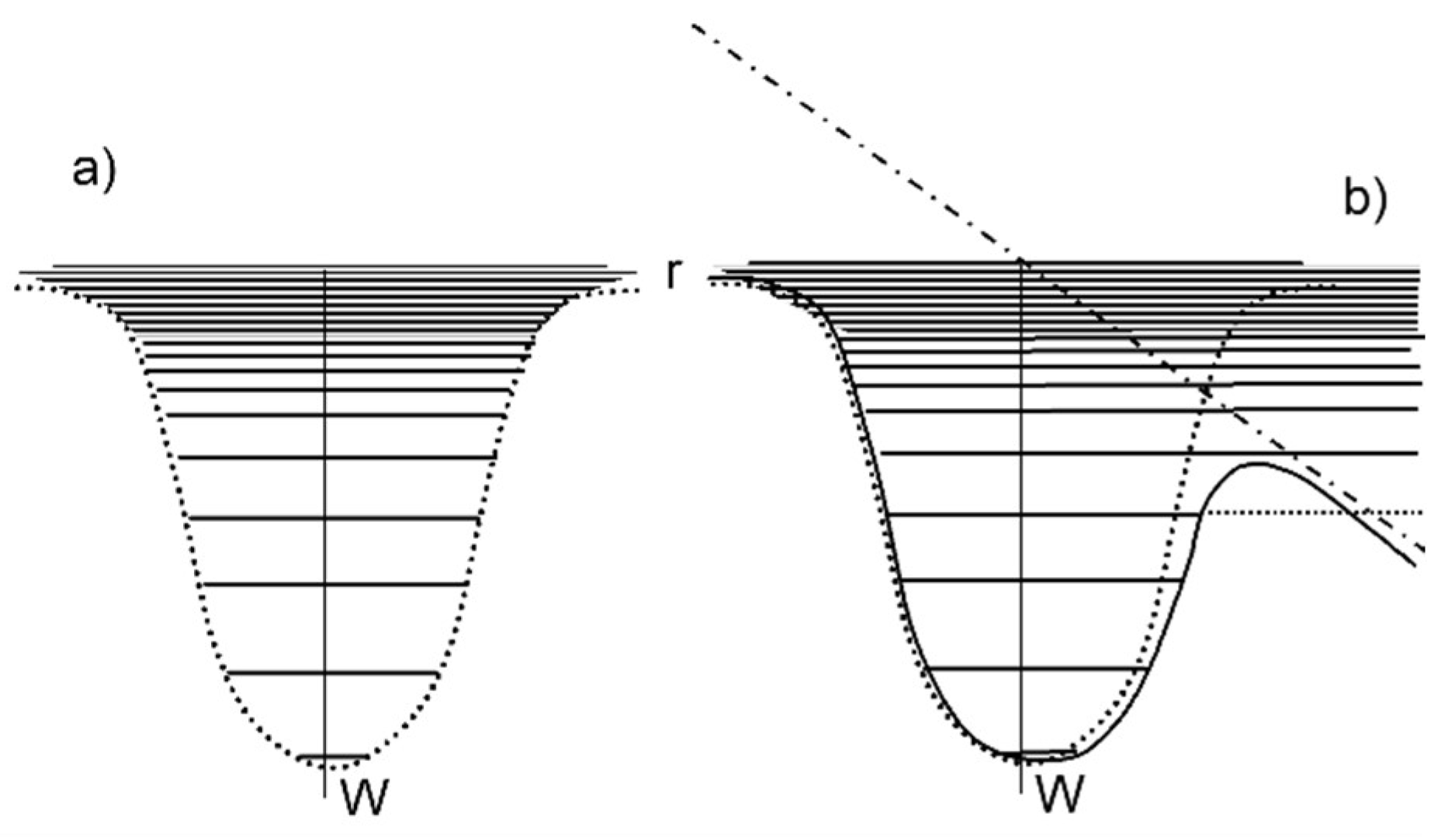
Genesis of Surface Structures
4.3. Modeling of Surface Modifications
4.3.1. Outline of the Self-Organization Model
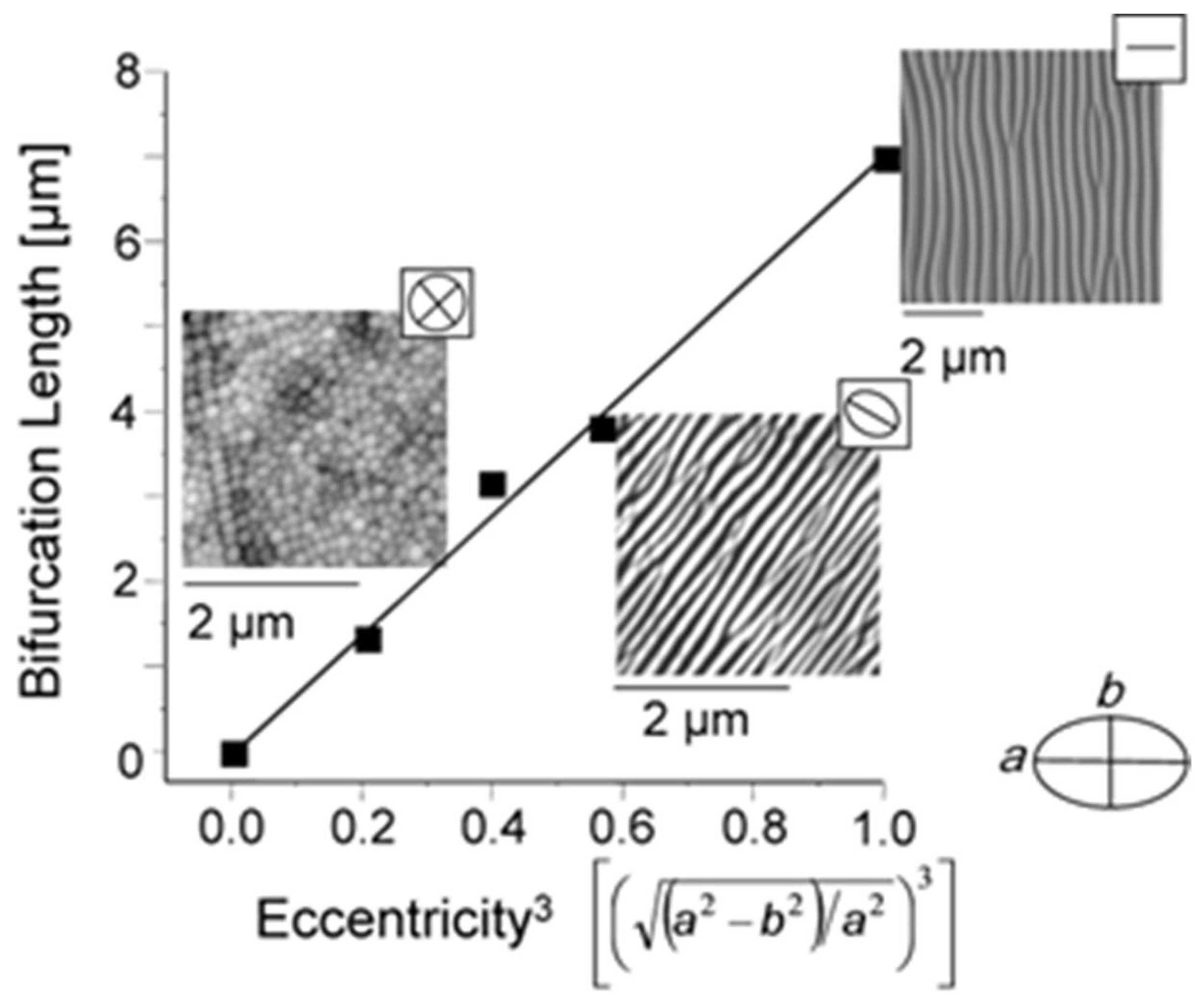
4.3.2. Laser Polarization in the Self-Organization Model
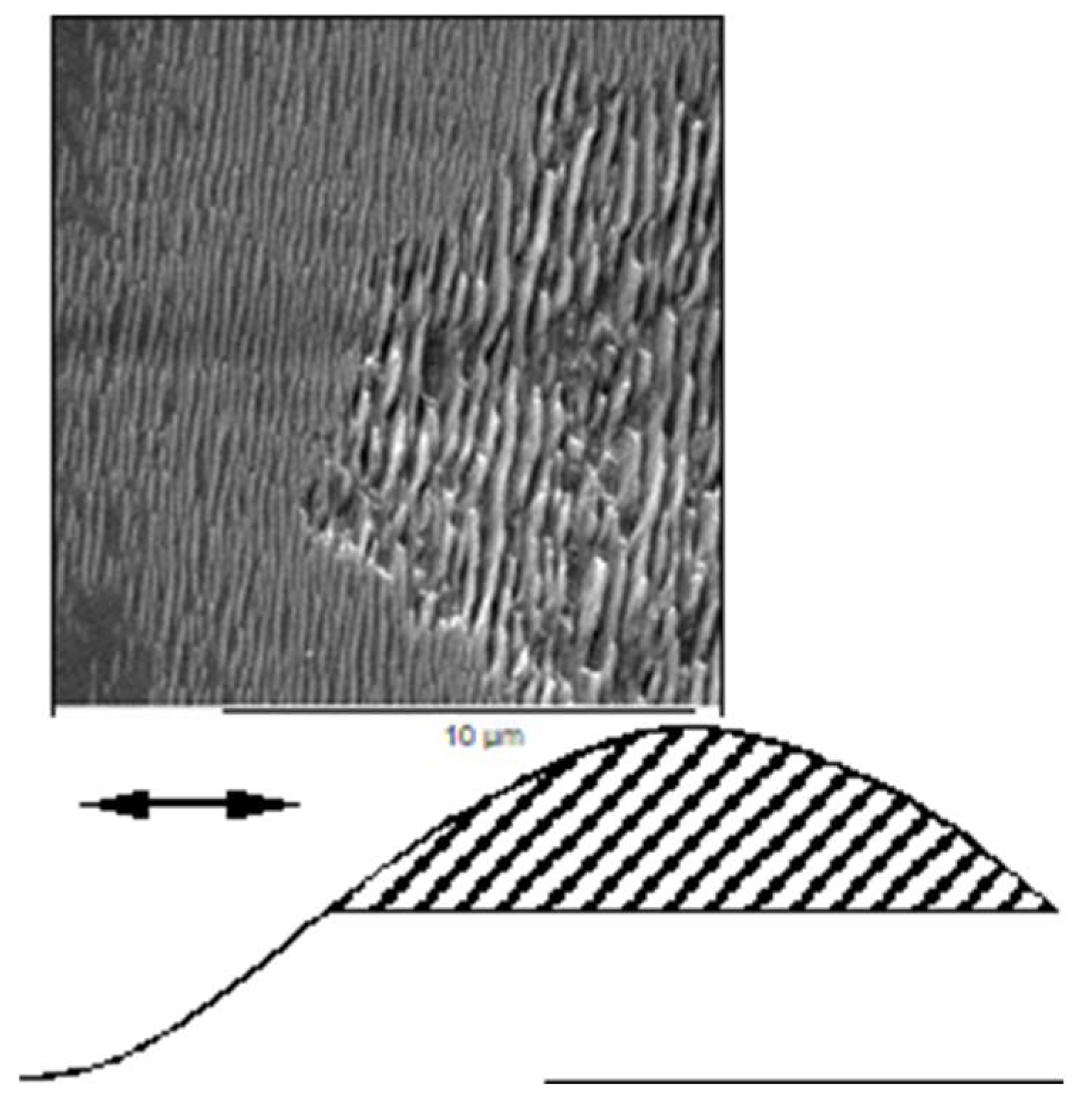
Anisotropic Energy Diffusion to the Surface
Anisotropy Induced by Laser Polarization
- (1)
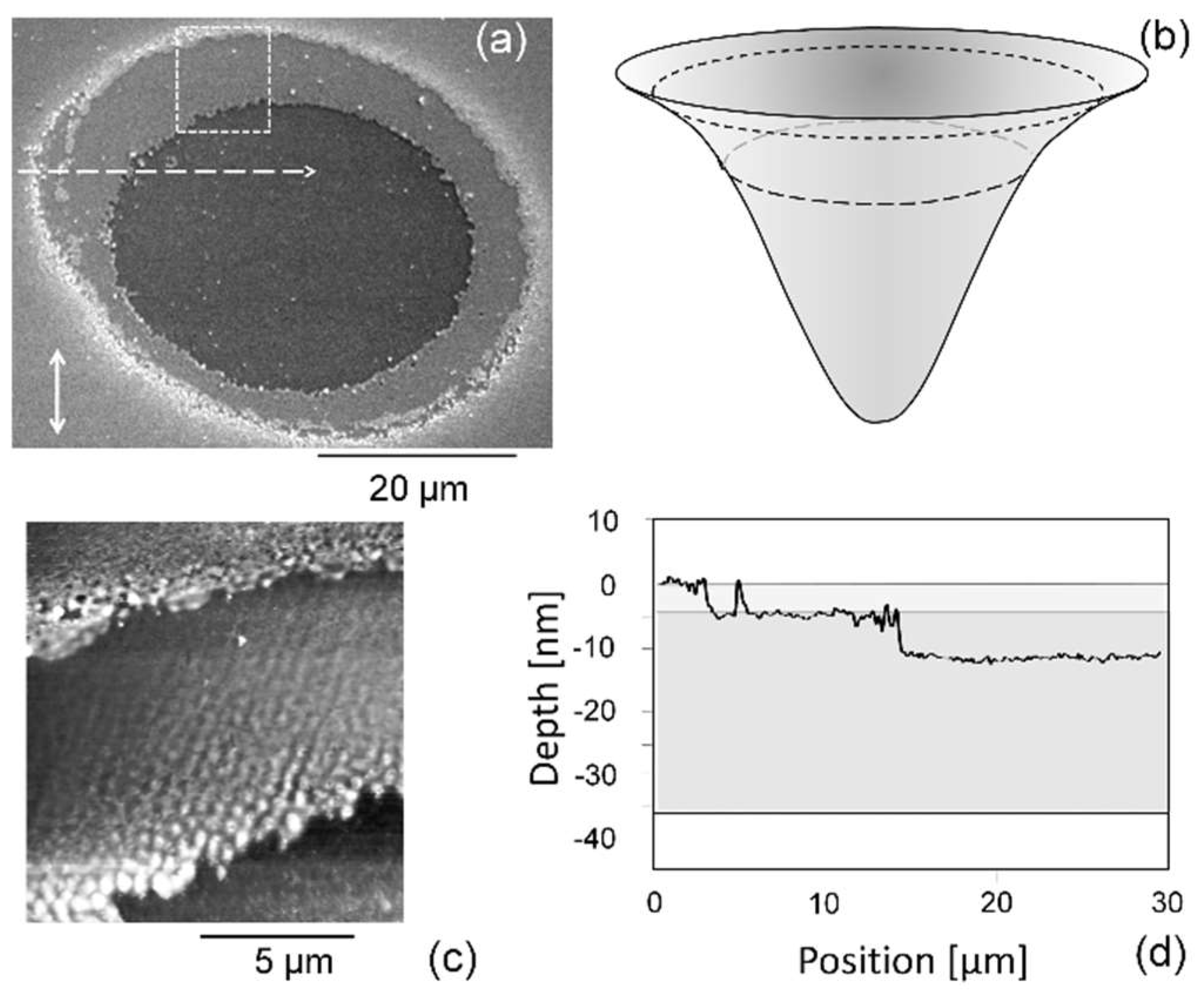
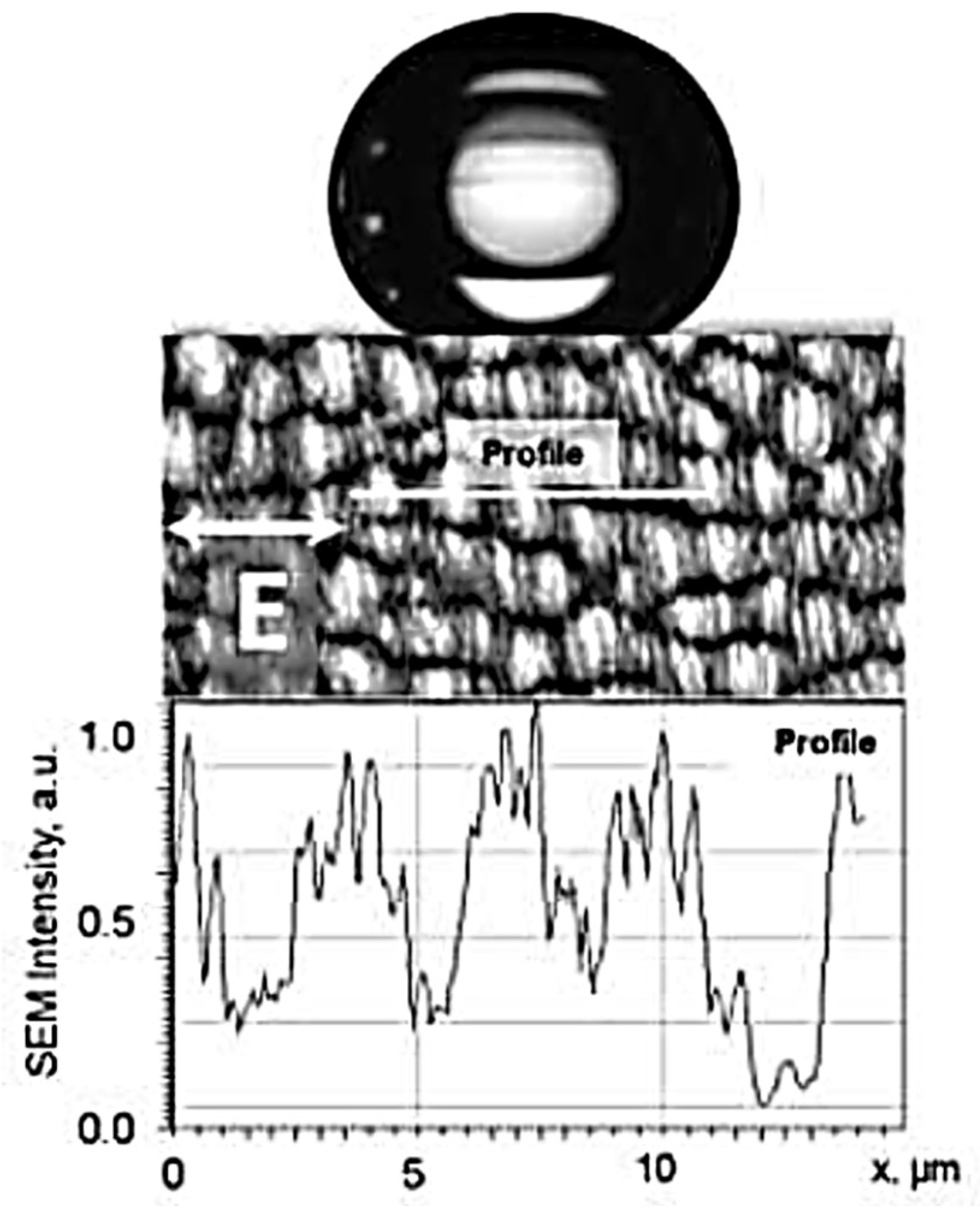
- The ablation spot does not reflect the (continuous) Gaussian beam profile. Instead, the ring is sharply bordered and only the polymeric cover is removed there, not any of the magnetic layer. Further, the ablation of the magnetic layer in the central disk is of about constant depth, disregarding the fluence variations across the beam profile. This suggests two distinctly different coupling or ablation thresholds;
- (2)
- The uncovered surface of the magnetic layer in the ring is regularly structured. The morphology looks very similar to the LIPSS. However, it is not compatible with any polarization influence.
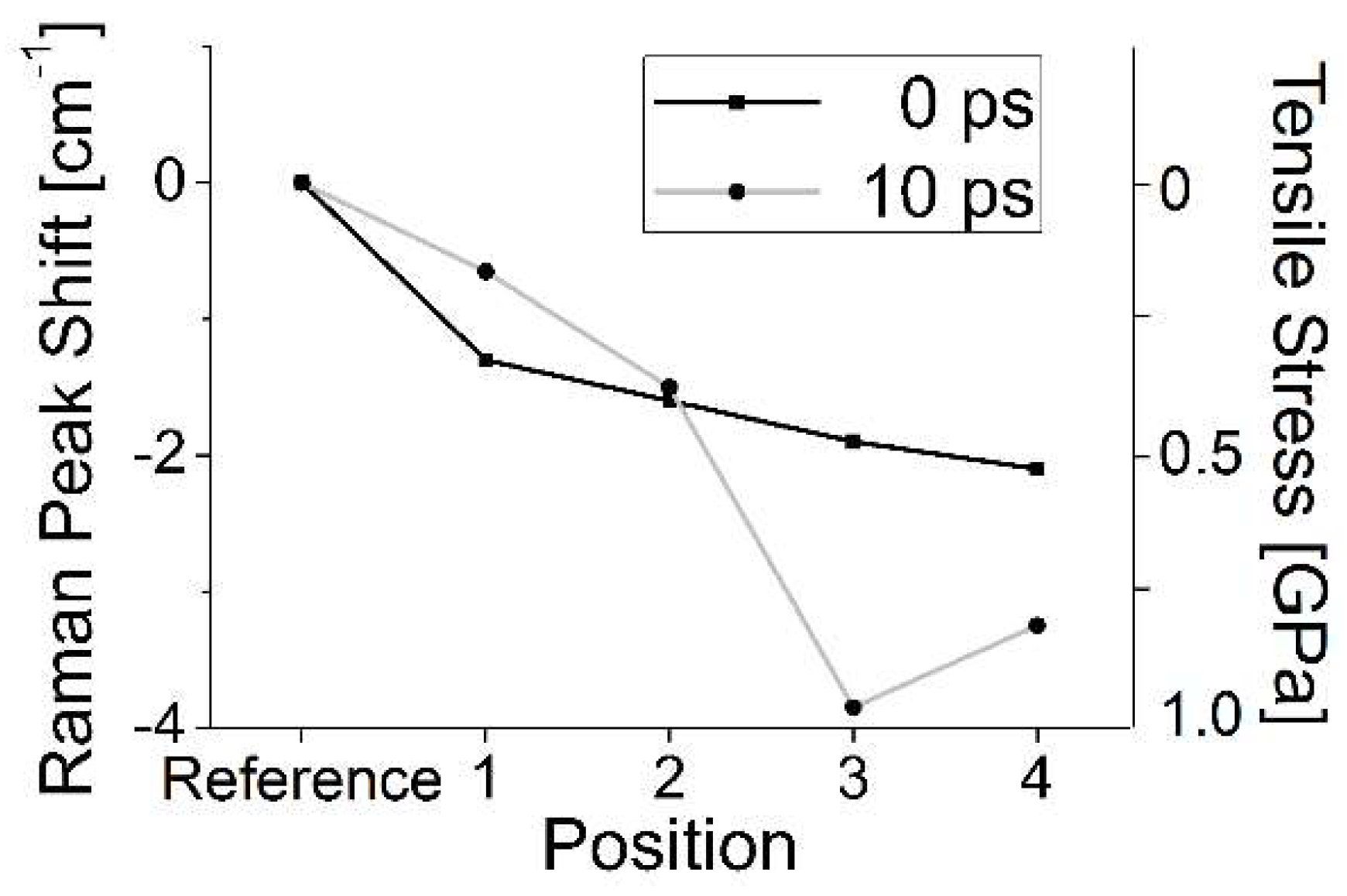
5. Surface Functionalization
5.1. Modification of Electric Surface Potential
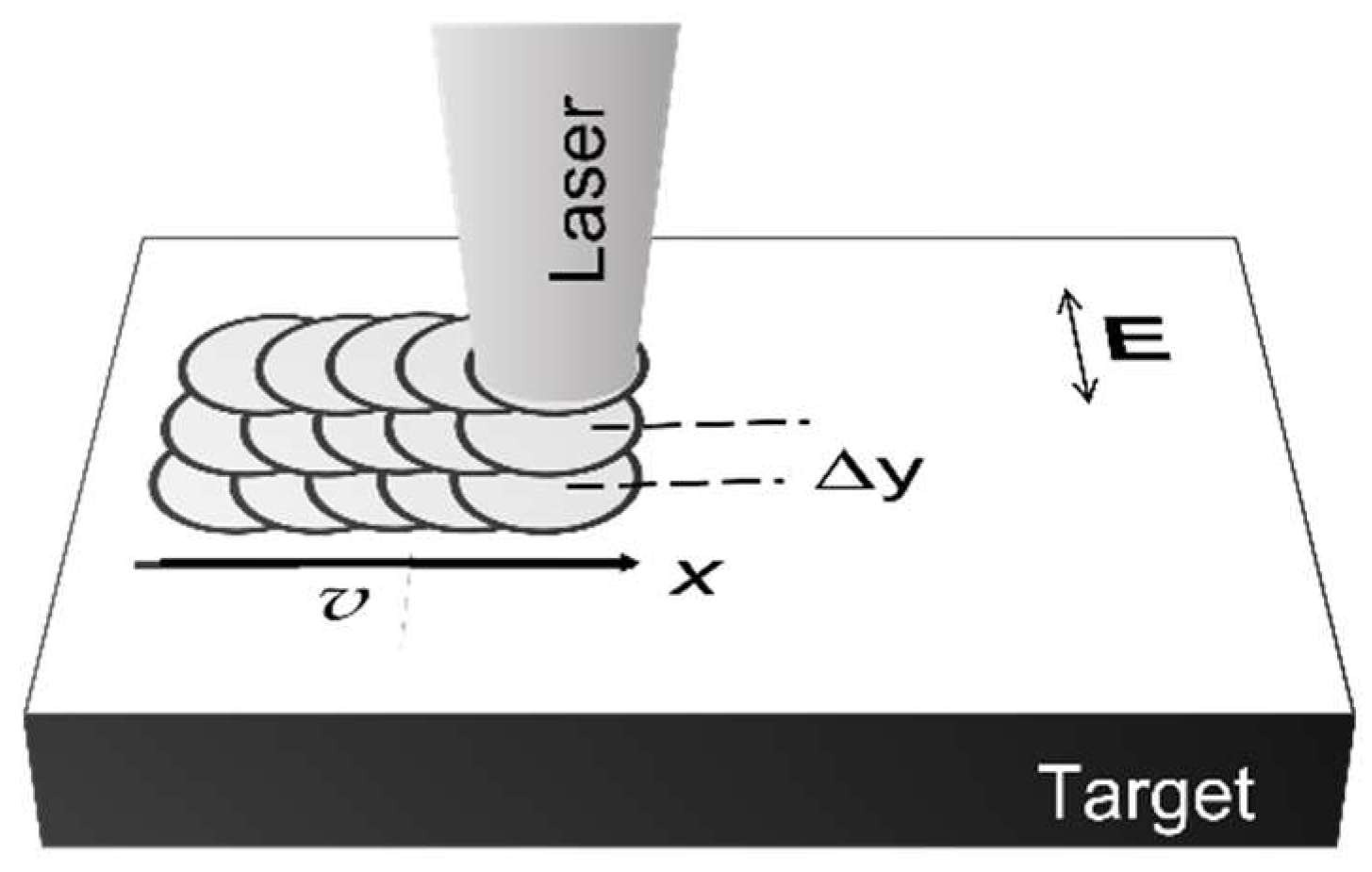
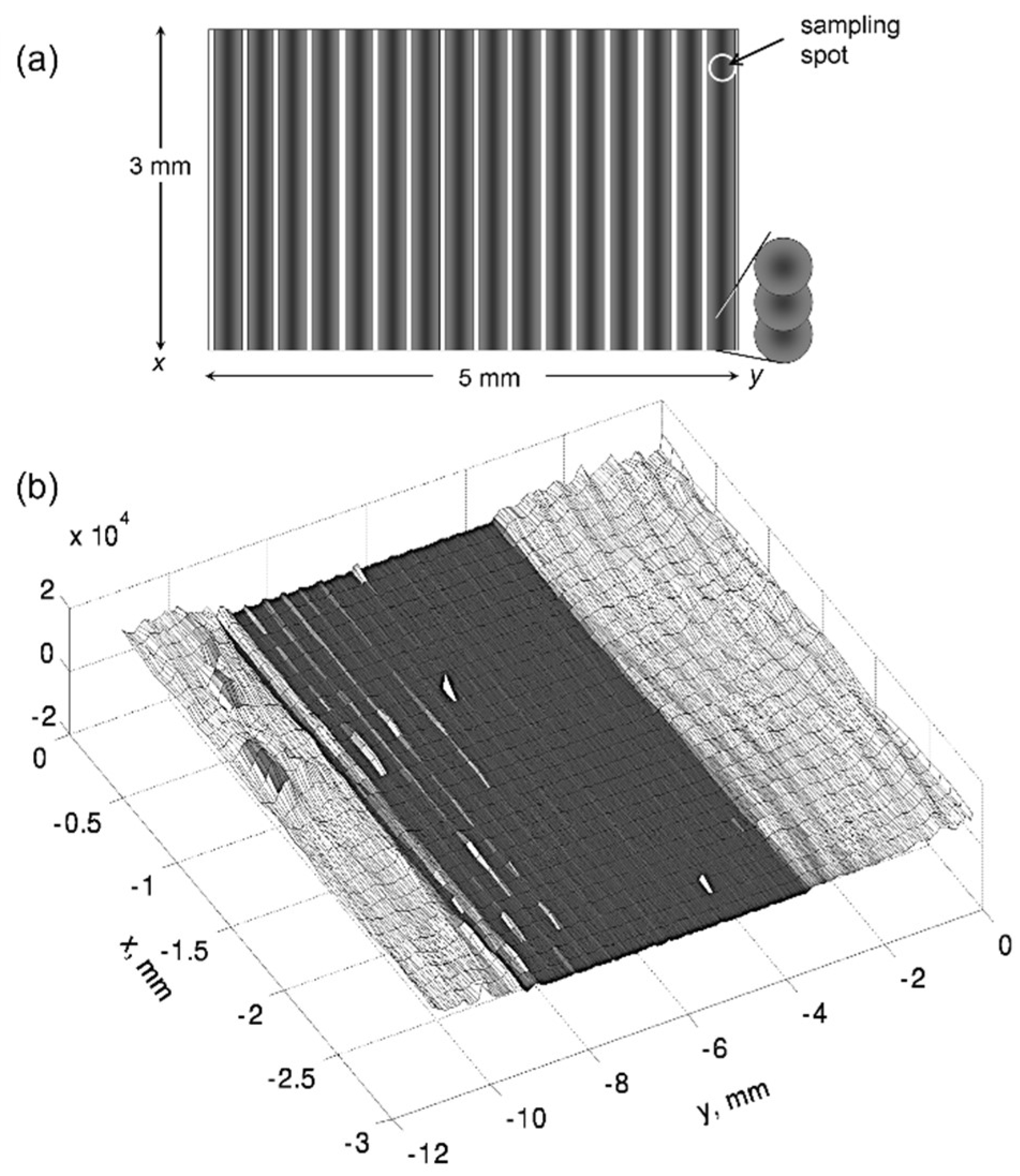
5.2. Large-Area Coverage
5.3. Applications
5.3.1. Color
5.3.2. Wettability
Funding
Acknowledgments
Conflicts of Interest
References
- Maiman, T.H. Stimulated Optical Radiation in Ruby. Nature 1960, 187, 493–494. [Google Scholar] [CrossRef]
- Bass, M. (Ed.) Laser Materials Processing; Elsevier: Amsterdam, The Netherlands, 1983. [Google Scholar]
- Stehn, W.; Mazumder, J. Laser Material Processing; Springer: London, UK, 2010. [Google Scholar]
- Schaaf, P. (Ed.) Laser Processing of Materials; Springer Series on Materials Science: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Laser Institute of America. LIA Handbook of Laser Materials Processing; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Franken, P.; Hill, A.; Peters, C.; Weinreich, G. Generation of Optical Harmonics. Phys. Rev. Lett. 1961, 7, 118–119. [Google Scholar] [CrossRef]
- von Allmen, M. Laser-Beam Interaction with Materials; Springer: Berlin/Heidelberg, Germany, 1987. [Google Scholar]
- Garrison, B.; Srinivasan, R. Laser ablation of organic polymers: Microscopic models for photochemical and thermal processes. J. Appl. Phys. 1984, 57, 2909–2914. [Google Scholar] [CrossRef]
- Petzoldt, S.; Reif, J.; Matthias, E. Laser plasma threshold of metals. Appl. Surf. Sci. 1996, 96–98, 199–204. [Google Scholar] [CrossRef]
- Shugaev, M.; Wu, C.; Armbruster, O.; Naghilou, A.; Brouwer, N.; Ivanov, D.; Derrien, T.-Y.; Bulgakowa, N.; Kautek, W.; Rethfeld, B.; et al. Fundamentals of ultrafast laser-material interaction. MRS Bulletin. 2016, 41, 960–968. [Google Scholar] [CrossRef]
- Schneider, T.; Wolfframm, D.; Reif, J. Ultrafast Pump-Probe Second Harmonic Generation—Always a Reliable Tool to Study Surface Dynamics? Phys. Stat. Sol. A 1999, 175, 177. [Google Scholar] [CrossRef]
- Schneider, T.; Wolfframm, D.; Mitzner, R.; Reif, J. Ultrafast Transient Grating in Barium Fluoride. In Novel Lasers and Devices—Basic Aspects; Leuchs, G., Mitzner, R., Reif, J., Eds.; OSA Technical Digest. Opt. Soc. America: Munich, Germany, 1999; p. 145. [Google Scholar]
- Schneider, T.; Wolfframm, D.; Mitzner, R.; Reif, J. Ultrafast optical switching by instantaneous laser-induced grating formation and self-diffraction in barium fluoride. Appl. Phys. B 1999, 68, 749–751. [Google Scholar] [CrossRef]
- Schmid, R.; Schneider, T.; Reif, J. Ultrafast Transient Grating in Barium Fluoride: Efficient Instantaneous Optical Switching, Frequency Conversion and Simple Logic Operations on a Femtosecond Time Scale. In Ultrafast Electronics and Optoelectronics, Chen, Y.-K., Knox, W., Rodwell, M., Eds.; OSA Trends in Optics and Photonics. Opt. Soc. America: Munich, Germany, 2001; Volume 49, p. 111. [Google Scholar]
- Schmid, R.; Schneider, T.; Reif, J. Optical Processing on a Femtosecond Time Scale. Opt. Commun. 2002, 207, 155–160. [Google Scholar] [CrossRef]
- Schneider, T.; Reif, J. Influence of an ultrafast transient refractive index grating on nonlinear optical phenomena. Phys. Rev. A 2002, 65, 023801. [Google Scholar] [CrossRef]
- Schmid, R.; Hänel, M.; Reif, J. Ultrafast transient grating in transparent dielectrics: Shaping of ultrashort pulses with excellent temporal and spectral characteristics and ultrafast pulse-labeling. In SuD1 in Optica Proc.: Controlling Light with Light: Photorefractive Effects, Photosensitivity, Fiber Gratings, Photonic Materials and More; OSA/Optica Publishing Group: Squaw Creek, CA, USA, 2007; ISBN 1-55752-848-9. [Google Scholar]
- Abraham, H.; Lemoine, J. Disparition instantanée du phénomène de Kerr. C.R. Acad. Sci. 1899, 129, 206–208. [Google Scholar]
- Bonse, J.; Baudach, J.; Krüger, J.; Kautek, W.; Lenzner, M. Femtosecond laser ablation of silicon—Modification thresholds and morphology. Appl. Phys. A 2002, 74, 19–25. [Google Scholar] [CrossRef]
- Srinivasan, R.; Braren, B. Ultraviolet Laser Ablation of Organic Polymers. Chem. Rev. 1989, 89, 1303–1308. [Google Scholar] [CrossRef]
- Keldysh, L. Ionization in the Field of a Strong Electromagnetic Wave. J. Exp. Theor. Phys. 1965, 20, 1307–1314. [Google Scholar]
- Reif, J. High Power Laser Interaction with the Surface of Wide Band-Gap Materials. Opt. Eng. 1989, 28, 1122. [Google Scholar] [CrossRef]
- Petite, G.; Martin, P.; Trainham, R.; Agostini, P.; Guizard, S.; Jollet, F.; Duraud, J.; Böhmer, K.; Reif, J. Charged Particle Emission by Laser Irradiated Surfaces. In Laser Ablation—Mechanisms and Applications; Miller, J., Haglund, R., Eds.; Lecture Notes in Physics 389; Springer: Berlin/Heidelberg, Germany, 1991; p. 224. [Google Scholar]
- Henyk, M.; Vogel, N.; Wolfframm, D.; Tempel, A.; Reif, J. Femtosecond Laser Ablation from Dielectric Materials: Comparison to Arc Discharge Erosion. Appl. Phys. A 1999, 69, S355–S358. [Google Scholar] [CrossRef]
- Henyk, M.; Mitzner, R.; Wolfframm, D.; Reif, J. Laser Induced Ion Emission from Dielectrics. Appl. Surf. Sci. 2000, 154–155, 249–255. [Google Scholar] [CrossRef]
- Stoian, R.; Ashkenasi; Rosenfeld, A.; Campbell, E. Coulomb explosion in ultrashort pulsed laser ablation of Al2O3. Phys. Rev. B 2000, 62, 13167. [Google Scholar] [CrossRef]
- Henyk, M.; Costache, F.; Reif, J. Femtosecond Laser Ablation from Sodium Chloride and Barium Fluoride. Appl. Surf. Sci. 2002, 186, 381–384. [Google Scholar] [CrossRef]
- Reif, J.; Costache, F.; Henyk, M. Explosive ion emission from ionic crystals induced by ultra-short laser pulses—Influence on surface morphology. Proc. SPIE 2003, 4948, 380–387. [Google Scholar]
- Costache, F.; Reif, J. Femtosecond Laser Induced Coulomb Explosion from Calcium Fluoride. Thin Solid Films 2004, 453–454, 334–339. [Google Scholar] [CrossRef]
- Henyk, M.; Wolfframm, D.; Reif, J. Ultra short laser pulse induced particle emission from wide bandgap materials. Appl. Surf. Sci. 2000, 168, 263–266. [Google Scholar] [CrossRef]
- Reif, J.; Costache, F. Femtosecond Laser Interaction with Solid Surfaces: Explosive Ablation and Self-Assembly of Ordered Nanostructures. Adv. At. Mol. Opt. Phys. 2006, 53, 228–249. [Google Scholar]
- Costache, F.; Kouteva-Arguirova, S.; Reif, J. Sub-damage-threshold femtosecond laser ablation rom crystalline Si: Surface nanostructures and phase transformation. Appl. Phys. A 2004, 79, 1429–1432. [Google Scholar] [CrossRef]
- Roeterdink, W.; Juurlink, L.; Vaughan, O.; Diez, J.D.; Bonn, M.; Kleyn, A. Coulomb explosion in femtosecond laser ablation of Si(111). Appl. Phys. Lett. 2003, 82, 4190. [Google Scholar] [CrossRef]
- Reif, J.; Costache, F.; Eckert, S.; Henyk, M. Mechanisms of ultra-short laser pulse ablation from ionic crystals. Appl. Phys. A 2004, 79, 1229–1231. [Google Scholar] [CrossRef]
- Henyk, M. Negative ion emission from ionic crystals upon ultra-short laser pulse irradiation. Appl. Surf. Sci. 2003, 208–209, 71. [Google Scholar] [CrossRef]
- Crain, J.; Ackland, G.; Maclean, J.; Piltz, R.; Hatton, P.; Pawley, G. Reversible pressure-induced structural transitions between metastable phases of silicon. Phys. Rev. B 1994, 50, 13043. [Google Scholar] [CrossRef]
- Henyk, M.; Costache, F.; Reif, J. Ultra short laser pulse ablation from sodium chloride—The role of laser induced color centers. Appl. Surf. Sci. 2002, 197–198, 90–95. [Google Scholar] [CrossRef]
- Itoh, N.; Stoneham, A. Materials Modification by Electronic Excitation; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Bass, M.; Barrett, H. Laser-Induced Damage Probability at 1.06 µm and 0.69 µm. Optica 1973, 12, 690–699. [Google Scholar]
- Jee, Y.; Becker, M.; Walser, R. Laser-induced damage on single-crystal metal surfaces. J. Opt. Soc. Am. B 1988, 5, 648. [Google Scholar] [CrossRef]
- Petzoldt, S.; Elg, A.; Reif, J.; Matthias, E. Shockwave Detection, an Efficient Way to Determine Multiple-Pulse Damage Thresholds. In Laser Induced Damage in Optical Materials: 1989; Bennett, H., Chase, L., Guenther, A., Newnam, B., Soileau, M., Eds.; NIST Special Publication 801/SPIE Proceedings Series; NIST: Gaithersburg, MD, USA, 1990; Volume 1438, p. 180. [Google Scholar]
- Costache, F.; Eckert, S.; Reif, J. Near-damage threshold femtosecond laser irradiation of dielectric surfaces: Desorbed ion kinetics and defect dynamics. Appl. Phys. A 2008, 92, 897–902. [Google Scholar] [CrossRef]
- Reif, J. Processing with Ultrashort Laser Pulses, Ch. 6. In Laser Processing of Materials; Schaaf, P., Ed.; Springer Ser. Mater. Sci.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 139, pp. 113–129. [Google Scholar]
- Phipps, C.R.; Dreyfus, R.W. Laser Ablation and Plasma Formation. In Laser Ionization Mass Analysis, Chemical Physics Monographs; Vertes, A., Gijbels, R., Adams, F., Eds.; University of Antwerp: Antwerp, Belgium, 1993; Volume 124, pp. 369–441. [Google Scholar]
- Langdon, A. Nonlinear Inverse Bremsstrahlung and Heated Electron Distributions. Appl. Phys. Lett. 1980, 44, 575. [Google Scholar] [CrossRef]
- Kaiser, A.; Rethfeld, B.; Vicanek, M.; Simon, G. Microscopic processes in dielectrics under irradiation by subpicosecond laser pulses. Phys. Rev. B 2000, 61, 11437. [Google Scholar] [CrossRef]
- Arnold, D.; Cartier, E. Theory of laser-induced free-electron heating and impact ionization in wide-band-gap solids. Phys. Rev. B 1992, 46, 15102. [Google Scholar] [CrossRef] [PubMed]
- Sokolowski-Tinten, K.; Bialkowski, J.; von der Linde, D. Ultrafast laser-induced order-disorder transitions in semiconductors. Phys. Rev. B 1995, 51, 14186. [Google Scholar] [CrossRef] [PubMed]
- Anisimov, S.I.; Kapeliovich, B.; Perel’man, T. Electron emission from metal surfaces exposed to ultrashort laser pulses. Sov. Phys. JETP 1974, 39, 375. [Google Scholar]
- Rethfeld, B.; Sokolowski-Tinten, K.; von der Linde, D.; Anisimov, S. Timescales in the response of materials to femtosecond laser excitation. Appl. Phys. A 2004, 79, 767–769. [Google Scholar] [CrossRef]
- Jeschke, H.; Garcia, M.; Lenzner, M.; Bonse, J.; Krüger, J.; Kautek, W. Laser ablation thresholds of silicon for different pulse durations: Theory and experiment. Appl. Surf. Sci. 2002, 197–198, 839. [Google Scholar] [CrossRef]
- Danielzik, B.; Harten, P.; Sokolowski-Tinten, K.; von der Linde, D. Picosecond Laser-Induced Solid-Liquid Phase Transformations in Gallium Arsenide and Silicon. MRS Proc. 1987, 100, 471. [Google Scholar] [CrossRef]
- Lindenberg, A.; Larsson, J.; Sokolowski-Tinten, K.; Gaffney, K.J.; Blome, C.; Synnergren, O.; Sheppard, J.; Caleman, C.; Macphee, A.G.; Weinstein, D.; et al. Atomic Scale Visualization of Inertial Dynamics. Science 2005, 308, 392–395. [Google Scholar] [CrossRef]
- Lindenberg, A.; Engemann, S.; Gaffney, K.J.; Sokolowski-Tinten, K.; Larsson, J.; Hillyard, P.B.; Reis, D.A.; Fritz, D.M.; Arthur, A.J.; Akre, R.A.; et al. X-Ray Diffuse Scattering Measurements of Nucleation Dynamics at Femtosecond Resolution. Phys. Rev. Lett. 2008, 100, 135502. [Google Scholar] [CrossRef] [PubMed]
- Rousse, A.; Rischel, C.; Fourmaux, S.; Uschmann, I.; Sebban, S.; Grillon, G.; Balcou, P.; Förster, E.; Geindre, J.; Audebert, P.; et al. Non-thermal melting in semiconductors measured at femtosecond resolution. Nature 2001, 410, 65–68. [Google Scholar] [CrossRef] [PubMed]
- Costache, F.; Eckert, S.; Reif, J. Dynamics of laser induced desorption from dielectric surfaces on a sub-picosecond timescale. Appl. Surf. Sci. 2006, 252, 4416–4419. [Google Scholar] [CrossRef]
- Reif, J.; Costache, F.; Eckert, S. The role of energy and phase relaxation (T1 and T2) in ultrafast laser ablation. J. Phys. Conf. Ser. 2007, 59, 1–4. [Google Scholar] [CrossRef]
- Schmidt; Husinsky, W.; Betz, G. Dynamics of Laser Desorption and Ablation of Metals at the Threshold on the Femtosecond Time Scale. Phys. Rev. Lett. 2000, 85, 3516. [Google Scholar] [CrossRef] [PubMed]
- Miotello, A.; Kelly, R. Critical assessment of thermal models for laser sputtering at high fluences. Appl. Phys. Lett. 1995, 67, 3535. [Google Scholar] [CrossRef]
- Cahn, R. Materials science: Melting and the surface. Nature 1986, 323, 668–669. [Google Scholar] [CrossRef]
- Miotello, A.; Kelly, R. Laser-induced phase explosion: New physical problems when a condensed phase approaches the thermodynamic critical temperature. Appl. Phys. A 1999, 69, S67–S73. [Google Scholar] [CrossRef]
- Reif, J. Material Response to Laser Energy Deposition (Thermal and Hyperthermal Processes), Ch. 2. In Lasers in Materials Science; Castillejo, M., Ossi, P., Zhigilei, L., Eds.; Springer Ser. Mater. Sci.; Springer: Berlin/Heidelberg, Germany, 2014; Volume 191. [Google Scholar]
- Cuerno, R.; Barabási, A.-L. Dynamic Scaling of Ion-Sputtered Surfaces. Phys. Rev. Lett. 1995, 74, 4746. [Google Scholar] [CrossRef]
- Birnbaum, M. Semiconductor Surface Damage Produced by Ruby Lasers. J. Appl. Phys. 1965, 36, 3688. [Google Scholar] [CrossRef]
- Siegrist, M.; Kaech, G.; Kneubühl, F.K. Formation of a periodic wave structure on the dry surface of a solid by TEA-CO2-laser pulses. Appl. Phys. 1973, 2, 45. [Google Scholar] [CrossRef]
- van Driel, H.M.; Sipe, J.; Young, J.F. Laser-Induced Periodic Surface Structure on Solids: A Universal Phenomenon. Phys. Rev. Lett. 1982, 49, 1955. [Google Scholar] [CrossRef]
- Keilmann, F.; Bai, Y.H. Periodic surface structures frozen into CO2 laser-melted quartz. Appl. Phys. A 1982, 29, 9. [Google Scholar] [CrossRef]
- Fauchet, P.M.; Siegman, A.E. Observations of higher-order laser-induced surface ripples on (111) germanium. Appl. Phys. A 1983, 32, 135. [Google Scholar] [CrossRef]
- Reif, J.; Costache, F.; Henyk, M.; Pandelov, S. Ripples Revisited: Non-Classical Morphology at the Bottom of Femtosecond Laser Ablation Craters in Transparent Dielectrics. Appl. Surf. Sci. 2002, 197–198, 891–895. [Google Scholar] [CrossRef]
- Costache, F.; Henyk, M.; Reif, J. Modification of Dielectric Surfaces with Ultra-Short Laser Pulses. Appl. Surf. Sci. 2002, 186, 352–357. [Google Scholar] [CrossRef]
- Bonse, J.; Gräf, S. Ten Open Questions about Laser-Induced Periodic Surface Structures. Nanomaterials 2021, 11, 3326. [Google Scholar] [CrossRef]
- Bonse, J.; Höhm, S.; Kirner, S.; Rosenfeld, A.; Krüger, J. Laser-Indued Periodic Surface Structures—A Scientific Evergreen. IEEE J. Sel. Top. Quant. Electron. 2017, 23, 9000615. [Google Scholar] [CrossRef]
- Fraggelakis, F.; Mincuzzi, G.; Mamnek-Hönninger, I.; Lopez, J.; Kling, R. Generation of micro- and nano-morphologies on a stainless steel surface irradiated with 257 nm femtosecond pulses. RSC Adv. 2018, 8, 16082–16087. [Google Scholar] [CrossRef]
- Varlamova, O.; Reif, J.; Varlamov, S.; Bestehorn, M. The laser polarization as control parameter in the formation of laser-induced periodic surface structures: Comparison of numerical and experimental results. Appl. Surf. Sci. 2011, 257, 5465–5469. [Google Scholar] [CrossRef]
- Reif, J.; Varlamova, O.; Costache, F. Femtosecond laser induced nanostructure formation: Self-organization control parameters. Appl. Phys. A 2008, 92, 1019–1024. [Google Scholar] [CrossRef]
- Razi, S.; Varlamova, O.; Reif, J.; Bestehorn, M.; Varlamov, S.; Mollabashi, M.; Mandanipour, K.; Ratzke, M. Birth of periodic Micro/Nano structures on 316L stainless steel surface following femtosecond laser irradiation; single and multi scanning study. Opt. Laser Technol. 2018, 104, 8–16. [Google Scholar] [CrossRef]
- Varlamova, O.; Bounhalli, M.; Reif, J. Influence of irradiation dose on laser-induced surface nanostructures on silicon. Appl. Surf. Sci. 2013, 278, 62–66. [Google Scholar] [CrossRef]
- Varlamova, O.; Ratzke, M.; Reif, J. Feedback Effect on the Self-Organized Nanostructures Formation on Silicon upon Femtosecond Laser Ablation. Solid State Phenom. 2009, 156–158, 535. [Google Scholar] [CrossRef]
- Bonse, J.; Krüger, J. Pulse number dependence of laser-induced periodic surface structures for femtosecond laser irradiation of silicon. J. Appl. Phys. 2010, 108, 034903. [Google Scholar] [CrossRef]
- Schade, M.; Varlamova, O.; Reif, J.; Blumtritt, H.; Erfurth, W.; Leipner, H. High-resolution investigations of ripple structures formed by femtosecond laser irradiation of silicon. Anal. Bioanal. Chem. 2010, 396, 1905–19011. [Google Scholar] [CrossRef] [PubMed]
- Höche, T.; Ruthe, D.; Petsch, T. Low-fluence femtosecond-interaction with a Mo/Si multilayer stack. Appl. Phys. A 2004, 79, 961. [Google Scholar] [CrossRef]
- Zhang, G.; Gu, D.; Gan, F. Femtosecond laser-induced crystallization in amorphous Sb-rich AgInSbTe films. Solid State Commun. 2004, 131, 211. [Google Scholar] [CrossRef]
- Frost, F.; Ziberi, A.; Schindler, A.; Rauschenbach, B. Surface engineering with ion beams: From self-organized nanostructures to ultra-smooth surfaces. Appl. Phys. A 2008, 91, 551–559. [Google Scholar] [CrossRef]
- Reif, J.; Costache, F.; Eckert, S.; Kouteva-Arguirova, S.; Bestehorn, M.; Georgescu, I.; Semerok, A.; Martin, P.; Gobert, O.; Seifert, W. Formation of self-organized regular nanostructures upon femtosecond laser ablation. Proc. SPIE 2004, 5662, 737. [Google Scholar]
- Erlebacher, J.; Aziz, M.; Chason, E.; Sinclair, M.; Floro, J. Spontaneous Pattern Formation on Ion Bombarded Si(001). Phys. Rev. Lett. 1999, 82, 2330. [Google Scholar] [CrossRef]
- Hashida, M.; Nishii, T.; Miyasaka, Y.; Sakagami, H.; Shimizu, M.; Inoue, A.; Sakabe, S. Orientation of periodic grating structures controlled by double-pulse irradiation. Appl. Phys. A 2016, 122, 484. [Google Scholar] [CrossRef]
- Rohloff, M.; Das, S.; Höhm, S.; Grunwald, R.; Rosenfeld, A.; Krüger, J.; Bonse, J. Formation of laser-induced periodic surface structures on fused silica upon multiple cross-polarized double-femtosecond-laser-pulse irradiation sequences. J. Appl. Phys. 2011, 110, 014910. [Google Scholar] [CrossRef]
- Barberoglou, M.; Gray, D.; Magoulakis, E.; Fotakis, F.; Loukakos, P.; Stratakis, E. Controlling ripples’ periodicity using temporally delayed femtosecond laser double pulses. Opt. Express 2013, 21, 18501–18508. [Google Scholar] [CrossRef]
- Höhm, S.; Herzlieb, M.; Rosenfeld, A.; Krüger, J.; Bonse, J. Dynamics of the formation of laser-induced periodic surface structures (LIPSS) upon femtosecond two-color double-pulse irradiation of metals, semiconductors, and dielectrics. Appl. Surf. Sci. 2016, 374, 331–338. [Google Scholar] [CrossRef]
- Gemini, L.; Myasaka, M.H.Y.; Inoue, S.; Limpouch, J.; Mocek, T.; Sakabe, S. Periodic surface structures on titanium self-organized upon double femtosecond pulse exposures. Appl. Surf. Sci. 2015, 336, 349–353. [Google Scholar] [CrossRef]
- Reif, J.; Varlamova, O.; Bounhalli, M.; Muth, M.; Arguirov, T. Nanostructure formation upon femtosecond ablation from silicon: Effect of double pulses. Appl. Surf. Sci. 2012, 258, 9491–9495. [Google Scholar] [CrossRef]
- Gregorčič, P.; Sedlaček, M.; Podgornik, B.; Reif, J. Formation of laser-induced periodic surface structures (LIPSS) on tool steel by multiple picosecond laser pulses of different polarizations. Appl. Surf. Sci. 2016, 387, 698–706. [Google Scholar] [CrossRef]
- Costache, F.A. Dynamics of Ultra-short Laser Pulse Interaction with Solids at the Origin of Nanoscale Surface Modification. Ph.D. Thesis, BTU, Cottbus, Germany, 2006. [Google Scholar]
- Reif, J.; Costache, F.; Bestehorn, M. Self-organized surface nano-structuring by femtosecond laser processing; Chapter 9. In Recent Advances in Laser Processing of Materials; Perriere, J., Millon, E., Fogarassy, E., Eds.; Elsevier: Amsterdam, The Netherlands, 2006; p. 275. [Google Scholar]
- Tomita, T.; Kinoshita, K.; Matsuo, S.; Hashimoto, S. Distinct Fine and Course Ripples on 4H-SiC Single Crystal Induced by Femtosecond Laser Irradiation. Jpn. J. Appl. Phys. 2006, 45, L444. [Google Scholar] [CrossRef]
- Miyaji, G.; Miyazaki, K. Role of multiple shots of femtosecond laser pulses in periodic surface nanoablation. Appl. Phys. Lett. 2013, 103, 07910. [Google Scholar] [CrossRef]
- Couillard, M.; Borowiec, A.; Haugen, H.; Preston, J. Subsurface modifications in indium phosphide induced by single and multiple femtosecond laser pulses: A study on the formation of periodic ripples. J. Appl. Phys. 2007, 101, 033519. [Google Scholar] [CrossRef]
- Samaltianos, N.; Logothetidis, S.; Perrie, W.; Romani, S.; Potter, R.; Edwardson, S.; French, P.; Sharp, M.; Dearden, G.; Watkins, K. Silicon nanoparticles generated by femtosecond laser ablation in a liquid environment. J. Nanopart. Res. 2010, 12, 573. [Google Scholar] [CrossRef]
- Reif, J. Basic Physics of Femtosecond Laser Ablation, Ch. 2. In Laser-Surface Interactions for New Materials Production; Miotello, A., Ossi, P., Eds.; Springer Ser. Mater. Sci.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 130. [Google Scholar]
- Reif, J.; Varlamova, O.; Ratzke, M.; Schade, M.; Leipner, H.; Arguirov, T. Multipulse feedback in self-organized ripples formation upon femtosecond laser ablation from silicon. Appl. Phys. A 2010, 101, 361–365. [Google Scholar] [CrossRef]
- Reif, J.; Varlamova, O.; Bounhalli, M.; Arguirov, T. Long-Time Feedback in the Formation of Self-Organized Nanostructures upon Multipulse Femtosecond Laser Ablation. In International Symposium on High Power Laser Ablation 2010, AIP Conference Proceedings 1278; Phipps, C., Ed.; AIP Melville: New York, NY, USA, 2010; pp. 446–456. [Google Scholar]
- Varlamova, O.; Reif, J. Evolution of Femtosecond Laser Induced Surface Structures at Low Number of Pulses near the Ablation Threshold. J. Laser Micro/Nanoeng. 2013, 8, 300. [Google Scholar] [CrossRef]
- Varlamova, O.; Martens, C.; Ratzke, M.; Reif, J. Genesis of femtosecond-induced nanostructures on solid surfaces. Appl. Opt. 2014, 53, I10–I15. [Google Scholar] [CrossRef] [PubMed]
- Savolainen, J.-M.; Christensen, M.; Balling, P. Material swelling as the first step in the ablation of metals by ultrashort laser pulses. Phys. Rev. B 2011, 84, 193410. [Google Scholar] [CrossRef]
- Bonse, J.; Gräf, S. Maxwell Meets Marangoni—A Review of Theories on Laser-Induced Periodic Surface Structures. Laser Photon. Rev. 2020, 14, 2000215. [Google Scholar]
- Skolski, J.; Römer, G.; Obona, J.V.; Ocelik; Veld, A.H.; De Hosson, J. Laser-induced periodic surface structures: Fingerprints of light localization. Phys. Rev. B 2012, 85, 075320. [Google Scholar] [CrossRef]
- Costache, F.; Henyk, M.; Reif, J. Surface patterning on insulators upon femtosecond laser ablation. Appl. Surf. Sci. 2003, 208–209, 486–491. [Google Scholar] [CrossRef]
- Reif, J.; Varlamova, O.; Uhlig, S.; Varlamov, S.; Bestehorn, M. On the physics of self-organized nanostructure formation upon femtosecond laser ablation. Appl. Phys. A 2014, 117, 179–184. [Google Scholar] [CrossRef]
- Sigmund, P. Theory of Sputtering. I. Sputtering Yield of Amorphous and Polycrystalline Targets. Phys. Rev. 1969, 184, 383–416. [Google Scholar]
- Sigmund, P. A mechanism of surface micro-roughening by ion bombardment. J. Mat. Sci. 1973, 8, 1545–1553. [Google Scholar] [CrossRef]
- Kardar, M.; Parisi, G.; Zhang, Y. Dynamic Scaling of Growing Interfaces. Phys. Rev. Lett. 1986, 56, 889. [Google Scholar] [CrossRef]
- Varlamova, O.; Costache, F.; Reif, J.; Bestehorn, M. Self-organized pattern formation upon femtosecond laser ablation by circular polarized light. Appl. Surf. Sci. 2006, 252, 4702–4706. [Google Scholar] [CrossRef]
- Kuramoto, Y. Diffusion-Induced Chaos in Reaction Systems. Prog. Theor. Phys. Suppl. 1978, 64, 346–367. [Google Scholar] [CrossRef]
- Sivashinsky, G. Nonlinear analysis of hydrodynamic instability in laminar flames—I. Derivation of basic equations. Acta Astronautica. 1977, 4, 1177–1206. [Google Scholar] [CrossRef]
- Zangwill, A. Physics at Surfaces; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Reif, J.; Varlamova, O.; Varlamov, S.; Bestehorn, M. The role of asymmetric excitation in self-organized nanostructure formation upon femtosecond laser ablation. AIP Conf. Proc. 2012, 1464, 428–441. [Google Scholar]
- Reif, J.; Varlamova, O.; Varlamov, S.; Bestehorn, M. The role of asymmetric excitation in self-organized nanostructure formation upon femtosecond laser ablation. Appl. Phys. A 2011, 104, 969–973. [Google Scholar] [CrossRef]
- Varlamova, O.; Reif, J.; Varlamov, S.; Bestehorn, M. Self-organized Surface Patterns Originating from Laser-Induced Instability; Ch. 1. In Progress in Nonlinear Nano-Optics; Sakabe, S., Lienau, C., Grunwald, R., Eds.; Ser. Nano-Opt. Nanophot. 2; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Varlamova, O.; Reif, J.; Varlamov, S.; Bestehorn, M. Modeling of the Laser Polarization as Control Parameter in Self-Organized Surface Pattern Formation. J. Nanosci. Nanotechnol. 2011, 11, 9274–9281. [Google Scholar] [CrossRef]
- Miyaji, G.; Miyazaki, K. Origin of periodicity in nanostructuring on thin film surfaces ablated with femtosecond laser pulses. Opt. Express 2008, 16, 16265. [Google Scholar] [CrossRef]
- Bonse, J.; Rosenfeld, A.; Krüger, J. On the role of surface plasmon polaritons in the formation of laser-induced periodic surface structures upon irradiation of silicon by femtosecond laser pulses. J. Appl. Phys. 2009, 106, 104910. [Google Scholar] [CrossRef]
- Garrelie, F.; Colombier, J.; Tonchev, F.P.S.; Faure, N.; Bounhalli, M.; Reynaud, S.; Parriaux, O. Evidence of surface plasmon resonance in ultrafast laser-induced ripples. Opt. Express 2011, 19, 9035. [Google Scholar] [CrossRef] [PubMed]
- Reif, J.; Varlamova, O.; Ratzke, M.; Uhlig, S. Laser-Induced Periodic Surface Structures of Thin, Complex Multi-Component Films. Appl. Phys. A 2016, 122, 338. [Google Scholar] [CrossRef]
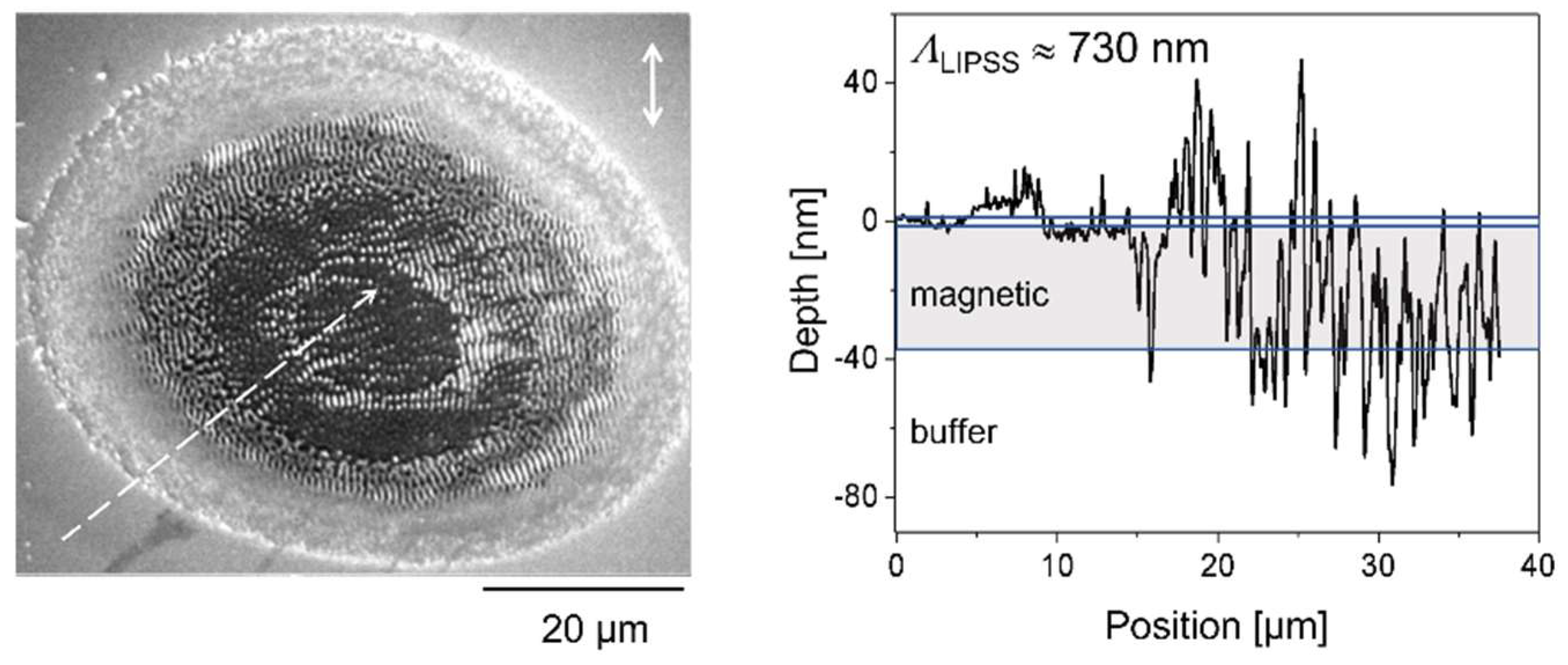
- Czajkowski, K.; Ratzke, M.; Varlamova, O.; Reif, J. Femtosecond-laser-induced periodic surface structures on magnetic layer targets: The role of magnetization. Appl. Surf. Sci. 2017, 417, 84–87. [Google Scholar] [CrossRef]
- Hornyak, G.; Moore, J.; Tibbals, H.; Dutta, J. Fundamentals of Nanotechnology; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group: Abingdon, UK, 2008. [Google Scholar]
- McFadyen, I.; Fullerton, E.; Carey, M. Nanostructured Materials in Information Storage. MRS Bull. 2008, 33, 831–837. [Google Scholar]
- Hunger, E.; Pietsch, H.; Petzoldt, S.; Matthias, E. Multishot ablation of polymer and metal films at 248 nm. Appl. Surf. Sci. 1992, 54, 227–231. [Google Scholar] [CrossRef]
- Lahtinen, T.; Shirahata, Y.; Yao, L.; Franke, K.; Venkataiah, G.; Taniyama, T.; van Dijken, S. Alternating domains with uniaxial and biaxial magnetic anisotropy in epitaxial Fe films on BaTiO3. Appl. Phys. Lett. 2012, 101, 262405. [Google Scholar]
- Li, W.; Zhou, W.; Lenox, P.; Seki, T.; Takanashi, K.; Jander, A.; Dhagat, P. Magnetostriction Measurements of L10 Fe50Pt(50–x)Pdx Thin Films. IEEE Trans. Magn. 2015, 51, 2504904. [Google Scholar] [CrossRef]
- Reif, J. Surface Functionalization by Laser-Induced Structuring. Ch. 3. In Advances in the Application of Lasers in Materials Science; Ossi, P., Ed.; Springer Ser. Mater. Sci.; Springer: Berlin/Heidelberg, Germany, 2018; Volume 274. [Google Scholar]
- Bonse, J. Quo Vadis LIPSS?—Recent and Future Trends on Laser-Induced Periodic Surface Structures. Nanomaterials 2020, 10, 1950. [Google Scholar] [CrossRef]
- Vorobyev, A.; Guo, C. Direct femtosecond laser surface nano/microstructuring and its applications. Laser Photonics Rev. 2012, 7, 385–407. [Google Scholar] [CrossRef]
- Reif, J.; Ratzke, M.; Varlamova, O.; Costache, F. Electrical Properties of Laser-Ablation-Initiated Self-Organized Nanostructures on Silicon Surface. Mater. Sci. Eng. B 2006, 134, 114–117. [Google Scholar] [CrossRef]
- Varlamova, O.; Costache, F.; Ratzke, M.; Reif, J. Control parameters in pattern formation upon femtosecond laser ablation. Appl. Surf. Sci. 2007, 253, 7932–7936. [Google Scholar] [CrossRef]
- Gottmann, J.; Wagner, R. Sub-wavelength ripple formation on dielectric and metallic materials induced by tightly focused femto-second laser radiation. Proc. SPIE 2006, 6106, 61061R. [Google Scholar]
- Gedvilas, M.; Račiukaitis, G.; Regelskis, K.; Gečys, P. Formation of Gratings by Self-Organization of the Chromium Thin Film on the Glass Substrate under Irradiation with Laser Pulses. JLMN 2008, 3, 58–62. [Google Scholar] [CrossRef]
- Hörstmann-Jungemann, M.; Gottmann, J.; Wortmann, D. Nano- and Microstructuring of SiO2 and Sapphire with Fs-laser Induced Selective Etching. JLMN 2009, 4, 135–140. [Google Scholar] [CrossRef]
- Zamfirescu, M.; Ulmeanu, M.; Jipa, F.; Cretu, O.; Moldovan, A.; Epurescu, G.; Dinescu, M.; Dabu, R. Femtosecond Laser Induced Periodic Surface Structures on ZnO Thin Films. JLMN 2009, 4, 7–10. [Google Scholar] [CrossRef]
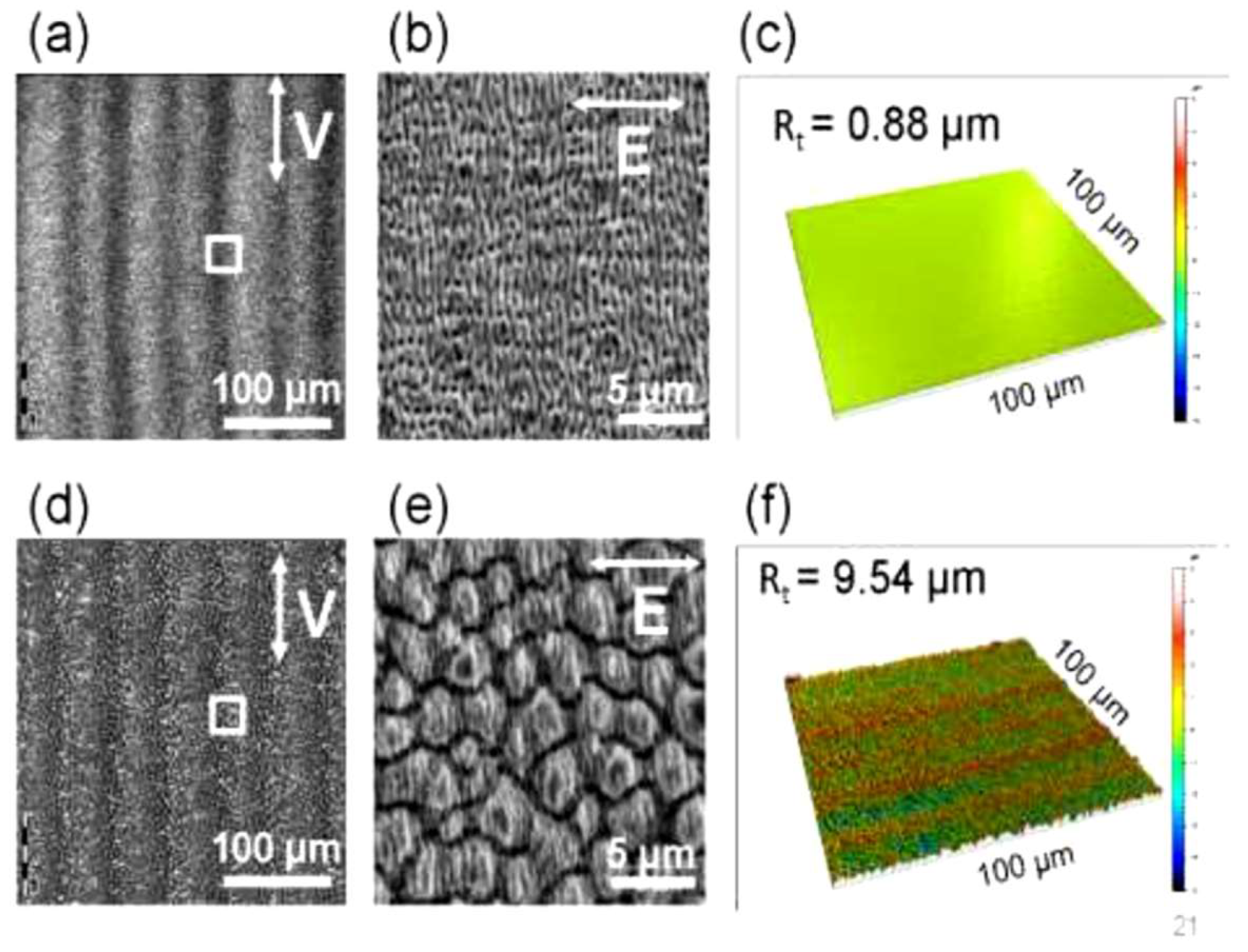
- Varlamova, O.; Hoefner, K.; Ratzke, M.; Reif, J.; Sarker, D. Modification of surface properties of solids by femtosecond LIPSS writing: Comparative studies on silicon and stainless steel. Appl. Phys. A 2017, 123, 725. [Google Scholar] [CrossRef]
- Reif, J.; Martens, C.; Uhlig, S.; Ratzke, M.; Varlamova, O.; Valette, S.; Benayoun, S. On large area LIPSS coverage by multiple pulses. Appl. Surf. Sci. 2015, 336, 249–254. [Google Scholar] [CrossRef]
- Sun, H.; Li, J.; Liu, M.; Yang, D.; Li, F. A Review of Effects of Femtosecond Laser Parameters on Metal Surface Properties. Coatings 2022, 12, 1596. [Google Scholar] [CrossRef]
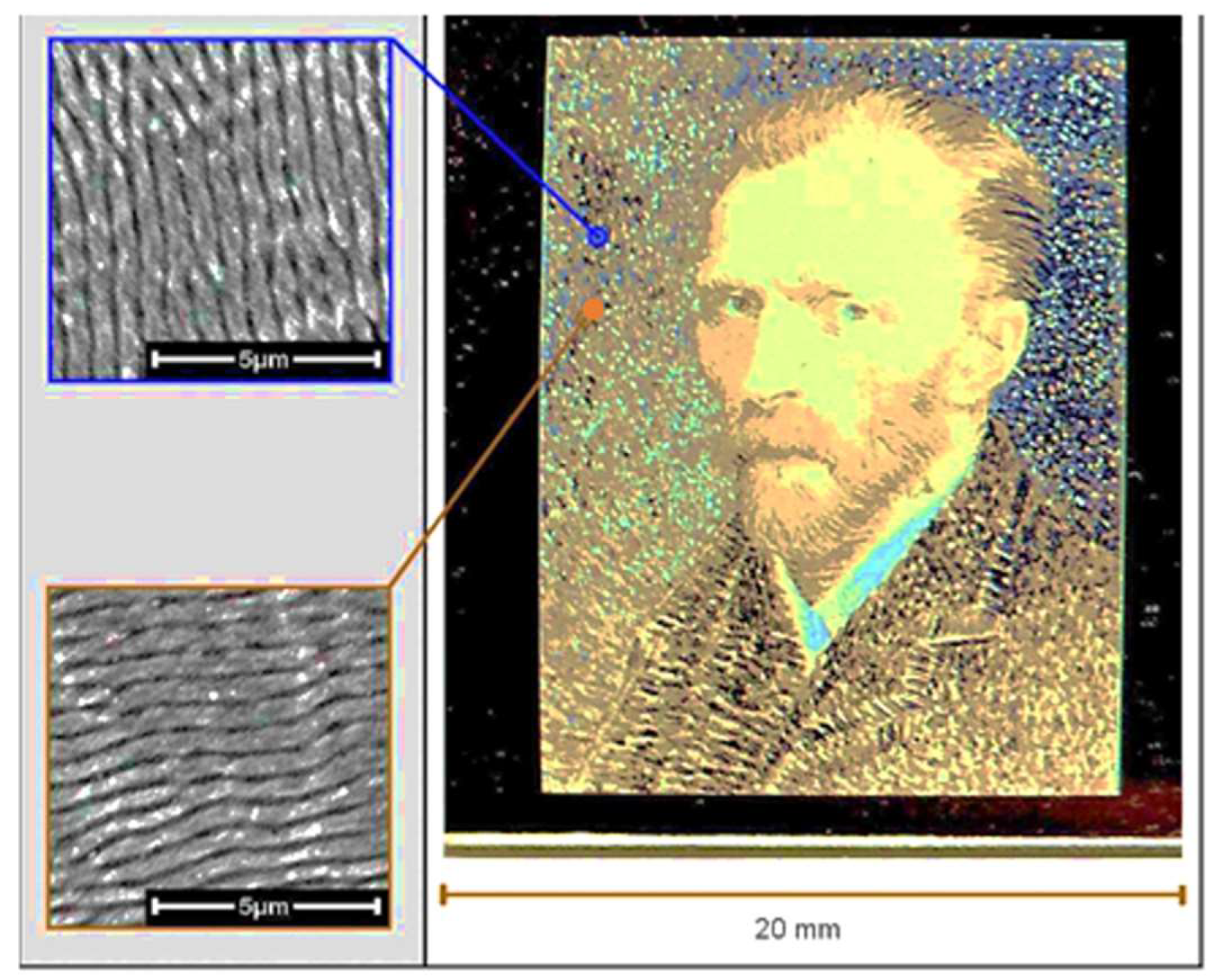
- Dusser, B.B.; Sagan, Z.; Soder, H.; Faure, N.; Colombier, J.; Jourlin, M.; Audouard, E. Controlled nanostructrures formation by ultra fast laser pulses for color marking. Opt. Express 2010, 18, 2913–2924. [Google Scholar] [CrossRef]
- Dusser, B.; Audouard, E.; Jourlin, M.; Soder, H.; Foucou, A. Method and Device for Marking a Surface Using Controlled Periodic Nanostructures. Patent WO/2009/090324, 2007. [Google Scholar]
- Her, T.-H.; Finlay, R.; Wu, C.; Deliwala, S.; Mazur, E. Microstructuring of silicon with femtosecond laser pulses. Appl. Phys. Lett. 1998, 73, 1673. [Google Scholar] [CrossRef]
- Wu, C.; Crouch, C.; Zhao, L.; Carey, J.; Younkin, R.; Levinson, J.; Mazur, E.; Farrell, R.; Gothoskar, P.; Karger, A. Near-unity below-band-gap absorption by microstructured silicon. Appl. Phys. Lett. 2001, 78, 1850. [Google Scholar] [CrossRef]
- Zorba; Persano, L.; Pisignano, D.; Athanassiou, A.; Stratakis, E.; Cingolani, R.; Tzanetakis, P.; Fotakis, C. Making silicon hydrophobic: Wettability control by two-lengthscale simultaneous patterning with femtosecond laser irradiation. Nanotechnology 2006, 17, 3234. [Google Scholar] [CrossRef] [PubMed]
- Groenendijk, M.; Meijer, J. Microstructuring using femtosecond pulsed laser ablation. J. Laser Appl. 2006, 18, 227–235. [Google Scholar] [CrossRef]
- Groenendijk, M. Fabrication of Super Hydrophobic Surfaces by fs Laser Pulses. Laser Tech. J. 2008, 5, 44–47. [Google Scholar] [CrossRef]
- Vorobyev, A.; Guo, C. Metal pumps liquid uphill. Appl. Phys. Lett. 2009, 94, 224102. [Google Scholar] [CrossRef]
- Vorobyev, A.; Guo, C. Laser turns silicon superwicking. Opt. Express 2010, 18, 6455–6460. [Google Scholar] [CrossRef]
- Barberoglou, M.; Zorba; Stratakis, E.; Spanakis, E.; Tzanetakis, P.; Anastasiadis, S.; Fotakis, C. Bio-inspired water repellent surfaces produced by ultrafast laser structuring of silicon. Appl. Surf. Sci. 2009, 255, 5425–5429. [Google Scholar] [CrossRef]
- Bizi-Bandoki, P.; Benayoun, S.; Valette, S.; Beaugiraud, B.; Audouard, E. Modifications of roughness and wettability properties of metals induced by femtosecond laser treatment. Appl. Surf. Sci. 2011, 257, 5213–5218. [Google Scholar] [CrossRef]
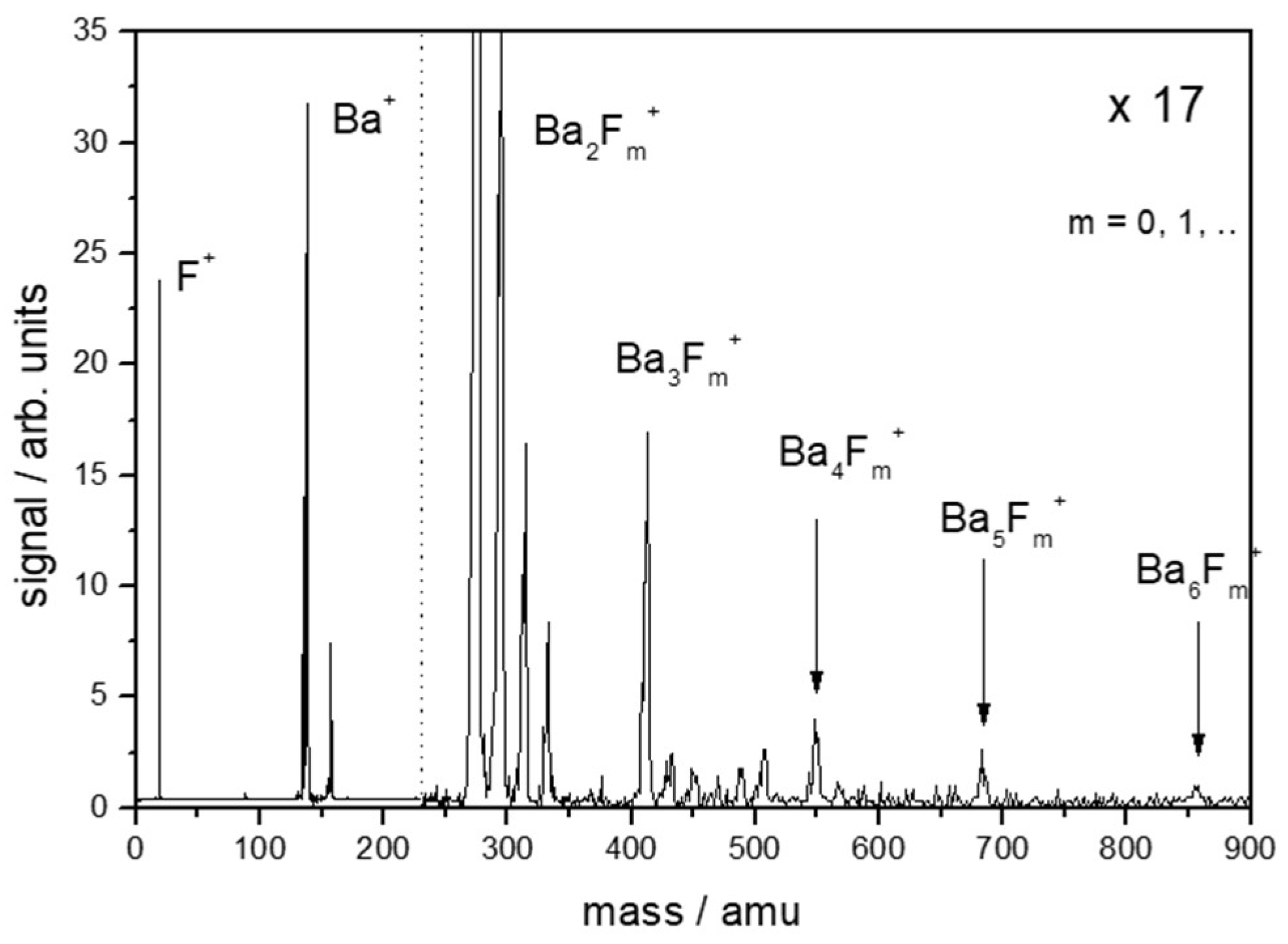
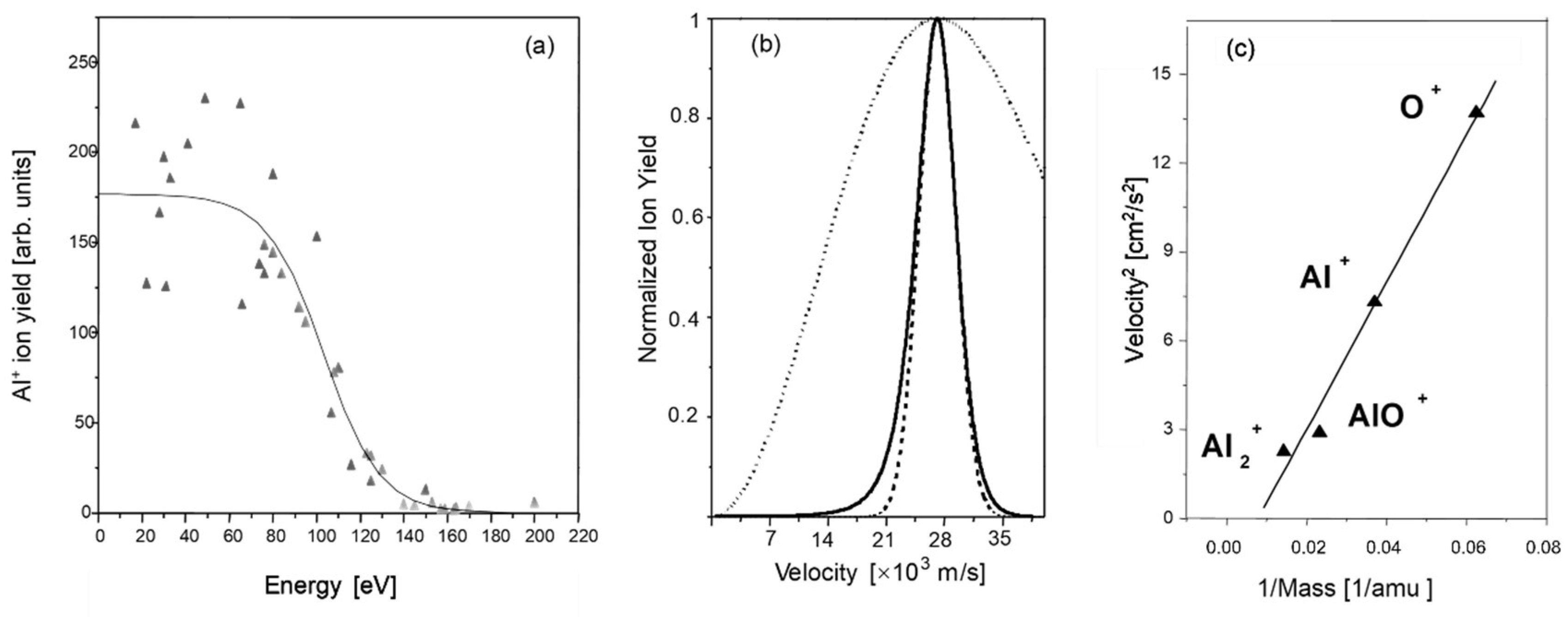
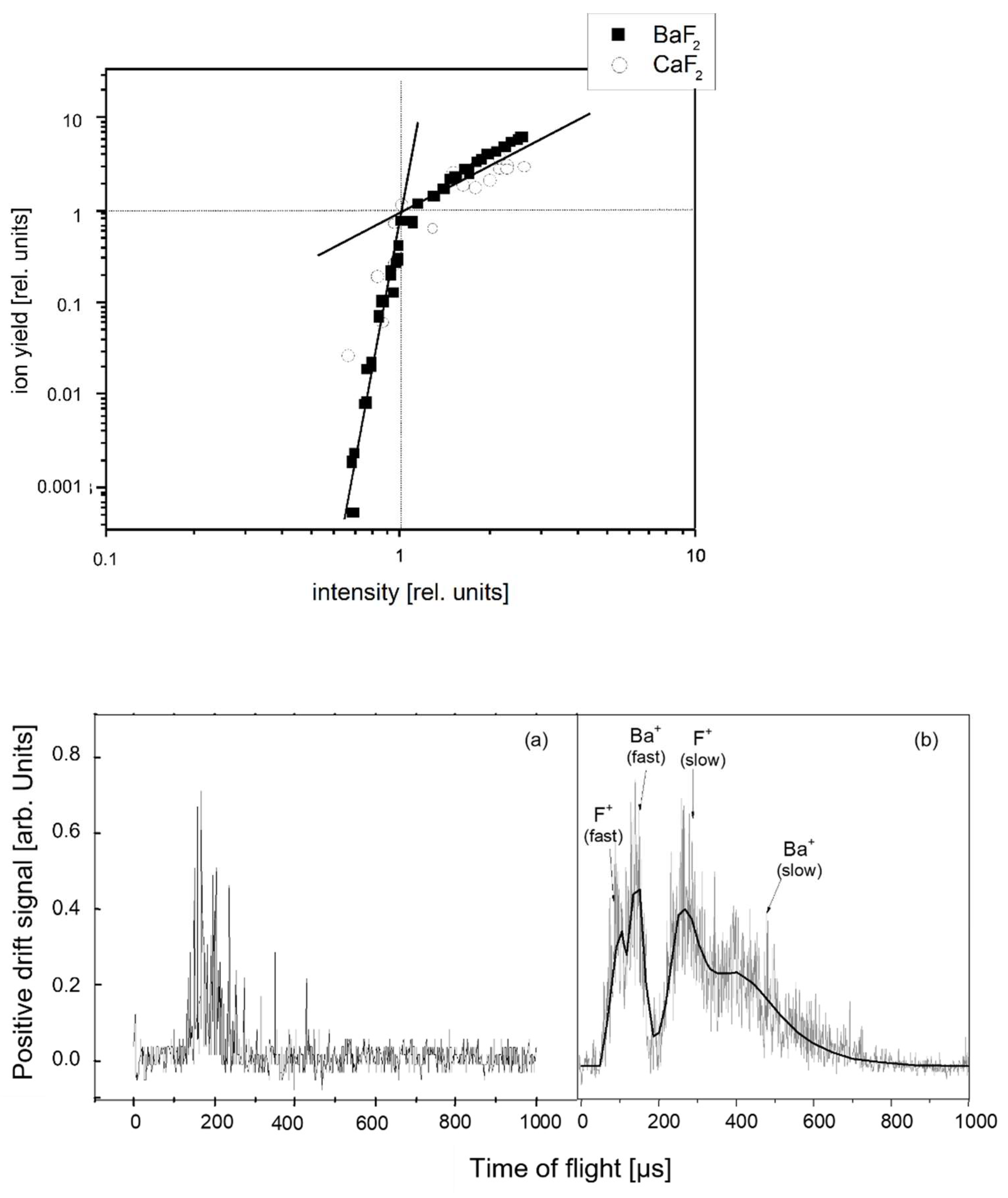
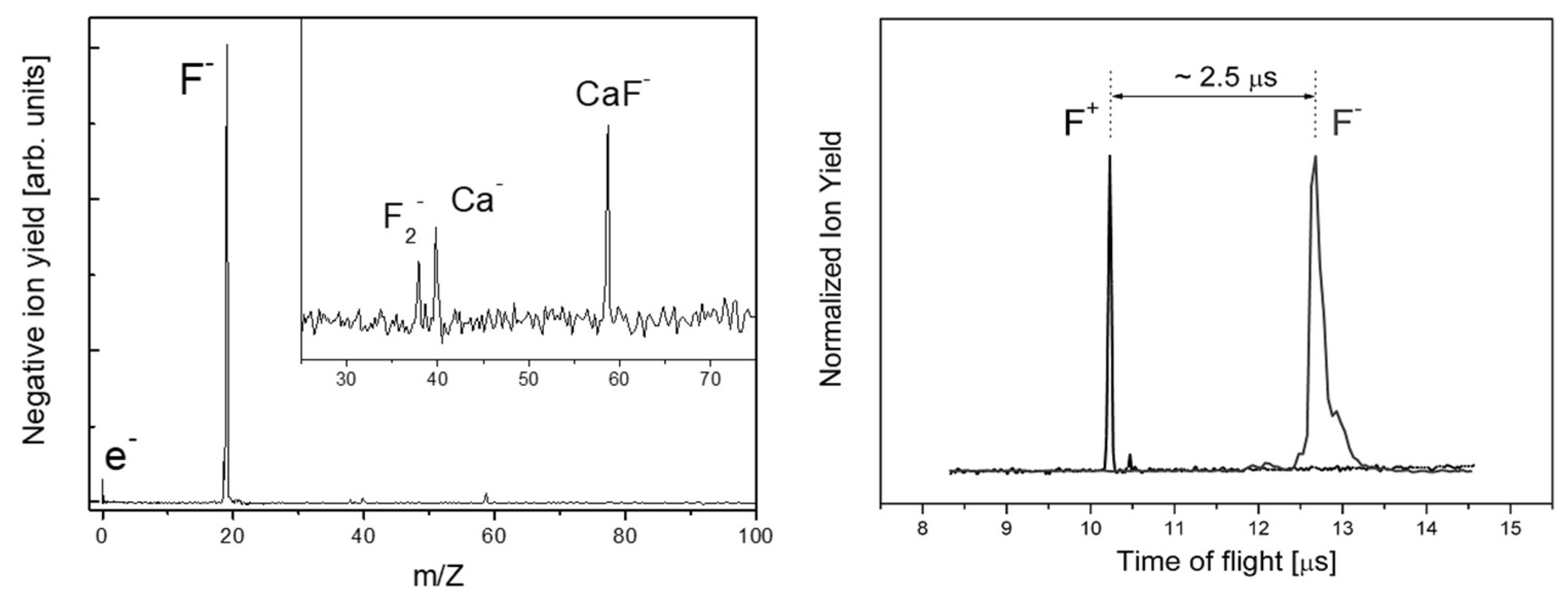
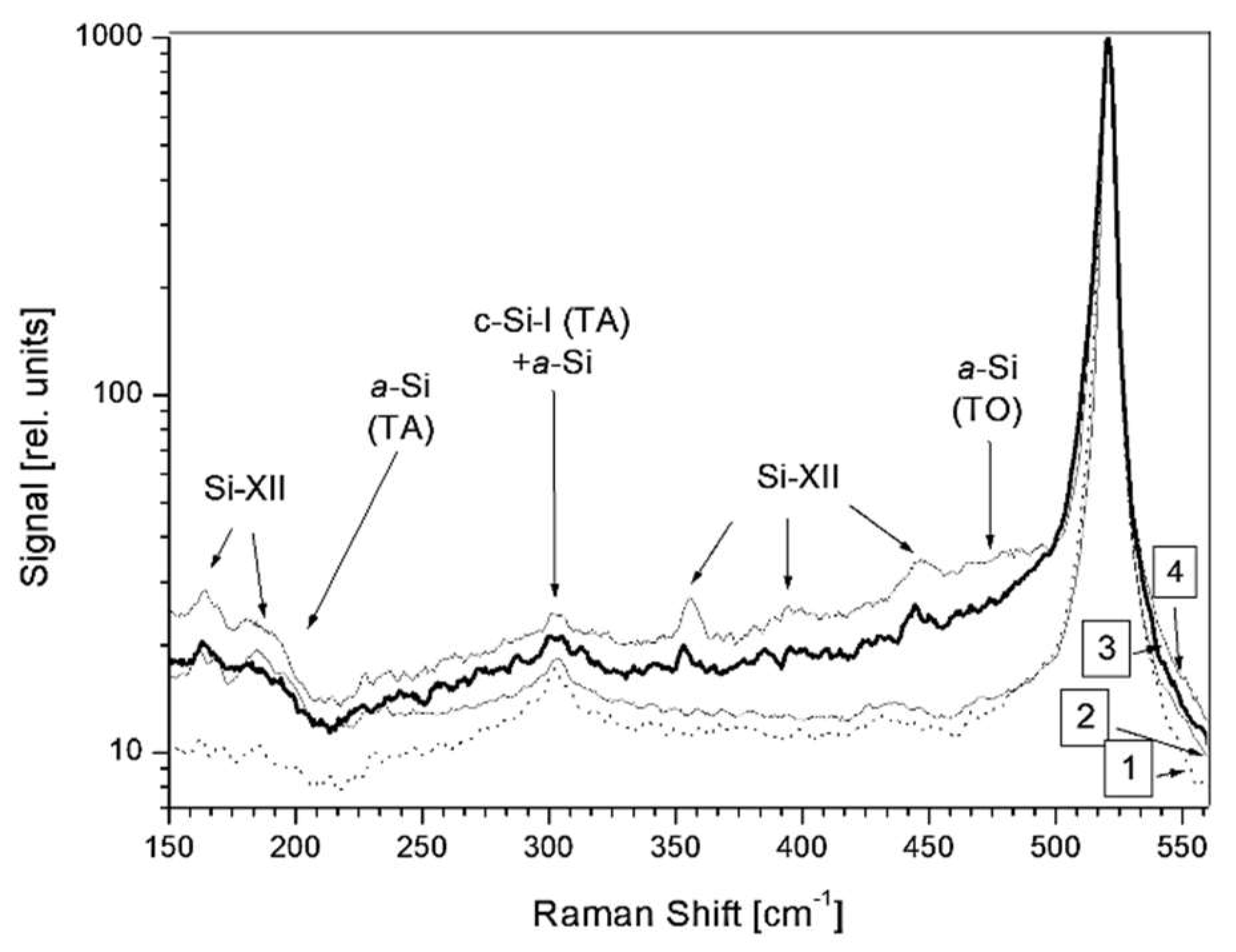
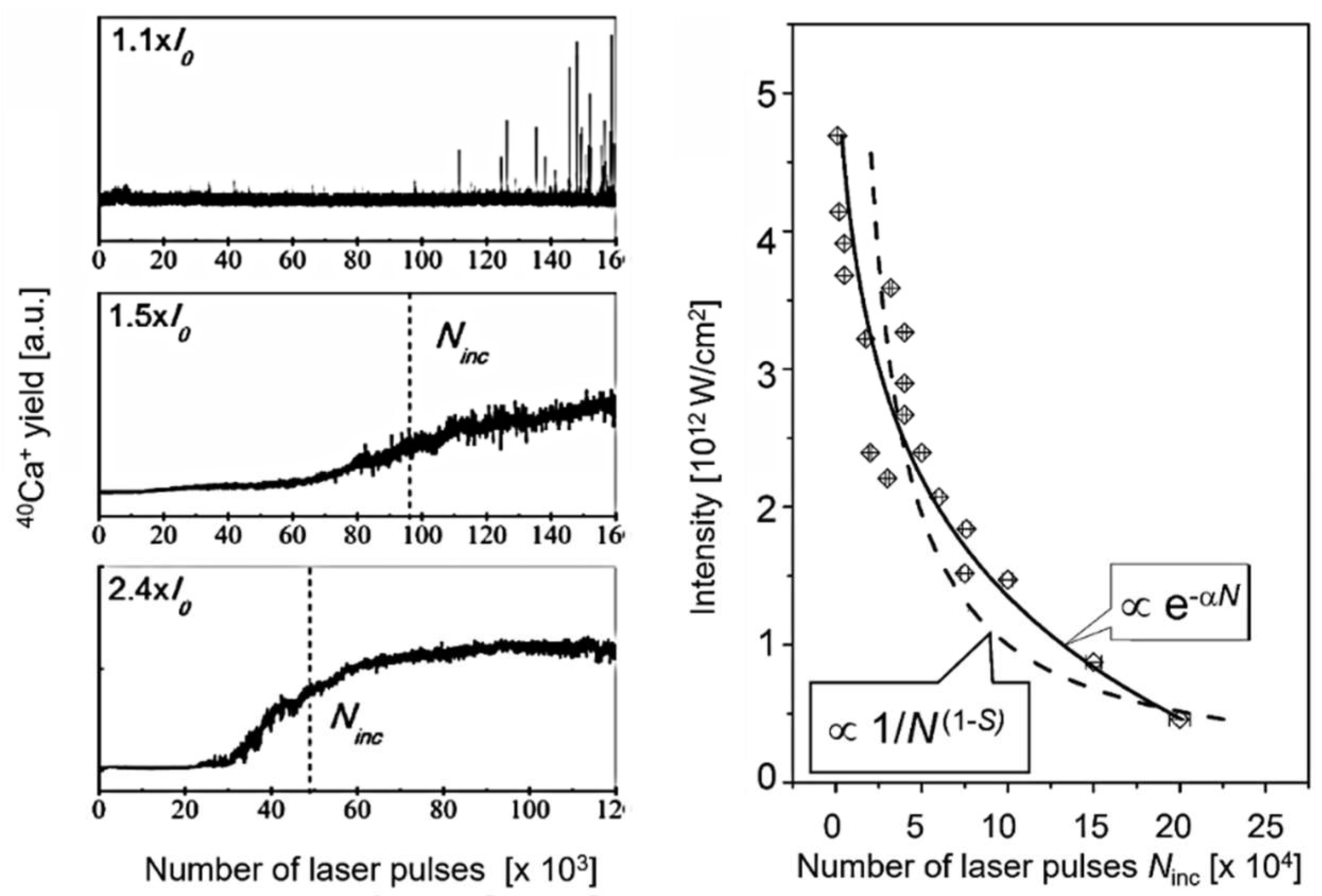
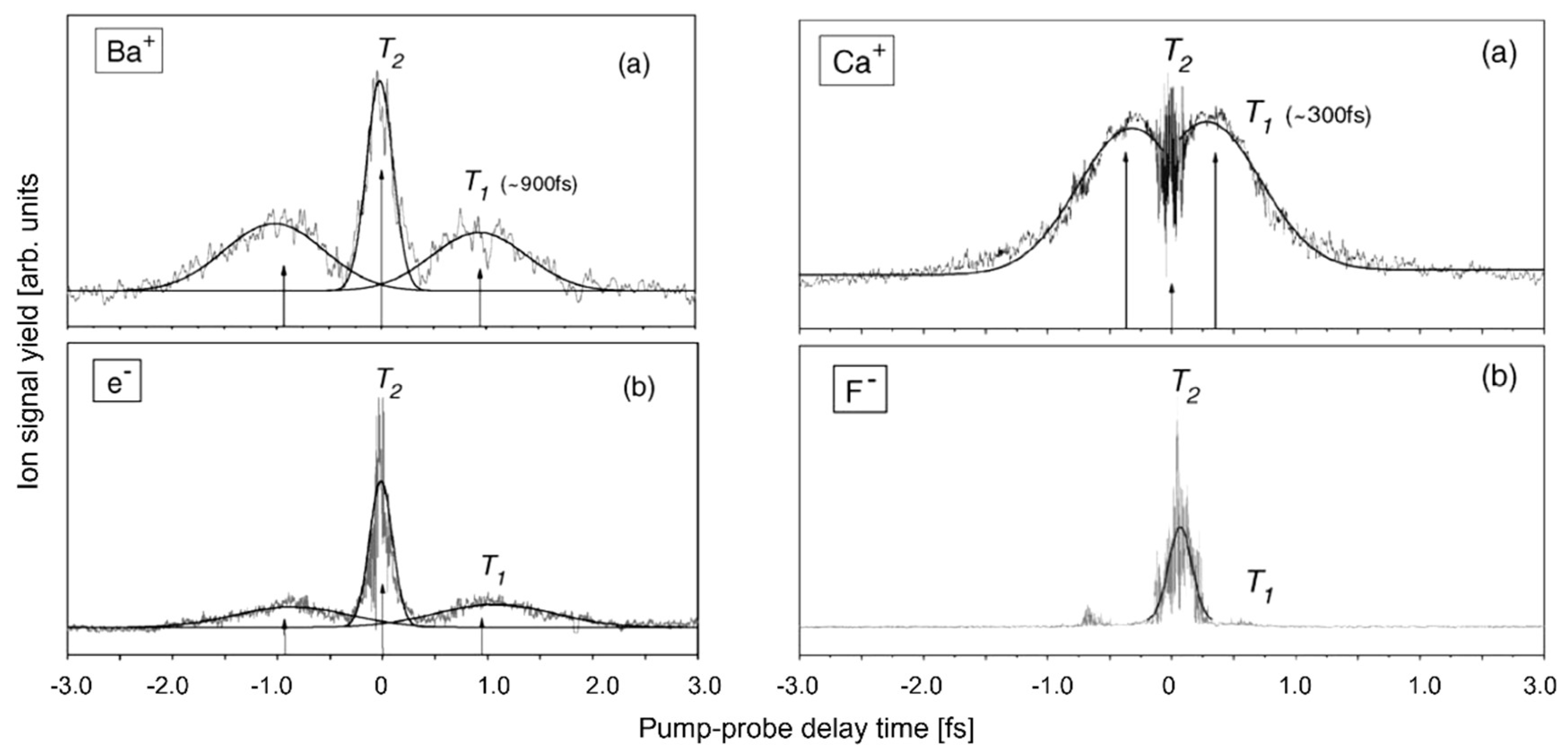











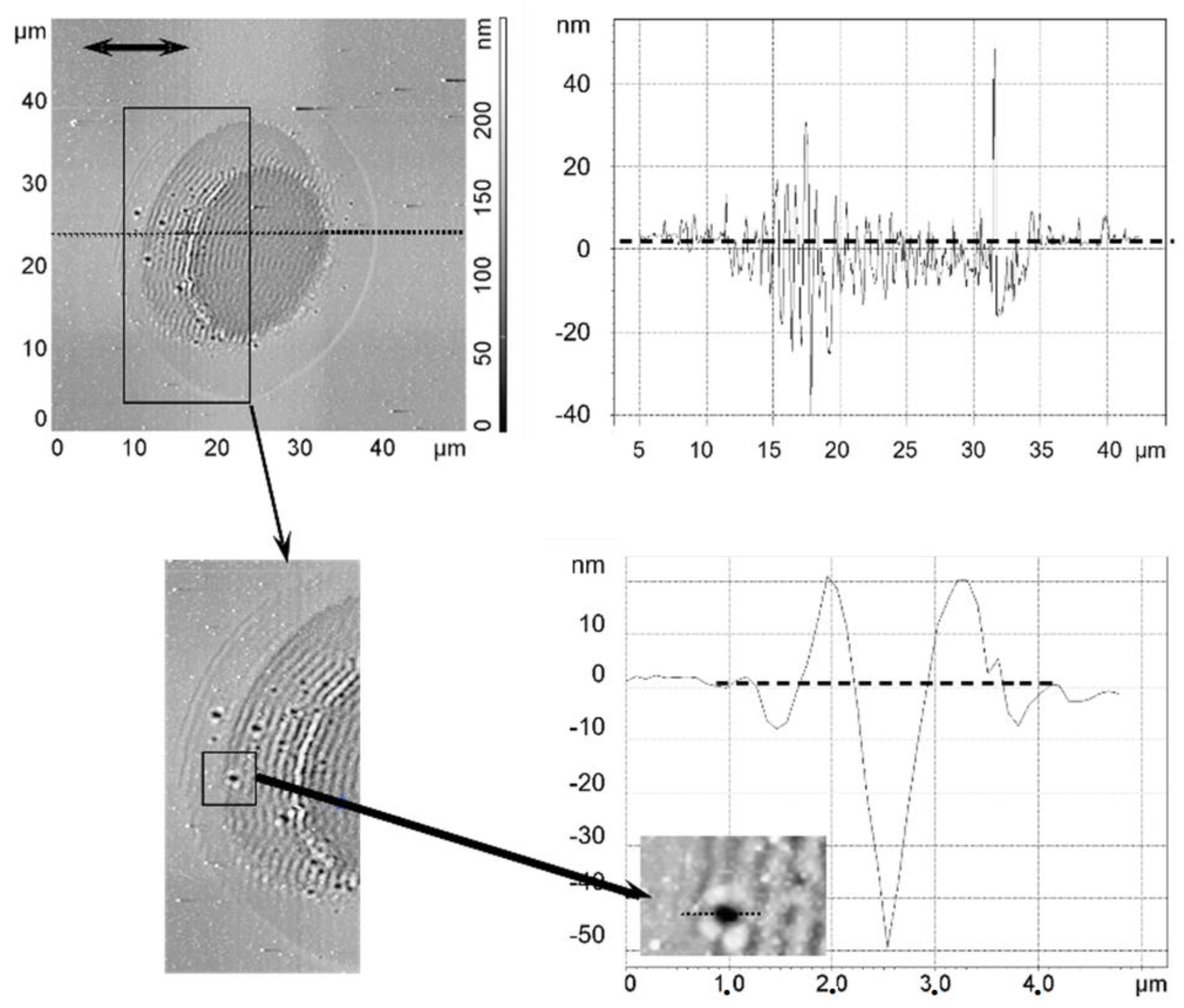




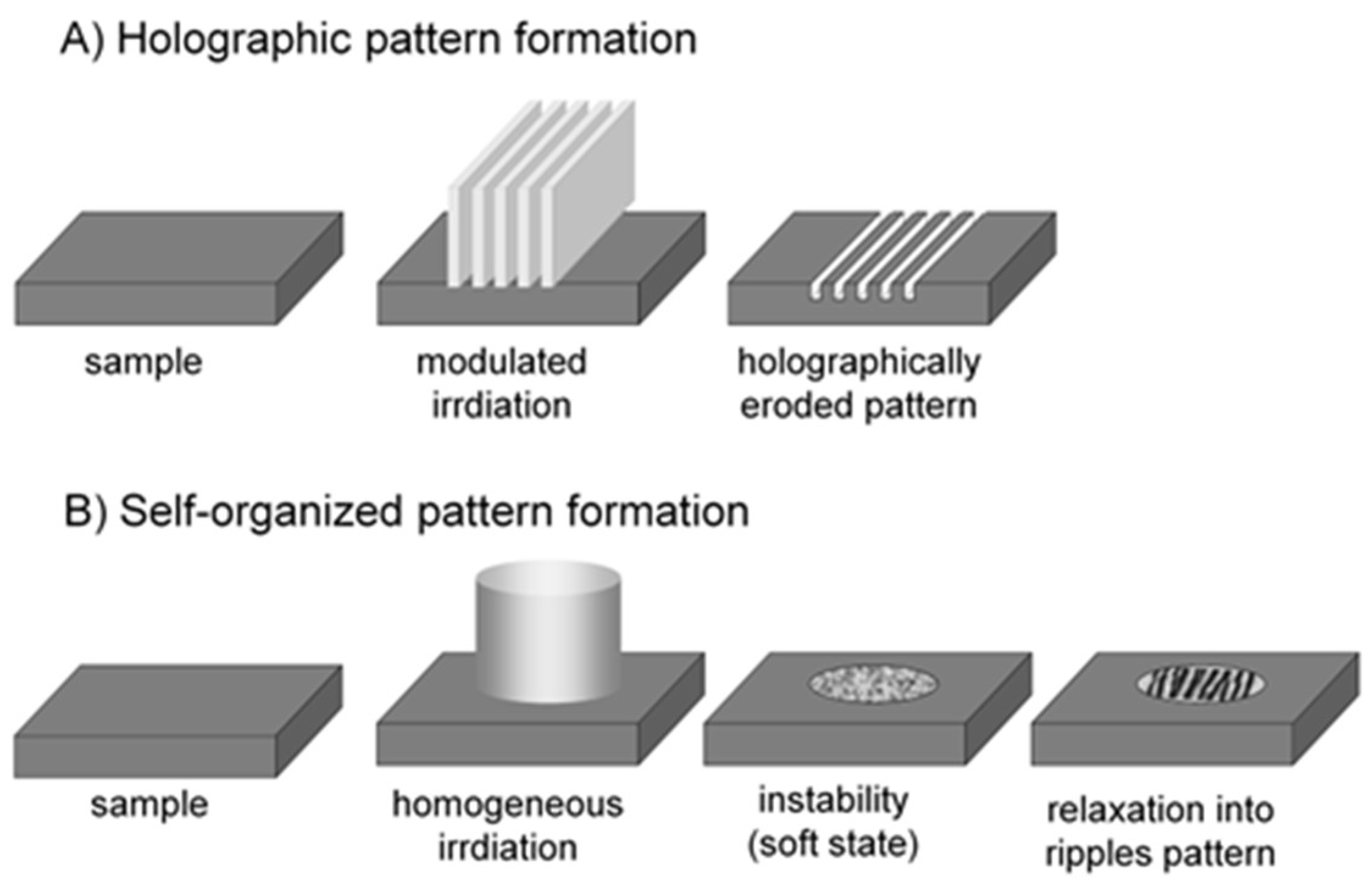


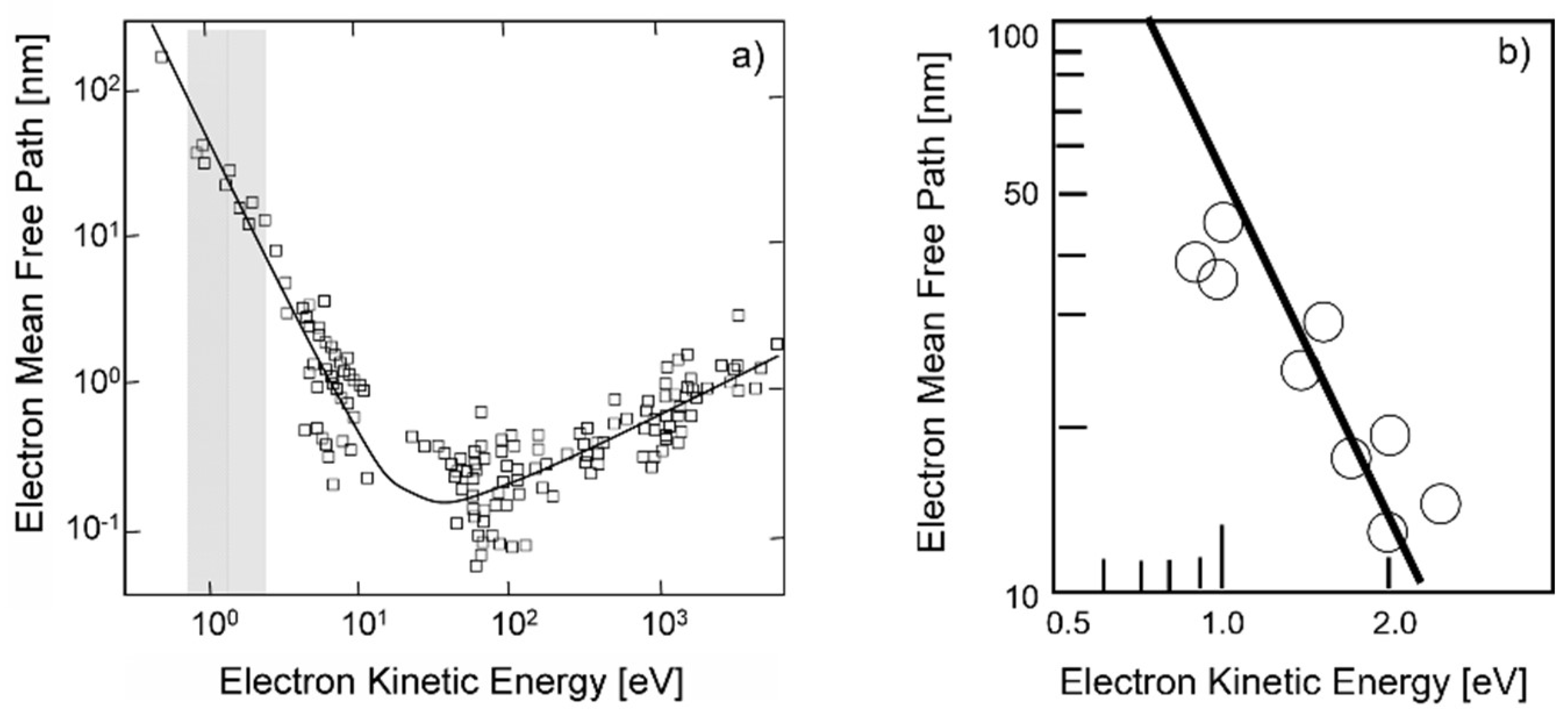
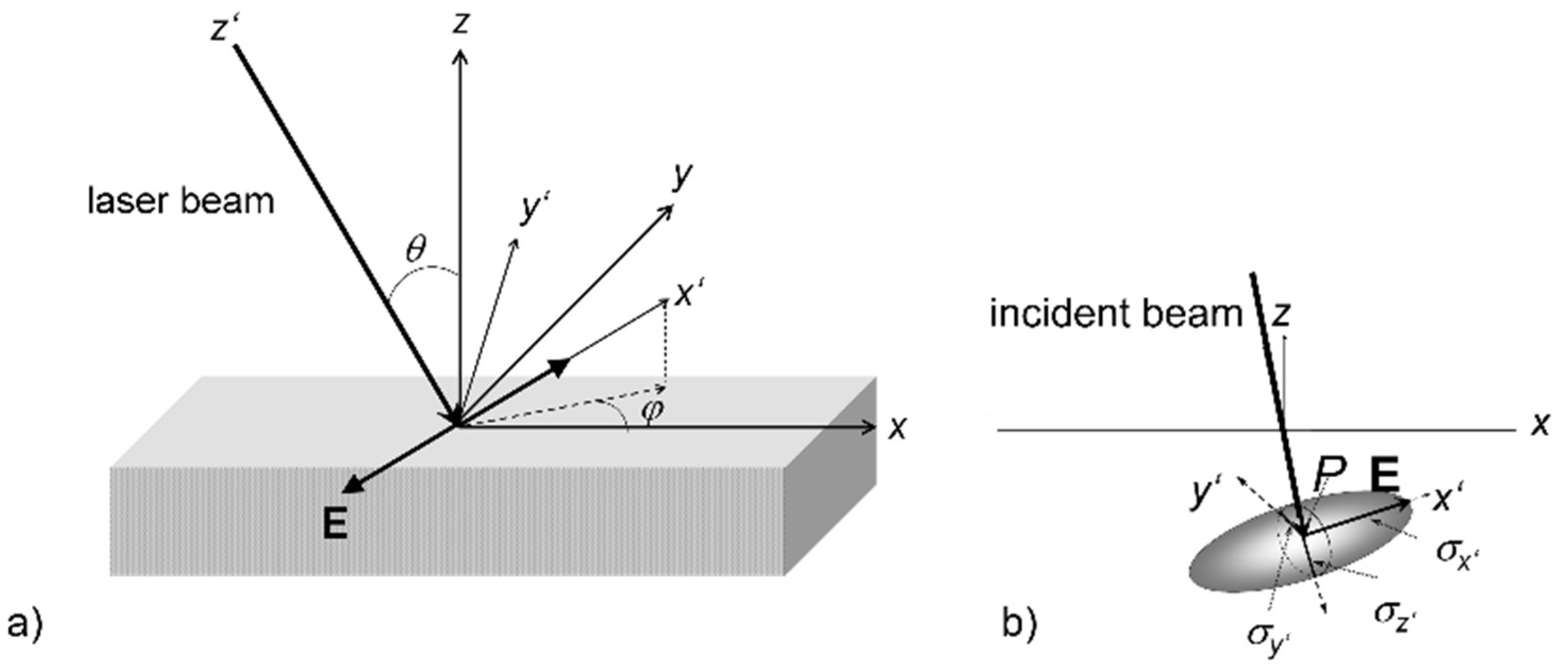





| Chemical Elements (%) | O | C | Fe | Cr | Ni |
|---|---|---|---|---|---|
| Irradiation Dose | |||||
| Non irradiated | 0.19 | 1.79 | 71.34 | 17.10 | 8.12 |
| 20 pulses/spot | 1.79 | 3.25 | 69.30 | 16.46 | 7.60 |
| 200 pulses/spot | 4.92 | 4.41 | 65.90 | 15.66 | 7.48 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reif, J. Dynamics and Processes on Laser-Irradiated Surfaces. Nanomaterials 2023, 13, 379. https://doi.org/10.3390/nano13030379
Reif J. Dynamics and Processes on Laser-Irradiated Surfaces. Nanomaterials. 2023; 13(3):379. https://doi.org/10.3390/nano13030379
Chicago/Turabian StyleReif, Juergen. 2023. "Dynamics and Processes on Laser-Irradiated Surfaces" Nanomaterials 13, no. 3: 379. https://doi.org/10.3390/nano13030379
APA StyleReif, J. (2023). Dynamics and Processes on Laser-Irradiated Surfaces. Nanomaterials, 13(3), 379. https://doi.org/10.3390/nano13030379





