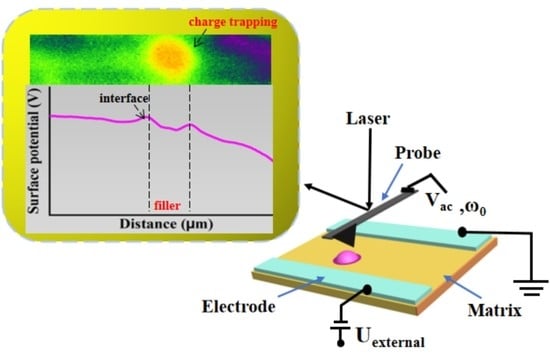
Interfacial Insight of Charge Transport in BaTiO3/Epoxy Composites
Abstract
:1. Introduction
2. Materials and Methods
2.1. Raw Materials
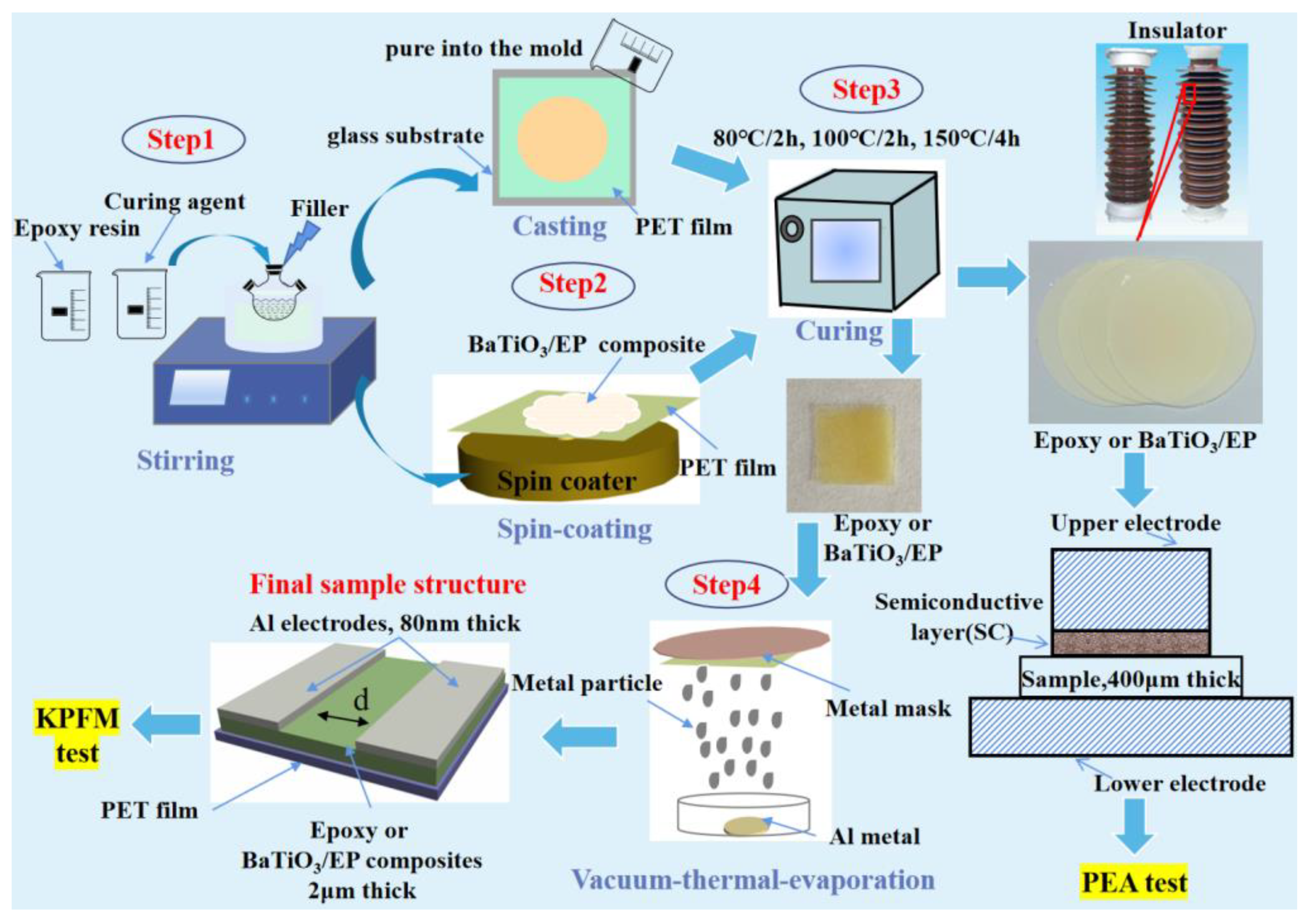
2.2. Sample Preparation
2.3. Characterization
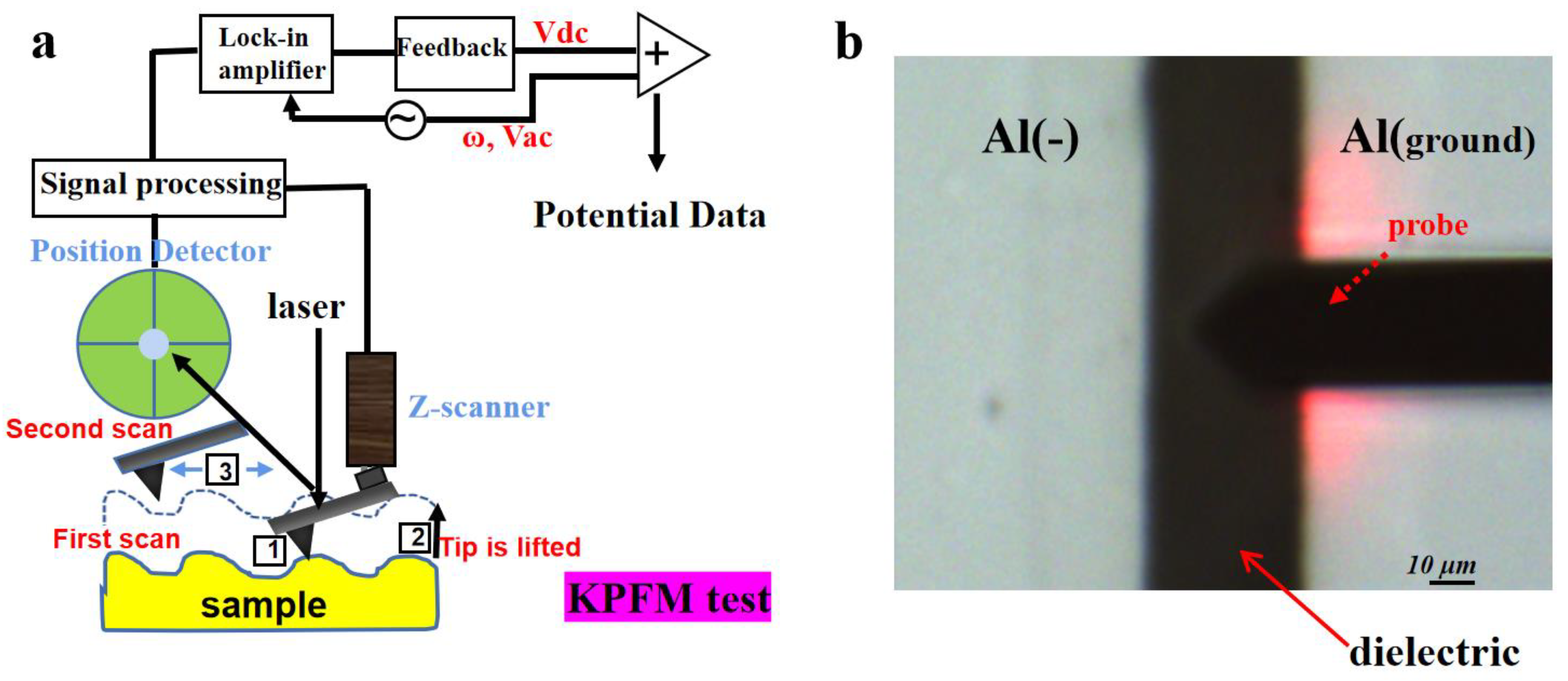
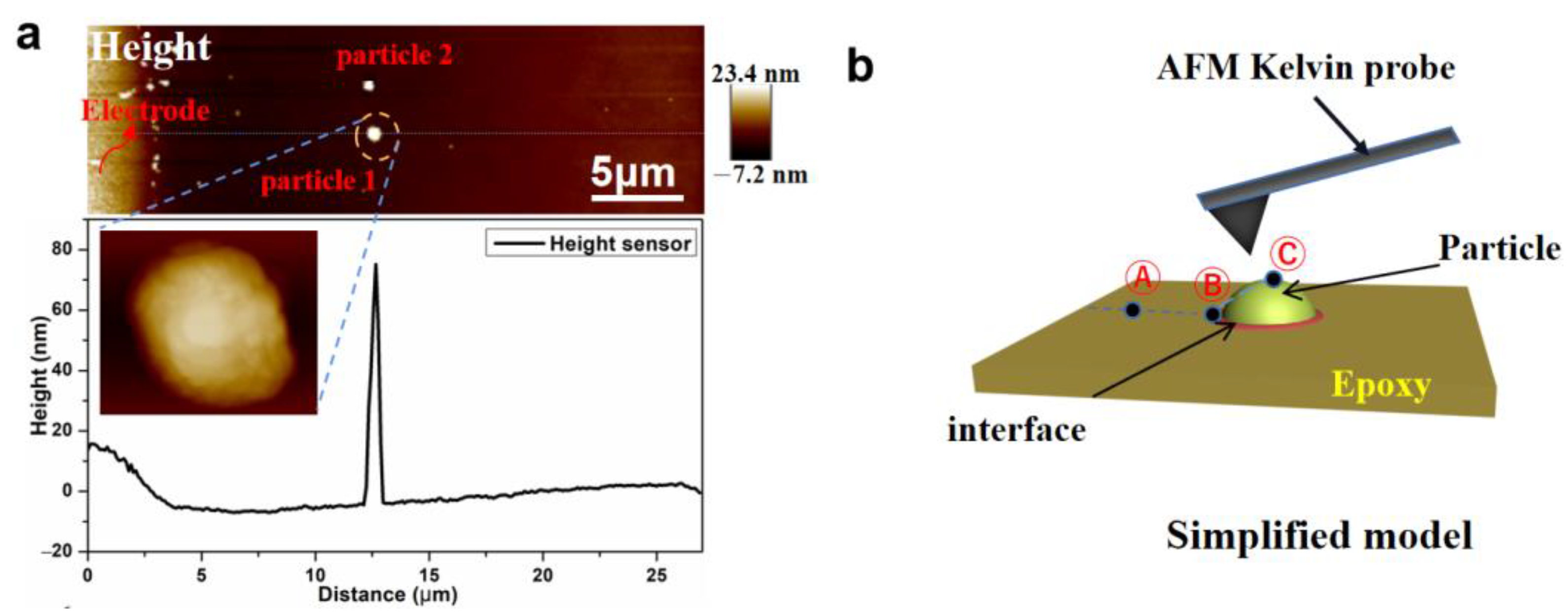
2.4. KPFM Measurement
3. Results and Discussion
3.1. Morphology of the BTO/EP Composite
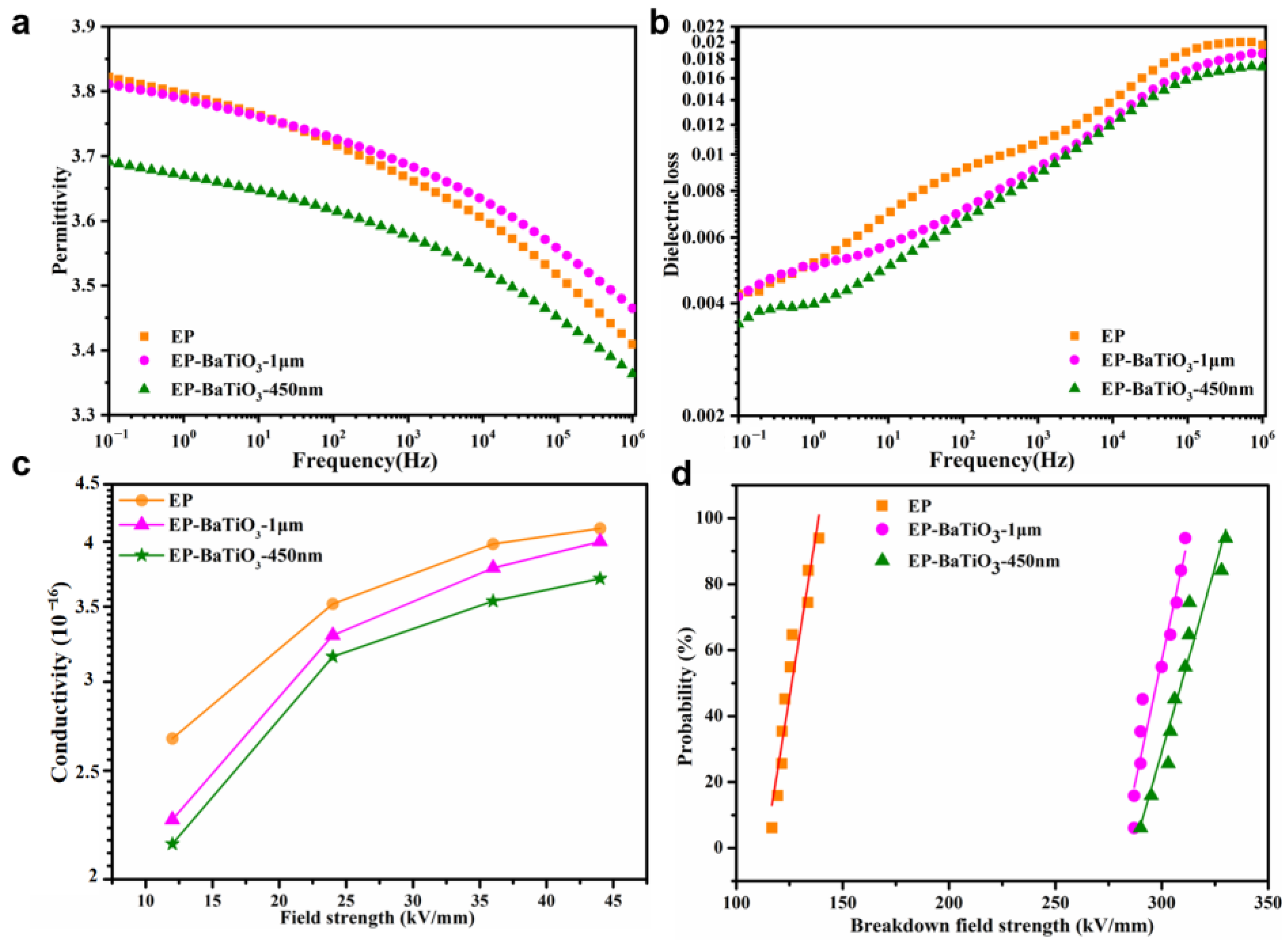
3.2. Dielectric Properties of the BTO/EP Composite
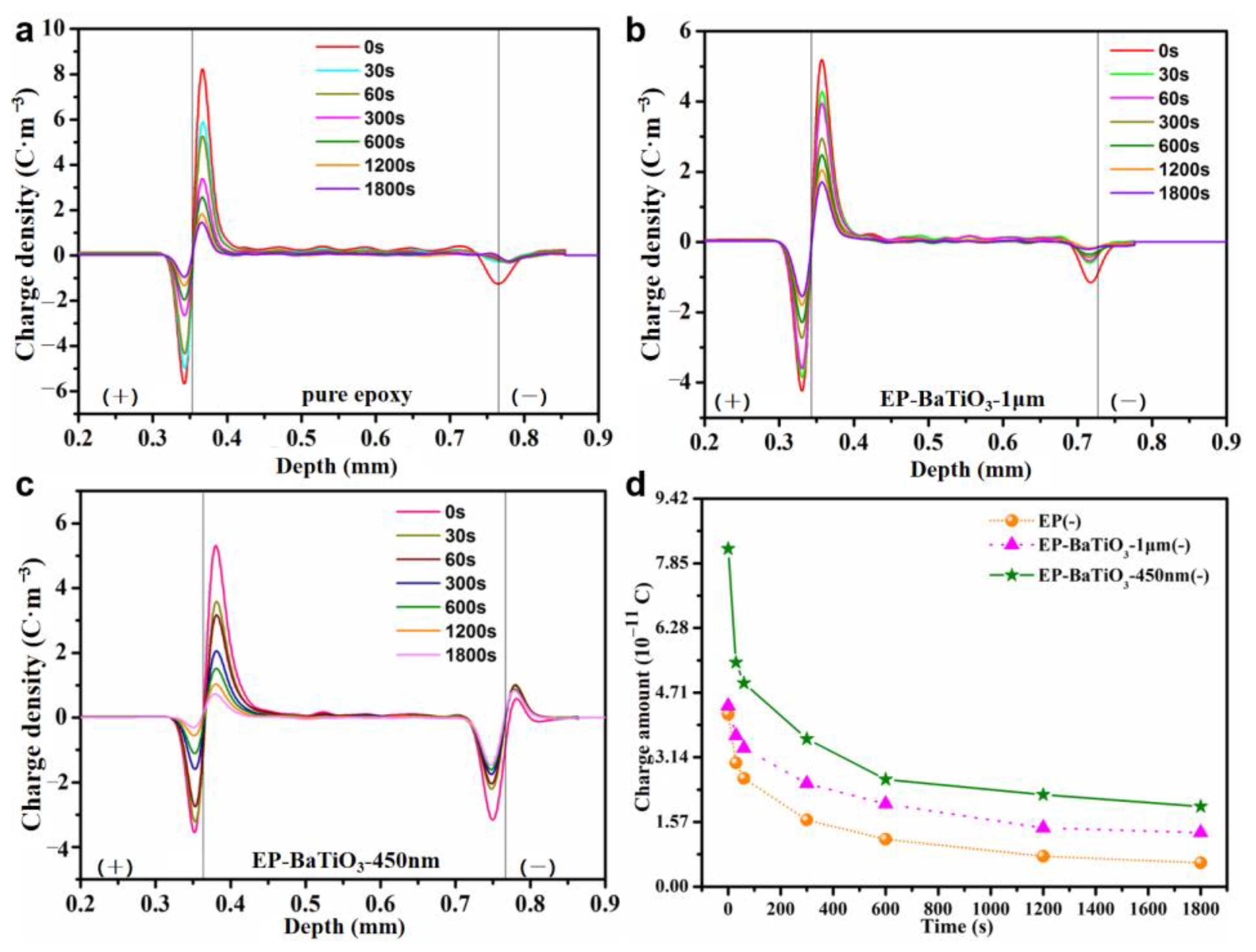
3.3. Space Charge Analysis via the PEA Method
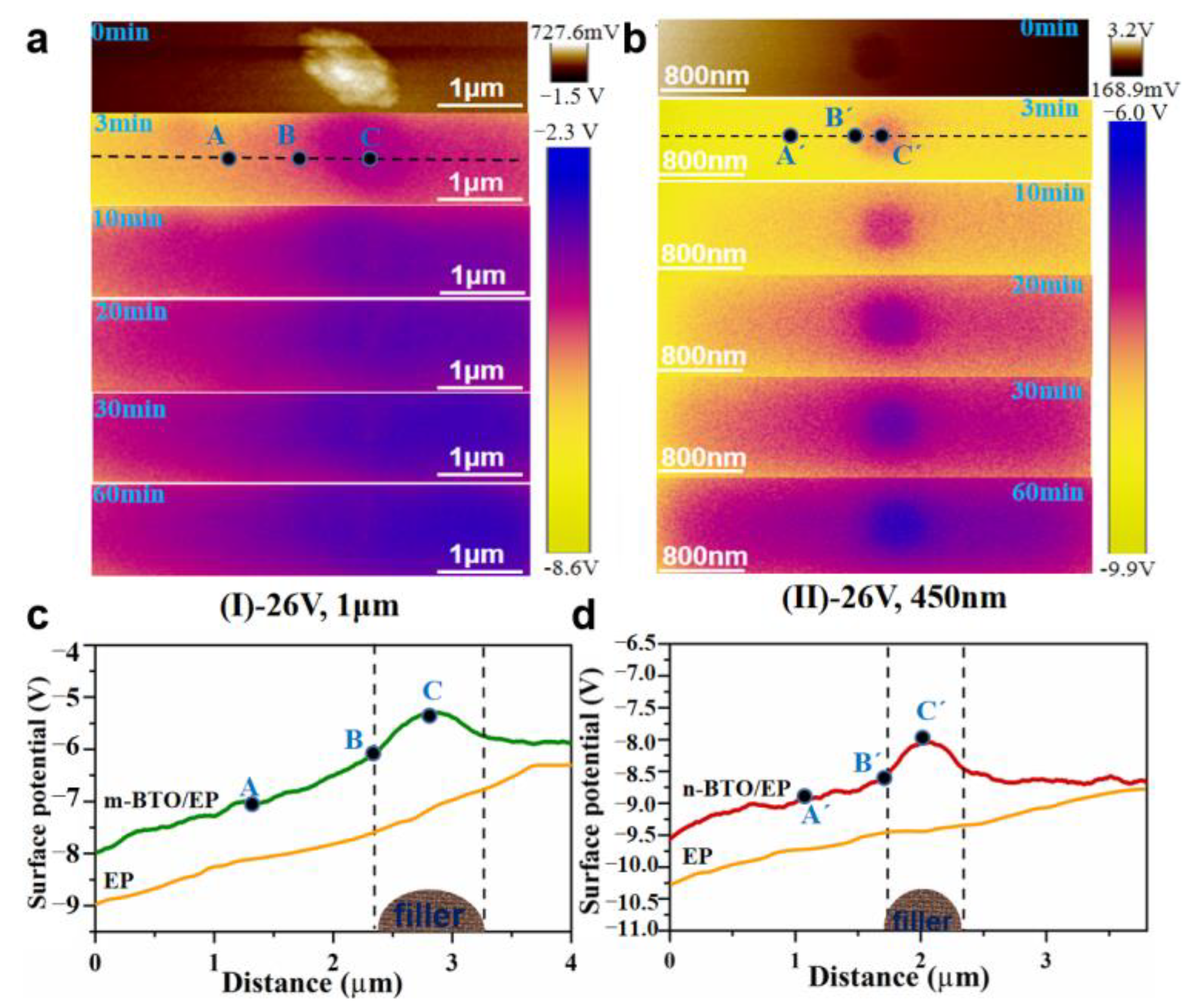
3.4. Charge Distribution and Transport Behavior at the Interface Region of BTO/EP under Bias
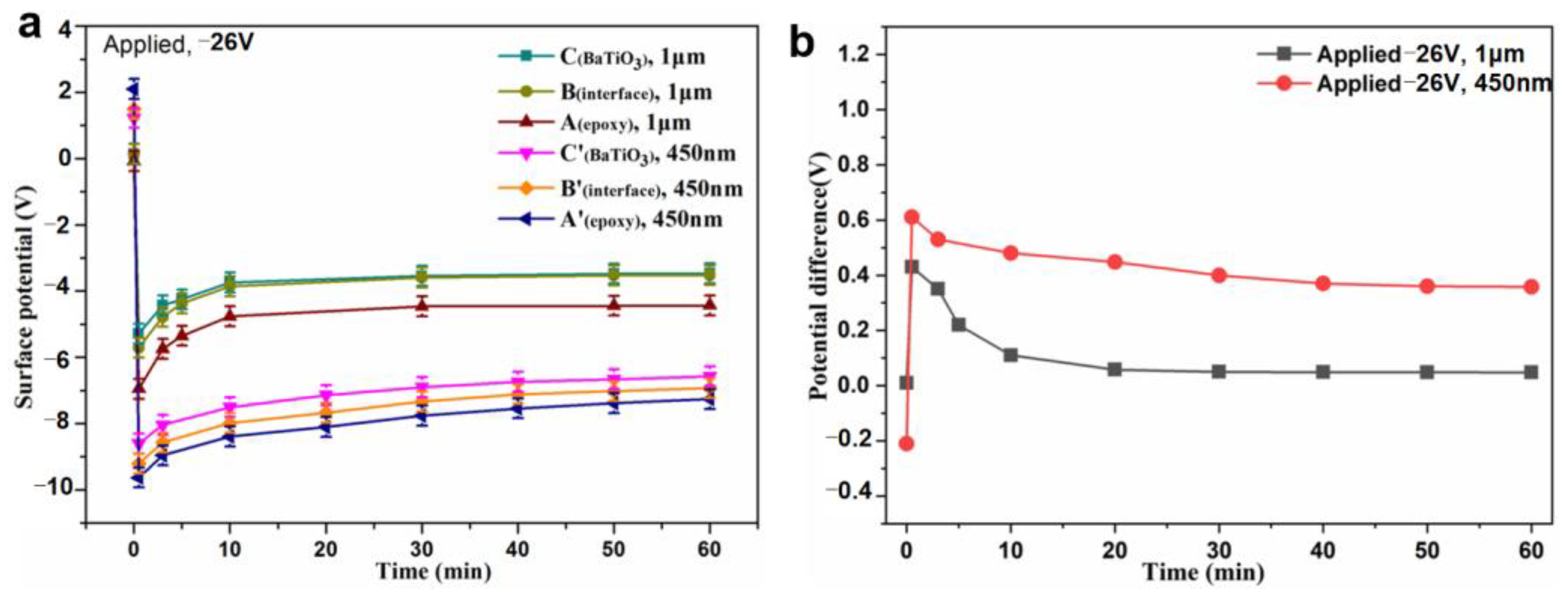
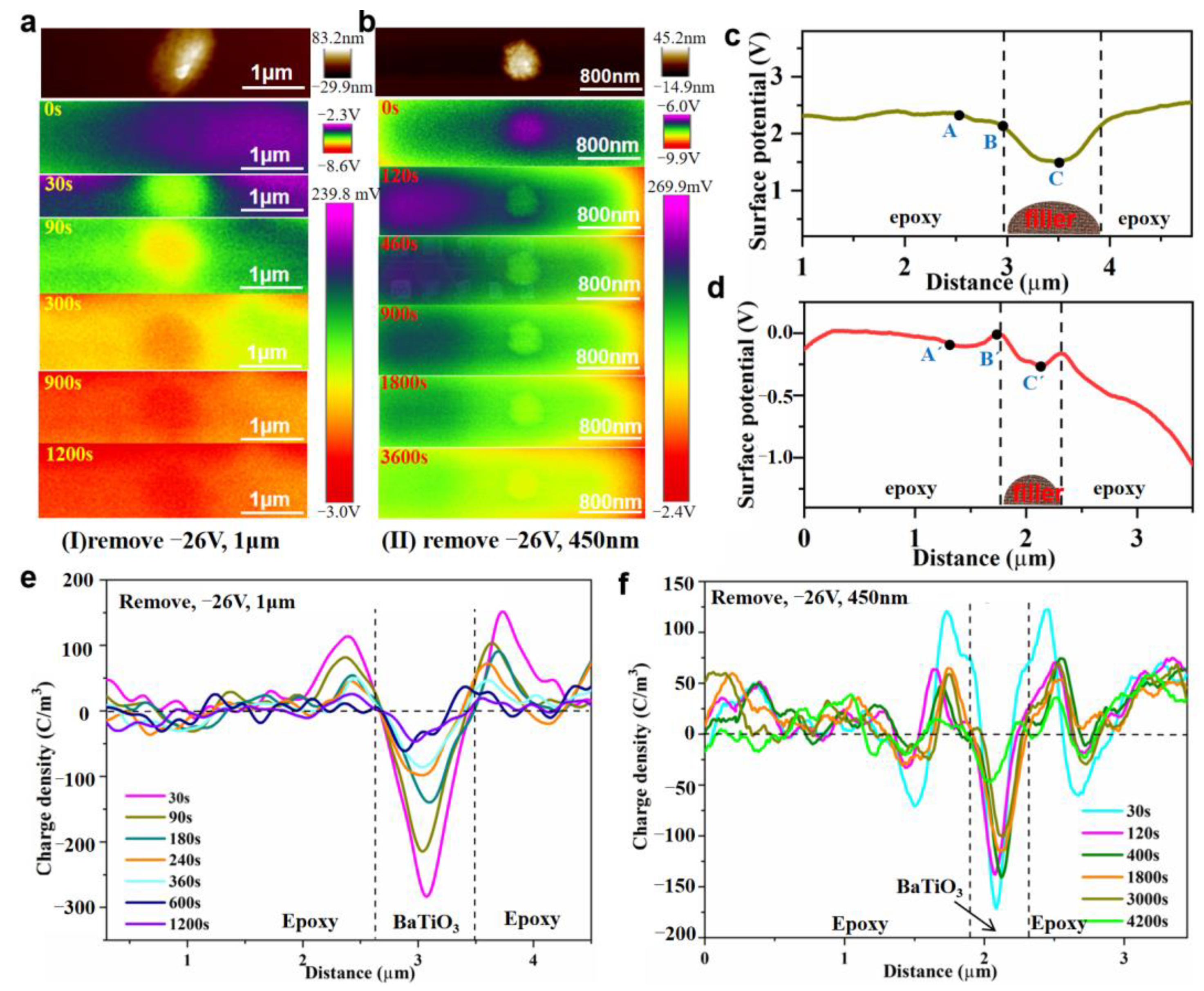
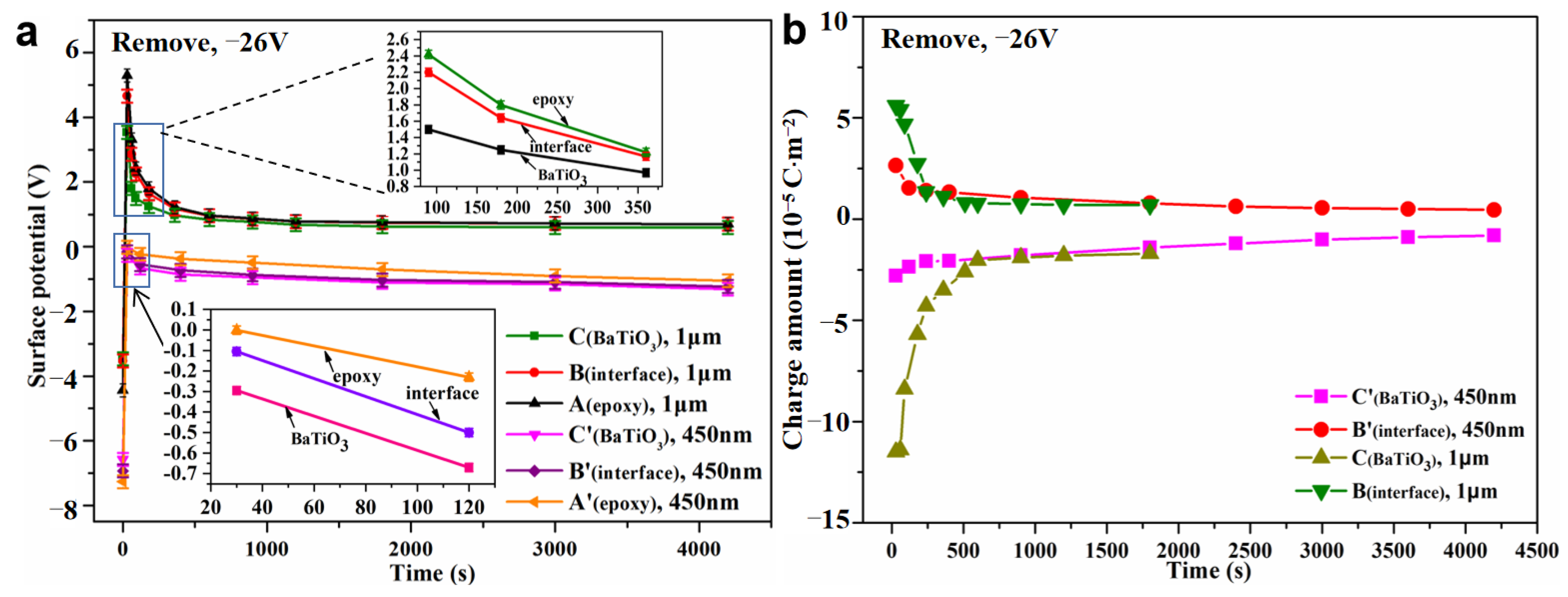
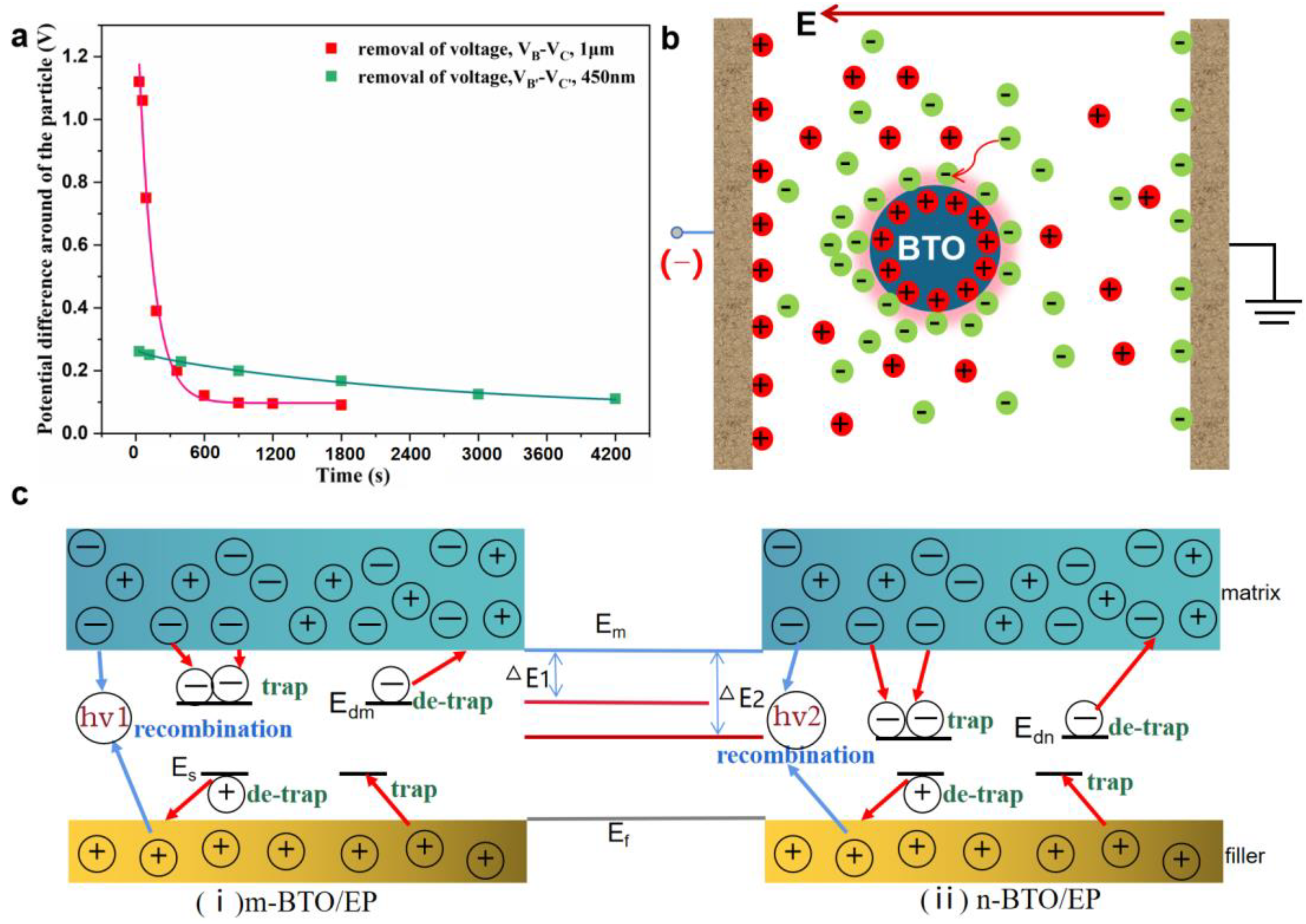
3.5. Charge Transport Behavior at the Interface Region of BTO/EP after Removal of Voltage
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Heger, G.; Vermeulen, H.; Holtzhausen, J.P.; Vosloo, W.A. Comparative Study of Insulator Materials Exposed to High Voltage AC and DC Surface Discharges. IEEE Trans. Dielectr. Electr. Insul. 2010, 17, 513–520. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Ding, Y.; Yuan, Z.; Peng, H.; Wu, J.; Yin, Y.; Tao, H.; Luo, F. Space-Charge Accumulation and Its Impact on High-Voltage Power Module Partial Discharge Under DC and PWM Waves: Testing and Modeling. IEEE Trtans. Power. Electr. 2021, 36, 11097–11108. [Google Scholar] [CrossRef]
- Zhao, X.; Pu, L.; Xu, Z.; Chen, G.; Duan, W.; Sun, H.; Ju, Z. Interfacial space charge characteristic of PPLP insulation for HVDC Cables. High Volt. 2020, 5, 628–635. [Google Scholar] [CrossRef]
- Li, Z.; Okamoto, K.; Ohki, Y.; Tanaka, T. Effects of Nano-Filler Addition on Partial Discharge Resistance and Dielectric Breakdown Strength of Micro-Al2O3/Epoxy Composite. IEEE Trans. Dielectr. Electr. Insul. 2010, 17, 654–663. [Google Scholar] [CrossRef]
- Li, S.; Xie, D.; Lei, Q. Understanding Insulation Failure of Nanodielectrics: Tailoring Carrier Energy. High Volt. 2020, 5, 643–649. [Google Scholar] [CrossRef]
- Jo, J.; Kim, S.; Jin, J.-T.; Huh, S.-R. Development of Waveguide DC Break for Power Transmission at 2.45 GHz and 100-kV Insulation. IEEE Microw. Wirel. Compon. Lett. 2020, 30, 339–342. [Google Scholar] [CrossRef]
- Mei, H.; Jiang, H.; Chen, J. Detection of Internal Defects of Full-Size Composite Insulators Based on Microwave Technique. IEEE T. Instrum. Meas. 2021, 99, 1–10. [Google Scholar] [CrossRef]
- Okabe, S.; Ueta, G.; Nojima, K. Resistance Characteristics and Electrification Characteristics of GIS Epoxy Insulators under DC Voltage. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 1260–1267. [Google Scholar] [CrossRef]
- Shen, Z.K.; Wang, X.L.; Xin, Z.Y. Analytical model for the spatiotemporal permittivity of uncured-composite devices in an AC electric field. J. Phy. D Appl Phys. 2021, 54, 155302. [Google Scholar] [CrossRef]
- Liang, X.; Li, X.; Tang, Y. Hyperbranched epoxy resin-grafted graphene oxide for efficient and all-purpose epoxy resin modification. J.Colloid. Interf. Sci. 2022, 611, 105–117. [Google Scholar] [CrossRef]
- Bai, T.; Wang, D.; Yan, J. Wetting mechanism and interfacial bonding performance of bamboo fiber reinforced epoxy resin composites. Compos. Sci. Technol. 2021, 213, 108951. [Google Scholar] [CrossRef]
- Bi, X.; Di, H.; Liu, J.; Meng, Y.; Song, Y.; Meng, W.; Qu, H.; Fang, L.; Song, P.; Xu, J. A core–shell-structured APP@COFs hybrid for enhanced flame retardancy and mechanical property of epoxy resin (EP). Adv.Compos. Hybrid. Mater 2022, 5, 1743–1755. [Google Scholar] [CrossRef]
- He, S.; Luo, C.; Zheng, Y. Improvement in the charge dissipation performance of epoxy resin composites by incorporating amino-modified boron nitride nanosheets. Mater. Lett 2021, 298, 130009. [Google Scholar] [CrossRef]
- Lee, S.Y.; Chong, M.; Kim, H.; Park, S. Effect of chemically reduced graphene oxide on epoxy nanocomposites for flexural behaviors. Carbon. Lett. 2014, 5, 67–70. [Google Scholar] [CrossRef] [Green Version]
- Jian, R.K.; Lin, X.B.; Liu, Z.Q.; Zhang, J. Rationally designed zinc borate@ZIF-8 core-shell nanorods for curing epoxy resins along with low flammability and high mechanical property. Compos. B. Eng. 2010, 200, 108349. [Google Scholar] [CrossRef]
- Thakur, Y.; Zhang, T.; Iacob, C.; Yang, T.; Bernholc, J.; Chen, L.Q.; Runt, J.; Zhang, Q.M. Enhancement of the Dielectric Response in Polymer Nanocomposites with Low Dielectric Constant Fillers. Nanoscale 2017, 9, 10992–10997. [Google Scholar] [CrossRef]
- Zhang, B.; Chen, X.; Lu, W.; Zhang, Q.M.; Bernholc, J. Morphology-Induced Dielectric Enhancement in Polymer Nanocomposites. Nanoscale 2021, 13, 10933–10942. [Google Scholar] [CrossRef]
- Guo, L.; Ding, S.L.; Yuan, S.; Gou, X.F. Study on the thermal properties and insulation resistance of epoxy resin modified by hexagonal boron nitride. e-Polym 2021, 21, 681–690. [Google Scholar] [CrossRef]
- Lu, F.C.; Ruan, H.O.; Song, J.X. Enhanced surface insulation and depressed dielectric constant for Al2O3/epoxy composites through plasma fluorination of filler. J. Phys. D Appl. Phys. 2019, 52, 155201. [Google Scholar] [CrossRef]
- Li, Z.; Hu, J.; Ma, L. Shape memory CTBN/epoxy resin/cyanate ester ternary resin and their carbon fiber reinforced composites. J. Appl. Polym. Sci. 2019, 137, 48756–48763. [Google Scholar] [CrossRef]
- Zhou, W.Y.; Cao, G.Z.; Yuan, M.X.; Zhong, S.L.; Wang, Y.D. Core–Shell Engineering of Conductive Fillers toward Enhanced Dielectric Properties: A Universal Polarization Mechanism in Polymer Conductor Composites. Adv.Mater. 2022, 35, 2207829. [Google Scholar] [CrossRef]
- Tian, Y.; Zhou, W.Y.; Peng, W.W.; Zhou, J.J.; Li, T. Insights into concomitant enhancements of dielectric properties and thermal conductivity of PVDF composites filled with core@ double-shell structured Zn@ZnO@PS particles. J. Appl. Polym. Sci. 2022, 139, e53069. [Google Scholar]
- Peng, S.; Dang, B.; Zhou, Y.; Hu, J.; He, J. Functionalized TiO2 Nanoparticles Tune the Aggregation Structure and Trapping Property of Polyethylene Nanocomposites. J. Phys. Chem. C. 2016, 120, 24754–24761. [Google Scholar] [CrossRef]
- Leng, J.; Szymoniak, P.; Kang, N.-J.; Wang, D.-Y.; Wurm, A.; Schick, C.; Schönhals, A. Influence of Interfaces on the Crystallization Behavior and the Rigid Amorphous Phase of Poly(l-Lactide)-Based Nanocomposites with Different Layered Doubled Hydroxides as Nanofiller. Polymer 2019, 184, 121929. [Google Scholar] [CrossRef]
- Zheng, H.R.; Li, Y.Q.; Wu, M.Y.; Yang, L.; He, L.; Wen, G.J. Effect of the electrode-bulk interface on the dielectric properties of BBZT ceramics. Ceram Int. 2020, 46, 21243–21247. [Google Scholar] [CrossRef]
- Feng, Y.F.; Dai, Y.M.; Sun, J.J. Simultaneously obtained high permittivity and low loss in 2-2 fluoro-polymer/anti-ferroelectric ceramic composites from interface effect. Mater. Res. Express. 2018, 5, 026302. [Google Scholar] [CrossRef]
- Teyssedre, G.; Zheng, F.; Boudou, L.; Laurent, C. Charge Trap Spectroscopy in Polymer Dielectrics: A Critical Review. J. Phys. D Appl. Phys. 2021, 54, 263001. [Google Scholar] [CrossRef]
- Yang, K.; Chen, W.; Zhao, Y. Enhancing Dielectric Strength of Epoxy Polymers by Constructing Interface Charge Traps. ACS Appl. Mater Interf. 2021, 13, 25850–25857. [Google Scholar] [CrossRef]
- Wang, X.; Lv, Z.; Wu, K.; Chen, X.; Tu, D.; Dissado, L.A. Study of the factors that suppress space charge accumulation in LDPE nanocomposites. IEEE Trans. Dielect. Electr. Insul. 2014, 21, 1670–1679. [Google Scholar] [CrossRef]
- Tian, F.; Zhang, J.; Xiao, P.; Hou, C. Interface trapping effects on the charge transport characteristics of LDPE/ZnO nanocomposites. IEEE Trans. Dielect. Electr. Insul. 2017, 24, 1888–1895. [Google Scholar] [CrossRef]
- Wang, Z.; Meng, G.; Wang, L.; Tian, L.; Chen, S.; Kong, B.; Cheng, Y.H. Simultaneously enhanced dielectric properties and through-plane thermal conductivity of epoxy composites with alumina and boron nitride nanosheets. Sci. Rep. 2021, 11, 2495. [Google Scholar] [CrossRef] [PubMed]
- Peng, B.; Yuan, L.; Liang, G.; Gu, A. Getting self-healing ability and ultra-low dielectric loss for high-k epoxy resin composites through building networks based on Li0.3Ti0.02Ni0.68O grafted carbon nanotube bundles with unique surface architecture. Appl. Surf. Sci. 2021, 536, 147955. [Google Scholar] [CrossRef]
- Peng, S.; Luo, Z.; Shaojie, W.; Liang, J.; Yuan, C.; Yuan, Z.; Hu, J.; Jinliang, H.; Li, Q. Mapping the Space Charge at Nanoscale in Dielectric Polymer Nanocomposites. ACS Appl Mater Inter. 2020, 12, 53425–53434. [Google Scholar] [CrossRef] [PubMed]
- Kumara, J.; Serdyuk, Y.; Gubanski, S.M. Surface potential decay on LDPE and LDPE/Al2O3 nano-composites: Measurements and modeling. IEEE Trans. Dielect Electr. Insul. 2016, 23, 3466–3475. [Google Scholar] [CrossRef]
- Mahtabani, A.; Rytoluoto, I.; Anyszka, R. On the Silica Surface Modification and Its Effect on Charge Trapping and Transport in PP Based Dielectric Nanocomposites. ACS Appl. Polym. Mater. 2020, 2, 3148–3160. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, L.; Li, D. Space charge property at the interface in low-density polyethylene/MgO three-layered nanocomposites. Modern Phys. Lett B. 2019, 33, 1950210. [Google Scholar]
- Tanaka, T. A Novel Concept for Electronic Transport in Nanoscale Spaces Formed by Islandic Multi-Cored Nanoparticles. In Proceedings of the 2016 IEEE International Conference on Dielectrics (ICD), Montpellier, France, 3–7 July 2016; IEEE: Montpellier, France, 2016; pp. 23–26. [Google Scholar]
- Zhao, H.; Yan, Z.; Yang, J.; Zheng, C.; Wang, X.; Han, B. TwoPhase Interface and Its Charging Behavior in Polyethylene Nanocomposite. High. Volt. Eng. 2017, 43, 2781–2790. [Google Scholar]
- Tanaka, T.; Kozako, M.; Fuse, N.; Ohki, Y. Proposal of a MultiCore Model for Polymer Nanocomposite Dielectrics. IEEE Trans. Dielect. Electr. Insul. 2005, 12, 669–681. [Google Scholar] [CrossRef]
- Lewis, T.J. Interfaces Are the Dominant Feature of Dielectrics at the Nanometric Level. IEEE Trans. Dielect. Electr. Insul. 2004, 11, 739–753. [Google Scholar] [CrossRef]
- Jakob, D.S.; Wang, H.; Xu, X.G. Pulsed Force Kelvin Probe Force Microscopy. ACS Nano 2020, 14, 4839–4848. [Google Scholar] [CrossRef]
- Faliya, K.; Kliem, H.; Dias, C. Space charge measurements with Kelvin probe force microscopy. IEEE Trans. Dielect Electr. Insul. 2017, 24, 1913–1922. [Google Scholar] [CrossRef]
- Peng, S.; Zeng, Q.; Yang, X.; Hu, J.; Qiu, X.; He, J. Local Dielectric Property Detection of the Interface between Nanoparticle and Polymer in Nanocomposite Dielectrics. Sci. Rep 2016, 6, 38978. [Google Scholar] [CrossRef]
- Jia, B.; Zhou, J.; Chen, Y.; Guo, H.; Wu, K. Charge transport at different interfce in epoxy composites. Nanotechnology 2022, 33, 12. [Google Scholar] [CrossRef]
- Mortreuil, F.; Villeneuve-Faure, C.; Boudou, L. Charge injection phenomena at the metal/dielectric interface investigated by Kelvin probe force microscopy. J. Phys. D Appl. Phys. 2017, 50, 175302. [Google Scholar] [CrossRef] [Green Version]
- Tsagaropoulos, G.; Eisenberg, A. Dynamic Mechanical Study of the Factors Affecting the Two Glass Transition Behavior of Filled Polymers.Similarities and Differences with Random Ionomers. Macromolecules 1995, 28, 6067–6077. [Google Scholar] [CrossRef]
- Awan, I.T.; Rivera, V.; Nogueira, I.C.; Pereira-Da-Silva, M.A.; Li, M.S.; Ferreira, S.O.; Marega, E. Growth process and grain boundary defects in Er doped BaTiO3 processed by EB-PVD: A study by XRD, FTIR, SEM and AFM. Appl. Surf. Sci. 2019, 493, 982–993. [Google Scholar]
- Lv, H.; Guo, Y.; Wu, G.; Ji, G.; Zhao, Y.; Xu, Z.J. Interface Polarization Strategy to Solve Electromagnetic Wave Interference Issue. Acs Appl. Mater. Inter. 2017, 9, 5660–5668. [Google Scholar] [CrossRef]
- Dong, J.; Shao, Z.; Wang, Y.; Lv, Z.; Wang, X.; Wu, K.; Li, W.; Zhang, C. Effect of Temperature Gradient on Space Charge Behavior in Epoxy Resin and Its Nanocomposites. IEEE Trans. Dielect Electr. Insul. 2017, 24, 1537–1546. [Google Scholar] [CrossRef]
- Finney, D.J. Statistical Methods in Genetics’ by Sir Ronald A Fisher. Int. J. Epidemiol. 2010, 39, 339–340. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Deng, H.; Li, P.; Yu, B. Infrared gas detection based on an adaptive Savitzky-Golay algorithm. Appl. Phys B. 2015, 120, 207–216. [Google Scholar] [CrossRef]
- Sadeghi, M.; Behnia, F.; Amiri, R. Window Selection of the Savitzky–Golay Filters for Signal Recovery from Noisy Measurements. IEEE Trans. Instrum. Meas. 2020, 9, 5418–5427. [Google Scholar] [CrossRef]
- Villeneuve-Faure, C.; Boudou, L.; Makasheva, K.; Teyssedre, G. Atomic force microscopy developments for probing space charge at sub-micrometer scale in thin dielectric films. IEEE Trans. Dielect. Electr. Insul. 2016, 23, 713–720. [Google Scholar] [CrossRef]
- Ho, S.H.; Chang, T.C.; Lu, Y.H.; Wang, B.W. High-k shallow traps observed by charge pumping with varying discharging times. J. Appl. Phys. 2013, 114, 174506. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Min, D.; Li, S. Understanding the Conduction and Breakdown Properties of Polyethylene Nanodielectrics: Effect of Deep Traps. IEEE Trans. Dielect. Electr. Insul. 2016, 23, 564–572. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, B.; Zhou, J.; Chen, J.; Zhang, Z.; Wang, Y.; Lv, Z.; Wu, K. Interfacial Insight of Charge Transport in BaTiO3/Epoxy Composites. Nanomaterials 2023, 13, 406. https://doi.org/10.3390/nano13030406
Jia B, Zhou J, Chen J, Zhang Z, Wang Y, Lv Z, Wu K. Interfacial Insight of Charge Transport in BaTiO3/Epoxy Composites. Nanomaterials. 2023; 13(3):406. https://doi.org/10.3390/nano13030406
Chicago/Turabian StyleJia, Beibei, Jun Zhou, Jiaxin Chen, Zixuan Zhang, Yang Wang, Zepeng Lv, and Kai Wu. 2023. "Interfacial Insight of Charge Transport in BaTiO3/Epoxy Composites" Nanomaterials 13, no. 3: 406. https://doi.org/10.3390/nano13030406
APA StyleJia, B., Zhou, J., Chen, J., Zhang, Z., Wang, Y., Lv, Z., & Wu, K. (2023). Interfacial Insight of Charge Transport in BaTiO3/Epoxy Composites. Nanomaterials, 13(3), 406. https://doi.org/10.3390/nano13030406