Nanostructure, Plastic Deformation, and Influence of Strain Rate Concerning Ni/Al2O3 Interface System Using a Molecular Dynamic Study (LAMMPS)
Abstract
1. Introduction
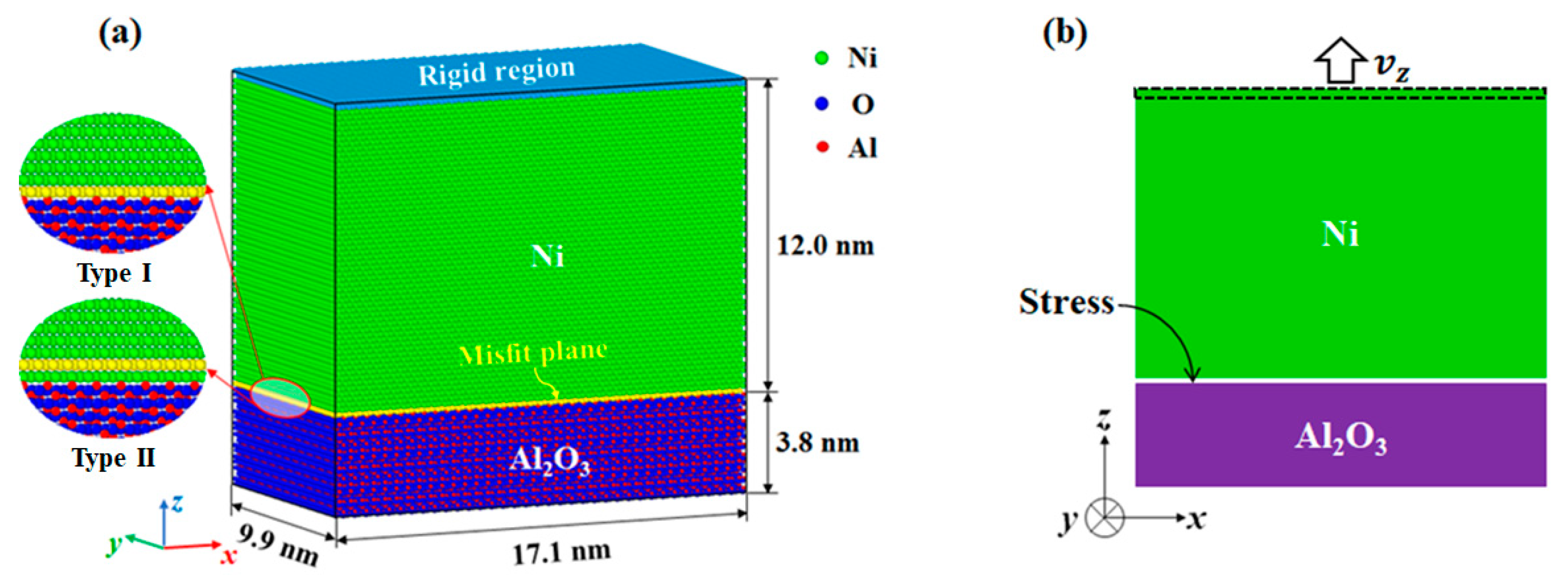
2. Models and Methods
3. Results
3.1. Validation of the Potential and Interface Model
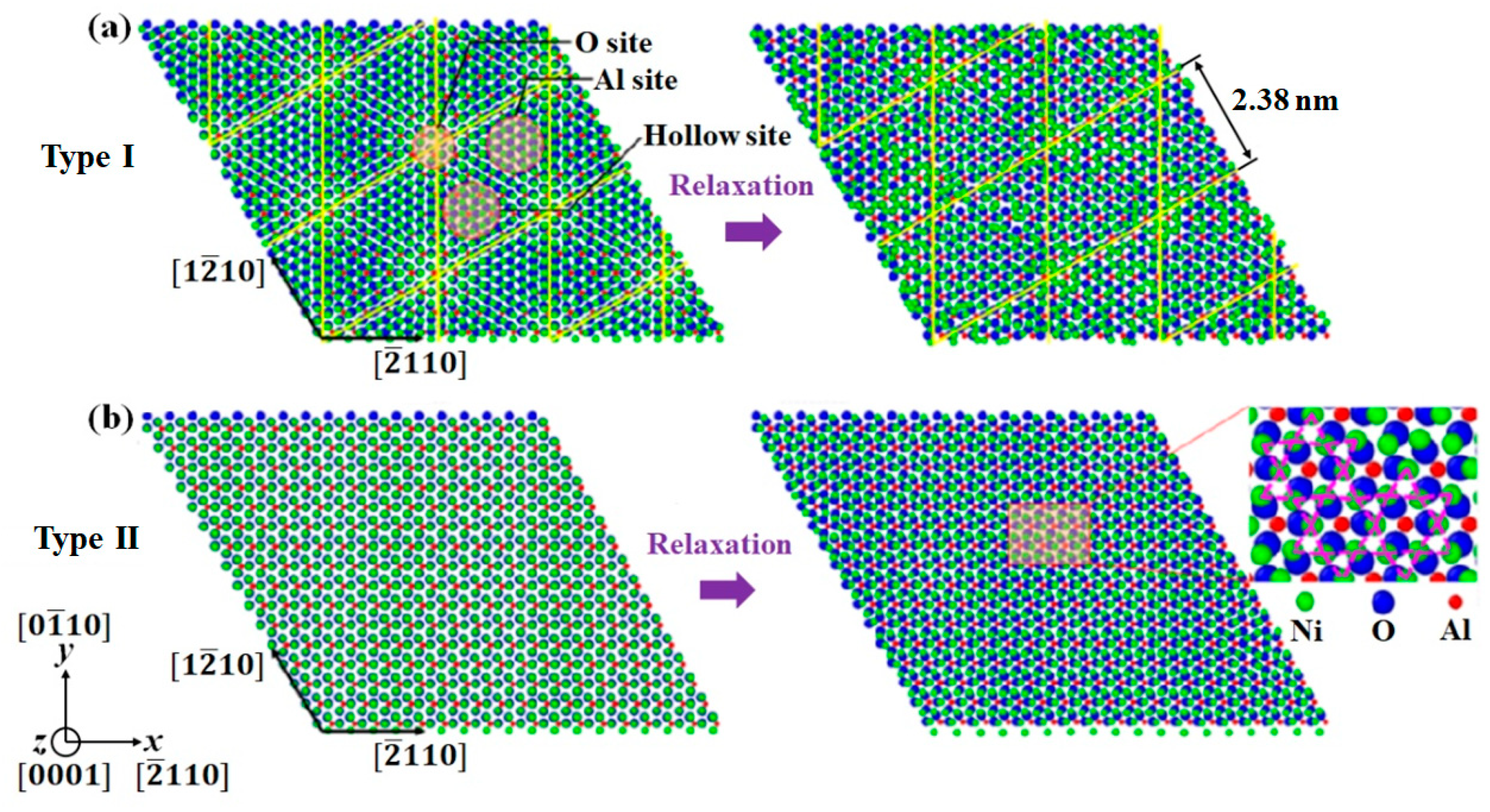
3.2. Interface Nanostructure
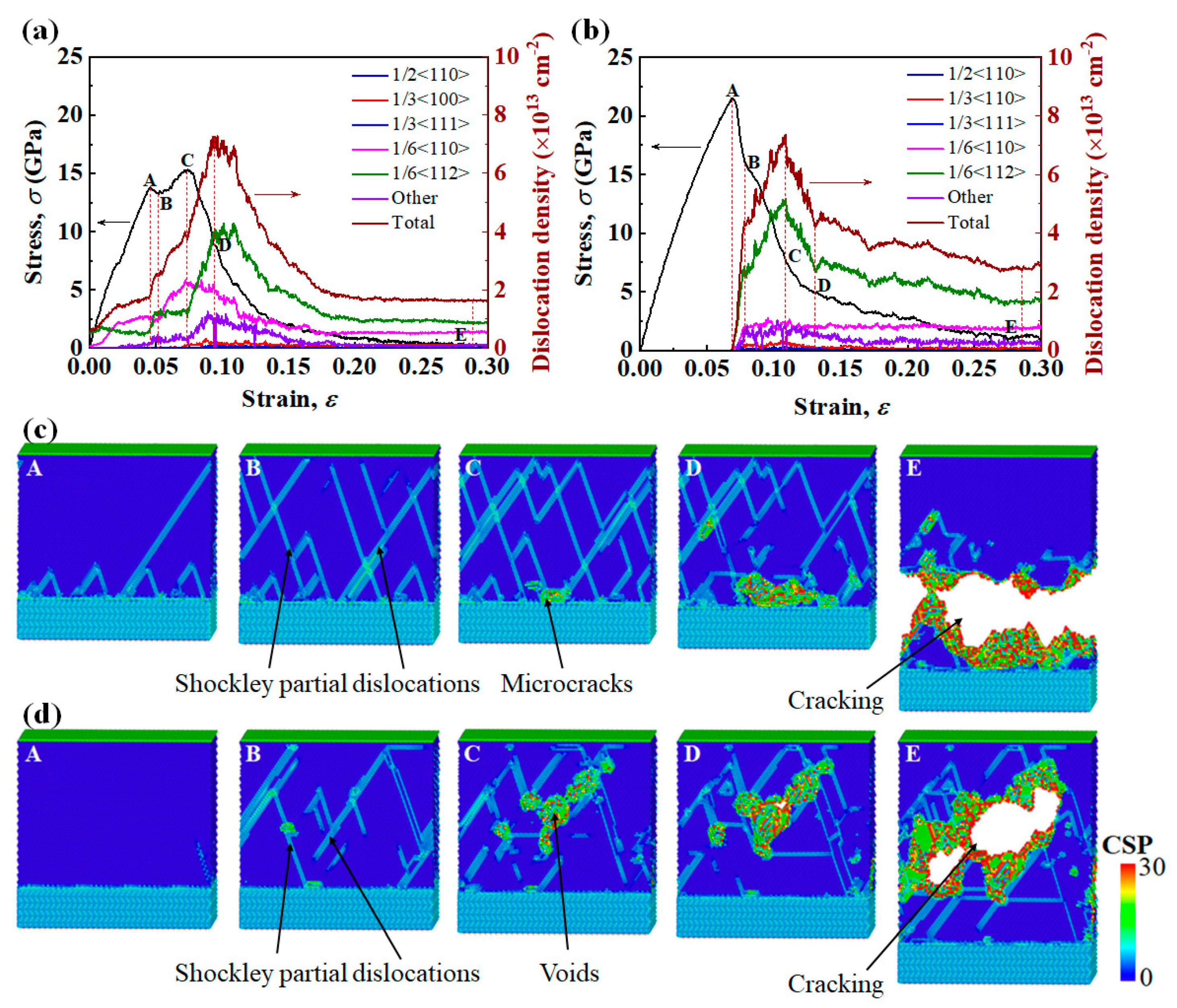
3.3. Tensile Fracture Mechanisms
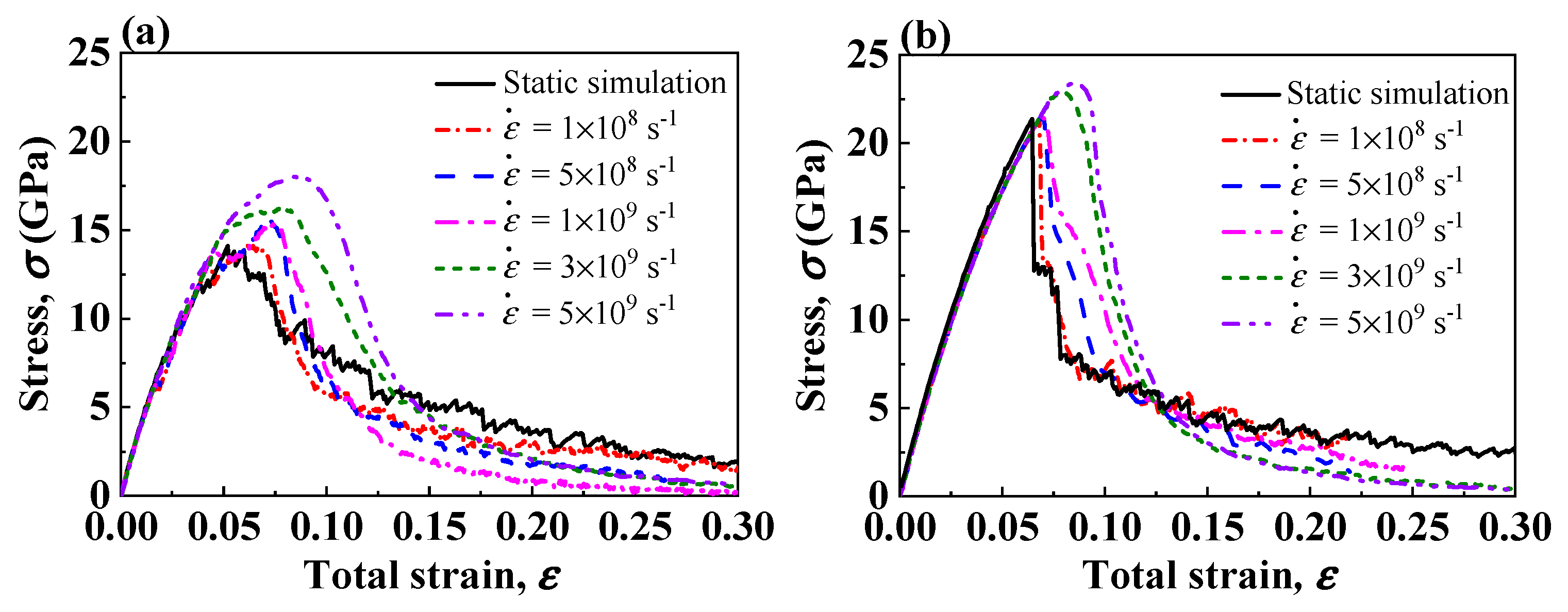
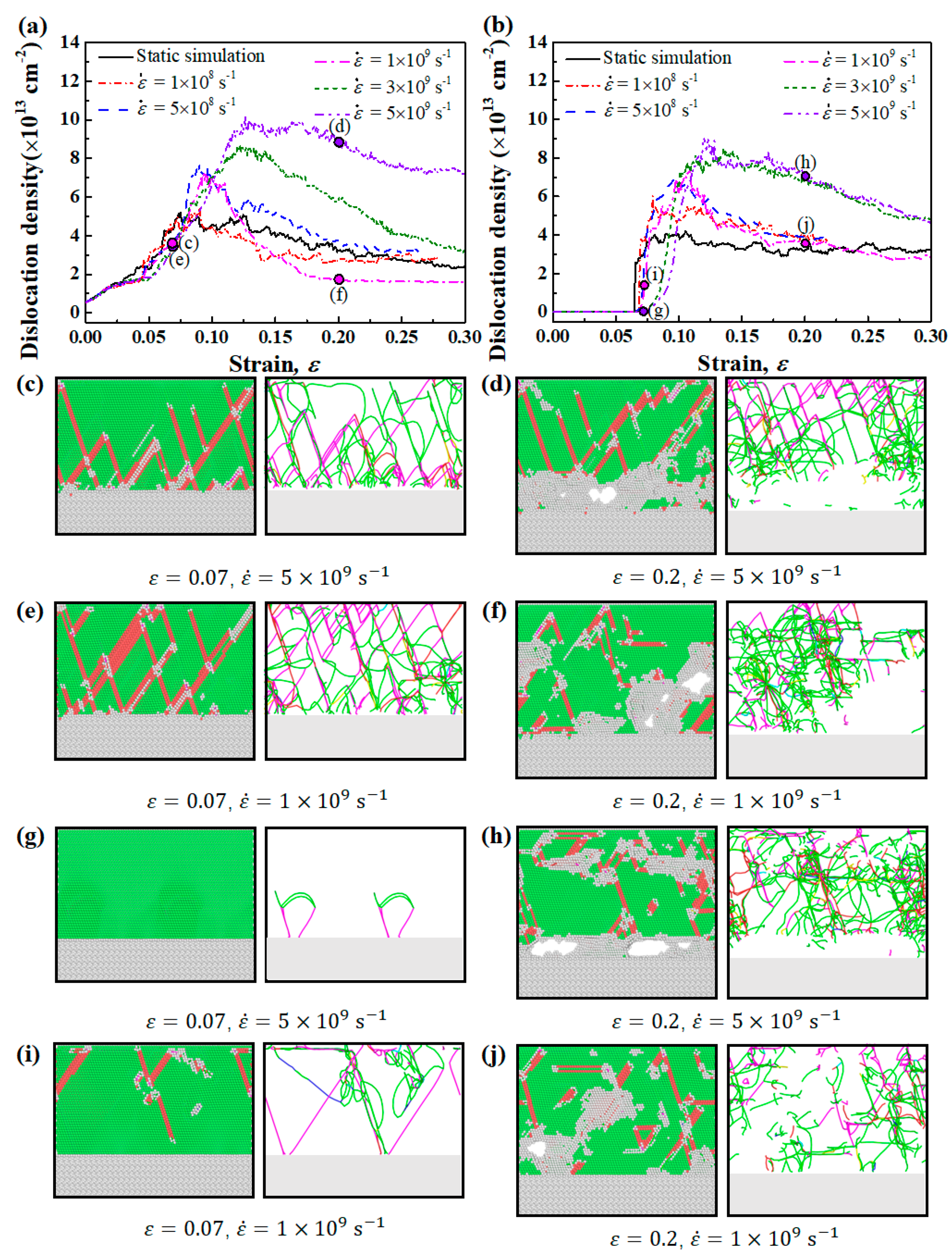
3.4. Effect of Strain Rate
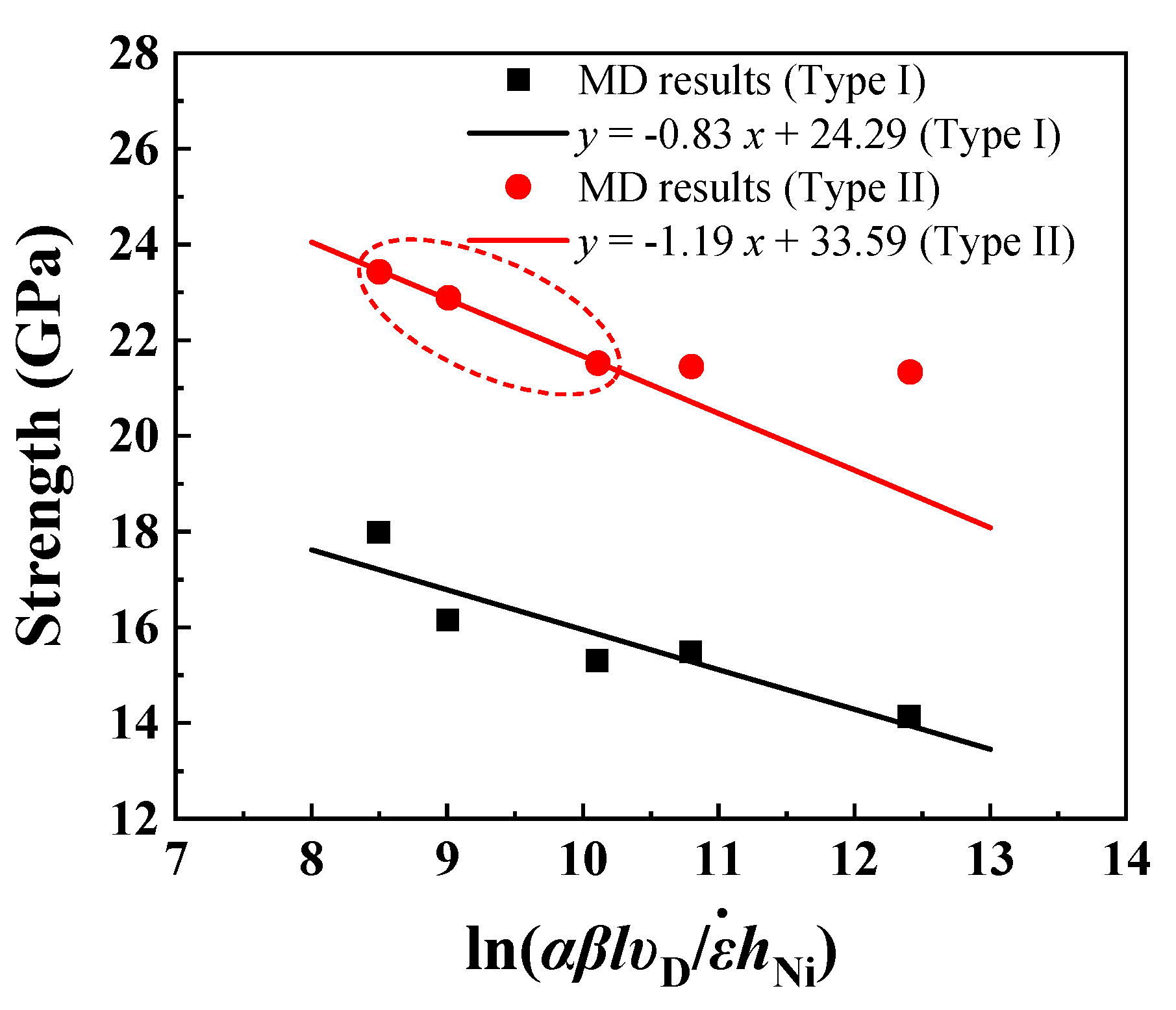
4. Discussion
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Evans, A.G.; Mumm, D.R.; Hutchinson, J.W.; Meier, G.H.; Pettic, F.S. Mechanisms controlling the durability of thermal barrier coatings. Prog. Mater. Sci. 2001, 46, 505–553. [Google Scholar] [CrossRef]
- Kumar, V.; Kandasubramanian, B. Processing and design methodologies for advanced and novel thermal barrier coatings for engineering applications. Particuology 2016, 27, 1–28. [Google Scholar] [CrossRef]
- Peters, M.; Leyens, C.; Schulz, U.; Kaysser, W.A. EB-PVD thermal barrier coatings for aeroengines and gas turbines. Adv. Eng. Mater. 2001, 3, 193–204. [Google Scholar] [CrossRef]
- Smith, J.; Scheibel, J.; Classen, D.; Paschke, S.; Elbel, S.; Fick, K.; Carlson, D. Thermal barrier coating validation testing for industrial gas turbine combustion hardware. J. Eng. Gas Turbines Power-Trans. Asme 2016, 138, 031508. [Google Scholar] [CrossRef]
- Tailor, S.; Singh, M.; Doub, A.V. Synthesis and characterization of yttria-stabilized zirconia (YSZ) nano-clusters for thermal barrier coatings (TBCs) applications. J. Clust. Sci. 2016, 27, 1097–1107. [Google Scholar] [CrossRef]
- Boissonnet, G.; Bonnet, G.; Pasquet, A.; Bourhila, N.; Pedraza, F. Evolution of thermal insulation of plasma-sprayed thermal barrier coating systems with exposure to high temperature. J. Eur. Ceram. Soc. 2019, 39, 2111–2121. [Google Scholar] [CrossRef]
- Zhang, W.; Smith, J.R.; Wang, X.G.; Evans, A.G. Influence of sulfur on the adhesion of the nickel/alumina interface. Phys. Rev. B 2003, 67, 245414. [Google Scholar] [CrossRef]
- Shi, S.; Tanaka, S.; Kohyama, M. First-principles investigation of the atomic and electronic structures of α-Al2O3(0001)/Ni(111) Interfaces. J. Am. Ceram. Soc. 2007, 90, 2429–2440. [Google Scholar] [CrossRef]
- Bao, Z.; Guo, X.; Shang, F. An atomistic investigation into the nature of fracture of Ni/Al2O3 interface with yttrium dopant under tension. Eng. Fract. Mech. 2015, 150, 239–247. [Google Scholar] [CrossRef]
- Guo, X.; Shang, F. Reinvestigation of the tensile strength and fracture property of Ni(111)/α-Al2O3(0001) interfaces by first-principle calculations. Comput. Mater. Sci. 2011, 50, 1711–1716. [Google Scholar] [CrossRef]
- Wang, X.G.; Smith, J.; Evans, A. Phase diagram for the Ni/Al2O3 interface and relationships to adhesion. Phys. Rev. B 2006, 74, 081403. [Google Scholar] [CrossRef]
- Wei, Y.; Hutchinson, J.W. Toughness of Ni/Al2O3 interfaces as dependent on micron-scale plasticity and atomistic-scale separation. Philos. Mag. 2008, 88, 3841–3859. [Google Scholar] [CrossRef]
- Gupta, P.; Pal, S.; Yedla, N. Molecular dynamics based cohesive zone modeling of Al (metal)–Cu50Zr50 (metallic glass) interfacial mechanical behavior and investigation of dissipative mechanisms. Mater. Des. 2016, 105, 41–50. [Google Scholar] [CrossRef]
- Salehinia, I.; Wang, J.; Bahr, D.F.; Zbib, H.M. Molecular dynamics simulations of plastic deformation in Nb/NbC multilayers. Int. J. Plast. 2014, 59, 119–132. [Google Scholar] [CrossRef]
- Sazgar, A.; Movahhedy, M.R.; Mahnama, M.; Sohrabpour, S. A molecular dynamics study of bond strength and interface conditions in the Al/Al2O3 metal–ceramic composites. Comput. Mater. Sci. 2015, 109, 200–208. [Google Scholar] [CrossRef]
- Zhou, Y.; Yang, W.; Hu, M.; Yang, Z. The typical manners of dynamic crack propagation along the metal/ceramics interfaces: A molecular dynamics study. Comput. Mater. Sci. 2016, 112, 27–33. [Google Scholar] [CrossRef]
- Damadam, M.; Shao, S.; Ayoub, G.; Zbib, H.M. Recent advances in modeling of interfaces and mechanical behavior of multilayer metallic/ceramic composites. J. Mater. Sci. 2017, 53, 5604–5617. [Google Scholar] [CrossRef]
- Damadam, M.; Shao, S.; Salehinia, I.; Ayoub, G.; Zbib, H.M. Molecular dynamics simulations of mechanical behavior in nanoscale ceramic–metallic multilayer composites. Mater. Res. Lett. 2017, 5, 306–313. [Google Scholar] [CrossRef]
- Florando, J.N.; El-Dasher, B.S.; Chen, C.; Swift, D.C.; Barton, N.R.; McNaney, J.M.; Ramesh, K.T.; Hemker, K.J.; Kumar, M. Effect of strain rate and dislocation density on the twinning behavior in tantalum. AIP Adv. 2016, 6, 045120. [Google Scholar] [CrossRef]
- Chen, J.; Mathaudhu, S.N.; Thadhani, N.; Dongare, A.M. Correlations between dislocation density evolution and spall strengths of Cu/Ta multilayered systems at the atomic scales: The role of spacing of KS interfaces. Materialia 2019, 5, 100192. [Google Scholar] [CrossRef]
- Thompson, C.B.; Randle, V.A. Study of twinning in nickel. Scr. Mater. 1996, 35, 385–390. [Google Scholar] [CrossRef]
- El-Danaf, E.; Kalidindi, S.R.; Doherty, R.D. Influence of grain size and stacking-fault energy on deformation twinning in fcc metals. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 1999, 30, 1223–1233. [Google Scholar] [CrossRef]
- Mahajan, S.; Bartlett, A.F. Influence of prior mechanical and thermal treatments on shock-induced substructures in molybdenum. Acta Metall. 1971, 19, 1111–1119. [Google Scholar]
- Boucher, N.A.; Christian, J.W. The influence of pre-strain on deformation twinning in niobium single crystals. Acta Metall. 1972, 20, 581–591. [Google Scholar] [CrossRef]
- Long, Y.; Chen, N.X. Interface reconstruction and dislocation networks for a metal/alumina interface: An atomistic approach. J. Phys. Condens. Matter 2008, 20, 135005. [Google Scholar] [CrossRef]
- Meltzman, H.; Mordehai, D.; Kaplan, W.D. Solid–solid interface reconstruction at equilibrated Ni–Al2O3 interfaces. Acta Mater. 2012, 60, 4359–4369. [Google Scholar] [CrossRef]
- Duffy, D.M.; Harding, J.H.; Stoneham, A.M. Atomistic modelling of the metal-oxide interfaces with image interactions. Acta Metall. Mater. 1992, 40, S11–S16. [Google Scholar] [CrossRef]
- Finnis, M.W. Metal-ceramic cohesion and the image interaction. Acta Metall. Mater. 1992, 40, S25–S37. [Google Scholar]
- Endou, A.; Teraishi, K.; Yajima, K.; Yokoyama, K. Potential energy surface and dynamics of Pd/MgO(001) system as investigated by periodic density functional calculations and classical molecular dynamics simulations. Jpn. J. Appl. Phys. 2000, 39, 4255–4260. [Google Scholar]
- Vervisch, W.; Mottet, C.; Goniakowski, J. Theoretical study of the atomic structure of Pd nanoclusters deposited on a MgO(100) surface. Phys. Rev. B 2002, 65, 245411. [Google Scholar] [CrossRef]
- Yao, Y.G.; Wang, T.C.; Wang, C.Y. Peierls-Nabarro model of interfacial misfit dislocation: An analytic solution. Phys. Rev. B 1999, 59, 8232–8236. [Google Scholar] [CrossRef]
- Zhang, Z.; Long, Y.; Cazottes, S.; Daniel, R.; Mitterer, C.; Dehm, G. The peculiarity of the metal-ceramic interface. Sci. Rep. 2015, 5, 11460. [Google Scholar] [CrossRef]
- Long, Y.; Chen, N.X. Atomistic simulation of misfit dislocation in metal/oxide interfaces. Comput. Mater. Sci. 2008, 42, 426–433. [Google Scholar] [CrossRef]
- Long, Y.; Chen, N.X. Pair potential approach for metal/Al2O3 interface. J. Phys. Condens. Matter 2007, 19, 196216. [Google Scholar] [CrossRef]
- Mishin, Y.; Farkas, D.; Mehl, M.J. Papaconstantopoulos, D.A. Interatomic potentials for monoatomic metals from experimental data and at initio calculations. Phys. Rev. B 1999, 59, 3393–3407. [Google Scholar] [CrossRef]
- Vitek, V.; Gutekunst, G.; Mayer, J.; Rühle, M. Atomic structure of misfit dislocations in metal-ceramic interfaces. Philos. Mag. A 1995, 71, 1219–1239. [Google Scholar] [CrossRef]
- Wang, J.; Hoagland, R.G.; Hirth, J.P.; Misra, A. Atomistic modeling of the interaction of glide dislocations with “weak” interfaces. Acta Mater. 2008, 56, 5685–5693. [Google Scholar] [CrossRef]
- Gall, K.; Horstemeyer, M.F.; Schilfgaarde, M.V.; Baskes, M.I. Atomistic simulations on the tensile debonding of an aluminum-silicon interface. J. Mech. Phys. Solids 2000, 48, 2183–2212. [Google Scholar] [CrossRef]
- Nosé, S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 2006, 52, 255–268. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef]
- Pandre, S.; Mhatre, V.; Kotkunde, N.; Kumar, S.S. Strain hardening behavior of DP 590 steel using dislocation density based Kock-Mecking model. Mater. Today Proc. 2021, 46, 9323–9327. [Google Scholar] [CrossRef]
- Buzaud, E.; Lee, W.S.; Chou, C.W.; Cosculluela, A.; Couque, H.; Cadoni, E. Dynamic deformation behaviour and dislocation substructure of AZ80 magnesium alloy over a wide range of temperatures. EPJ Web Conf. 2018, 183, 03010. [Google Scholar]
- Keller, C.; Hug, E. Kocks-Mecking analysis of the size effects on the mechanical behavior of nickel polycrystals. Int. J. Plast. 2017, 98, 106–122. [Google Scholar] [CrossRef]
- Stechmann, G.; Zaefferer, S.; Raabe, D. Molecular statics simulation of CdTe grain boundary structures and energetics using a bond-order potential. Model. Simul. Mater. Sci. Eng. 2018, 26, 045009. [Google Scholar] [CrossRef]
- Taketomi, S.; Matsumoto, R.; Hagihara, S. Molecular statics simulation of the effect of hydrogen concentration on {112} edge dislocation mobility in alpha Iron. ISIJ Int. 2017, 57, 2058–2064. [Google Scholar] [CrossRef]
- Fu, X.Q.; Liang, L.H.; Wei, Y.G. Atomistic simulation study on the shear behavior of Ag/MgO interface. Comput. Mater. Sci. 2018, 155, 116–128. [Google Scholar] [CrossRef]
- Kelchner, C.L.; Plimpton, S.J.; Hamilton, J.C. Dislocation nucleation and defect structure during surface indentation. Phys. Rev. B 1998, 58, 11085–11088. [Google Scholar] [CrossRef]
- Stukowski, A.; Bulatov, V.V.; Arsenlis, A. Automated identification and indexing of dislocations in crystal interfaces. Model. Simul. Mater. Sci. Eng. 2012, 20, 085007. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015102. [Google Scholar] [CrossRef]
- Batyrev, I.G.; Alavi, A.; Finnis, M.W. Equilibrium and adhesion of Nb/sapphire: The effect of oxygen partial pressure. Phys. Rev. B 2000, 62, 4698–4706. [Google Scholar] [CrossRef]
- Wang, X.G.; Chaka, A.; Scheffler, M. Effect of the environment on alpha-Al2O3 (0001) surface structures. Phys. Rev. Lett. 2000, 84, 3650–3653. [Google Scholar] [CrossRef]
- Łodziana, Z.; Nørskov, J.K.; Stoltze, P. The stability of the hydroxylated (0001) surface of α-Al2O3. J. Chem. Phys. 2003, 118, 11179–11188. [Google Scholar] [CrossRef]
- Long, Y.; Chen, N.X.; Wang, H.Y. Theoretical investigations of misfit dislocations in Pd/MgO(001) interfaces. J. Phys. Condens. Matter 2005, 17, 6149–6172. [Google Scholar] [CrossRef]
- Lin, Z.J.; Peng, X.H.; Huang, C.; Fu, T.; Wang, Z.C. Atomic structure, electronic properties and generalized stacking fault energy of diamond/c-BN multilayer. RSC Adv. 2017, 7, 29599–29605. [Google Scholar] [CrossRef]
- Cornil, D.; Rivolta, N.; Mercier, V.; Wiame, H.; Beljonne, D.; Cornil, J. Enhanced adhesion energy at oxide/Ag interfaces for low-emissivity glasses: Theoretical insight into doping and vacancy effects. ACS Appl. Mater. Interfaces 2020, 12, 40838–40849. [Google Scholar] [CrossRef]
- Jiang, Y.; Wei, Y.G.; Smith, J.R.; Hutchinson, J.W.; Evans, A.G. First principles based predictions of the toughness of a metal/oxide interface. Int. J. Mater. Res. 2010, 101, 8–15. [Google Scholar] [CrossRef]
- Brandl, C.; Derlet, P.M.; Swygenhoven, H.V. Strain rates in molecular dynamics simulations of nanocrystalline metals. Philos. Mag. 2009, 89, 3465–3475. [Google Scholar] [CrossRef]
- Zhang, Z.P.; Kou, J.X.; Chen, L.Q.; Guo, J.Y.; Duan, X.Y.; Shan, B.; Duan, X.B. From stacking fault to phase transformation: A quantitative model of plastic deformation of CoCrFeMnNi under different strain rates. Intermetallics 2022, 146, 107585. [Google Scholar] [CrossRef]
- Zepeda-Ruiz, L.A.; Stukowski, A.; Oppelstrup, T.; Bulatov, V.V. Probing the limits of metal plasticity with molecular dynamics simulations. Nature 2017, 550, 492–495. [Google Scholar] [CrossRef]
- Zhang, X. A model on twinning-induced crack kinking out of a metal-ceramics interface. Int. J. Fract. 2008, 152, 27–35. [Google Scholar] [CrossRef]
- Ramachandramoorthy, R.; Gao, W.; Bernal, R.; Espinosa, H. High strain rate tensile testing of silver nanowires: Rate-dependent brittle-to-ductile transition. Nano Lett. 2016, 16, 255–263. [Google Scholar] [CrossRef]
- Abdolrahim, N.; Zbib, H.M.; Bahr, D.F. Multiscale modeling and simulation of deformation in nanoscale metallic multilayer systems. Int. J. Plast. 2014, 52, 33–50. [Google Scholar] [CrossRef]
- Zhu, T.; Li, J.; Samanta, A.; Leach, A.; Gall, K. Temperature and strain-rate dependence of surface dislocation nucleation. Phys. Rev. Lett. 2008, 100, 025502. [Google Scholar] [CrossRef]
- Bian, X.; Wang, G.; Wang, Q.; Sun, B.; Hussain, I.; Zhai, Q.; Mattern, N.; Bednarcik, J.; Eckert, J. Cryogenic-temperature-induced structural transformation of a metallic glass. Mater. Res. Lett. 2016, 5, 284–291. [Google Scholar] [CrossRef]
- Tanaka, M.; Izumi, D.; Yoshimura, N.; Shigesato, G.; Hoshino, M.; Ushioda, K.; Higashida, K. Temperature dependence of activation volume on Cu content of ultra-low carbon steel. Philos. Mag. 2017, 97, 2915–2930. [Google Scholar] [CrossRef]
- Swygenhoven, H.V. Grain boundaries and dislocations. Science 2002, 296, 66–67. [Google Scholar] [CrossRef]
- Wu, X.L.; Zhu, Y.T.; Wei, Y.G.; Wei, Q. Strong strain hardening in nanocrystalline nickel. Phys. Rev. Lett. 2009, 103, 205504. [Google Scholar] [CrossRef]
- Long, Y.; Chen, N.X. Theoretical study of misfit dislocation in interface dynamics. Comput. Mater. Sci. 2008, 44, 721–727. [Google Scholar] [CrossRef]



| ID | Size (Lattice) | Tensile Velocities (m/s) | Strain Rate (s−1) | Initial Nanostructure |
|---|---|---|---|---|
| S1 | 24 24 3 (Al2O3)-15(Ni) | 1.27 | 1 108 | Type I |
| S2 | 24 24 3 (Al2O3)-15(Ni) | 6.35 | 5 108 | Type I |
| S3 | 24 24 3 (Al2O3)-15(Ni) | 12.70 | 1 109 | Type I |
| S4 | 24 24 3 (Al2O3)-15(Ni) | 38.12 | 3 109 | Type I |
| S5 | 24 24 3 (Al2O3)-15(Ni) | 63.51 | 5 109 | Type I |
| S6 | 24 24 3 (Al2O3)-15(Ni) | 1.24 | 1 108 | Type II |
| S7 | 24 24 3 (Al2O3)-15(Ni) | 6.20 | 5 108 | Type II |
| S8 | 24 24 3 (Al2O3)-15(Ni) | 12.41 | 1 109 | Type II |
| S9 | 24 24 3 (Al2O3)-15(Ni) | 37.20 | 3 109 | Type II |
| S10 | 24 24 3 (Al2O3)-15(Ni) | 62.03 | 5 109 | Type II |
| Mode | or USFE (J/m2) | ||
|---|---|---|---|
| This Work | Ab Initio | ||
| Tension | Ni on O | 1.21 | 1.44 [9], 1.48 [10] 1.90 [34] |
| Ni on Al | 0.62 | 1.01 [34] | |
| Ni on hollow | 1.10 | 1.24 [34] | |
| Shear | <112> | 1.76 | 1.78 [57] |
| <110> | 0.76 | 1.07 [57] | |
| Interface Type | (GPa) | (GPa) | b3 | |
|---|---|---|---|---|
| Type I | 24.29 | 0.83 | 0.0010 | 0.0025 |
| Type II | 33.59 | 1.19 | 0.0007 | 0.0024 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, X. Nanostructure, Plastic Deformation, and Influence of Strain Rate Concerning Ni/Al2O3 Interface System Using a Molecular Dynamic Study (LAMMPS). Nanomaterials 2023, 13, 641. https://doi.org/10.3390/nano13040641
Fu X. Nanostructure, Plastic Deformation, and Influence of Strain Rate Concerning Ni/Al2O3 Interface System Using a Molecular Dynamic Study (LAMMPS). Nanomaterials. 2023; 13(4):641. https://doi.org/10.3390/nano13040641
Chicago/Turabian StyleFu, Xueqiong. 2023. "Nanostructure, Plastic Deformation, and Influence of Strain Rate Concerning Ni/Al2O3 Interface System Using a Molecular Dynamic Study (LAMMPS)" Nanomaterials 13, no. 4: 641. https://doi.org/10.3390/nano13040641
APA StyleFu, X. (2023). Nanostructure, Plastic Deformation, and Influence of Strain Rate Concerning Ni/Al2O3 Interface System Using a Molecular Dynamic Study (LAMMPS). Nanomaterials, 13(4), 641. https://doi.org/10.3390/nano13040641







