Anomalous Optical Properties of KTN:Li Ferroelectric Supercrystals
Abstract
:1. Introduction
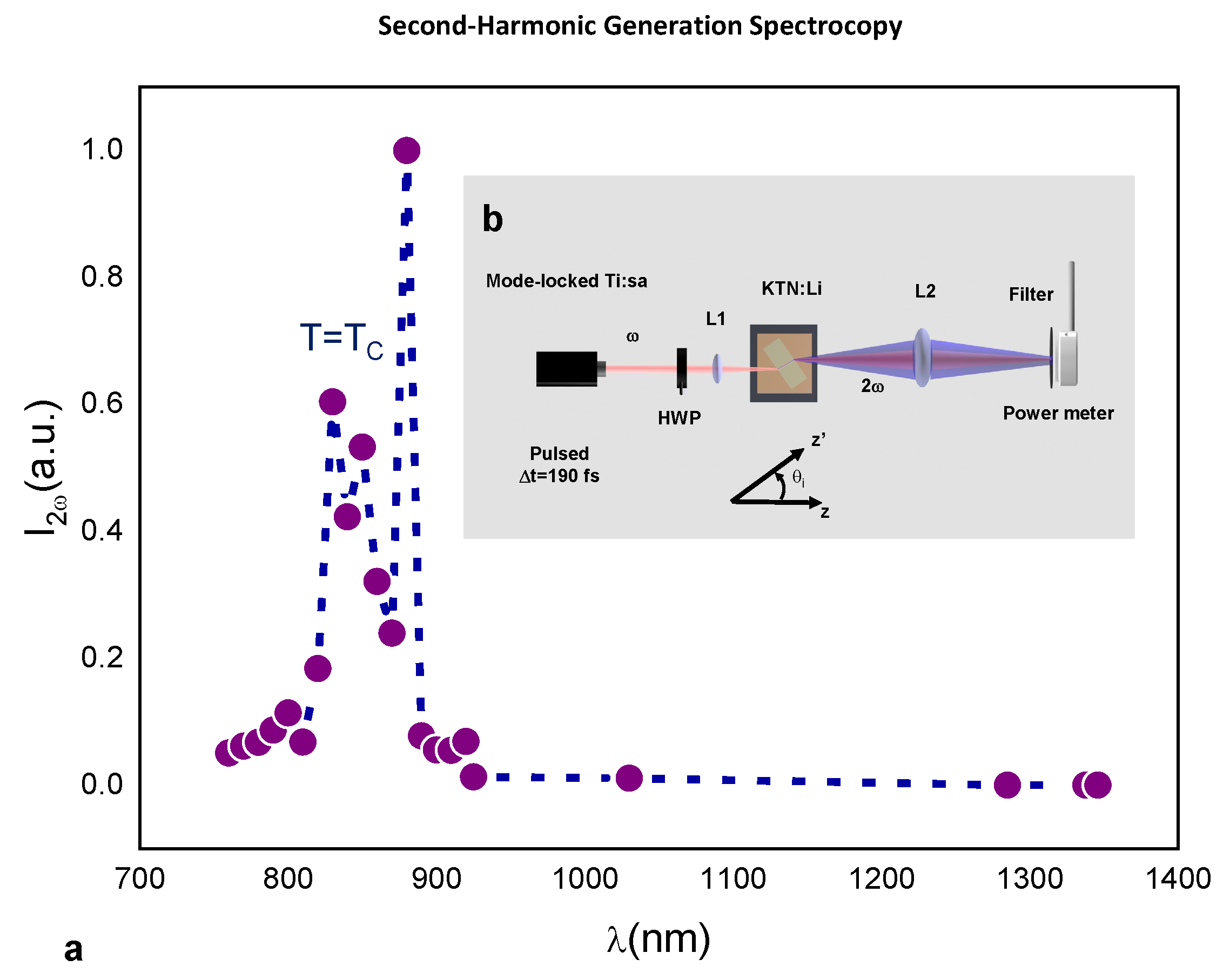
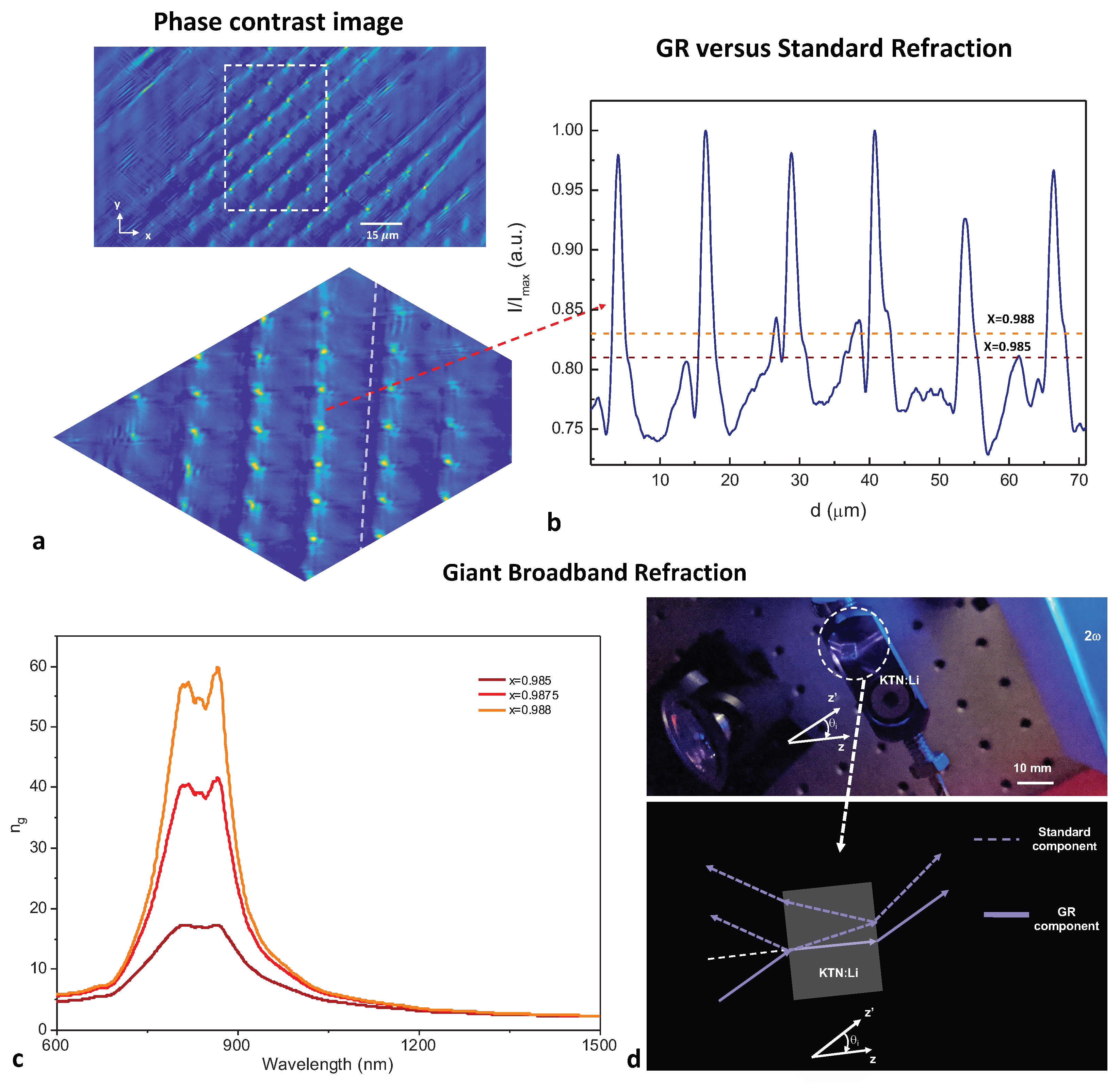
2. Results
3. Discussion and Conclusions
4. Methods
4.1. Material
4.2. Optical Setup
4.3. SHG Setup
4.4. Phase-Contrast Imaging
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pierangeli, D.; Ferraro, M.; Di Mei, F.; Di Domenico, G.; De Oliveira, C.E.M.; Agranat, A.J.; DelRe, E. Super-crystals in composite ferroelectrics. Nat. Commun. 2016, 7, 10674. [Google Scholar] [CrossRef] [Green Version]
- Ferraro, M.; Pierangeli, D.; Flammini, M.; Di Domenico, G.; Falsi, L.; Di Mei, F.; Agranat, A.J.; DelRe, E. Observation of polarization-maintaining light propagation in depoled compositionally disordered ferroelectrics. Opt. Lett. 2017, 42, 3856–3859. [Google Scholar] [CrossRef]
- Falsi, L.; Aversa, M.; Di Mei, F.; Pierangeli, D.; Xin, F.; Agranat, A.J.; DelRe, E. Direct Observation of Fractal-Dimensional Percolation in the 3D Cluster Dynamics of a Ferroelectric Supercrystal. Phys. Rev. Lett. 2016, 126, 037601. [Google Scholar] [CrossRef]
- Li, C.; Wang, X.; Wu, Y.; Liang, F.; Wang, F.; Zhao, X.; Yu, H.; Zhang, H. Three-dimensional nonlinear photonic crystal in naturally grown potassium–tantalate–niobate perovskite ferroelectrics. Light Sci. Appl. 2020, 9, 193. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, Q.X.; Liu, H.L.; Wang, X.P.; He, S.; Li, X.J.; Wu, P.F. Switching effects of spontaneously formed superlattices in relaxor ferroelectrics. Opt. Mat. Express 2019, 9, 4081–4089. [Google Scholar] [CrossRef]
- Yang, Q.; Zhang, X.; Liu, H.; Wang, X.; Ren, Y.; He, S.; Li, X.; Wu, P. Dynamic relaxation process of a 3D super crystal structure in a Cu:KTN crystal. Chin. Opt. Lett. 2020, 18, 021901. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, X.; Tian, G.; Zheng, L.; Liang, F.; Zhang, S.; Yu, H.; Zhang, H. Inverse Design of Ferroelectric-Order in Perovskite Crystal for Self-Powered Ultraviolet Photodetection. Adv. Mater. 2022, 34, 2105108. [Google Scholar] [CrossRef]
- Hadjimichael, M.; Li, Y.; Zatterin, E.; Chahine, G.A.; Conroy, M.; Moore, K.; O’Connell, E.N.; Petr, C.; Pavel, O.; Marton, P.; et al. Metal–ferroelectric supercrystals with periodically curved metallic layers. Nat. Mater. 2021, 20, 495–502. [Google Scholar] [CrossRef]
- Choi, K.J.; Biegalski, M.; Li, Y.L.; Sharan, A.; Schubert, J.; Uecker, R.; Reiche, P.; Chen, Y.B.; Pan, X.Q.; Gopalan, V.; et al. Enhancement of ferroelectricity in strained BaTiO3 thin films. Science 2004, 306, 1005–1009. [Google Scholar] [CrossRef] [Green Version]
- Scott, J.F. Applications of modern ferroelectrics. Science 2007, 315, 954. [Google Scholar] [CrossRef]
- Wang, J.; Nagano, K.; Shimada, T.; Kitamura, T. Strainmediated multilevel ferroelectric random access memory operating through a magnetic field. RSC Adv. 2014, 4, 45382. [Google Scholar] [CrossRef]
- Wang, G.; Lu, Z.; Li, Y.; Li, L.; Ji, H.; Feteira, A.; Zhou, D.; Wang, D.; Zhang, S.; Reaney, I.M. Electroceramics for high-energy density capacitors: Current status and future perspectives. Chem. Rev. 2021, 121, 6124–6172. [Google Scholar] [CrossRef]
- Lo Presti, L.; Parravicini, J.; Soave, R.; Parravicini, G.; Mauri, M.; Loconte, L.; Di Mei, F.; Falsi, L.; Tartara, L.; Binetti, S.; et al. Observation of an exotic lattice structure in the transparent KTa1−xNbxO3 perovskite supercrystal. Phys. Rev. B 2020, 102, 214110. [Google Scholar] [CrossRef]
- Falsi, L.; Tartara, L.; Di Mei, F.; Flammini, M.; Parravicini, J.; Pierangeli, D.; Parravicini, G.; Xin, F.; DiPorto, P.; Agranat, A.J.; et al. Constraint-free wavelength conversion supported by giant optical refraction in a 3D perovskite supercrystal. Commun. Mater. 2020, 1, 76. [Google Scholar] [CrossRef]
- Di Mei, F.; Falsi, L.; Flammini, M.; Pierangeli, D.; Di Porto, P.; Agranat, A.J.; DelRe, E. Giant broadband refraction in the visible in a ferroelectric perovskite. Nat. Photon. 2018, 12, 734–738. [Google Scholar] [CrossRef]
- Shim, H.; Monticone, F.; Miller, O.D. Fundamental Limits to the Refractive Index of Transparent Optical Materials. Adv. Mater. 2021, 33, 2103946. [Google Scholar] [CrossRef]
- Pashkin, A.; Železný, V.; Petzelt, J. Infrared spectroscopy of KTa1−xNbxO3 crystals. J. Phys. Condens. Matter. 2005, 17, L265. [Google Scholar] [CrossRef] [PubMed]
- Zeleznỳ, V.; Bursík, J.; Vanek, P. CSD ceramic K(Ta, Nb)O3 thin films and their characterization by infrared spectroscopy. J. Phys. IV 2005, 128, 71–76. [Google Scholar]
- Kojima, S.; Rahaman, M.M.; Sase, R.; Hoshina, T.; Tsurumi, T. Vibrational dynamics of ferroelectric K(Ta1−xNbx)O3 studied by far-infrared spectroscopic ellipsometry and Ramanscattering. JPN. J. Appl. Phys. 2018, 57, 11UB05. [Google Scholar] [CrossRef]
- Rahaman, M.; Imai, T.; Sakamoto, T.; Kojima, S. Fano resonance of Li-doped KTa1−xNbxO3 single crystals studied by Raman scattering. Sci. Rep. 2016, 6, 23898. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Hlinka, J.; Bokov, A.; Ye, Z.G.; Ondrejkovic, P.; Petzelt, J.; Bellaiche, L. Fano resonance and dipolar relaxation in lead-free relaxors. Nat. Commun. 2014, 5, 5100. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Liang, F.; Wang, X.; Wang, J.; Yu, H.; Zhang, H. Temperature dependent Raman spectroscopic study of Fano resonance in perovskite ferroelectric KTa1−xNbxO3 single crystal. Opt. Mater. Express 2022, 12, 247–255. [Google Scholar] [CrossRef]
- Nichelatti, E. Complex refractive index of a slab from reflectance and transmittance: Analytical solution. J. Opt. A: Pure Appl. Opt. 2002, 4, 400–403. [Google Scholar] [CrossRef]
- D’Arco, A.; Tomarchio, L.; Dolci, V.; Di Pietro, P.; Perucchi, A.; Mou, S.; Petrarca, M.; Lupi, S. Broadband Anisotropic Optical Properties of the Terahertz Generator HMQ-TMS Organic Crystal. Condens. Matter. 2020, 5, 47. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, Q.; Tian, G.; Zheng, L.; Liang, F.; Wang, X.; Wang, D.; Sang, Y.; Liu, H.; Wang, J.; et al. Periodically Poled Nonlinear Photonic Crystal KTa0.51Nb0.49O3. Adv. Opt. Mater. 2022, 10, 2201010. [Google Scholar] [CrossRef]
- Birks, E.; Kundzinsh, M.; Nitiss, E.; Ignatans, R.; Dunce, M.; Antonova, M.; Sternberg, A. Study of Tetragonal Phase in 0.4Na1/2Bi1/2TiO3-(0.6 − x)SrTiO3-xPbTiO3 Solid Solutions by Second-Harmonic Generation. Ferroelectrics 2015, 485, 53–57. [Google Scholar] [CrossRef]
- Stoica, V.A.; Laanait, N.; Dai, C.; Hong, Z.; Yuan, Y.; Zhang, Z.; Lei, S.; McCarter, M.R.; Yadav, A.; Damodaran, A.R.; et al. Optical creation of a supercrystal with three-dimensional nanoscale periodicity. Nat. Mater. 2019, 18, 377–383. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xiao, J.; Zhu, H.; Wang, Y.; Feng, W.; Hu, Y.; Dasgupta, A.; Han, Y.; Wang, Y.; Muller, D.A.; Martin, L.W.; et al. Intrinsic two-dimensional ferroelectricity with dipole locking. Phys. Rev. Lett. 2018, 120, 227601. [Google Scholar] [CrossRef] [Green Version]
- Zhang, M.Y.; Wang, Z.X.; Li, Y.N.; Shi, L.Y.; Wu, D.; Lin, T.; Zhang, S.J.; Liu, Y.Q.; Liu, Q.M.; Wang, J.; et al. Light-Induced Subpicosecond Lattice Symmetry Switch in MoTe2. Phys. Rev. X 2019, 9, 021036. [Google Scholar] [CrossRef] [Green Version]
- Wei, D.; Wang, C.; Wang, H.; Hu, X.; Wei, D.; Fang, X.; Zhang, Y.; Wu, D.; Hu, Y.; Li, J.; et al. Experimental demonstration of a three-dimensional lithium niobate nonlinear photonic crystal. Nat. Photon. 2018, 12, 596–600. [Google Scholar] [CrossRef]
- Xu, T.; Switkowski, K.; Chen, X.; Liu, S.; Koynov, K.; Yu, H.; Zhang, H.; Wang, J.; Sheng, Y.; Krolikowski, W. Three-dimensional nonlinear photonic crystal in ferroelectric barium calcium titanate. Nat. Photon. 2018, 12, 591–595. [Google Scholar] [CrossRef]
- Choy, T.C. Effective Medium Theory: Principles and Applications; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Lupi, S.; Baldassarre, L.; Mansart, B.; Perucchi, A.; Barinov, A.; Dudin, P.; Papalazarou, E.; Rodolakis, F.; Rueff, J.P.; Itié, J.P.; et al. A microscopic view on the Mott transition in chromium-doped V2O3. Nat. Commun. 2010, 1, 105. [Google Scholar] [CrossRef] [Green Version]
- Chang, D.E.; Vuletic, V.; Lukin, M.D. Quantum nonlinear optics—Photon by photon. Nat. Photon. 2014, 8, 685–694. [Google Scholar] [CrossRef] [Green Version]
- Hell, S.W. Far-field optical nanoscopy. Science 2007, 316, 1153–1158. [Google Scholar] [CrossRef] [Green Version]
- Born, M.; Wolf, E. Principles of Optics; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Khorasaninejad, M.; Chen, W.T.; Devlin, R.C.; Oh, J.; Zhu, A.Y.; Capasso, F. Metalenses at visible wavelengths: Diffraction-limited focusing and subwavelength resolution imaging. Science 2016, 352, 1190–1194. [Google Scholar] [CrossRef] [Green Version]
- Chang, T.; Kim, J.U.; Kang, S.K.; Kim, H.; Kim, D.K.; Lee, Y.H.; Shin, J. Broadband giant-refractive-index material based on mesoscopic space-filling curves. Nat. Commun. 2016, 7, 12661. [Google Scholar] [CrossRef] [Green Version]
- Choi, M.; Lee, S.H.; Kim, Y.; Kang, S.B.; Shin, J.; Kwak, M.H.; Kang, K.-Y.; Lee, Y.-H.; Park, N.; Min, B. A terahertz metamaterial with unnaturally high refractive index. Nature 2011, 470, 369–373. [Google Scholar] [CrossRef]
- Lin, D.; Fan, P.; Hasman, E.; Brongersma, M.L. Dielectric gradient metasurface optical elements. Science 2014, 345, 298–302. [Google Scholar] [CrossRef]
- Kuznetsov, A.I.; Miroshnichenko, A.E.; Brongersma, M.L.; Kivshar, Y.S.; Luk’yanchuk, B. Optically resonant dielectric nanostructures. Science 2016, 354, aag2472. [Google Scholar] [CrossRef] [Green Version]
- Brongersma, M.L.; Cui, Y.; Fan, S. Light management for photovoltaics using high-index nanostructures. Nat. Mater. 2014, 13, 451–460. [Google Scholar] [CrossRef]
- Yablonovitch, E. Statistical ray optics. JOSA 1982, 72, 899–907. [Google Scholar] [CrossRef]
- Baba, T. Slow light in photonic crystals. Nat. Photon. 2008, 2, 465–473. [Google Scholar] [CrossRef]
- Hellwig, H.; Liebertz, J.; Bohatý, L. Linear optical properties of the monoclinic bismuth borate BiB3O6. J. Appl. Phys. 2000, 88, 240–244. [Google Scholar] [CrossRef]
- Petrov, V.; Ghotbi, M.; Kokabee, O.; Esteban-Martin, A.; Noack, F.; Gaydardzhiev, A.; Nikolov, I.; Tzankov, P.; Buchvarov, I.; Miyata, K.; et al. Femtosecond nonlinear frequency conversion based on BiB3O6. Laser Photon. Rev. 2010, 4, 53–98. [Google Scholar] [CrossRef]
- Zubko, P.; Wojdeł, J.C.; Hadjimichael, M.; Fernandez-Pena, S.; Sené, A.; Luk’yanchuk, I.; Triscone, J.-M.; Íñiguez, J. Negative capacitance in multidomain ferroelectric superlattices. Nature 2016, 534, 524–528. [Google Scholar] [CrossRef] [Green Version]
- Bokov, A.A.; Ye, Z.G. Dielectric relaxation in relaxor ferroelectrics. J. Adv. Dielectr. 2012, 2, 1241010. [Google Scholar] [CrossRef]
- Shvartsman, V.V.; Lupascu, D.C. Lead-free relaxor ferroelectrics. J. Am. Ceram. Soc. 2012, 95, 1–26. [Google Scholar] [CrossRef]
- De Oliveira, C.E.M.; Orr, G.; Axelrold, N.; Agranat, A.J. Controlled composition modulation in potassium lithium tantalate niobate crystals grown by off centered TSSG method. J. Cryst. Growth. 2004, 273, 203–206. [Google Scholar] [CrossRef]
- Agranat, A.J.; deOliveira, C.E.M.; Orr, G. Dielectric electrooptic gratings in potassium lithium tantalate niobate. J. Non-Cryst. Sol. 2007, 353, 4405–4410. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Falsi, L.; Macis, S.; Gelkop, Y.; Tartara, L.; Bonaventura, E.; Di Pietro, P.; Perucchi, A.; Garcia, Y.; Perepelitsa, G.; DelRe, E.; et al. Anomalous Optical Properties of KTN:Li Ferroelectric Supercrystals. Nanomaterials 2023, 13, 899. https://doi.org/10.3390/nano13050899
Falsi L, Macis S, Gelkop Y, Tartara L, Bonaventura E, Di Pietro P, Perucchi A, Garcia Y, Perepelitsa G, DelRe E, et al. Anomalous Optical Properties of KTN:Li Ferroelectric Supercrystals. Nanomaterials. 2023; 13(5):899. https://doi.org/10.3390/nano13050899
Chicago/Turabian StyleFalsi, Ludovica, Salvatore Macis, Yehonatan Gelkop, Luca Tartara, Eleonora Bonaventura, Paola Di Pietro, Andrea Perucchi, Yehudit Garcia, Galina Perepelitsa, Eugenio DelRe, and et al. 2023. "Anomalous Optical Properties of KTN:Li Ferroelectric Supercrystals" Nanomaterials 13, no. 5: 899. https://doi.org/10.3390/nano13050899
APA StyleFalsi, L., Macis, S., Gelkop, Y., Tartara, L., Bonaventura, E., Di Pietro, P., Perucchi, A., Garcia, Y., Perepelitsa, G., DelRe, E., Agranat, A. J., & Lupi, S. (2023). Anomalous Optical Properties of KTN:Li Ferroelectric Supercrystals. Nanomaterials, 13(5), 899. https://doi.org/10.3390/nano13050899










