A Theoretical Study of Interband Absorption Spectra of Spherical Sector Quantum Dots under the Effect of a Powerful Resonant Laser
Abstract
:1. Introduction
2. Theoretical Framework
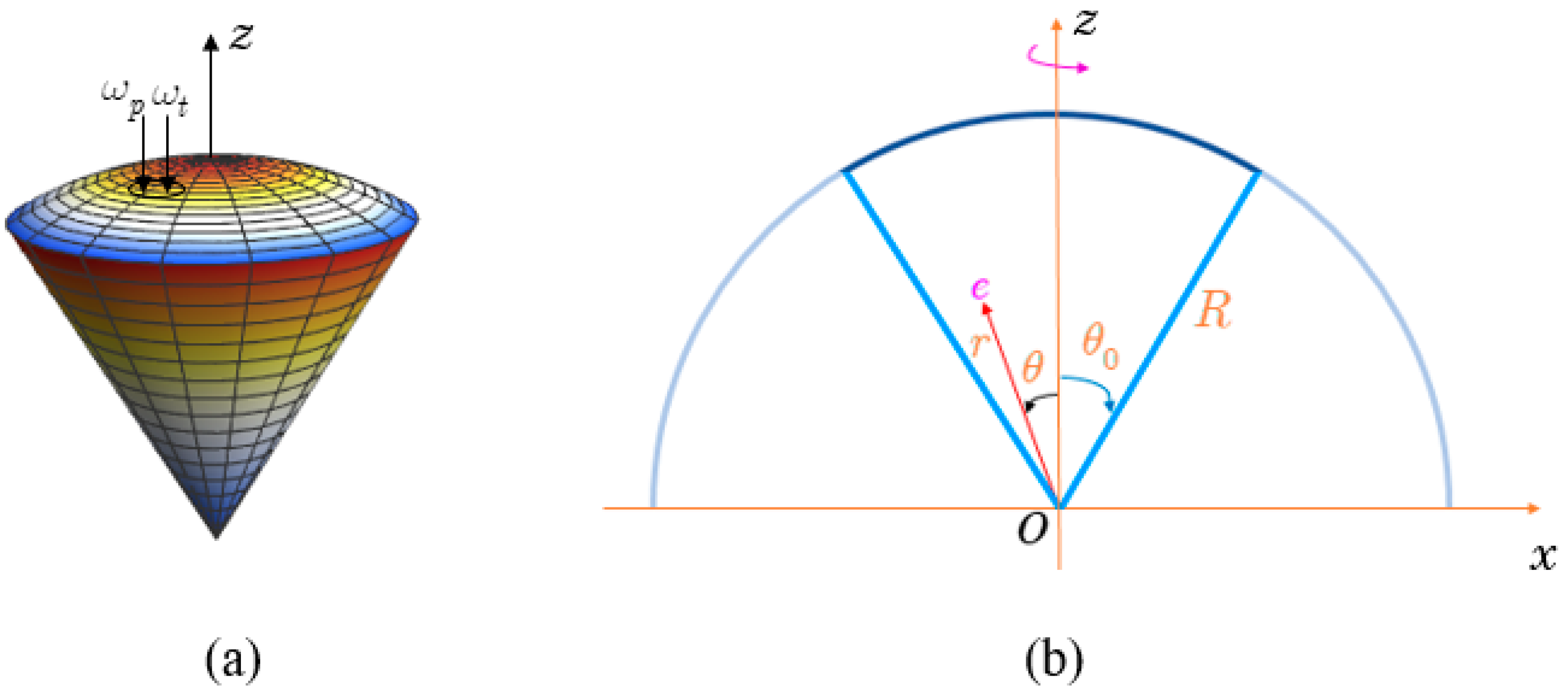
2.1. The Wave Function and Energy Levels of Particles
2.2. The Intraband Optical Transition Matrix Element
2.3. The Interband Absorption Spectra in the Absence of a Pump Field
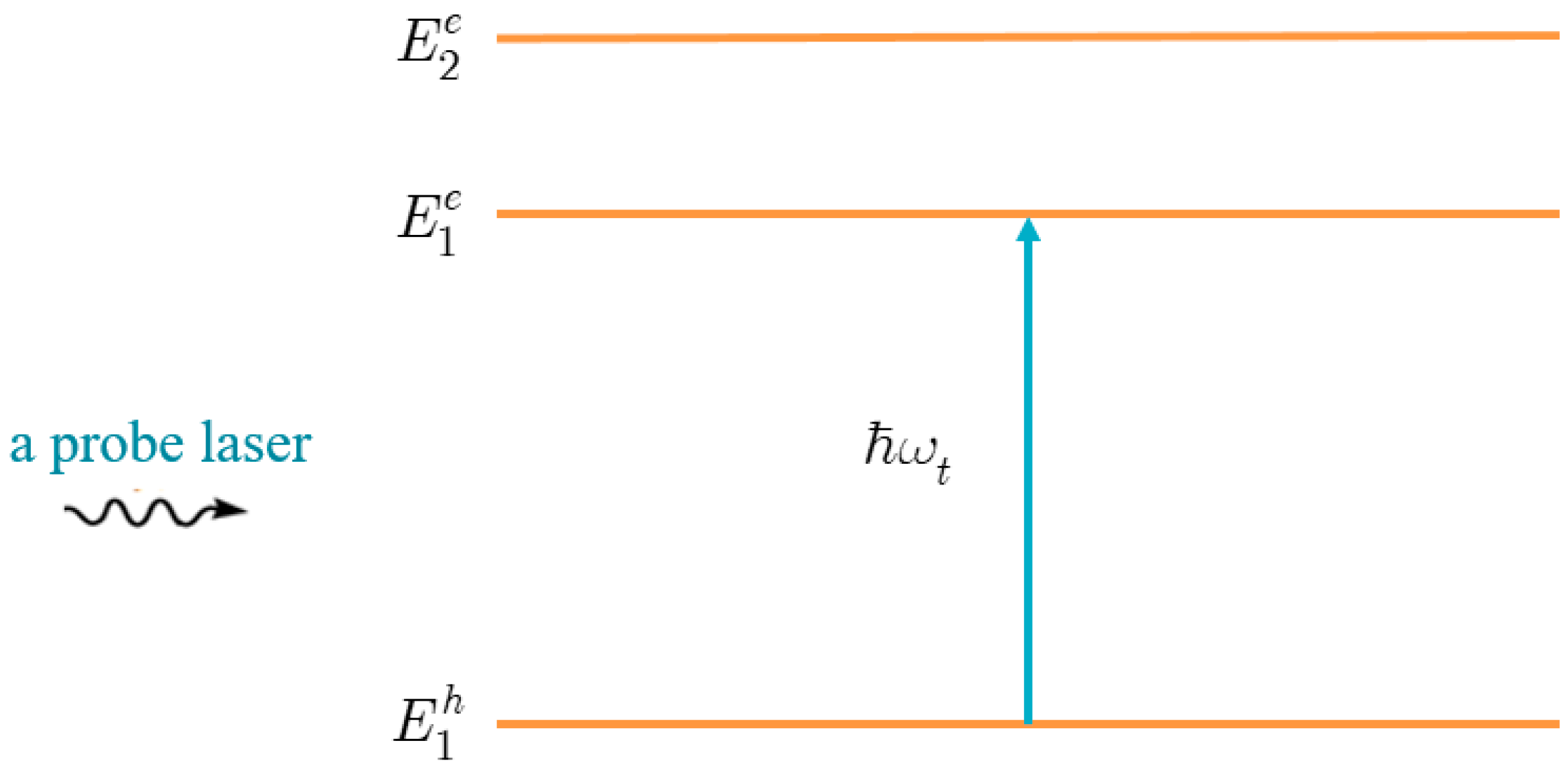
2.4. The Interband Absorption Spectra in the Presence of a Pump Field
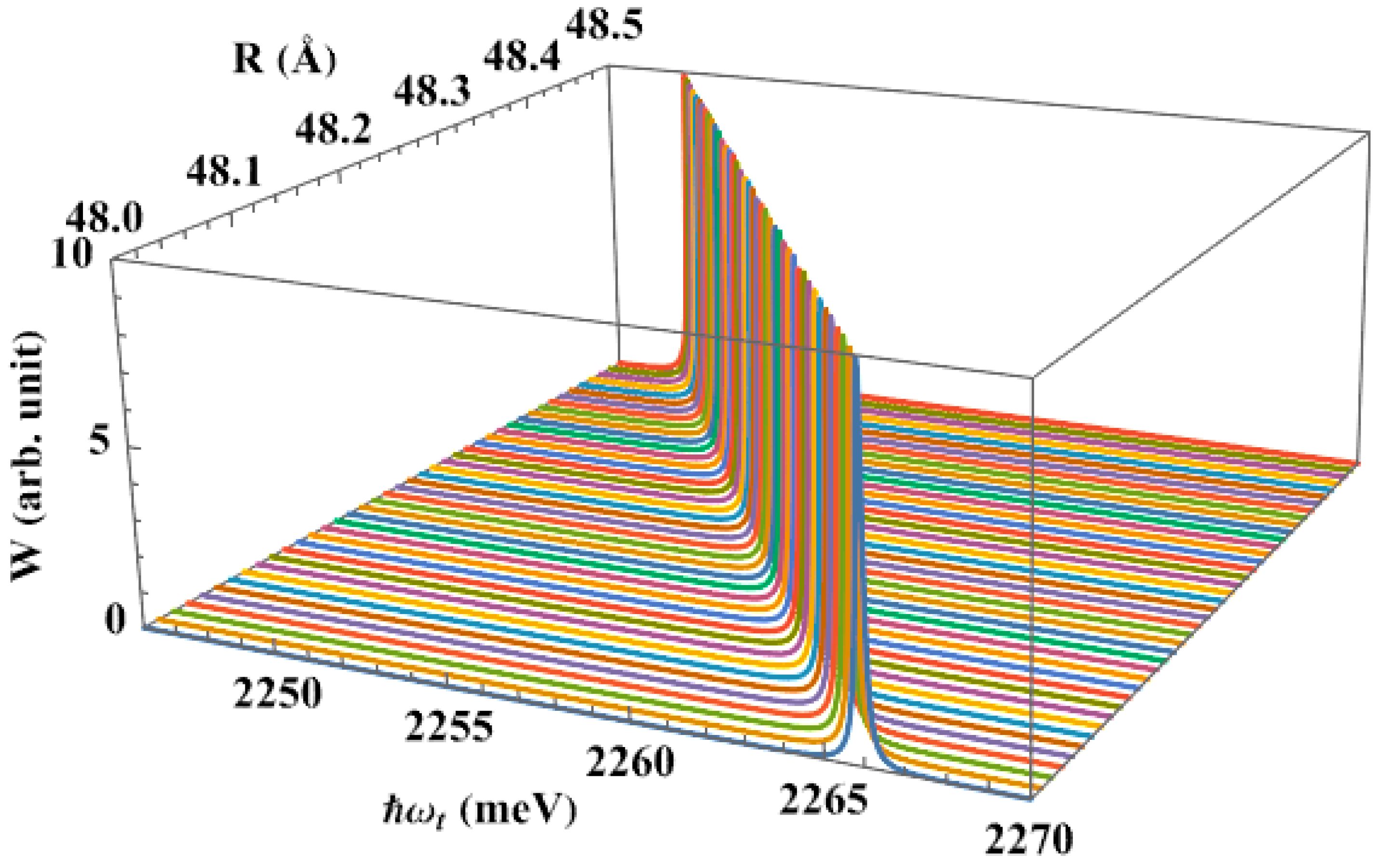
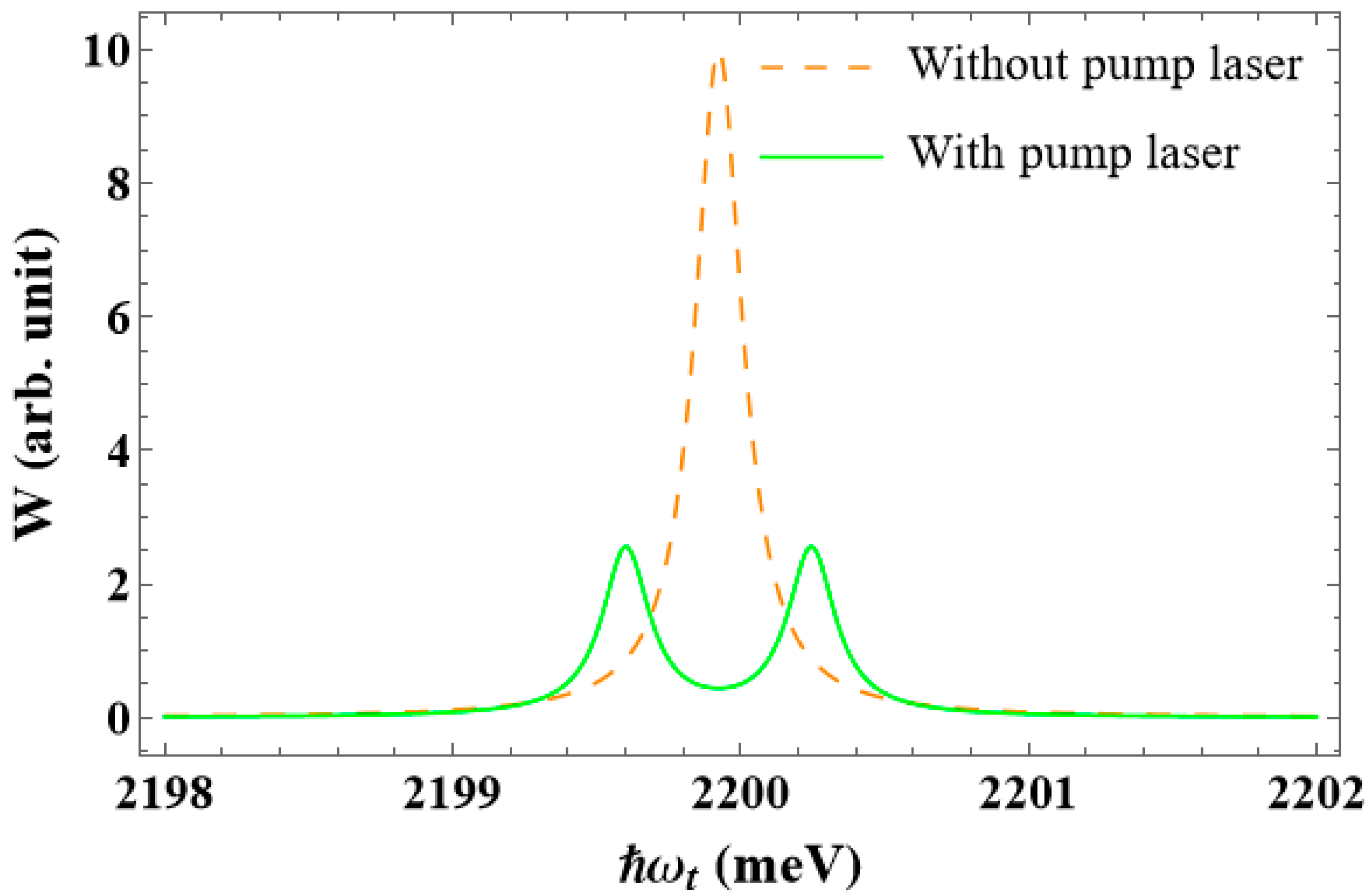
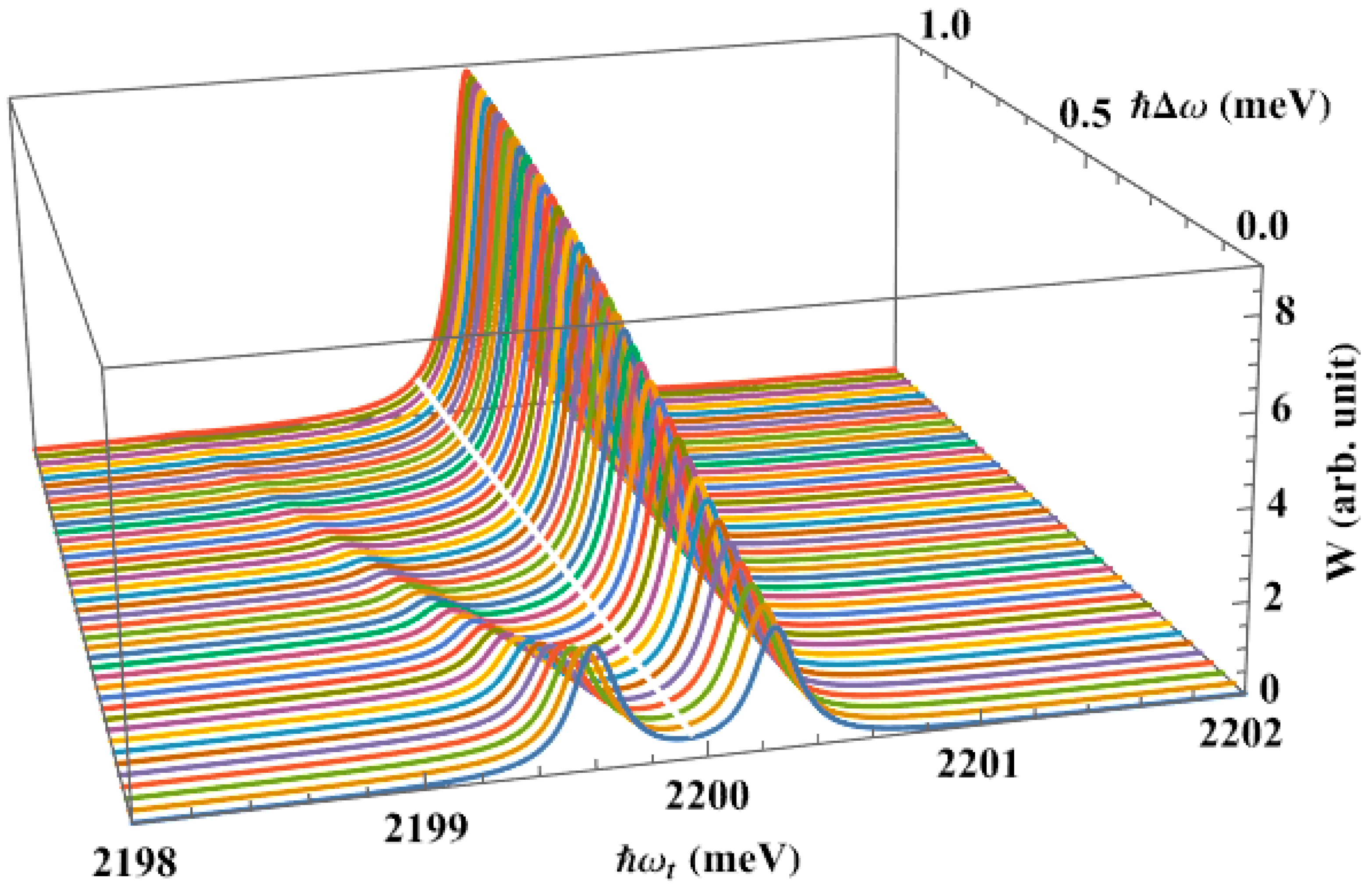
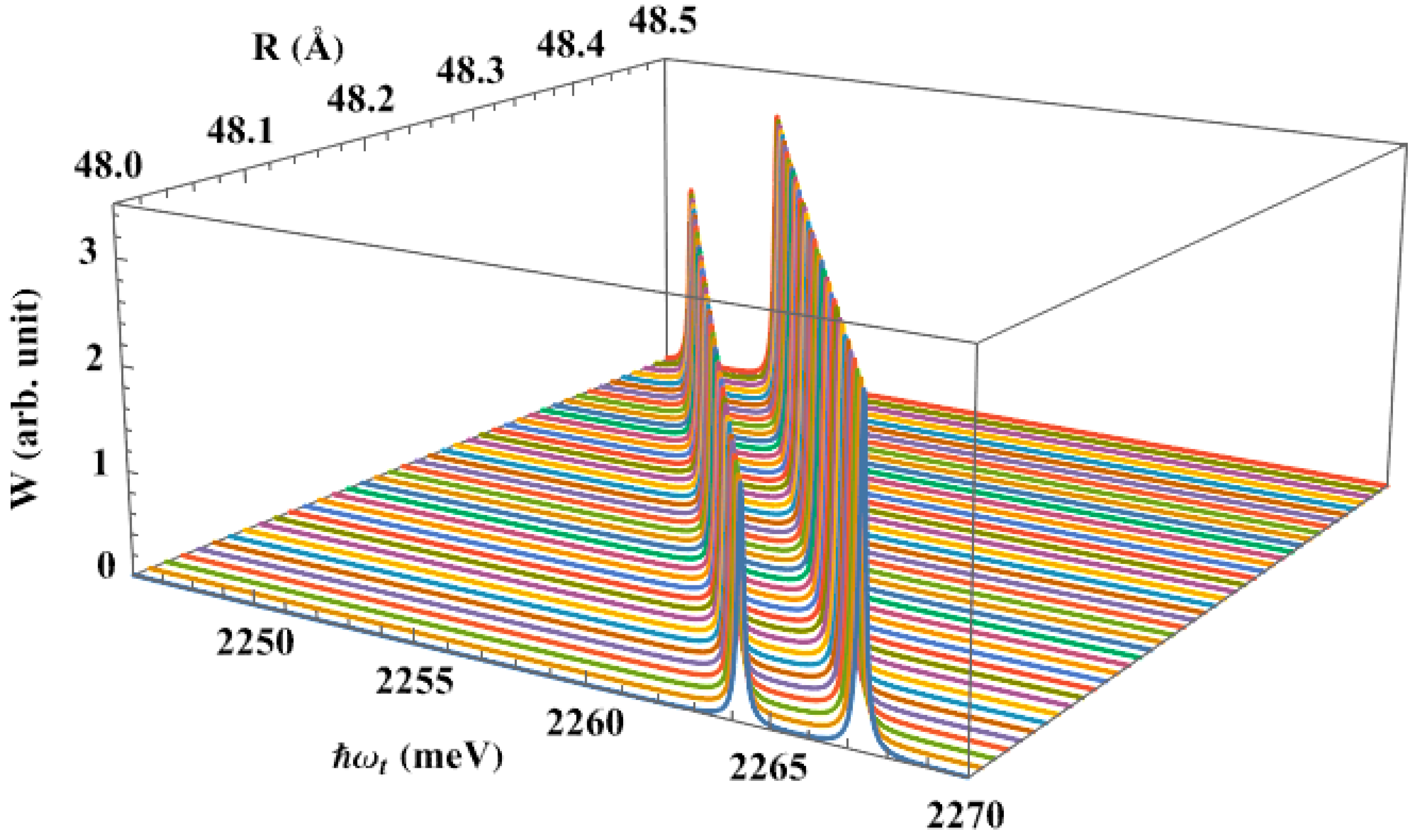
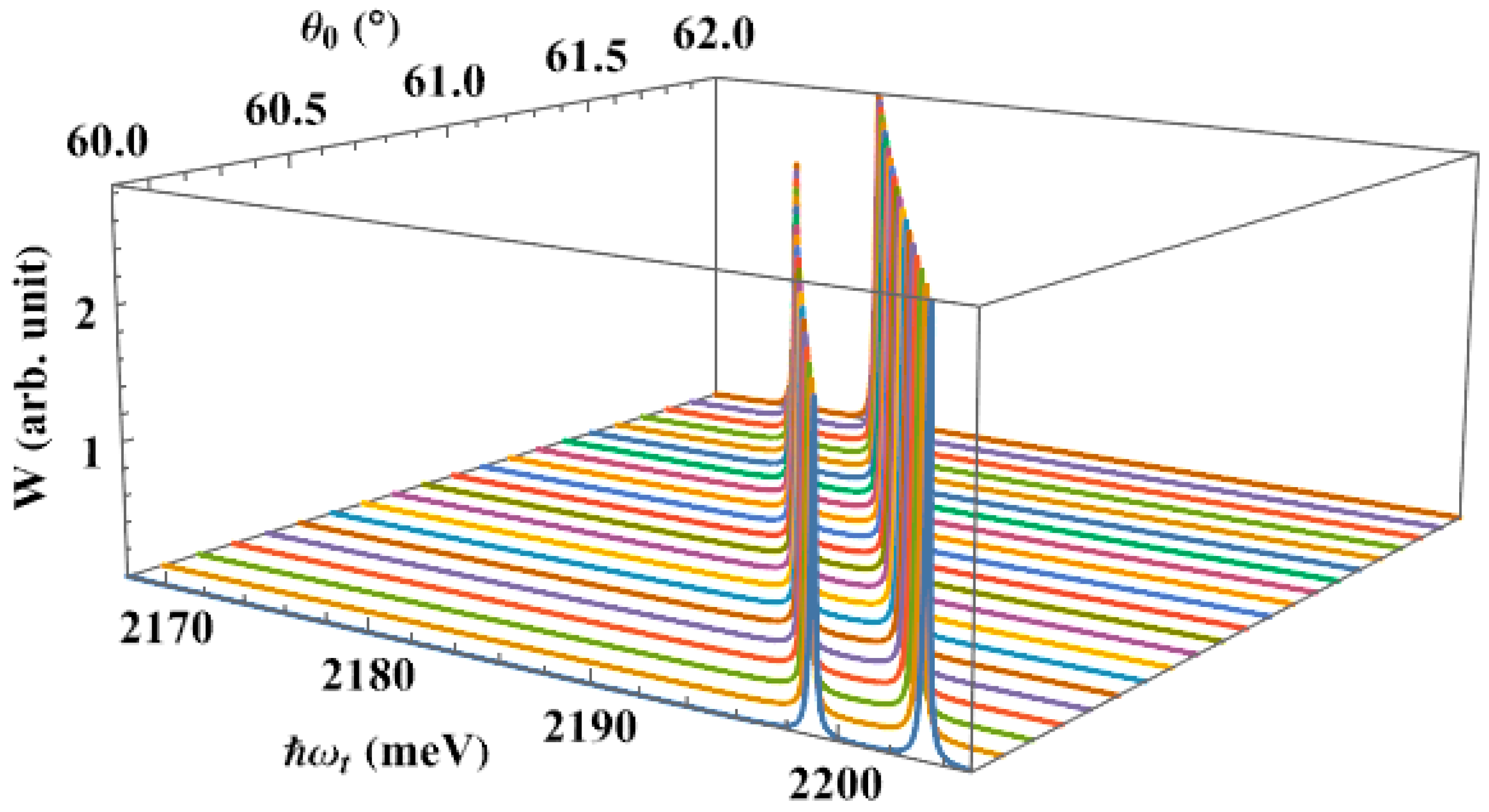
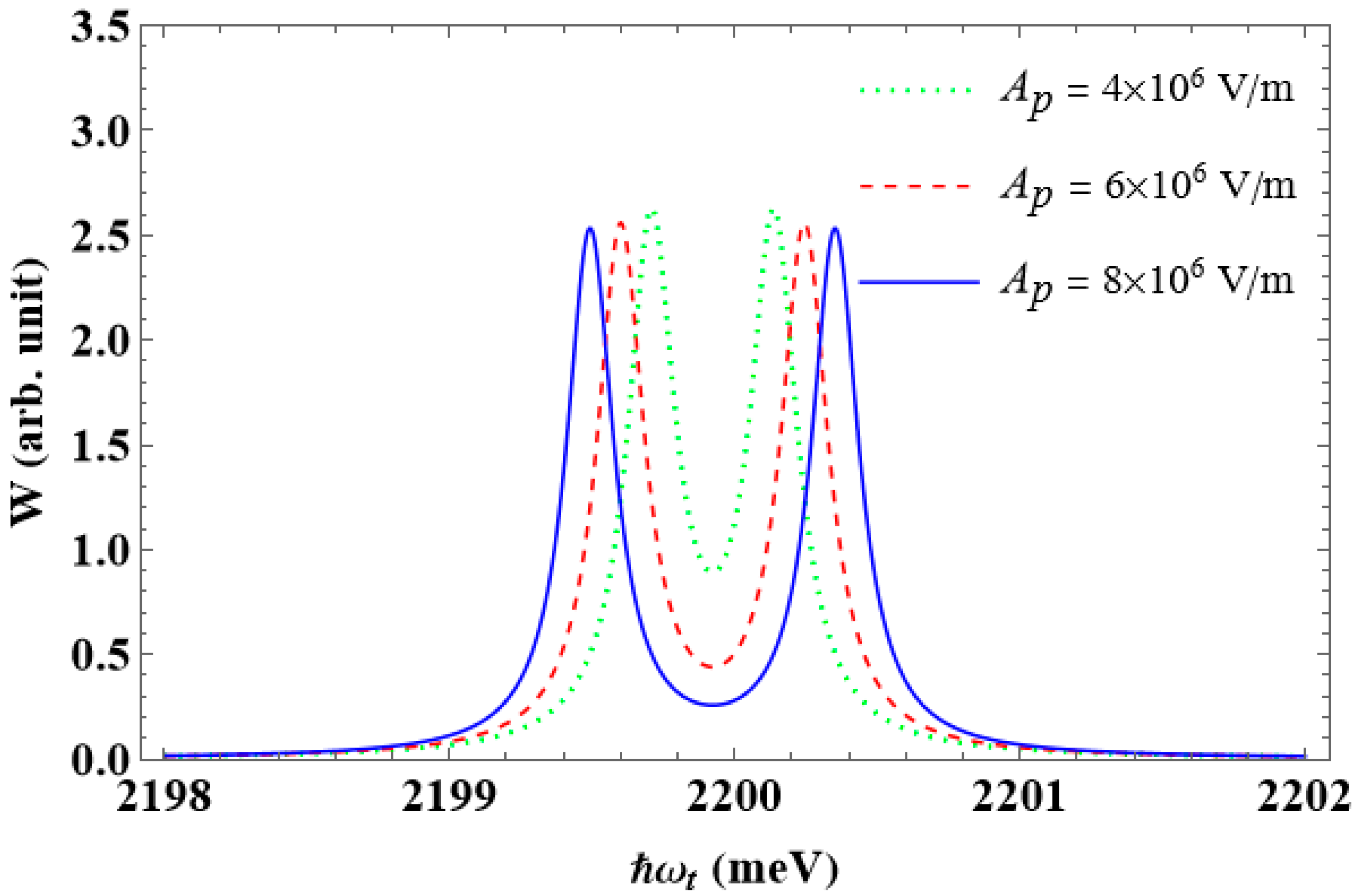
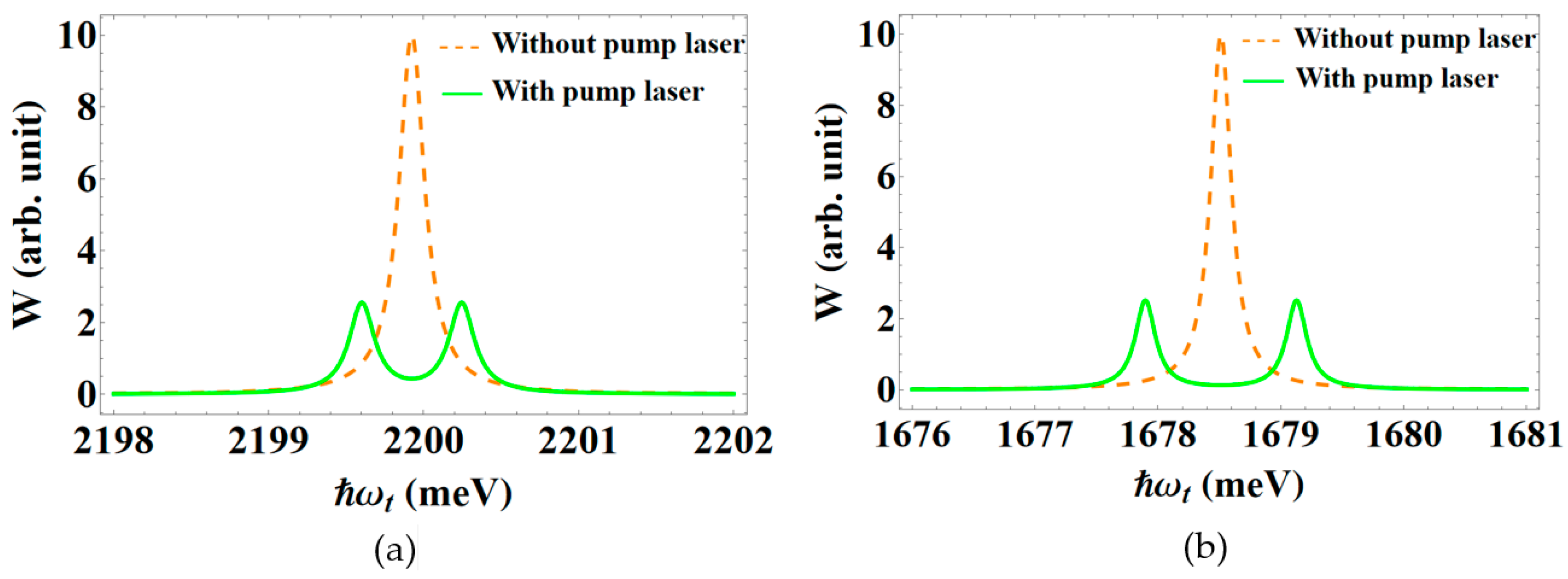
3. Numerical Results and Discussions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, W.; Coleman, J.J. Semiconductor quantum dots. Curr. Opin. Solid State Mater. Sci. 2016, 20, 352–360. [Google Scholar] [CrossRef]
- Kim, T.H.; Jun, S.; Cho, K.S.; Choi, B.L.; Jang, E. Bright and stable quantum dots and their applications in full-color displays. MRS Bull. 2013, 38, 712–720. [Google Scholar] [CrossRef]
- Biju, V.; Muraleedharan, D.; Nakayama, K.; Shinohara, Y.; Itoh, T.; Baba, Y.; Ishikawa, M. Quantum dot-insect neuropeptide conjugates for fluorescence imaging, transfection, and nucleus targeting of living cells. Langmuir 2007, 23, 10254–10261. [Google Scholar] [CrossRef] [PubMed]
- Towe, E.; Pan, D. Semiconductor quantum-dot nanostructures: Their application in a new class of infrared photodetectors. IEEE J. Sel. Top. Quantum Electron. 2000, 6, 408–421. [Google Scholar] [CrossRef]
- De Rinaldis, S.; D’Amico, I.; Biolatti, E.; Rinaldi, R.; Cingolani, R.; Rossi, F. Intrinsic exciton-exciton coupling in GaN-based quantum dots: Application to solid-state quantum computing. Phys. Rev. B 2002, 65, 081309. [Google Scholar] [CrossRef] [Green Version]
- Arakawa, Y.; Holmes, M.J. Progress in quantum-dot single photon sources for quantum information technologies: A broad spectrum overview. Appl. Phys. Rev. 2020, 7, 021309. [Google Scholar] [CrossRef]
- Arzhanov, A.I.; Savostianov, A.O.; Magaryan, K.A.; Karimullin, K.R.; Naumov, A.V. Photonics of semiconductor quantum dots: Applied aspects. Photonics Russ. 2022, 16, 96. [Google Scholar]
- Azam, N.; Ali, M.N.; Khan, T.J. Carbon Quantum Dots for Biomedical Applications: Review and Analysis. Front. Mater. 2021, 8, 700403. [Google Scholar] [CrossRef]
- Farzin, M.A.; Abdoos, H. A critical review on quantum dots: From synthesis toward applications in electrochemical biosensors for determination of disease-related biomolecules. Talanta 2021, 224, 121828. [Google Scholar] [CrossRef]
- Marent, A.; Nowozin, T.; Geller, M.; Bimberg, D. The QD-Flash: A quantum dot-based memory device. Semicond. Sci. Technol. 2011, 26, 014026. [Google Scholar] [CrossRef]
- Bonato, L.; Arikan, I.F.; Desplanque, L.; Coinon, C.; Wallart, X.; Wang, Y.; Ruterana, P.; Bimberg, D. Hole localization energy of 1.18 eV in GaSb quantum dots embedded in GaP. Phys. Status Solidi B 2016, 253, 1869. [Google Scholar] [CrossRef] [Green Version]
- Abramkin, D.S.; Atuchin, V.V. Novel InGaSb/AlP Quantum Dots for Non-Volatile Memories. Nanomaterials 2022, 12, 3794. [Google Scholar] [CrossRef] [PubMed]
- Petrushkov, M.O.; Abramkin, D.S.; Emelyanov, E.A.; Putyato, M.A.; Komkov, O.S.; Firsov, D.D.; Vasev, A.V.; Yesin, M.Y.; Bakarov, A.K.; Loshkarev, I.D.; et al. Dislocation Filter Based on LT-GaAs Layers for Monolithic GaAs/Si Integration. Nanomaterials 2022, 12, 4449. [Google Scholar] [CrossRef] [PubMed]
- Tang, M.; Chen, S.; Wu, J.; Jiang, Q.; Dorogan, V.G.; Benamara, M.; Mazur, Y.I.; Salamo, G.J.; Seeds, A.; Liu, H. 13-μm InAs/GaAs quantum-dot lasers monolithically grown on Si substrates using InAlAs/GaAs dislocation filter layers. Opt. Express 2014, 22, 11528. [Google Scholar] [CrossRef]
- Wan, Y.; Zhang, Z.; Chao, R.; Norman, J.; Jung, D.; Shang, C.; Li, Q.; Kennedy, M.J.; Liang, D.; Zhang, C.; et al. Monolithically integrated InAs/InGaAs quantum dot photodetectors on silicon substrates. Opt. Express 2017, 25, 27715. [Google Scholar] [CrossRef]
- Hiruma, K.; Yazawa, M.; Katsuyama, T.; Ogawa, K.; Haraguchi, K.; Koguchi, M.; Kakibayashi, H. Growth and optical properties of nanometer-scale GaAs and InAs whiskers. J. Appl. Phys. 1995, 77, 447–462. [Google Scholar] [CrossRef]
- Melnik, R.V.N.; Willatzen, M. Bandstructures of conical quantum dots with wetting layers. Nanotechnology 2003, 15, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Schamp, C.T.; Jesser, W.A.; Shivaram, B.S. Growth of GaAs nano ice cream cones by dual wavelength pulsed laser ablation. Appl. Surf. Sci. 2007, 253, 6326–6329. [Google Scholar] [CrossRef]
- Lozovski, V.; Piatnytsia, V. The analytical study of electronic and optical properties of pyramid-like and cone-like quantum dots. J. Comput. Theor. Nanosci. 2011, 8, 2335–2343. [Google Scholar] [CrossRef]
- Khordad, R.; Bahramiyan, H. Study of impurity position effect in pyramid and cone like quantum dots. Eur. Phys. J. Appl. Phys. 2014, 67, 20402. [Google Scholar] [CrossRef]
- Khordad, R.; Bahramiyan, H. Optical properties of a GaAs cone-like quantum dot: Second and third-harmonic generation. Opt. Spectrosc. 2014, 117, 447–452. [Google Scholar] [CrossRef]
- Eduard, M.K.; Lyudvig, S.P.; Vanik, A.S.; Hayk, A.S. Quasi-Conical Quantum Dot: Electron States and Quantum Transitions. Commun. Theor. Phys. 2015, 63, 255–260. [Google Scholar] [CrossRef] [Green Version]
- Hayrapetyan, D.B.; Kazaryan, E.M.; Sarkisyan, H.A. Magneto-absorption in conical quantum dot ensemble: Possible applications for QD LED. Opt. Commun. 2016, 371, 138–143. [Google Scholar] [CrossRef]
- Bahramiyan, H. Electric field and impurity effect on nonlinear optical rectification of a double cone like quantum dot. Opt. Mater. 2018, 75, 187–195. [Google Scholar] [CrossRef]
- Khordad, R.; Rastegar Sedehi, H.R.; Bahramiyan, H. Simultaneous effects of impurity and electric field on entropy behavior in double cone-like quantum dot. Commun. Theor. Phys. 2018, 69, 95–100. [Google Scholar] [CrossRef]
- Vinasco, J.A.; Radu, A.; Duque, C.A. Propiedades electrónicas de un anillo cuántico elíptico con sección transversal rectangular. Rev. EIA 2019, 16, 77–87. [Google Scholar] [CrossRef] [Green Version]
- El Aouami, A.; Feddi, E.; El-Yadri, M.; Aghoutane, N.; Dujardin, F.; Duque, C.A.; Phuc, H.V. Electronic states and optical properties of single donor in GaN conical quantum dot with spherical edge. Superlattices Microstruct. 2018, 114, 214–224. [Google Scholar] [CrossRef]
- Mora-Ramos, M.E.; El Aouma, A.; Feddi, E.; Radu, A.; Restrepo, R.L.; Vinasco, J.A.; Duque, C.A. Donor impurity energy and optical absorption in spherical sector quantum dots. Heliyon 2020, 6, e03194. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Heyn, C.; Radu, A.; Vinasco, J.A.; Laroze, D.; Restrepo, R.L.; Tulupenko, V.; Hieu, N.N.; Phuc, H.V.; Mora-Ramosi, M.E.; Ojeda, J.H.; et al. Exciton states in conical quantum dots under applied electric and magnetic fields. Opt. Laser Technol. 2021, 139, 106953. [Google Scholar] [CrossRef]
- Mysyrowicz, A.; Hulin, D.; Antonetti, A.; Migus, A.; Masselink, W.T.; Morkoç, H. ‘Dressed excitons’ in a multiple-quantum-well structure: Evidence for an optical Stark effect with femtosecond response time. Phys. Rev. Lett. 1986, 56, 2748–2751. [Google Scholar] [CrossRef]
- Von Lehmen, A.; Chemla, D.S.; Heritage, J.P.; Zucker, J.E. Optical Stark effect on excitons in GaAs quantum wells. Opt. Lett. 1986, 11, 609–611. [Google Scholar] [CrossRef]
- Hulin, D.; Mysyrowicz, A.; Antonetti, A.; Migus, A.; Masselink, W.T.; Morkoç, H.; Peyghambarian, N. Ultrafast all-optical gate with subpicosecond on and off response time. Appl. Phys. Lett. 1986, 49, 749–751. [Google Scholar] [CrossRef]
- Hulin, D.; Antonetti, A.; Joffre, M.; Migus, A.; Mysyrowicz, A.; Peyghambarian, N.; Gibbs, H.M. Subpicosecond all-optical logic gate: An application of the optical Stark effect. Rev. Phys. Appliquée 1987, 22, 1269–1271. [Google Scholar] [CrossRef]
- Ahn, D. Enhancement of the Stark effect in coupled quantum wells for optical switching devices. IEEE J. Quantum Electron. 1989, 25, 2260–2265. [Google Scholar] [CrossRef]
- Combescot, M. Semiconductors in strong laser fields: From polariton to exciton optical Stark effect. Phys. Rep. 1992, 221, 167–249. [Google Scholar] [CrossRef]
- Schmitt-Rink, S.; Chemla, D.S. Collective excitations and the dynamical Stark effect in a coherently driven exciton system. Phys. Rev. Lett. 1986, 57, 2752–2755. [Google Scholar] [CrossRef] [PubMed]
- Combescot, M.; Combescot, R. Excitonic Stark shift: A coupling to ‘semivirtual’ biexcitons. Phys. Rev. Lett. 1988, 61, 117–120. [Google Scholar] [CrossRef] [PubMed]
- Schmitt-Rink, S.; Chemla, D.S.; Haug, H. Nonequilibrium theory of the optical Stark effect and spectral hole burning in semiconductors. Phys. Rev. B 1988, 37, 941–955. [Google Scholar] [CrossRef]
- Combescot, M. Polarisation effects for the excitonic Stark shift at all detunings. Solid State Commun. 1988, 68, 471–475. [Google Scholar] [CrossRef]
- Lindberg, M.; Koch, S.W. Transient oscillations and dynamic Stark effect in semiconductors. Phys. Rev. B 1988, 38, 7607–7614. [Google Scholar] [CrossRef]
- Fröhlich, D.; Reimann, K.; Wille, R. Optical Stark effect of excitons in semiconductors. J. Lumin. 1987, 38, 235–238. [Google Scholar] [CrossRef]
- Ell, C.; Müller, J.F.; El Sayed, K.; Banyai, L.; Haug, H. Evaluation of the Hartree-Fock theory of the excitonic optical Stark effect. Phys. Status Solid (b) 1988, 150, 393–399. [Google Scholar] [CrossRef]
- Lindberg, M.; Koch, S.W. Theory of the optical Stark effect in semiconductors under ultrashort-pulse excitation. Phys. Status Solid (b) 1988, 150, 379–385. [Google Scholar] [CrossRef]
- Combescot, M.; Combescot, R. Optical Stark effect of the exciton: Biexcitonic origin of the shift. Phys. Rev. B 1989, 40, 3788–3801. [Google Scholar] [CrossRef] [PubMed]
- Ell, C.; Müller, J.F.; El Sayed, K.; Haug, H. Influence of many-body interactions on the excitonic optical Stark effect. Phys. Rev. Lett. 1989, 62, 304–307. [Google Scholar] [CrossRef] [PubMed]
- Combescot, M.; Betbeder-Matibet, O. On the exciton red-shift in the optical Stark effect. Solid State Commun. 1990, 75, 163–165. [Google Scholar] [CrossRef]
- Bobrysheva, A.I.; Shmiglyuk, M.I.; Pavlov, V.G. Optical exciton Stark effect and quantum beats at exciton quasienergy levels in quantum wells. Phys. Solid State 1997, 39, 1147–1149. [Google Scholar] [CrossRef]
- Quang, N.H. The optical Stark effect of the exciton due to dynamical coupling between quantized states of the electron and hole in quantum wells. Int. J. Mod. Phys. B 1993, 7, 3405–3413. [Google Scholar] [CrossRef]
- Wang, S.; Kang, Y.; Han, C. Transverse Stark effect in the optical absorption in a square semiconducting quantum wire. J. Semicond. 2013, 34, 102001. [Google Scholar] [CrossRef]
- Sangalli, D.; Perfetto, E.; Stefanucci, G.; Marini, A. An ab-initio approach to describe coherent and non-coherent exciton dynamics. Eur. Phys. J. B 2018, 91, 171. [Google Scholar] [CrossRef] [Green Version]
- Rustagi, A.; Kemper, A.F. Coherent excitonic quantum beats in time-resolved photoemission measurements. Phys. Rev. B 2019, 99, 125303. [Google Scholar] [CrossRef] [Green Version]
- Zielińska-Raczyńska, S.; Czajkowski, G.; Ziemkiewicz, D. Quantum confined Stark effect in wide parabolic quantum wells: Real density matrix approach. Eur. Phys. J. B 2015, 88, 338. [Google Scholar] [CrossRef] [Green Version]
- Altevogt, T.; Zimmermann, R. Nonclassical gain in the optical Stark effect: Density matrix approach. J. Phys. B Atom. Mol. Phys. 1999, 32, 4719–4728. [Google Scholar] [CrossRef]
- Tai, K.; Hegarty, J.; Tsang, W.T. Observation of optical Stark effect in InGaAs/InP multiple quantum wells. Appl. Phys. Lett. 1987, 51, 152–154. [Google Scholar] [CrossRef]
- Knox, W.H.; Chemla, D.S.; Miller, D.A.B.; Stark, J.B.; Schmitt-Rink, S. Femtosecond ac Stark effect in semiconductor quantum wells: Extreme low- and high-intensity limits. Phys. Rev. Lett. 1989, 62, 1189–1192. [Google Scholar] [CrossRef] [PubMed]
- Mysyrowicz, A.; Hulin, D. Optical Stark effect in GaAs quantum wells. J. Phys. Colloq. 1988, 49, C2-175–C2-177. [Google Scholar] [CrossRef]
- Unold, T.; Mueller, K.; Lienau, C.; Elsaesser, T.; Wieck, A.D. Optical Stark effect in a quantum dot: Ultrafast control of single exciton polarizations. Phys. Rev. Lett. 2004, 92, 157401. [Google Scholar] [CrossRef] [Green Version]
- Biswas, C.; Jeong, H.; Jeong, M.S.; Yu, W.J.; Pribat, D.; Lee, Y.H. Quantum dot-carbon nanotube hybrid phototransistor with an enhanced optical Stark effect. Adv. Funct. Mater. 2013, 23, 3653–3660. [Google Scholar] [CrossRef]
- Hulin, D.; Joffre, M. Excitonic optical Stark redshift: The biexciton signature. Phys. Rev. Lett. 1990, 65, 3425–3428. [Google Scholar] [CrossRef]
- Garmire, E.I.; Maradudin, A.I.A.; Rebane, K.K. Volume 2 the Physics of Optical Phenomena and Their Use as Probes of Matter. In Laser Optics of Condensed Matter; Springer Science+Business Media, LCC: New York, NY, USA, 1991. [Google Scholar]
- Fröhlich, D.; Neumann, C.; Uebbing, B.; Wille, R. Experimental investigation of three-level optical Stark effect in semiconductors. Phys. Status Solidi (B) 1990, 159, 297–307. [Google Scholar] [CrossRef]
- Thao, D.N.; Bao, L.T.N.; Phuoc, D.D.; Quang, N.H. A theoretical study of the optical Stark effect in InGaAs/InAlAs quantum dots. Semicond. Sci. Technol. 2017, 32, 025014. [Google Scholar] [CrossRef]
- Kumar, A. Fundamentals of Quantum Mechanics; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Fox, M. Optical Properties of Solids; Oxford University Press: Oxford, UK; New York, NY, USA, 2001. [Google Scholar]
- Bala, K.J.; Peter, A.J.; Lee, C.W. Interband and intersubband optical transition energies in a Ga0.7In0.3N/GaN quantum dot. Optik 2019, 183, 1106–1113. [Google Scholar] [CrossRef]
- Nakwaski, W. Effective masses of electrons and heavy holes in GaAs, InAs, A1As and their ternary compounds. Physica B 1995, 210, 1–25. [Google Scholar] [CrossRef]
- Casey, H.C., Jr.; Panish, M.B. Heterostructure Lasers; Academic Press: Cambridge, MA, USA, 1978; p. 157. [Google Scholar]
- Tarucha, S.; Okamoto, H.; Iwasa, Y.; Miura, N. Exciton binding energy in GaAs quantum wells deduced from magneto-optical absorption measurement. Solid State Commun. 1984, 52, 815–819. [Google Scholar] [CrossRef]
- Lelong, P.; Bastard, G. Binding energies of excitons and charged excitons in quantum dots. Solid State Commun. 1996, 98, 819–823. [Google Scholar] [CrossRef]
- Zhao, Z.-R.; Liang, X.X. Phonon effect on exciton binding energies in cylindrical quantum wires in the presence of an electric field. Chin. J. Phys. 2011, 49, 259. [Google Scholar]
- Yücel, M.B.; Sari, H.; Duque, C.M.; Duque, C.A.; Kasapoglu, E. Theoretical study of the exciton binding energy and exciton absorption in different hyperbolic-type quantum wells under applied electric, magnetic, and intense laser fields. Int. J. Mol. Sci. 2022, 23, 11429. [Google Scholar] [CrossRef]
- Bao, L.T.N.; Phuoc, D.D.; Hien, L.T.D.; Thao, D.N. On the optical Stark effect of excitons in InGaAs prolate ellipsoidal quantum dots. J. Nanomater. 2021, 2021, 5586622. [Google Scholar] [CrossRef]


| n | ||
|---|---|---|
| 1 | (0, 4.08369) | 8.28148 |
| 2 | (1, 6.8354) | 11.4695 |
| 3 | (2, 9.37328) | 14.3338 |
| 4 | (0, 10.0386) | 15.0764 |
| 5 | (1, 12.9083) | 18.2505 |
| 6 | (2, 15.6154) | 21.2108 |
| 7 | (0, 16.0248) | 21.6562 |
| 8 | (1, 18.9364) | 24.8094 |
| 9 | (2, 21.721) | 27.8050 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hien, L.T.D.; Bao, L.T.N.; Phuoc, D.D.; Kim, H.J.; Duque, C.A.; Thao, D.N. A Theoretical Study of Interband Absorption Spectra of Spherical Sector Quantum Dots under the Effect of a Powerful Resonant Laser. Nanomaterials 2023, 13, 1020. https://doi.org/10.3390/nano13061020
Hien LTD, Bao LTN, Phuoc DD, Kim HJ, Duque CA, Thao DN. A Theoretical Study of Interband Absorption Spectra of Spherical Sector Quantum Dots under the Effect of a Powerful Resonant Laser. Nanomaterials. 2023; 13(6):1020. https://doi.org/10.3390/nano13061020
Chicago/Turabian StyleHien, Le Thi Dieu, Le Thi Ngoc Bao, Duong Dinh Phuoc, Hye Jung Kim, C. A. Duque, and Dinh Nhu Thao. 2023. "A Theoretical Study of Interband Absorption Spectra of Spherical Sector Quantum Dots under the Effect of a Powerful Resonant Laser" Nanomaterials 13, no. 6: 1020. https://doi.org/10.3390/nano13061020
APA StyleHien, L. T. D., Bao, L. T. N., Phuoc, D. D., Kim, H. J., Duque, C. A., & Thao, D. N. (2023). A Theoretical Study of Interband Absorption Spectra of Spherical Sector Quantum Dots under the Effect of a Powerful Resonant Laser. Nanomaterials, 13(6), 1020. https://doi.org/10.3390/nano13061020






