Ga-In Alloy Segregation within a Porous Glass as Studied by SANS
Abstract
:1. Introduction
2. Materials and Methods
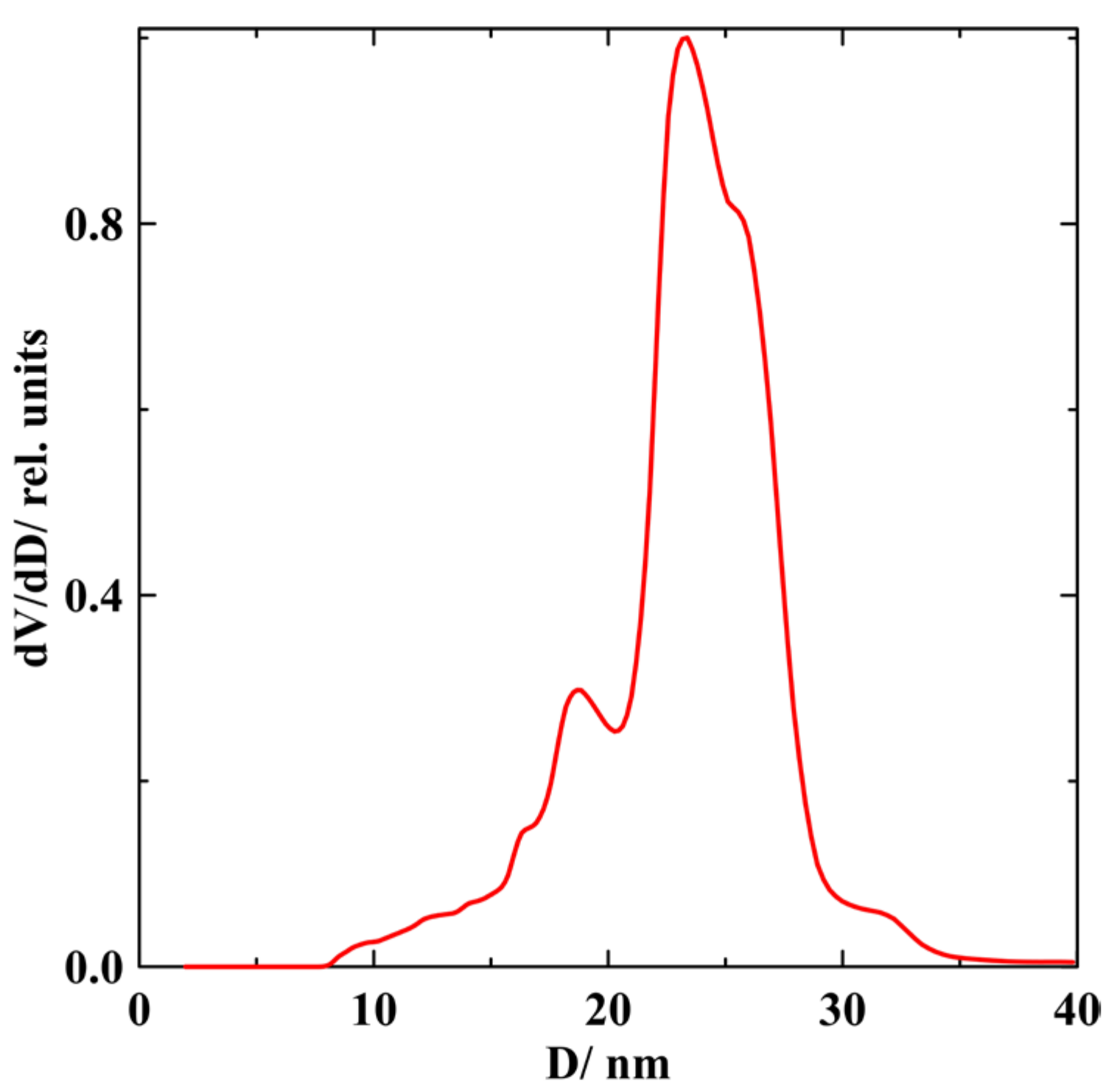
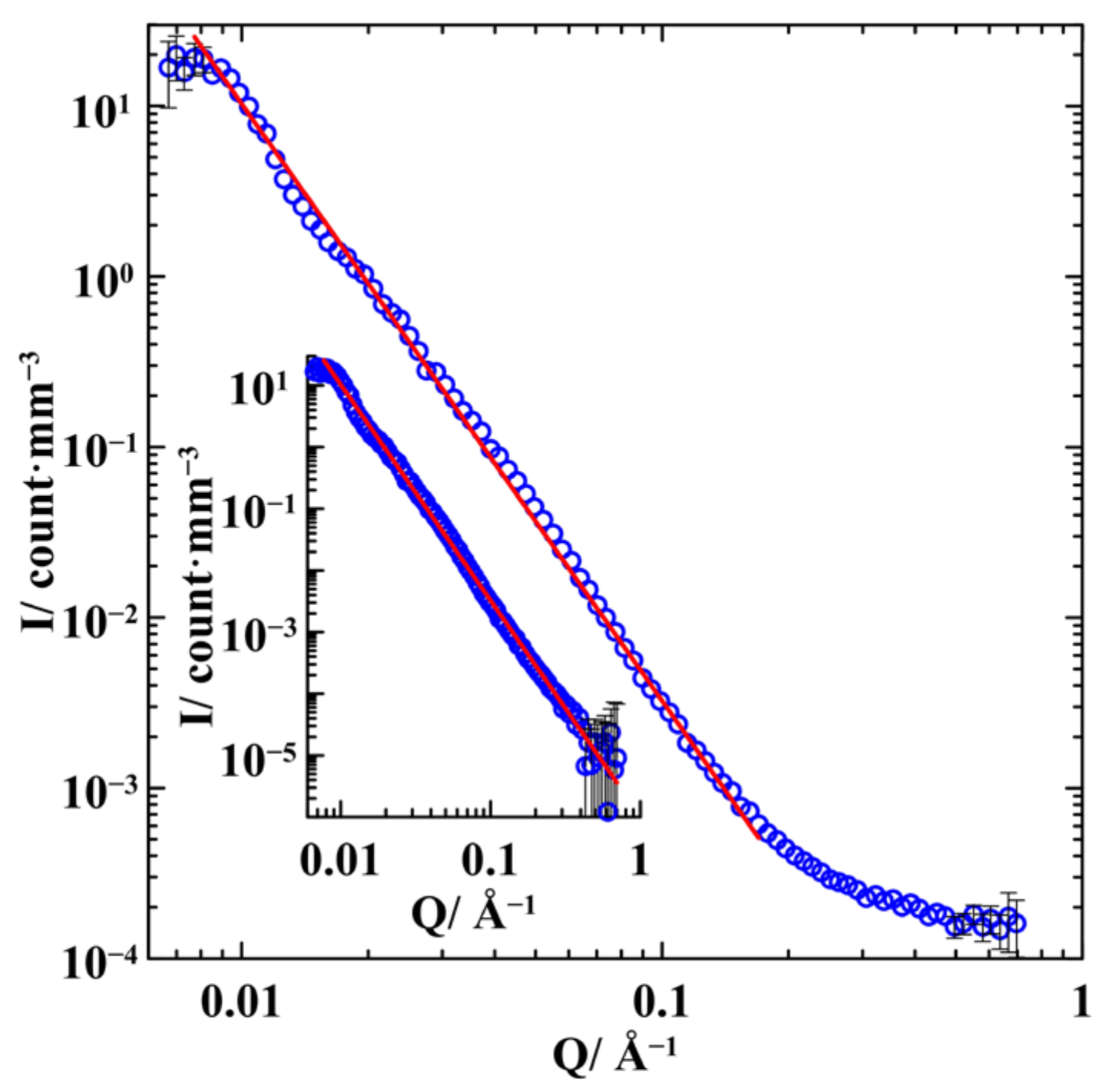
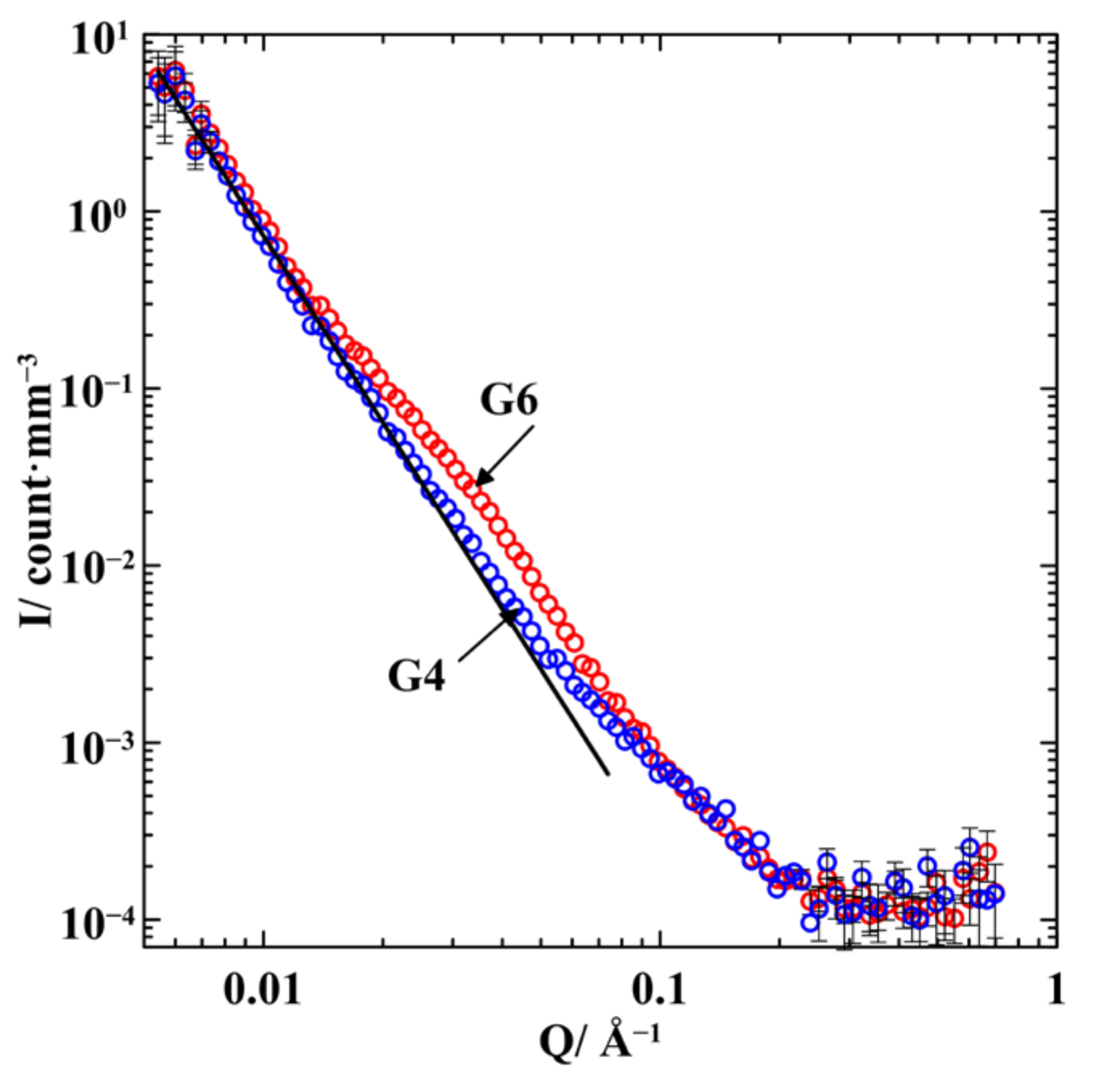
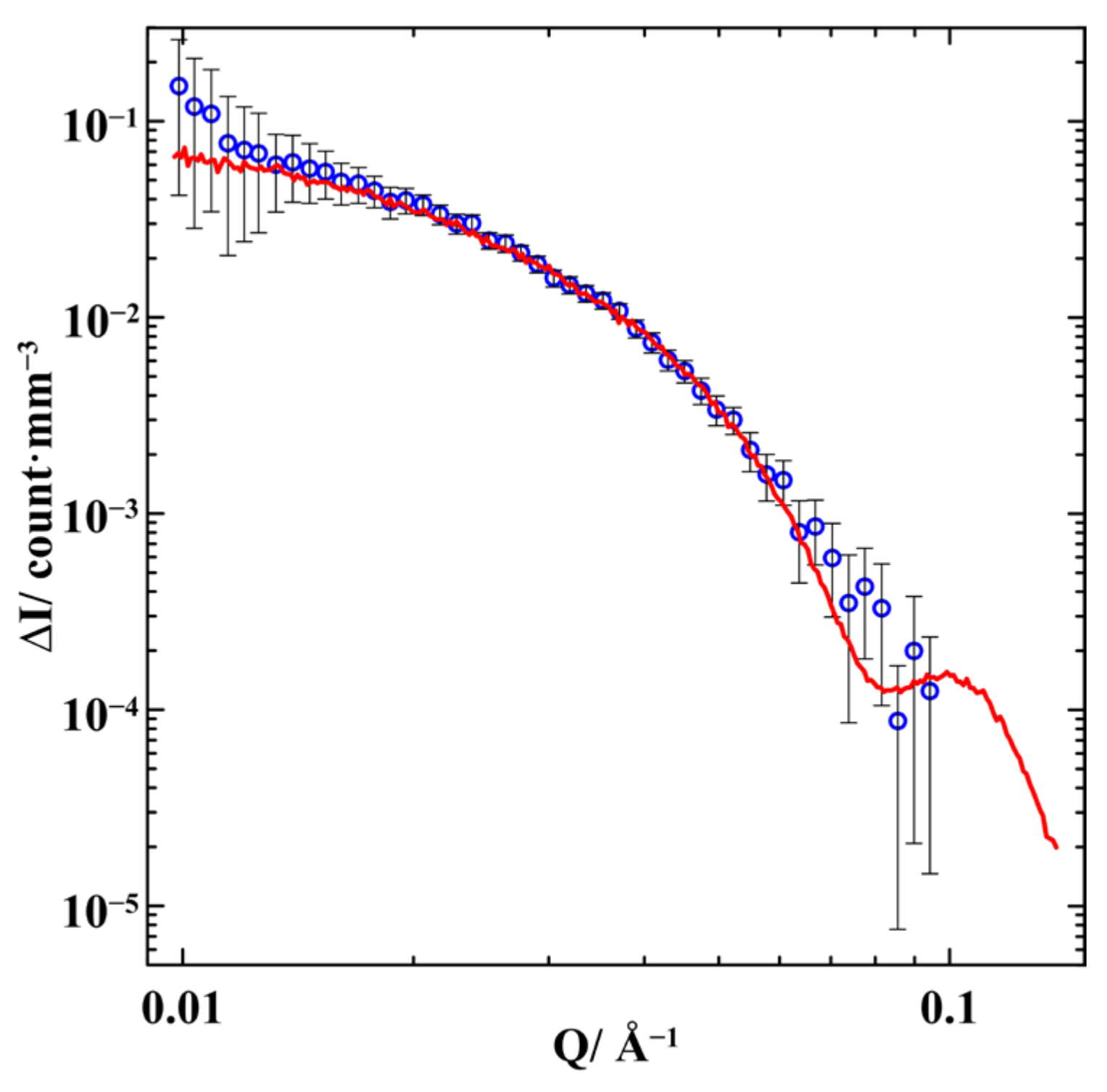
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Z.; Guo, Y.; Zong, Y.; Li, K.; Wang, S.; Cao, H.; Teng, C. Ga Based Particles, Alloys and Composites: Fabrication and Applications. Nanomaterials 2021, 11, 2246. [Google Scholar] [CrossRef] [PubMed]
- Bo, G.; Ren, L.; Xu, X.; Du, Y.; Dou, S. Recent progress on liquid metals and their applications. Adv. Phys. X 2018, 3, 1446359. [Google Scholar] [CrossRef] [Green Version]
- Xiong, Y.; Lu, X. Metallic Nanostructures. From Controlled Synthesis to Applications; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Noohi, Z.; Nosouhian, S.; Niroumand, B.; Timelli, G. Use of Low Melting Point Metals and Alloys (Tm < 420 °C) as Phase Change Materials: A Review. Metals 2022, 12, 945. [Google Scholar] [CrossRef]
- Song, H.; Kim, T.; Kang, S.; Jin, H.; Lee, K.; Yoon, H.J. Ga-Based Liquid Metal Micro/Nanoparticles: Recent Advances and Applications. Small 2019, 15, 1903391. [Google Scholar] [CrossRef]
- Akyildiz, K.; Kim, J.-H.; So, J.-H.; Koo, H.-J. Recent progress on micro- and nanoparticles of gallium-based liquid metals: From preparation to applications. J. Ind. Eng. Chem. 2022, 116, 120–141. [Google Scholar] [CrossRef]
- Won, P.; Jeong, S.; Majidi, C.; Ko, S.H. Recent advances in liquid-metal-based wearable electronics and materials. iScience 2021, 24, 102698. [Google Scholar] [CrossRef]
- Anderson, T.J.; Ansara, I. The Ga-In (Gallium-Indium) System. J. Phase Equilib. 1991, 12, 64–72. [Google Scholar] [CrossRef]
- Lu, H.M.; Shuai, J.; Meng, X.K. Size-Dependent Eutectic Temperature of Ag-Pb Alloy Nanoparticles. J. Nanosci. Nanotechnol. 2013, 13, 1480–1483. [Google Scholar] [CrossRef]
- Yasuda, H.; Mori, H. Phase diagrams in nanometer-sized alloy systems. J. Cryst. Growth 2002, 237, 234–238. [Google Scholar] [CrossRef]
- Schamp, C.T.; Jesser, W.A. Two-phase equilibrium in individual nanoparticles of Bi-Sn. Metall. Mater. Trans. A 2006, 37, 1825–1829. [Google Scholar] [CrossRef]
- Jesser, W.A.; Shneck, R.Z.; Gile, W.W. Solid-liquid equilibria in nanoparticles of Pb-Bi alloys. Phys. Rev. B 2004, 69, 13. [Google Scholar] [CrossRef]
- Shin, S.J.; Guzman, J.; Yuan, C.W.; Liao, C.Y.; Boswell-Koller, C.N.; Stone, P.R.; Dubon, O.D.; Minor, A.M.; Watanabe, M.; Beeman, J.W.; et al. Embedded Binary Eutectic Alloy Nanostructures: A New Class of Phase Change Materials. Nano Lett. 2010, 10, 2794–2798. [Google Scholar] [CrossRef]
- Likholetova, M.V.; Charnaya, E.V.; Shevchenko, E.V.; Lee, M.K.; Chang, L.-J.; Kumzerov, Y.A.; Fokin, A.V. Magnetic Studies of Superconductivity in the Ga-Sn Alloy Regular Nanostructures. Nanomaterials 2023, 13, 280. [Google Scholar] [CrossRef]
- Shevchenko, E.V.; Charnaya, E.V.; Lee, M.K.; Chang, L.-J.; Likholetova, M.V.; Lezova, I.E.; Kumzerov, Y.A.; Fokin, A.V. Superconductivity in a Ga-Ag nanocomposite with dendritic morphology. Physica C 2020, 574, 1353666. [Google Scholar] [CrossRef]
- Shevtsova, O.D.; Likholetova, M.V.; Charnaya, E.V.; Shevchenko, E.V.; Kumzerov, Y.A.; Fokin, A.V. Ac susceptibility of the superconducting porous glass/Ga−In−Sn nanocomposite. Phys. Solid State 2022, 64, 38–43. [Google Scholar] [CrossRef]
- Latysheva, E.N.; Pirozerskii, A.L.; Charnaya, E.V.; Kumzerov, Y.A.; Fokin, A.V.; Nedbai, A.I.; Bugaev, A.S. Polymorphism of Ga-In alloys in nanoconfinement conditions. Phys. Solid State 2015, 57, 131–135. [Google Scholar] [CrossRef]
- Podorozhkin, D.Y.; Tien, C.; Charnaya, E.V.; Lee, M.K.; Chang, L.J.; Michel, D.; Haase, J.; Kumzerov, Y.A. Slowdown of atomic diffusion in liquid gallium–indium alloy under different nanoconfinements. Physica B 2012, 407, 2063–2067. [Google Scholar] [CrossRef]
- Pirozerskii, A.L.; Charnaya, E.V.; Lee, M.K.; Chang, L.J.; Nedbai, A.I.; Kumzerov, Y.A.; Fokin, A.V.; Samoilovich, M.I.; Lebedeva, E.L.; Bugaev, A.S. Acoustic and NMR Investigations of Melting and Crystallization of Indium-Gallium Alloys in Pores of Synthetic Opal Matrices. Acoust. Phys. 2016, 62, 306–312. [Google Scholar] [CrossRef]
- Nefedov, D.Y.; Charnaya, E.V.; Uskov, A.V.; Antonenko, A.O.; Podorozhkin, D.Y.; Haase, J.; Kumzerov, Y.A.; Fokin, A.V. Stabilization of β-Ga structure in nanostructured Ga-In alloy. Appl. Magn. Reson. 2021, 52, 1721–1727. [Google Scholar] [CrossRef]
- Nefedov, D.Y.; Podorozhkin, D.Y.; Charnaya, E.V.; Uskov, A.V.; Haase, J.; Kumzerov, Y.A.; Fokin, A.V. Liquid-liquid transition in supercooled gallium alloys under nanoconfinement. J. Phys. Condens. Matter 2019, 31, 255101. [Google Scholar] [CrossRef]
- Uskov, A.V.; Charnaya, E.V.; Kuklin, A.I.; Lee, M.K.; Chang, L.J.; Kumzerov, Y.A.; Fokin, A.V. SANS Studies of the Gallium-Indium Alloy Structure within Regular Nanopores. Nanomaterials 2022, 12, 2245. [Google Scholar] [CrossRef] [PubMed]
- Feigin, L.A.; Svergun, D.I. Structure Analysis by Small-Angle X-ray and Neutron Scattering; Springer: New York, NY, USA, 1987. [Google Scholar]
- Mohammed, A.S.A.; Carino, A.; Testino, A.; Andalibi, M.R.; Cervellino, A. A dilute gold nanoparticle suspension as small-angle X-ray scattering standard for an absolute scale using an extended Guinier approximation. J. Appl. Crystallogr. 2019, 52, 344–350. [Google Scholar] [CrossRef] [Green Version]
- Sinha, S.K. 6. Small-Angle Scattering from Porous Materials. Exp. Methods Phys. Sci. 1999, 35, 223–262. [Google Scholar] [CrossRef]
- Hohr, A.; Neumann, H.B.; Schmidt, P.W.; Pfeifer, P.; Avnir, D. Fractal surface and cluster structure of controlled-pore glasses and Vycor porous glass as revealed by small-angle x-ray and neutron scattering. Phys. Rev. B 1988, 38, 1462–1467. [Google Scholar] [CrossRef]
- Rauch, H.; Waschkowski, W. Neutron Scattering Lengths in ILL Neutron Data Booklet, 2nd ed.; Dianoux, A.-J., Lander, G., Eds.; Old City Publishing: Philidelphia, PA, USA, 2003. [Google Scholar]
- Ivicheva, S.N.; Amarantov, S.V.; Kargin, Y.F.; Volkov, V.V. Structural Parameters of Ordered Nanocomposites Based on Opal Matrices in Accordance with the Data of Small-Angle X-ray and Neutron Scattering: Simulation of Structural and Size Dispersion Characteristics of Nanocomposites. Part II. Nanotechnol. Russ. 2018, 13, 565–577. [Google Scholar] [CrossRef]
- Pötschke, D.; Ballauff, M.; Lindner, P.; Fischer, M.; Vögtle, F. Analysis of the Structure of Dendrimers in Solution by Small-Angle Neutron Scattering Including Contrast Variation. Macromolecules 1999, 32, 4079–4087. [Google Scholar] [CrossRef]
- Aronson, B.J.; Blanford, C.F.; Stein, A. Solution-Phase Grafting of Titanium Dioxide onto the Pore Surface of Mesoporous Silicates: Synthesis and Structural Characterization. Chem. Mater. 1997, 9, 2842–2851. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uskov, A.V.; Charnaya, E.V.; Kuklin, A.I.; Lee, M.K.; Chang, L.-J.; Kumzerov, Y.A.; Fokin, A.V. Ga-In Alloy Segregation within a Porous Glass as Studied by SANS. Nanomaterials 2023, 13, 1357. https://doi.org/10.3390/nano13081357
Uskov AV, Charnaya EV, Kuklin AI, Lee MK, Chang L-J, Kumzerov YA, Fokin AV. Ga-In Alloy Segregation within a Porous Glass as Studied by SANS. Nanomaterials. 2023; 13(8):1357. https://doi.org/10.3390/nano13081357
Chicago/Turabian StyleUskov, Andrei V., Elena V. Charnaya, Aleksandr I. Kuklin, Min Kai Lee, Lieh-Jeng Chang, Yurii A. Kumzerov, and Aleksandr V. Fokin. 2023. "Ga-In Alloy Segregation within a Porous Glass as Studied by SANS" Nanomaterials 13, no. 8: 1357. https://doi.org/10.3390/nano13081357
APA StyleUskov, A. V., Charnaya, E. V., Kuklin, A. I., Lee, M. K., Chang, L.-J., Kumzerov, Y. A., & Fokin, A. V. (2023). Ga-In Alloy Segregation within a Porous Glass as Studied by SANS. Nanomaterials, 13(8), 1357. https://doi.org/10.3390/nano13081357





