Multipole Excitations and Nonlocality in 1d Plasmonic Nanostructures
Abstract
1. Introduction
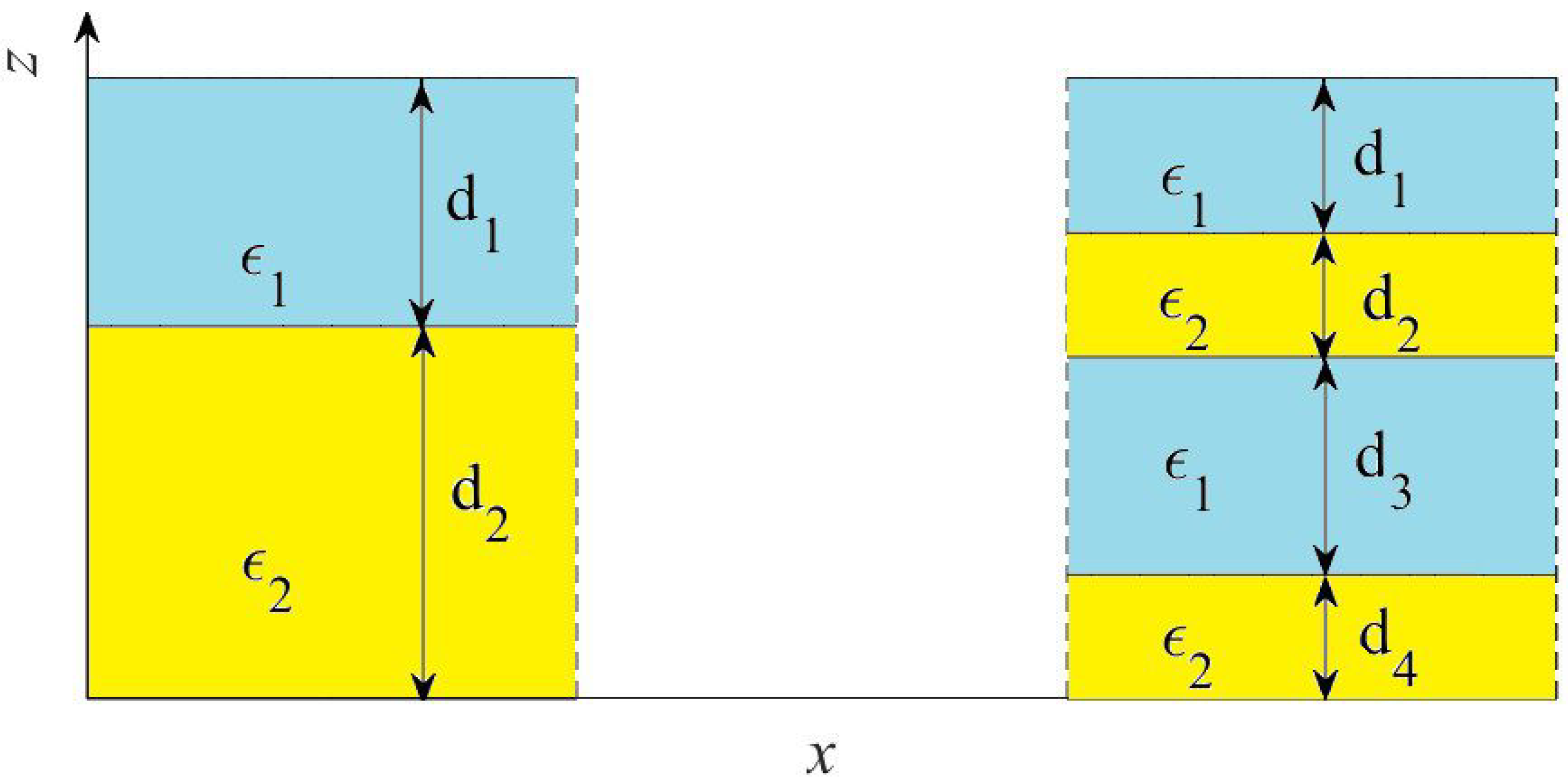
2. Geometry and Assumptions
- (1)
- We deal with nonmagnetic, homogeneous, isotropic dielectric, and plasmonic layers. Although multipolar excitations can occur in all-dielectric nanostructures due to retardation effects, this usually takes place at sizes where the long-wavelength multipole expansion is no longer accurate. In contrast, in plasmonic multilayered nanostructures strong optical nonlocality can occur for moderate size unit cells as a result from excitation of surface plasmon polaritons (SPPs). Currently, plasmonic MMs offer rich opportunities to control the light intensity and polarization, as well as the near-field heat transfer and local density of states on the subwavelength scale [26,27].
- (2)
- We neglect intrinsic nonlocality of constituent layers. It means that the vectors of the electric displacement and magnetic fields D and H at any point of space can be written in terms of the spatially averaged electric and induction fields, E and B, at the same point. It is necessary to keep in mind that in some cases, especially for thin metal layers and gaps, the local response model for their permittivity may become inaccurate [28,29,30].
- (3)
- To reduce the number of material parameters, we deal only with two-phase MMs. It implies that if the filling factors of the constituents 1 and 2 are and , respectively, it is always . At the same time, multiphase MMs with arbitrary number of different phases within unit cell can be studied using our technique.
- (4)
- For simplicity, only microgeometries with two-layer and four-layer unit cells are considered as shown in Figure 1. We note that any three-layer microgeometry cannot be realized when dealing with 1d two-phase MMs.
- (5)
- Herein, we limit ourselves to considering only the fundamental mode, which propagates along the interfaces () with the electric field, oriented along the optical axis (TM polarization). This means that we consider only one diagonal component () of the nonlocal effective permittivity tensor . Thus, in what follows we implicitly assume that . This choice is not accidental. It is motivated by the fact that this component can vary in wide limits, that gives rise to numerous potential applications [31,32,33,34].
3. Formalism and Techniques Used
4. Simulation Results
4.1. Material Parameters
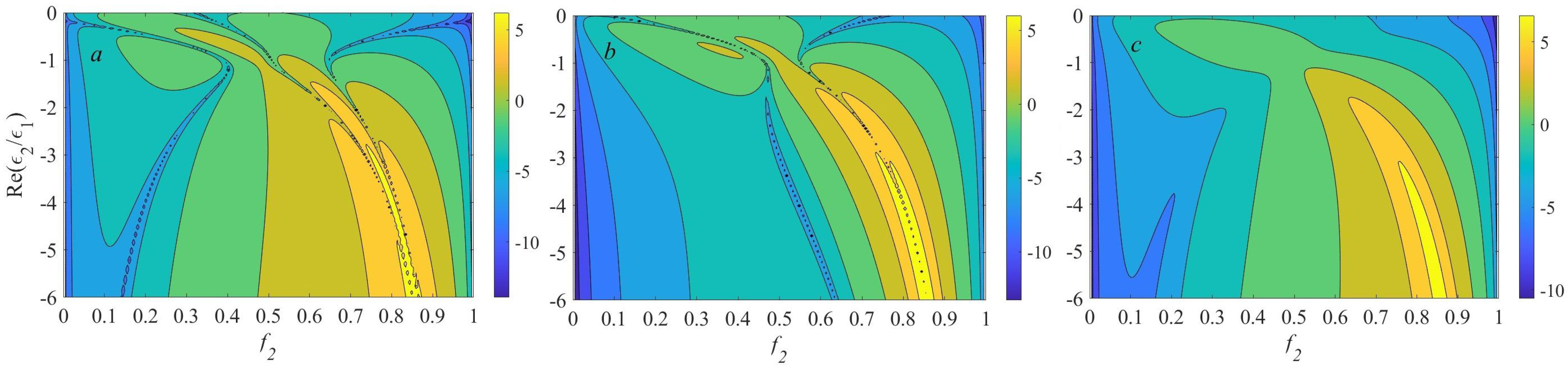
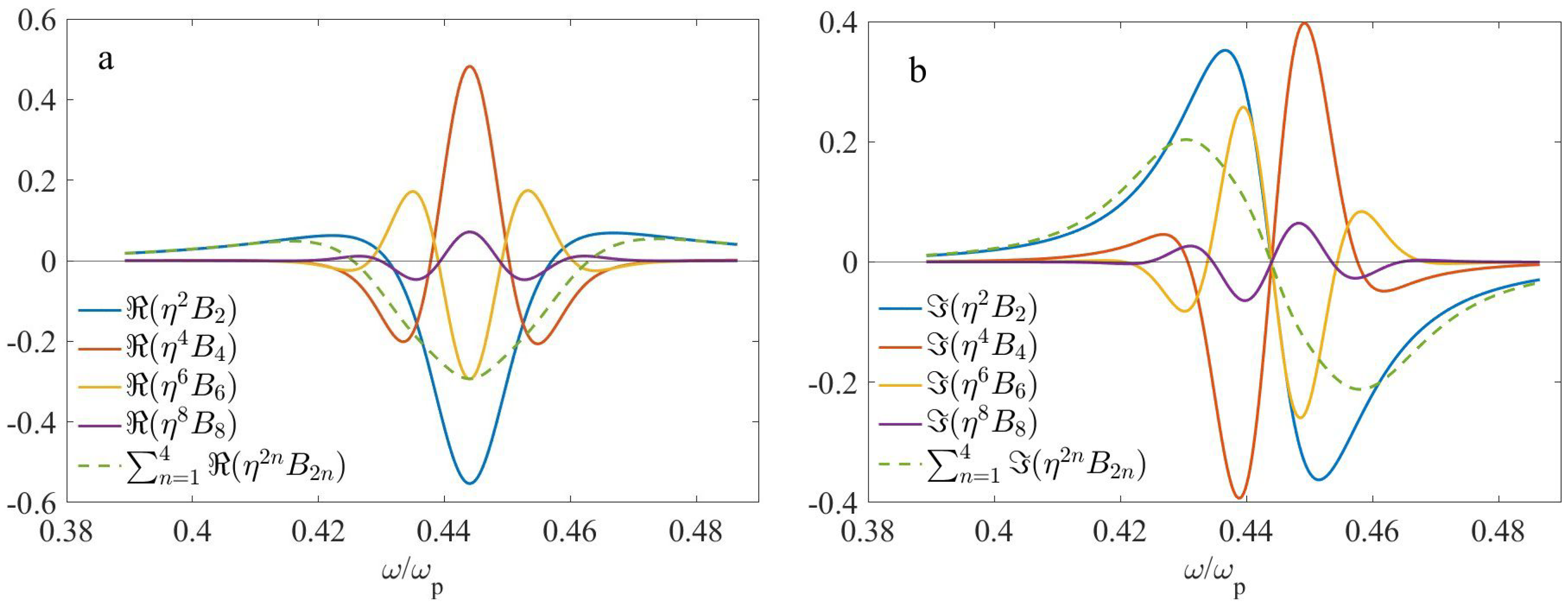
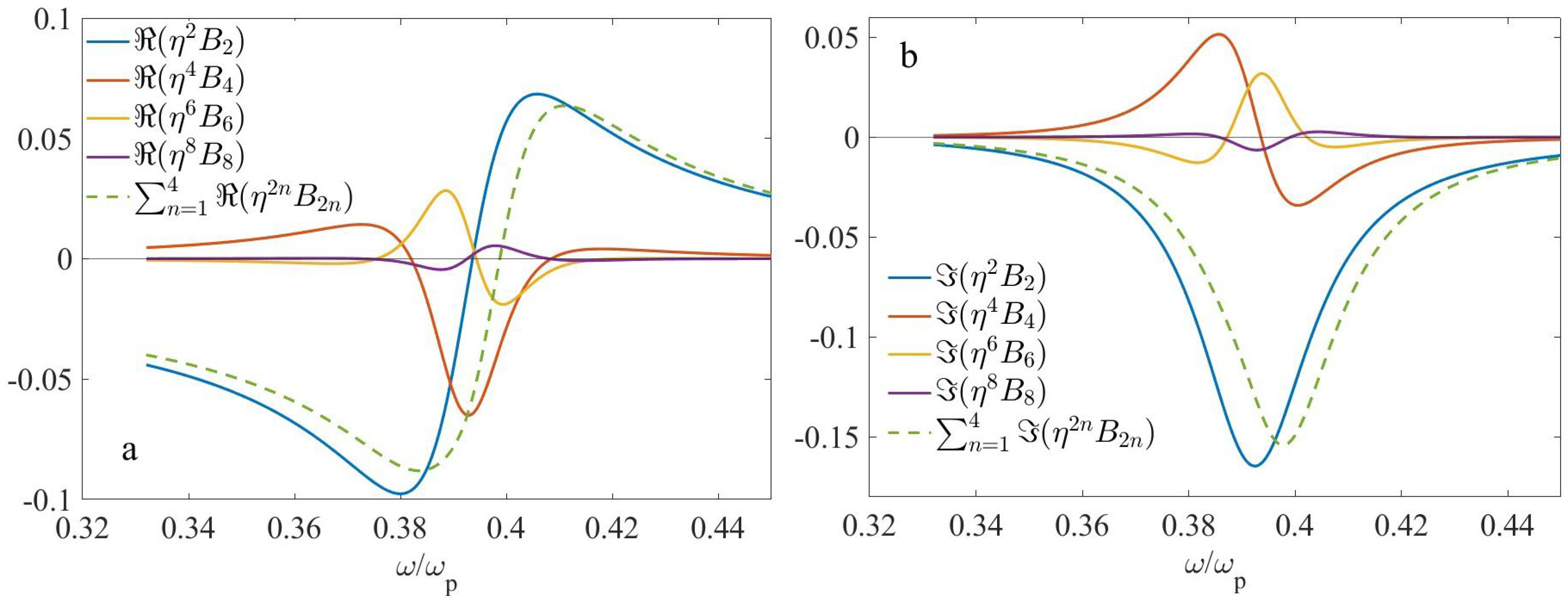
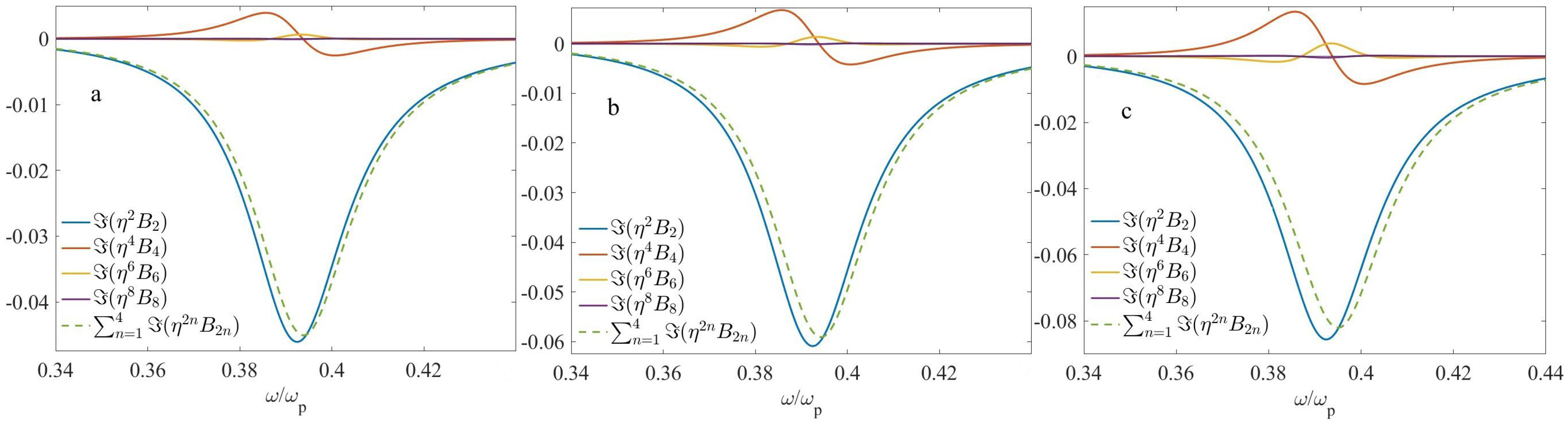
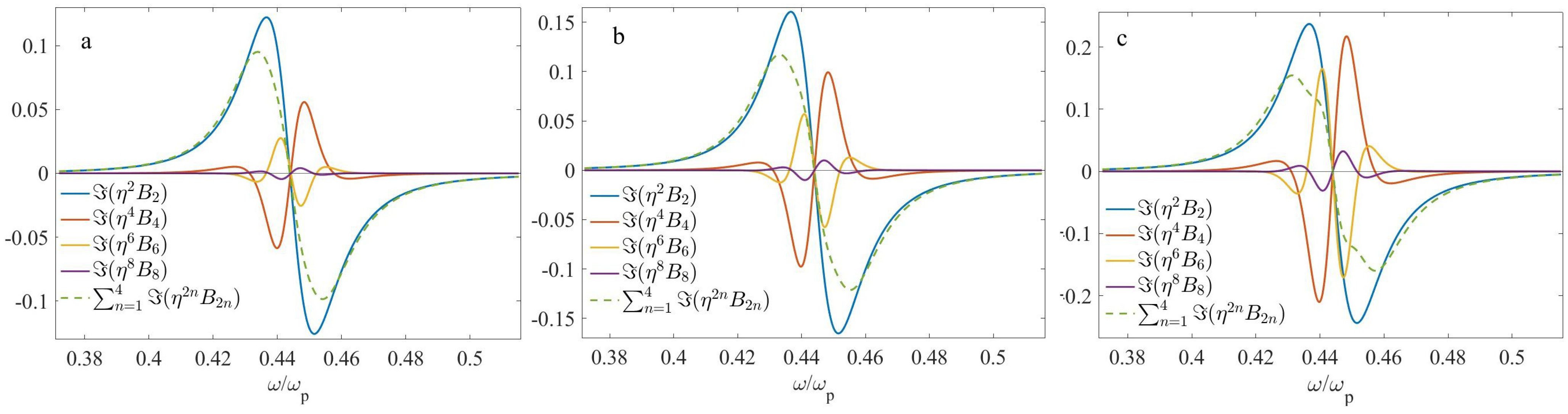
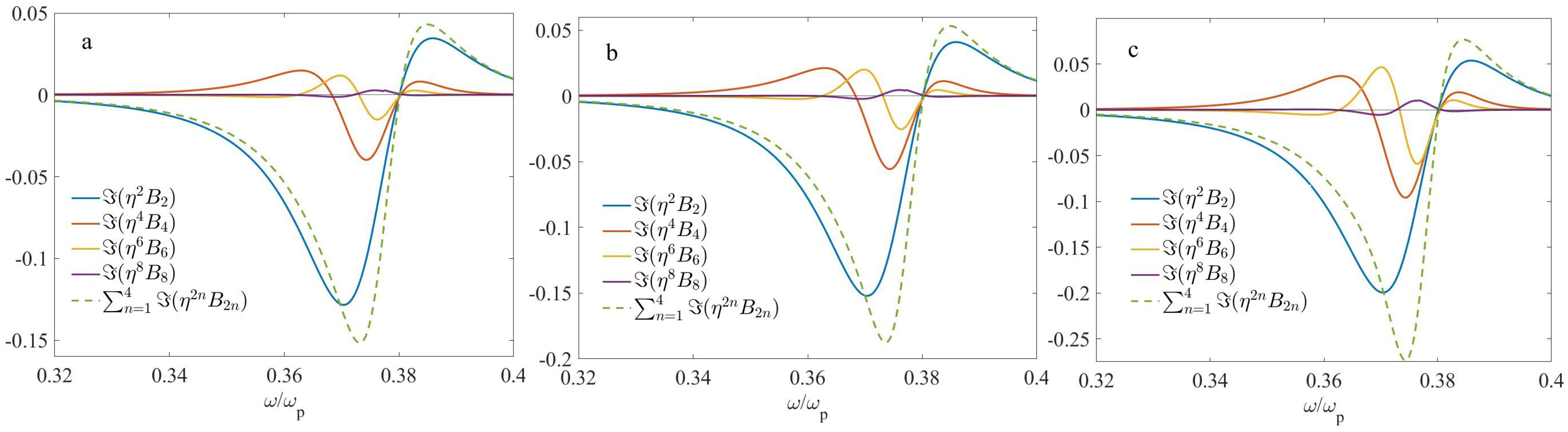
4.2. Two-Layer Microgeometry
4.3. Four-Layer Microgeometry
5. Discussion
6. Conclusions
- (1)
- When the dielectric phase content prevails (), particular nonlocal terms can be large, but overall nonlocality can be moderate due to their mutual compensation.
- (2)
- When , symmetry of the term is opposite to that of other nonlocal contribution terms under consideration.
- (3)
- When the plasmonic phase content prevails (), strong nonlocality can occur.
- (4)
- The spectra of multipolar excitations of the MMs with four-layer unit cell reproduce main features of MMs with two-layer unit cell, but nonlocality in the former case is weaker.
- (5)
- Higher asymmetry in four-layer arrangements enhances nonlocality.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ED | electric dipole |
| MD | magnetic dipole |
| EQ | electric quadrupole |
| MQ | magnetic quadrupole |
| EO | electric octopole |
| MM | Metamaterial |
| SPP | surface plasmon polariton |
| TMM | transfer matrix method |
| IR | infrared |
| 1d | one-dimensional |
Appendix A
References
- Draine, B.T.; Flatau, P.J. Discrete-dipole approximation for periodic targets: Theory and tests. J. Opt. Soc. Am. A 2008, 25, 2693–2703. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Kivshar, Y.S. Multipolar interference effects in nanophotonics. Phil. Trans. R. Soc. A 2017, 375, 20160317. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Kivshar, Y.S. Generalized Kerker effects in nanophotonics and meta-optics. Opt. Exp. 2018, 26, 13085–13105. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Wang, G.P.; Zhang, S. A nonlocal effective medium description of topological Weyl metamaterials. Laser Photon. Rev. 2021, 15, 2100129. [Google Scholar] [CrossRef]
- Yu, C.Y.; Zeng, Q.C.; Yu, C.J.; Han, C.Y.; Wang, C.M. Scattering analysis and efficiency optimization of dielectric Pancharatnam–Berry-Phase metasurfaces. Nanomaterials 2021, 11, 586. [Google Scholar] [CrossRef]
- Ziolkowski, R.W. Mixtures of multipoles—should they be in your EM toolbox? IEEE Open J. Ant. Propag. 2022, 3, 154–188. [Google Scholar] [CrossRef]
- Raab, R.E.; de Lange, O.L. Symmetry constraints for electromagnetic constitutive relations. J. Opt. Pure Appl. Opt. 2001, 3, 446–451. [Google Scholar] [CrossRef]
- De Lange, O.L.; Raab, R.E. Completion of multipole theory for the electromagnetic response fields D and H. Proc. R. Soc. Lond. A 2003, 459, 1325–1337. [Google Scholar] [CrossRef]
- Raab, R.E.; de Lange, O.L. Transformed multipole theory of the response fields D and H to electric octopole-magnetic quadrupole order. Proc. R. Soc. Lond. A 2005, 461, 595–608. [Google Scholar] [CrossRef]
- Luk’yanchuk, B.; Zheludev, N.I.; Maier, S.A.; Halas, N.J.; Nordlander, P.; Giessen, H.; Chong, C.T. The Fano resonance in plasmonic nanostructures and metamaterials. Nature Mater. 2010, 9, 707–714. [Google Scholar] [CrossRef]
- Cho, D.J.; Wang, F.; Zhang, X.; Shen, Y.R. Contribution of the electric quadrupole resonance in optical metamaterials. Phys. Rev. B 2008, 78, 121101. [Google Scholar] [CrossRef]
- Alu, A.; Engheta, N. Guided propagation along quadrupolar chains of plasmonic nanoparticles. Phys. Rev. B 2009, 79, 235412. [Google Scholar] [CrossRef]
- Grahn, P.; Shevchenko, A.; Kaivola, M. Electromagnetic multipole theory for optical nanomaterials. New J. Phys. 2012, 14, 093033. [Google Scholar] [CrossRef]
- Silveirinha, M. Boundary conditions for quadrupolar metamaterials. New J. Phys. 2014, 16, 083042. [Google Scholar] [CrossRef]
- Wells, B.; Kudyshev, Z.A.; Litchinitser, N.; Podolskiy, V.A. Nonlocal effects in transition hyperbolic metamaterials. ACS Photon. 2017, 4, 2470–2478. [Google Scholar] [CrossRef]
- Lim, W.X.; Han, S.; Gupta, M.; MacDonald, K.F.; Singh, R. Near-infrared linewidth narrowing in plasmonic Fano-resonant metamaterials via tuning of multipole contributions. Appl. Phys. Lett. 2017, 111, 061104. [Google Scholar] [CrossRef]
- Dirdal, C.A.; Hågenvik, H.O.; Haave, H.A.; Skaar, J. Higher order multipoles in metamaterial homogenization. IEEE Trans. Antennas Propag. 2018, 66, 6403–6407. [Google Scholar] [CrossRef]
- Babicheva, V.E.; Evlyukhin, A.B. Analytical model of resonant electromagnetic dipole-quadrupole coupling in nanoparticle arrays. Phys. Rev. B 2019, 99, 195444. [Google Scholar] [CrossRef]
- Mun, J.; So, S.; Jang, J.; Rho, J. Describing meta-atoms using the exact higher-order polarizability tensors. ACS Photon. 2020, 7, 1153–1162. [Google Scholar] [CrossRef]
- Liu, F.; Peng, P.; Du, Q.J.; Ke, M. Effective medium theory for photonic crystals with quadrupole resonances. Opt. Lett. 2021, 46, 4597–4600. [Google Scholar] [CrossRef]
- Rahimzadegan, A.; Karamanos, T.D.; Alaee, R.; Lamprianidis, A.G.; Beutel, D.; Boyd, R.W.; Rockstuhl, B. A comprehensive multipolar theory for periodic metasurfaces. Adv. Opt. Mater. 2022, 10, 2102059. [Google Scholar] [CrossRef]
- Xia, S.X.; Zhai, X.; Huang, Y.; Wang, L.L.; Wen, S.C. Multi-band perfect plasmonic absorptions using rectangular graphene gratings. Opt. Lett. 2017, 42, 3052–3055. [Google Scholar] [CrossRef] [PubMed]
- Xia, S.X.; Zhai, X.; Wang, L.L.; Wen, S.C. Plasmonically induced transparency in double-layered graphene nanoribbons. Photon. Res. 2018, 6, 692–702. [Google Scholar] [CrossRef]
- Xia, S.; Zhai, X.; Wang, L.; Xiang, Y.; Wen, S. Plasmonically induced transparency in phase-coupled graphene nanoribbons. Phys. Rev. B 2022, 106, 075401. [Google Scholar] [CrossRef]
- Castaldi, G.; Alu, A.; Galdi, V. Boundary effects of weak nonlocality in multilayered dielectric metamaterials. Phys. Rev. Appl. 2018, 10, 034060. [Google Scholar] [CrossRef]
- Boriskina, S.V.; Tong, J.K.; Zhou, J.; Chiloyan, V.; Chen, G. Enhancement and tunability of near-field radiative heat transfer mediated by surface plasmon polaritons in thin plasmonic films. Photonics 2015, 2, 659–683. [Google Scholar] [CrossRef]
- Wang, P.; Krasavin, A.V.; Liu, L.; Jiang, Y.; Li, Z.; Guo, X.; Tong, L.; Zayats, A.V. Molecular plasmonics with metamaterials. Chem. Phys. 2022, 122, 15031–15081. [Google Scholar] [CrossRef]
- Garcia de Abajo, F.J. Nonlocal effects in the plasmons of strongly interacting nanoparticles, dimers, and waveguides. J. Phys. Chem. 2008, 112, 17983–17987. [Google Scholar] [CrossRef]
- Moreau, A.; Ciraci, C.; Smith, D.R. Impact of nonlocal response on metallodielectric multilayers and optical patch antennas. Phys. Rev. B 2013, 87, 045401. [Google Scholar] [CrossRef]
- Benedicto, J.; Polles, R.; Ciraci, C.; Centeno, E.; Smith, D.R.; Moreau, A. Numerical tool to take nonlocal effects into account in metallo-dielectric multilayers. J. Opt. Soc. Am. A 2015, 32, 1581–1588. [Google Scholar] [CrossRef]
- Goncharenko, A.V.; Venger, E.F.; Pinchuk, A.O. Homogenization of quasi-1d metamaterials and the problem of extended bandwidth. Opt. Exp. 2014, 22, 2429–2442. [Google Scholar] [CrossRef] [PubMed]
- Hemmati, F.; Magnusson, R. Applicability of Rytov’s full effective-medium formalism to the physical description and design of resonant metasurfaces. ACS Photon. 2020, 7, 3177–3187. [Google Scholar] [CrossRef]
- Goncharenko, A.V.; Fitio, V.; Silkin, V. Broadening the absorption bandwidth based on heavily doped semiconductor nanostructures. Opt. Exp. 2022, 30, 472788. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Lin, Y.; Yu, K.W.; Wang, G.P. All-angle broadband ENZ metamaterials. New J. Phys. 2022, 24, 073016. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Electrodynamics of Continuous Media. In Course of Theoretical Physics; Elsevier: Oxford, UK, 2004; Volume 8. [Google Scholar]
- Lalanne, J.; Lemercier-Lalanne, D. On the effective medium theory of subwavelength periodic structures. J. Mod. Opt. 1996, 43, 2063–2085. [Google Scholar] [CrossRef]
- Li, L. Effective-medium permittivity of one-dimensional gratings of vertically invariant and laterally arbitrary permittivity distribution. J. Mod. Opt. 2019, 66, 850–856. [Google Scholar] [CrossRef]
- Skaar, J.; Hågenvik, H.O.; Dirdal, C.A. Four definitions of magnetic permeability for periodic metamaterials. Phys. Rev. B 2019, 99, 064407. [Google Scholar] [CrossRef]
- Forcella, D.; Prada, C.; Carminati, R. Causality, nonlocality, and negative refraction. Phys. Rev. Lett. 2017, 118, 134301. [Google Scholar] [CrossRef]
- Pitarke, J.M.; Silkin, V.M.; Chulkov, E.V.; Echenique, P.M. Theory of surface plasmons and surface-plasmon polaritons. Rep. Prog. Phys. 2007, 70, 1–87. [Google Scholar] [CrossRef]
- Yeh, P.; Yariv, A.; Hong, C.S. Electromagnetic propagation in periodic stratified media. I. General theory. J. Opt. Soc. Am. 1977, 67, 423–438. [Google Scholar] [CrossRef]
- Wang, A.; Yin, C.; Cao, Z. Progress in Planar Optical Waveguides (Springer Tracts in Modern Physics; Springer-Verlag GmbH: Berlin, Germany; Shanghai Jiao Tong University Press: Shanghai, China, 2008; Volume 266. [Google Scholar]
- Sun, L.; Yang, X.; Gao, J. Analysis of nonlocal effective permittivity and permeability in symmetric metal–dielectric multilayer metamaterials. J. Opt. 2016, 18, 065101. [Google Scholar] [CrossRef]
- Rytov, S.M. Electromagnetic properties of a finely stratified medium. Sov. Phys. JETP 1956, 2, 466–475. [Google Scholar]
- Naik, C.V.; Shalaev, V.M.; Boltasseva, A. Alternative plasmonic materials: Beyond gold and silver. Adv. Mater. 2013, 25, 3264–3294. [Google Scholar] [CrossRef]
- Feigenbaum, E.; Diest, K.; Atwater, H.A. Unity-order index change in transparent conducting oxides at visible grequencies. Nano Lett. 2010, 10, 2111–2116. [Google Scholar] [CrossRef] [PubMed]
- Helseth, L.E. Tunable plasma response of a metal/ferromagnetic composite material. Phys. Rev. B 2005, 72, 033409. [Google Scholar] [CrossRef]
- Wu, Y.; Ou, P.; Zhang, L.; Lin, Y.; Yang, J. Controlling the null photonic gap and zero refractive index in photonic superlattices with temperature-controllable-refractive-index materials. J. Opt. Soc. Am. B 2020, 37, 1008–1020. [Google Scholar] [CrossRef]
| Label | ||||||
|---|---|---|---|---|---|---|
| 0.25 | 0.2 | 0.25 | 0.3 | 0.005 | a | |
| 0.5 | 0.25 | 0.15 | 0.25 | 0.35 | 0.02 | b |
| 0.25 | 0.1 | 0.25 | 0.4 | 0.045 | c |
| Label | ||||||
|---|---|---|---|---|---|---|
| 0.4 | 0.1 | 0.3 | 0.2 | 0.05 | a | |
| 0.3 | 0.5 | 0.1 | 0.2 | 0.2 | 0.09 | b |
| 0.6 | 0.1 | 0.1 | 0.2 | 0.17 | c |
| Label | ||||||
|---|---|---|---|---|---|---|
| 0.2 | 0.3 | 0.25 | 0.25 | 0.005 | a | |
| 0.55 | 0.2 | 0.35 | 0.25 | 0.2 | 0.015 | b |
| 0.2 | 0.4 | 0.25 | 0.15 | 0.035 | c |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goncharenko, A.V.; Silkin, V.M. Multipole Excitations and Nonlocality in 1d Plasmonic Nanostructures. Nanomaterials 2023, 13, 1395. https://doi.org/10.3390/nano13081395
Goncharenko AV, Silkin VM. Multipole Excitations and Nonlocality in 1d Plasmonic Nanostructures. Nanomaterials. 2023; 13(8):1395. https://doi.org/10.3390/nano13081395
Chicago/Turabian StyleGoncharenko, Anatoliy V., and Vyacheslav M. Silkin. 2023. "Multipole Excitations and Nonlocality in 1d Plasmonic Nanostructures" Nanomaterials 13, no. 8: 1395. https://doi.org/10.3390/nano13081395
APA StyleGoncharenko, A. V., & Silkin, V. M. (2023). Multipole Excitations and Nonlocality in 1d Plasmonic Nanostructures. Nanomaterials, 13(8), 1395. https://doi.org/10.3390/nano13081395






