Magnetostrictive and Magnetoactive Effects in Piezoelectric Polymer Composites
Abstract
:1. Introduction
1.1. Magnetostrictive Composites
1.2. Magnetoactive Composites
2. Coexistence of the Magnetostrictive and Magnetoactive ME Effects
3. Superposition of the Effects: Qualitative View
4. Energy Functional of the Composite Film
- For CFO: Gauss, applied magnetic field kOe, anisotropy field kOe, reference magnetostriction coefficient ppm, dielectric permeability , Young modulus GPa, Poisson coefficient .
- For PVDF: dielectric permeability , Young modulus GPa, Poisson coefficient ; the piezocoefficients are , , in CGS units. The particle radius is set to nm.
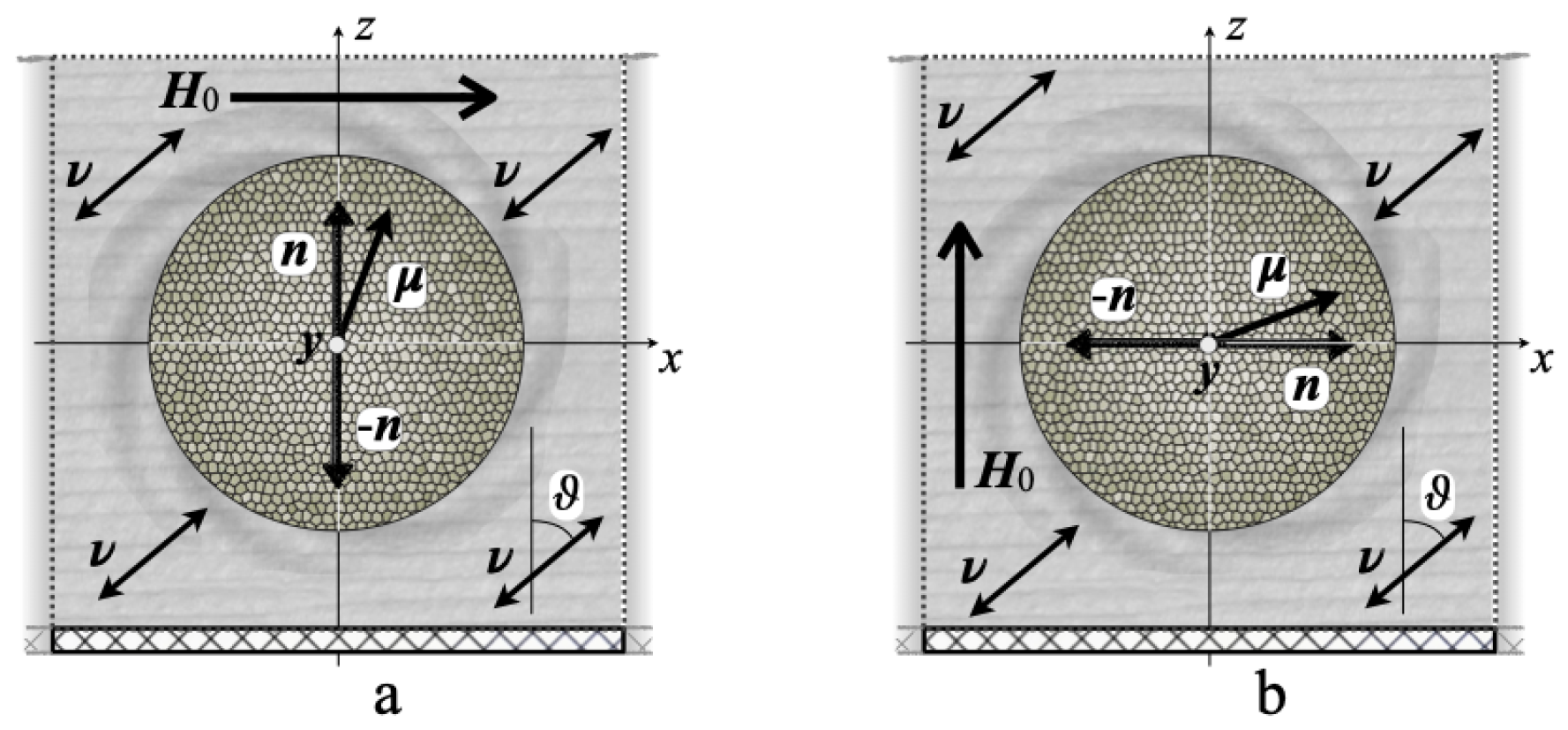
5. Finite-Element Calculation
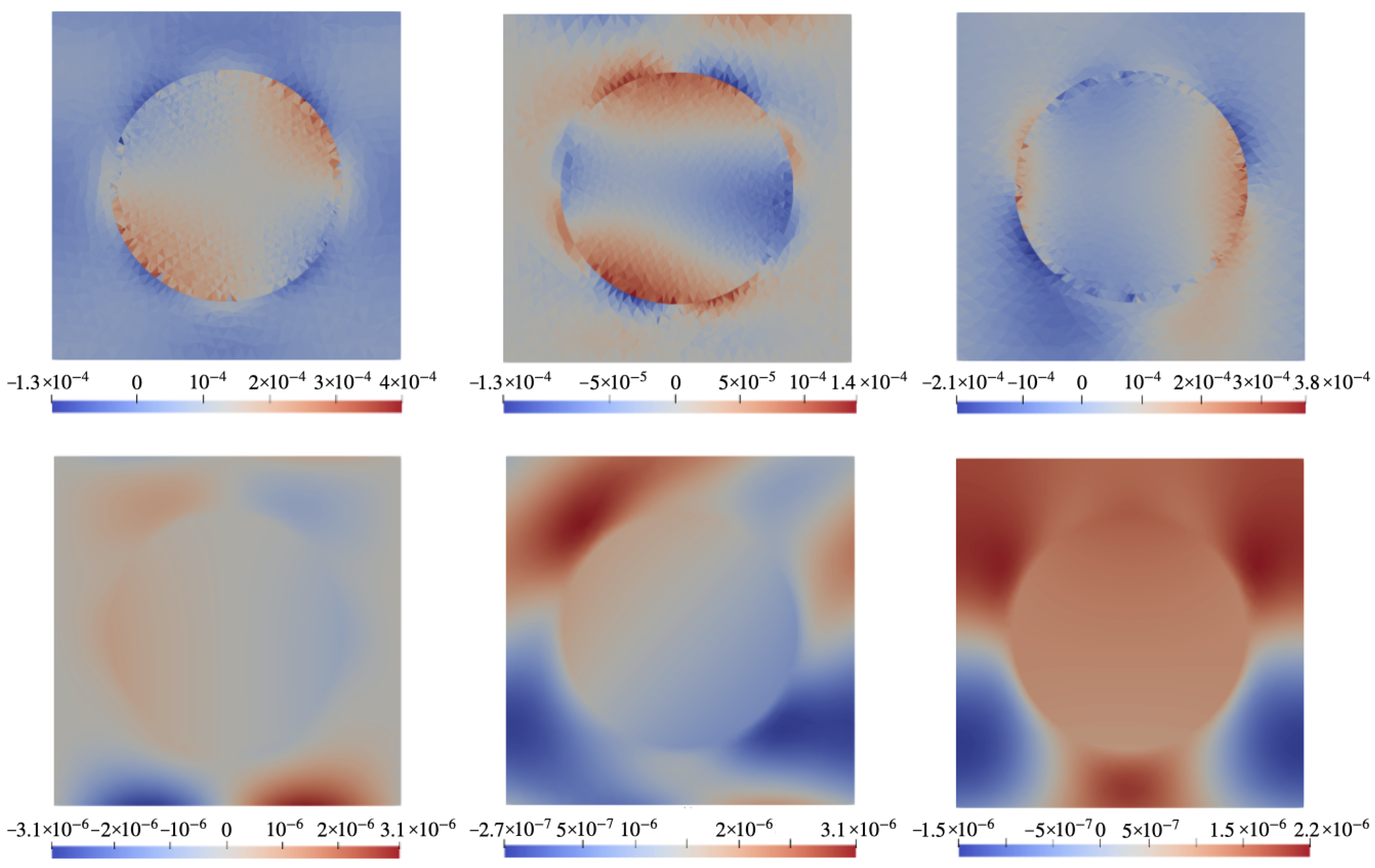
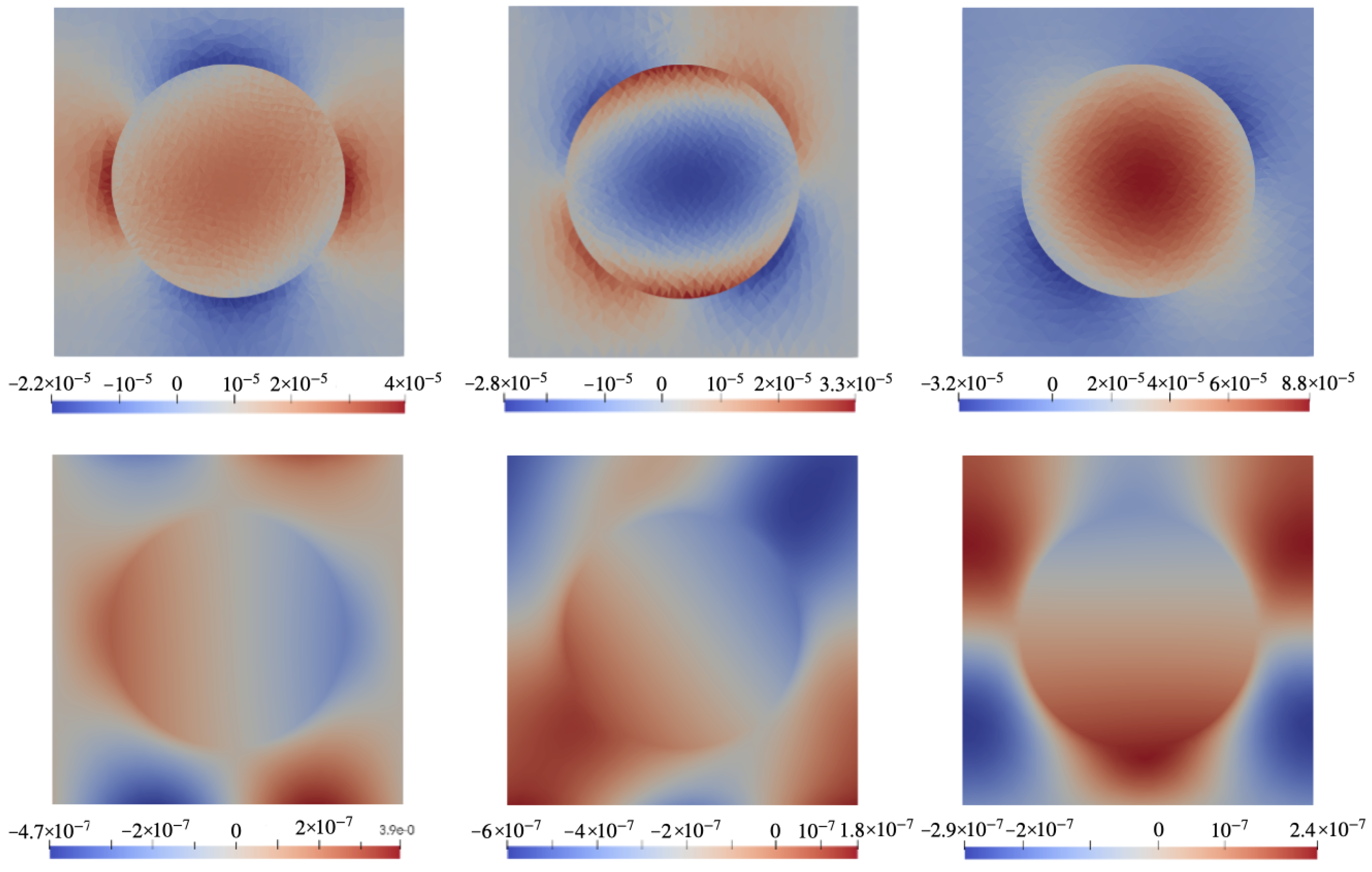
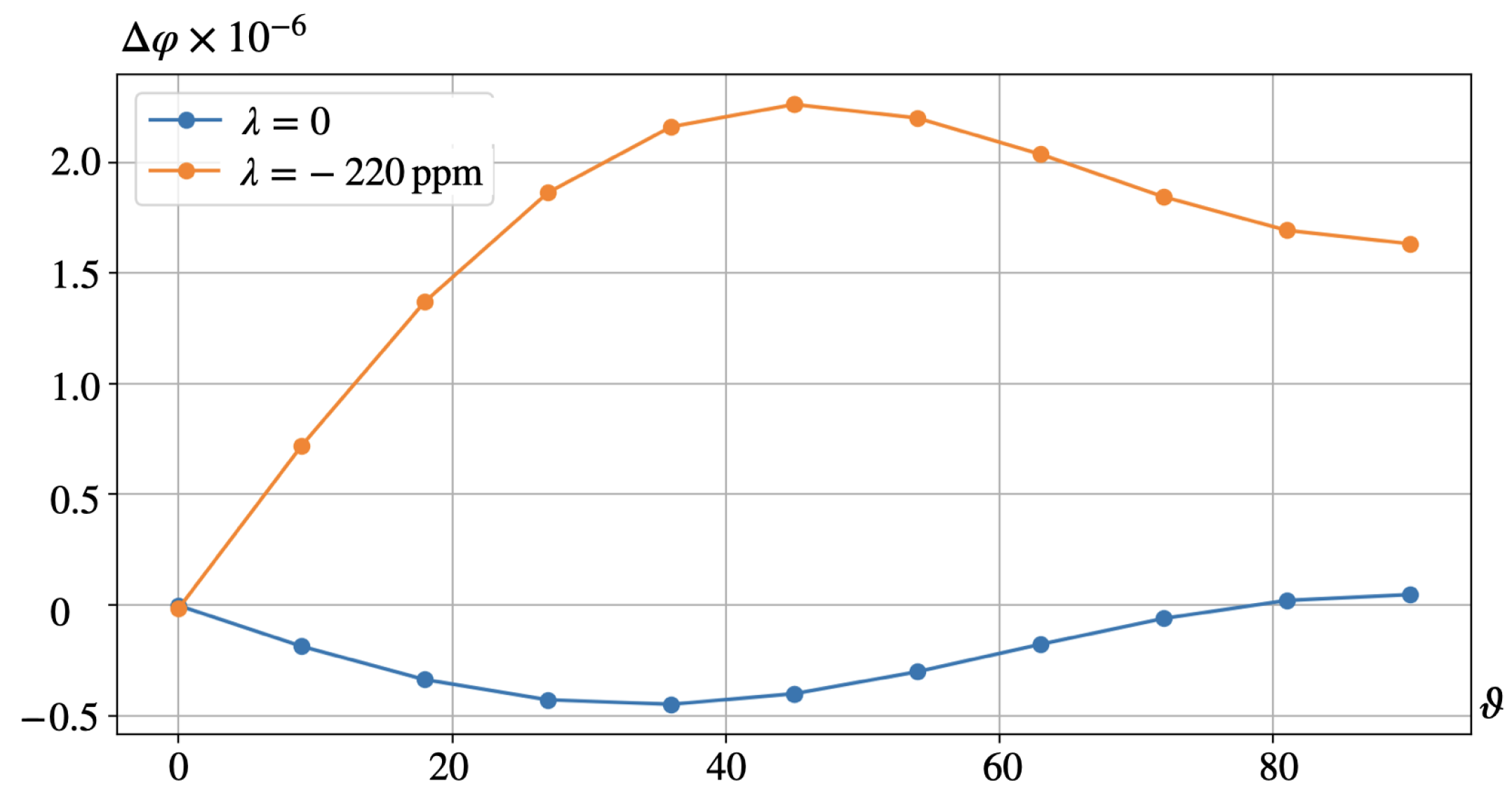
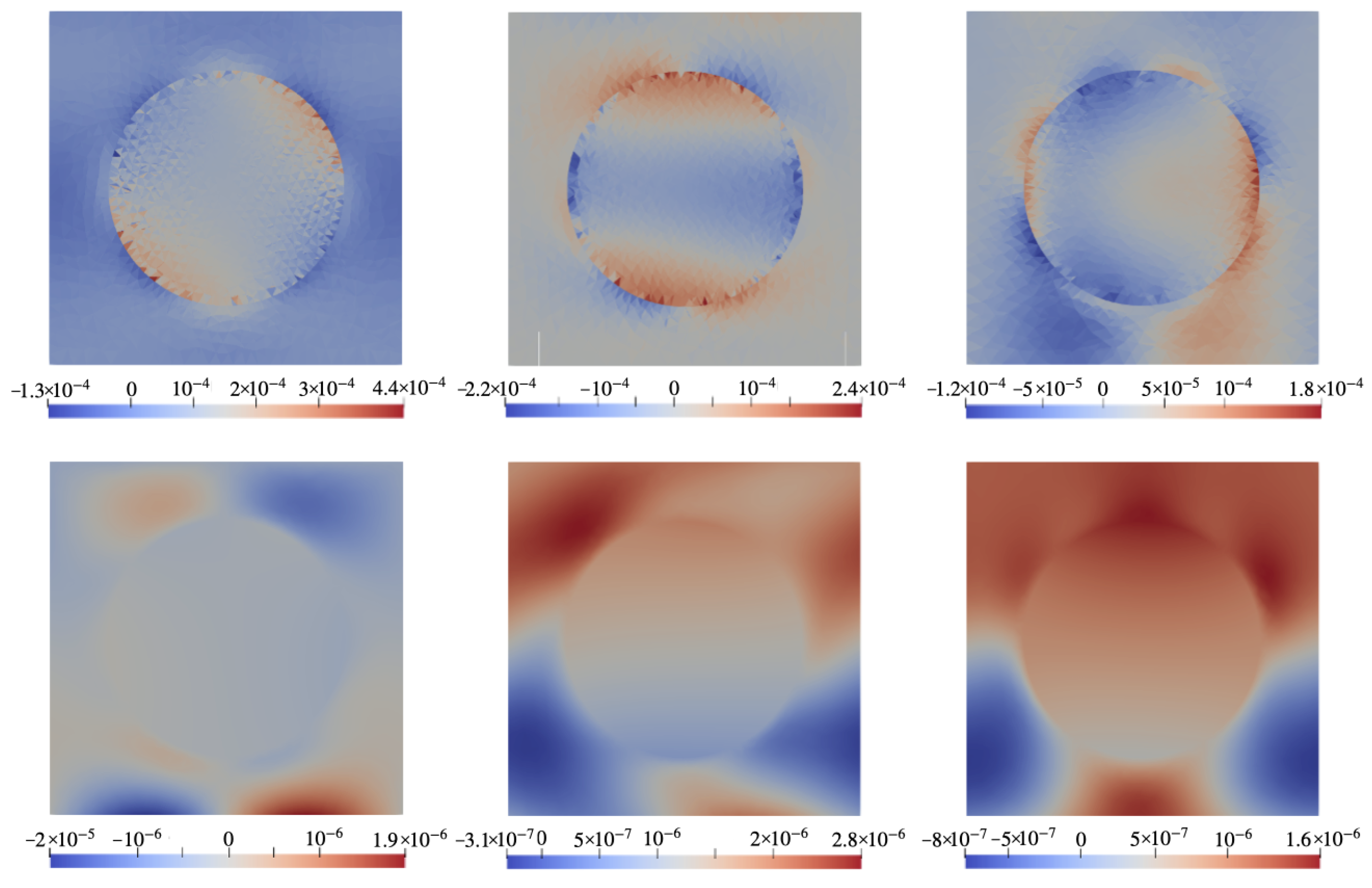
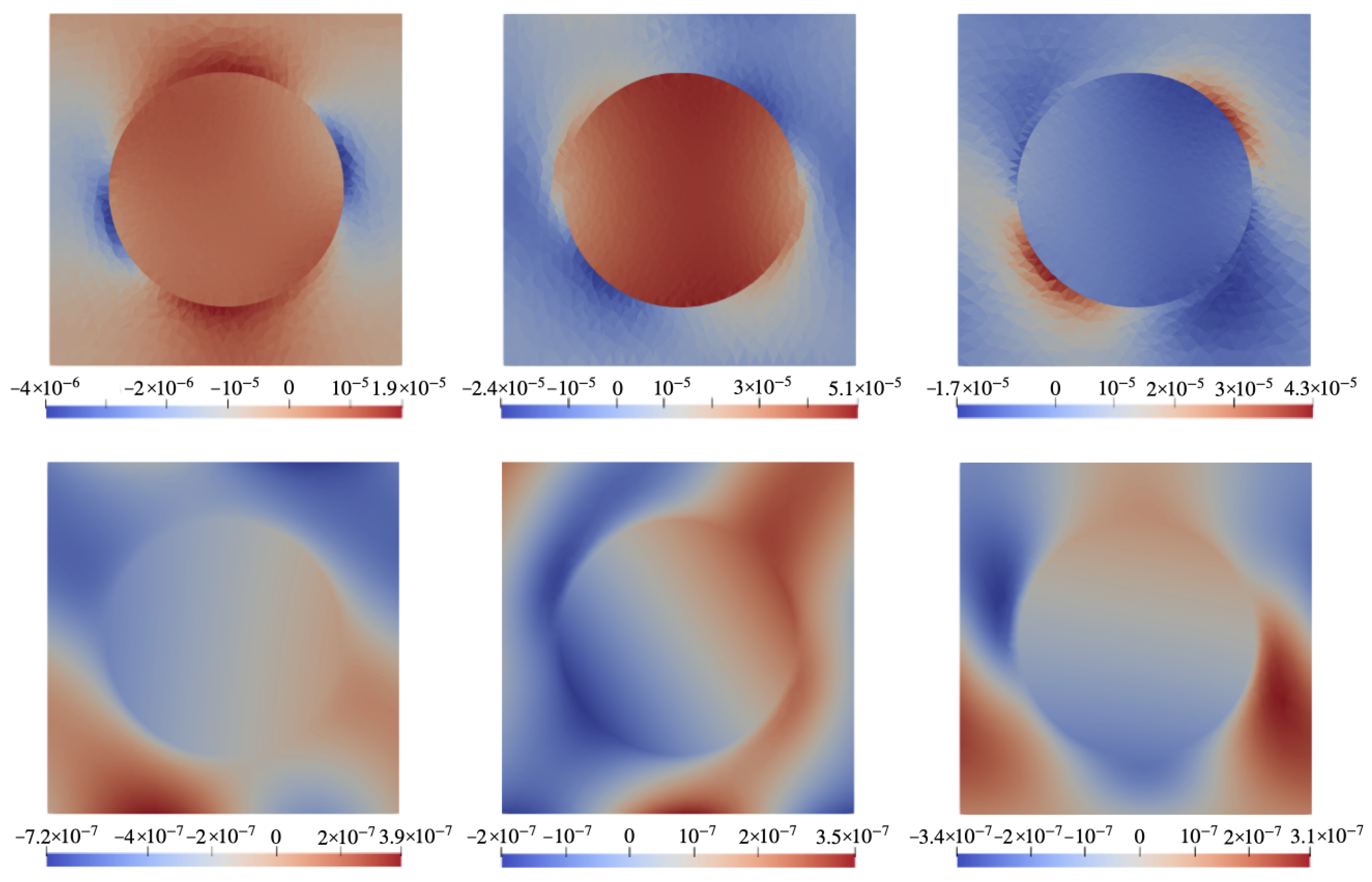
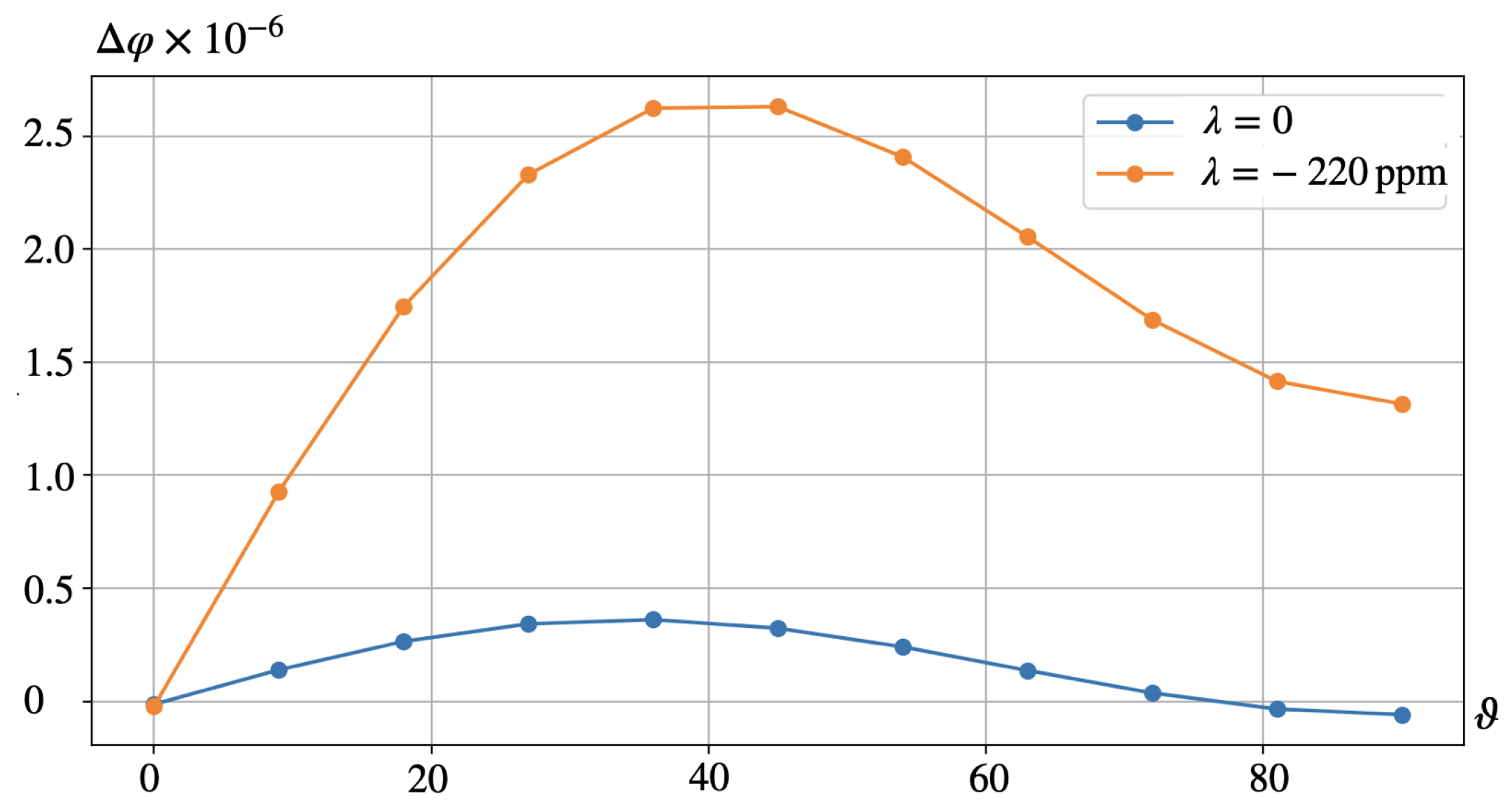
6. Results
6.1. Configuration A
6.2. Configuration B
7. Discussion
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Derivation of the Energy Functional
Appendix B. Magnetostriction of a Uniaxial Particle
Appendix C. Piezoelectric Strain Response of Uniaxially Oriented Matrix
References
- Liang, X.; Matyushov, A.; Hayes, P.; Schell, V.; Dong, C.; Chen, H.; He, Y.; Will-Cole, A.; Quandt, E.; Martins, P.; et al. Roadmap on magnetoelectric materials and devices. IEEE Trans. Magn. 2021, 57, 400157. [Google Scholar] [CrossRef]
- Fernandes, C.L.; Correia, D.M.; Tariq, M.; Esperança, J.M.S.S.; Martins, P.; Lanceros-Méndez, S. Multifunctional magnetoelectric sensing and bending actuator response of polymer-based hybrid materials with magnetic ionic liquids. Nanomaterials 2023, 13, 2186. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Meng, X.; Fu, G.; Han, T.; Xu, F.; Putson, C.; Liu, X. Enhanced polarization effect of flexible magnetoelectric PVDF-TrFE/Fe3O4 smart nanocomposites for nonvolatile memory application. ACS Appl. Electron. Mater. 2023, 5, 1844–1852. [Google Scholar] [CrossRef]
- Pourhosseiniasl, M.; Gao, X.; Kamalisiahroudi, S.; Yu, Z.; Chu, Z.; Yang, J.; Lee, H.; Dong, S. Versatile power and energy conversion of magnetoelectric composite materials with high efficiency via electromechanical resonance. NanoEnergy 2020, 70, 104506. [Google Scholar] [CrossRef]
- Jiang, J.; Liu, S.; Feng, L.; Zhao, D. A review of piezoelectric vibration energy harvesting with magnetic coupling based on different structural characteristics. Micromachines 2021, 12, 436. [Google Scholar] [CrossRef] [PubMed]
- Sasmal, A.; Sen, S.; Chelvane, J.A.; Arockiarajan, A. PVDF based flexible magnetoelectric composites for capacitive energy storage, hybrid mechanical energy harvesting and self-powered magnetic field detection. Polymer 2023, 281, 126141. [Google Scholar] [CrossRef]
- Díaz, E.; Valle, M.B.; Ribeiro, S.; Lanceros-Méndez, S.; Barandiarán, J.M. Development of magnetically active scaffolds for bone regeneration. Nanomaterials 2018, 8, 678. [Google Scholar] [CrossRef]
- Kapat, K.; Shubhra, Q.T.H.; Zhou, M.; Leeuwenburgh, S. Piezoelectric nano-biomaterials for biomedicine and tissue regeneration. Adv. Funct. Mater. 2020, 30, 19009045. [Google Scholar] [CrossRef]
- Kopyl, S.; Surmenev, R.; Surmeneva, M.; Fetisov, Y.; Kholkin, A. Magnetoelectric effect: Principles and applications in biology and medicine—A review. Mater. Today Bio 2021, 12, 100149. [Google Scholar] [CrossRef]
- Silva, C.A.; Fernandes, M.M.; Ribeiro, C.; Lanceros-Méndez, S. Two- and three-dimensional piezoelectric scaffolds for bone tissue engineering. Colloids Surfaces B Biointerfaces 2022, 218, 112708. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, C.; Liu, Y.; Ding, Q.; Wang, T.; Li, H.; Wu, H.; Ma, T. Harnessing electromagnetic fields to assist bone tissue engineering. Stem Cell Res. Ther. 2023, 14, 7. [Google Scholar] [CrossRef] [PubMed]
- Sharma, M.; Madras, G.; Bose, S. Process induced electroactive polymorph in PVDF: Effect on dielectric and ferroelectric properties. Phys. Chem. Chem. Phys. 2014, 16, 14792–14799. [Google Scholar] [CrossRef] [PubMed]
- Ruan, L.; Yao, X.; Chang, Y.; Zhou, L.; Qin, G.; Zhang, X. Properties and applications of the β phase poly(vinylidene fluoride). Polymers 2018, 10, 228. [Google Scholar] [CrossRef] [PubMed]
- Nivedhitha, D.M.; Subramanian, J. Polyvinylidene fluoride, an advanced futuristic smart polymer material: A comprehensive review. Polym. Adv. Technol. 2023, 34, 474–505. [Google Scholar] [CrossRef]
- Correia, D.M.; Gonçalves, R.; Ribeiro, C.; Sencadas, V.; Botelho, G.; Ribelles, J.G.; Lanceros-Méndez, S. Electrosprayed poly(vinylidene fluoride) microparticles for tissue engineering applications. RSC Adv. 2014, 4, 33013–33021. [Google Scholar] [CrossRef]
- Gonçalves, R.; Martins, P.; Correia, D.M.; Sencadas, V.; Vilas, J.L.; León, L.M.; Botelho, G.; Lanceros-Méndez, S. Development of magnetoelectric CoFe2O4/poly(vinylidene fluoride) microspheres. RSC Adv. 2015, 5, 35852–35857. [Google Scholar] [CrossRef]
- Omelyanchik, A.; Antipova, V.; Gritsenko, C.; Kolesnikova, V.; Murzin, D.; Han, Y.; Turutin, A.V.; Kubasov, I.V.; Kislyuk, A.M.; Ilina, T.S.; et al. Boosting magnetoelectric effect in polymer-based nanocomposites. Nanomaterials 2021, 11, 1154. [Google Scholar] [CrossRef]
- Martins, L.A.; Ródenas-Rochina, J.; Salazar, D.; Cardoso, V.F.; Ribelles, J.L.G.; Lanceros-Méndez, S. Microfluidic processing of piezoelectric and magnetic responsive electroactive microspheres. ACS Appl. Polym. Mater. 2017, 4, 5368–5379. [Google Scholar] [CrossRef]
- Stolbov, O.V.; Ignatov, A.A.; Rodionova, V.V.; Raikher, Y.L. Modelling the effect of particle arrangement on the magnetoelectric response of a polymer multiferroic film. Soft Matter 2023, 19, 4029–4040. [Google Scholar] [CrossRef]
- Martins, P.; Larrea, A.; Gonçalves, R.; Botelho, G.; Ramana, E.V.; Mendiratta, S.K.; Sebastian, V.; Lanceros-Méndez, S. Novel anisotropic magnetoelectric effect on #-FeO(OH)/P(VDF-TrFE) multiferroic composites. ACS Appl. Mater. Interfaces 2015, 7, 1122–1129. [Google Scholar] [CrossRef]
- Gutiérrez, J.; Martins, P.; Gonçalves, R.; Sencadas, V.; Lasheras, A.; Lanceros-Méndez, S.; Barandiarán, J.M. Synthesis, physical and magnetic properties of BaFe12O19 / P(VDF-TrFE) multifunctional composites. Eur. Polym. J. 2015, 69, 224–231. [Google Scholar] [CrossRef]
- Anithakumari, P.; Mandal, B.P.; Abdelhamid, E.; Naik, R.; Tyagi, A.K. Enhancement of dielectric, ferroelectric and magneto-dielectric properties in PVDF-BaFe12O19 composites. RSC Adv. 2016, 6, 16073–16080. [Google Scholar] [CrossRef]
- Gonçalves, R.; Larrea, A.; Zheng, T.; Higgins, M.J.; Sebastian, V.; Lanceros-Méndez, S.; Martins, P. Synthesis of highly magnetostrictive nanostructures and their application in a polymer-based magnetoelectric sensing device. Eur. Polym. J. 2016, 84, 685–692. [Google Scholar] [CrossRef]
- Alnassar, M.Y.; Ivanov, Y.P.; Kosel, J. Flexible magnetoelectric nanocomposites with tunable properties. Adv. Electron. Mater. 2016, 2, 1600081. [Google Scholar] [CrossRef]
- Nan, C.-W.; Bichurin, M.I.; Dong, S.; Viehland, D.; Srinivasan, G. Multiferroic magnetoelectric composites: Historical perspective, status, and future directions. J. Appl. Phys. 2008, 103, 031101. [Google Scholar] [CrossRef]
- Ma, J.; Hu, J.; Li, Z.; Nan, C.-W. Recent progress in multiferroic magnetoelectric composites: From bulk to thin films. Adv. Mater. 2011, 23, 1062–1087. [Google Scholar] [CrossRef]
- Acosta, M.; Novak, N.; Rojas, V.; Patel, S.; Vaish, R.; Koruza, J.; Rossetti, G.A.; Rödel, J. BaTiO3-based piezoelectrics: Fundamentals, current status, and perspectives. Appl. Phys. Rev. 2018, 4, 041305. [Google Scholar] [CrossRef]
- Ferson, N.D.; Uhl, A.M.; Andrew, J.S. Piezoelectric and magnetoelectric scaffolds for tissue regeneration and biomedicine: A Review. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2020, 68, 229–241. [Google Scholar] [CrossRef]
- Meng, Y.; Chen, G.; Huang, M. Piezoelectric materials: Properties, advancements, and design strategies for high-temperature applications. Nanomaterials 2022, 12, 1171. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, X.; Wang, X.; Fang, C.; Weng, G.J. Magnetic, mechanical, electrical properties and coupling effects of particle reinforced piezoelectric polymer matrix composites. Compos. Struct. 2022, 304, 116450. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Electrodynamics of Continuous Media, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 1984. [Google Scholar]
- FEniCS Project. Available online: http://www.fenicsproject.org (accessed on 8 September 2023).
- Bickford, L.R.; Pappis, J.; Stull, J.L. Magnetostriction and permeability of magnetite and cobalt-substituted magnetite. Phys. Rev. 1955, 99, 1210–1214. [Google Scholar] [CrossRef]
- Bozort, R.M.; Tilden, E.F.; Williams, A.J. Anisotropy and magnetostriction of some ferrites. Phys. Rev. 1955, 99, 1788–1798. [Google Scholar] [CrossRef]
- Gonçalves, R.; Larrea, A.; Sebastian, M.S.; Sebastian, V.; Martins, P.; Lanceros-Méndez, S. Synthesis and size dependent magnetostrictive response of ferrite nanoparticles and their application on magnetoelectric polymer-based multiferroic sensors. J. Mater. Chem. C 2016, 4, 10701–10706. [Google Scholar] [CrossRef]
- de Groot, C.H.; de Kort, K. Magnetoelastic anisotropy in NdFeB permanent magnets. J. Appl. Phys. 1999, 85, 8312–8316. [Google Scholar] [CrossRef]
- Licei, F.; Rinaldi, S. Magnetostriction of some hexagonal ferrites. J. Appl. Phys. 1981, 52, 2442–2443. [Google Scholar] [CrossRef]
- Cui, Y.; Sui, Y.; Wei, P.; Lv, Y.; Cong, C.; Meng, X.; Ye, H.; Zhou, Q. Rationalizing the dependence of poly (vinylidene difluoride) (PVDF) rheological performance on the nano-silica. Nanomaterials 2023, 13, 1096. [Google Scholar] [CrossRef]
- Tang, B.; Zhuang, J.; Wang, L.; Zhang, B.; Lin, S.; Jia, F.; Dong, L.; Wang, Q.; Cheng, K.; Weng, W. Harnessing cell dynamic responses on magnetoelectric nanocomposite films to promote osteogenic differentiation. ACS Appl. Mater. Interfaces 2018, 10, 7841–7851. [Google Scholar] [CrossRef]
- Bustamante, R.; Dorfmann, A.; Ogden, R.W. On boundary conditions in nonlinear magneto- and electroelasticity. In Constitutive Models for Rubber; Balkema-Proceedings and Monographs in Engineering, Water, and Earth Sciences; Boukamel, A., Laiarinandrasana, L., Meo, S., Verron, E., Eds.; Taylor & Francis: London, UK, 2008; Volume 5, pp. 339–344. [Google Scholar]
- Ogden, R.W. Non-Linear Elastic Deformations; Dover: New York, NY, USA, 1984. [Google Scholar]
- Ueberschlag, P. PVDF piezoelectric polymer. Sens. Rev. 2001, 21, 118–125. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stolbov, O.V.; Raikher, Y.L. Magnetostrictive and Magnetoactive Effects in Piezoelectric Polymer Composites. Nanomaterials 2024, 14, 31. https://doi.org/10.3390/nano14010031
Stolbov OV, Raikher YL. Magnetostrictive and Magnetoactive Effects in Piezoelectric Polymer Composites. Nanomaterials. 2024; 14(1):31. https://doi.org/10.3390/nano14010031
Chicago/Turabian StyleStolbov, Oleg V., and Yuriy L. Raikher. 2024. "Magnetostrictive and Magnetoactive Effects in Piezoelectric Polymer Composites" Nanomaterials 14, no. 1: 31. https://doi.org/10.3390/nano14010031
APA StyleStolbov, O. V., & Raikher, Y. L. (2024). Magnetostrictive and Magnetoactive Effects in Piezoelectric Polymer Composites. Nanomaterials, 14(1), 31. https://doi.org/10.3390/nano14010031







