Topography and Nonlinear Optical Properties of Thin Films Containing Iodide-Based Hybrid Perovskites
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Deposition Technique of Thin Films
2.3. Surface Characterization of Thin Films
2.4. Spectroscopic Measurements
2.5. NLO Measurements
2.5.1. Interaction of Matter with a Strong Electromagnetic Field—The Process of Generating Higher Harmonics
2.5.2. Theoretical Models for Higher Harmonic Generation Analysis
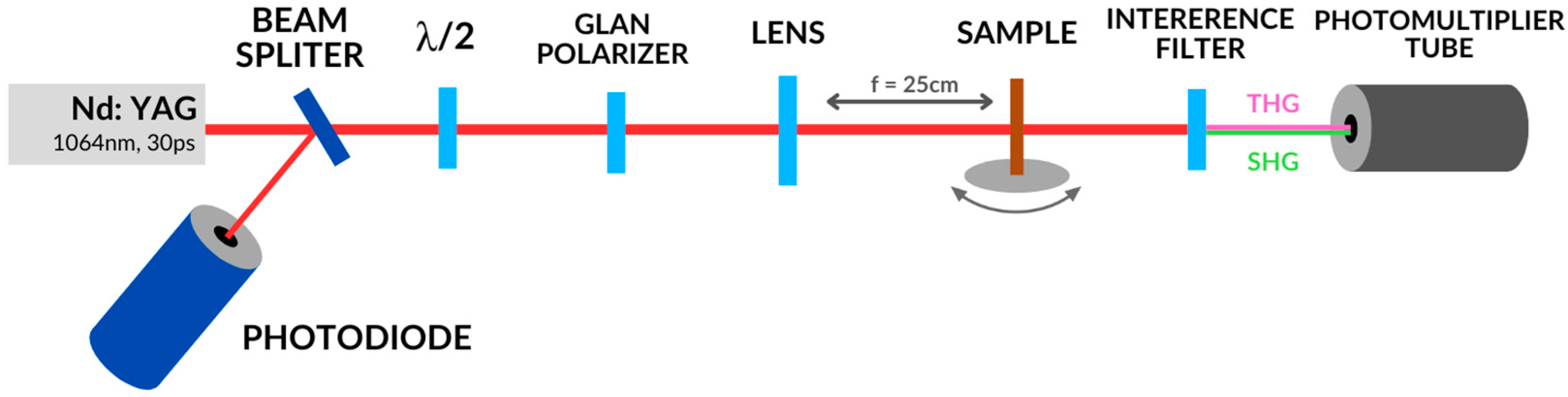
2.5.3. SHG and THG Apparatus
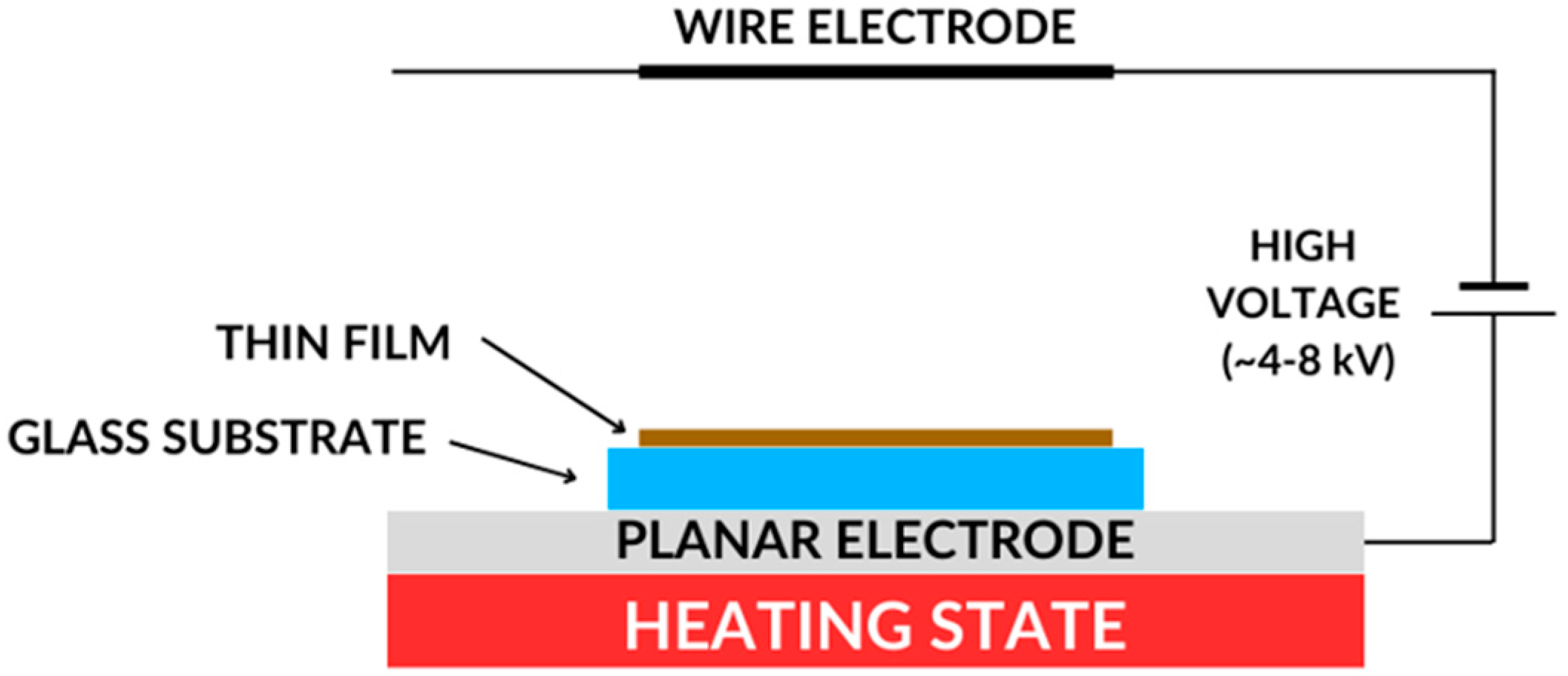
2.5.4. Corona Poling Technique
3. Results and Discussion
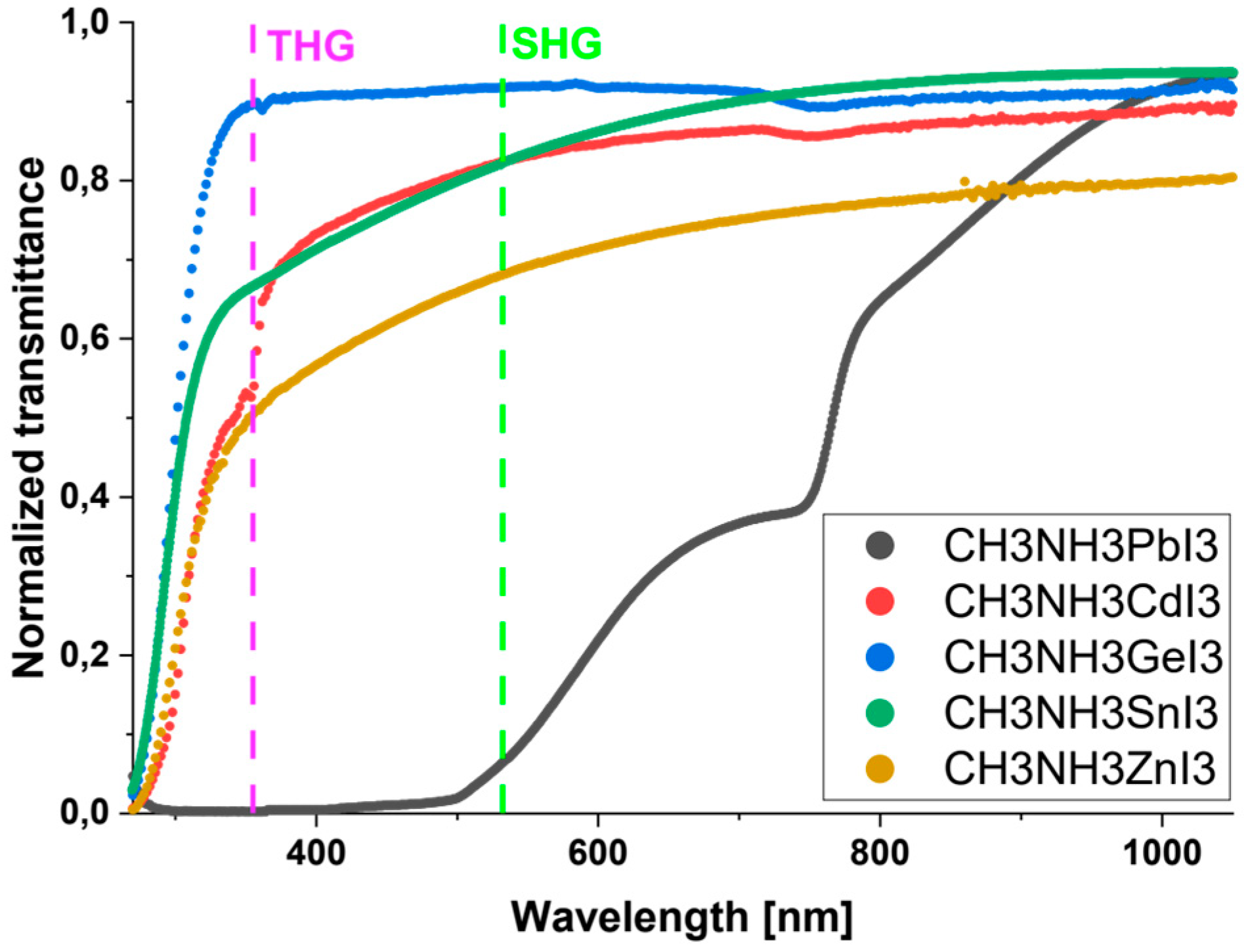
3.1. Transmittance
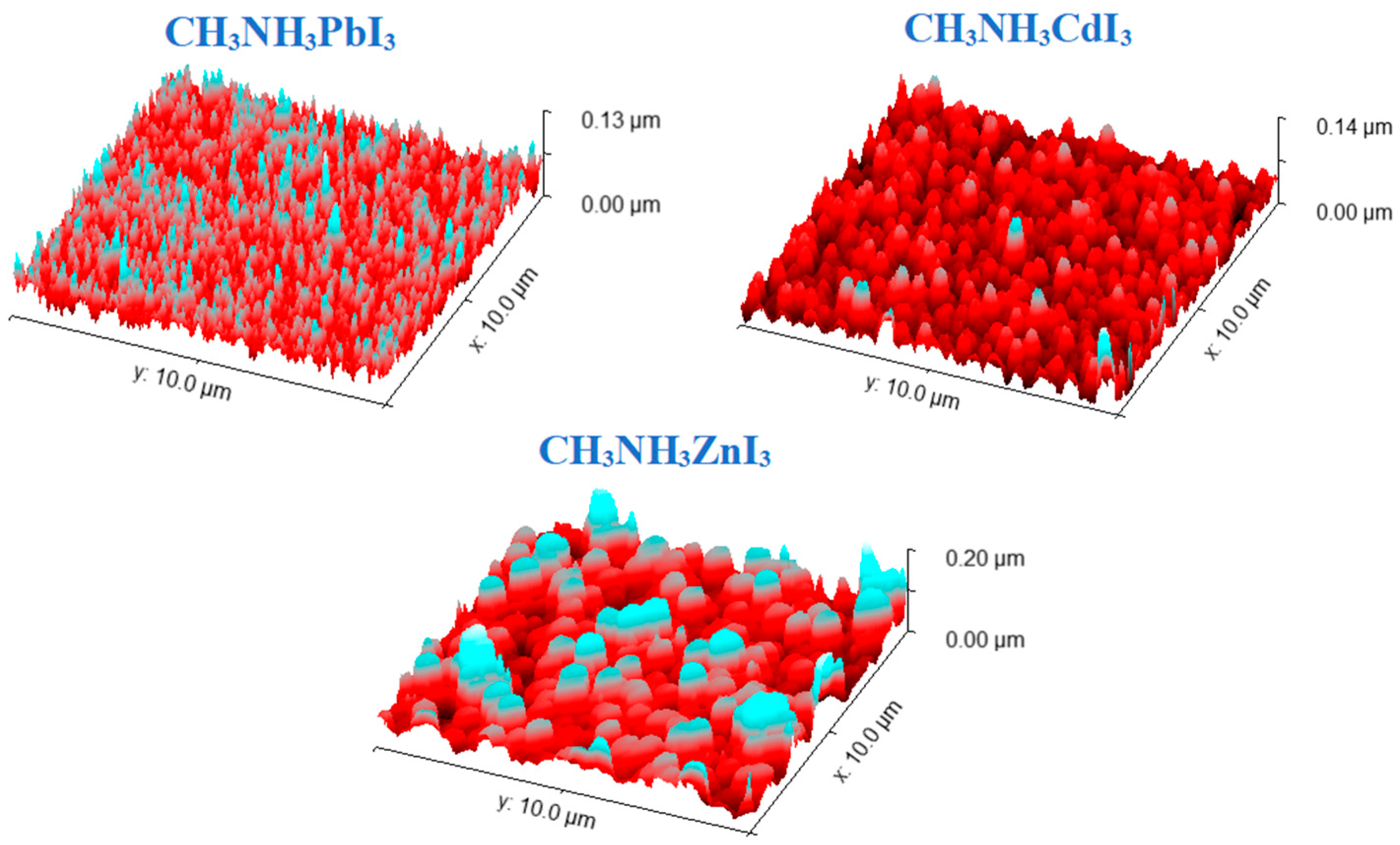
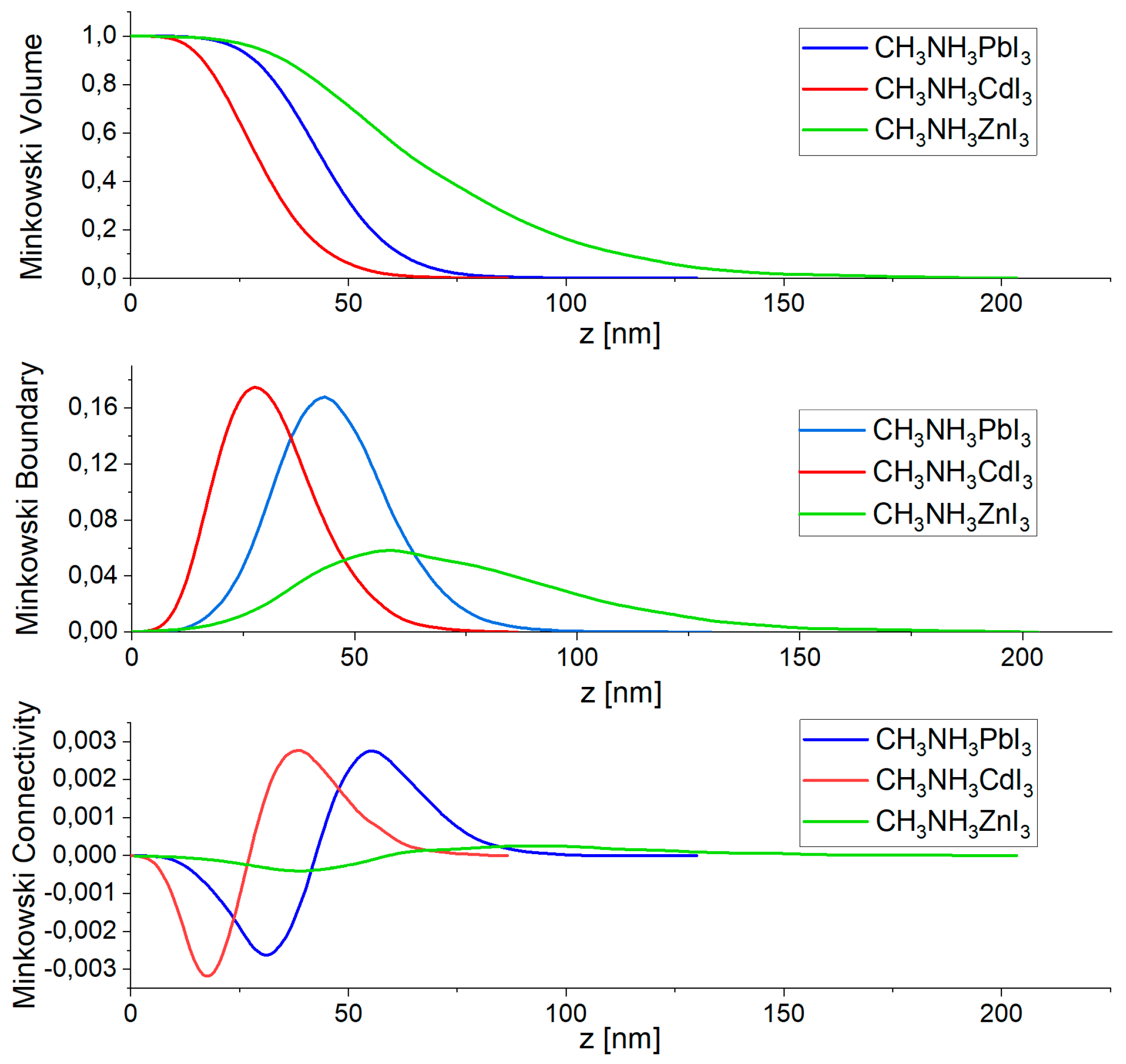
3.2. AFM Analysis
| Material | Thickness [nm] | Average Crystallite Height [nm] | Medium Roughness [nm] |
|---|---|---|---|
| CH3NH3PbI3 | 300.0 | 45.2 | 13.2 |
| CH3NH3CdI3 | 175.0 | 32.7 | 12.5 |
| CH3NH3GeI3 | 70.0 | − | − |
| CH3NH3SnI3 | 253.0 | − | − |
| CH3NH3ZnI3 | 260.0 | 71.0 | 30.8 |
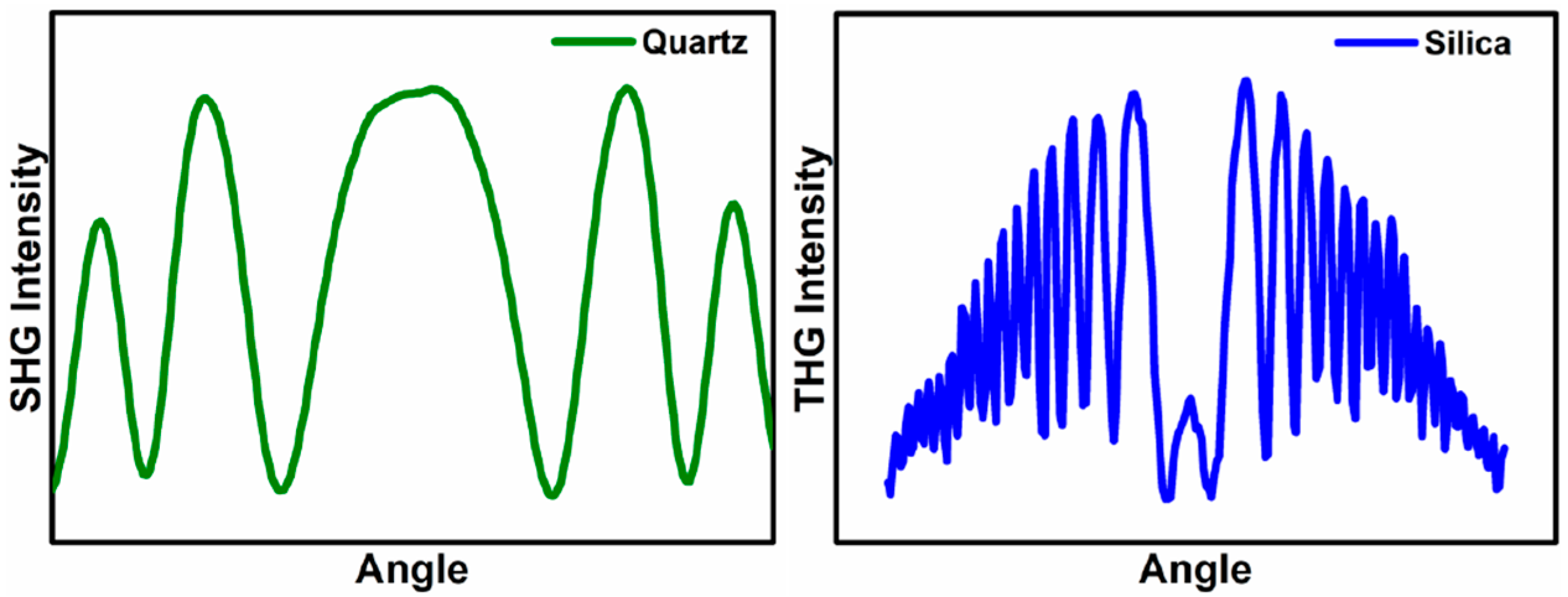
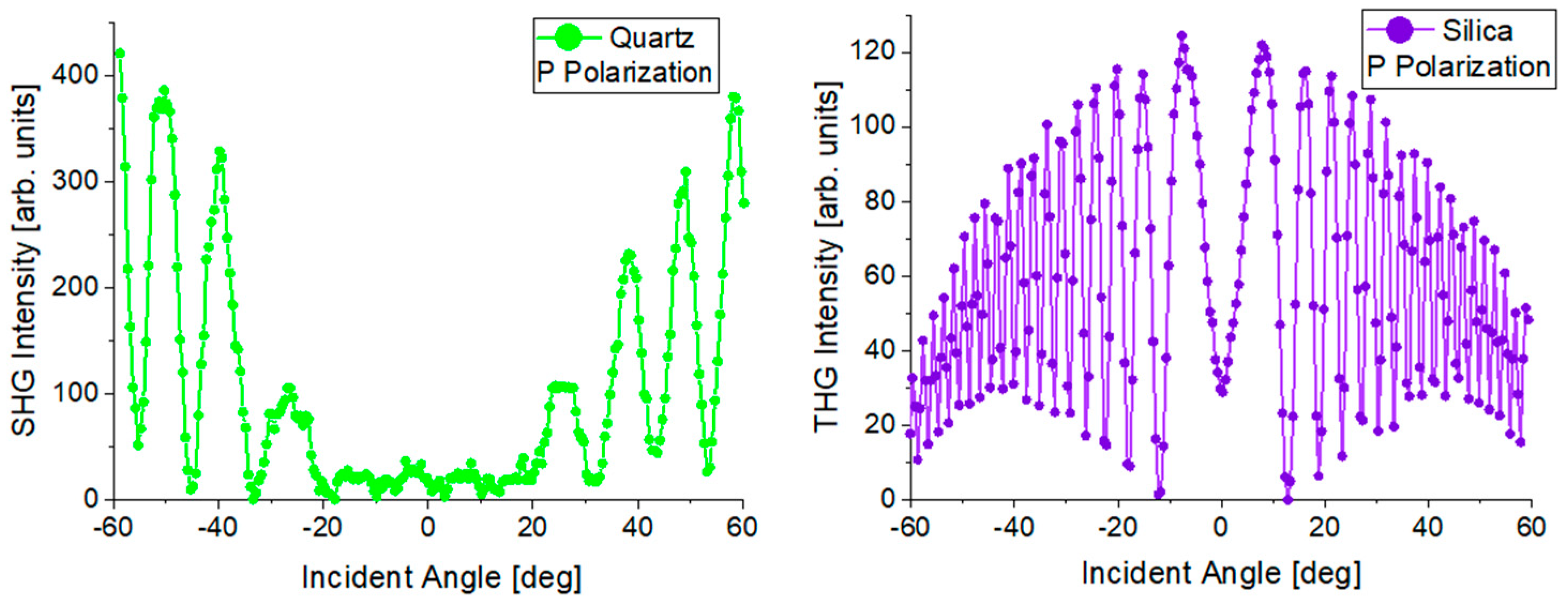
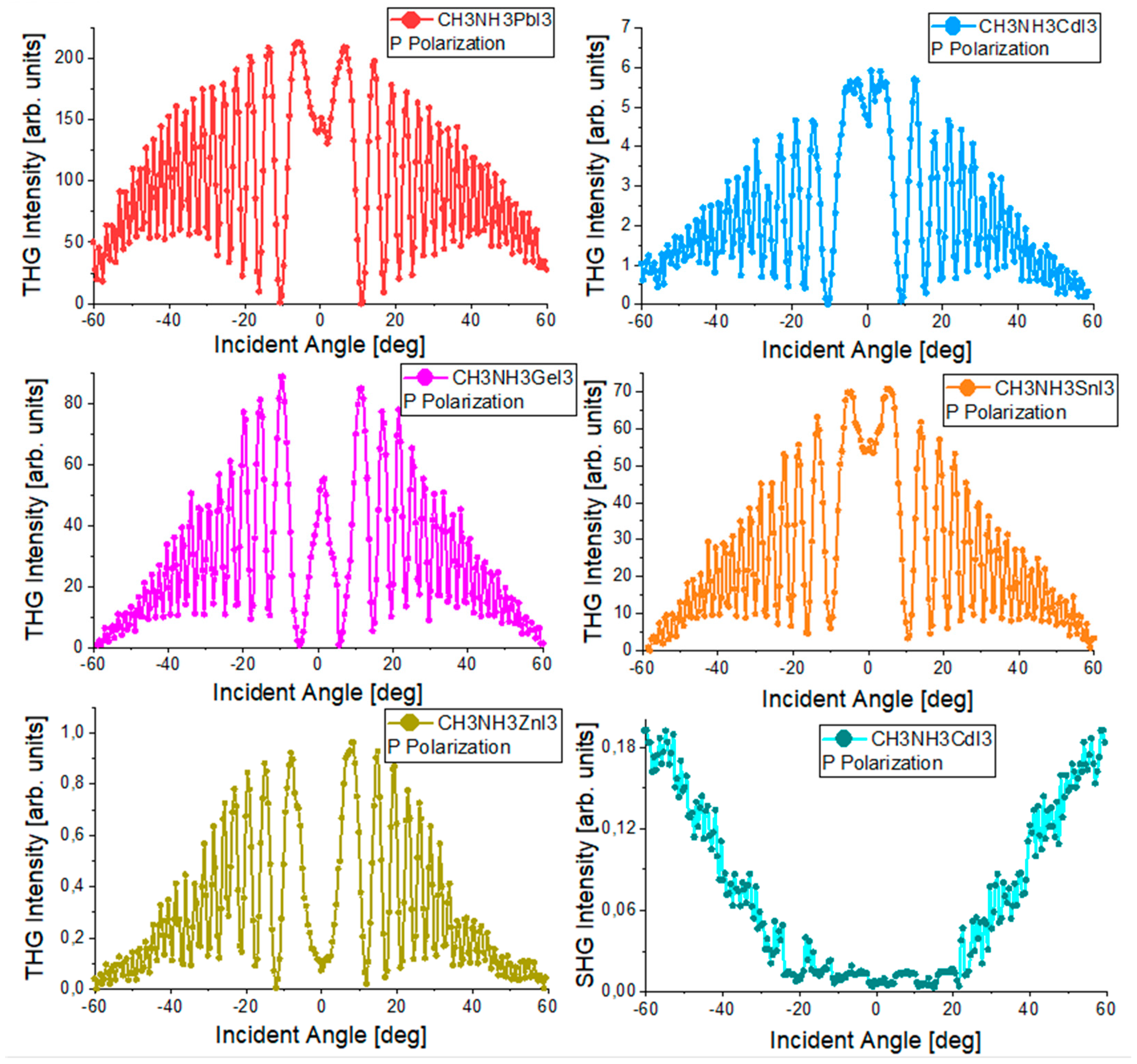
3.3. SHG and THG Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abu Baker, A.M.; Boltaev, G.S.; Iqbal, M.; Pylnev, M.; Hamdan, N.M.; Alnaser, A.S. Giant Third-Order Nonlinear Response of Mixed Perovskite Nanocrystals. Materials 2022, 15, 389. [Google Scholar] [CrossRef]
- Wang, G.; Liu, T.; Wang, B.; Gu, H.; Wei, Q.; Zhang, Z.; He, J.; Li, M.; Xing, G. Hot-carrier tunable abnormal nonlinear absorption conversion in quasi-2D perovskite. Nat. Commun. 2022, 13, 6935. [Google Scholar] [CrossRef] [PubMed]
- Szwagierczak, D. Wytwarzanie i Właściwości Nieferroelektrycznych Materiałów Perowskitowych o Bardzo Wysokiej Przenikalności Elektrycznej; Instytut Technologii Elektronowej: Warszawa, Poland, 2011. [Google Scholar]
- Whitfield, P.S.; Herron, N.; Guise, W.E.; Page, K.; Cheng, Y.Q.; Milas, I.; Crawford, M.K. Structures, Phase Transitions and Tricritical Behavior of the Hybrid Perovskite Methyl Ammonium Lead Iodide. Sci. Rep. 2016, 6, 35685. [Google Scholar] [CrossRef] [PubMed]
- Fu, Y.; Zhu, H.; Chen, J.; Hautzinger, M.P.; Zhu, X.-Y.; Jin, S. Metal halide perovskite nanostructures for optoelectronic applications and the study of physical properties. Nat. Rev. Mater. 2019, 4, 169–188. [Google Scholar] [CrossRef]
- Yuan, Y.; Giri, G.; Ayzner, A.L.; Zoombelt, A.P.; Mannsfeld, S.C.B.; Chen, J.; Nordlund, D.; Toney, M.F.; Huang, J.; Bao, Z. Ultra-high mobility transparent organic thin film transistors grown by an off-centre spin-coating method. Nat. Commun. 2014, 5, 3005. [Google Scholar] [CrossRef] [PubMed]
- Park, N.-G. Perovskite solar cells: An emerging photovoltaic technology. Mater. Today 2015, 18, 65–72. [Google Scholar] [CrossRef]
- Chowdhury, T.A.; Bin Zafar, A.; Islam, S.-U.; Shahinuzzaman, M.; Islam, M.A.; Khandaker, M.U. Stability of perovskite solar cells: Issues and prospects. RSC Adv. 2023, 13, 1787–1810. [Google Scholar] [CrossRef]
- Kojima, A.; Teshima, K.; Shirai, Y.; Miyasaka, T. Organometal Halide Perovskites as Visible-Light Sensitizers for Photovoltaic Cells. J. Am. Chem. Soc. 2009, 131, 6050–6051. [Google Scholar] [CrossRef]
- Tang, H.; He, S.; Peng, C. A Short Progress Report on High-Efficiency Perovskite Solar Cells. Nanoscale Res. Lett. 2017, 12, 410. [Google Scholar] [CrossRef]
- Petrus, M.L.; Schlipf, J.; Li, C.; Gujar, T.P.; Giesbrecht, N.; Müller-Buschbaum, P.; Thelakkat, M.; Bein, T.; Hüttner, S.; Docampo, P. Capturing the Sun: A Review of the Challenges and Perspectives of Perovskite Solar Cells. Adv. Energy Mater. 2017, 7, 1700264. [Google Scholar] [CrossRef]
- Hutchinson, G.; Milburn, G. Nonlinear quantum optical computing via measurement. J. Mod. Opt. 2004, 51, 1211–1222. [Google Scholar] [CrossRef]
- Lee, J.S.; Farmakidis, N.; Wright, C.D.; Bhaskaran, H. Polarization-selective reconfigurability in hybrized-active-dielectric nanowires. Sci. Adv. 2022, 8, eabn9459. [Google Scholar] [CrossRef] [PubMed]
- Ortíz-Trejo, F.; Trejo-Valdez, M.; Campos-López, J.P.; Castro-Chacón, J.H.; Torres-Torres, C. Multipath Data Storage by Third-Order Nonlinear Optical Properties in Znic Oxide Nanostructures. Appl. Sci. 2020, 10, 5688. [Google Scholar] [CrossRef]
- Arivuoli, D. Fundamentals on Nonlinear Optical Materials. Pramana J. Phys. 2001, 57, 871–883. [Google Scholar] [CrossRef]
- Dhama, R.; Panahpour, A.; Pihlava, T.; Ghindani, D.; Caglayan, H. All-optical switching based on plasmon induced Enhancement of Index of Refraction. Nat. Commun. 2022, 13, 3114. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Bai, X.; Muñoz, J.A.; Dai, Y.; Das, S.; Wang, Y.; Sun, Z. Coherent modulation of chiral nonlinear optics with crystal symmetry. Light Sci. Appl. 2022, 11, 216. [Google Scholar] [CrossRef]
- McKenna, T.P.; Stokowski, H.S.; Ansari, V.; Mishra, J.; Jankowski, M.; Sarabalis, C.J.; Herrmann, J.F.; Langrock, C.; Fejer, M.M.; Safavi-Naeini, A.H. Ultra-low-power second-order nonlinear optics on a chip. Nat. Commun. 2022, 13, 4532. [Google Scholar] [CrossRef]
- Yi, R.; Zhang, X.; Li, C.; Zhao, B.; Wang, J.; Li, Z.; Gan, X.; Li, L.; Li, Z.; Zhang, F.; et al. Self-frequency-conversion nanowire lasers. Light Sci. Appl. 2022, 11, 120. [Google Scholar] [CrossRef]
- Liu, X.; Guo, Q.; Qiu, J. Emerging Low-Dimensional Materials for Nonlinear Optics and Ultrafast Photonics. Adv. Mater. 2017, 29, 1605886. [Google Scholar] [CrossRef]
- Starodumov, A.; Zenteno, L.; Arzate, N. Nonlinear-optical modulator for high-power fiber lasers. Opt. Lett. 1997, 22, 286–288. [Google Scholar] [CrossRef]
- Shen, Y. Surface properties probed by second-harmonic and sum-frequency generation. Nature 1989, 337, 519–525. [Google Scholar] [CrossRef]
- Ghader, A.; Behruzi, M.; Ara, M.H.M.; Ghaznavi, H.; Ardakani, A.A. Nonlinear optical response of cancer cells following conventional and nano-technology based treatment strategies: Results of chemo-, thermo- and radiation therapies. Photodiagnosis Photodyn. Ther. 2022, 37, 102686. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Zhao, X.; Li, H.; Zheng, Y.; Chen, X. Dynamic computer-generated nonlinear optical holograms in a non-collinear second-harmonic generation process. Opt. Lett. 2018, 43, 3236–3239. [Google Scholar] [CrossRef] [PubMed]
- Campagnola, P.J.; Wei, M.-D.; Lewis, A.; Loew, L.M. High-Resolution Nonlinear Optical Imaging of Live Cells by Second Harmonic Generation. Biophys. J. 1999, 77, 3341–3349. [Google Scholar] [CrossRef]
- Zawadzka, A.; Marjanowska, A.; Płóciennik, P.; Korcala, A.; Wisniewski, K.; Sahraoui, B. Properties and applications of hybrid organic-inorganic halide perovskites thin films. In Proceedings of the Organic Photonic Materials and Devices XXII, San Francisco, CA, USA, 5–6 February 2020; p. 112770S. [Google Scholar] [CrossRef]
- El Ouedghiri-Idrissi, I.; Lougdali, M.; Makir, Z.; Niasse, O.A.; Sofiani, Z. Photoluminescence of organic thin film Copper phthalocyanine CuPc for LED application. Mater. Today Proc. 2022, 66, 76–79. [Google Scholar] [CrossRef]
- Calisi, N.; Galvanetto, E.; Borgioli, F.; Martinuzzi, S.M.; Bacci, T.; Caporali, S. Thin films deposition of fully inorganic metal halide perovskites: A review. Mater. Sci. Semicond. Process. 2022, 147, 106721. [Google Scholar] [CrossRef]
- Anoua, R.; Lifi, H.; Touhtouh, S.; El Jouad, M.; Hajjaji, A.; Bakasse, M.; Płociennik, P.; Zawadzka, A. Optical and morphological properties of Curcuma longa dye for dye-sensitized solar cells. Enviromental Sci. Pollut. Res. 2021, 28, 57860–57871. [Google Scholar] [CrossRef]
- Laouid, A.; Belghiti, A.A.; Wisniewski, K.; Hajjaji, A.; Zawadzka, A. Structural and optical properties of DCM thin films prepared by PVD. Mater. Today Proc. 2022, 66, 63–67. [Google Scholar] [CrossRef]
- Maiman, T. Stimulated Optical Radiation in Ruby. Nature 1960, 187, 493–494. [Google Scholar] [CrossRef]
- Franken, P.A.; Hill, A.E.; Peters, C.W.; Weinreich, G. Generation Of Optical Harmonics. Phys. Rev. Lett. 1961, 7, 118–119. [Google Scholar] [CrossRef]
- Ducuing, J.; Bloembergen, N. Statistical Fluctuations in Nonlinear Optical Processes. Phys. Rev. 1964, 133, A1493. [Google Scholar] [CrossRef]
- Buckingham, A.; Orr, B. Molecular hyperpolarisabilities. Q. Rev. Chem. Soc. 1967, 21, 195–212. [Google Scholar] [CrossRef]
- Yahya, M.; Nural, Y.; Seferoglu, Z. Recent advances in the nonlinear optical (NLO) properties of phthalocyanines: A review. Dye. Pigment. 2022, 198, 109960. [Google Scholar] [CrossRef]
- Zawadzka, A. Cienkie Warstwy i Nanostruktury Cienkowarstwowe—Eksperymentalne Metody Wytwarzania i Badania Właściwości; Wydawnictwo Naukowe Uniwersytetu Mikołaja Kopernika: Toruń, Poland, 2016; ISBN 978-83-231-3513-5. [Google Scholar]
- Lougdali, M.; El Kouari, Y.; Zazoui, M.; Abboud, Y.; Zawadzka, A.; Migalska-Zalas, A.; Waszkowska, K.; Sahraoui, B. Photoluminescence and nonlinear optical properties of Nickel bis-(8-hydroxyquinoline) thin film. Mater. Chem. Phys. 2022, 284, 126031. [Google Scholar] [CrossRef]
- Mydlova, L.; Sahraoui, B.; Waszkowska, K.; El Karout, H.; Makowska-Janusik, M.; Migalska-Zalas, A. Computational and Experimental Study of Nonlinear Optical Susceptibilities of Composite Materials Based on PVK Polymer Matrix and Benzonitrile Derivatives. Materials 2022, 15, 2073. [Google Scholar] [CrossRef]
- Na Quan, L.; Park, Y.; Guo, P.; Gao, M.; Jin, J.; Huang, J.; Copper, J.K.; Schwartzberg, A.; Schaller, R.; Limmer, D.T.; et al. Vibrational relaxation dynamics in layered perovskite quantum wells. Proc. Natl. Acad. Sci. USA 2021, 118, e2104425118. [Google Scholar] [CrossRef] [PubMed]
- Batignani, G.; Fumero, G.; Kandada, A.R.S.; Cerullo, G.; Gandini, M.; Ferrante, C.; Petrozza, A.; Scopigno, T. Probing femtosecond lattice displacement upon photo-carrier generation in lead halide perovskite. Nat. Commun. 2018, 9, 1971. [Google Scholar] [CrossRef] [PubMed]
- Park, M.; Neukirch, A.J.; Reyes-Lillo, S.E.; Lai, M.; Ellis, S.R.; Dietze, D.; Neaton, J.B.; Yang, P.; Tretiak, S.; Mathies, R.A. Excited-state vibrational dynamics toward the polaron in methylammonium lead iodide perovskite. Nat. Commun. 2018, 9, 2525. [Google Scholar] [CrossRef]
- Zawadzka, A.; Płóciennik, P.; Strzelecki, J.; Łukasiak, Z.; Sahraoui, B. Photophysical properties of Alq3 thin films. Opt. Mater. 2014, 36, 91–97. [Google Scholar] [CrossRef]
- Abdelwahab, I.; Grinblat, G.; Leng, K.; Li, Y.; Chi, X.; Rusydi, A.; Maier, S.A.; Loh, K.P. Highly Enhanced Third-Harmonic Generation in 2D Perovskites at Excitonic Resonances. ACS Nano 2018, 12, 644–650. [Google Scholar] [CrossRef]
- Mirershadi, S.; Ahmadi-Kandjani, S.; Zawadzka, A.; Rouhbakhsh, H.; Sahraoui, B. Third order nonlinear optical properties of organometal halide perovskite by means of the Z-scan technique. Chem. Phys. Lett. 2016, 647, 7–13. [Google Scholar] [CrossRef]
- Stoumpos, C.C.; Frazer, L.; Clark, D.J.; Kim, Y.S.; Rhim, S.H.; Freeman, A.J.; Ketterson, J.B.; Jang, J.I.; Kanatzidis, M.G. Hybrid Germanium Iodide Perovskite Semiconductors: Active Lone Pairs, Structural Distortions, Direct and Indirect Energy Gaps, and Strong Nonlinear Optical Properties. J. Am. Chem. Soc. 2015, 137, 6804–6819. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Huang, Y.; Xu, X.; Fan, Z.; Khurgin, J.B.; Xiong, Q. Nonlinear optical properties of halide perovskites and their applications. Appl. Phys. Rev. 2020, 7, 041313. [Google Scholar] [CrossRef]


| Material | Parameters | |||
|---|---|---|---|---|
| Density [gcm−3] | Z-Factor | Rate [As−1] | Melting Point [°C] | |
| CH3NH3I | 2.22 | 1 | 0.2 | ~145 |
| PbI2 | 6.16 | ~400 | ||
| CdI2 | 5.67 | ~390 | ||
| GeI2 | 4.32 | ~460 | ||
| SnI2 | 5.28 | ~320 | ||
| ZnI2 | 4.74 | ~445 | ||
| Laser | Nd: YAG |
|---|---|
| Laser wavelength | 1064 nm |
| Laser energy | 95 µJ |
| Pulse duration | 30 ps |
| Repetition rate | 10 Hz |
| Material | T532 nm [%] | A532nm | T355nm [%] | A355nm | α532nm [cm−1] | α355nm [cm−1] |
|---|---|---|---|---|---|---|
| CH3NH3PbI3 | 6.36 | 1.20 | 0.24 | 2.62 | 92,755.00 | 202,930.00 |
| CH3NH3CdI3 | 82.34 | 0.08 | 53.05 | 0.28 | 11,215.00 | 36,587.00 |
| CH3NH3GeI3 | 91.74 | 0.04 | 89.33 | 0.05 | 12,439.00 | 16,280.00 |
| CH3NH3SnI3 | 82.25 | 0.08 | 66.63 | 0.18 | 7801.00 | 27,334.00 |
| CH3NH3ZnI3 | 68.04 | 0.17 | 51.02 | 0.30 | 14,958.00 | 26,141.00 |
| Material | Lee Model | Kubodera–Kobayashi Model | |
|---|---|---|---|
| χ(2) [pmV−1] after CP | χ(3) [10−22 m2 V−2] | ||
| P Polarization | S Polarization | ||
| Quartz | 1 | - | |
| Silica | - | 2 | |
| CH3NH3PbI3 | - | - | 118.20 ± 3.97 |
| CH3NH3CdI3 | 0.06 ± 0.01 | - | 71.49 ± 4.09 |
| CH3NH3GeI3 | - | - | 71.12 ± 10.20 |
| CH3NH3SnI3 | - | - | 47.73 ± 1.89 |
| CH3NH3ZnI3 | - | - | 43.10 ± 2.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marjanowska, A.; El Karout, H.; Guichaoua, D.; Sahraoui, B.; Płóciennik, P.; Zawadzka, A. Topography and Nonlinear Optical Properties of Thin Films Containing Iodide-Based Hybrid Perovskites. Nanomaterials 2024, 14, 50. https://doi.org/10.3390/nano14010050
Marjanowska A, El Karout H, Guichaoua D, Sahraoui B, Płóciennik P, Zawadzka A. Topography and Nonlinear Optical Properties of Thin Films Containing Iodide-Based Hybrid Perovskites. Nanomaterials. 2024; 14(1):50. https://doi.org/10.3390/nano14010050
Chicago/Turabian StyleMarjanowska, Agnieszka, Houda El Karout, Dominique Guichaoua, Bouchta Sahraoui, Przemysław Płóciennik, and Anna Zawadzka. 2024. "Topography and Nonlinear Optical Properties of Thin Films Containing Iodide-Based Hybrid Perovskites" Nanomaterials 14, no. 1: 50. https://doi.org/10.3390/nano14010050
APA StyleMarjanowska, A., El Karout, H., Guichaoua, D., Sahraoui, B., Płóciennik, P., & Zawadzka, A. (2024). Topography and Nonlinear Optical Properties of Thin Films Containing Iodide-Based Hybrid Perovskites. Nanomaterials, 14(1), 50. https://doi.org/10.3390/nano14010050








