Spatially Structured Optical Pump for Laser Generation Tuning
Abstract
1. Introduction
2. Methodology and the Laser Setup
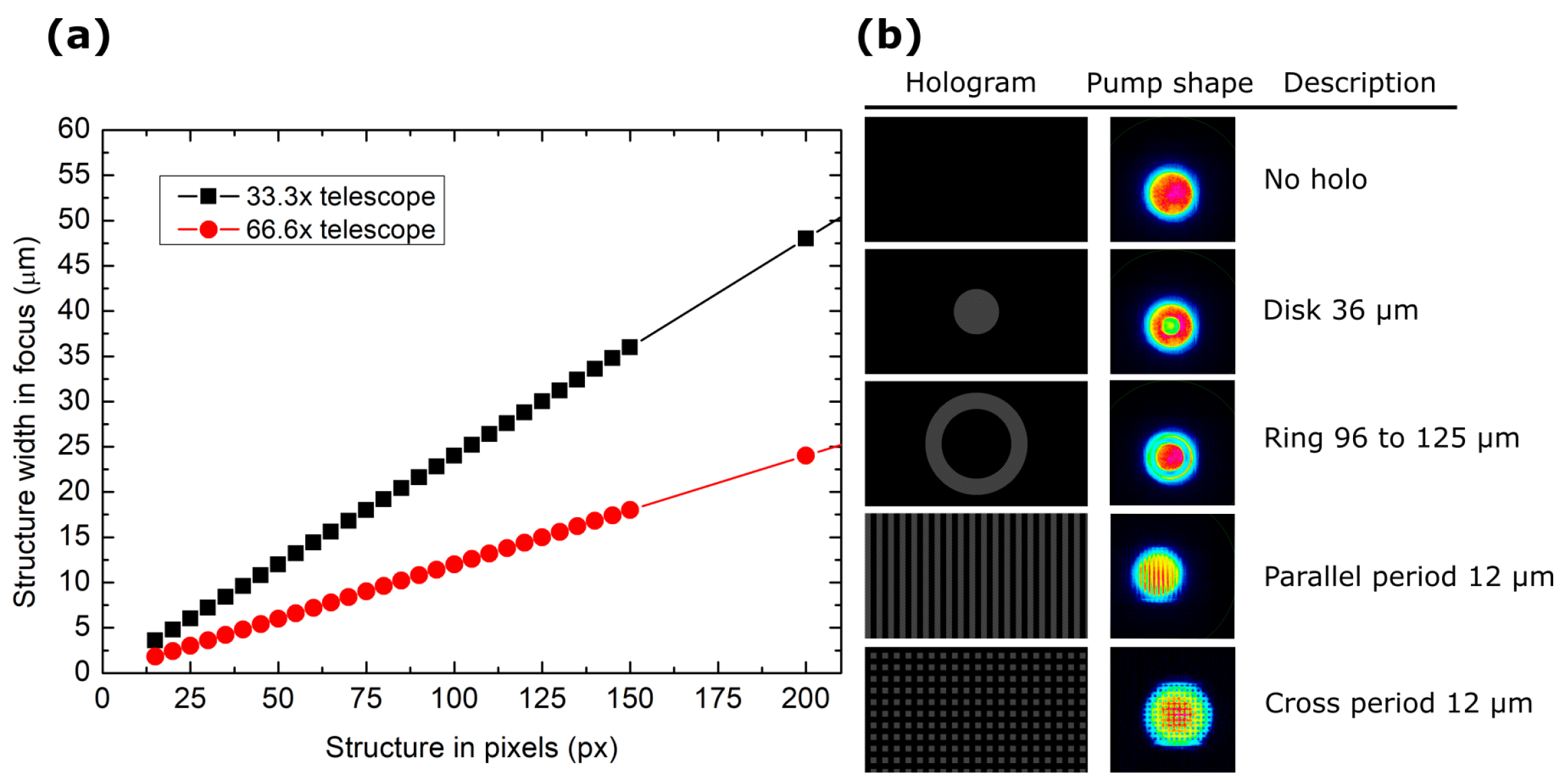
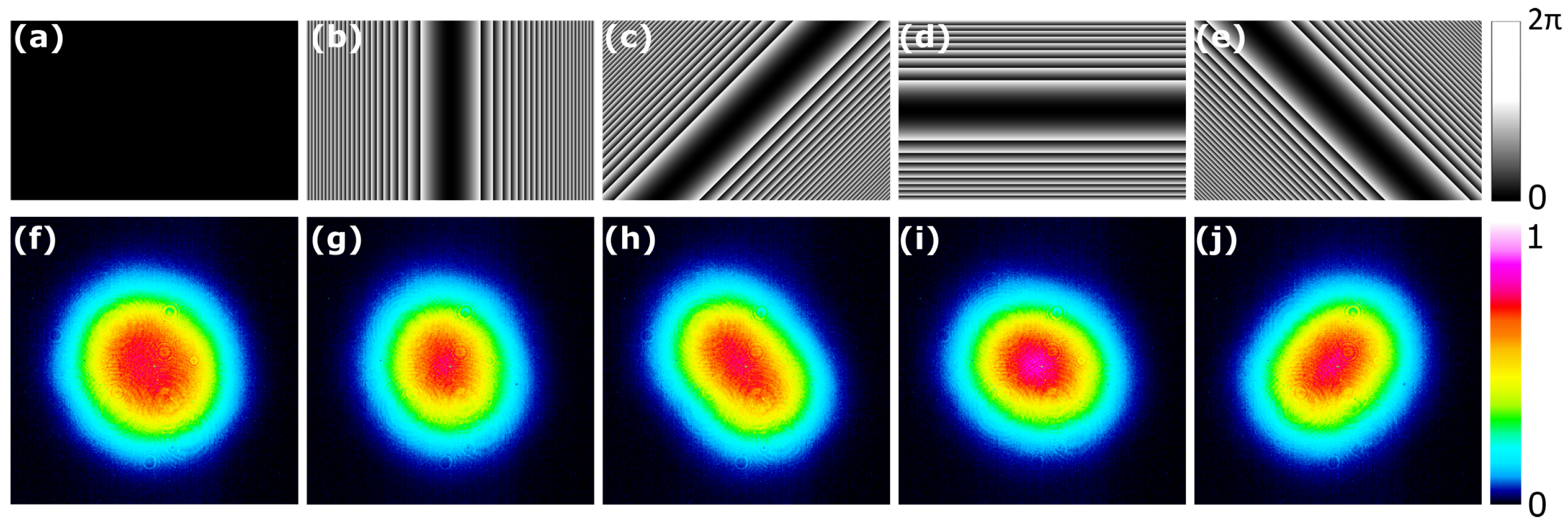
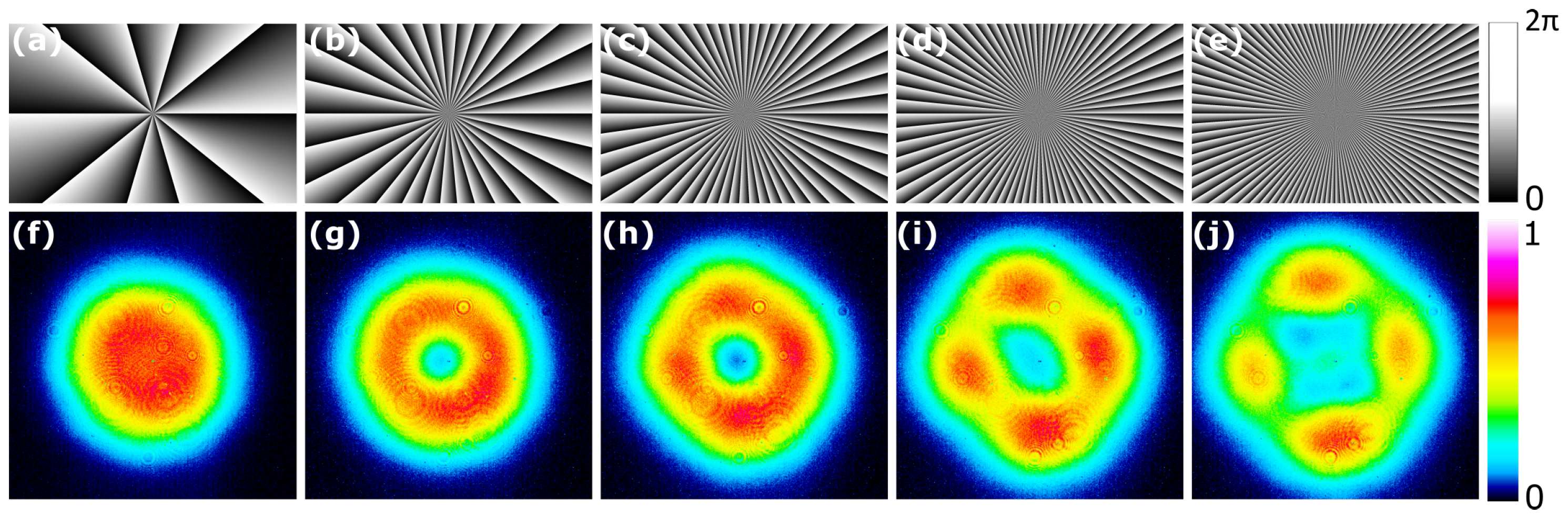
2.1. Models for Phase Mask Selection
2.2. Experimental Setup
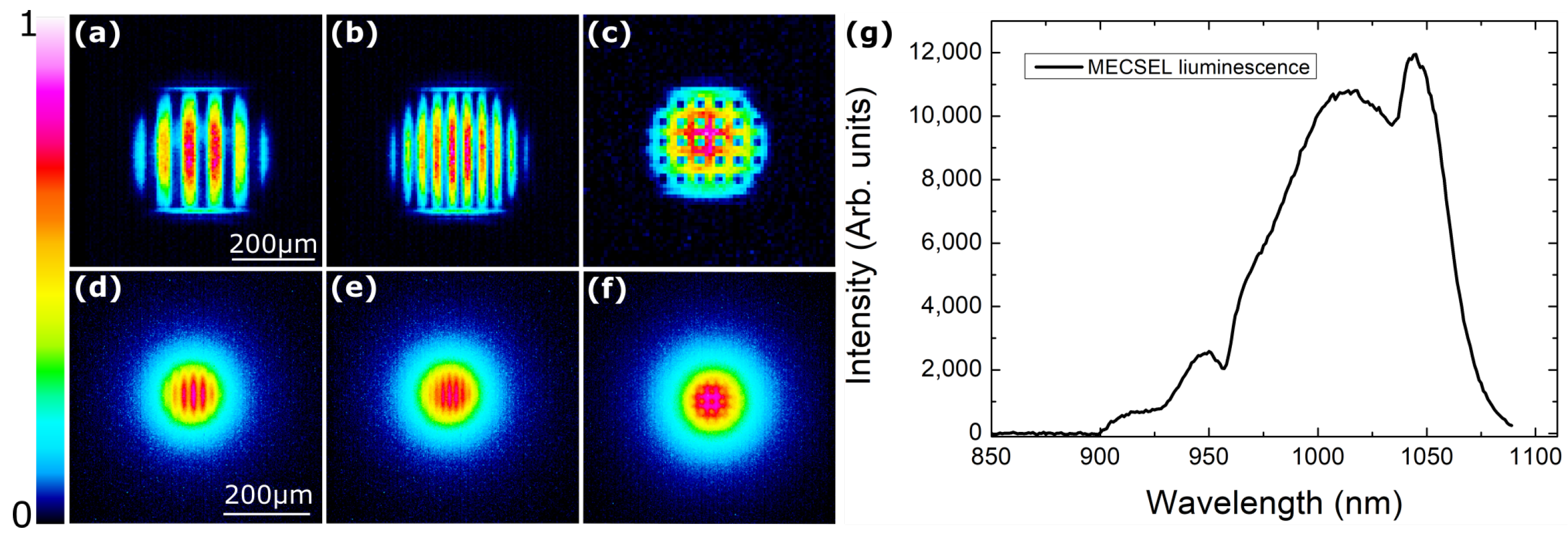
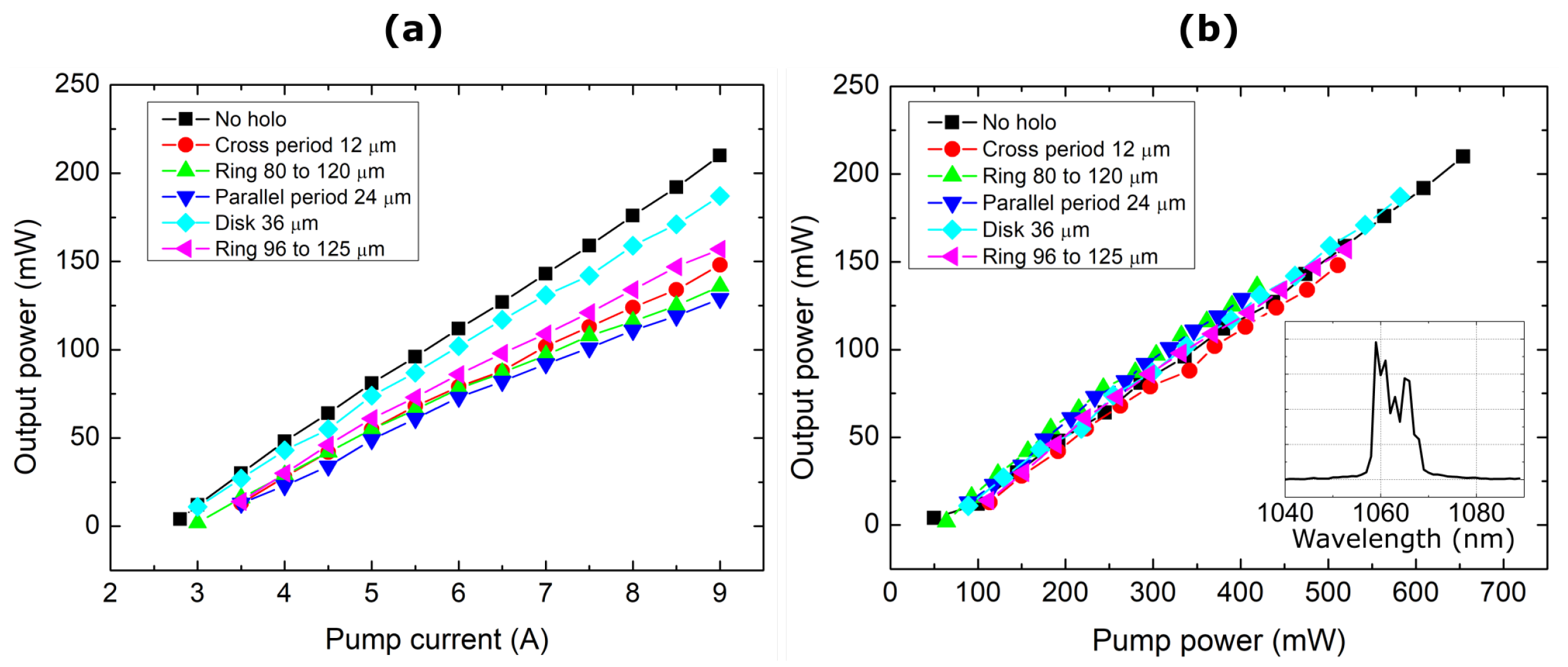
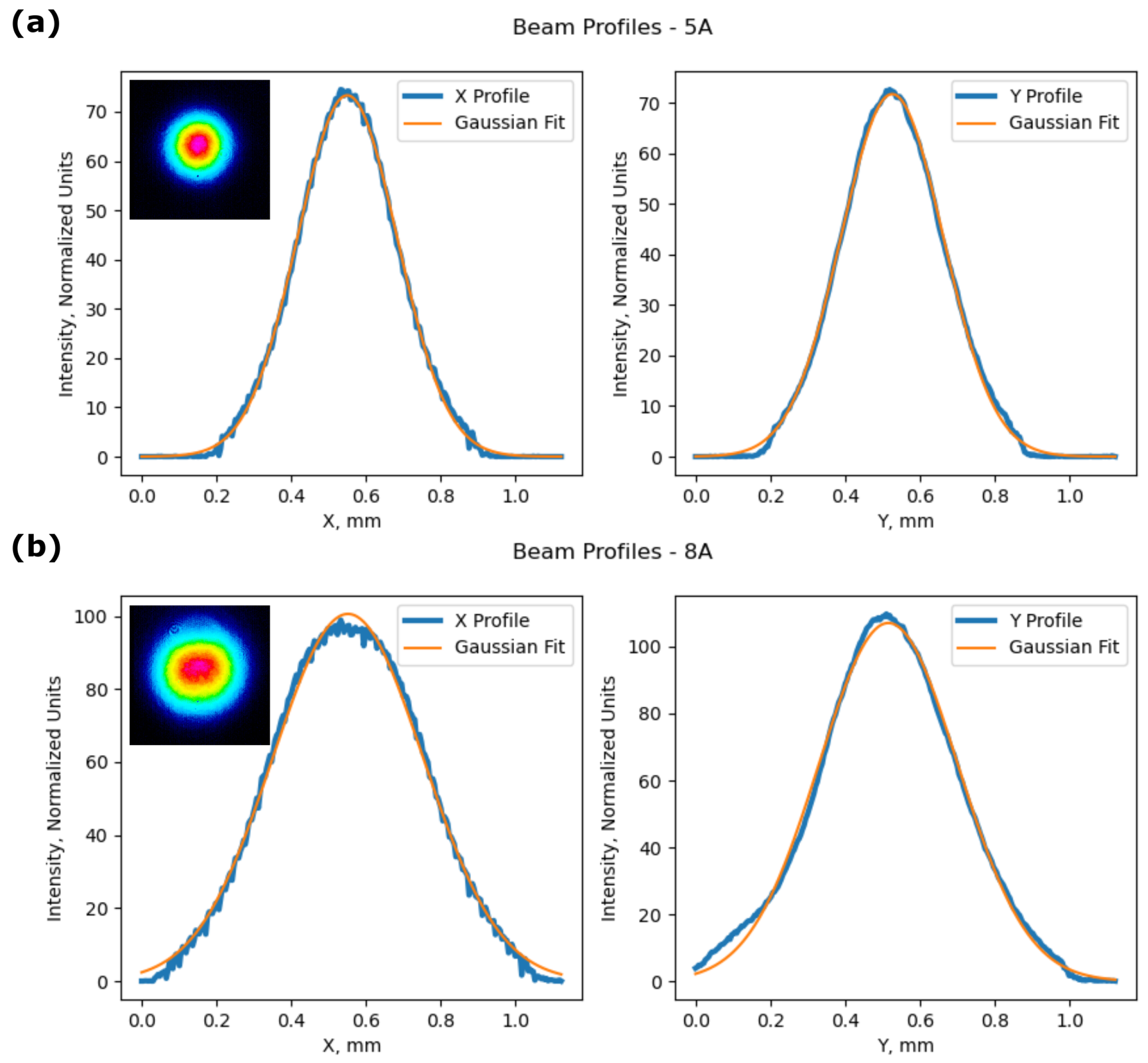
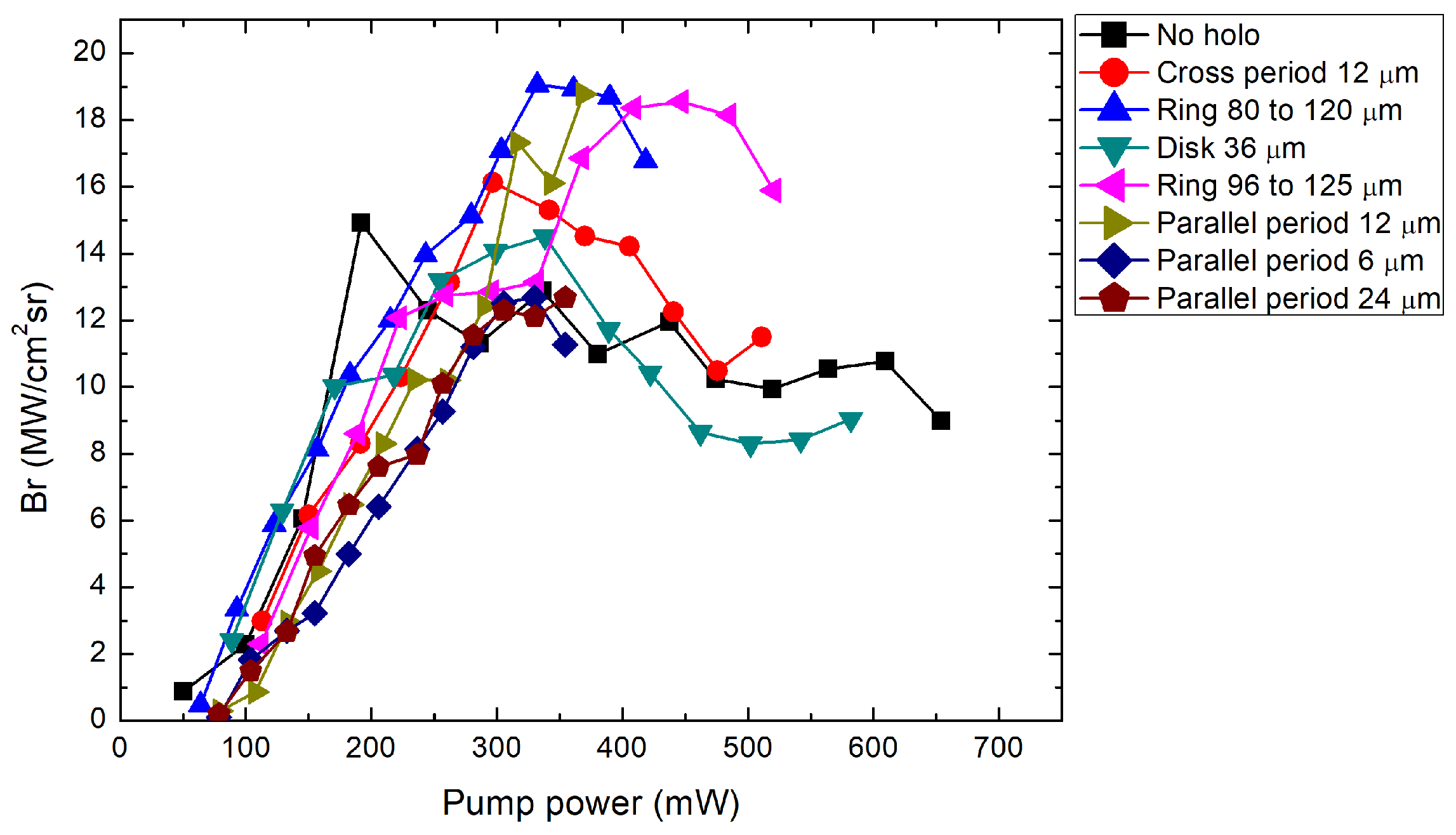
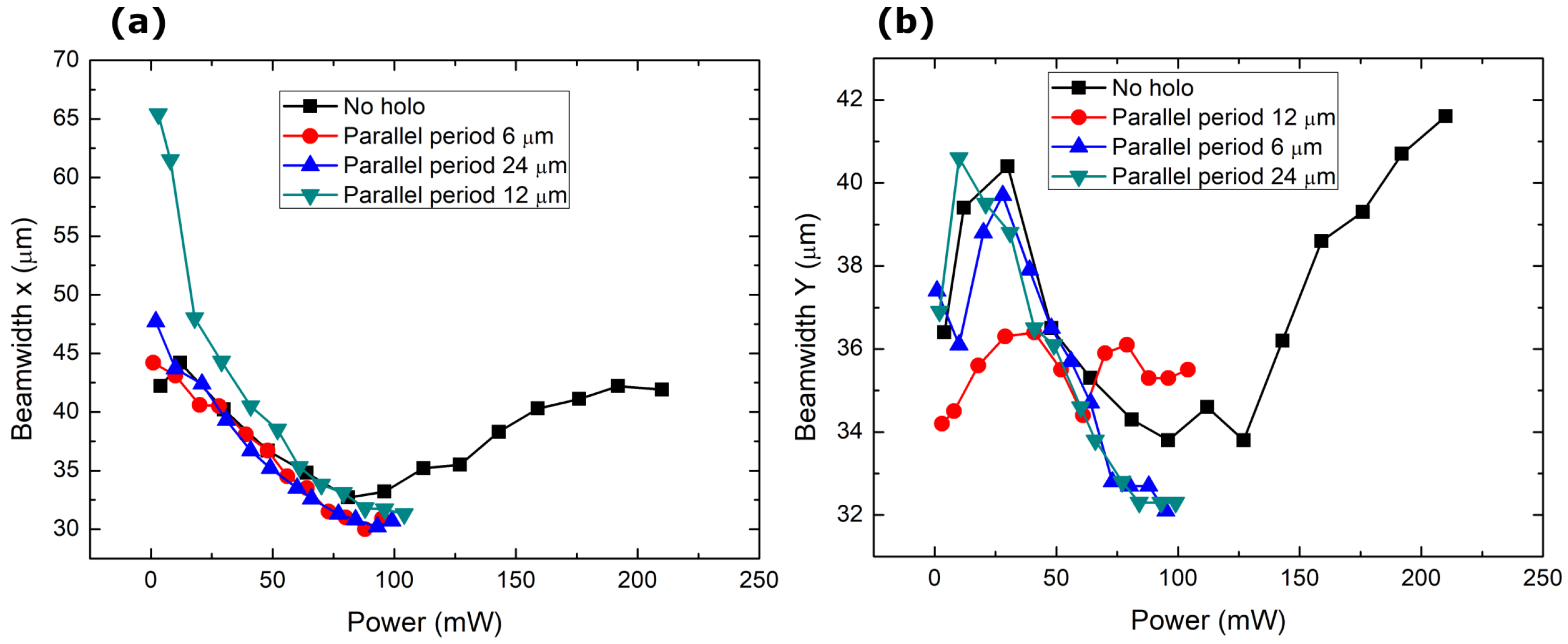
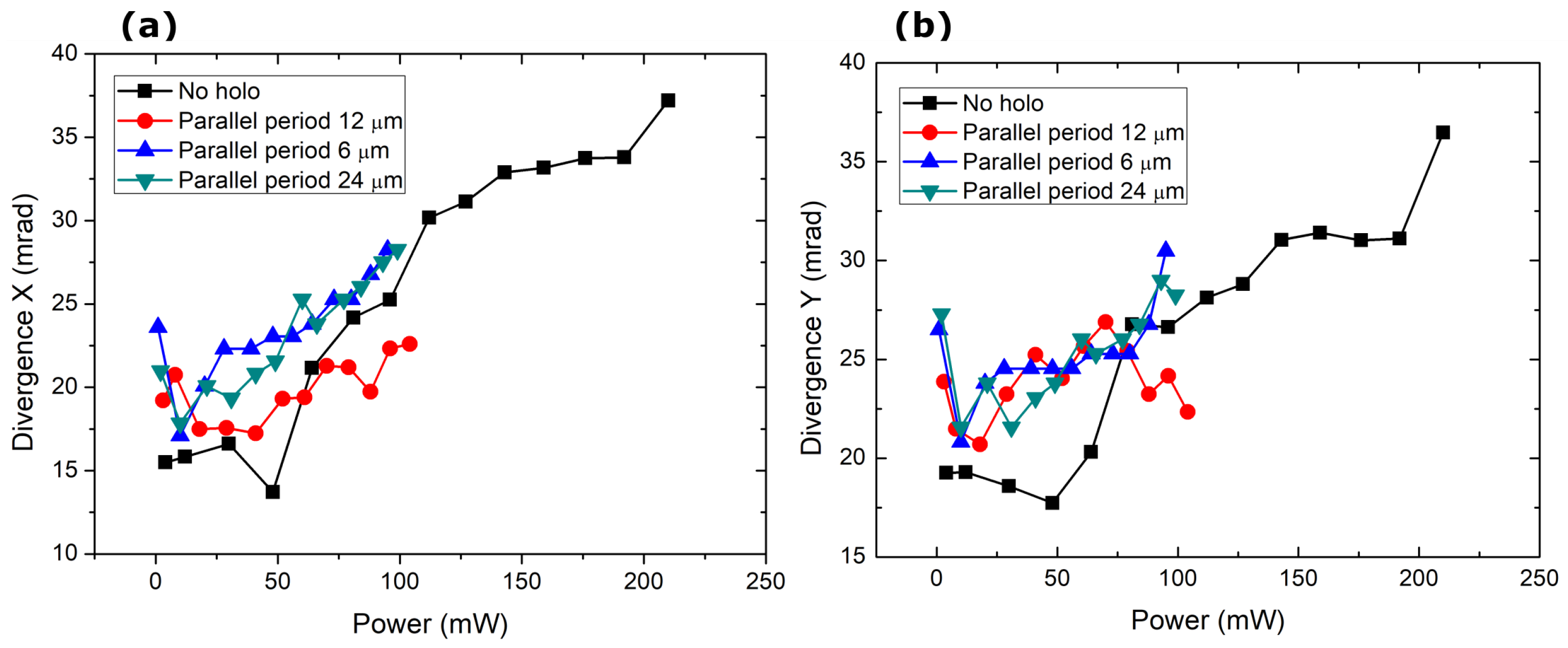
3. Results
4. Materials and Methods
5. Discussion and Outlook
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SLM | Spatial Light Modulator |
| OC | Output Coupler |
| CCD | Charge Coupled Device |
| LG | Laguerre Gauss |
| VCSEL | Vertical Cavity Surface-Emitting Lasers |
| VECSEL | Vertical External Cavity Surface-Emitting Lasers |
| PCSEL | Photonic Crystal Surface-Emitting Lasers |
| PhC | Photonic Crystal |
| GL | Gain/Loss |
| CW | Continuous Wave |
| QCW | Quasi Continuous Wave |
| MECSEL | Membrane External Cavity Surface-Emitting Lasers |
| MEXL | Membrane eXternal cavity Lasers |
| DBR | Distributed Bragg Reflector |
| BAS | Broad Area Semiconductor |
| HR | High Reflecting |
| AR | Anti Reflecting |
References
- Siegman, A.E. Defining, measuring, and optimizing laser beam quality. In Proceedings of the SPIE 1868; Bhowmik, A., Ed.; SPIE: Bellingham, WA, USA, 1993; Volume V, pp. 2–12. [Google Scholar] [CrossRef]
- Shukla, P.; Lawrence, J.; Zhang, Y. Understanding laser beam brightness: A review and new prospective in material processing. Opt. Laser Technol. 2015, 75, 40–51. [Google Scholar] [CrossRef]
- Brauch, U.; Röcker, C.; Graf, T.; Abdou Ahmed, M. High-Power, High-Brightness Solid-State Laser Architectures and Their Characteristics; Springer: Berlin/Heidelberg, Germany, 2022; Volume 128, pp. 1–32. [Google Scholar] [CrossRef]
- Mukhopadhyay, P.K.; Ranganathan, K.; George, J.; Sharma, S.; Nathan, T. Effect of absorbed pump power on the quality of output beam from monolithic microchip lasers. Pramana 2002, 58, 657–668. [Google Scholar] [CrossRef]
- Plukys, M.; Gaizauskas, E.; Gailevicius, D.; Staliunas, K. Transverse modes and beam spatial quality in microchip lasers. Phys. Rev. A 2023, 107, 043505. [Google Scholar] [CrossRef]
- Vysotskii, D.V.; Elkin, N.N.; Napartovich, A.P.; Kozlovskii, V.I.; Lavrushin, B.M. Simulation of a longitudinally electron-beam-pumped nanoheterostructure semiconductor laser. Quantum Electron. 2009, 39, 1028–1032. [Google Scholar] [CrossRef]
- Laurain, A.; Hader, J.; Moloney, J.V. Modeling and experimental investigation of transverse mode dynamics in VECSEL. In Proceedings of the Vertical External Cavity Surface Emitting Lasers (VECSELs) IX, San Francisco, CA, USA, 5–6 February 2019; p. 12. [Google Scholar] [CrossRef]
- Staliunas, K.; Sánchez-Morcillo, V. Transverse Patterns in Nonlinear Optical Resonators; Springer Tracts in Modern Physics; Springer: Berlin/Heidelberg, Germany, 2003; Volume 183. [Google Scholar] [CrossRef]
- Ahmed, W.W.; Kumar, S.; Herrero, R.; Botey, M.; Radziunas, M.; Staliunas, K. Stabilization of flat-mirror vertical-external-cavity surface-emitting lasers by spatiotemporal modulation of the pump profile. Phys. Rev. A At. Mol. Opt. Phys. 2015, 92, 043829. [Google Scholar] [CrossRef]
- Tiaw, K.S.; Hong, M.H.; Teoh, S.H. Precision laser micro-processing of polymers. J. Alloys Compd. 2008, 449, 228–231. [Google Scholar] [CrossRef]
- Daykin, J.; Woods, J.R.C.; Bek, R.; Jetter, M.; Michler, P.; Mills, B.; Horak, P.; Wilkinson, J.S.; Apostolopoulos, V. Bi-frequency operation in a membrane external-cavity surface-emitting laser. PLoS ONE 2023, 18, e0289223. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, B. Analysis of beam quality for the laser beams after spectral beam combining. Optik 2010, 121, 1236–1242. [Google Scholar] [CrossRef]
- Sakata, R.; Ishizaki, K.; De Zoysa, M.; Fukuhara, S.; Inoue, T.; Tanaka, Y.; Iwata, K.; Hatsuda, R.; Yoshida, M.; Gelleta, J.; et al. Dually modulated photonic crystals enabling high-power high-beam-quality two-dimensional beam scanning lasers. Nat. Commun. 2020, 11, 3487. [Google Scholar] [CrossRef] [PubMed]
- Hughes, D.; Barr, J. Laser diode pumped solid state lasers. J. Phys. D Appl. Phys. 1992, 25, 563. [Google Scholar] [CrossRef][Green Version]
- Spreemann, M.; Eppich, B.; Schnieder, F.; Wenzel, H.; Erbert, G. Modal behavior, spatial coherence, and beam quality of a high-power gain-guided laser array. IEEE J. Quantum Electron. 2010, 46, 1619–1625. [Google Scholar] [CrossRef]
- Huang, M.; Zhao, F.; Cheng, Y.; Xu, N.; Xu, Z. Large area uniform nanostructures fabricated by direct femtosecond laser ablation. Opt. Express 2008, 16, 19354–19365. [Google Scholar] [CrossRef] [PubMed]
- Mercier, B.; Rousseau, J.P.; Jullien, A.; Antonucci, L. Nonlinear beam shaper for femtosecond laser pulses, from Gaussian to flat-top profile. Opt. Commun. 2010, 283, 2900–2907. [Google Scholar] [CrossRef]
- Vetter, C.; Giust, R.; Furfaro, L.; Billet, C.; Froehly, L.; Courvoisier, F. High aspect ratio structuring of glass with ultrafast bessel beams. Materials 2021, 14, 6749. [Google Scholar] [CrossRef] [PubMed]
- Hazra, L.N. Laser Beam Shaping. In Proceedings of the 2008 2nd National Workshop on Advanced Optoelectronic Materials and Devices, Varanasi, India, 22–24 December 2008; pp. 108–109. [Google Scholar]
- Morizur, J.F.; Nicholls, L.; Jian, P.; Armstrong, S.; Treps, N.; Hage, B.; Hsu, M.; Bowen, W.; Janousek, J.; Bachor, H.A. Programmable unitary spatial mode manipulation. J. Opt. Soc. Am. A 2010, 27, 2524. [Google Scholar] [CrossRef] [PubMed]
- Dickey, F. Laser Beam Shaping: Theory and Techniques, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Naidoo, D.; Godin, T.; Fromager, M.; Cagniot, E.; Passilly, N.; Forbes, A.; Aït-Ameur, K. Transverse mode selection in a monolithic microchip laser. Opt. Commun. 2011, 284, 5475–5479. [Google Scholar] [CrossRef]
- Lin, D.; Andrew Clarkson, W. End-pumped Nd:YVO4 laser with reduced thermal lensing via the use of a ring-shaped pump beam. Opt. Lett. 2017, 42, 2910. [Google Scholar] [CrossRef]
- Tahir Jamal, M.; Hansen, A.K.; Tawfieq, M.; Andersen, P.E.; Jensen, O.B. Influence of pump beam shaping and noise on performance of a direct diode-pumped ultrafast Ti:sapphire laser. Opt. Express 2020, 28, 31754. [Google Scholar] [CrossRef]
- Seghilani, M.; Myara, M.; Sagnes, I.; Chomet, B.; Bendoula, R.; Garnache, A. Self-mixing in low-noise semiconductor vortex laser: Detection of a rotational Doppler shift in backscattered light. Opt. Lett. 2015, 40, 5778. [Google Scholar] [CrossRef]
- Seghilani, M.S.; Myara, M.; Sellahi, M.; Legratiet, L.; Sagnes, I.; Beaudoin, G.; Lalanne, P.; Garnache, A. Vortex Laser based on III-V semiconductor metasurface: Direct generation of coherent Laguerre-Gauss modes carrying controlled orbital angular momentum. Sci. Rep. 2016, 6, 38156. [Google Scholar] [CrossRef]
- Sagnes, I.; Myara, M.; Garnache, A.; Sellahi, M.; Seghilani, M.S.; Beaudoin, G.; Lafosse, X.; Legratiet, L.; Lalanne, P. Generation of New Spatial and Temporal Coherent States Using VECSEL Technology: VORTEX, High Order Laguerre-Gauss Mode, Continuum Source. In Proceedings of the International Conference on Space Optics—ICSO 2014, Tenerife, Spain, 6–10 October 2014; SPIE: Bellingham, WA, USA, 2017; Volume 10563, p. 23. [Google Scholar] [CrossRef]
- Zhang, Z.; Hai, L.; Fu, S.; Gao, C. Advances on Solid-State Vortex Laser. Photonics 2022, 9, 215. [Google Scholar] [CrossRef]
- Voss, A.; Abdou-Ahmed, M.; Neugebauer, C.; Giesen, A.; Graf, T. Intracavity beam shaping for high power thin-disk lasers. In Proceedings of the XVI International Symposium on Gas Flow, Chemical Lasers, and High-Power Lasers, Gmunden, Austria, 4–8 September 2006; Volume 6346, p. 63461U. [Google Scholar] [CrossRef]
- Yang, P.; Liu, Y.; Yang, W.; Ao, M.W.; Hu, S.J.; Xu, B.; Jiang, W.H. Adaptive mode optimization of a continuous-wave solid-state laser using an intracavity piezoelectric deformable mirror. Opt. Commun. 2007, 278, 377–381. [Google Scholar] [CrossRef]
- Ngcobo, S.; Litvin, I.; Burger, L.; Forbes, A. A digital laser for on-demand laser modes. Nat. Commun. 2013, 4, 2289. [Google Scholar] [CrossRef]
- Lukowski, M.L.; Meyer, J.T.; Hessenius, C.; Wright, E.M.; Fallahi, M. Generation of high-power spatially structured beams using vertical external cavity surface emitting lasers. Opt. Express 2017, 25, 25504. [Google Scholar] [CrossRef]
- Litvin, I.A.; King, G.; Strauss, H. Beam shaping laser with controllable gain. Appl. Phys. B Lasers Opt. 2017, 123, 174. [Google Scholar] [CrossRef]
- Yoshida, M.; De Zoysa, M.; Ishizaki, K.; Kunishi, W.; Inoue, T.; Izumi, K.; Hatsuda, R.; Noda, S. Photonic-crystal lasers with high-quality narrow-divergence symmetric beams and their application to LiDAR. J. Phys. Photonics 2021, 3, 022006. [Google Scholar] [CrossRef]
- Litvin, I.A. Implementation of intra-cavity beam shaping technique to enhance pump efficiency. J. Mod. Opt. 2012, 59, 241–244. [Google Scholar] [CrossRef]
- Naidoo, D.; Litvin, I.A.; Forbes, A. Brightness enhancement in a solid-state laser by mode transformation: Publisher’s note. Optica 2018, 5, 1135. [Google Scholar] [CrossRef]
- Bouzid, O.; Hasnaoui, A.; Ait-Ameur, K. Simple intra-cavity beam shaping for generating a shape-invariant flat-top laser beam. Optik 2020, 201, 163494. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, Q.; Shan, X.; Miao, Y.; Gao, X. Generation of high-order Gaussian beams by resonator with deformed steel wire. Optik 2019, 183, 124–130. [Google Scholar] [CrossRef]
- Alford, W.J.; Fetzer, G.J.; Epstein, R.J.; Sandalphon; Van Lieu, N.; Ranta, S.; Tavast, M.; Leinonen, T.; Guina, M. Optically pumped semiconductor lasers for precision spectroscopic applications. IEEE J. Quantum Electron. 2013, 49, 719–727. [Google Scholar] [CrossRef]
- Tropper, A.C.; Foreman, H.D.; Garnache, A.; Wilcox, K.G.; Hoogland, S.H. Vertical-external-cavity semiconductor lasers. J. Phys. D Appl. Phys. 2004, 37, R75. [Google Scholar] [CrossRef]
- Lee, J.H.; Kim, J.Y.; Lee, S.M.; Yoo, J.R.; Kim, K.S.; Cho, S.H.; Lim, S.J.; Kim, G.B.; Hwang, S.M.; Kim, T.; et al. 9.1-W high-efficient continuous-wave end-pumped vertical-external-cavity surface-emitting semiconductor laser. IEEE Photonics Technol. Lett. 2006, 18, 2117–2119. [Google Scholar] [CrossRef]
- Sanchez, F.; Chardon, A. Transverse modes in microchip lasers. J. Opt. Soc. Am. B 1996, 13, 2869. [Google Scholar] [CrossRef]
- Fan, L.; Fallahi, M.; Murray, J.T.; Bedford, R.; Kaneda, Y.; Zakharian, A.R.; Hader, J.; Moloney, J.V.; Stolz, W.; Koch, S.W. Tunable high-power high-brightness linearly polarized vertical-external-cavity surface-emitting lasers. Appl. Phys. Lett. 2006, 88, 021105. [Google Scholar] [CrossRef]
- Guina, M.; Rantamäki, A.; Härkönen, A. Optically pumped VECSELs: Review of technology and progress. J. Phys. D Appl. Phys. 2017, 50, 383001. [Google Scholar] [CrossRef]
- Broda, A.; Jezewski, B.; Szymanski, M.; Muszalski, J. High-Power 1770 nm Emission of a Membrane External-Cavity Surface-Emitting Laser. IEEE J. Quantum Electron. 2020, 57, 2400106. [Google Scholar] [CrossRef]
- Giesen, A.; Hügel, H.; Voss, A.; Wittig, K.; Brauch, U.; Opower, H. Scalable concept for diode-pumped high-power solid-state lasers. Appl. Phys. B Lasers Opt. 1994, 58, 365–372. [Google Scholar] [CrossRef]
- Iakovlev, V.; Walczak, J.; Gebski, M.; Sokół, A.K.; Wasiak, M.; Gallo, P.; Sirbu, A.; Sarzała, R.P.; Dems, M.; Czyszanowski, T.; et al. Double-diamond high-contrast-gratings vertical external cavity surface emitting laser. J. Phys. D Appl. Phys. 2014, 47, 065104. [Google Scholar] [CrossRef]
- Keeler, G.A.; Serkland, D.K.; Geib, K.M.; Peake, G.M.; Mar, A. Single transverse mode operation of electrically pumped vertical-external-cavity surface-emitting lasers with micromirrors. IEEE Photonics Technol. Lett. 2005, 17, 522–524. [Google Scholar] [CrossRef]
- Grineviciute, L.; Babayigit, C.; Gailevičius, D.; Bor, E.; Turduev, M.; Purlys, V.; Tolenis, T.; Kurt, H.; Staliunas, K. Angular filtering by Bragg photonic microstructures fabricated by physical vapour deposition. Appl. Surf. Sci. 2019, 481, 353–359. [Google Scholar] [CrossRef]
- Grineviciute, L.; Babayigit, C.; Gailevičius, D.; Peckus, M.; Turduev, M.; Tolenis, T.; Vengris, M.; Kurt, H.; Staliunas, K. Nanostructured Multilayer Coatings for Spatial Filtering. Adv. Opt. Mater. 2021, 9, 2001730. [Google Scholar] [CrossRef]
- Babayigit, C.; Grineviciute, L.; Nikitina, J.; Melnikas, S.; Gailevicius, D.; Staliunas, K. Inverse designed photonic crystals for spatial filtering. Appl. Phys. Lett. 2023, 122, 244103. [Google Scholar] [CrossRef]
- Hirose, K.; Liang, Y.; Kurosaka, Y.; Watanabe, A.; Sugiyama, T.; Noda, S. Watt-class high-power, high-beam-quality photonic-crystal lasers. Nat. Photonics 2014, 8, 406–411. [Google Scholar] [CrossRef]
- Gawali, S.; Gailevičius, D.; Garre-Werner, G.; Purlys, V.; Cojocaru, C.; Trull, J.; Montiel-Ponsoda, J.; Staliunas, K. Photonic crystal spatial filtering in broad aperture diode laser. Appl. Phys. Lett. 2019, 115, 141104. [Google Scholar] [CrossRef]
- Gawali, S.; Medina, J.; Gailevičius, D.; Purlys, V.; Garre-Werner, G.; Cojocaru, C.; Trull, J.; Botey, M.; Herrero, R.; Montiel-Ponsoda, J.; et al. Spatial filtering in edge-emitting lasers by intracavity chirped photonic crystals. J. Opt. Soc. Am. B 2020, 37, 2856. [Google Scholar] [CrossRef]
- King, B.C.; Rae, K.J.; McKenzie, A.F.; Boldin, A.; Kim, D.; Gerrard, N.D.; Li, G.; Nishi, K.; Takemasa, K.; Sugawara, M.; et al. Coherent power scaling in photonic crystal surface emitting laser arrays. AIP Adv. 2021, 11, 015017. [Google Scholar] [CrossRef]
- Gailevicius, D.; Koliadenko, V.; Purlys, V.; Peckus, M.; Taranenko, V.; Staliunas, K. Photonic Crystal Microchip Laser. Sci. Rep. 2016, 6, 34173. [Google Scholar] [CrossRef]
- Smirnov, A.M.; Golinskaya, A.D.; Ezhova, K.V.; Mantsevich, V.N.; Dneprovskii, V.S. Self-Diffraction at a Dynamic Photonic Crystal Formed in a Colloidal Solution of Quantum Dots. JETP Lett. 2016, 104, 674–678. [Google Scholar] [CrossRef]
- Smirnov, A.M.; Ezhova, K.V.; Mantsevich, V.N.; Dneprovskii, V.S. Dynamic photonic crystal in a colloidal quantum-dot solution: Formation, structure analysis, and dimensionality switching. Opt. Lett. 2020, 45, 2415. [Google Scholar] [CrossRef]
- Ishaaya, A.A.; Davidson, N.; Friesem, A.A. Passive laser beam combining With intracavity interferometric combiners. IEEE J. Sel. Top. Quantum Electron. 2009, 15, 301–311. [Google Scholar] [CrossRef]
- Fernández-Pousa, C.R.; Flores-Arias, M.T.; Bao, C.; Pérez, M.V.; Gómez-Reino, C. Talbot conditions, Talbot resonators, and first-order systems. J. Opt. Soc. Am. A 2003, 20, 638. [Google Scholar] [CrossRef]
- Ciofini, M.; Lapucci, A. Guided Talbot resonators for annular laser sources. J. Opt. A Pure Appl. Opt. 2000, 2, 223–227. [Google Scholar] [CrossRef]
- Cassarly, W.J.; Finlan, J.M.; Waarts, R.; Mehuys, D.; Flood, K.M.; Ehlert, J.C.; Nam, D.; Welch, D. Intracavity phase correction of an external Talbot cavity laser with the use of liquid crystals. Opt. Lett. 1992, 17, 607. [Google Scholar] [CrossRef]
- Herrero, R.; Botey, M.; Radziunas, M.; Staliunas, K. Beam shaping in spatially modulated broad area semiconductor amplifiers. In Proceedings of the 2013 Conference on Lasers & Electro-Optics Europe & International Quantum Electronics Conference CLEO EUROPE/IQEC, Munich, Germany, 12–16 May 2013; Volume 37, pp. 5253–5255. [Google Scholar] [CrossRef]
- Salter, P.S.; Iqbal, Z.; Booth, M.J. Analysis of the Three-Dimensional Focal Positioning Capability of Adaptive Optic Elements. Int. J. Optomechatroni. 2013, 7, 1–14. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kontenis, G.; Gailevicius, D.; Taranenko, V.; Staliunas, K. Spatially Structured Optical Pump for Laser Generation Tuning. Nanomaterials 2024, 14, 49. https://doi.org/10.3390/nano14010049
Kontenis G, Gailevicius D, Taranenko V, Staliunas K. Spatially Structured Optical Pump for Laser Generation Tuning. Nanomaterials. 2024; 14(1):49. https://doi.org/10.3390/nano14010049
Chicago/Turabian StyleKontenis, Gabrielius, Darius Gailevicius, Victor Taranenko, and Kestutis Staliunas. 2024. "Spatially Structured Optical Pump for Laser Generation Tuning" Nanomaterials 14, no. 1: 49. https://doi.org/10.3390/nano14010049
APA StyleKontenis, G., Gailevicius, D., Taranenko, V., & Staliunas, K. (2024). Spatially Structured Optical Pump for Laser Generation Tuning. Nanomaterials, 14(1), 49. https://doi.org/10.3390/nano14010049





