Description of Short-Range Interactions of Carbon-Based Materials with a Combined AIREBO and ZBL Potential
Abstract
:1. Introduction
2. Materials and Methods
2.1. Interatomic Potential Description
2.2. Interatomic Potential Integration
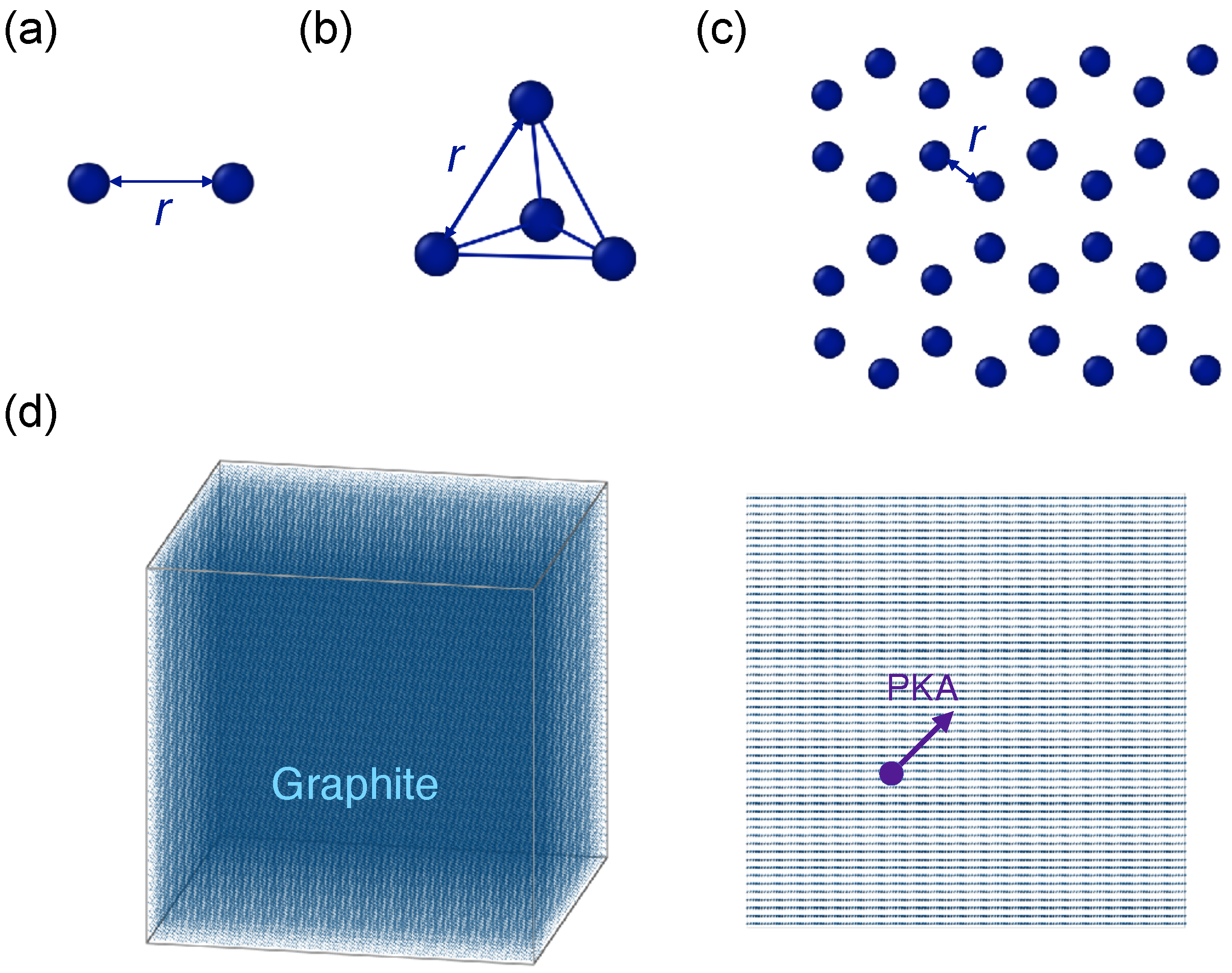
2.3. Simulation Setup for Potential Comparison
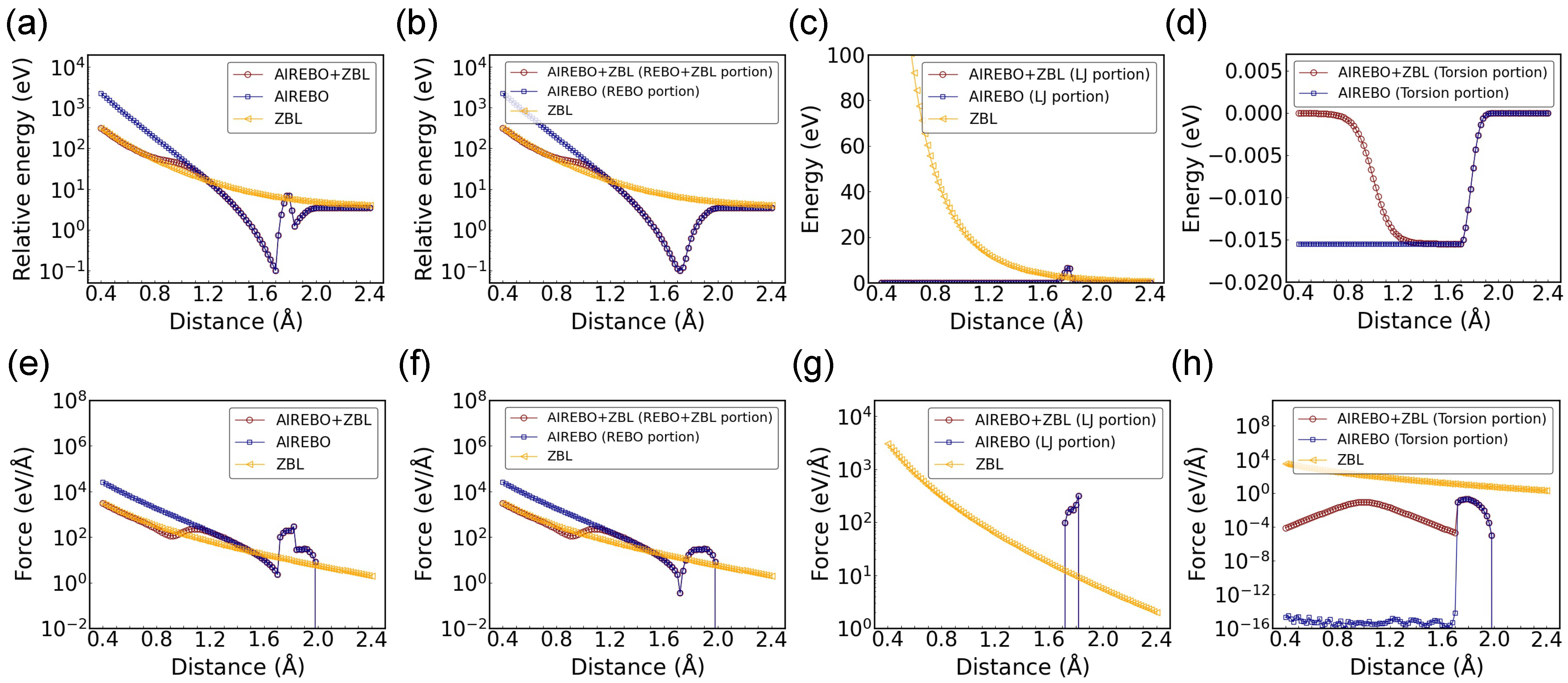
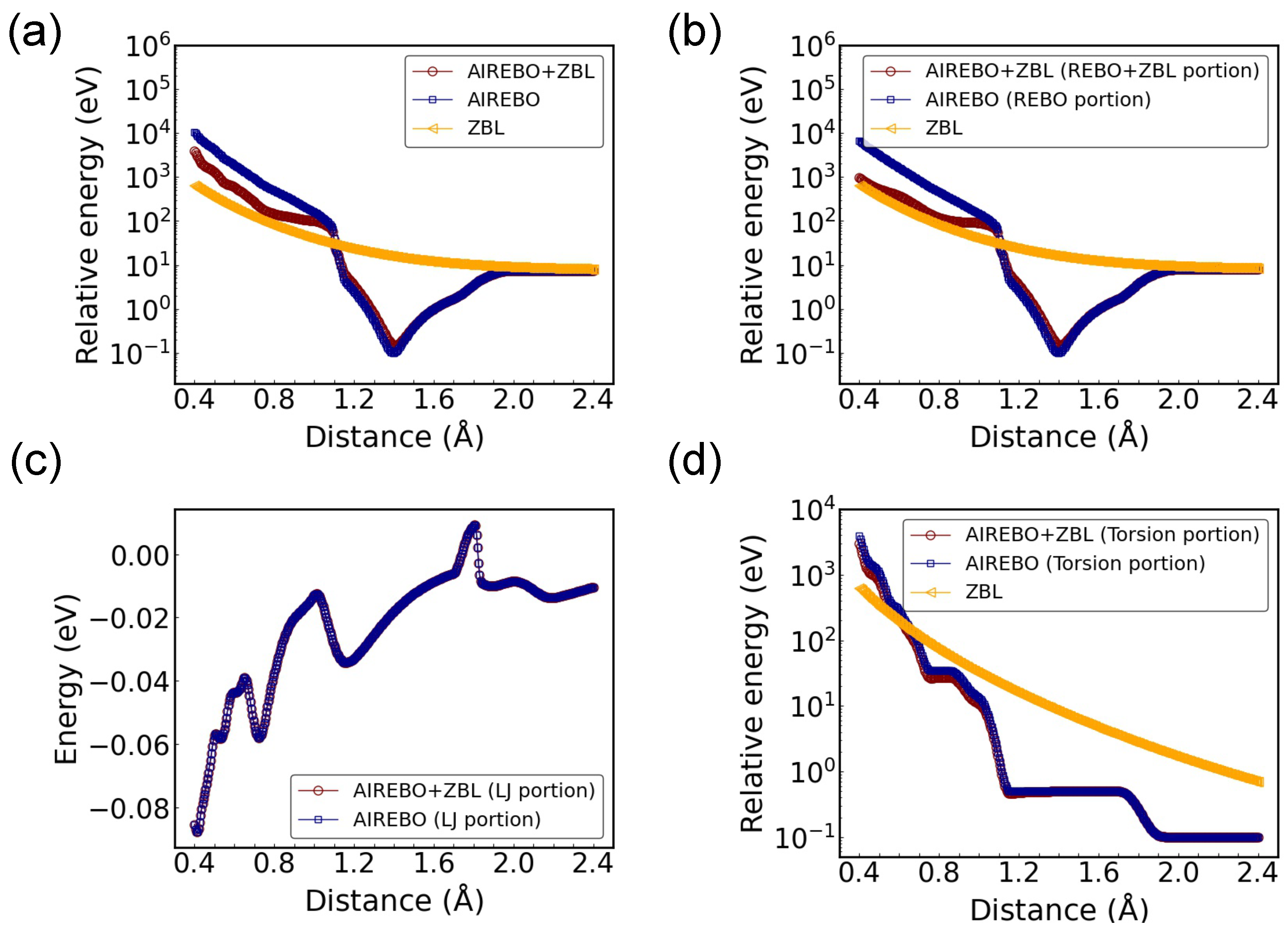
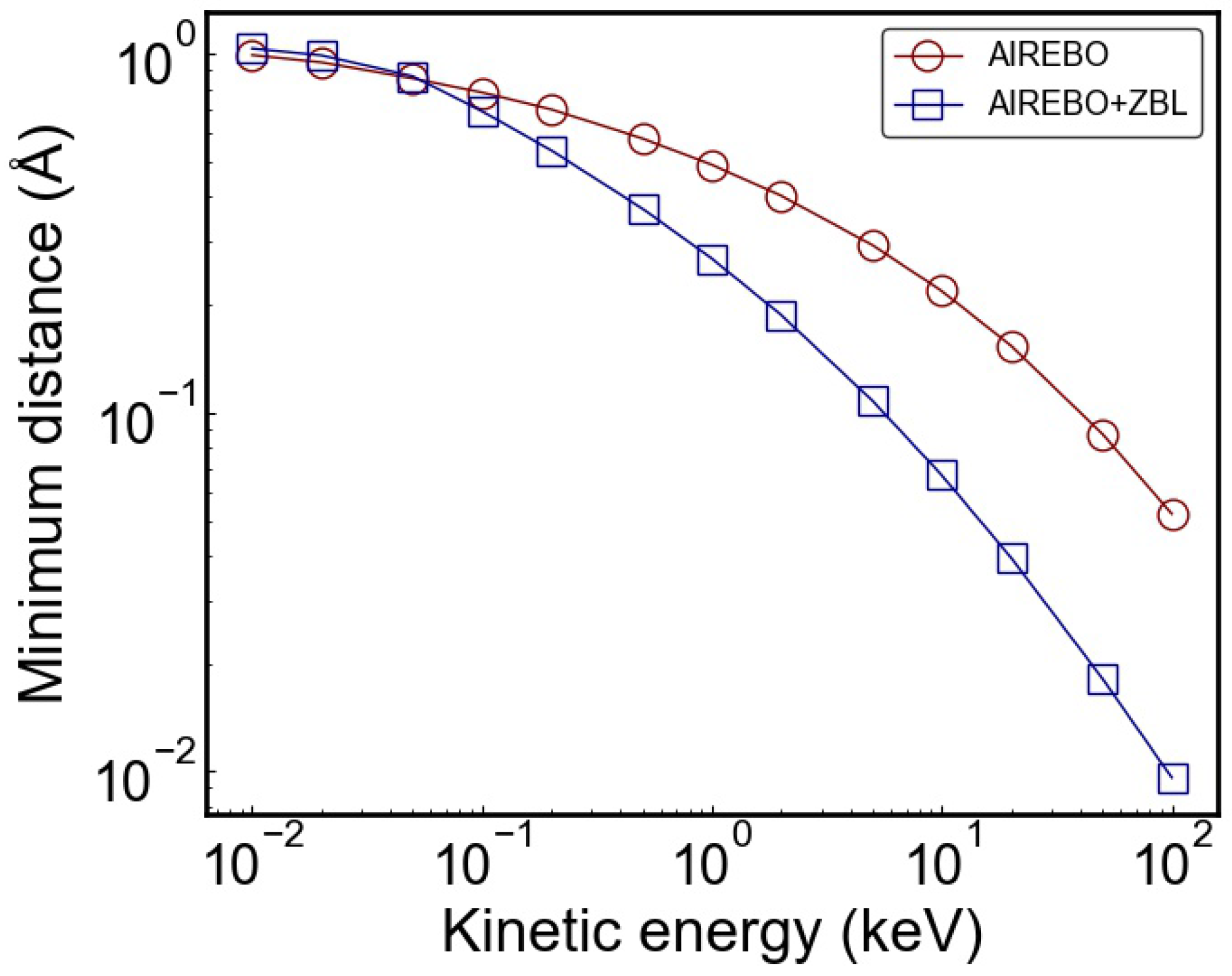
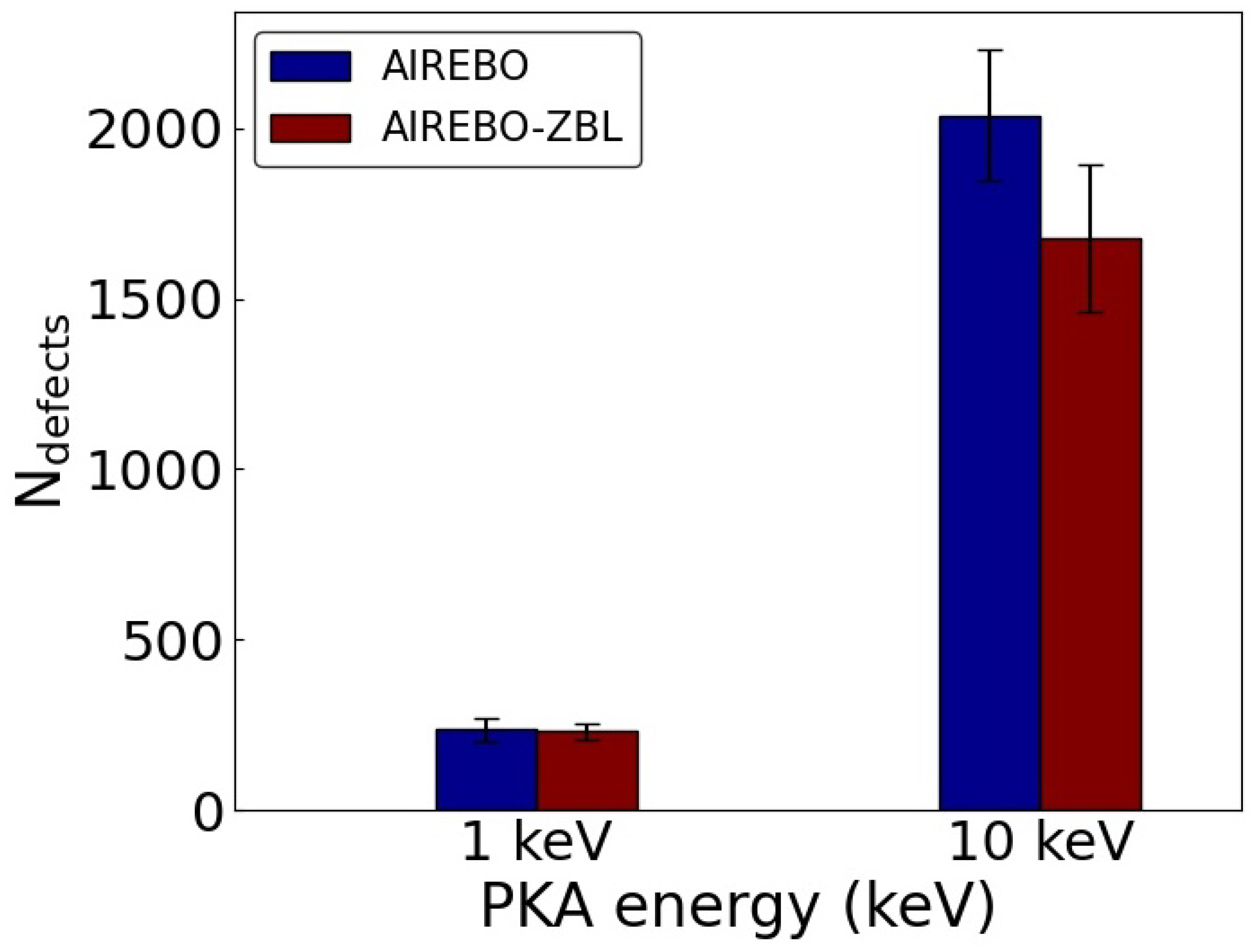
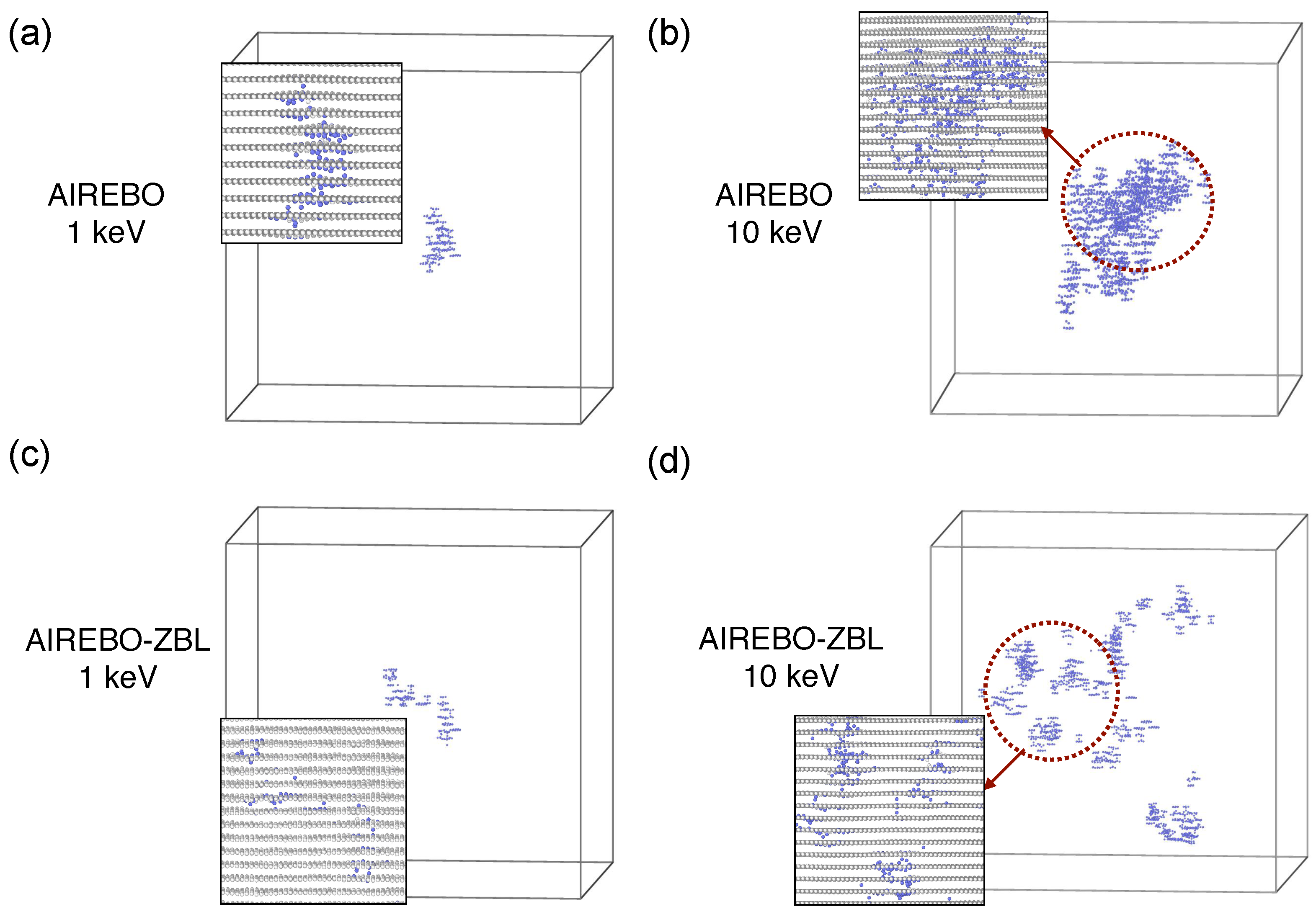
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AIREBO | adaptive intermolecular reactive empirical bond-order |
| LAMMPS | large-scale atomic/molecular massively parallel simulator |
| LJ | Lennard-Jones |
| MD | molecular dynamics |
| PKA | primary knock-on atom |
| REBO | reactive empirical bond-order |
| ZBL | Ziegler-Biersack-Littmark |
References
- Shi, T.; Peng, Q.; Bai, Z.; Gao, F.; Jovanovic, I. Proton irradiation of graphene: Insights from atomistic modeling. Nanoscale 2019, 11, 20754–20765. [Google Scholar] [CrossRef] [PubMed]
- Walker, R.; Shi, T.; Silva, E.; Jovanovic, I.; Robinson, J. Radiation effects on two-dimensional materials. Phys. Status Solidi (A) 2016, 213, 3065–3077. [Google Scholar] [CrossRef]
- Su, S.; Xue, J. Facile fabrication of subnanopores in graphene under ion irradiation: Molecular dynamics simulations. ACS Appl. Mater. Interfaces 2021, 13, 12366–12374. [Google Scholar] [CrossRef] [PubMed]
- Lehtinen, O.; Kotakoski, J.; Krasheninnikov, A.; Tolvanen, A.; Nordlund, K.; Keinonen, J. Effects of ion bombardment on a two-dimensional target: Atomistic simulations of graphene irradiation. Phys. Rev. B 2010, 81, 153401. [Google Scholar] [CrossRef]
- Wu, X.; Zhao, H.; Pei, J. Fabrication of nanopore in graphene by electron and ion beam irradiation: Influence of graphene thickness and substrate. Comput. Mater. Sci. 2015, 102, 258–266. [Google Scholar] [CrossRef]
- Dai, J.; Zhang, C.; Mao, F.; Cheng, W.; Zhang, F.S. Dynamical processes of low-energy carbon ion collision with the graphene supported by diamond. Eur. Phys.-J.-Appl. Phys. 2014, 67, 30402. [Google Scholar] [CrossRef]
- Wu, X.; Zhu, X. Molecular dynamics simulations of ion beam irradiation on graphene/MoS2 heterostructure. Sci. Rep. 2021, 11, 21113. [Google Scholar] [CrossRef]
- Zhao, S.; Xue, J. Modification of graphene supported on SiO2 substrate with swift heavy ions from atomistic simulation point. Carbon 2015, 93, 169–179. [Google Scholar] [CrossRef]
- Luketić, K.T.; Gajović, A.; Karlušić, M. High-energy heavy ions as a tool for production of nanoporous graphene. Appl. Surf. Sci. 2024, 669, 160593. [Google Scholar] [CrossRef]
- Delaunay, R.; Gatchell, M.; Mika, A.; Domaracka, A.; Adoui, L.; Zettergren, H.; Cederquist, H.; Rousseau, P.; Huber, B.A. Shock-driven formation of covalently bound carbon nanoparticles from ion collisions with clusters of C60 fullerenes. Carbon 2018, 129, 766–774. [Google Scholar] [CrossRef]
- Kumar, R.; Mohan, K.; Augusthy, A.; Bari, S.; Parhi, A.P.; Kelkar, A.H.; Chakravarty, S.; Shukla, N. Tunable room temperature ferromagnetism in fullerene thin film induced by 1 MeV proton microbeam irradiation. Thin Solid Film. 2022, 755, 139350. [Google Scholar] [CrossRef]
- Krasheninnikov, A.; Nordlund, K. Irradiation effects in carbon nanotubes. Nucl. Instruments Methods Phys. Res. Sect. Beam Interact. Mater. Atoms 2004, 216, 355–366. [Google Scholar] [CrossRef]
- Stepanov, A.; Filippov, G. Channeling of low energy atomic particles in carbon nanotubes with heterojunctions. Nucl. Instruments Methods Phys. Res. Sect. Beam Interact. Mater. Atoms 2017, 402, 263–266. [Google Scholar] [CrossRef]
- Pomoell, J.; Krasheninnikov, A.; Nordlund, K.; Keinonen, J. Ion ranges and irradiation-induced defects in multiwalled carbon nanotubes. J. Appl. Phys. 2004, 96, 2864–2871. [Google Scholar] [CrossRef]
- Nordlund, K.; Keinonen, J.; Mattila, T. Formation of ion irradiation induced small-scale defects on graphite surfaces. Phys. Rev. Lett. 1996, 77, 699. [Google Scholar] [CrossRef]
- Zeng, J.; Liu, J.; Yao, H.J.; Zhai, P.F.; Zhang, S.X.; Guo, H.; Hu, P.P.; Duan, J.L.; Mo, D.; Hou, M.D.; et al. Comparative study of irradiation effects in graphite and graphene induced by swift heavy ions and highly charged ions. Carbon 2016, 100, 16–26. [Google Scholar] [CrossRef]
- Daulton, T.; Kirk, M.; Lewis, R.; Rehn, L. Production of nanodiamonds by high-energy ion irradiation of graphite at room temperature. Nucl. Instruments Methods Phys. Res. Sect. Beam Interact. Mater. Atoms 2001, 175, 12–20. [Google Scholar] [CrossRef]
- Guo, B.; Liu, Q.; Chen, E.; Zhu, H.; Fang, L.; Gong, J.R. Controllable N-doping of graphene. Nano Lett. 2010, 10, 4975–4980. [Google Scholar] [CrossRef]
- Nanda, G.; Goswami, S.; Watanabe, K.; Taniguchi, T.; Alkemade, P.F. Defect control and n-doping of encapsulated graphene by helium-ion-beam irradiation. Nano Lett. 2015, 15, 4006–4012. [Google Scholar] [CrossRef]
- Naitou, Y.; Iijima, T.; Ogawa, S. Direct nano-patterning of graphene with helium ion beams. Appl. Phys. Lett. 2015, 106. [Google Scholar] [CrossRef]
- Zhao, S.; Xue, J. Tuning the band gap of bilayer graphene by ion implantation: Insight from computational studies. Phys. Rev. B 2012, 86, 165428. [Google Scholar] [CrossRef]
- Liu, J.; Liang, T.; Lai, W.; Liu, Y. Morphology evolution and defect distribution in irradiated graphite from molecular dynamics. Comput. Mater. Sci. 2018, 155, 246–255. [Google Scholar] [CrossRef]
- Qin, X.; Yan, W.; Guo, X.; Gao, T.; Xie, Q. Molecular dynamics simulations of Si ion substituted graphene by bombardment. IOP Conf. Ser.: Mater. Sci. Eng. 2018, 394, 022020. [Google Scholar] [CrossRef]
- Ziegler, J.F.; Biersack, J.P. The stopping and range of ions in matter. In Treatise on Heavy-Ion Science: Volume 6: Astrophysics, Chemistry, and Condensed Matter; Springer: Berlin/Heidelberg, Germany, 1985; pp. 93–129. [Google Scholar]
- Qiu, R.; Chen, Y.; Liao, X.; He, X.; Yang, W.; Hu, W.; Deng, H. Finnis–Sinclair-type potential for atomistic simulation of defects behaviour in V-Ti-Ta ternary system. J. Nucl. Mater. 2021, 557, 153231. [Google Scholar] [CrossRef]
- Zhang, Z.; Su, Z.; Zhang, B.; Yu, Q.; Ding, J.; Shi, T.; Lu, C.; Ritchie, R.O.; Ma, E. Effect of local chemical order on the irradiation-induced defect evolution in CrCoNi medium-entropy alloy. Proc. Natl. Acad. Sci. USA 2023, 120, e2218673120. [Google Scholar] [CrossRef]
- Stuart, S.J.; Tutein, A.B.; Harrison, J.A. A reactive potential for hydrocarbons with intermolecular interactions. J. Chem. Phys. 2000, 112, 6472–6486. [Google Scholar] [CrossRef]
- Amini, M.; Azadegan, B. The role of various heterostructures on radiation tolerance of Cu-based nanocomposites. Phys. Scr. 2023, 98, 115406. [Google Scholar] [CrossRef]
- Gu, J.; Huang, L.; Shi, W. Atomic simulations of effect on thermal conductivity of ion-irradiated graphene. Phys. B Condens. Matter 2019, 554, 40–44. [Google Scholar] [CrossRef]
- Wu, X. Influence of Particle Beam Irradiation on the Structure and Properties of Graphene; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Qi, J.; Komvopoulos, K. A molecular dynamics analysis of ion irradiation of ultrathin amorphous carbon films. J. Appl. Phys. 2016, 120, 125311. [Google Scholar] [CrossRef]
- Rosandi, Y.; Urbassek, H.M. Subsurface and interface channeling of keV ions in graphene/SiC. Nucl. Instruments Methods Phys. Res. Sect. Beam Interact. Mater. Atoms 2014, 340, 5–10. [Google Scholar] [CrossRef]
- Verkhoturov, S.V.; Gołuński, M.; Verkhoturov, D.S.; Czerwinski, B.; Eller, M.J.; Geng, S.; Postawa, Z.; Schweikert, E.A. Hypervelocity cluster ion impacts on free standing graphene: Experiment, theory, and applications. J. Chem. Phys. 2019, 150, 160901. [Google Scholar] [CrossRef] [PubMed]
- Abdol, M.A.; Sadeghzadeh, S.; Jalaly, M.; Khatibi, M.M. Constructing a three-dimensional graphene structure via bonding layers by ion beam irradiation. Sci. Rep. 2019, 9, 8127. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.; Shao, L. Using irradiation-induced defects as pinning sites to minimize self-alignment in twisted bilayer graphene. Appl. Phys. Lett. 2021, 118, 151602. [Google Scholar] [CrossRef]
- Tian, J.; Zheng, T.; Yang, J.; Kong, S.; Xue, J.; Wang, Y.; Nordlund, K. Capacity of graphite’s layered structure to suppress the sputtering yield: A molecular dynamics study. Appl. Surf. Sci. 2015, 337, 6–11. [Google Scholar] [CrossRef]
- Marian, J.; Zepeda-Ruiz, L.; Gilmer, G.; Bringa, E.; Rognlien, T. Simulations of Carbon Sputtering in Fusion Reactor Divertor Plates; Technical Report; Lawrence Livermore National Laboratory (LLNL): Livermore, CA, USA, 2005. [Google Scholar]
- Delgado, D.; Vila, R. Statistical molecular dynamics study of displacement energies in diamond. J. Nucl. Mater. 2011, 419, 32–38. [Google Scholar] [CrossRef]
- Zhou, B.; Zhang, W.; Gong, W.B.; Wang, S.; Ren, C.L.; Wang, C.B.; Zhu, Z.Y.; Huai, P. Molecular dynamics simulation of damage to coiled carbon nanotubes under C ion irradiation. Chin. Phys. Lett. 2013, 30, 113402. [Google Scholar] [CrossRef]
- Arnold, A.J.; Shi, T.; Jovanovic, I.; Das, S. Extraordinary radiation hardness of atomically thin MoS2. ACS Appl. Mater. Interfaces 2019, 11, 8391–8399. [Google Scholar] [CrossRef]
- Walker, R.C.; Shi, T.; Jariwala, B.; Jovanovic, I.; Robinson, J.A. Stability of the tungsten diselenide and silicon carbide heterostructure against high energy proton exposure. Appl. Phys. Lett. 2017, 111, 143104. [Google Scholar] [CrossRef]
- Shi, T.; Walker, R.C.; Jovanovic, I.; Robinson, J.A. Effects of energetic ion irradiation on WSe2/SiC heterostructures. Sci. Rep. 2017, 7, 4151. [Google Scholar] [CrossRef]
- Liang, T.; Phillpot, S.R.; Sinnott, S.B. Parametrization of a reactive many-body potential for Mo–S systems. Phys. Rev. B 2009, 79, 245110. [Google Scholar] [CrossRef]
- Stewart, J.A.; Spearot, D. Atomistic simulations of nanoindentation on the basal plane of crystalline molybdenum disulfide (MoS)2. Model. Simul. Mater. Sci. Eng. 2013, 21, 045003. [Google Scholar] [CrossRef]
- Han, Y.; Li, M.Y.; Jung, G.S.; Marsalis, M.A.; Qin, Z.; Buehler, M.J.; Li, L.J.; Muller, D.A. Sub-nanometre channels embedded in two-dimensional materials. Nat. Mater. 2018, 17, 129–133. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Christie, H.; Robinson, M.; Roach, D.; Ross, D.; Suarez-Martinez, I.; Marks, N.A. Simulating radiation damage cascades in graphite. Carbon 2015, 81, 105–114. [Google Scholar] [CrossRef]
- Husnayani, I.; Majidi, M. Radiation damage study on graphite from multiple cascade events in molecular dynamics simulation. J. Phys. Conf. Ser. 2021, 1816, 012073. [Google Scholar] [CrossRef]
- Tersoff, J. New empirical approach for the structure and energy of covalent systems. Phys. Rev. B 1988, 37, 6991. [Google Scholar] [CrossRef]
- Byggmästar, J.; Nordlund, K.; Djurabekova, F. Gaussian approximation potentials for body-centered-cubic transition metals. Phys. Rev. Mater. 2020, 4, 093802. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Shi, T.; Sun, Y.; Cai, X.; Gao, R.; Peng, Q.; Lu, P.; Lu, C. Description of Short-Range Interactions of Carbon-Based Materials with a Combined AIREBO and ZBL Potential. Nanomaterials 2024, 14, 1423. https://doi.org/10.3390/nano14171423
Li J, Shi T, Sun Y, Cai X, Gao R, Peng Q, Lu P, Lu C. Description of Short-Range Interactions of Carbon-Based Materials with a Combined AIREBO and ZBL Potential. Nanomaterials. 2024; 14(17):1423. https://doi.org/10.3390/nano14171423
Chicago/Turabian StyleLi, Jing, Tan Shi, Yichao Sun, Xintian Cai, Rui Gao, Qing Peng, Peng Lu, and Chenyang Lu. 2024. "Description of Short-Range Interactions of Carbon-Based Materials with a Combined AIREBO and ZBL Potential" Nanomaterials 14, no. 17: 1423. https://doi.org/10.3390/nano14171423
APA StyleLi, J., Shi, T., Sun, Y., Cai, X., Gao, R., Peng, Q., Lu, P., & Lu, C. (2024). Description of Short-Range Interactions of Carbon-Based Materials with a Combined AIREBO and ZBL Potential. Nanomaterials, 14(17), 1423. https://doi.org/10.3390/nano14171423






