Targeted Polariton Flow Through Tailored Photonic Defects
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
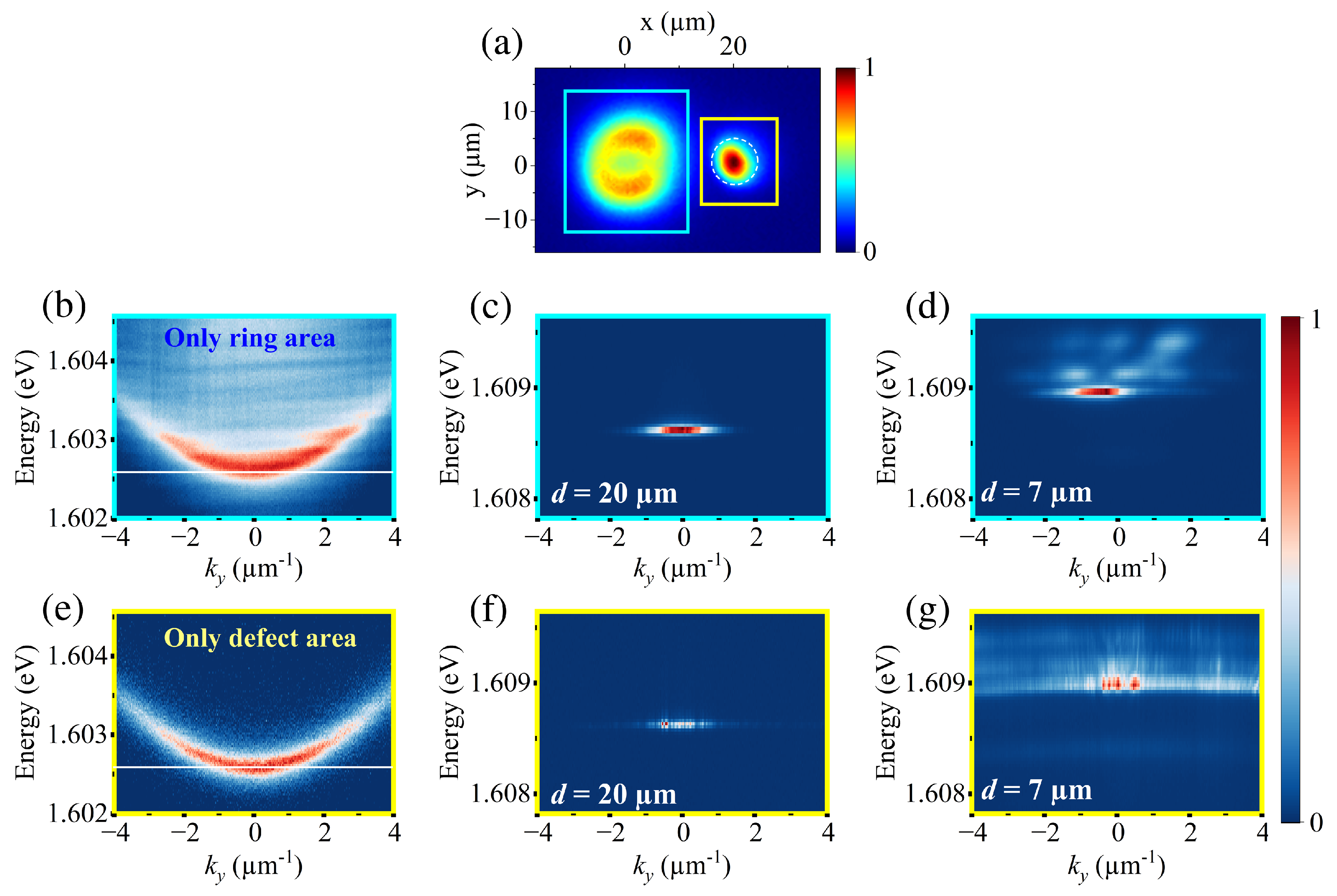
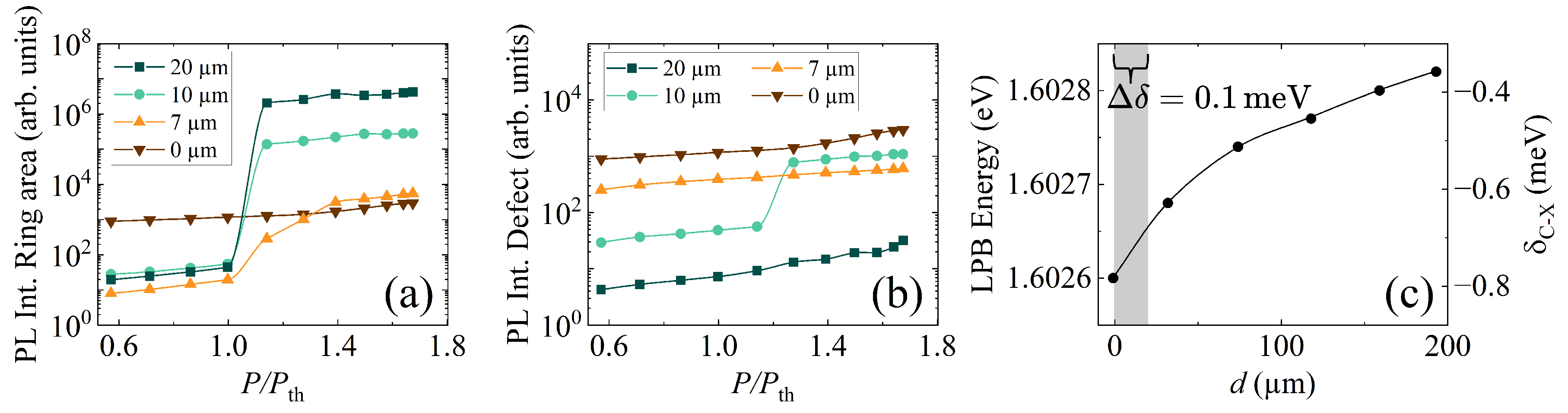
3.1. Polariton Flow Near Photonic Defects
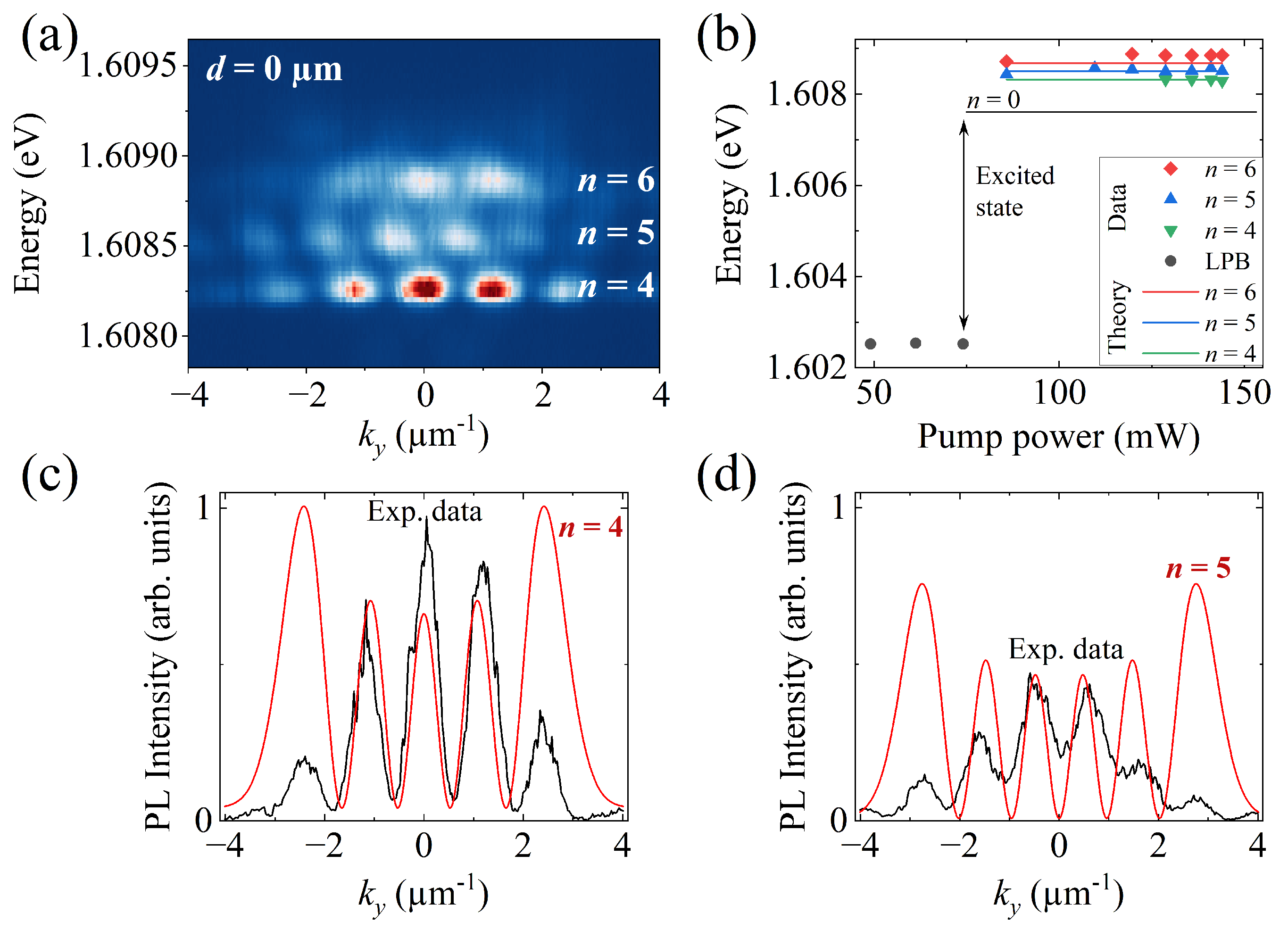
3.2. Generation of a Quantum Harmonic Oscillator Potential
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DBR | distributed Bragg reflector |
| SLM | spatial light modulator |
| PL | photoluminescence |
| power threshold | |
| LPB | lower polariton branch |
| QHO | Quantum Harmonic Oscillator |
References
- Kanshu, A.; Rüter, C.E.; Kip, D.; Shandarov, V.M. Optically-induced defect states in photonic lattices: Formation of defect channels, directional couplers, and disordered lattices leading to Anderson-like light localization. Appl. Phys. B 2009, 95, 537–543. [Google Scholar] [CrossRef]
- Blanco-Redondo, A.; Andonegui, I.; Collins, M.J.; Harari, G.; Lumer, Y.; Rechtsman, M.C.; Eggleton, B.J.; Segev, M. Topological Optical Waveguiding in Silicon and the Transition between Topological and Trivial Defect States. Phys. Rev. Lett. 2016, 116, 163901. [Google Scholar] [CrossRef] [PubMed]
- Vashistha, V.; Krawczyk, M.; Serebryannikov, A.E.; Serebryannikov, A.E.; Vandenbosch, G.A.E. Light guiding, bending, and splitting via local modification of interfaces of a photonic waveguide. Opt. Lett. 2019, 44, 4725–4728. [Google Scholar] [CrossRef]
- Rozas, E.; Beierlein, J.; Yulin, A.; Klaas, M.; Suchomel, H.; Egorov, O.; Shelykh, I.A.; Peschel, U.; Schneider, C.; Klembt, S.; et al. Impact of the Energetic Landscape on Polariton Condensates’ Propagation along a Coupler. Adv. Opt. Mater. 2020, 8, 2000650. [Google Scholar] [CrossRef]
- Wang, D.S.; Yelin, S.F.; Flick, J. Defect Polaritons from First Principles. ACS Nano 2021, 15, 15142–15152. [Google Scholar] [CrossRef]
- Wang, D.S.; Ciccarino, C.J.; Flick, J.; Narang, P. Hybridized Defects in Solid-State Materials as Artificial Molecules. ACS Nano 2021, 15, 5240–5248. [Google Scholar] [CrossRef]
- Shi, L.; Xu, S.; Xiong, D.; Wang, L.; Yang, P.; Chu, P.K. Analysis of defect states in optical microcavities based on the photonic quantum well structure. Opt. Commun. 2020, 458, 124880. [Google Scholar] [CrossRef]
- Romero, E.; Valenzuela, V.M.; Kermany, A.R.; Sementilli, L.; Iacopi, F.; Bowen, W.P. Engineering the Dissipation of Crystalline Micromechanical Resonators. Phys. Rev. Appl. 2020, 13, 044007. [Google Scholar] [CrossRef]
- Hu, T.; Li, D.; Shan, Q.; Dong, Y.; Xiang, H.; Choy, W.C.H.; Zeng, H. Defect Behaviors in Perovskite Light-Emitting Diodes. ACS Mater. Lett. 2021, 3, 1702–1728. [Google Scholar] [CrossRef]
- Gagel, P.; Harder, T.H.; Betzold, S.; Egorov, O.A.; Beierlein, J.; Suchomel, H.; Emmerling, M.; Wolf, A.; Peschel, U.; Höfling, S.; et al. Electro-optical Switching of a Topological Polariton Laser. ACS Photonics 2022, 9, 405–412. [Google Scholar] [CrossRef]
- McDougall, N.L.; Partridge, J.G.; Nicholls, R.J.; Russo, S.P.; McCulloch, D.G. Influence of point defects on the near edge structure of hexagonal boron nitride. Phys. Rev. B 2017, 96, 144106. [Google Scholar] [CrossRef]
- Mackoit-Sinkevičienė, M.; Maciaszek, M.; Van de Walle, C.G.; Alkauskas, A. Carbon dimer defect as a source of the 4.1 eV luminescence in hexagonal boron nitride. Appl. Phys. Lett. 2019, 115, 212101. [Google Scholar] [CrossRef]
- Zemła, M.R.; Czelej, K.; Kamińska, P.; Van de Walle, C.G.; Majewski, J.A. Electronic structure and magneto-optical properties of silicon-nitrogen-vacancy complexes in diamond. Phys. Rev. B 2020, 102, 115102. [Google Scholar] [CrossRef]
- Jiang, Y.; Niu, C.; Lin, D.L. Resonance tunneling through photonic quantum wells. Phys. Rev. B 1999, 59, 9981–9986. [Google Scholar] [CrossRef]
- Qiao, F.; Zhang, C.; Wan, J.; Zi, J. Photonic quantum-well structures: Multiple channeled filtering phenomena. Appl. Phys. Lett. 2000, 77, 3698–3700. [Google Scholar] [CrossRef]
- Yamamoto, Y.; Slusher, R.E. Optical Processes in Microcavities. Phys. Today 1993, 46, 66–73. [Google Scholar] [CrossRef]
- Vahala, K.J. Optical microcavities. Nature 2003, 424, 839–846. [Google Scholar] [CrossRef]
- Kavokin, A.V.; Baumberg, J.J.; Malpuech, G.; Laussy, F.P. Microcavities; Oxford University Press: Oxford, UK, 2017; Volume 21. [Google Scholar]
- Weisbuch, C.; Nishioka, M.; Ishikawa, A.; Arakawa, Y. Observation of the coupled exciton-photon mode splitting in a semiconductor quantum microcavity. Phys. Rev. Lett. 1992, 69, 3314–3317. [Google Scholar] [CrossRef]
- Kavokin, A.; Malpuech, G. Cavity Polaritons; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Kasprzak, J.; Richard, M.; Kundermann, S.; Baas, A.; Jeambrun, P.; Keeling, J.M.J.; Marchetti, F.M.; Szymańska, M.H.; André, R.; Staehli, J.L.; et al. Bose–Einstein condensation of exciton polaritons. Nature 2006, 443, 409–414. [Google Scholar] [CrossRef]
- Aristov, D.; Baryshev, S.; Töpfer, J.D.; Sigurðsson, H.; Lagoudakis, P.G. Directional planar antennae in polariton condensates. Appl. Phys. Lett. 2023, 123, 121101. [Google Scholar] [CrossRef]
- Winkler, K.; Flayac, H.; Klembt, S.; Schade, A.; Nevinskiy, D.; Kamp, M.; Schneider, C.; Höfling, S. Exciton-polariton flows in cross-dimensional junctions. Phys. Rev. B 2017, 95, 201302. [Google Scholar] [CrossRef]
- Wertz, E.; Amo, A.; Solnyshkov, D.D.; Ferrier, L.; Liew, T.C.H.; Sanvitto, D.; Senellart, P.; Sagnes, I.; Lemaître, A.; Kavokin, A.V.; et al. Propagation and Amplification Dynamics of 1D Polariton Condensates. Phys. Rev. Lett. 2012, 109, 216404. [Google Scholar] [CrossRef] [PubMed]
- Amo, A.; Liew, T.C.H.; Adrados, C.; Houdré, R.; Giacobino, E.; Kavokin, A.V.; Bramati, A. Exciton–polariton spin switches. Nat. Photonics 2010, 4, 361–366. [Google Scholar] [CrossRef]
- Gao, T.; Eldridge, P.S.; Liew, T.C.H.; Tsintzos, S.I.; Stavrinidis, G.; Deligeorgis, G.; Hatzopoulos, Z.; Savvidis, P.G. Polariton condensate transistor switch. Phys. Rev. B 2012, 85, 235102. [Google Scholar] [CrossRef]
- Antón, C.; Liew, T.C.H.; Sarkar, D.; Martín, M.D.; Hatzopoulos, Z.; Eldridge, P.S.; Savvidis, P.G.; Viña, L. Operation speed of polariton condensate switches gated by excitons. Phys. Rev. B 2014, 89, 235312. [Google Scholar] [CrossRef]
- Ma, X.; Berger, B.; Aßmann, M.; Driben, R.; Meier, T.; Schneider, C.; Höfling, S.; Schumacher, S. Realization of all-optical vortex switching in exciton-polariton condensates. Nat. Commun. 2020, 11, 897. [Google Scholar] [CrossRef]
- Ballarini, D.; De Giorgi, M.; Cancellieri, E.; Houdré, R.; Giacobino, E.; Cingolani, R.; Bramati, A.; Gigli, G.; Sanvitto, D. All-optical polariton transistor. Nat. Commun. 2013, 4, 1778. [Google Scholar] [CrossRef]
- Ghosh, S.; Liew, T.C.H. Quantum computing with exciton-polariton condensates. NPJ Quantum Inf. 2020, 6, 16. [Google Scholar] [CrossRef]
- Marsault, F.; Nguyen, H.S.; Tanese, D.; Lemaître, A.; Galopin, E.; Sagnes, I.; Amo, A.; Bloch, J. Realization of an all optical exciton-polariton router. Appl. Phys. Lett. 2015, 107, 201115. [Google Scholar] [CrossRef]
- Flayac, H.; Savenko, I.G. An exciton-polariton mediated all-optical router. Appl. Phys. Lett. 2013, 103, 201105. [Google Scholar] [CrossRef]
- Kavokin, A.; Liew, T.C.H.; Schneider, C.; Lagoudakis, P.G.; Klembt, S.; Hoefling, S. Polariton condensates for classical and quantum computing. Nat. Rev. Phys. 2022, 4, 435–451. [Google Scholar] [CrossRef]
- Sanvitto, D.; Pigeon, S.; Amo, A.; Ballarini, D.; De Giorgi, M.; Carusotto, I.; Hivet, R.; Pisanello, F.; Sala, V.G.; Guimaraes, P.S.S.; et al. All-optical control of the quantum flow of a polariton condensate. Nat. Photonics 2011, 5, 610–614. [Google Scholar] [CrossRef]
- Steger, M.; Gautham, C.; Snoke, D.W.; Pfeiffer, L.; West, K. Slow reflection and two-photon generation of microcavity exciton–polaritons. Optica 2015, 2, 1–5. [Google Scholar] [CrossRef]
- Pieczarka, M.; Biegańska, D.; Schneider, C.; Höfling, S.; Klembt, S.; Sęk, G.; Syperek, M. Crossover from exciton-polariton condensation to photon lasing in an optical trap. Opt. Express 2022, 30, 17070–17079. [Google Scholar] [CrossRef] [PubMed]
- Orfanakis, K.; Tzortzakakis, A.F.; Petrosyan, D.; Savvidis, P.G.; Ohadi, H. Ultralong temporal coherence in optically trapped exciton-polariton condensates. Phys. Rev. B 2021, 103, 235313. [Google Scholar] [CrossRef]
- Askitopoulos, A.; Ohadi, H.; Kavokin, A.V.; Hatzopoulos, Z.; Savvidis, P.G.; Lagoudakis, P.G. Polariton condensation in an optically induced two-dimensional potential. Phys. Rev. B 2013, 88, 041308. [Google Scholar] [CrossRef]
- Snoke, D.W.; Hartwell, V.; Beaumariage, J.; Mukherjee, S.; Yoon, Y.; Myers, D.M.; Steger, M.; Sun, Z.; Nelson, K.A.; Pfeiffer, L.N. Reanalysis of experimental determinations of polariton-polariton interactions in microcavities. Phys. Rev. B 2023, 107, 165302. [Google Scholar] [CrossRef]
- Rozas, E.; Sedov, E.; Brune, Y.; Höfling, S.; Kavokin, A.; Aßmann, M. Polariton–dark exciton interactions in bistable semiconductor microcavities. Phys. Rev. B 2023, 108, 165411. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rozas, E.; Brune, Y.; West, K.; Baldwin, K.W.; Pfeiffer, L.N.; Beaumariage, J.; Alnatah, H.; Snoke, D.W.; Aßmann, M. Targeted Polariton Flow Through Tailored Photonic Defects. Nanomaterials 2024, 14, 1691. https://doi.org/10.3390/nano14211691
Rozas E, Brune Y, West K, Baldwin KW, Pfeiffer LN, Beaumariage J, Alnatah H, Snoke DW, Aßmann M. Targeted Polariton Flow Through Tailored Photonic Defects. Nanomaterials. 2024; 14(21):1691. https://doi.org/10.3390/nano14211691
Chicago/Turabian StyleRozas, Elena, Yannik Brune, Ken West, Kirk W. Baldwin, Loren N. Pfeiffer, Jonathan Beaumariage, Hassan Alnatah, David W. Snoke, and Marc Aßmann. 2024. "Targeted Polariton Flow Through Tailored Photonic Defects" Nanomaterials 14, no. 21: 1691. https://doi.org/10.3390/nano14211691
APA StyleRozas, E., Brune, Y., West, K., Baldwin, K. W., Pfeiffer, L. N., Beaumariage, J., Alnatah, H., Snoke, D. W., & Aßmann, M. (2024). Targeted Polariton Flow Through Tailored Photonic Defects. Nanomaterials, 14(21), 1691. https://doi.org/10.3390/nano14211691







