Vertical Electric-Field-Induced Switching from Strong to Asymmetric Strong–Weak Confinement in GaAs Cone-Shell Quantum Dots Using Transparent Al-Doped ZnO Gates
Abstract
:1. Introduction
2. Methods
3. Results
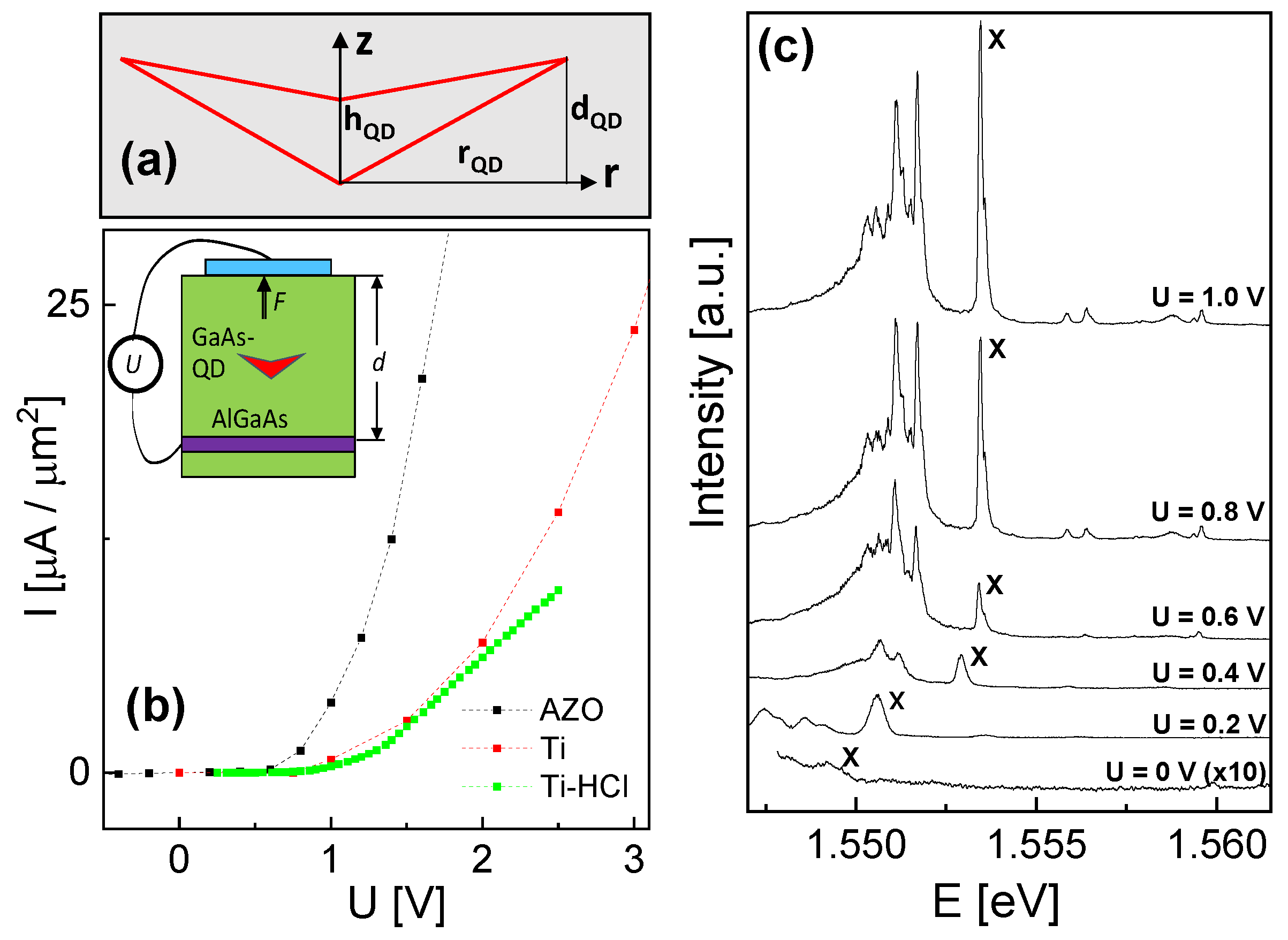
3.1. Gate Material
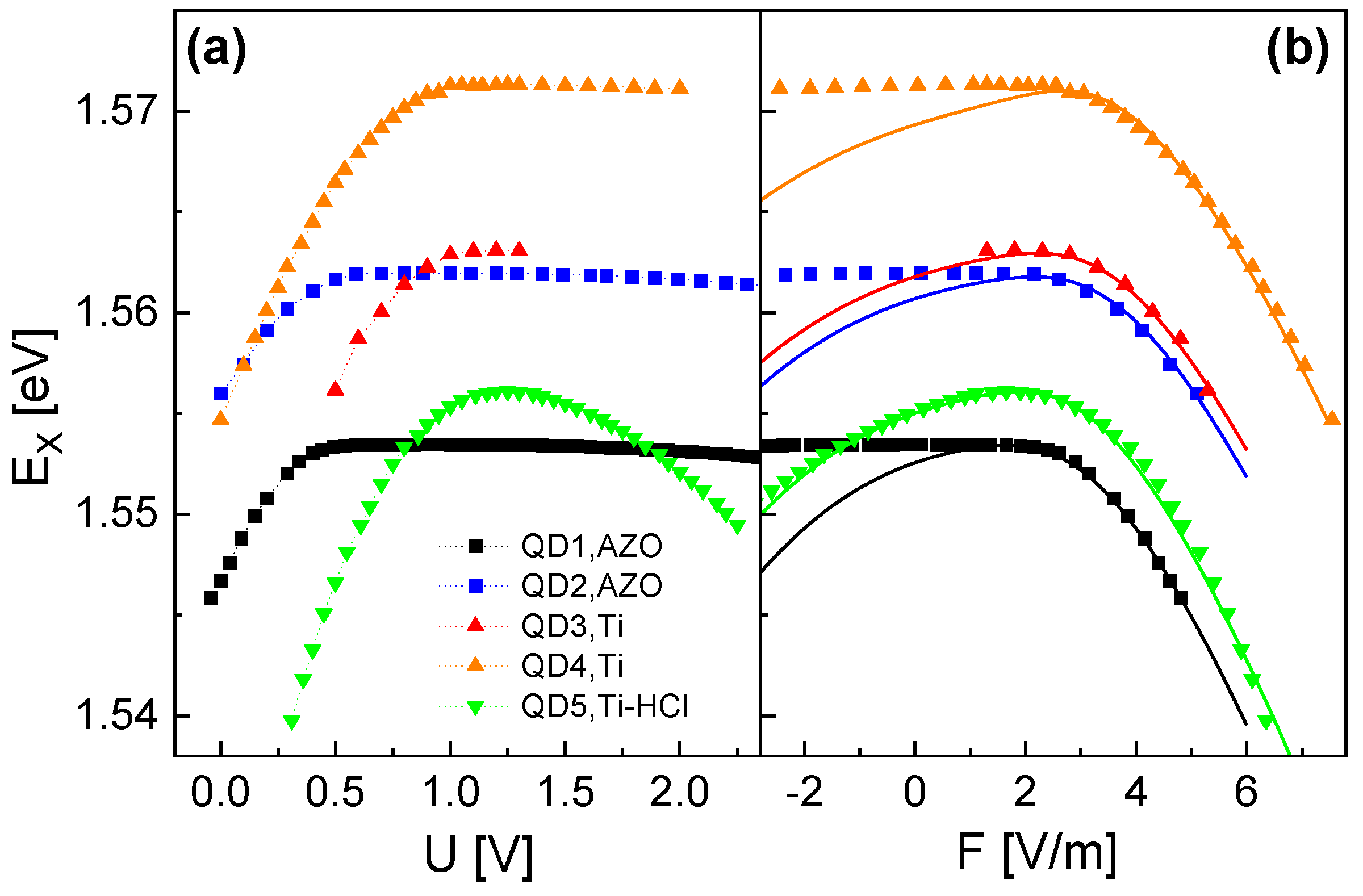
3.2. Stark Shift
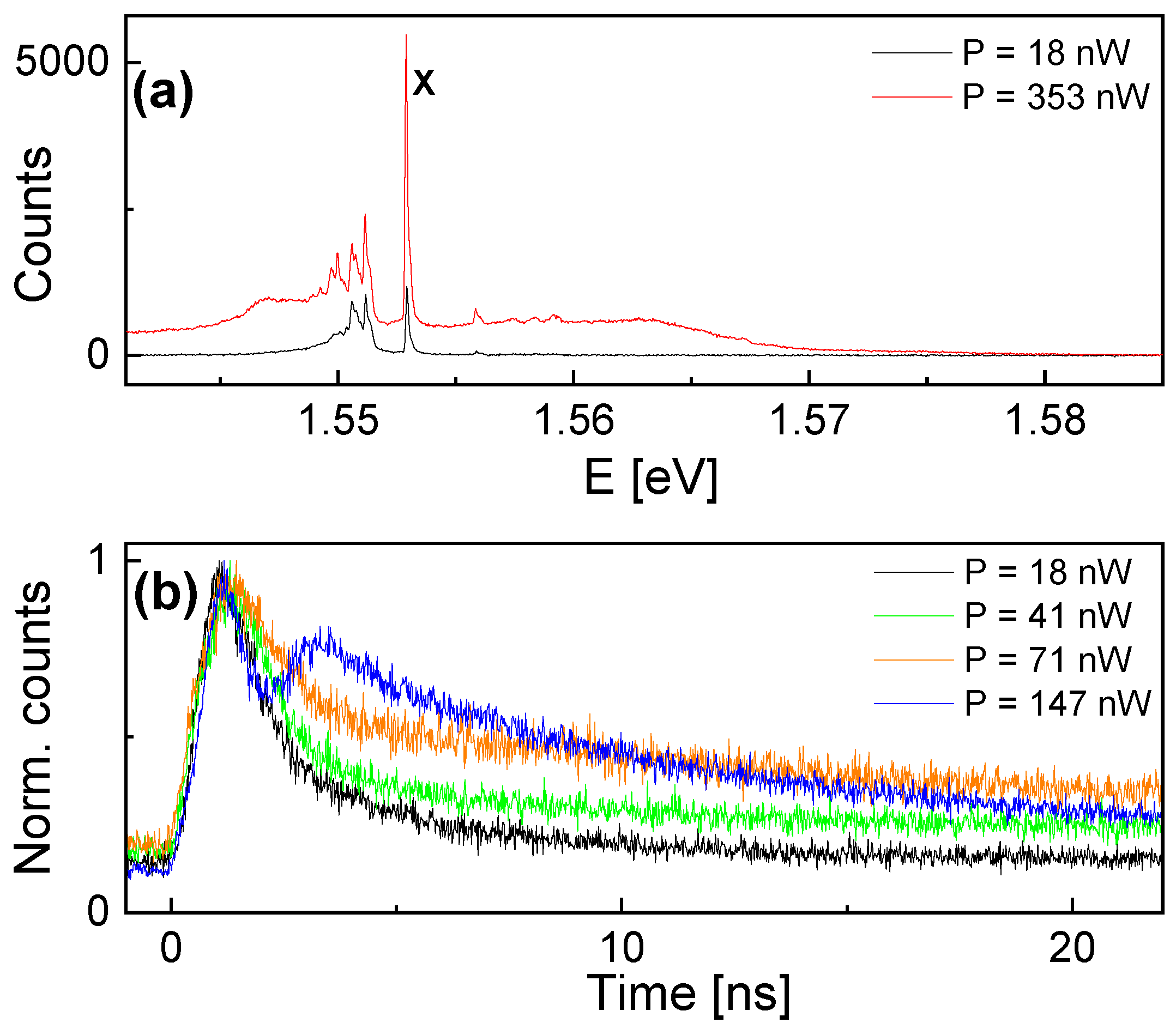
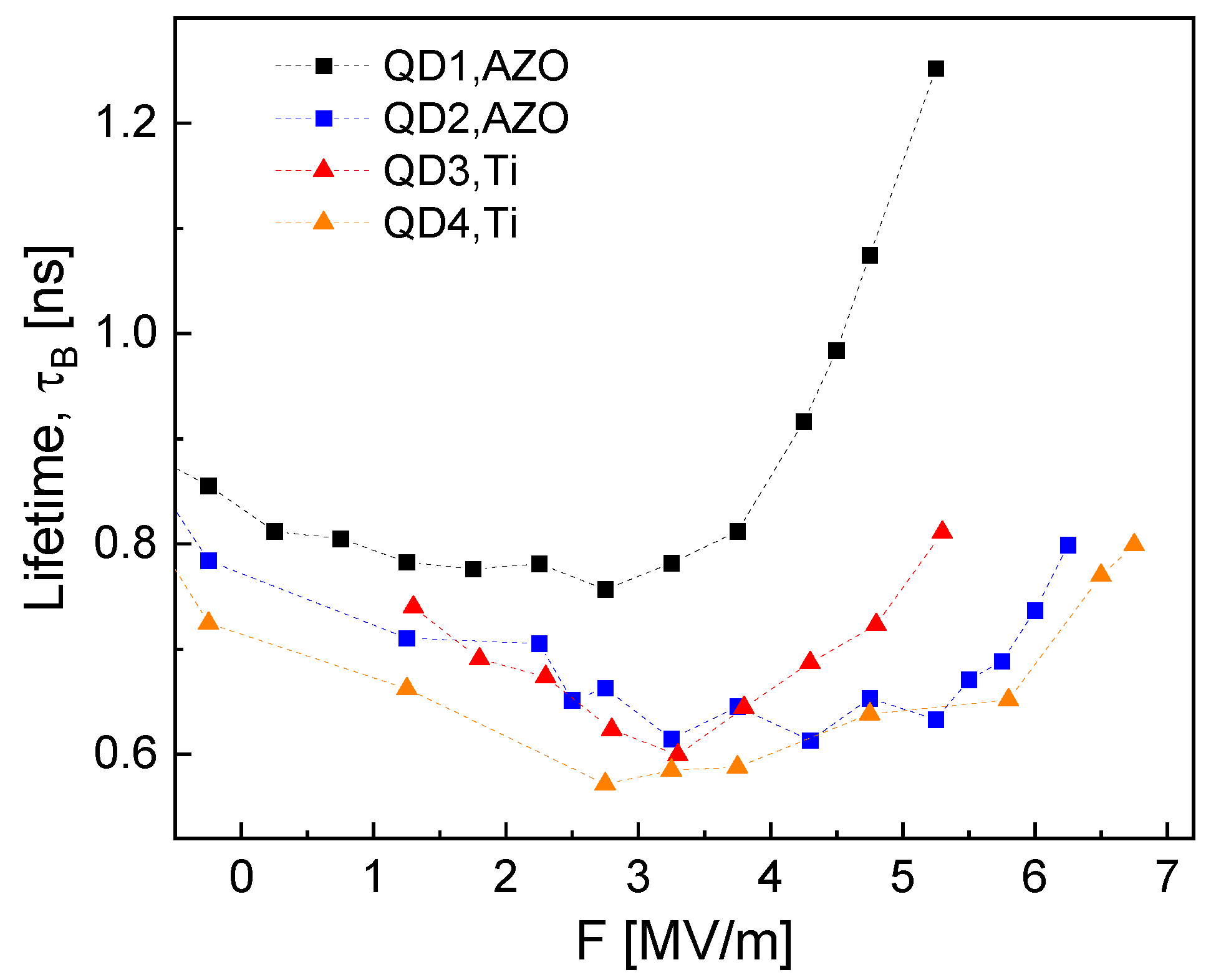
3.3. Lifetime
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dalgarno, P.A.; Smith, J.M.; McFarlane, J.; Gerardot, B.D.; Karrai, K.; Badolato, A.; Petroff, P.M.; Warburton, R.J. Coulomb interactions in single charged self-assembled quantum dots: Radiative lifetime and recombination energy. Phys. Rev. B 2008, 77, 245311. [Google Scholar] [CrossRef]
- Giessen, H.; Woggon, U.; Fluegel, B.; Mohs, G.; Hu, Y.Z.; Koch, S.W.; Peyghambarian, N. Quantum dots in the strong confinement regime: A model system for gain in quasi zero-dimensional semiconductors. Chem. Phys. 1996, 210, 71–78. [Google Scholar] [CrossRef]
- Okuno, T.; Lipovskii, A.A.; Ogawa, T.; Amagai, I.; Masumoto, Y. Strong confinement of PbSe and PbS quantum dots. J. Lumin. 2000, 87–89, 491–493. [Google Scholar] [CrossRef]
- Tighineanu, P.; Daveau, R.; Lee, E.H.; Song, J.D.; Stobbe, S.; Lodahl, P. Decay dynamics and exciton localization in large GaAs quantum dots grown by droplet epitaxy. Phys. Rev. B 2013, 88, 155320. [Google Scholar] [CrossRef]
- Ning, J.Q.; Zheng, C.C.; Zhang, X.H.; Xu, S.J. Strong quantum confinement effect and reduced Fröhlich exciton–phonon coupling in ZnO quantum dots embedded inside a SiO2 matrix. Nanoscale 2015, 7, 17482–17487. [Google Scholar] [CrossRef]
- Purcell, E.M. Spontaneous Emission Probabilities at Radio Frequencies. Phys. Rev. 1946, 69, 1946. [Google Scholar]
- Badolato, A.; Hennessy, K.; Atatüre, M.; Dreiser, J.; Hu, E.; Petroff, P.M.; Imamoğlu, A. Deterministic Coupling of Single Quantum Dots to Single Nanocavity Modes. Science 2005, 308, 1158–1161. [Google Scholar] [CrossRef]
- Jordan, M.; Androvitsaneas, P.; Clark, R.N.; Trapalis, A.; Farrer, I.; Langbein, W.; Bennett, A.J. Probing Purcell enhancement and photon collection efficiency of InAs quantum dots at nodes of the cavity electric field. Phys. Rev. Res. 2024, 6, L022004. [Google Scholar] [CrossRef]
- Phillips, C.L.; Brash, A.J.; Godsland, M.; Martin, N.J.; Foster, A.; Tomlinson, A.; Dost, R.; Babazadeh, N.; Sala, E.M.; Wilson, L.; et al. Purcell-enhanced single photons at telecom wavelengths from a quantum dot in a photonic crystal cavity. Sci. Rep. 2024, 14, 4450. [Google Scholar] [CrossRef]
- Hanamura, E. Very large optical nonlinearity of semiconductor microcrystallites. Phys. Rev. B 1988, 37, 1273–1279. [Google Scholar] [CrossRef]
- Musiał, A.; Gold, P.; Andrzejewski, J.; Löffler, A.; Misiewicz, J.; Höfling, S.; Forchel, A.; Kamp, M.; Sęk, G.; Reitzenstein, S. Toward weak confinement regime in epitaxial nanostructures: Interdependence of spatial character of quantum confinement and wave function extension in large and elongated quantum dots. Phys. Rev. B 2014, 90, 045430. [Google Scholar] [CrossRef]
- Stobbe, S.; Schlereth, T.W.; Höfling, S.; Forchel, A.; Hvam, J.M.; Lodahl, P. Large quantum dots with small oscillator strength. Phys. Rev. B 2010, 82, 233302. [Google Scholar] [CrossRef]
- Stobbe, S.; Kristensen, P.T.; Mortensen, J.E.; Hvam, J.M.; Mørk, J.; Lodahl, P. Spontaneous emission from large quantum dots in nanostructures: Exciton-photon interaction beyond the dipole approximation. Phys. Rev. B 2012, 86, 085304. [Google Scholar] [CrossRef]
- Heyn, C.; Ranasinghe, L.; Deneke, K.; Alshaikh, A.; Duque, C.A.; Hansen, W. Strong Electric Polarizability of Cone–Shell Quantum Structures for a Large Stark Shift, Tunable Long Exciton Lifetimes, and a Dot-to-Ring Transformation. Nanomaterials 2023, 13, 857. [Google Scholar] [CrossRef] [PubMed]
- Luo, W.; Cao, L.; Shi, Y.; Wan, L.; Zhang, H.; Li, S.; Chen, G.; Li, Y.; Li, S.; Wang, Y.; et al. Recent progress in quantum photonic chips for quantum communication and internet. Light Sci. Appl. 2023, 12, 175. [Google Scholar] [CrossRef]
- Heyn, C.; Stemmann, A.; Köppen, T.; Strelow, C.; Kipp, T.; Grave, M.; Mendach, S.; Hansen, W. Highly uniform and strain-free GaAs quantum dots fabricated by filling of self-assembled nanoholes. Appl. Phys. Lett. 2009, 94, 183113–183115. [Google Scholar] [CrossRef]
- Heyn, C.; Gräfenstein, A.; Pirard, G.; Ranasinghe, L.; Deneke, K.; Alshaikh, A.; Bester, G.; Hansen, W. Dot-Size Dependent Excitons in Droplet-Etched Cone-Shell GaAs Quantum Dots. Nanomaterials 2022, 12, 2981. [Google Scholar] [CrossRef]
- Heyn, C.; Ranasinghe, L.; Alshaikh, A.; Duque, C.A. Cone-Shell Quantum Structures in Electric and Magnetic Fields as Switchable Traps for Photoexcited Charge Carriers. Nanomaterials 2023, 13, 1696. [Google Scholar] [CrossRef]
- Peng, J.; Zhao, P.; Venugopal, R.; Deneke, K.; Haugg, S.; Blick, R.; Zierold, R. Thermal Sight: A Position-Sensitive Detector for a Pinpoint Heat Spot. Small Sci. 2024, 4, 2400091. [Google Scholar] [CrossRef]
- Mendez, E.; Bastard, G.; Chang, L.; Esaki, L.; Morkoc, H.; Fischer, R. Effect of an electric field on the luminescence of GaAs quantum wells. Phys. Rev. B 1982, 26, 7101–7104. [Google Scholar] [CrossRef]
- Miller, D.A.B.; Chemla, D.S.; Damen, T.C.; Gossard, A.C.; Wiegmann, W.; Wood, T.H.; Burrus, C.A. Band-Edge Electroabsorption in Quantum Well Structures: The Quantum-Confined Stark Effect. Phys. Rev. Lett. 1984, 53, 2173–2176. [Google Scholar] [CrossRef]
- Empedocles, S.A.; Bawendi, M.G. Quantum-Confined Stark Effect in Single CdSe Nanocrystallite Quantum Dots. Science 1997, 278, 2114–2117. [Google Scholar] [CrossRef] [PubMed]
- Heller, W.; Bockelmann, U.; Abstreiter, G. Electric-field effects on excitons in quantum dots. Phys. Rev. B 1998, 57, 6270–6273. [Google Scholar] [CrossRef]
- Finley, J.J.; Sabathil, M.; Vogl, P.; Abstreiter, G.; Oulton, R.; Tartakovskii, A.I.; Mowbray, D.J.; Skolnick, M.S.; Liew, S.L.; Cullis, A.G.; et al. Quantum-confined Stark shifts of charged exciton complexes in quantum dots. Phys. Rev. B 2004, 70, 201308. [Google Scholar] [CrossRef]
- Bennett, A.J.; Patel, R.B.; Joanna, S.S.; Christine, A.N.; David, A.F.; Andrew, J.S. Giant Stark effect in the emission of single semiconductor quantum dots. Appl. Phys. Lett. 2010, 97, 031104. [Google Scholar] [CrossRef]
- Heyn, C.; Ranasinghe, L.; Zocher, M.; Hansen, W. Shape-Dependent Stark Shift and Emission-Line Broadening of Quantum Dots and Rings. J. Phys. Chem. C 2020, 124, 19809–19816. [Google Scholar] [CrossRef]
- Fomin, V.M. (Ed.) Physics of Quantum Rings; NanoScience and Technology; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
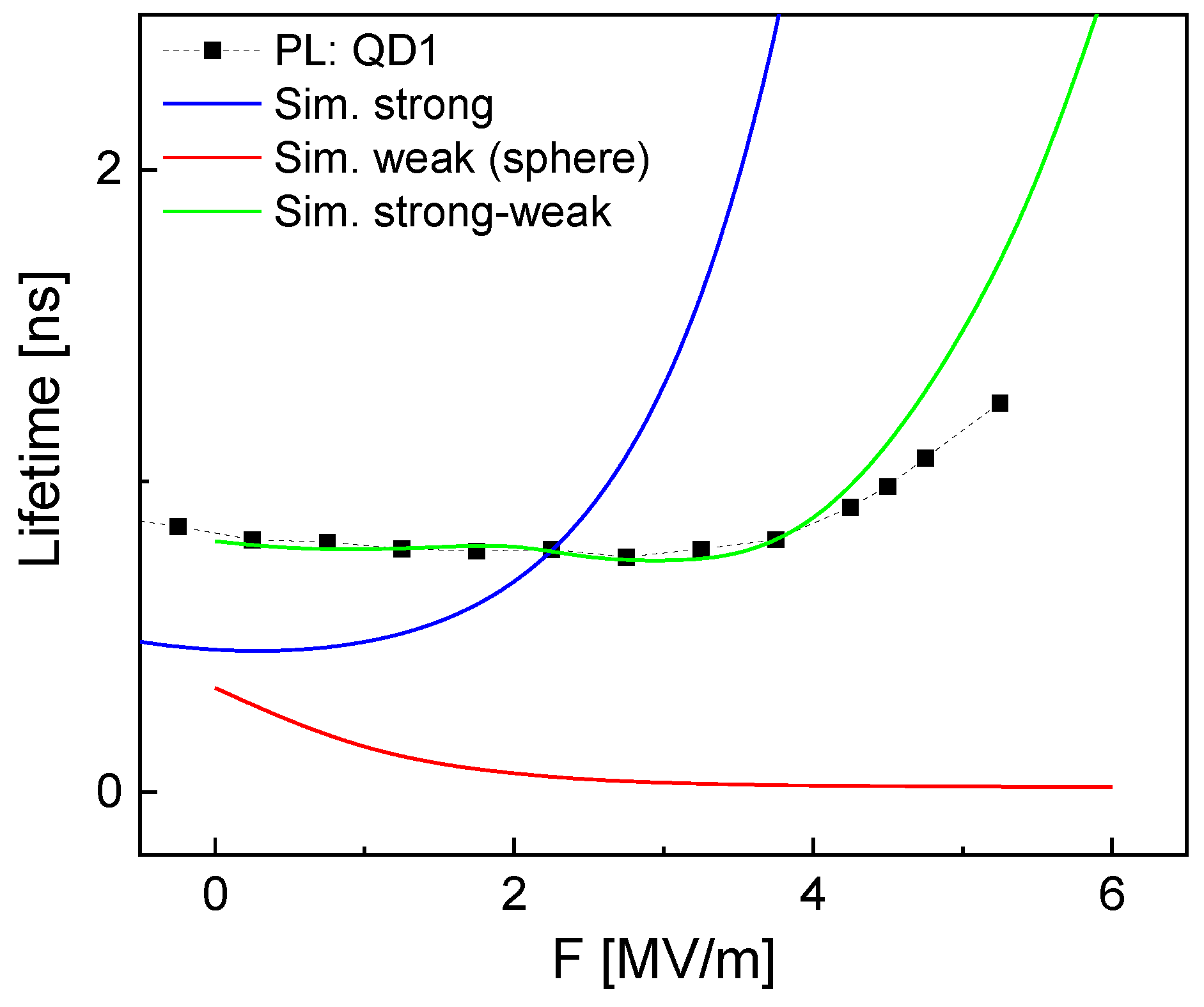
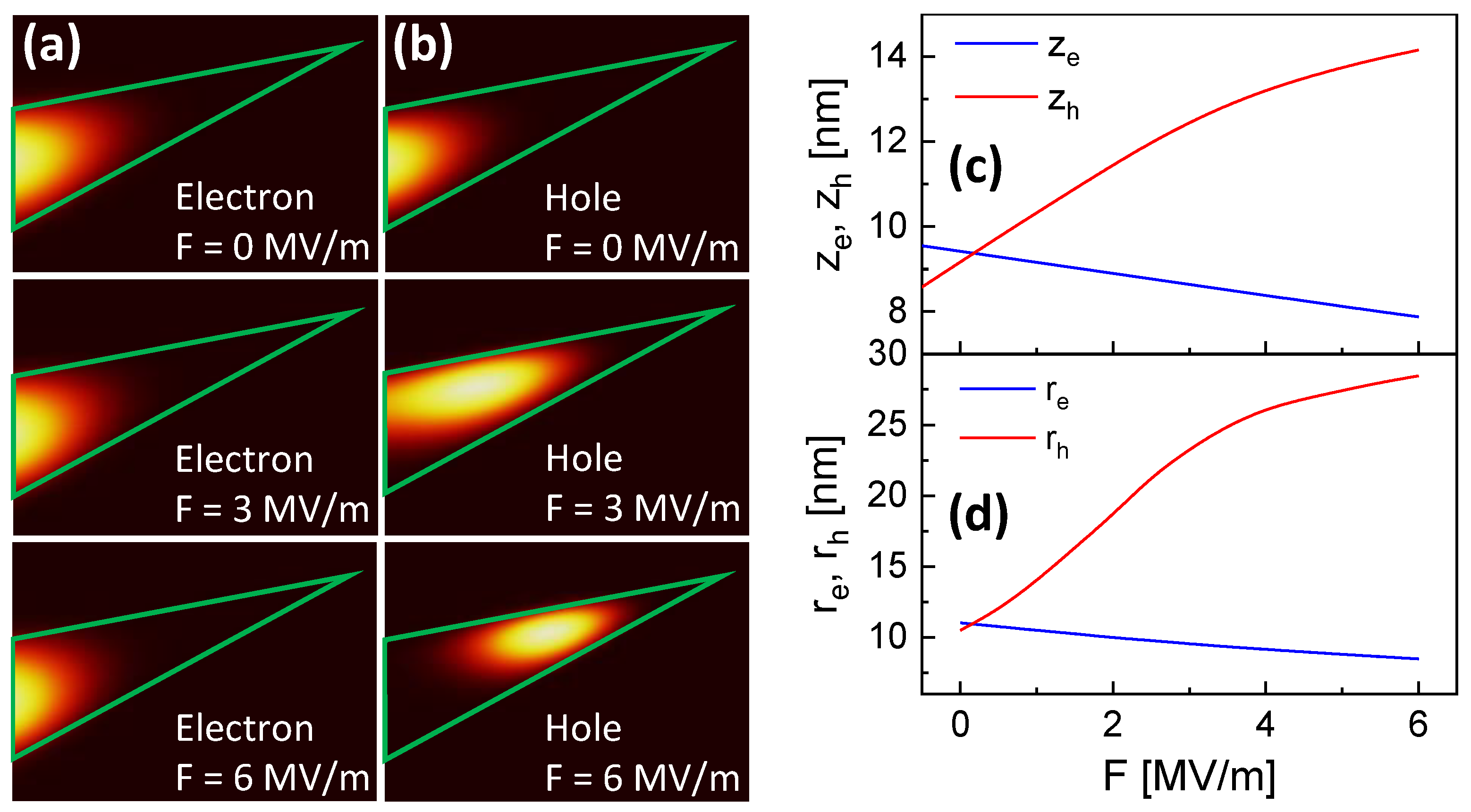
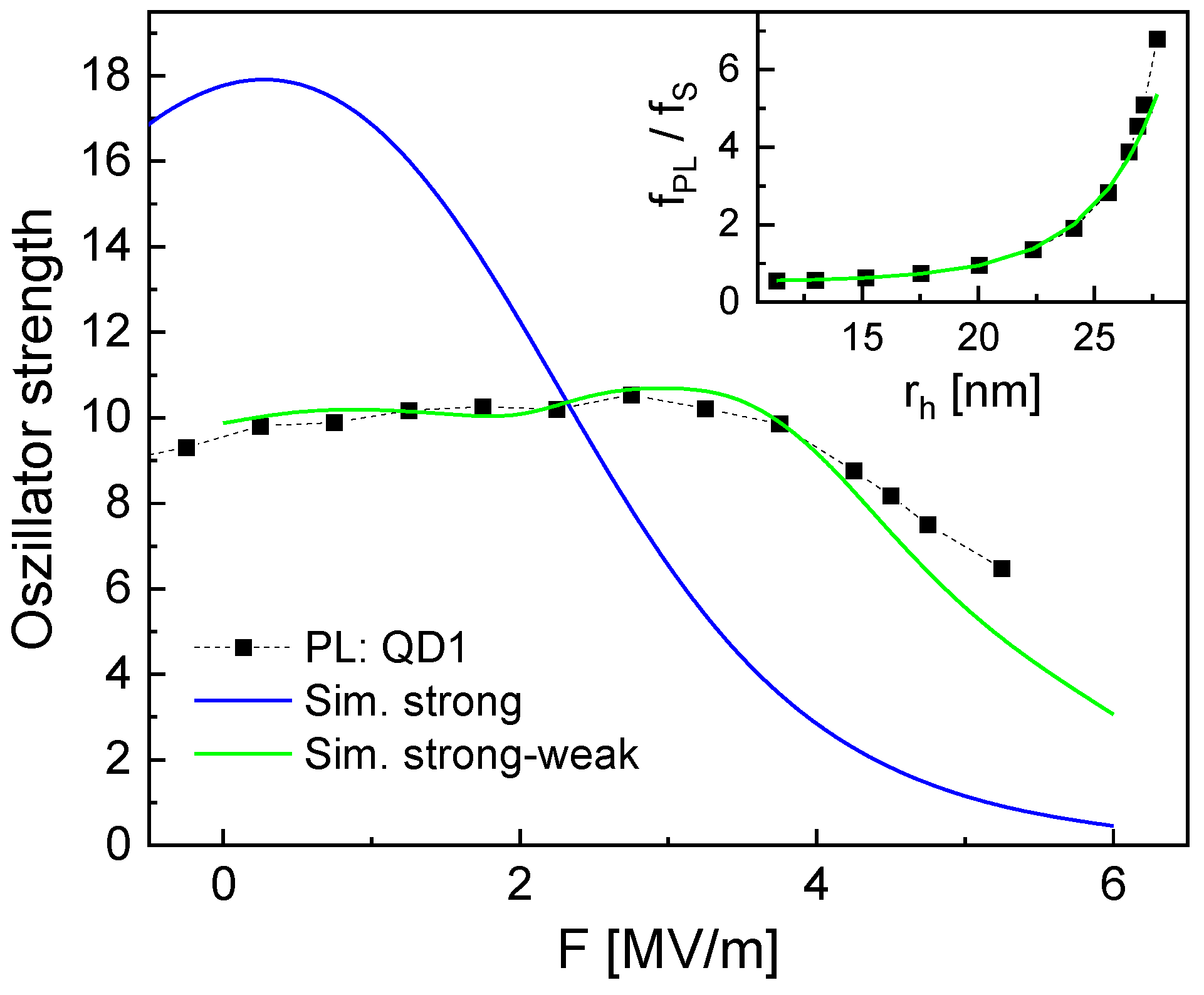
| Dot | Gate Material | HCl Dip | [eV] | [V] | [nm] | [nm] | [nm] | (F = 3 MV/m) [ns] |
|---|---|---|---|---|---|---|---|---|
| QD1 | AZO | no | 1.5534 | 0.92 | 35.0 | 19.0 | 13.5 | 0.77 |
| QD2 | AZO | no | 1.5619 | 1.02 | 33.0 | 18.0 | 11.9 | 0.63 |
| QD3 | Ti | no | 1.5631 | 1.56 | 33.0 | 18.0 | 11.7 | 0.61 |
| QD4 | Ti | no | 1.5713 | 1.51 | 33.0 | 18.0 | 10.5 | 0.58 |
| QD5 | Ti | yes | 1.5560 | 1.58 | 35.0 | 19.0 | 12.8 | – |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshaikh, A.; Peng, J.; Zierold, R.; Blick, R.H.; Heyn, C. Vertical Electric-Field-Induced Switching from Strong to Asymmetric Strong–Weak Confinement in GaAs Cone-Shell Quantum Dots Using Transparent Al-Doped ZnO Gates. Nanomaterials 2024, 14, 1712. https://doi.org/10.3390/nano14211712
Alshaikh A, Peng J, Zierold R, Blick RH, Heyn C. Vertical Electric-Field-Induced Switching from Strong to Asymmetric Strong–Weak Confinement in GaAs Cone-Shell Quantum Dots Using Transparent Al-Doped ZnO Gates. Nanomaterials. 2024; 14(21):1712. https://doi.org/10.3390/nano14211712
Chicago/Turabian StyleAlshaikh, Ahmed, Jun Peng, Robert Zierold, Robert H. Blick, and Christian Heyn. 2024. "Vertical Electric-Field-Induced Switching from Strong to Asymmetric Strong–Weak Confinement in GaAs Cone-Shell Quantum Dots Using Transparent Al-Doped ZnO Gates" Nanomaterials 14, no. 21: 1712. https://doi.org/10.3390/nano14211712
APA StyleAlshaikh, A., Peng, J., Zierold, R., Blick, R. H., & Heyn, C. (2024). Vertical Electric-Field-Induced Switching from Strong to Asymmetric Strong–Weak Confinement in GaAs Cone-Shell Quantum Dots Using Transparent Al-Doped ZnO Gates. Nanomaterials, 14(21), 1712. https://doi.org/10.3390/nano14211712






