Deciphering Surface-Localized Structure of Nanodiamonds
Abstract
:1. Introduction
2. Calculation Method
3. Results and Discussion
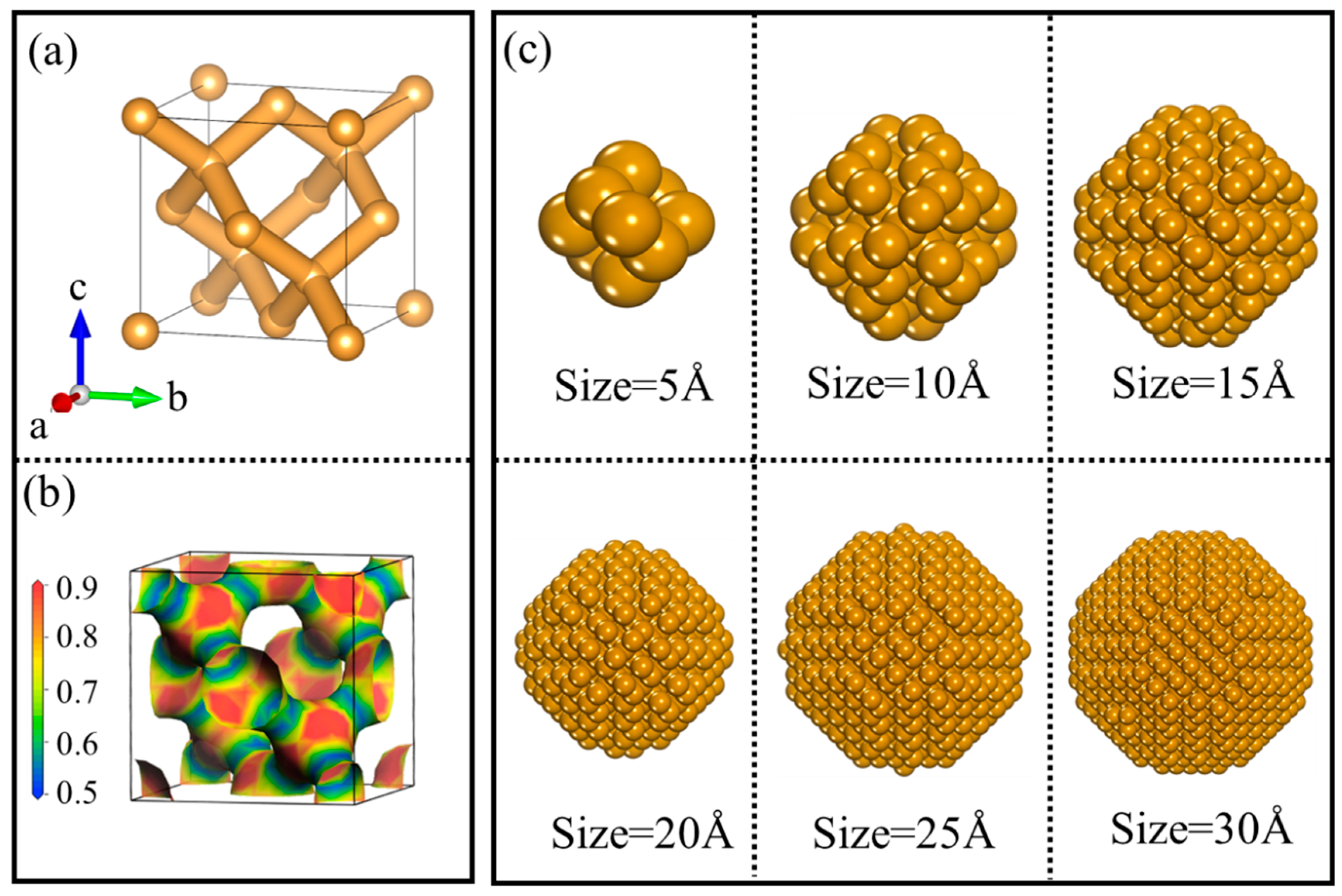
3.1. Structural Characterization of NDs
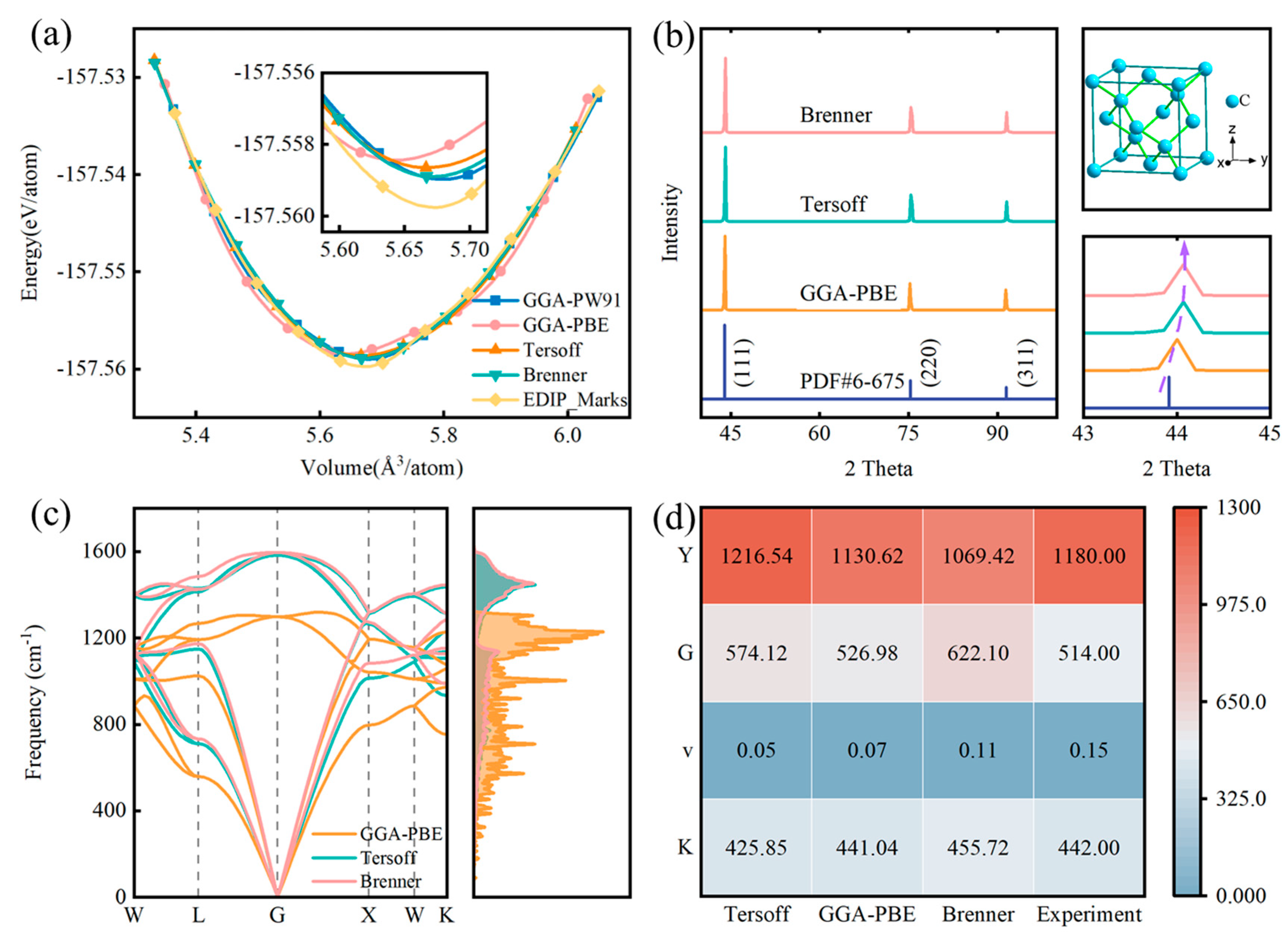
3.2. Selection and Validation of Diamond Interatomic Potential
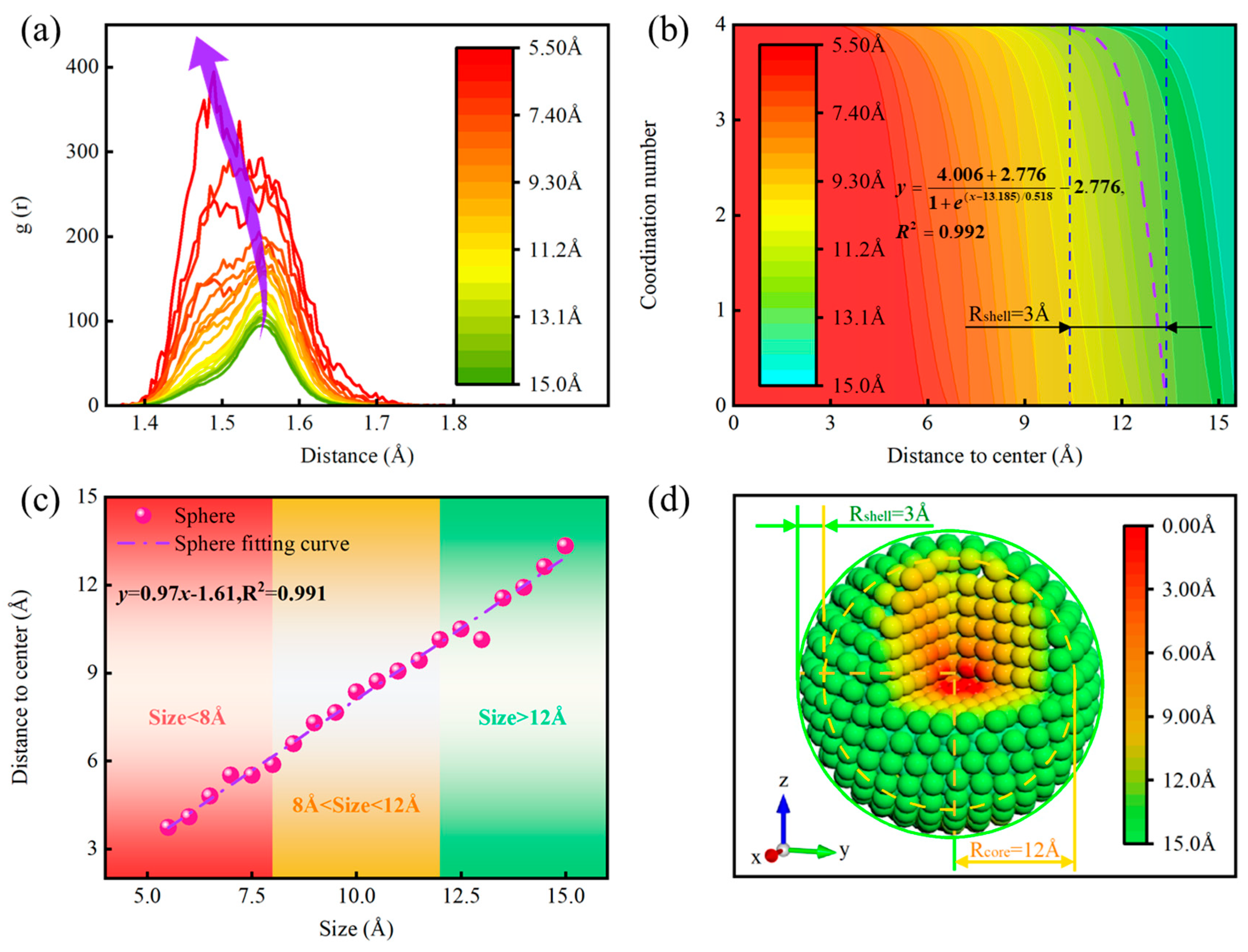
3.3. Fine Structure Anatomy
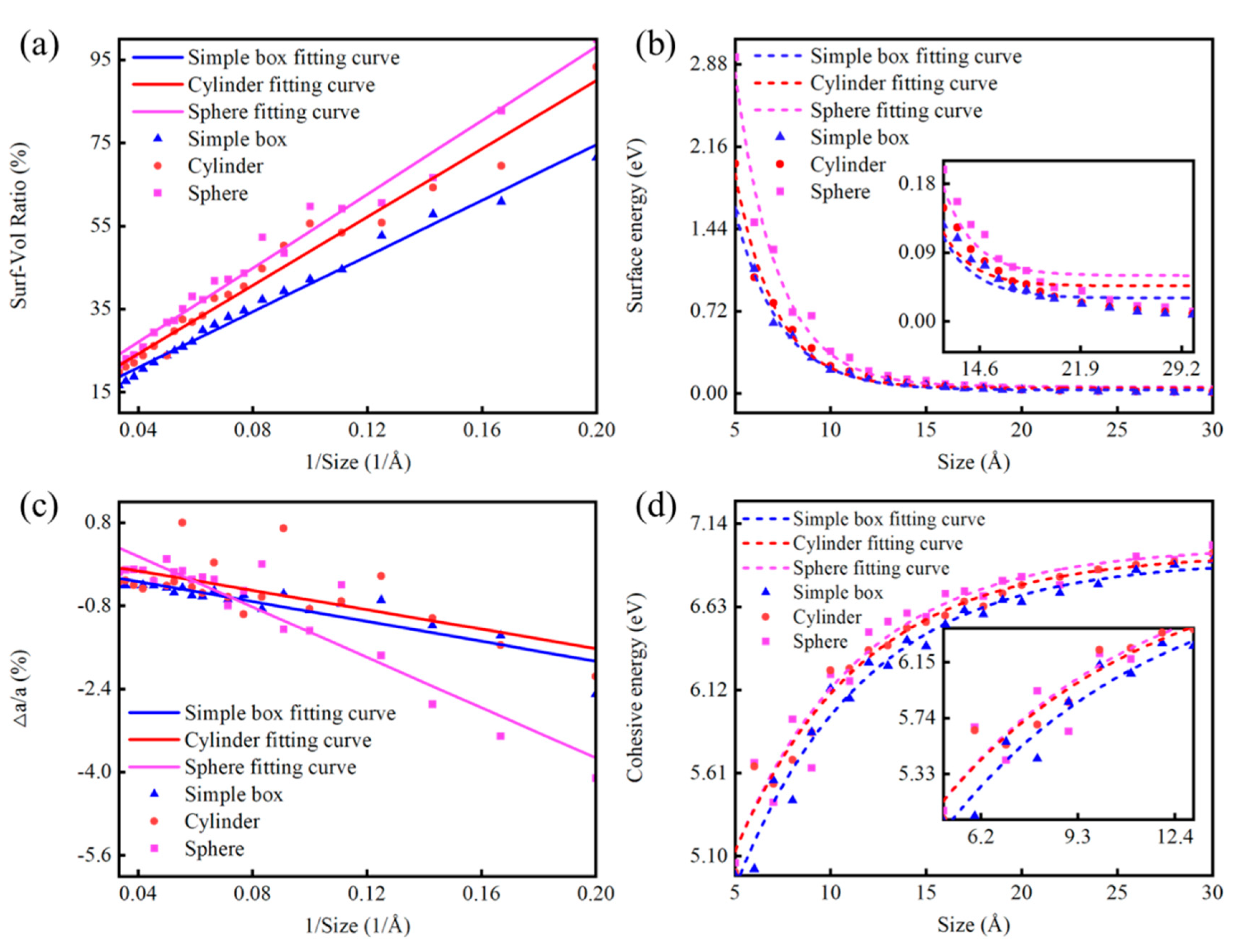
3.3.1. Size Effect of Diamond NPs
3.3.2. Layer-by-Layer Dissection of ND Particles
3.3.3. Surface Amorphous Structure Modulation
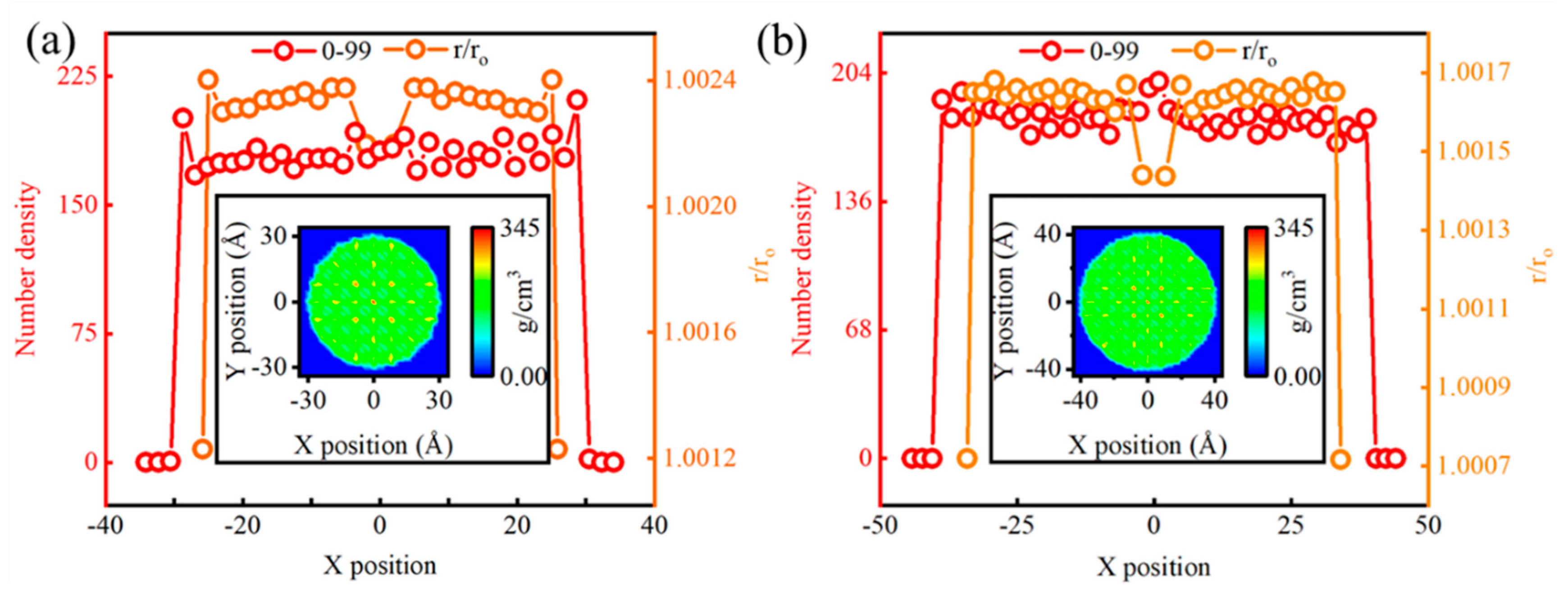
3.4. Comparative Verification
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Langer, R.; Weissleder, R. Nanotechnology. JAMA 2015, 313, 135–136. [Google Scholar] [CrossRef]
- Lowry, G.V.; Avellan, A.; Gilbertson, L.M. Opportunities and challenges for nanotechnology in the agri-tech revolution. Nat. Nanotechnol. 2019, 14, 517–522. [Google Scholar] [CrossRef]
- Nile, S.H.; Baskar, V.; Selvaraj, D.; Nile, A.; Xiao, J.; Kai, G. Nanotechnologies in food science: Applications, recent trends, and future perspectives. Nano-Micro Lett. 2020, 12, 45. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Li, J.; Dong, B.; Wang, F.; Fan, C.; Zuo, X. DNA nanotechnology-empowered nanoscopic imaging of biomolecules. Chem. Soc. Rev. 2021, 50, 5650–5667. [Google Scholar] [CrossRef] [PubMed]
- Keller, A.A.; Ehrens, A.; Zheng, Y.; Nowack, B. Developing trends in nanomaterials and their environmental implications. Nat. Nanotechnol. 2023, 18, 834–837. [Google Scholar] [CrossRef]
- Gloag, L.; Mehdipour, M.; Chen, D.; Tilley, R.D.; Gooding, J.J. Advances in the application of magnetic nanoparticles for sensing. Adv. Mater. 2019, 31, 1904385. [Google Scholar] [CrossRef]
- Luo, W.; Shen, D.; Zhang, R.; Zhang, B.; Wang, Y.; Dou, S.X.; Liu, H.K.; Yang, J. Nanoparticles: Germanium Nanograin Decoration on Carbon Shell: Boosting Lithium-Storage Properties of Silicon Nanoparticles. Adv. Funct. Mater. 2016, 26, 7799. [Google Scholar] [CrossRef]
- Mitchell, M.J.; Billingsley, M.M.; Haley, R.M.; Wechsler, M.E.; Peppas, N.A.; Langer, R. Engineering precision nanoparticles for drug delivery. Nat. Rev. Drug Discov. 2021, 20, 101–124. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Nehra, M.; Kedia, D.; Dilbaghi, N.; Tankeshwar, K.; Kim, K.-H. Nanodiamonds: Emerging face of future nanotechnology. Carbon 2019, 143, 678–699. [Google Scholar] [CrossRef]
- Wang, H.; Cui, Y. Nanodiamonds for energy. Carbon Energy 2019, 1, 13–18. [Google Scholar] [CrossRef]
- Reina, G.; Zhao, L.; Bianco, A.; Komatsu, N. Chemical functionalization of nanodiamonds: Opportunities and challenges ahead. Angew. Chem. Int. Ed. 2019, 58, 17918–17929. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.; Sun, M.; Yang, S.; Gan, G.; Bu, S.; Zhu, A.; Lin, D.; Zhang, T.; Luan, C.; Zhi, C. Multifunctional Nanodiamond Interfacial Layer for Ultra-Stable Zinc-Metal Anodes. Adv. Energy Mater. 2024, 14, 2401479. [Google Scholar] [CrossRef]
- Shao, P.; Tian, J.; Yang, F.; Duan, X.; Gao, S.; Shi, W.; Luo, X.; Cui, F.; Luo, S.; Wang, S. Identification and regulation of active sites on nanodiamonds: Establishing a highly efficient catalytic system for oxidation of organic contaminants. Adv. Funct. Mater. 2018, 28, 1705295. [Google Scholar] [CrossRef]
- Matsubara, H.; Kikugawa, G.; Bessho, T.; Ohara, T. Evaluation of thermal conductivity and its structural dependence of a single nanodiamond using molecular dynamics simulation. Diam. Relat. Mater. 2020, 102, 107669. [Google Scholar] [CrossRef]
- Chen, Z.; Walsh, A.G.; Zhang, P. Structural Analysis of Single-Atom Catalysts by X-ray Absorption Spectroscopy. Acc. Chem. Res. 2024, 57, 521–532. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Jin, C.; Li, Y.; Shen, W. Dynamic behavior of metal nanoparticles for catalysis. Nano Today 2018, 20, 101–120. [Google Scholar] [CrossRef]
- Martín-Sánchez, C.; Sánchez-Iglesias, A.; Barreda-Argüeso, J.A.; Polian, A.; Liz-Marzán, L.M.; Rodríguez, F. Behavior of au nanoparticles under pressure observed by in situ small-angle x-ray scattering. ACS Nano 2022, 17, 743–751. [Google Scholar] [CrossRef]
- Nathanson, M.; Kanhaiya, K.; Pryor, A.; Miao, J.; Heinz, H. Atomic-scale structure and stress release mechanism in core-shell nanoparticles. ACS Nano 2018, 12, 12296–12304. [Google Scholar] [CrossRef]
- Pan, Y.; Chen, S. First-principles investigation of the structure, mechanical and hydrogen adsorption behavior of NiPt nanoparticle. Int. J. Energy Res. 2020, 44, 10970–10981. [Google Scholar] [CrossRef]
- Orekhov, N.; Ostroumova, G.; Stegailov, V. High temperature pure carbon nanoparticle formation: Validation of AIREBO and ReaxFF reactive molecular dynamics. Carbon 2020, 170, 606–620. [Google Scholar] [CrossRef]
- Tolbert, S.; Alivisatos, A. Size dependence of a first order solid-solid phase transition: The wurtzite to rock salt transformation in CdSe nanocrystals. Science 1994, 265, 373–376. [Google Scholar] [CrossRef]
- Okeke, G.; Hammond, R.B.; Joseph Antony, S.J. Influence of size and temperature on the phase stability and thermophysical properties of anatase TiO 2 nanoparticles: Molecular dynamics simulation. J. Nanoparticle Res. 2013, 15, 1–9. [Google Scholar] [CrossRef]
- Song, P.; Wen, D. Molecular dynamics simulation of a core− shell structured metallic nanoparticle. J. Phys. Chem. C 2010, 114, 8688–8696. [Google Scholar] [CrossRef]
- Wang, Y.; Kiziltas, A.; Blanchard, P.; Walsh, T.R. Calculation of 1D and 2D densities in VMD: A flexible and easy-to-use code. Comput. Phys. Commun. 2021, 266, 108032. [Google Scholar] [CrossRef]
- Segall, M.; Lindan, P.J.; Probert, M.A.; Pickard, C.J.; Hasnip, P.J.; Clark, S.; Payne, M. First-principles simulation: Ideas, illustrations and the CASTEP code. J. Phys. Condens. Matter 2002, 14, 2717. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Hedin, L. New method for calculating the one-particle Green’s function with application to the electron-gas problem. Phys. Rev. 1965, 139, A796. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Gale, J.D.; Rohl, A.L. The general utility lattice program (GULP). Mol. Simul. 2003, 29, 291–341. [Google Scholar] [CrossRef]
- Tersoff, J. New empirical approach for the structure and energy of covalent systems. Phys. Rev. B 1988, 37, 6991. [Google Scholar] [CrossRef] [PubMed]
- Tersoff, J. Modeling solid-state chemistry: Interatomic potentials for multicomponent systems. Phys. Rev. B 1989, 39, 5566. [Google Scholar] [CrossRef] [PubMed]
- Brenner, D.W. Empirical potential for hydrocarbons for use in simulating the chemical vapor deposition of diamond films. Phys. Rev. B 1990, 42, 9458. [Google Scholar] [CrossRef]
- Luo, J.; Zhou, C.; Cheng, Y.; Liu, L. Assessing the EDIP potential for atomic simulation of carbon diffusion, segregation and solubility in silicon melt. J. Cryst. Growth 2020, 546, 125785. [Google Scholar] [CrossRef]
- Lejaeghere, K.; Van Speybroeck, V.; Van Oost, G.; Cottenier, S. Error estimates for solid-state density-functional theory predictions: An overview by means of the ground-state elemental crystals. Crit. Rev. Solid State Mater. Sci. 2014, 39, 1–24. [Google Scholar] [CrossRef]
- Zhu, B.; Meng, J.; Yuan, W.; Zhang, X.; Yang, H.; Wang, Y.; Gao, Y. Reshaping of metal nanoparticles under reaction conditions. Angew. Chem. Int. Ed. 2020, 59, 2171–2180. [Google Scholar] [CrossRef]
- Zuo, L.; Humbert, M.; Esling, C. Elastic properties of polycrystals in the Voigt-Reuss-Hill approximation. J. Appl. Crystallogr. 1992, 25, 751–755. [Google Scholar] [CrossRef]
- Vila, F.D.; Hayashi, S.T.; Moore, J.M.; Rehr, J.J. Molecular dynamics simulations of supported Pt nanoparticles with a hybrid Sutton–Chen potential. J. Phys. Chem. C 2016, 120, 14883–14891. [Google Scholar] [CrossRef]
- Symianakis, E.; Kucernak, A. Embedded atom method interatomic potentials fitted upon density functional theory calculations for the simulation of binary PtNi nanoparticles. Comput. Mater. Sci. 2017, 133, 185–193. [Google Scholar] [CrossRef]
- Yu, X.; Zhan, Z. The effects of the size of nanocrystalline materials on their thermodynamic and mechanical properties. Nanoscale Res. Lett. 2014, 9, 516. [Google Scholar] [CrossRef] [PubMed]
- Nosé, S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
- Plimpton, S.; Crozier, P.; Thompson, A. LAMMPS-large-scale atomic/molecular massively parallel simulator. Sandia Natl. Lab. 2007, 18, 43. [Google Scholar]
- Feldman, J.L.; Allen, P.B.; Bickham, S.R. Numerical study of low-frequency vibrations in amorphous silicon. Phys. Rev. B 1999, 59, 3551. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695. [Google Scholar] [CrossRef]
- Norman, G.; Starikov, S.; Stegailov, V. Atomistic simulation of laser ablation of gold: Effect of pressure relaxation. J. Exp. Theor. Phys. 2012, 114, 792–800. [Google Scholar] [CrossRef]
- Erdemir, A.; Martin, J.M. Superior wear resistance of diamond and DLC coatings. Curr. Opin. Solid State Mater. Sci. 2018, 22, 243–254. [Google Scholar] [CrossRef]
- Xiao, S.; Hu, W.; Yang, J. Melting temperature: From nanocrystalline to amorphous phase. J. Chem. Phys. 2006, 125, 184504. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, C.; Chithra, S.; Malviya, K.; Sinha, S.; Chattopadhyay, K. Size dependent microstructure for Ag–Ni nanoparticles. Acta Mater. 2011, 59, 6501–6509. [Google Scholar] [CrossRef]
- Wang, H.; Gu, X.-K.; Zheng, X.; Pan, H.; Zhu, J.; Chen, S.; Cao, L.; Li, W.-X.; Lu, J. Disentangling the size-dependent geometric and electronic effects of palladium nanocatalysts beyond selectivity. Sci. Adv. 2019, 5, eaat6413. [Google Scholar] [CrossRef]
- Riley, D. Lattice constant of diamond and the C–C single bond. Nature 1944, 153, 587–588. [Google Scholar] [CrossRef]
- Li, X.; Ke, P.; Zheng, H.; Wang, A. Structural properties and growth evolution of diamond-like carbon films with different incident energies: A molecular dynamics study. Appl. Surf. Sci. 2013, 273, 670–675. [Google Scholar] [CrossRef]
- Rowe, P.; Csányi, G.; Alfè, D.; Michaelides, A. Development of a machine learning potential for graphene. Phys. Rev. B 2018, 97, 054303. [Google Scholar] [CrossRef]
- Gray, K.J. Electromagnetic window properties of CVD diamond. In Proceedings of the Diamond Optics V, San Diego, CA, USA, 20 November 1992; pp. 203–208. [Google Scholar]
- Altammar, K.A. A review on nanoparticles: Characteristics, synthesis, applications, and challenges. Front. Microbiol. 2023, 14, 1155622. [Google Scholar] [CrossRef]
- Yu, X.; Zhan, Z.; Rong, J.; Liu, Z.; Li, L.; Liu, J. Vacancy formation energy and size effects. Chem. Phys. Lett. 2014, 600, 43–45. [Google Scholar] [CrossRef]
- Liu, J.; Papadakis, R.; Li, H. Experimental observation of size-dependent behavior in surface energy of gold nanoparticles through atomic force microscope. Appl. Phys. Lett. 2018, 113, 083108. [Google Scholar] [CrossRef]
- Yu, X.; Rong, J.; Zhan, Z.; Liu, Z.; Liu, J. Effects of grain size and thermodynamic energy on the lattice parameters of metallic nanomaterials. Mater. Des. 2015, 83, 159–163. [Google Scholar] [CrossRef]
- Yu, X.; Liu, X.; Zhang, K.; Hu, Z. The lattice contraction of nanometre-sized Sn and Bi particles produced by an electrohydrodynamic technique. J. Phys. Condens. Matter 1999, 11, 937. [Google Scholar] [CrossRef]
- Sun, C.Q.; Tay, B.; Zeng, X.; Li, S.; Chen, T.; Zhou, J.; Bai, H.; Jiang, E. Bond-order–bond-length–bond-strength (bond-OLS) correlation mechanism for the shape-and-size dependence of a nanosolid. J. Phys. Condens. Matter 2002, 14, 7781. [Google Scholar] [CrossRef]
- Van Hoang, V. Molecular dynamics simulation of liquid and amorphous Fe nanoparticles. Nanotechnology 2009, 20, 295703. [Google Scholar] [CrossRef] [PubMed]
- Panich, A. Nuclear magnetic resonance studies of nanodiamond surface modification. Diam. Relat. Mater. 2017, 79, 21–31. [Google Scholar] [CrossRef]
- Pezeshki, S.; Lin, H. Recent developments in QM/MM methods towards open-boundary multi-scale simulations. Mol. Simul. 2015, 41, 168–189. [Google Scholar] [CrossRef]
- Tzeliou, C.E.; Mermigki, M.A.; Tzeli, D. Review on the QM/MM methodologies and their application to metalloproteins. Molecules 2022, 27, 2660. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, Z.; Meng, K.; Lu, Y.; Rong, J.; Wei, Y.; Zhang, Y.; Yu, X.; Hou, H. High catalytic activity of amorphous/crystalline heterostructures in Au nanoparticles: A theoretical investigation. Mater. Today Commun. 2023, 37, 107190. [Google Scholar] [CrossRef]
- Magomedov, M. Random packing of monoatomic structures. J. Struct. Chem. 2008, 49, 156–159. [Google Scholar] [CrossRef]
- Skrobas, K.; Stelmakh, S.; Gierlotka, S.; Palosz, B. A model of density waves in atomic structure of nanodiamond by molecular dynamics simulations. Diam. Relat. Mater. 2019, 91, 1–14. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, L.; He, Z.; Chen, K.; Li, H.; Wu, Y.; Ye, J.; Hou, H.; Rong, J.; Yu, X. Deciphering Surface-Localized Structure of Nanodiamonds. Nanomaterials 2024, 14, 2024. https://doi.org/10.3390/nano14242024
Ma L, He Z, Chen K, Li H, Wu Y, Ye J, Hou H, Rong J, Yu X. Deciphering Surface-Localized Structure of Nanodiamonds. Nanomaterials. 2024; 14(24):2024. https://doi.org/10.3390/nano14242024
Chicago/Turabian StyleMa, Li, Zhijie He, Keyuan Chen, Hanqing Li, Yongzhi Wu, Jueyi Ye, Hongying Hou, Ju Rong, and Xiaohua Yu. 2024. "Deciphering Surface-Localized Structure of Nanodiamonds" Nanomaterials 14, no. 24: 2024. https://doi.org/10.3390/nano14242024
APA StyleMa, L., He, Z., Chen, K., Li, H., Wu, Y., Ye, J., Hou, H., Rong, J., & Yu, X. (2024). Deciphering Surface-Localized Structure of Nanodiamonds. Nanomaterials, 14(24), 2024. https://doi.org/10.3390/nano14242024





