Constructing Dynamical Symmetries for Quantum Computing: Applications to Coherent Dynamics in Coupled Quantum Dots
Abstract
:1. Introduction
2. Dynamical Symmetries
3. The Evolution Operator in a Product Form
4. Explicit Solution of the Two-Coupled Level System
5. Generalization to a N-Coupled Level System
6. Applications to the Electronic Dynamics of CdSe Nanoparticles
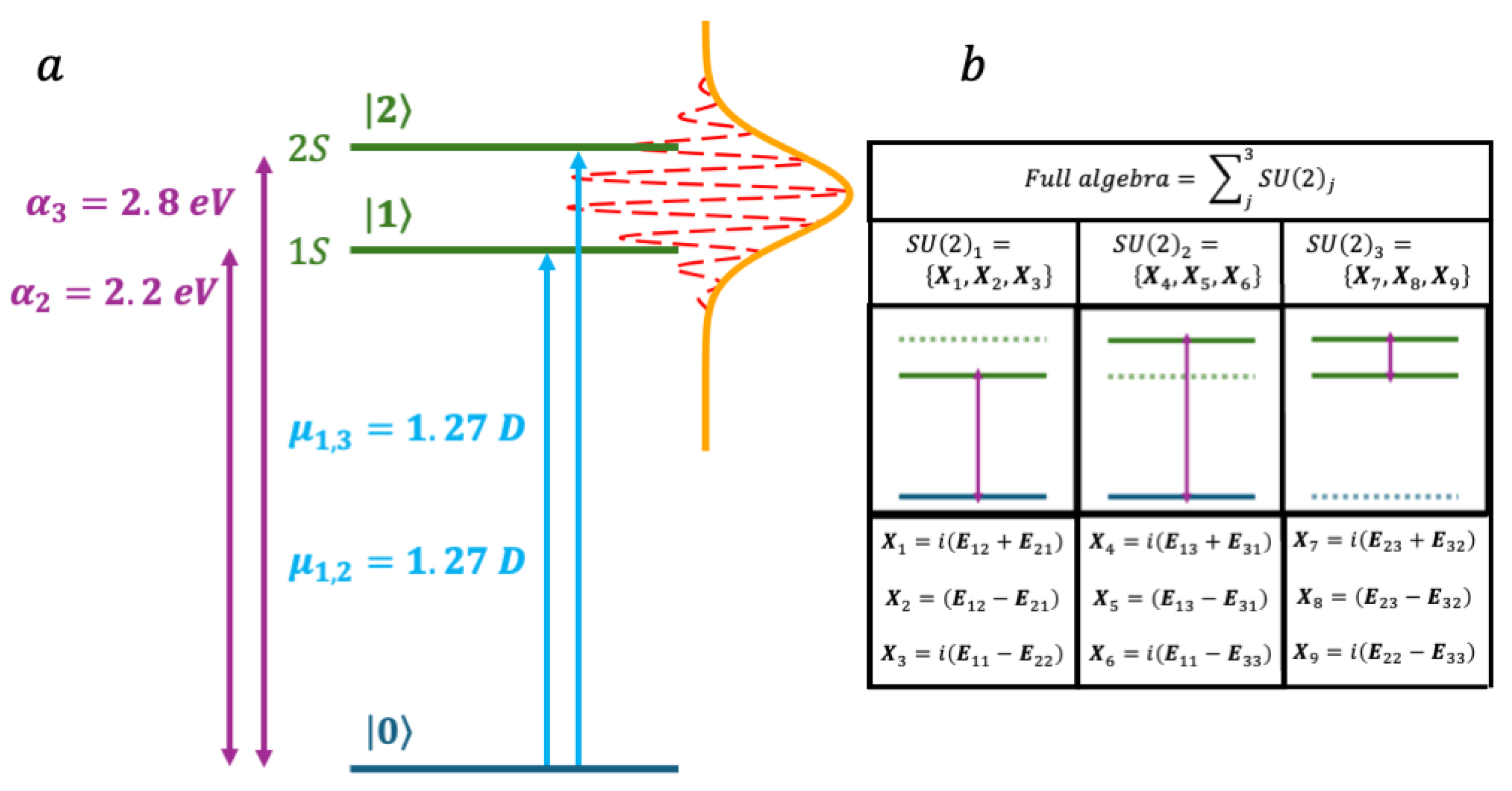
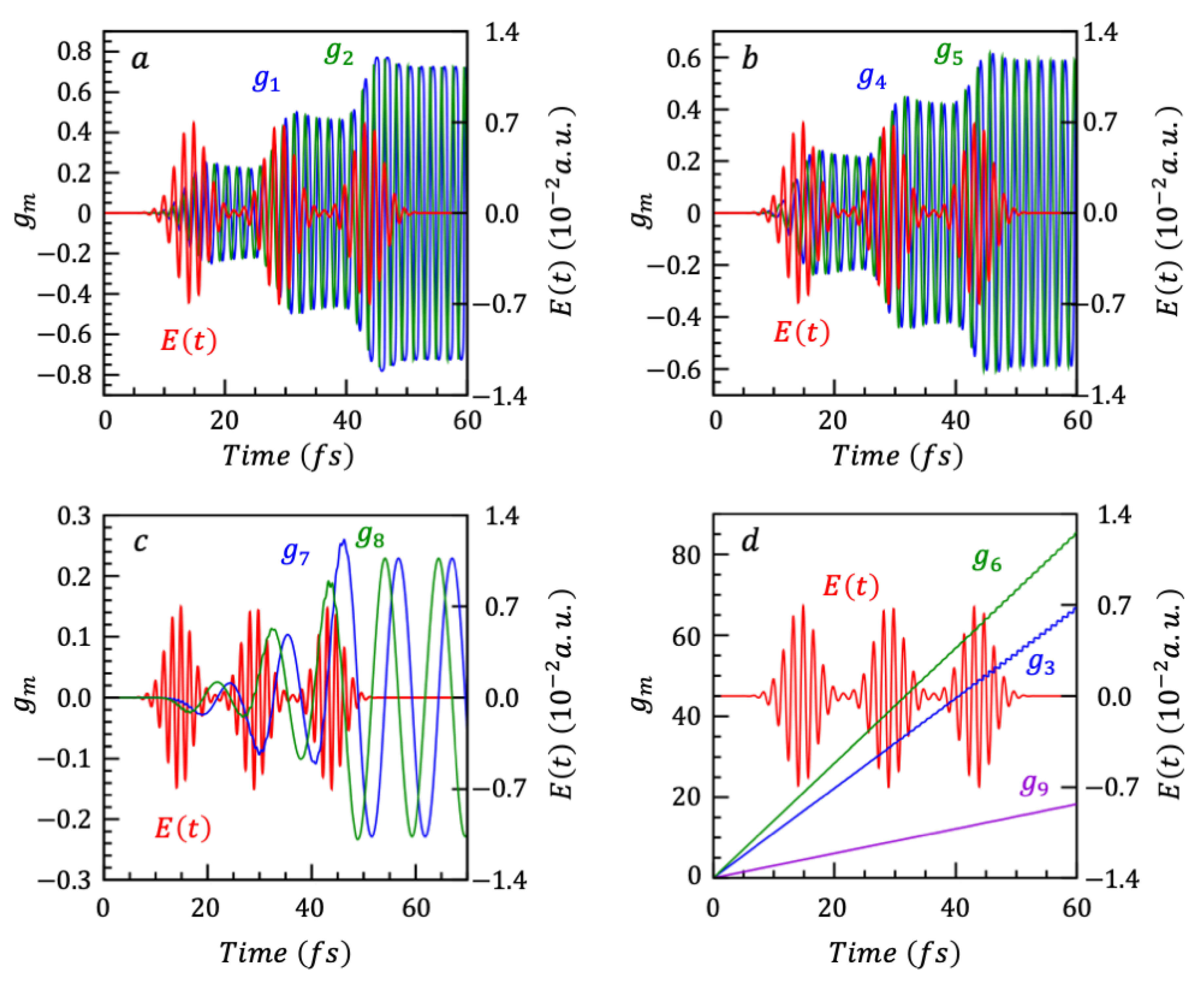
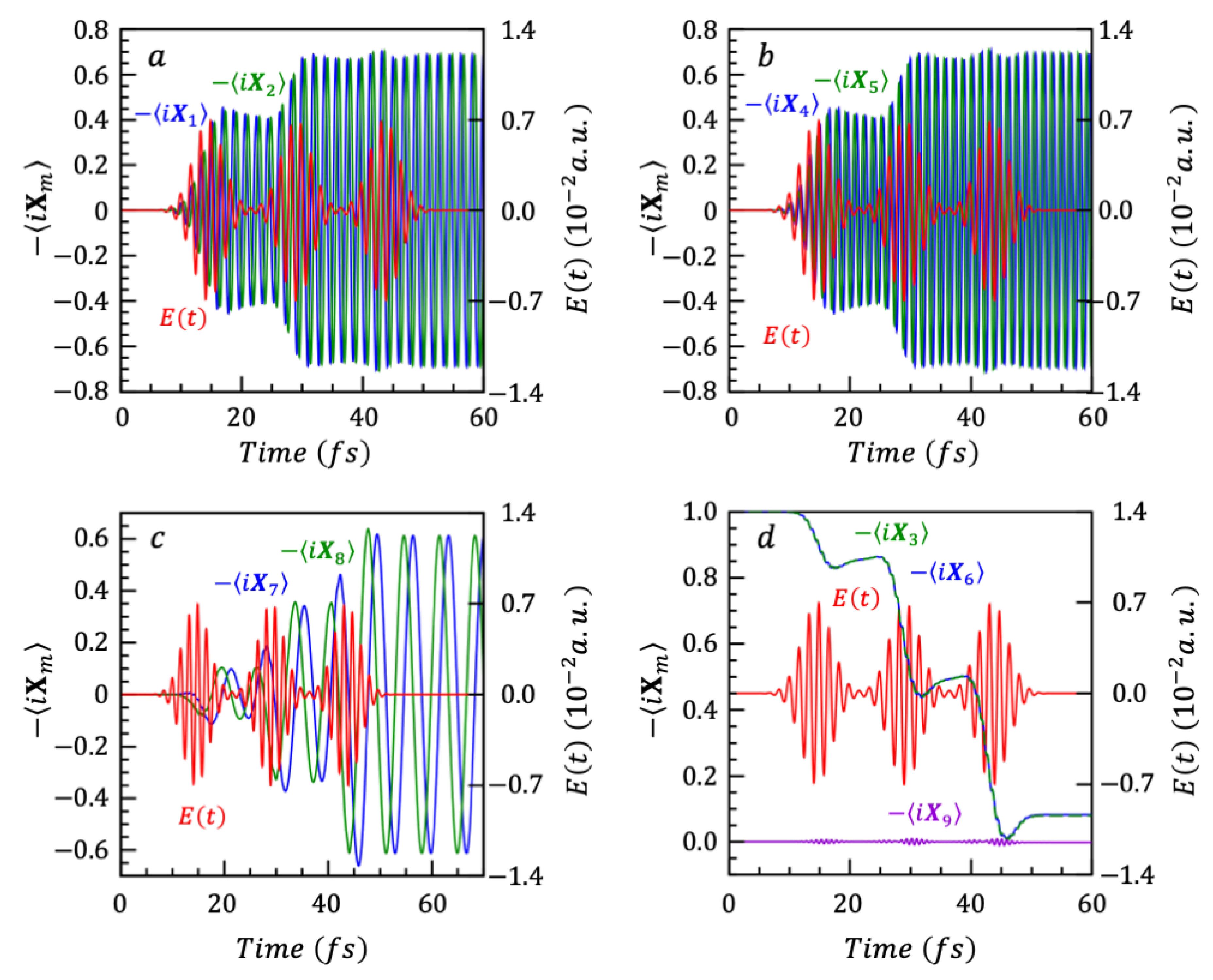
6.1. Electronic Dynamics for a Single CdSe Nanoparticle: An N = 3 Model
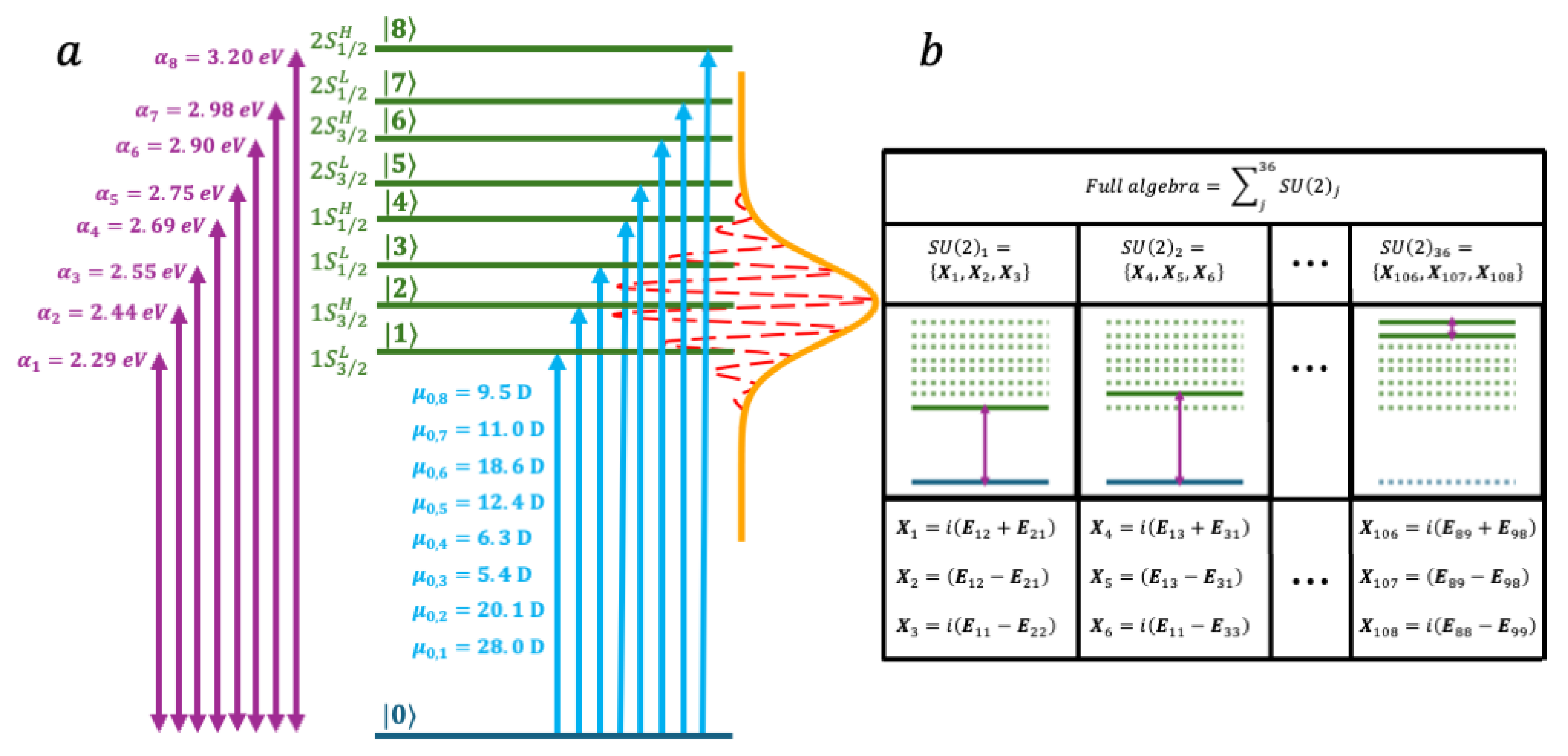
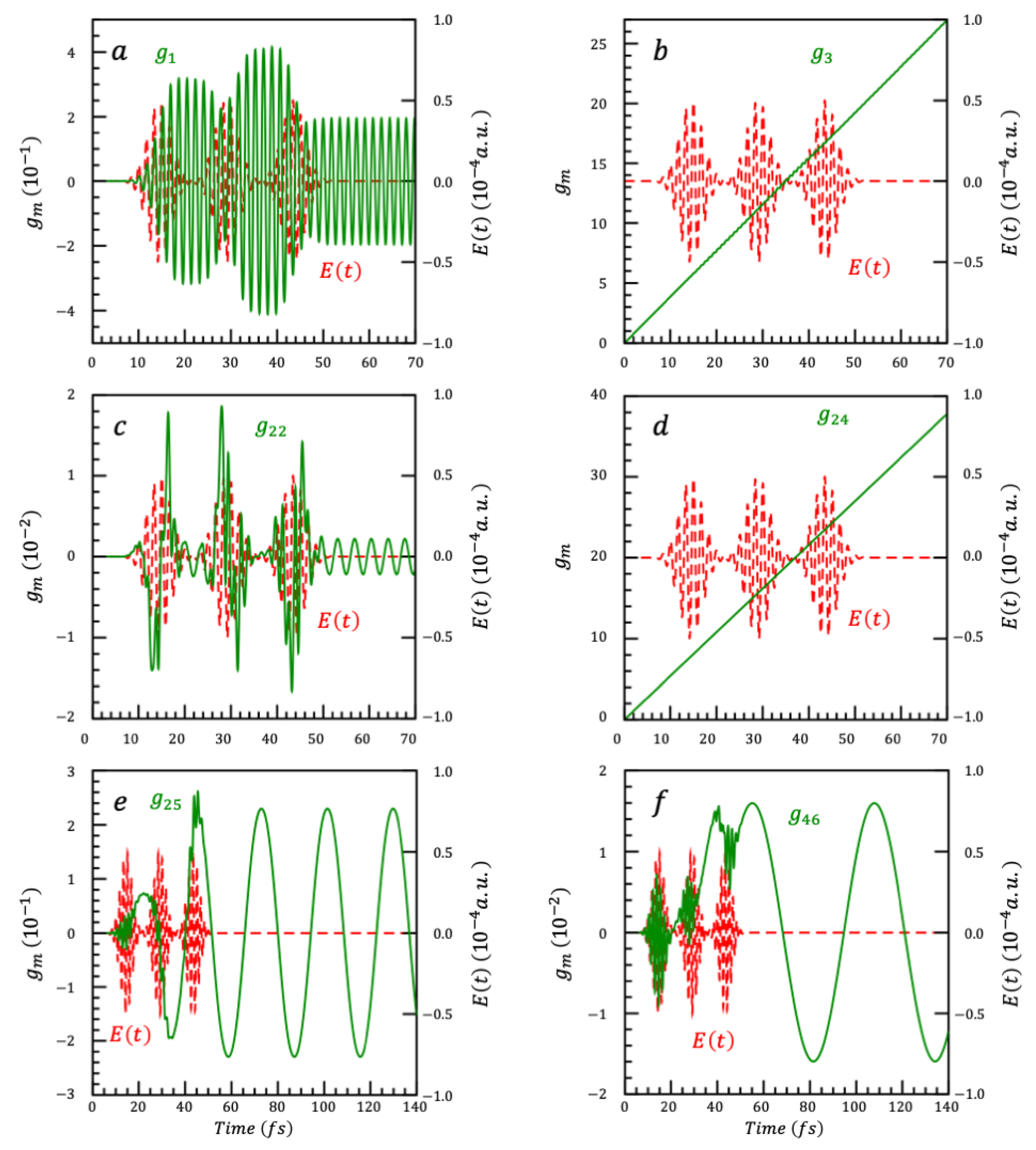
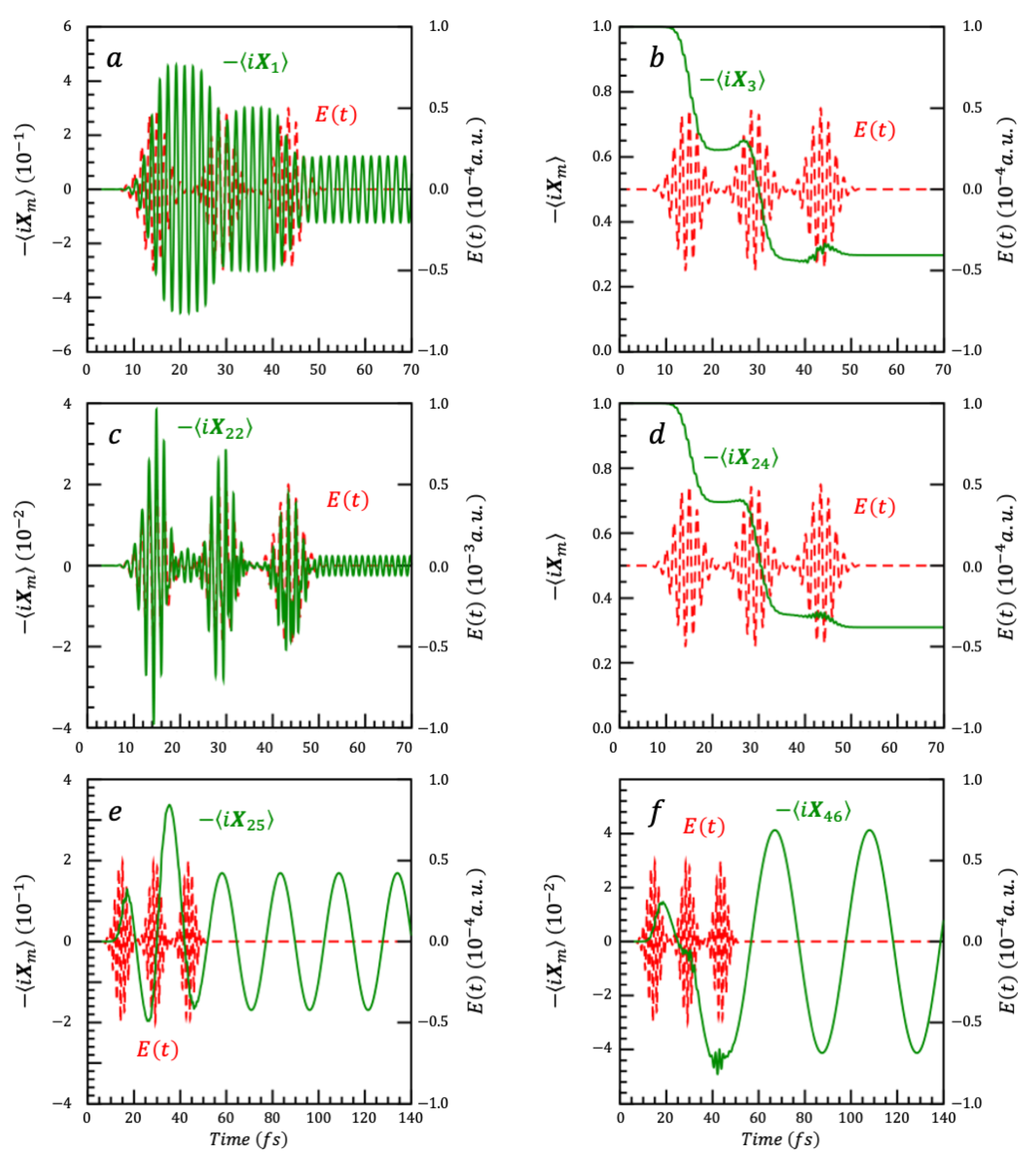
6.2. Electronic Dynamics in a Nine-Level Dimer of CdSe Nanoparticles
7. Conclusions and Perspectives
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cotton, A.F. Chemical Applications of GroupTheory, 3rd ed.; Wiley & Sons: Chichester, UK, 1990. [Google Scholar]
- Lewis, H.R., Jr.; Riesenfeld, W.B. An Exact Quantum Theory of the Time-Dependent Harmonic Oscillator and of a Charged Particle in a Time-Dependent Electromagnetic Field. J. Math. Phys. 1969, 10, 1458–1473. [Google Scholar] [CrossRef]
- Magnus, W. On the exponential solution of differential equations for a linear operator. Commun. Pure Appl. Math. 1954, 7, 649–673. [Google Scholar] [CrossRef]
- Pechukas, P.; Light, J.C. On the Exponential Form of Time-Displacement Operators in Quantum Mechanics. J. Chem. Phys. 1966, 44, 3897–3912. [Google Scholar] [CrossRef]
- Wilcox, R.M. Exponential Operators and Parameter Differentiation in Quantum Physics. J. Math. Phys. 1967, 8, 962–982. [Google Scholar] [CrossRef]
- Hioe, F.T.; Eberly, J.H. N-Level Coherence Vector and Higher Conservation Laws in Quantum Optics and Quantum Mechanics. Phys. Rev. Lett. 1981, 47, 838–841. [Google Scholar] [CrossRef]
- Rasetti, M. Generalized definition of coherent states and dynamical groups. Int. J. Theor. Phys. 1975, 13, 425–430. [Google Scholar] [CrossRef]
- Dattoli, G.; Di Lazzaro, P.; Torre, A. SU(1,1), SU(2), and SU(3) coherence-preserving Hamiltonians and time-ordering techniques. Phys. Rev. A 1987, 35, 1582–1589. [Google Scholar] [CrossRef] [PubMed]
- Dattoli, G.; Richetta, M.; Schettini, G.; Torre, A. Lie algebraic methods and solutions of linear partial differential equations. J. Math. Phys. 1990, 31, 2856–2863. [Google Scholar] [CrossRef]
- Dattoli, G.; Torre, A. Cayley–Klein parameters and evolution of two- and three-level systems and squeezed states. J. Math. Phys. 1990, 31, 236–240. [Google Scholar] [CrossRef]
- Dattoli, G.; Torre, A. Matrix representation of the evolution operator for theSU(3) dynamics. Il Nuovo Cimento B (1971–1996) 1991, 106, 1247–1256. [Google Scholar] [CrossRef]
- Altafini, C. Explicit Wei-Norman formulae for matrix Lie groups. In Proceedings of the Proc 41st IEEE Conference on Decision and Control, Las Vegas, NE, USA, 10–13 December 2002; pp. 2714–2719. [Google Scholar]
- Altafini, C. Parameter differentiation and quantum state decomposition for time varying Schrödiner equations. Rep. Math. Phys. 2003, 52, 381–400. [Google Scholar] [CrossRef]
- Wei, J.; Norman, E. Lie Algebraic Solution of Linear Differential Equations. J. Math. Phys. 1963, 4, 575–581. [Google Scholar] [CrossRef]
- Wei, J.; Norman, E. On Global Representations of the Solutions of Linear Differential Equations as a Product of Exponentials. Proc. Am. Math. So. 1964, 15, 327–334. [Google Scholar] [CrossRef]
- Fano, U. Description of States in Quantum Mechanics by Density Matrix and Operator Techniques. Rev. Mod. Phys. 1957, 29, 74–93. [Google Scholar] [CrossRef]
- Olver, P.J. Introduction to Partial Differential Equations; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Miller, W. Lie Theory and Special Functions; Academic Press: New York, NY, USA, 1968. [Google Scholar]
- Malkin, I.A.; Man’ko, V.I.; Trifonov, D.A. Dynamical symmetry of nonstationary systems. Il Nuovo Cimento A 1971, 4, 773–792. [Google Scholar] [CrossRef]
- Katzin, G.H.; Levine, J. Dynamical symmetries and constants of the motion for classical particle systems. J. Math. Phys. 1974, 15, 1460–1470. [Google Scholar] [CrossRef]
- Dragt, A.J.; Forest, E. Computation of nonlinear behavior of Hamiltonian systems using Lie algebraic methods. J. Math. Phys. 1983, 24, 2734–2744. [Google Scholar] [CrossRef]
- Engelhardt, G.; Cao, J. Dynamical Symmetries and Symmetry-Protected Selection Rules in Periodically Driven Quantum Systems. Phys. Rev. Lett. 2021, 126, 090601. [Google Scholar] [CrossRef]
- Kikoin, K.; Kiselev, M.; Avishai, Y. Dynamical Symmetries for Nanostructures; Springer: Vienna, Austria, 2012. [Google Scholar]
- Moehlis, J.; Knobloch, E. Equivalent dynamical systems. Scholarpedia 2007, 2, 2510. [Google Scholar] [CrossRef]
- Wulfman, C.E. Dynamical Symmetry; Worl Scientific: Singapore, 2010. [Google Scholar]
- Barut, A.; Bohm, A.; Ne’eman, Y. Dynamical Groups and Spectrum Generating Algebras; World Scientific Publishing Company: Singapore, 1988; p. 1168. [Google Scholar]
- Alhassid, Y.; Levine, R.D. Collision experiments with partial resolution of final states: Maximum entropy procedure and surprisal analysis. Phys. Rev. C 1979, 20, 1775–1788. [Google Scholar] [CrossRef]
- Alhassid, Y.; Levine, R.D. Connection between the maximal entropy and the scattering theoretic analyses of collision processes. Phys. Rev. A 1978, 18, 89–116. [Google Scholar] [CrossRef]
- Aronson, E.B.; Malkin, I.A.; Manko, V.I. Dynamical Symmetries in quamtum Mechanics. Sov. J. Part. Nucl. 1974, 5, 47–67. [Google Scholar]
- Levine, R.D. Dynamical symmetries. J. Phys. Chem. 1985, 89, 2122–2129. [Google Scholar] [CrossRef]
- Leviatan, A. Partial dynamical symmetries. Prog. Part. Nucl. Phys. 2011, 66, 93–143. [Google Scholar] [CrossRef]
- Pfeifer, P.; Levine, R.D. A stationary formulation of time-dependent problems in quantum mechanics. J. Chem. Phys. 1983, 79, 5512–5519. [Google Scholar] [CrossRef]
- Vilemkin, N.J. Special Functions and the Theory of Group Representations; American Mathematical Society: Providence, RI, USA, 1968. [Google Scholar]
- Klauder, J.R.; Skagerstant, B.-S. Coherent States; World Scientific: Singapore, 1985. [Google Scholar]
- Sternberg, S. Group Theory and Physics; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Perelomov, A.M. Coherent states for arbitrary Lie group. Commun. Math. Phys. 1972, 26, 222–236. [Google Scholar] [CrossRef]
- Gilmore, R. On the properties of coherent states. Rev. Mex. Física 1974, 23, 143–187. [Google Scholar]
- Dodonov, V.V.; Malkin, I.A.; Man’ko, V.I. Integrals of the motion, green functions, and coherent states of dynamical systems. Int. J. Theor. Phys. 1975, 14, 37–54. [Google Scholar] [CrossRef]
- Penson, K.A.; Solomon, A.I. New generalized coherent states. J. Math. Phys. 1999, 40, 2354–2363. [Google Scholar] [CrossRef]
- Solomon, A.I. Group Theory of Superfluidity. J. Math. Phys. 1971, 12, 390–394. [Google Scholar] [CrossRef]
- Mukamel, S. Principles of Nonlinear Optical Spectroscopy; Oxford University Press: Melbourne, VIC, Australia, 1995. [Google Scholar]
- Hamilton, J.R.; Amarotti, E.; Dibenedetto, C.N.; Striccoli, M.; Levine, R.D.; Collini, E.; Remacle, F. Harvesting a Wide Spectral Range of Electronic Coherences with Disordered Quasi-Homo Dimeric Assemblies at Room Temperature. Adv. Quantum Technol. 2022, 5, 2200060. [Google Scholar] [CrossRef]
- Collini, E. 2D Electronic Spectroscopic Techniques for Quantum Technology Applications. J. Phys. Chem. C 2021, 125, 13096–13108. [Google Scholar] [CrossRef] [PubMed]
- Dibenedetto, C.N.; Fanizza, E.; De Caro, L.; Brescia, R.; Panniello, A.; Tommasi, R.; Ingrosso, C.; Giannini, C.; Agostiano, A.; Curri, M.L.; et al. Coupling in quantum dot molecular hetero-assemblies. Mater. Res. Bull. 2022, 146, 111578. [Google Scholar] [CrossRef]
- Kagan, C.R.; Bassett, L.C.; Murray, C.B.; Thompson, S.M. Colloidal Quantum Dots as Platforms for Quantum Information Science. Chem. Rev. 2021, 121, 3186–3233. [Google Scholar] [CrossRef]
- Koley, S.; Cui, J.; Panfil, Y.E.; Banin, U. Coupled Colloidal Quantum Dot Molecules. Acc. Chem. Res. 2021, 54, 1178–1188. [Google Scholar] [CrossRef] [PubMed]
- Rebentrost, P.; Stopa, M.; Aspuru-Guzik, A. Förster Coupling in Nanoparticle Excitonic Circuits. Nano Lett. 2010, 10, 2849–2856. [Google Scholar] [CrossRef] [PubMed]
- Spittel, D.; Poppe, J.; Meerbach, C.; Ziegler, C.; Hickey, S.G.; Eychmüller, A. Absolute Energy Level Positions in CdSe Nanostructures from Potential-Modulated Absorption Spectroscopy (EMAS). ACS Nano 2017, 11, 12174–12184. [Google Scholar] [CrossRef] [PubMed]
- Loss, D.; DiVincenzo, D.P. Quantum computation with quantum dots. Phys. Rev. A 1998, 57, 120–126. [Google Scholar] [CrossRef]
- Kane, B.E. A silicon-based nuclear spin quantum computer. Nature 1998, 393, 133–137. [Google Scholar] [CrossRef]
- Imamoglu, A. Are quantum dots useful for quantum computation? Phys. E Low-Dimens. Syst. Nanostructures 2003, 16, 47–50. [Google Scholar] [CrossRef]
- Hanson, R.; Kouwenhoven, L.P.; Petta, J.R.; Tarucha, S.; Vandersypen, L.M.K. Spins in few-electron quantum dots. Rev. Mod. Phys. 2007, 79, 1217–1265. [Google Scholar] [CrossRef]
- Harvey, S.P. Quantum Dots/Spin Qubits. arXiv 2022, arXiv:2204.04261. [Google Scholar] [CrossRef]
- Collini, E.; Gattuso, H.; Bolzonello, L.; Casotto, A.; Volpato, A.; Dibenedetto, C.N.; Fanizza, E.; Striccoli, M.; Remacle, F. Quantum Phenomena in Nanomaterials: Coherent Superpositions of Fine Structure States in CdSe Nanocrystals at Room Temperature. J. Phys. Chem. C 2019, 123, 31286–31293. [Google Scholar] [CrossRef]
- Collini, E.; Gattuso, H.; Kolodny, Y.; Bolzonello, L.; Volpato, A.; Fridman, H.T.; Yochelis, S.; Mor, M.; Dehnel, J.; Lifshitz, E.; et al. Room-Temperature Inter-Dot Coherent Dynamics in Multilayer Quantum Dot Materials. J. Phys. Chem. C 2020, 124, 1622–16231. [Google Scholar] [CrossRef]
- Gattuso, H.; Levine, R.D.; Remacle, F. Massively parallel classical logic via coherent dynamics of an ensemble of quantum systems with dispersion in size. Proc. Natl. Acad. Sci. USA 2020, 117, 21022. [Google Scholar] [CrossRef]
- Komarova, K.; Gattuso, H.; Levine, R.D.; Remacle, F. Quantum Device Emulates the Dynamics of Two Coupled Oscillators. J. Phys. Chem. Lett. 2020, 11, 6990–6995. [Google Scholar] [CrossRef]
- Tishby, N.Z.; Levine, R.D. Time evolution via a self-consistent maximal-entropy propagation: The reversible case. Phys. Rev. A 1984, 30, 1477–1490. [Google Scholar] [CrossRef]
- Claveau, Y.; Arnaud, B.; Matteo, S.D. Mean-field solution of the Hubbard model: The magnetic phase diagram. Eur. J. Phys. 2014, 35, 035023. [Google Scholar] [CrossRef]
- Montorsi, A.; Rasetti, M.; Solomon, A.I. Dynamical superalgebra and supersymmetry for a many-fermion system. Phys. Rev. Lett. 1987, 59, 2243–2246. [Google Scholar] [CrossRef] [PubMed]
- Dirac, P.A.M. The quantum theory of tghe emission and the absorption of radiation. Proc. R. Soc. Lond. A 1927, 114, 243–265. [Google Scholar]
- Remacle, F.; Levine, R.D. A quantum information processing machine for computing by observables. Proc. Natl. Acad. Sci. USA 2023, 120, e2220069120. [Google Scholar] [CrossRef]
- Hioe, F.T.; Eberly, J.H. Nonlinear constants of motion for three-level quantum systems. Phys. Rev. A 1982, 25, 2168–2171. [Google Scholar] [CrossRef]
- Brus, L. Electronic wave functions in semiconductor clusters: Experiment and theory. J. Phys. Chem. 1986, 90, 2555–2560. [Google Scholar] [CrossRef]
- Efros, A.L.; Rosen, M.; Kuno, M.; Nirmal, M.; Norris, D.J.; Bawendi, M. Band-edge exciton in quantum dots of semiconductors with a degenerate valence band: Dark and bright exciton states. Phys. Rev. B 1996, 54, 4843–4856. [Google Scholar] [CrossRef]
- Norris, D.J.; Bawendi, M.G. Measurement and assignment of the size-dependent optical spectrum in CdSe quantum dots. Phys. Rev. B 1996, 53, 16338–16346. [Google Scholar] [CrossRef] [PubMed]
- Prezhdo, O.V. Photoinduced Dynamics in Semiconductor Quantum Dots: Insights from Time-Domain ab Initio Studies. Acc. Chem. Res. 2009, 42, 2005–2016. [Google Scholar] [CrossRef]
- Klimov, V.I. (Ed.) Nanocrystal Quantum Dots; CRC Press: Boca Raton, FI, USA, 2010. [Google Scholar]
- Hyeon-Deuk, K.; Prezhdo, O.V. Multiple Exciton Generation and Recombination Dynamics in Small Si and CdSe Quantum Dots: An Ab Initio Time-Domain Study. ACS Nano 2012, 6, 1239–1250. [Google Scholar] [CrossRef]
- Seiler, H.; Palato, S.; Sonnichsen, C.; Baker, H.; Kambhampati, P. Seeing Multiexcitons through Sample Inhomogeneity: Band-Edge Biexciton Structure in CdSe Nanocrystals Revealed by Two-Dimensional Electronic Spectroscopy. Nano Lett. 2018, 18, 2999–3006. [Google Scholar] [CrossRef] [PubMed]
- Trivedi, D.J.; Wang, L.; Prezhdo, O.V. Auger-Mediated Electron Relaxation Is Robust to Deep Hole Traps: Time-Domain Ab Initio Study of CdSe Quantum Dots. Nano Lett. 2015, 15, 2086–2091. [Google Scholar] [CrossRef] [PubMed]
- Palato, S.; Seiler, H.; Nijjar, P.; Prezhdo, O.; Kambhampati, P. Atomic fluctuations in electronic materials revealed by dephasing. Proc. Natl. Acad. Sci. USA 2020, 117, 11940–11946. [Google Scholar] [CrossRef]
- Cassette, E.; Pensack, R.D.; Mahler, B.; Scholes, G.D. Room-temperature exciton coherence and dephasing in two-dimensional nanostructures. Nat. Commun. 2015, 6, 6086. [Google Scholar] [CrossRef]
- Turner, D.B.; Hassan, Y.; Scholes, G.D. Exciton Superposition States in CdSe Nanocrystals Measured Using Broadband Two-Dimensional Electronic Spectroscopy. Nano Lett. 2012, 12, 880–886. [Google Scholar] [CrossRef]
- Caram, J.R.; Zheng, H.; Dahlberg, P.D.; Rolczynski, B.S.; Griffin, G.B.; Dolzhnikov, D.S.; Talapin, D.V.; Engel, G.S. Exploring size and state dynamics in CdSe quantum dots using two-dimensional electronic spectroscopy. J. Chem. Phys. 2014, 140, 084701. [Google Scholar] [CrossRef]
- Caram, J.R.; Zheng, H.; Dahlberg, P.D.; Rolczynski, B.S.; Griffin, G.B.; Fidler, A.F.; Dolzhnikov, D.S.; Talapin, D.V.; Engel, G.S. Persistent Interexcitonic Quantum Coherence in CdSe Quantum Dots. J. Phys. Chem. Lett. 2014, 5, 196–204. [Google Scholar] [CrossRef]
- Kim, J.; Wong, C.Y.; Scholes, G.D. Exciton Fine Structure and Spin Relaxation in Semiconductor Colloidal Quantum Dots. Acc. Chem. Res. 2009, 42, 1037–1046. [Google Scholar] [CrossRef]
- Wong, C.Y.; Scholes, G.D. Biexcitonic Fine Structure of CdSe Nanocrystals Probed by Polarization-Dependent Two-Dimensional Photon Echo Spectroscopy. J. Phys. Chem. A 2011, 115, 3797–3806. [Google Scholar] [CrossRef]
- Gattuso, H.; Fresch, B.; Levine, R.D.; Remacle, F. Coherent Exciton Dynamics in Ensembles of Size-Dispersed CdSe Quantum Dot Dimers Probed via Ultrafast Spectroscopy: A Quantum Computational Study. Appl. Sci. 2020, 10, 1328. [Google Scholar] [CrossRef]
- Collini, E.; Gattuso, H.; Levine, R.D.; Remacle, F. Ultrafast fs coherent excitonic dynamics in CdSe quantum dots assemblies addressed and probed by 2D electronic spectroscopy. J. Chem. Phys. 2021, 154, 014301. [Google Scholar] [CrossRef]
- Hamilton, J.R.; Amarotti, E.; Dibenedetto, C.N.; Striccoli, M.; Levine, R.D.; Collini, E.; Remacle, F. Time-Frequency Signatures of Electronic Coherence of Colloidal CdSe Quantum Dot Dimer Assemblies Probed at Room Temperature by Two-Dimensional Electronic Spectroscopy. Nanomaterials 2023, 13, 2096. [Google Scholar] [CrossRef] [PubMed]
- Chae, E.; Choi, J.; Kim, J. An elementary review on basic principles and developments of qubits for quantum computing. Nano Converg. 2024, 11, 11. [Google Scholar] [CrossRef]
- Lucas, A. Ising formulations of many NP problems. Front. Phys. 2014, 2, 5. [Google Scholar] [CrossRef]
- Xia, R.; Bian, T.; Kais, S. Electronic Structure Calculations and the Ising Hamiltonian. J. Phys. Chem. B 2018, 122, 3384–3395. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamilton, J.R.; Levine, R.D.; Remacle, F. Constructing Dynamical Symmetries for Quantum Computing: Applications to Coherent Dynamics in Coupled Quantum Dots. Nanomaterials 2024, 14, 2056. https://doi.org/10.3390/nano14242056
Hamilton JR, Levine RD, Remacle F. Constructing Dynamical Symmetries for Quantum Computing: Applications to Coherent Dynamics in Coupled Quantum Dots. Nanomaterials. 2024; 14(24):2056. https://doi.org/10.3390/nano14242056
Chicago/Turabian StyleHamilton, James R., Raphael D. Levine, and Francoise Remacle. 2024. "Constructing Dynamical Symmetries for Quantum Computing: Applications to Coherent Dynamics in Coupled Quantum Dots" Nanomaterials 14, no. 24: 2056. https://doi.org/10.3390/nano14242056
APA StyleHamilton, J. R., Levine, R. D., & Remacle, F. (2024). Constructing Dynamical Symmetries for Quantum Computing: Applications to Coherent Dynamics in Coupled Quantum Dots. Nanomaterials, 14(24), 2056. https://doi.org/10.3390/nano14242056







