Abstract
We report on DFT-TDDFT studies of the structural, electronic and vibrational properties of nanocapsules and the effect of encapsulation of homonuclear diatomic halogens (, and ) and chalcogens ( and ) on the interaction of the nanocapsules with the divalent magnesium cation. In particular, to foretell whether these BN nanostructures could be proper negative electrodes for magnesium-ion batteries, the structural, vibrational and electronic properties, as well as the interaction energy and the cell voltage, which is important for applications, have been computed for each system, highlighting their differences and similarities. The encapsulation of halogen and chalcogen diatomic molecules increases the cell voltage, with an effect enhanced down groups 16 and 17 of the periodic table, leading to better performing anodes and fulfilling a remarkable cell voltage of 3.61 V for the iodine-encapsulated system.
1. Introduction
Materials are key components in the sphere of energy production, transformation and storage, and first-principle calculations play a critical role in designing and optimizing new advanced energy materials able to meet the high performance requirements of an efficient and sustainable use of electrical energy [1]. The growing electrified world has been dominated by lithium-ion battery (LIB) technology since the 1990s, when LIBs became the backbone of portable electronics, enabling the convenient storage and utilization of energy [2,3,4]. However, market concerns are rising over lithium resource depletion, which will cause the price of lithium to skyrocket with the escalating implementation of LIBs in the automotive industry and the risk of limiting the wide-scale adoption of electric vehicles [5,6,7,8]. Therefore, over the years, numerous earth-abundant metals have been investigated in order to replace lithium in batteries, and the consensus prevailing in the scientific community affirms that the trajectory of rechargeable batteries hinges significantly on the exploration and advancement of alternative battery chemistries. The technologies proposed include sodium, potassium, magnesium, calcium, aluminum and zinc as the active material, and among all these elements, magnesium is one of the most promising materials for the replacement of lithium [9,10,11,12,13,14,15,16,17,18].
Magnesium ranks among the decadal elements as the most prevalent element in the Earth’s crust. It is non-toxic and is characterized by non-monopolized extraction processes, complete recyclability, an elevated theoretical specific capacity, substantial volumetric energy density and a low redox potential. This underscores magnesium’s growing significance as both a supplemental and alternate element in the evolution of the next generation of power sources [19,20,21,22,23,24]. In addition to the better energy capacities, magnesium-ion batteries (MIBs), which share the same working principle as LIBs, have numerous other advantages over them [25,26,27]. First of all, magnesium is safer than lithium; it does not form toxic compounds, and thus manufacturing MIBs would be more efficient and environmentally friendly. Despite the extensive research over the last decade, MIB technology has yet to be in the initial phase, and this is primarily attributable to the evidence that the active materials conventionally suitable for LIBs are deemed merely satisfactory for MIBs [28,29,30]. Overcoming these challenges requires multidisciplinary efforts to develop novel electrodes and electrolytes that can efficiently store and release magnesium ions during charging and discharging cycles [31,32,33]. The successful adoption of this technology could revolutionize the energy storage landscape, offering superior energy density, augmented safety and a diminished environmental impact [34].
The optimal anode materials for MIBs should exhibit several key characteristics. These include the reversible retention of significant quantities of ions, environmental friendliness, cost-effectiveness and high electronic as well as ionic conductivity. Additionally, they should refrain from undergoing chemical reactions or dissolution in the electrolyte. Nanomaterials play a pivotal role in advancing ion battery technologies due to their proven efficacy as electrode candidates, offering superior ionic and electronic conductivity when compared with their bulk counterparts [35,36,37,38,39,40,41,42,43,44,45,46,47,48,49]. The synergy between materials science and high-performance computing (HPC) has opened exciting opportunities for accelerating the discovery of novel electrode nanomaterials. In fact, by leveraging HPC capabilities, researchers can employ sophisticated quantum mechanical calculations (e.g., DFT calculations) and molecular dynamics simulations to explore the properties of thousands of potential nanoelectrodes and tackle complex material design challenges [50,51,52]. This computational approach not only accelerates the research and development process but also significantly reduces the costs associated with experimental synthesis and testing, guiding experimental efforts toward the most promising candidates and thus accelerating the overall material discovery timeline.
Among nanomaterials, BN nanostructures (including nanosheets, nanotubes and nanocages, etc.) have sprung up as promising electrode materials thanks to their unique characteristics, exhibiting chemical and structural stability (suitable for use in corrosive environments), low toxicity, high thermal conductivity and excellent mechanical properties (ideal for better control of charge transport within the energy storage system) [53,54,55,56,57]. The characteristics of diverse nanostructured BN systems vary, contingent upon factors such as the synthesis technique, size, diameter and material shape. Notably, the mixed covalent-ionic B-N bond exerts a substantial influence on the structure of BN allotropes, affording the capability to form or linkage structures. Generally, BN is unsuitable for deployment as an anode electrode in rechargeable batteries due to its wide band gap energy range of 4–6 eV, rendering it an insulator. Additionally, the B-N bond exhibits limited movement, given the low degree of electron pair delocalization, leading to a scarcity of free electrons in BN [58,59,60]. Nevertheless, a diverse array of methodologies and approaches, encompassing vacancy creation, doping, defect engineering, composite formation, and judicious chemical functionalization, may be employed to proficiently modulate the bandgap (facilitating conductivity) and enhance both electron conductivity and cation– interaction on the BN surface. The latter is particularly critical for bolstering the alkali-ion storage capacity in a material [61,62,63,64].
Specifically, BN fullerene-like nanostructures have garnered attention since the fullerene’s discovery [65]. The smallest nanocage, , featuring tetragonal BN rings isolated by hexagonal BN rings, has become noteworthy following its synthesis by Oku et al. [66,67,68,69,70,71,72,73]. The potential application of nanocages as anode materials has been suggested for lithium-ion [74], sodium-ion [75] and magnesium-ion batteries [76,77]. Given the intriguing physical and chemical properties of , the preparation and characterization of fullerene dimers, such as , have garnered substantial attention both experimentally and theoretically. Wu et al. [78] identified the tubular form of as the most stable structure, resulting from the connection of two six-membered rings of . In this article, systematic calculations in the DFT framework are used to explore nanocapsules and the interaction of magnesium and magnesium ions with endonanocapsules (), particularly nanocapsules encapsulating homonuclear diatomic halogen and chalcogen molecules, to uncover if these systems are promising anodes for MIBs. This paper is organized as follows. In Section 2, we pose the computational methods and theoretical approaches employed to characterize these anodes. The formation energies, the interaction energies, the Raman and optical absorption spectra as well as the cell voltages are reported and examined in detail in Section 3 for the endonanocapsules. Lastly, our conclusions are gathered in Section 4.
2. Materials and Methods
2.1. Geometries and Energies
In the present contribution, outcomes derived from first-principles calculations within the density functional theory framework are found using the DMOL3 package [79,80,81] within Materials Studio [82]. The calculations incorporated the generalized gradient approximation with Perdew–Burke–Ernzerhof exchange-correlation functional [83,84,85] and Grimme’s DFT-D dispersion correction to account for van der Waals interactions [86,87,88]. Electronic wavefunctions were expanded using atom-centered basis functions defined on a dense numerical grid. The chosen basis set, double numerical plus polarization (DNP), was subject to a global cut-off radius of 4.5 Å. This cut-off value ensured atomic energies with an accuracy of 0.1 eV/atom, allowing for calculations without a significant loss of precision. Geometry optimizations were carried out by employing a scheme based on delocalized internal coordinates, and the convergence thresholds for the energy change, maximum force and maximum displacement during geometry optimization were set to Hartree, 0.002 Hartree/Å and 0.001 Å, respectively.
2.2. Electrochemical Reactions and Thermodynamics
The estimation of the interaction energy between Mg and Mg2+ with the designated endonanocapsule was conducted to assess the comparative efficacy of adsorption. This evaluation was performed using the following equation:
where are the total energies of the endonanocapsules with Mg or with Mg2+; is the energy of the geometry-optimized isolated endonanocapsule and is the total energy of the magnesium or magnesium ion. Considering the application of endonanocapsules as anodes in magnesium-ion batteries, the electrochemical reactions at the anode and cathode can be simplified as follows:
Therefore, the global reaction in the magnesium-ion battery cell will be
where is the Gibbs free energy change of the cell’s total reaction. For the theoretical assessment of the average open circuit intercalation potential () in this cell, the Nernst equation was employed:
where is the Faraday constant (96,500 C/mol) and z = +2 represents the charge of the divalent magnesium ion, which acts as a working cation in the electrolyte. The term was assessed initially while neglecting volume and entropy variations and solely taking into account the variation of the total energy, where . Therefore, the of the reaction considered above can be derived from the computed total energies as follows:
As deducible from the aforementioned equation, a heightened voltage () is anticipated for endonanocapsules, in which the interaction with the magnesium ion surpasses that with magnesium. Such systems may potentially serve as high-performance anode materials for magnesium-ion batteries. Afterward, to account for entropy effects, the Gibbs free energy change of the cell reaction, as described by Equation (3), was computed based on the outcomes derived from frequency analysis at 298.15 K and 1 atm of pressure:
where G is the zero-point energy-corrected Gibbs free energy of the investigated system [89]. The voltage was then calculated using the Nernst equation (Equation (4)). The formation energy for the B24N24 nanocage and that for the endonanocapsules are each defined as follows:
where and are the total energies of the primeval nanocage and of each endonanocapsule, respectively, whereas , and are the total energies per atom of the trigonal solid boron, N2 molecule and the halogen or chalcogen atom, respectively. The sign and value of the formation energies indicate a measure of the stability or instability for each system.
2.3. Raman and Optical Absorption Spectra
Raman spectroscopy exploits the Raman effect, involving the inelastic scattering of monochromatic light [90]. This interaction with the vibrations results in a shift in the energy of incident photons. The ensuing spectra are instrumental in investigating vibrational, rotational and other low-frequency modes in a system. The energy shift is dictated by the vibrational frequency, while the fraction of light undergoing inelastic scattering is determined by the spatial derivatives of the macroscopic polarization. In DMOL3, the Raman intensities and activities are computed using the finite differentiation technique. Multiple gradient calculations are executed under varying electric fields to generate the polarizability tensor derivative, which fundamentally defines the Raman activity. At a given incident light frequency and temperature, assuming a plane-polarized incident laser beam, the first-order differential Raman cross-section (intensity) for the Stokes component of the ith eigenmode far from resonance () [91] is calculated as follows:
where and are the unit vectors of the electric-field polarization for the scattered and incident light, respectively, is a normal-mode coordinate, is the frequency of the scattered light, is the polarizability tensor and is the Bose–Einstein statistical factor. Given that the frequency of the scattered light derives from the frequency of the incident light , according to , this enables the evaluation of Raman intensities under the experimental conditions T = 298.15 K and = 514.5 nm (green laser).
The time-dependent density functional theory in the linear response regime is a extremely efficient method for determining excitation energies and optical spectra [92]. Since the external field is small, it is treated as a time-dependent perturbation. Then, the linear response function (the frequency-dependent dynamic polarizability tensor) depends only on the ground state density, and it has poles at the excitation energies of the system, which can be computed by resolving the following eigenvalue problem [93,94]:
where represents the multi-determinantal excited states, represents the excitation energies and represents the matrix elements, with the labels describing the occupied orbitals and describing the unoccupied ones. Iterative diagonalization [95,96] is used to calculate the product of operating on the trial excitation vector .
3. Results and Discussion
3.1. Nanocapsule
The
nanocapsule was constructed by arranging 24 boron atoms and 24 nitrogen atoms in a specific pattern, resulting in an optimized hollow cage-like structure. At the GGA-PBE level of theory, the dimerization of
is observed through the breaking of four B (hexagonal rings close to hexagonal rings) single bonds and the consequent formation of four B=N bridges, all of which are 1.281 Å long. The stability of the dimers is confirmed by a negative formation energy = −0.48 eV/atom (see Table 1). At the baseline, the adsorption of Mg and magnesium ions at various initial sites was investigated, and the total energy minimum was found for the Mg adsorption, preferentially on B (see Figure 1b), as well as that for the Mg2+ adsorption on N (see Figure 1c). The distance between the B24N24 nanocapsule and the elemental Mg was 2.805 Å, whereas a decrease was observed in this quantity to 2.045 Å in the case of the cation Mg2+. This tendency was reflected in the interaction energy value (see Table 1), which was negative (−6.50 eV) in the case of Mg2+ adsorption and positive (+0.27 eV) in the case of Mg, and it was outlined by a bigger Lewis acid–base interaction regarding the ion.

Table 1.
Interaction energies (), HOMO-LUMO energy gap (), cell voltage at 298.15 K and 1 atm (), cell Gibbs free energy change () and formation energies () for the nanostructures investigated.
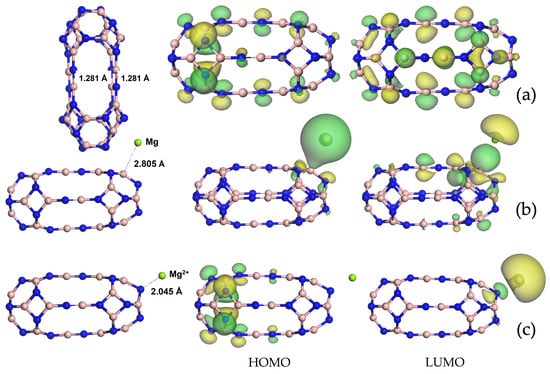
Figure 1.
Optimized structures and visualization of frontier molecular orbitals for the
nanocapsule (a), @Mg (b) and @Mg2+ (c). Nitrogen atoms are denoted in blue, boron atoms in pink and magnesium atoms in green. Distances are in Å.
Also, in terms of electronic properties, the effect of the Mg and Mg2+ adsorption was completely distinct, leading to an energy gap of 2.369 eV for the B24N24@Mg and 0.285 eV
for the B24N24@Mg2+. When considering the B24N24 nanocapsule as anode material for MIBs, the cell voltage calculated with Equation (4) was 3.38 V, which is much bigger than
the 2.7 V found in the literature for the B12N12 nanocage [76,77]. From Equation (4), it
is evident that a weaker Mg–B24N24 interaction combined with a stronger Mg2+–B24N24
interaction is conducive to an increased cell voltage, a quantity of fundamental importance
for rechargeable batteries. Additionally, the hollow structure of the B24N24 system provides
an excellent environment for encapsulating other molecules or nanoparticles.This fact
opens the possibility of encapsulating B24N24 with homonuclear diatomic molecules (see
Figure S1 in the Supplementary Materials) and examine whether a better Mg2+–B24N24
interaction can be obtained in the case of endonanocapsules.
3.2. Diatomic Halogen Endonanocapsules
Diatomic halogen encapsulation entails an enlargement of the nanocapsules, as visible in the relaxed structures in Figure S1 in the Supplementary Material, with an elongation of the B=N bridges. Their lengths increased when going from chlorine to iodine and became 1.289 Å for /, 1.301 Å for / and 1.311 Å for /. The same trend can be seen for the energy gap value (see Table 1), which was 1.473 eV for the system enclosing , 1.671 eV for the one with and 2.184 eV for the one with . The minimum total energy for the adsorption of both magnesium and magnesium ion onto / (see Figure 2a), / (see Figure 2b) and / (see Figure 2c) fell into its adsorption on N. The frontier molecular orbitals plotted for the three endonanocapsules show how the HOMO arose from the hybridization of p orbitals of N and B for /@ and /@, while for /@Mg2+, it arose from the hybridization of p orbitals of N, B and those of the encapsulated diatomic iodine, as confirmed by the pDOS in Figure 3a. The LUMO retained the spherical shape of the s orbital of Mg2+ for all the three systems. The distance from the endonanocapsules was 2.088 Å, 2.145 Å and 3.254 Å, while the Mg2+ was located at 2.042 Å, 2.046 Å and 2.081 Å from the /@Mg2+, Br2/B24N24@Mg2+ and /@Mg2+ structures, respectively.
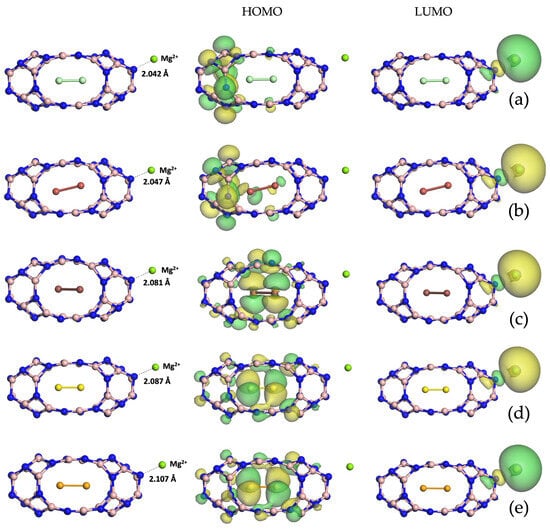
Figure 2.
Optimized structures and visualizations of frontier molecular orbitals for (from top to bottom) /@, Br2/B24N24@Mg2+ (b), /@, S2/B24N24@Mg2+ (d) and /@.
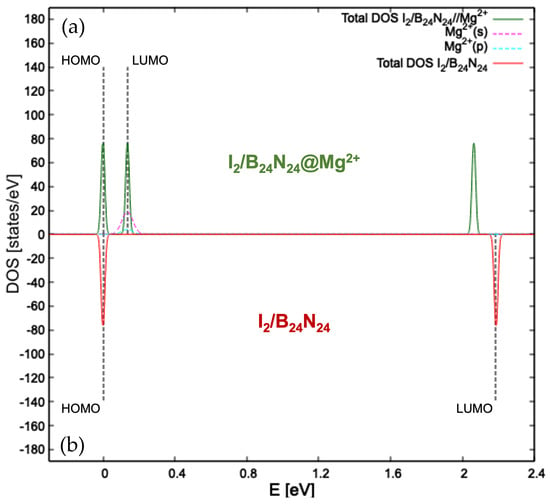
Figure 3.
Details of the atom- and angular momentum-projected DOS for /@Mg2+ (a) and the total density of states computed for / (b) at the GGA-PBE level of theory. The HOMO is taken to be zero for the energy scale. Dashed black lines indicate the HOMO and LUMO.
The increase in the distance between Mg2+ and the halogen endonanocapsules was
due to a more positive global Mulliken charge on the endonanocapsule, which was 1.007
for Cl2/B24N24@Mg2+, 1.017 for Br2/B24N24@Mg2+ or 1.122 for I2/B24N24@Mg2+, with these
values obtained with a progressively more negative Mulliken charge on the encapsulated
diatomic halogens. Moreover, it was found that a more negative Mulliken charge on the
enclosed molecule had two major effects: (1) boosting the interaction of the halogen endo-
nanocapsule with Mg2+, as evident from the interaction energy values (see Table 1), which
were −6.58 eV for Cl2/B24N24@Mg2+ in comparison with −7.24 eV for I2/B24N24@Mg2+,
and (2) diminishing the HOMO-LUMO energy gap at the PBE-GGA level to 0.289 eV for
Cl2/B24N24@Mg2+ and 0.136 eV for I2/B24N24@Mg2+. The insulator HOMO-LUMO gap of
B24N24 (4.261 eV) was thus reduced to improve conductivity.
To discern the nature of the chemical bonds and the subtleties in the atomic arrangements as well as predict the measurable features, Raman spectra were computed for B24N24
(see Figure 4a), I2/B24N24 (see Figure 4a) and I2/B24N24@Mg2+ (see Figure 4b). Raman
shifts reveal a wealth of information about the molecular vibrations, which rule the ther-
mal and electrical conductivity, thermal expansion and mechanical properties. Breathing
and deformation modes of the B-N π bonds appeared at 89.02 cm−1, 95.46 cm−1 and
281.25 cm−1 for B24N24, and at 116.51 cm−1, 162.52 cm−1 and 276.69 cm−1 for I2/B24N24
(see Tables S1 and S2 in the Supplementary Materials), since these vibrations involved light
atoms and strong bonds, while two librational modes at 43.64 cm−1 and 87.49 cm−1 and one
translational mode at 55.78 cm−1 of the encapsulated I2 occurred at a lower Raman shift for I2/B24N24 since these vibrations involved heavier atoms (see Figure 4a). Furthermore, with
regard to I2/B24N24@Mg2+, the analysis of the intensities and positions of the Raman peaks
unveiled rocking modes associated with the Mg2+ adsorbed onto the endonanocapsule at
52.66 cm−1, 59.31 cm−1 and 63.94 cm−1, while two librations of I2 occurred at 40.81 cm−1
and 79.69 cm−1, and one translation was observed at 97.45 cm−1 (see Figure 4b). The Mg2+
adsorption drastically changed the Raman spectrum for shifts above 80 cm−1. The intense
Raman peaks in the ranges of 80–190 cm−1 and 260–320 cm−1 still appeared in the spectrum
of I2/B24N24@Mg2+ (see Figure 4b), even though they were barely visible compared with
the more pronounced peaks associated with the modes of the magnesium ion.
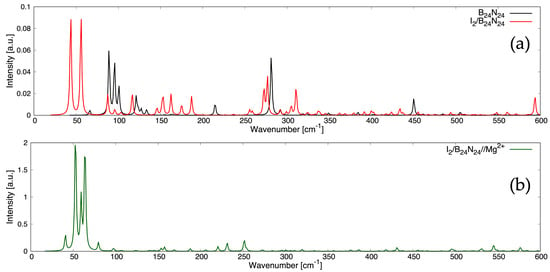
Figure 4.
Raman spectra of (a), / (a) and /@ (b) at T = 298.15 K and at an excitation wavelength λ = 514.5 nm.
The optical absorption spectra in TDDFT for B24N24 and I2/B24N24 at the ALDA-XC Kernel level of theory exhibited peaks above 4 eV and 2 eV, respectively (see Figure 5). The lowest energy peak arose from the weak HOMO-LUMO electronic excitation in I2/B24N24 at 2.35 eV, while the same excitation in B24N24 occurred at 4.29 eV. For B24N24, two rather intense peaks were observed, with one at 4.75 eV which corresponded to the excitation involving the p-states of N in the B-N π bonds (HOMO-3) and the LUMO and the other one, the highest energy peak, corresponding to the strong excitation between the p states of N (HOMO-6) and the p states of B (LUMO+1) in B24N24 at 5.14 eV. For I2/B24N24, four relevant peaks are visible in Figure 5: one at 3.83 eV involving the HOMO and the p states of B (LUMO+5), one at 4.50 eV involving the p states of I2 (HOMO-2) and the p states of B (LUMO+4), one at 5.06 eV corresponding to the electronic excitation between the p states of N (HOMO-20) and the p states of I2 (LUMO) and the last at 5.14 eV corresponding to the excitation between the I2 bond (HOMO-12) and the p states of B (LUMO+3). A detailed analysis of the positions of the absorption peaks in TDDFT and DFT is summarized in Tables S4 and S5 in the Supplementary Materials. In any case, the comparison of the absorption edges of B24N24 and I2/B24N24 shows that the absorption spectroscopy can be applied to discriminate the nanocapsules from the endonanocapsules.
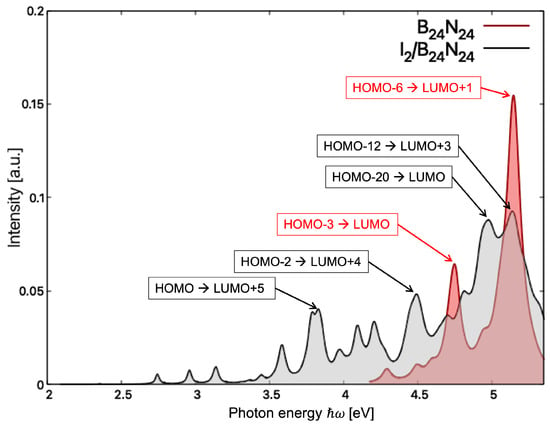
Figure 5.
Optical absorption spectra of (red) and / (gray), calculated within TDDFT with the ALDA-XC kernel. Transitions related to relevant peaks are shown.
The atom- and orbital-projected density of states of I2/B24N24 (see Figure 3b) show that HOMO and LUMO were separated well, resulting in a band gap of 2.184 eV. On the other side, the pDOS for I2/B24N24@Mg2+ (see Figure 3a) exhibited the frontier orbitals to be quite close in terms of energy, with the s orbital of the magnesium ion deeply contributing
to the LUMO. Its spherical shape is visible in Figure 2a–e, from which the halogen and
chalcogen molecules are independently encapsulated. Consequently, a further redshift of
the absorption edge is expected after Mg2+ adsorption. These facts suggest the idea, confirmed by the Mulliken population analysis, that diatomic halogen encapsulation leads to a cell voltage better than that of B24N24. In fact, calculations performed at 1 atm and 298.15 K (see Equation (5)) for the I2 endonanocapsule obtained a cell voltage of 3.61 V, exceeding the 3.38 V of the pristine nanocapsule (see Figure 6).
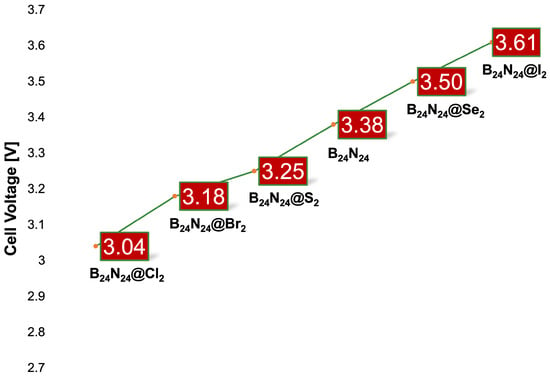
Figure 6.
Voltage trend at 298.15 K and 1 atm for the examined nanostructures.
3.3. Diatomic Chalcogen Endonanocapsules
The geometrically optimized structures of diatomic chalcogens encapsulating B24N24 (see Figure S1) display how the B=N bonds lengthened with an increase in the atomic number of the chalcogen atom, changing from 1.289 Å for the S2/B24N24 to 1.292 Å for the Se2/B24N24 in comparison with 1.281 Å for the pristine B24N24. The trend of the energy gaps was the same as that observed for the halogen endonanocapsules, even though the values were significantly smaller (see Table 1), being 0.004 eV for the S2 endonanocapsule and 0.037 eV for the Se2 endonanocapsule. The total energy minima for Mg and Mg2+ adsorption on S2/B24N24 (see Figure 2d) and S2/B24N24 (see Figure 2e) correspond to a position near an
N atom. The frontier molecular orbitals plotted for the two endonanocapsules show how the
HOMO arose from the hybridization of the p orbitals of N, B and those of the encapsulated
diatomic chalcogens for S2/B24N24@Mg2+
and Se2/B24N24@Mg2+, highlighting the charge
transfer from the encapsulated species to the B24N24 surface. The LUMO retained the
spherical shape of the s orbital of Mg2+ for both systems. It can be observed that both the Mg
and Mg2+ distances were comparable with those found for the chalcogen endonanocapsule. In fact, Mg was located at 2.107 Å and 2.140 Å from Se2/B24N24 and Se2/B24N24, respectively, while Mg2+ was within 2.087 Å from the nanocapsule enclosing S2 and 2.107 Å from the
one enclosing Se2. In the case of the chalcogen endonanocapsule, Mg2+ was even more distant, in agreement with a global Mulliken charge on the enonancapsule, which was more positive than the cases seen above (1.111 elementary charges for Se2/B24N24 and 1.154 for Se2/B24N24). The local Mulliken charge on the chalcogen molecule was negative, and as stated above, it was related to an improvement in the interaction energy with Mg2+, which was −6.94 eV for S2 encapsulation and −7.43 eV for Se2 encapsulation, as well as
a decrease in the PBE-GGA energy gap, which was 0.120 eV for S2/B24N24@Mg2+ and 0.086 eV for Se2/B24N24@Mg2+ (see Table 1). The cell voltage calculations carried out
at 1 atm and 298.15 K (see Equation (5)) returned 3.25 V and 3.50 V for the S2 and Se2
endonanocapsules, respectively. Despite the encapsulation, S2/B24N24 was less efficient
than the pristine nanocapsule as an anode for magnesium batteries. Instead, Se2/B24N24
was undoubtedly capable of reaching a voltage higher than that of B24N24 but still lower
than that observed for I2/B24N24.
The values of the open circuit potentials calculated in this DFT-TDDFT study for diatomic halogen and chalcogen B24N24 endonanocapsules are indeed significant in comparison with those obtained for other low-dimensional materials explored as anodes for MIBs via first principles calculations. In fact, earlier studies reported values for the open circuit potential such as ∼1.6 V for defective graphene [97], 0.89 V for a single layer of phosphorene [98] and 0.85 V for a single layer of WS2 [99].
4. Conclusions
The atomic arrangement of the B24N24 nanocapsule was highly symmetrical and stable, allowing it to retain its shape and structural integrity, which is essential for its potential applications in various fields, namely catalysis and energy storage inter alia. Moreover, its particular geometrical structure enables encapsulation with molecules, possibility being exploitable for enhancing the electrochemical properties of this nanomaterial.
Based on the DFT-TDDFT approach, this study investigated the effect of the encapsulation of homonuclear diatomic halogens and chalcogens and the interaction of the resulting endonanocapsules with the divalent magnesium cation. Indeed, we demonstrated that a stronger interaction with Mg2+ eads to an increased cell voltage, with a positive impact on
the performance of rechargeable magnesium batteries.
The Mulliken population analysis made clear that a more negative charge on the enclosed molecule has three important consequences: boosting the interaction of the halogen or chalcogen endonanocapsule with Mg2+, evident from the interaction energy
values; diminishing the HOMO-LUMO energy gap at the PBE-GGA level of theory and
obtaining a cell voltage better than that of the pristine B24N24. Given that I2/B24N24 turned
out to be capable of reaching the highest cell voltage among the studied systems, an in-depth investigation of this endonanocapsule was performed, including the calculation of
the Raman and optical adsorption spectra.
The Raman spectra were enabled to identify the main vibrations of the B-N π bonds, those of the encapsulated I2 molecule and those of the adsorbed magnesium ion. In parallel, the optical absorption spectra highlighted the characteristic electronic excitations of I2/B24N24, making a comparison with those of B24N24. While the analysis of the vibrational and optical properties shed light upon the nature of chemical bonds and the subtleties in atomic arrangements on one hand, on the other hand, it could drive the experimental characterization of these nanomaterials with both in situ and operando spectroscopy.
At least thus far, our studies of the geometry, the adsorption site, the interaction strength and the resulting cell voltage of the magnesium ion adsorption on B24N24 encapsulating a diatomic halogen or chalcogen molecule pave the way toward experimental preparation as anodes for magnesium-ion batteries. Moreover, the properties of these nanomaterials showed advanced performance, with a low environmental impact arising out of the natural abundance of Mg and I and the chemical inertness of BN.
In summary, our investigation of B24N24 encaspulation with homonuclear diatomic halogens and chalcogens, as well as the interaction of the resulting endonanocapsules with homonuclear diatomic
halogens and chalcogens, as well as the interaction of the resulting endonanocapsules
with Mg2+ cations, clearly indicates that a stronger interaction with these ions leads to an
increased cell voltage. Consequently, it enhances their performance as negative electrodes
for rechargeable magnesium batteries. In the case of the iodine-encapsulated anode, a
remarkable cell voltage of 3.61 V was reached.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/nano14030271/s1, Figure S1: Geometrically optimized structures and molecular orbitals plots for endonanocapsules; Figure S2: Geometrically optimized structures and molecular orbitals plots for endonanocapsules adsorbing Mg; Figure S3: Energy level diagram for diatomic iodine endonanocapsule; Table S1: Vibrational analysis of the BN nanocapsule; Table S2: Vibrational analysis of the diatomic iodine endonanocapsule; Table S3: Vibrational analysis of the diatomic iodine endonanocapsule adsorbing Mg-ion; Table S4: Optical absorption analysis of the BN nanocapsule; Table S5: Optical absorption analysis of the diatomic iodine endonanocapsule.
Author Contributions
Conceptualization, D.C. and O.P.; methodology, F.B. (Francesco Buonocore) and O.P.; validation, D.C., F.B. (Francesco Buonocore) and O.P.; formal analysis, D.C.; investigation, D.C.; resources, M.C. and F.B. (Francesco Buonocore); data curation, D.C.; writing—original draft preparation, D.C.; writing—review and editing, D.C., F.B. (Francesco Buonocore) and F.B. (Friedhelm Bechstedt); supervision, O.P., F.B. (Francesco Buonocore) and F.B. (Friedhelm Bechstedt); funding acquisition, M.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was carried out within the activities “Ricerca Sistema Elettrico” funded through contributions to research and development by the Italian Ministry of the Environment and Energy Security.
Data Availability Statement
Dataset available on request from the authors.
Acknowledgments
The authors thank M. Shundalau for the productive conversations. The computing resources and related technical support used for this work were provided by CRESCO/ENEAGRID High Performance Computing infrastructure and its staff [100].
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ALDA | Adiabatic local density approximation |
| BN | Boron nitride |
| DFT | Density functional theory |
| DFT-D | Dispersion-correction density functional theory |
| DOS | Density of states |
| GGA | Generalized gradient approximation |
| HOMO | Highest occupied molecular orbital |
| LIBs | Lithium-ion batteries |
| LUMO | Lowest unoccupied molecular orbital |
| MIBs | Magnesium-ion batteries |
| PBE | Perdew–Burke–Ernzerhof exchange-correlation functional |
| TDDFT | Time-dependent density functional theory |
| XC | Exchange-correlation |
References
- Jain, A.; Shin, Y.; Persson, K.A. Computational predictions of energy materials using density functional theory. Nat. Rev. Mater. 2016, 1, 1–13. [Google Scholar] [CrossRef]
- Scrosati, B. History of lithium batteries. J. Solid State Electrochem. 2011, 15, 1623–1630. [Google Scholar] [CrossRef]
- Goodenough, J.B.; Park, K.S. The Li-ion rechargeable battery: A perspective. J. Am. Chem. Soc. 2013, 135, 1167–1176. [Google Scholar] [CrossRef] [PubMed]
- Yoshino, A.; Tsubata, T.; Shimoyamada, M.; Satake, H.; Okano, Y.; Mori, S.; Yata, S. Development of a lithium-type advanced energy storage device. J. Electrochem. Soc. 2004, 151, A2180. [Google Scholar] [CrossRef]
- Berckmans, G.; Messagie, M.; Smekens, J.; Omar, N.; Vanhaverbeke, L.; Van Mierlo, J. Cost projection of state of the art lithium-ion batteries for electric vehicles up to 2030. Energies 2017, 10, 1314. [Google Scholar] [CrossRef]
- Ponrouch, A.; Bitenc, J.; Dominko, R.; Lindahl, N.; Johansson, P.; Palacín, M.R. Multivalent rechargeable batteries. Energy Storage Mater. 2019, 20, 253–262. [Google Scholar] [CrossRef]
- Thackeray, M.M.; Wolverton, C.; Isaacs, E.D. Electrical energy storage for transportation approaching the limits of, and going beyond, lithium-ion batteries. Energy Environ. Sci. 2012, 5, 7854–7863. [Google Scholar] [CrossRef]
- Duffner, F.; Wentker, M.; Greenwood, M.; Leker, J. Battery cost modeling: A review and directions for future research. Renew. Sustain. Energy Rev. 2020, 127, 109872. [Google Scholar] [CrossRef]
- Luntz, A. Beyond lithium ion batteries. J. Phys. Chem. Lett. 2015, 6, 300–301. [Google Scholar] [CrossRef] [PubMed]
- Delmas, C. Sodium and sodium-ion batteries: 50 years of research. Adv. Energy Mater. 2018, 8, 1703137. [Google Scholar] [CrossRef]
- Sharma, S.S.; Manthiram, A. Towards more environmentally and socially responsible batteries. Energy Environ. Sci. 2020, 13, 4087–4097. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, R.; Chen, T.; Lv, H.; Zhu, G.; Ma, L.; Wang, C.; Jin, Z.; Liu, J. Emerging non-lithium ion batteries. Energy Storage Mater. 2016, 4, 103–129. [Google Scholar] [CrossRef]
- Aurbach, D.; Lu, Z.; Schechter, A.; Gofer, Y.; Gizbar, H.; Turgeman, R.; Cohen, Y.; Moshkovich, M.; Levi, E. Prototype systems for rechargeable magnesium batteries. Nature 2000, 407, 724–727. [Google Scholar] [CrossRef]
- Zhang, X.; Tang, Y.; Zhang, F.; Lee, C.S. A novel aluminum-graphite dual-ion battery. Adv. Energy Mater. 2016, 6, 1502588. [Google Scholar] [CrossRef]
- Ji, B.; Zhang, F.; Song, X.; Tang, Y. A novel potassium-ion-based dual-ion battery. Adv. Mater. 2017, 29, 1700519. [Google Scholar] [CrossRef] [PubMed]
- Stievano, L.; de Meatza, I.; Bitenc, J.; Cavallo, C.; Brutti, S.; Navarra, M.A. Emerging calcium batteries. J. Power Sources 2021, 482, 228875. [Google Scholar] [CrossRef]
- Wang, M.; Jiang, C.; Zhang, S.; Song, X.; Tang, Y.; Cheng, H.M. Reversible calcium alloying enables a practical room-temperature rechargeable calcium-ion battery with a high discharge voltage. Nat. Chem. 2018, 10, 667–672. [Google Scholar] [CrossRef]
- Lu, S.; Yin, Z.; Liao, S.; Yang, B.; Liu, S.; Liu, M.; Yin, l.; Zheng, W. An asymmetric encoder-decoder model for Zn-ion battery lifetime prediction. Energy Rep. 2022, 8, 33–50. [Google Scholar] [CrossRef]
- Aurbach, D.; Gofer, Y.; Lu, Z.; Schechter, A.; Chusid, O.; Gizbar, H.; Cohen, Y.; Ashkenazi, V.; Moshkovich, M.; Turgeman, R.; et al. A short review on the comparison between Li battery systems and rechargeable magnesium battery technology. J. Power Sources 2001, 97, 28–32. [Google Scholar] [CrossRef]
- Ehrenberger, S.; Friedrich, H.E. Life-cycle assessment of the recycling of magnesium vehicle components. Jom 2013, 65, 1303–1309. [Google Scholar] [CrossRef]
- You, C.; Wu, X.; Yuan, X.; Chen, Y.; Liu, L.; Zhu, Y.; Fu, L.; Wu, Y.; Guo, Y.G.; van Ree, T. Advances in rechargeable Mg batteries. J. Mater. Chem. 2020, 8, 25601–25625. [Google Scholar] [CrossRef]
- Song, J.; Sahadeo, E.; Noked, M.; Lee, S.B. Mapping the challenges of magnesium battery. J. Phys. Chem. Lett. 2016, 7, 1736–1749. [Google Scholar] [CrossRef] [PubMed]
- Bitenc, J.; Dominko, R. Opportunities and challenges in the development of cathode materials for rechargeable Mg batteries. Front. Chem. 2018, 6, 634. [Google Scholar] [CrossRef]
- Chusid, O.; Gofer, Y.; Gizbar, H.; Vestfrid, Y.; Levi, E.; Aurbach, D.; Riech, I. Solid-state rechargeable magnesium batteries. Adv. Mater. 2003, 15, 627–630. [Google Scholar] [CrossRef]
- Bucur, C.B.; Gregory, T.; Oliver, A.G.; Muldoon, J. Confession of a magnesium battery. J. Phys. Chem. Lett. 2015, 6, 3578–3591. [Google Scholar] [CrossRef] [PubMed]
- Besenhard, J.O.; Winter, M. Advances in battery technology: Rechargeable magnesium batteries and novel negative-electrode materials for lithium ion batteries. Chemphyschem 2002, 3, 155–159. [Google Scholar] [CrossRef]
- Liu, F.; Wang, T.; Liu, X.; Fan, L.Z. Challenges and recent progress on key materials for rechargeable magnesium batteries. Adv. Energy Mater. 2021, 11, 2000787. [Google Scholar] [CrossRef]
- Dominko, R.; Bitenc, J.; Berthelot, R.; Gauthier, M.; Pagot, G.; Di Noto, V. Magnesium batteries: Current picture and missing pieces of the puzzle. J. Power Sources 2020, 478, 229027. [Google Scholar] [CrossRef]
- Levi, E.; Levi, M.D.; Chasid, O.; Aurbach, D. A review on the problems of the solid state ions diffusion in cathodes for rechargeable Mg batteries. J. Electroceram. 2009, 22, 13–19. [Google Scholar] [CrossRef]
- Bella, F.; De Luca, S.; Fagiolari, L.; Versaci, D.; Amici, J.; Francia, C.; Bodoardo, S. An overview on anodes for magnesium batteries: Challenges towards a promising storage solution for renewables. Nanomaterials 2021, 11, 810. [Google Scholar] [CrossRef]
- Pei, C.; Xiong, F.; Yin, Y.; Liu, Z.; Tang, H.; Sun, R.; An, Q.; Mai, L. Recent progress and challenges in the optimization of electrode materials for rechargeable magnesium batteries. Small 2021, 17, 2004108. [Google Scholar] [CrossRef]
- Deivanayagam, R.; Ingram, B.J.; Shahbazian-Yassar, R. Progress in development of electrolytes for magnesium batteries. Energy Stor. Mater. 2019, 21, 136–153. [Google Scholar] [CrossRef]
- Park, B.; Schaefer, J.L. Polymer electrolytes for magnesium batteries: Forging away from analogs of lithium polymer electrolytes and towards the rechargeable magnesium metal polymer battery. J. Electrochem. Soc. 2020, 167, 070545. [Google Scholar] [CrossRef]
- Shah, R.; Mittal, V.; Matsil, E.; Rosenkranz, A. Magnesium-ion batteries for electric vehicles: Current trends and future perspectives. Adv. Mech. Eng. 2021, 13, 16878140211003398. [Google Scholar] [CrossRef]
- Murray, R.W. Nanoelectrochemistry: Metal nanoparticles, nanoelectrodes, and nanopores. Chem. Rev. 2008, 108, 2688–2720. [Google Scholar] [CrossRef] [PubMed]
- Arrigan, D.W. Nanoelectrodes, nanoelectrode arrays and their applications. Analyst 2004, 129, 1157–1165. [Google Scholar] [CrossRef] [PubMed]
- Bruce, P.G.; Scrosati, B.; Tarascon, J.M. Nanomaterials for rechargeable lithium batteries. Angew. Chem. Int. Ed. 2008, 47, 2930–2946. [Google Scholar] [CrossRef] [PubMed]
- Poizot, P.L.S.G.; Laruelle, S.; Grugeon, S.; Dupont, L.; Tarascon, J.M. Nano-sized transition-metal oxides as negative-electrode materials for lithium-ion batteries. Nature 2000, 407, 496–499. [Google Scholar] [CrossRef] [PubMed]
- Zou, Y.; Gu, Y.; Hui, B.; Yang, X.; Liu, H.; Chen, S.; Cai, R.; Sun, J.; Zhang, X.; Yang, D. Nitrogen and sulfur vacancies in carbon shell to tune charge distribution of Co6Ni3S8 core and boost sodium storage. Adv. Energy Mater. 2020, 10, 1904147. [Google Scholar] [CrossRef]
- Tao, S.; Cai, J.; Cao, Z.; Song, B.; Deng, W.; Liu, Y.; Hou, H.; Zou, G.; Ji, X. Revealing the Valence Evolution of Metal Element in Heterostructures for Ultra-High Power Li-Ion Capacitors. Adv. Energy Mater. 2023, 13, 2301653. [Google Scholar] [CrossRef]
- Song, Z.; Zhang, G.; Deng, X.; Tian, Y.; Xiao, X.; Deng, W.; Hou, H.; Zou, G.; Ji, X. Strongly coupled interfacial engineering inspired by robotic arms enable high-performance sodium-ion capacitors. Adv. Funct. Mater. 2022, 32, 2205453. [Google Scholar] [CrossRef]
- Pomerantseva, E.; Bonaccorso, F.; Feng, X.; Cui, Y.; Gogotsi, Y. Energy storage: The future enabled by nanomaterials. Science 2019, 366, eaan8285. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, G.; Liu, K.; Cui, Y. Design of complex nanomaterials for energy storage: Past success and future opportunity. Acc. Chem. Res. 2017, 50, 2895–2905. [Google Scholar] [CrossRef]
- Cox, J.T.; Zhang, B. Nanoelectrodes: Recent advances and new directions. Annu. Rev. Anal. Chem. 2012, 5, 253–272. [Google Scholar] [CrossRef]
- Ozoemena, K.I.; Chen, S. Nanomaterials in Advanced Batteries and Supercapacitors; Springer International Publishing: Cham, Switzerland, 2016; p. 423. [Google Scholar]
- Wallace, G.G.; Chen, J.; Mozer, A.J.; Forsyth, M.; MacFarlane, D.R.; Wang, C. Nanoelectrodes: Energy conversion and storage. Mater. Today 2009, 12, 20–27. [Google Scholar] [CrossRef]
- Chen, B.; Humayun, M.; Li, Y.; Zhang, H.; Sun, H.; Wu, Y.; Wang, C. Constructing hierarchical fluffy CoO–Co4N@ NiFe-LDH nanorod arrays for highly effective overall water splitting and urea electrolysis. ACS Sustain. Chem. Eng. 2021, 9, 14180–14192. [Google Scholar] [CrossRef]
- Qin, M.; Chen, L.; Zhang, H.; Humayun, M.; Fu, Y.; Xu, X.; Xue, X.; Wang, C. Achieving highly efficient pH-universal hydrogen evolution by Mott-Schottky heterojunction of Co2P/Co4N. Chem. Eng. J. 2023, 454, 140230. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, L.; Zhang, H.; Humayun, M.; Duan, J.; Xu, X.; Bououdina, M.; Wang, C. Elaborately tailored NiCo2O4 for highly efficient overall water splitting and urea electrolysis. Green Chem. 2023, 25, 8181–8195. [Google Scholar] [CrossRef]
- Lusk, M.T.; Mattsson, A.E. High-performance computing for materials design to advance energy science. MRS Bull. 2011, 36, 169–174. [Google Scholar] [CrossRef]
- Correa-Baena, J.P.; Hippalgaonkar, K.; van Duren, J.; Jaffer, S.; Chandrasekhar, V.R.; Stevanovic, V.; Wadia, C.; Guha, S.; Buonassisi, T. Accelerating materials development via automation, machine learning, and high-performance computing. Joule 2018, 2, 1410–1420. [Google Scholar] [CrossRef]
- Pyzer-Knapp, E.O.; Pitera, J.W.; Staar, P.W.; Takeda, S.; Laino, T.; Sanders, D.P.; Sexton, J.; Smith, J.R.; Curioni, A. Accelerating materials discovery using artificial intelligence, high performance computing and robotics. npj Comput. Mater. 2022, 8, 84. [Google Scholar] [CrossRef]
- Golberg, D.; Bando, Y.; Huang, Y.; Terao, T.; Mitome, M.; Tang, C.; Zhi, C. Boron nitride nanotubes and nanosheets. ACS Nano 2010, 4, 2979–2993. [Google Scholar] [CrossRef]
- Weng, Q.; Wang, X.; Wang, X.; Bando, Y.; Golberg, D. Functionalized hexagonal boron nitride nanomaterials: Emerging properties and applications. Chem. Soc. Rev. 2016, 45, 3989–4012. [Google Scholar] [CrossRef]
- Pakdel, A.; Zhi, C.; Bando, Y.; Golberg, D. Low-dimensional boron nitride nanomaterials. Mater. Today 2012, 15, 256–265. [Google Scholar] [CrossRef]
- Jiang, X.F.; Weng, Q.; Wang, X.B.; Li, X.; Zhang, J.; Golberg, D.; Bando, Y. Recent progress on fabrications and applications of boron nitride nanomaterials: A review. J. Mater. Sci. Technol. 2015, 31, 589–598. [Google Scholar] [CrossRef]
- Merlo, A.; Mokkapati, V.R.S.S.; Pandit, S.; Mijakovic, I. Boron nitride nanomaterials: Biocompatibility and bio-applications. Biomater. Sci. 2018, 6, 2298–2311. [Google Scholar] [CrossRef] [PubMed]
- Mateti, S.; Sultana, I.; Chen, Y.; Kota, M.; Rahman, M.M. Boron Nitride-Based Nanomaterials: Synthesis and Application in Rechargeable Batteries. Batteries 2023, 9, 344. [Google Scholar] [CrossRef]
- Petrescu, M.I.; Balint, M.G. Structure and properties modifications in boron nitride. Part I: Direct polymorphic transformations mechanisms. UPB Sci. Bull. 2007, 69, 35–42. [Google Scholar]
- Han, R.; Liu, F.; Wang, X.; Huang, M.; Li, W.; Yamauchi, Y.; Sun, X.; Huang, Z. Functionalised hexagonal boron nitride for energy conversion and storage. J. Mater. Chem. 2020, 8, 14384–14399. [Google Scholar] [CrossRef]
- Pu, J.; Zhang, K.; Wang, Z.; Li, C.; Zhu, K.; Yao, Y.; Hong, G. Synthesis and modification of boron nitride nanomaterials for electrochemical energy storage: From theory to application. Adv. Funct. Mater. 2021, 31, 2106315. [Google Scholar] [CrossRef]
- Tang, C.; Bando, Y.; Huang, Y.; Yue, S.; Gu, C.; Xu, F.; Golberg, D. Fluorination and electrical conductivity of BN nanotubes. J. Am. Chem. Soc. 2005, 127, 6552–6553. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Y.-F.; Huang, S.-P.; Lin, W.; Chen, W.-K. BC2N/graphene heterostructure as a promising anode material for rechargeable Li-ion batteries by density functional calculations. J. Phys. Chem. C 2019, 123, 30809–30818. [Google Scholar] [CrossRef]
- Lei, W.; Qin, S.; Liu, D.; Portehault, D.; Liu, Z.; Chen, Y. Large scale boron carbon nitride nanosheets with enhanced lithium storage capabilities. Chem. Commun. 2013, 49, 352–354. [Google Scholar] [CrossRef]
- Kroto, H.W. The stability of the fullerenes C n, with n = 24, 28, 32, 36, 50, 60 and 70. Nature 1987, 329, 529–531. [Google Scholar] [CrossRef]
- Oku, T.; Nishiwaki, A.; Narita, I. Formation and atomic structure of B12N12 nanocage clusters studied by mass spectrometry and cluster calculation. Sci. Technol. Adv. Mater. 2004, 5, 635–638. [Google Scholar] [CrossRef]
- Jensen, F.; Toftlund, H. Structure and stability of C24 and B12N12 isomers. Chem. Phys. Lett. 1993, 201, 89–96. [Google Scholar] [CrossRef]
- Strout, D.L. Structure and stability of boron nitrides: Isomers of B12N12. J. Phys. Chem. 2000, 104, 3364–3366. [Google Scholar] [CrossRef]
- Matxain, J.M.; Eriksson, L.A.; Mercero, J.M.; Lopez, X.; Piris, M.; Ugalde, J.M.; Poater, J.; Matito, E.; Solá, M. New solids based on B12N12 fullerenes. J. Phys. Chem. C 2007, 111, 13354–13360. [Google Scholar] [CrossRef]
- Wang, J.; Ma, L.; Zhao, J.; Wang, B.; Wang, G. Stability and magnetic properties of transition metal atoms endohedral BnNn (n = 12–28) cages. J. Chem. Phys. 2008, 128, 084306. [Google Scholar] [CrossRef] [PubMed]
- Yap, Y.K. BCN Nanotubes and Related Nanostructures; Springer Science & Business Media: New York, NY, USA, 2009; Volume 6. [Google Scholar]
- Feng, L.; Lu, Y.; Kong, J.; Su, Z. Theoretical studies on the structure and properties of BN clusters (BN) n and endohedral metallo-BN clusters M@(BN) n. Comput. Theoretic. Chem. 2011, 964, 56–64. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, Z.; Wang, Q. Structures, electronic and magnetic properties of transition metal atoms encapsulated in B12N12 cage. Chem. Phys. Lett. 2020, 739, 136922. [Google Scholar] [CrossRef]
- Hosseini, J.; Rastgou, A.; Moradi, R. F-encapsulated B12N12 fullerene as an anode for Li-ion batteries: A theoretical study. J. Mol. Liq. 2017, 225, 913–918. [Google Scholar] [CrossRef]
- Nejati, K.; Hosseinian, A.; Bekhradnia, A.; Vessally, E.; Edjlali, L. Na-ion batteries based on the inorganic BN nanocluster anodes: DFT studies. J. Mol. Graph. Model. 2017, 74, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Shakerzadeh, E.; Mirzavand, H.; Mahdavifar, Z. A comparative DFT study on prospective application of C24, Si12C12, B12N12, B12P12, Al12N12, and Al12P12 nanoclusters as suitable anode materials for magnesium-ion batte- ries (MIBs). Phys. E Low-Dimens. Syst. Nanostruct. 2022, 140, 115161. [Google Scholar] [CrossRef]
- Corona, D.; Buonocore, F.; Celino, M.; Pulci, O. BN endofullerenes as anode materials for magnesium-ion batteries: A density functional theory study. Mater. Today Chem. 2023, 32, 101660. [Google Scholar] [CrossRef]
- Wu, H.S.; Xu, X.H.; Zhang, F.Q.; Jiao, H. New boron nitride B24N24 nanotube. J. Phys. Chem. A 2003, 107, 6609–6612. [Google Scholar] [CrossRef]
- Delley, B. An all-electron numerical method for solving the local density functional for polyatomic molecules. J. Chem. Phys. 1990, 92, 508–517. [Google Scholar] [CrossRef]
- Delley, B. From molecules to solids with the DMol 3 approach. J. Chem. Phys. 2000, 113, 7756–7764. [Google Scholar] [CrossRef]
- Delley, B.; Ellis, D.E. Efficient and accurate expansion methods for molecules in local density models. J. Chem. Phys. 1982, 76, 1949–1960. [Google Scholar] [CrossRef]
- BIOVIA, Dassault Systèmes. Materials Studio 2020; Dassault Systèmes: San Diego, CA, USA, 2019. [Google Scholar]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Ziesche, P.; Kurth, S.; Perdew, J.P. Density functionals from LDA to GGA. Comput. Mater. Sci. 1998, 11, 122–127. [Google Scholar] [CrossRef]
- Burke, K. Perspective on density functional theory. J. Chem. Phys. 2012, 136, 150901. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S. Density functional theory with London dispersion corrections. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 211–228. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Van Troeye, B.; Torrent, M.; Gonze, X. Interatomic force constants including the DFT-D dispersion contribution. Phys. Rev. B 2016, 93, 144304. [Google Scholar] [CrossRef]
- Hirano, T.; Tanabe, K. Molecular Orbital MOPAC Guidebook, 2nd ed.; Kaibundo Press: Tokyo, Japan, 1996. [Google Scholar]
- Loudon, R. The Raman effect in crystals. Adv. Phys. 1964, 13, 423–482. [Google Scholar] [CrossRef]
- Porezag, D.; Pederson, M.R. Infrared intensities and Raman-scattering activities within density-functional theory. Phys. Rev. B 1996, 54, 7830. [Google Scholar] [CrossRef]
- Ullrich, C.A.; Yang, Z.H. A brief compendium of time-dependent density functional theory. Braz. J. Phys. 2014, 44, 154–188. [Google Scholar] [CrossRef]
- Casida, M.E. Time-dependent density functional response theory for molecules. In Recent Advances In Density Functional Methods: (Part I); World Scientific: Singapore, 1995; pp. 155–192. [Google Scholar]
- Delley, B. Time dependent density functional theory with DMol3. J. Phys. Condens. Matter. 2010, 22, 384208. [Google Scholar] [CrossRef] [PubMed]
- Davidson, E.R. The iterative calculation of a few of the lowest eigenvalues and corresponding eigenvectors of large real-symmetric matrices. J. Comput. Phys. 1975, 17, 87–94. [Google Scholar] [CrossRef]
- Lanczos, C. An iteration method for the solution of the eigenvalue problem of linear differential and integral operators. J. Res. Natl. Bur. Stand. 1950, 45, 255. [Google Scholar] [CrossRef]
- Er, D.; Detsi, E.; Kumar, H.; Shenoy, V.B. Defective graphene and graphene allotropes as high-capacity anode materials for Mg ion batteries. ACS Energy Lett. 2016, 1, 638–645. [Google Scholar] [CrossRef]
- Jin, W.; Wang, Z.; Fu, Y.Q. Monolayer black phosphorus as potential anode materials for Mg-ion batteries. J. Mater. Sci. 2016, 51, 7355. [Google Scholar] [CrossRef]
- Vakili-Nezhaad, G.R.; Gujarathi, A.M.; Al Rawahi, N.; Mohammadi, M. Performance of WS2 monolayers as a new family of anode materials for metal-ion (Mg, Al and Ca) batteries. Mater. Chem. Phys. 2019, 230, 114. [Google Scholar] [CrossRef]
- Ponti, G.; Palombi, F.; Abate, D.; Ambrosino, F.; Aprea, G.; Bastianelli, T.; Beone, F.; Bertini, R.; Bracco, G.; Caporicci, M.; et al. The role of medium size facilities in the HPC ecosystem: The case of the new CRESCO4 cluster integrated in the ENEAGRID infrastructure. In Proceedings of the 2014 International Conference on High Performance Computing & Simulation (HPCS), Bologna, Italy, 21–25 July 2014; pp. 1030–1033. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).