Enhancing Silicon Solar Cell Performance Using a Thin-Film-like Aluminum Nanoparticle Surface Layer
Abstract
1. Introduction
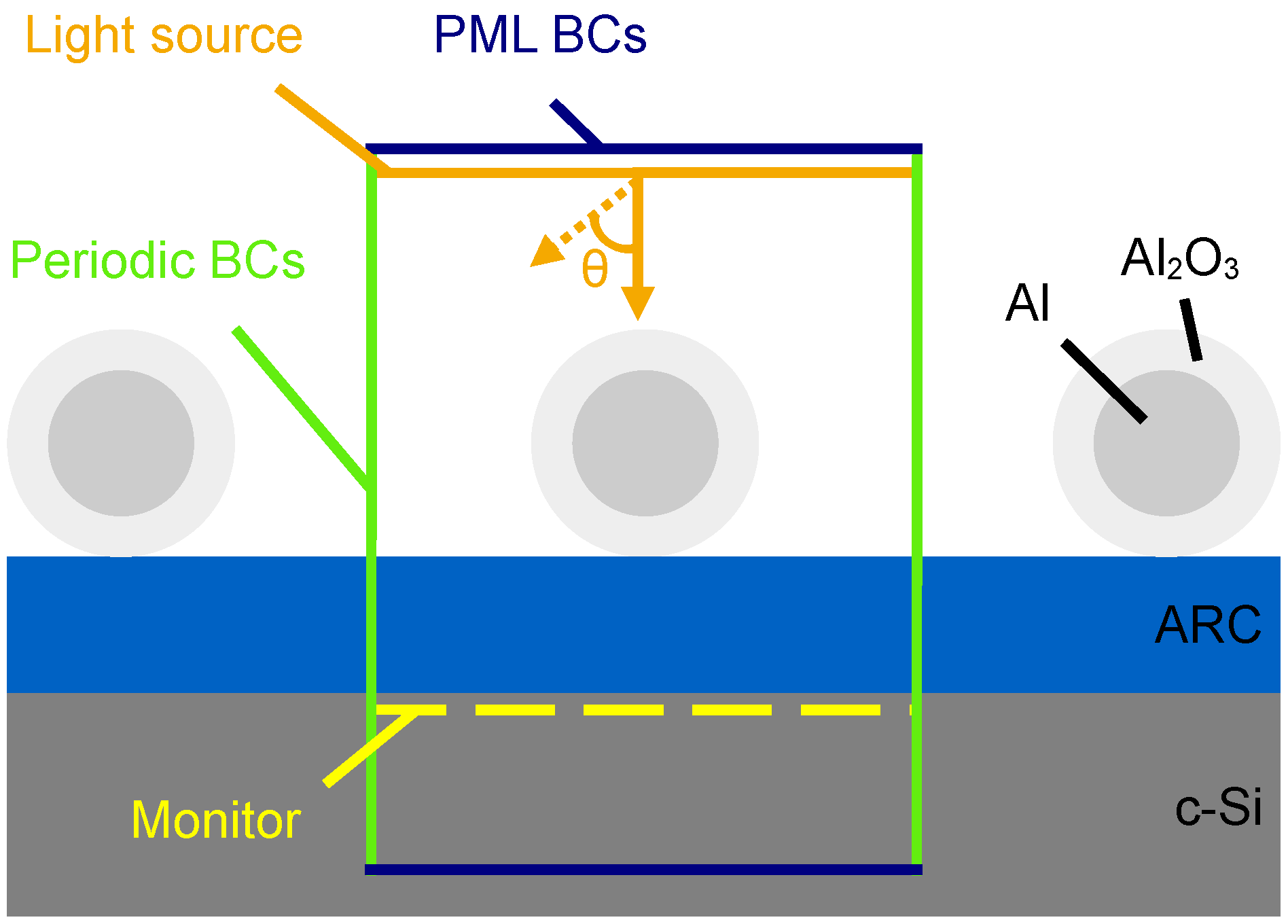
2. Materials and Methods
3. Results
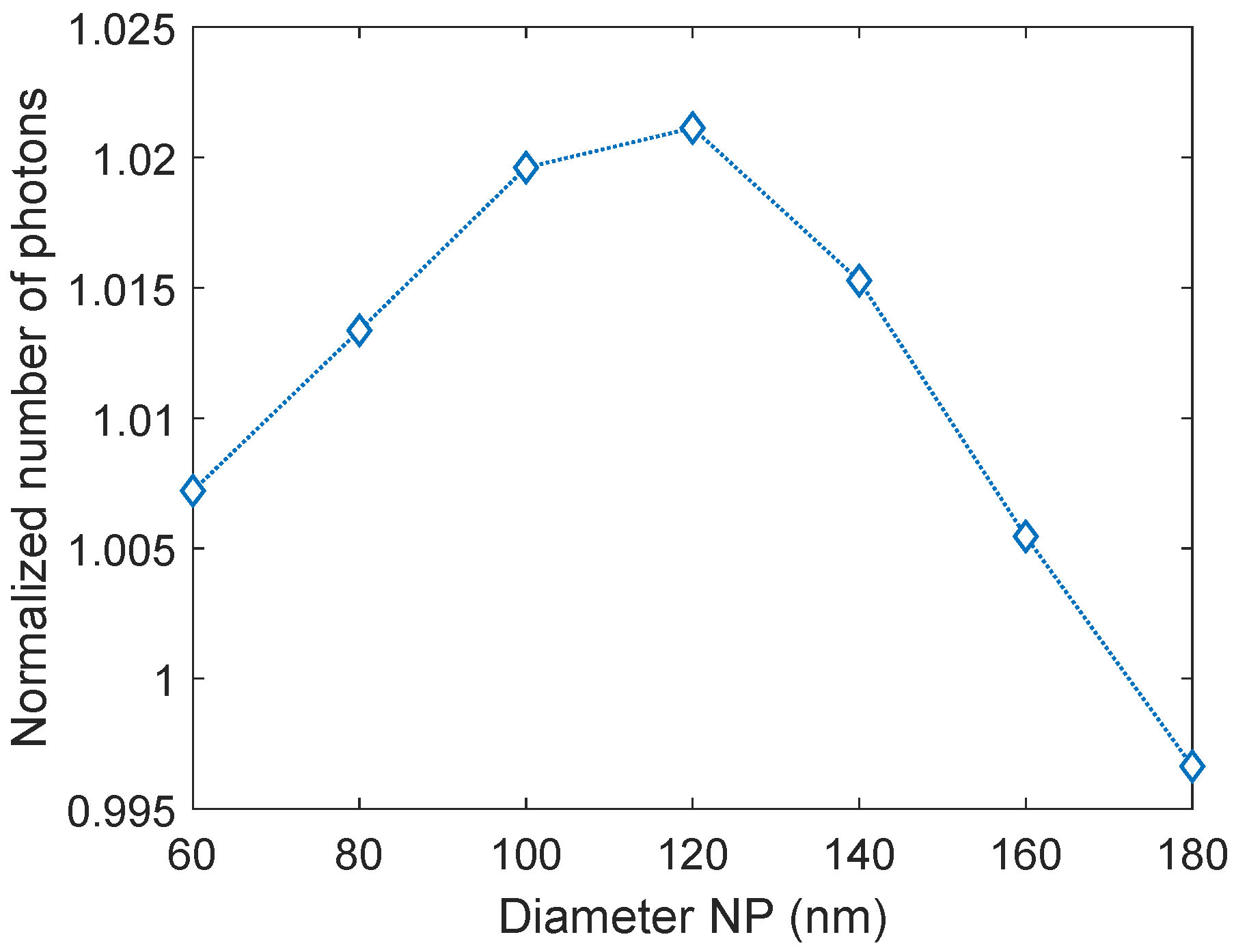
3.1. Size of Al Nanoparticles
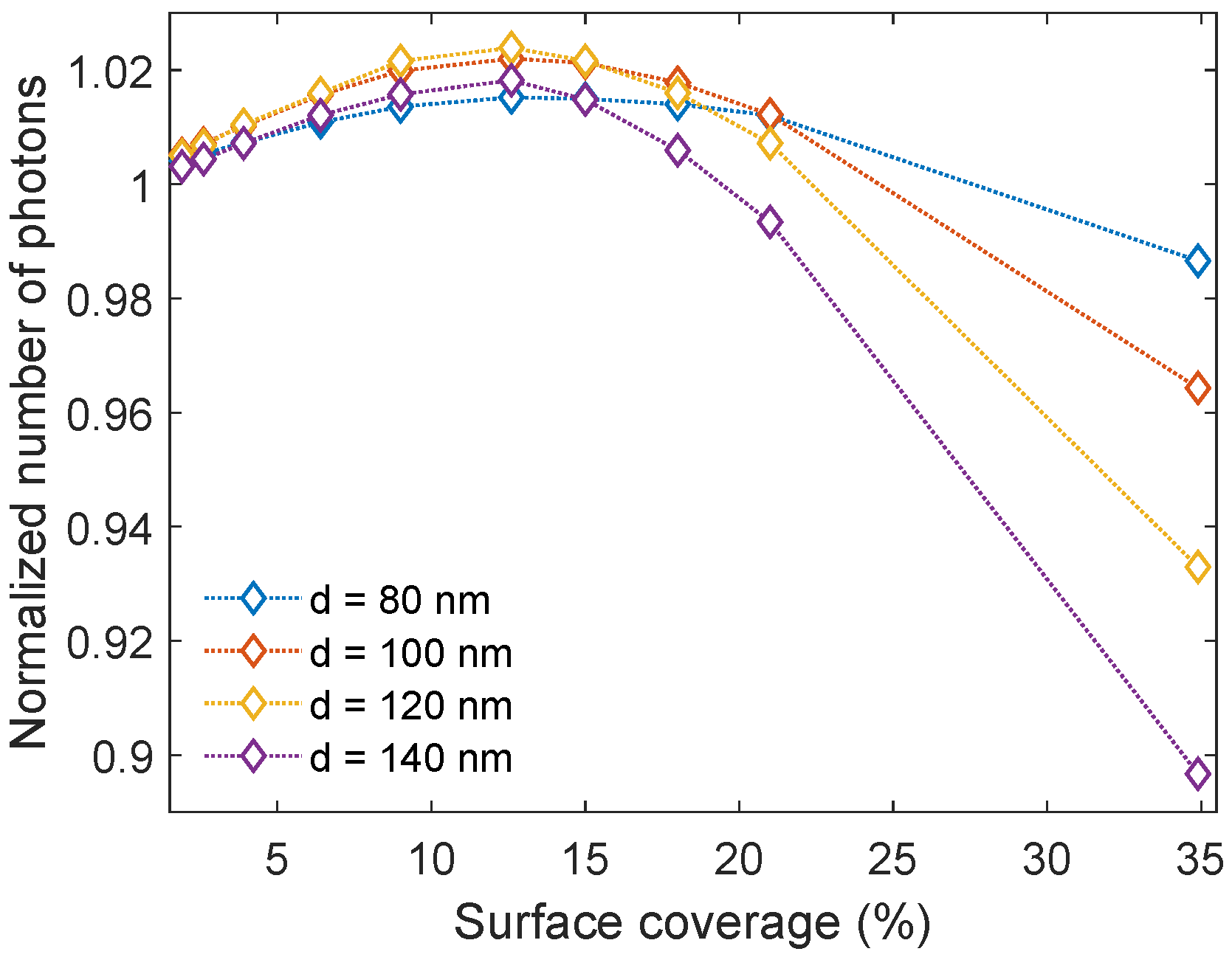
3.2. Surface Coverage of Al Nanoparticles
3.3. Oxide Layer Thickness of Al Nanoparticles
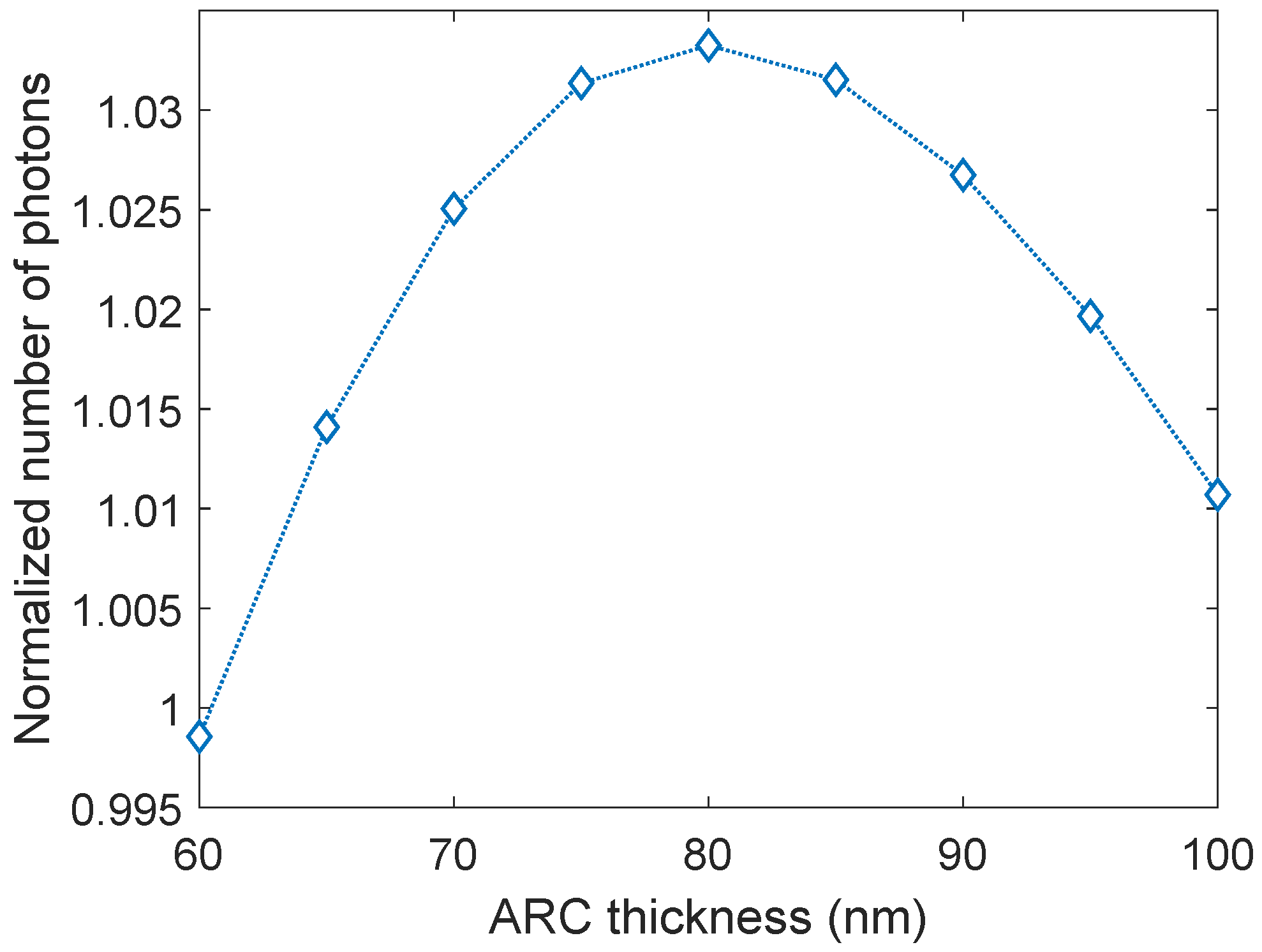
3.4. ARC Thickness
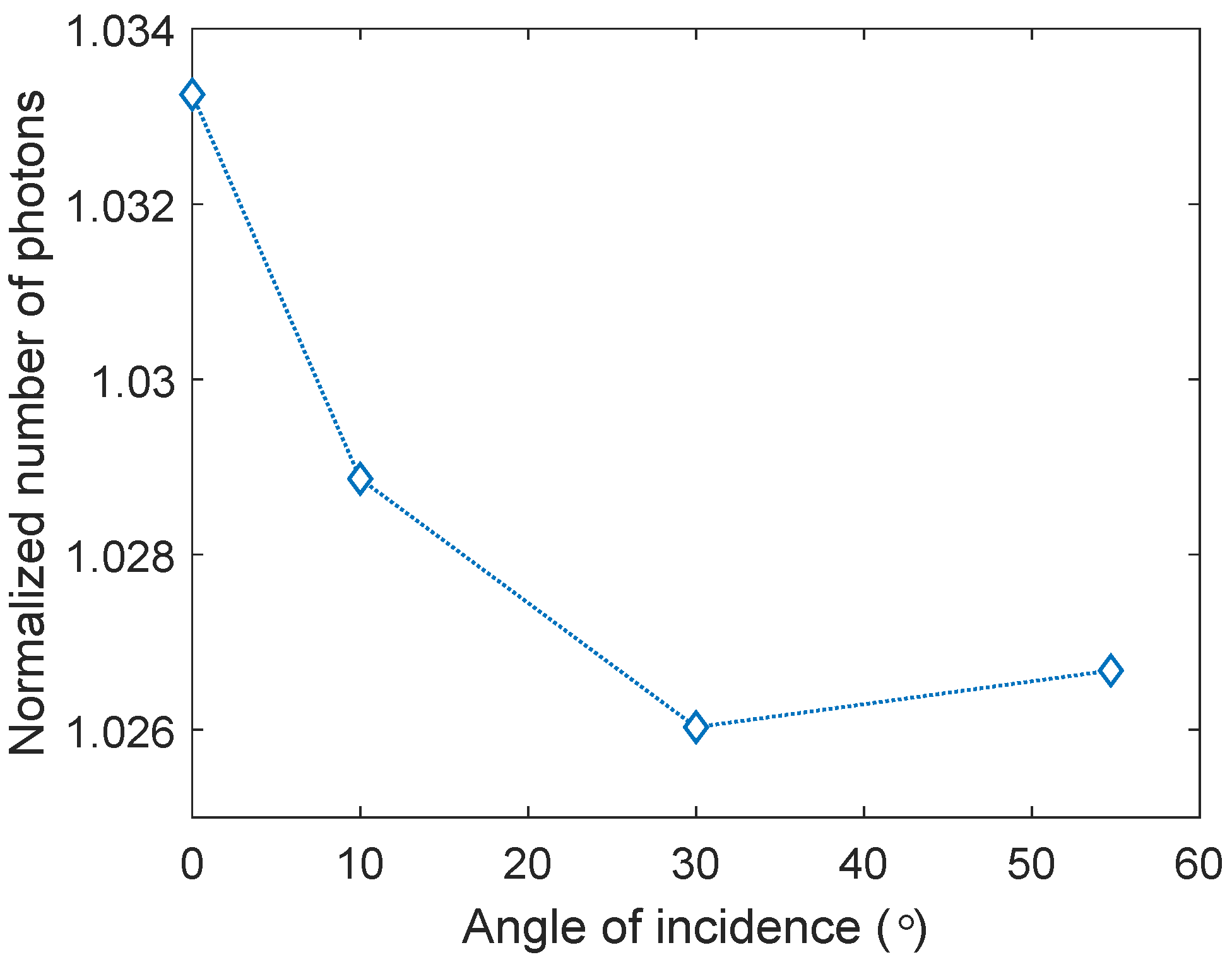
3.5. Angled Illumination
4. Discussion
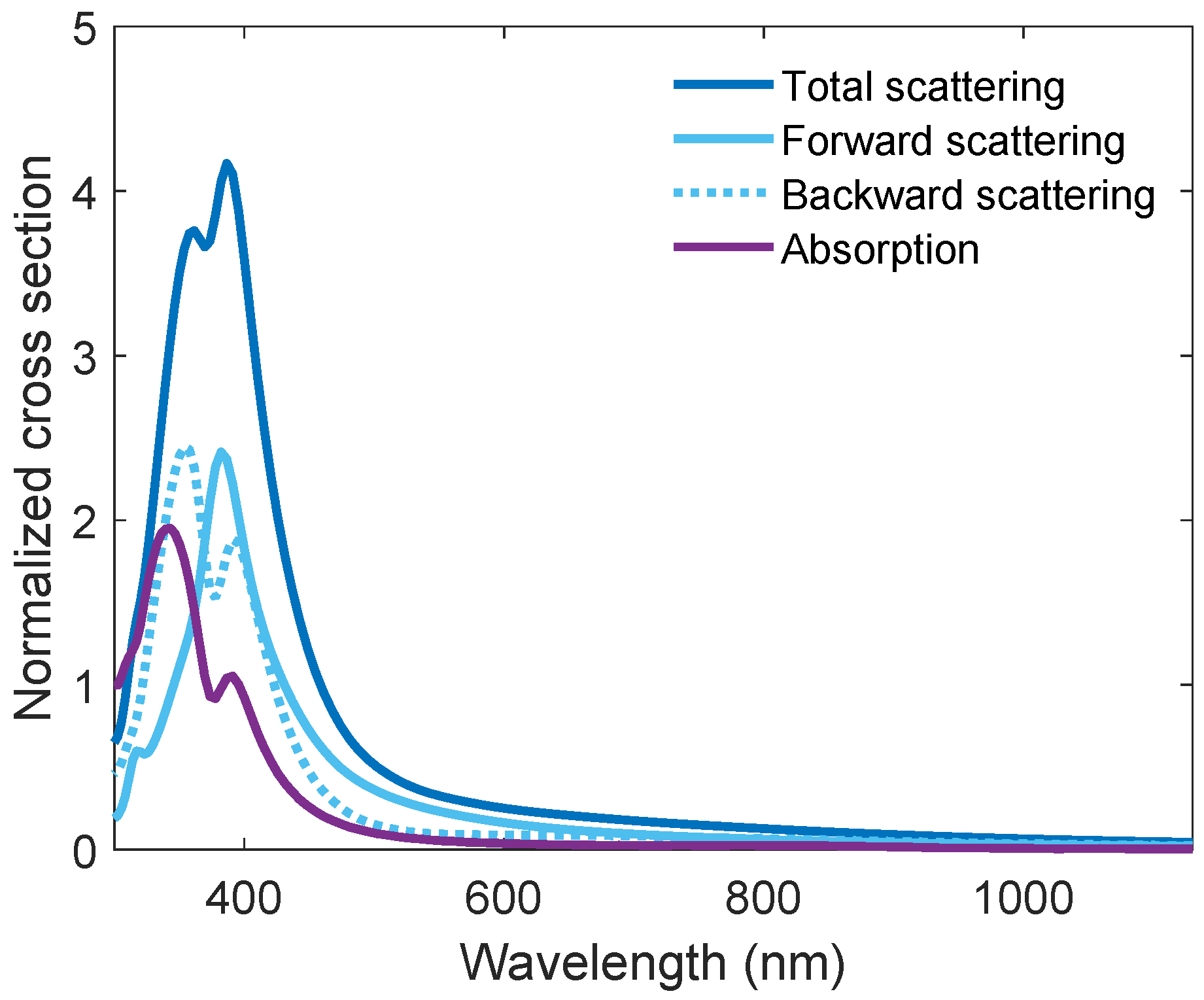
4.1. Light-Matter Interaction
4.2. Spectral Response for Optimized Device Design
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ARC | Anti-reflection coating |
| BC | Boundary condition |
| BFAST | Broadband Fixed Angle Source Technique |
| EMT | Effective medium theory |
| FDTD | Finite Difference Time Domain |
| LSPR | Localized surface plasmon resonance |
| PML | Perfectly matched layer |
| TFSF | Total-field-scattered-field |
References
- Andreani, L.C.; Bozzola, A.; Kowalczewski, P.; Liscidini, M.; Redorici, L. Silicon solar cells: Toward the efficiency limits. Adv. Phys. X 2019, 4, 1548305. [Google Scholar] [CrossRef]
- Shockley, W.; Queisser, H.J. Detailed Balance Limit of Efficiency of p-n Junction Solar Cells. J. Appl. Phys. 1961, 32, 510–519. [Google Scholar] [CrossRef]
- Hedayati, M.K.; Elbahri, M. Antireflective coatings: Conventional stacking layers and ultrathin plasmonic metasurfaces, a mini-review. Materials 2016, 9, 497. [Google Scholar] [CrossRef]
- Green, M.A. Lambertian light trapping in textured solar cells and light-emitting diodes: Analytical solutions. Prog. Photovoltaics Res. Appl. 2002, 10, 235–241. [Google Scholar] [CrossRef]
- Ushasree, P.M.; Bora, B. Silicon Solar Cells. In Solar Energy Capture Materials; Gibson, E.A., Ed.; Royal Society of Chemistry: London, UK, 2019; pp. 1–55. [Google Scholar] [CrossRef]
- Yablonovitch, E. Statistical ray optics. J. Opt. Soc. Am. 1982, 72, 899–907. [Google Scholar] [CrossRef]
- Buddhiraju, S.; Fan, S. Theory of solar cell light trapping through a nonequilibrium Green’s function formulation of Maxwell’s equations. Phys. Rev. B 2017, 96, 035304. [Google Scholar] [CrossRef]
- Callahan, D.M.; Munday, J.N.; Atwater, H.A. Solar Cell Light Trapping beyond the Ray Optic Limit. Nano Lett. 2012, 12, 214–218. [Google Scholar] [CrossRef]
- Ueno, K.; Oshikiri, T.; Sun, Q.; Shi, X.; Misawa, H. Solid-State Plasmonic Solar Cells. Chem. Rev. 2018, 118, 2955–2993. [Google Scholar] [CrossRef]
- Mandal, P.; Sharma, S. Progress in plasmonic solar cell efficiency improvement: A status review. Renew. Sustain. Energy Rev. 2016, 65, 537–552. [Google Scholar] [CrossRef]
- Pillai, S.; Beck, F.J.; Catchpole, K.R.; Ouyang, Z.; Green, M.A. The effect of dielectric spacer thickness on surface plasmon enhanced solar cells for front and rear side depositions. J. Appl. Phys. 2011, 109, 073105. [Google Scholar] [CrossRef]
- Nakayama, K.; Tanabe, K.; Atwater, H.A. Plasmonic nanoparticle enhanced light absorption in GaAs solar cells. Appl. Phys. Lett. 2008, 93, 121904. [Google Scholar] [CrossRef]
- Ho, C.; Yeh, D.; Su, V.; Yang, C.; Yang, P.; Pu, M.; Kuan, C.; Cheng, I.; Lee, S. Plasmonic multilayer nanoparticles enhanced photocurrent in thin film hydrogenated amorphous silicon solar cells. J. Appl. Phys. 2012, 112, 023113. [Google Scholar] [CrossRef]
- Notarianni, M.; Vernon, K.; Chou, A.; Aljada, M.; Liu, J.; Motta, N. Plasmonic effect of gold nanoparticles in organic solar cells. Sol. Energy 2014, 106, 23–37. [Google Scholar] [CrossRef]
- Yu, P.; Zhang, F.; Li, Z.; Zhong, Z.; Govorov, A.; Fu, L.; Tan, H.; Jagadish, C.; Wang, Z. Giant optical pathlength enhancement in plasmonic thin film solar cells using core-shell nanoparticles. J. Phys. D Appl. Phys. 2018, 51, 295106. [Google Scholar] [CrossRef]
- Spinelli, P.; Ferry, V.E.; van de Groep, J.; van Lare, M.; Verschuuren, M.A.; Schropp, R.E.I.; Atwater, H.A.; Polman, A. Plasmonic light trapping in thin-film Si solar cells. J. Opt. 2012, 14, 024002. [Google Scholar] [CrossRef]
- Maier, S.A. Plasmonics: Fundamentals and Applications, 1st ed.; Springer: New York, NY, USA, 2007; pp. 66–86. [Google Scholar] [CrossRef]
- Pelton, M.; Bryant, G. Introduction to Metal-Nanoparticle Plasmonics; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2013; pp. 13–45. [Google Scholar]
- Catchpole, K.R.; Polman, A. Design principles for particle plasmon enhanced solar cells. Appl. Phys. Lett. 2008, 93, 191113. [Google Scholar] [CrossRef]
- Beck, F.J.; Mokkapati, S.; Catchpole, K.R. Plasmonic light-trapping for Si solar cells using self-assembled, Ag nanoparticles. Prog. Photovoltaics Res. Appl. 2010, 18, 500–504. [Google Scholar] [CrossRef]
- Winans, J.D.; Hungerford, C.; Shome, K.; Rothberg, L.J.; Fauchet, P.M. Plasmonic effects in ultrathin amorphous silicon solar cells: Performance improvements with Ag nanoparticles on the front, the back, and both. Opt. Express 2015, 23, A92–A105. [Google Scholar] [CrossRef]
- Moulin, E.; Sukmanowski, J.; Schulte, M.; Gordijn, A.; Royer, F.; Stiebig, H. Thin-film silicon solar cells with integrated silver nanoparticles. Thin Solid Films 2008, 516, 6813–6817. [Google Scholar] [CrossRef]
- Beck, F.J.; Polman, A.; Catchpole, K.R. Tunable light trapping for solar cells using localized surface plasmons. J. Appl. Phys. 2009, 105, 114310. [Google Scholar] [CrossRef]
- Derkacs, D.; Lim, S.H.; Matheu, P.; Mar, W.; Yu, E.T. Improved performance of amorphous silicon solar cells via scattering from surface plasmon polaritons in nearby metallic nanoparticles. Appl. Phys. Lett. 2006, 89, 093103. [Google Scholar] [CrossRef]
- Hylton, N.P.; Li, X.F.; Giannini, V.; Lee, K.H.; Ekins-Daukes, N.J.; Loo, J.; Vercruysse, D.; Dorpe, P.V.; Sodabanlu, H.; Sugiyama, M.; et al. Loss mitigation in plasmonic solar cells: Aluminium nanoparticles for broadband photocurrent enhancements in GaAs photodiodes. Sci. Rep. 2013, 3, 2874. [Google Scholar] [CrossRef]
- Knight, M.W.; King, N.S.; Liu, L.; Everitt, H.; Nordlander, P.; Halas, N.J. Aluminum for Plasmonics. ACS Nano 2014, 8, 834–840. [Google Scholar] [CrossRef]
- Mukti, R.J.; Hossain, M.R.; Islam, A.; Mekhilef, S.; Horan, B. Increased absorption with Al nanoparticle at front surface of thin film silicon solar cell. Energies 2019, 12, 2602. [Google Scholar] [CrossRef]
- Hu, F.; Zhou, Z.Q.; Ma, L.; Zhang, C.; Zhou, W.J.; Lu, M. Enhancing the ultraviolet-visible-near infrared photovoltaic responses of crystalline-silicon solar cell by using aluminum nanoparticles. Phys. E 2017, 94, 174–177. [Google Scholar] [CrossRef]
- Zhang, Y.; Ouyang, Z.; Stokes, N.; Jia, B.; Shi, Z.; Gu, M. Low cost and high performance Al nanoparticles for broadband light trapping in Si wafer solar cells. Appl. Phys. Lett. 2012, 100, 151101. [Google Scholar] [CrossRef]
- Akimov, Y.A.; Koh, W.S. Resonant and nonresonant plasmonic nanoparticle enhancement for thin-film silicon solar cells. Nanotechnology 2010, 21, 235201. [Google Scholar] [CrossRef]
- Temple, T.L.; Bagnall, D.M. Optical properties of gold and aluminium nanoparticles for silicon solar cell applications. J. Appl. Phys. 2011, 109, 084343. [Google Scholar] [CrossRef]
- Singh, G.; Verma, S.S. Optimized size and period of Al nanoparticles for thin film GaAs solar cells. AIP Conf. Proc. 2018, 1953, 060014. [Google Scholar] [CrossRef]
- Matheu, P.; Lim, S.H.; Derkacs, D.; McPheeters, C.; Yu, E.T. Metal and dielectric nanoparticle scattering for improved optical absorption in photovoltaic devices. Appl. Phys. Lett. 2008, 93, 113108. [Google Scholar] [CrossRef]
- Parashar, P.K.; Sharma, R.P.; Komarala, V.K. Plasmonic silicon solar cell comprised of aluminum nanoparticles: Effect of nanoparticles’ self-limiting native oxide shell on optical and electrical properties. J. Appl. Phys. 2016, 120, 143104. [Google Scholar] [CrossRef]
- Zhang, Y.; Cai, B.; Jia, B. Ultraviolet plasmonic aluminium nanoparticles for highly efficient light incoupling on silicon solar cells. Nanomaterials 2016, 6, 95. [Google Scholar] [CrossRef]
- Hashmi, G.; Rashid, M.J.; Mahmood, Z.H.; Hoq, M.; Rahman, M.H. Investigation of the impact of different ARC layers using PC1D simulation: Application to crystalline silicon solar cells. J. Theor. Appl. Phys. 2018, 12, 327–334. [Google Scholar] [CrossRef]
- Langhammer, C.; Schwind, M.; Kasemo, B.; Zorić, I. Localized Surface Plasmon Resonances in Aluminum Nanodisks. Nano Lett. 2008, 8, 1461–1471. [Google Scholar] [CrossRef]
- Palik, E.D. Handbook of Optical Constants of Solids; Academic Press: San Diego, CA, USA, 1998; Volumes I–III. [Google Scholar]
- Philipp, H.R. Optical Properties of Silicon Nitride. J. Electrochem. Soc. 1973, 120, 295. [Google Scholar] [CrossRef]
- Collings, P.J. Simple measurement of the band gap in silicon and germanium. Am. J. Phys. 1980, 48, 197–199. [Google Scholar] [CrossRef]
- NREL. Reference Air Mass 1.5 Spectra. Available online: https://www.nrel.gov/grid/solar-resource/spectra-am1.5.html (accessed on 27 April 2023).
- Winderbaum, S.; Reinhold, O.; Yun, F. Reactive ion etching (RIE) as a method for texturing polycrystalline silicon solar cells. Sol. Energy Mater. Sol. Cells 1997, 46, 239–248. [Google Scholar] [CrossRef]
- Liang, B.; Bai, M.; Ma, H.; Ou, N.; Miao, J. Wideband analysis of periodic structures at oblique incidence by material independent FDTD algorithm. IEEE Trans. Antennas Propag. 2013, 62, 354–360. [Google Scholar] [CrossRef]
- Hu, J.; Chen, L.; Lian, Z.; Cao, M.; Li, H.; Sun, W.; Tong, N.; Zeng, H. Deep-Ultraviolet–Blue-Light Surface Plasmon Resonance of Al and Alcore/Al2O3shell in Spherical and Cylindrical Nanostructures. J. Phys. Chem. C 2012, 116, 15584–15590. [Google Scholar] [CrossRef]
- Fano, U. Effects of Configuration Interaction on Intensities and Phase Shifts. Phys. Rev. 1961, 124, 1866–1878. [Google Scholar] [CrossRef]
- Ershov, A.E.; Gerasimov, V.S.; Bikbaev, R.G.; Polyutov, S.P.; Karpov, S.V. Mode coupling in arrays of Al nanoparticles. J. Quant. Spectrosc. Radiat. Transfer 2020, 248, 106961. [Google Scholar] [CrossRef]
- Luk’yanchuk, B.; Zheludev, N.I.; Maier, S.A.; Halas, N.J.; Nordlander, P.; Giessen, H.; Chong, C.T. The Fano resonance in plasmonic nanostructures and metamaterials. Nat. Mater. 2010, 9, 707–715. [Google Scholar] [CrossRef]
- Garnett, J.C.M.; Larmor, J. XII. Colours in metal glasses and in metallic films. Philos. Trans. R. Soc. Lond. 1904, 203, 385–420. [Google Scholar] [CrossRef]
- Bruggeman, D.A.G. Berechnung verschiedener physikalischer Konstanten von heterogenen Substanzen. I. Dielektrizitätskonstanten und Leitfähigkeiten der Mischkörper aus isotropen Substanzen. Ann. Phys. 1935, 416, 636–664. (In German) [Google Scholar] [CrossRef]
- Centurioni, E. Generalized matrix method for calculation of internal light energy flux in mixed coherent and incoherent multilayers. Appl. Opt. 2005, 44, 7532–7539. [Google Scholar] [CrossRef]
- Yu, H.; Zhang, P.; Lu, S.; Yang, S.; Peng, F.; Chang, W.S.; Liu, K. Synthesis and Multipole Plasmon Resonances of Spherical Aluminum Nanoparticles. J. Phys. Chem. Lett. 2020, 11, 5836–5843. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; Huang, Y.F.; Jen, Y.J.; Ganguly, A.; Chen, K.H.; Chen, L.C. Anti-reflecting and photonic nanostructures. Mater. Sci. Eng. R Rep. 2010, 69, 1–35. [Google Scholar] [CrossRef]
- Lamprecht, B.; Schider, G.; Lechner, R.T.; Ditlbacher, H.; Krenn, J.R.; Leitner, A.; Aussenegg, F.R. Metal Nanoparticle Gratings: Influence of Dipolar Particle Interaction on the Plasmon Resonance. Phys. Rev. Lett. 2000, 2000, 4721–4724. [Google Scholar] [CrossRef]
- Haynes, C.L.; McFarl, A.D.; Zhao, L.; Van Duyne, R.P.; Schatz, G.C.; Gunnarsson, L. Nanoparticle Optics: The Importance of Radiative Dipole Coupling in Two-Dimensional Nanoparticle Arrays. J. Phys. Chem. B 2003, 107, 7337–7342. [Google Scholar] [CrossRef]
- Jaffe, R.L.; Taylor, W. The Physics of Energy; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar] [CrossRef]
- Landsberg, P.T.; Markvart, T. Chapter IA-3—Ideal Efficiencies. In Solar Cells, 2nd ed.; McEvoy, A., Castaner, L., Markvart, T., Eds.; Elsevier: Amsterdam, The Netherlands, 2013; pp. 55–66. [Google Scholar] [CrossRef]
- Ruhle, S. Tabulated values of the Shockley—Queisser limit for single junction solar cells. Solar Energy 2016, 130, 139–147. [Google Scholar] [CrossRef]


| Surface Coverage | 80 nm | 100 nm | 120 nm | 140 nm |
|---|---|---|---|---|
| 1.9% | 520 nm | 650 nm | 780 nm | 910 nm |
| 2.6% | 440 nm | 550 nm | 660 nm | 770 nm |
| 3.9% | 360 nm | 450 nm | 540 nm | 630 nm |
| 6.4% | 280 nm | 350 nm | 420 nm | 490 nm |
| 9.0% | 236 nm | 295 nm | 354 nm | 414 nm |
| 12.6% | 200 nm | 250 nm | 300 nm | 350 nm |
| 15.0% | 183 nm | 229 nm | 275 nm | 320 nm |
| 18.0% | 167 nm | 209 nm | 251 nm | 292 nm |
| 21.0% | 155 nm | 193 nm | 232 nm | 271 nm |
| 34.9% | 120 nm | 150 nm | 180 nm | 210 nm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fjell, M.D.; Lothe, J.B.; Halas, N.J.; Rosnes, M.H.; Holst, B.; Greve, M.M. Enhancing Silicon Solar Cell Performance Using a Thin-Film-like Aluminum Nanoparticle Surface Layer. Nanomaterials 2024, 14, 324. https://doi.org/10.3390/nano14040324
Fjell MD, Lothe JB, Halas NJ, Rosnes MH, Holst B, Greve MM. Enhancing Silicon Solar Cell Performance Using a Thin-Film-like Aluminum Nanoparticle Surface Layer. Nanomaterials. 2024; 14(4):324. https://doi.org/10.3390/nano14040324
Chicago/Turabian StyleFjell, Mirjam D., John Benjamin Lothe, Naomi J. Halas, Mali H. Rosnes, Bodil Holst, and Martin M. Greve. 2024. "Enhancing Silicon Solar Cell Performance Using a Thin-Film-like Aluminum Nanoparticle Surface Layer" Nanomaterials 14, no. 4: 324. https://doi.org/10.3390/nano14040324
APA StyleFjell, M. D., Lothe, J. B., Halas, N. J., Rosnes, M. H., Holst, B., & Greve, M. M. (2024). Enhancing Silicon Solar Cell Performance Using a Thin-Film-like Aluminum Nanoparticle Surface Layer. Nanomaterials, 14(4), 324. https://doi.org/10.3390/nano14040324







