The Effect of Impact Load on the Atomistic Scale Fracture Behavior of Nanocrystalline bcc Iron
Abstract
:1. Introduction
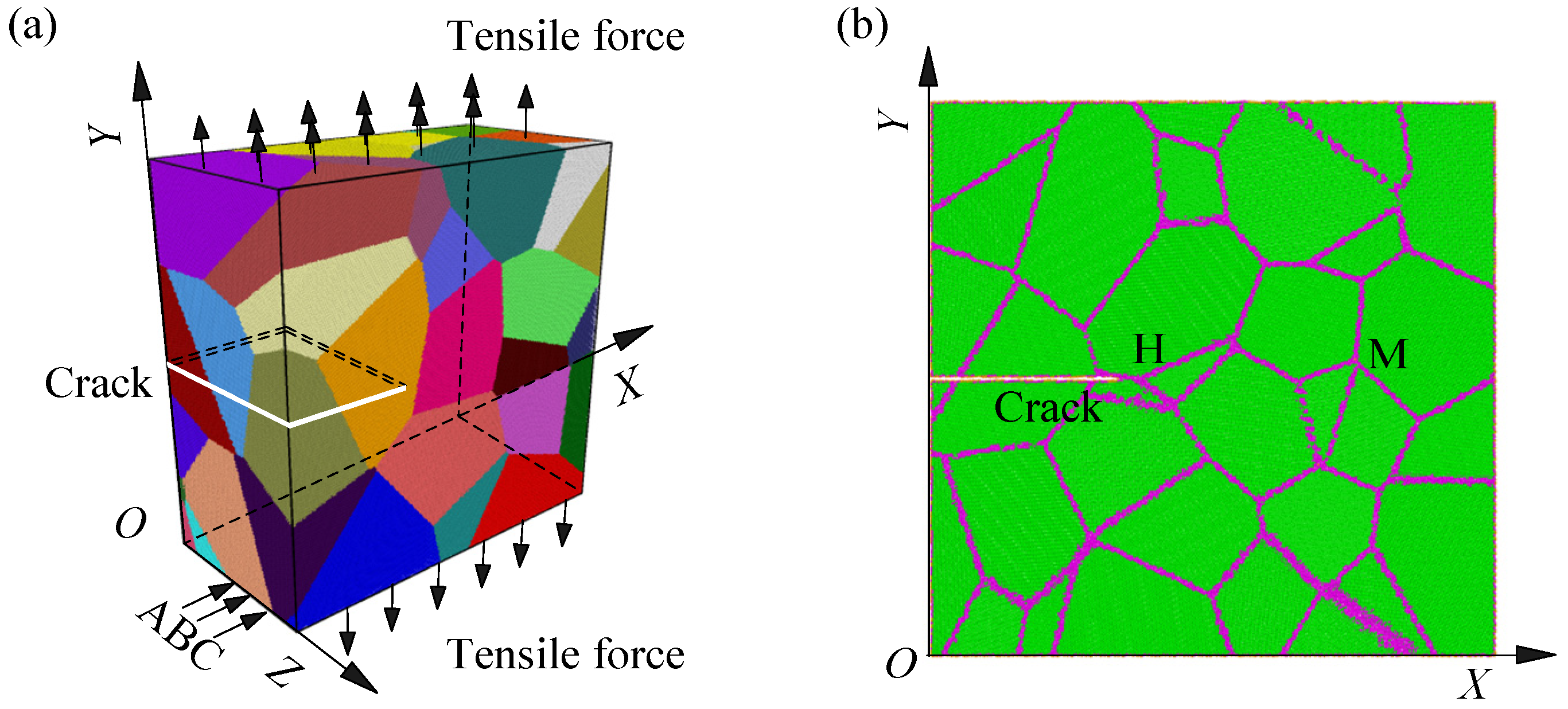
2. Model and Methods
3. Results and Discussions
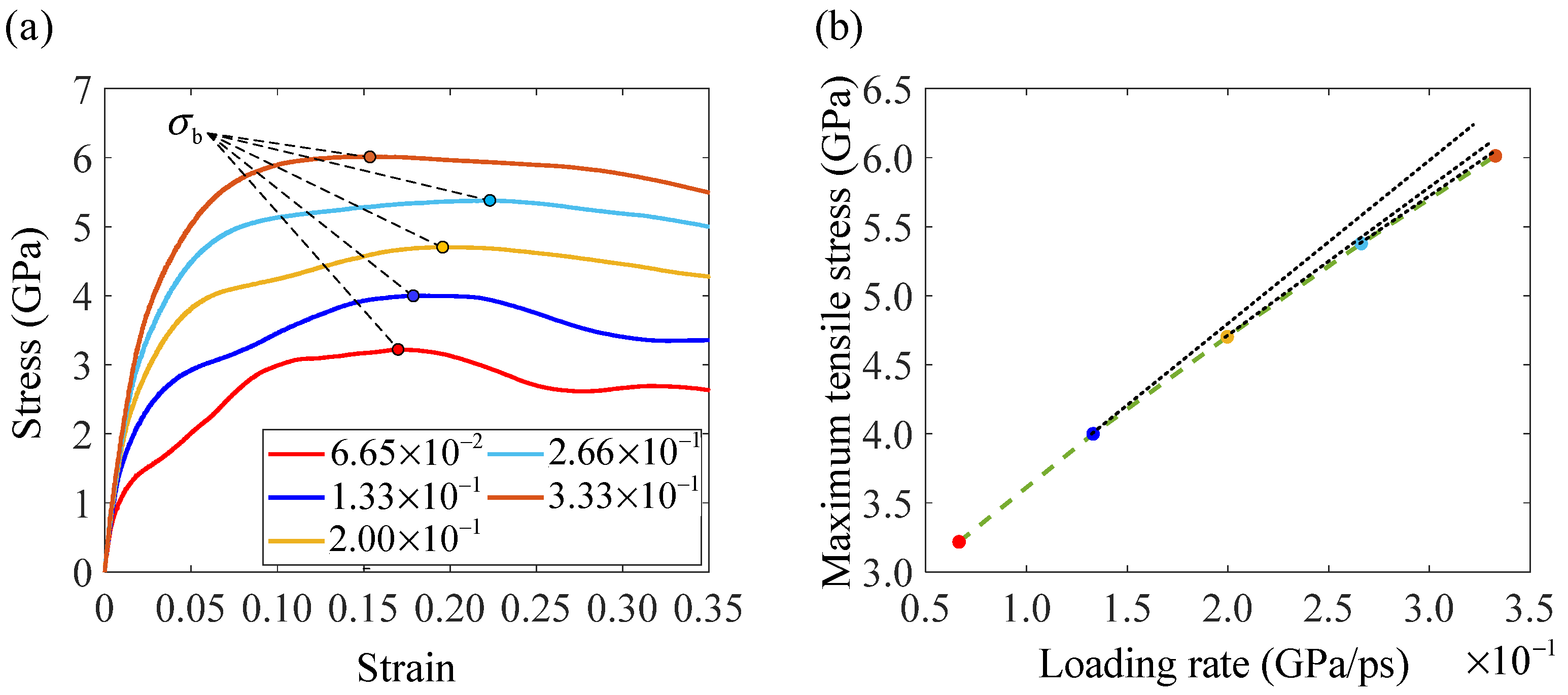
3.1. Engineering Stress–Strain Behaviors
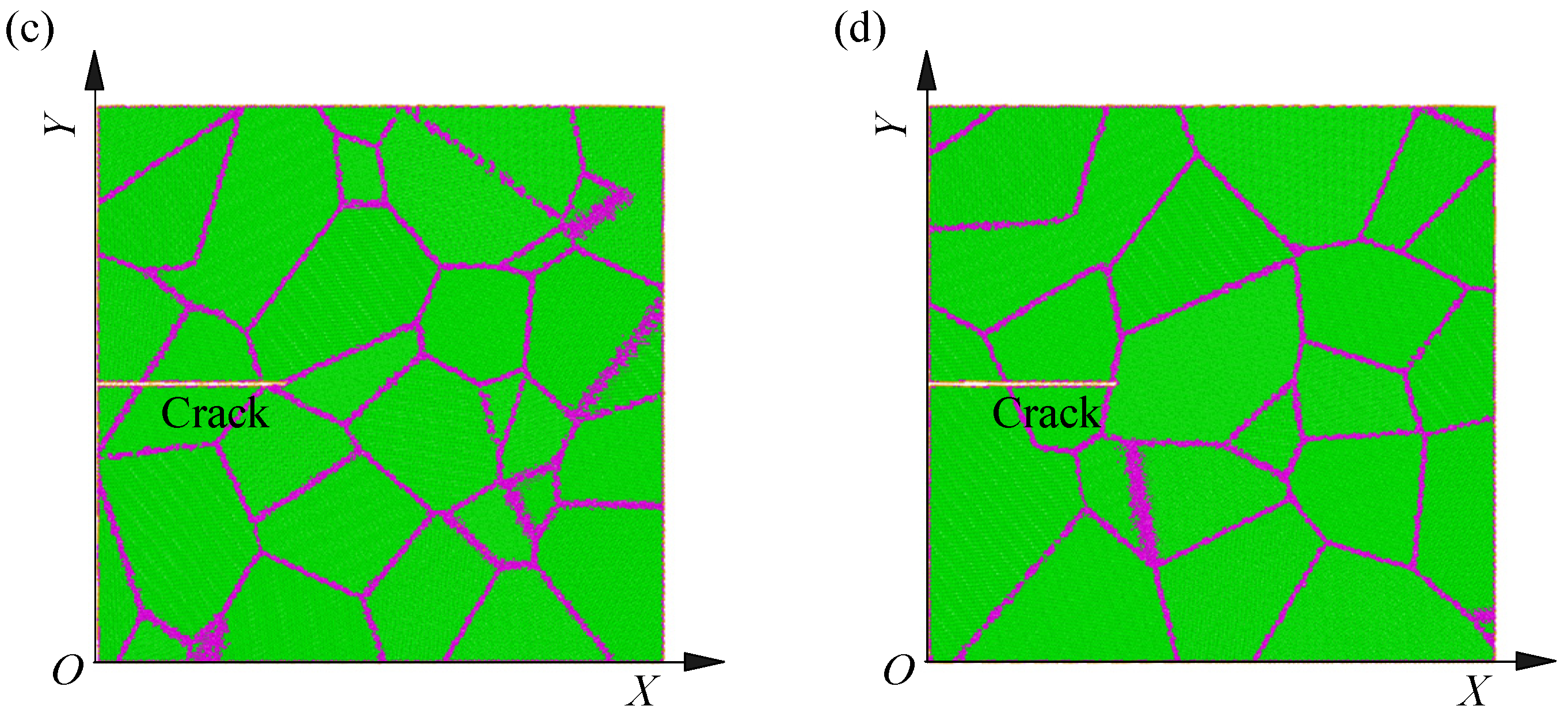
3.2. Crack Propagation Behaviors
3.3. Ductile–Brittle Characteristics
4. Conclusions
- (1)
- The engineering stress–strain behaviors of cracked nanocrystalline iron are very disparate under different loading rates. On the one hand, the ultimate tensile stress increases with an increase in loading rate in a weak, nonlinear way. On the other hand, plastic deformation will cause secondary hardening of the stress–strain behavior at a low loading rate but not at a high loading rate.
- (2)
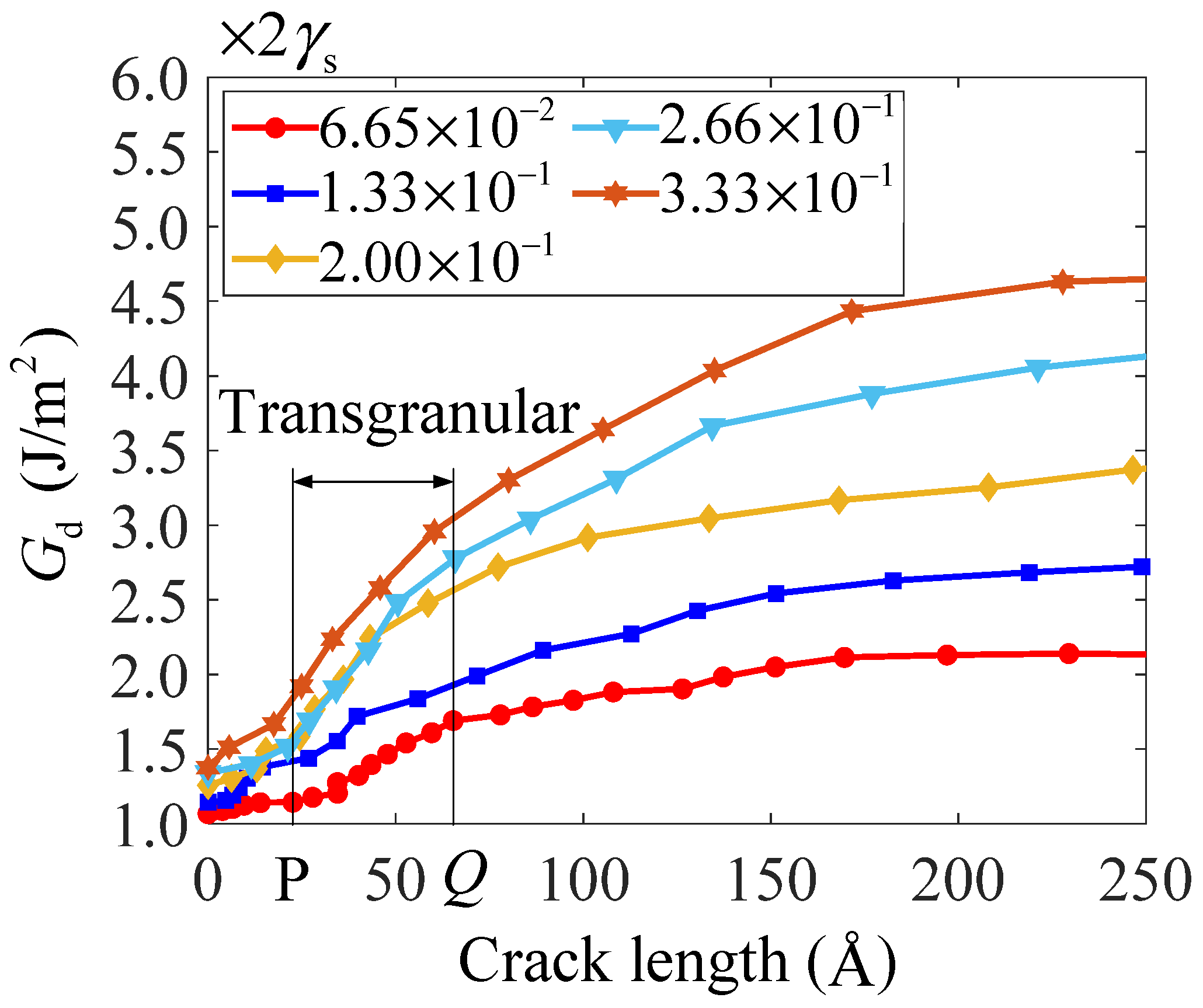
- Ductile–brittle characteristics of crack propagation on different cross-sections are very unique, and fast brittle cleavage on some cross-sections can accelerate ductile propagation on their adjacent cross-sections through intergranular decohesion. With the loading rate increasing, intergranular decohesion weakens, and more plastic behaviors are generated by grain boundary activities. The obvious grain boundary activities result in the formation of microvoids at the position far away from the crack tip and hinder crack propagation. The differences in crack propagation behavior and grain boundary activity under different loading rates determine whether secondary hardening occurs or not.
- (3)
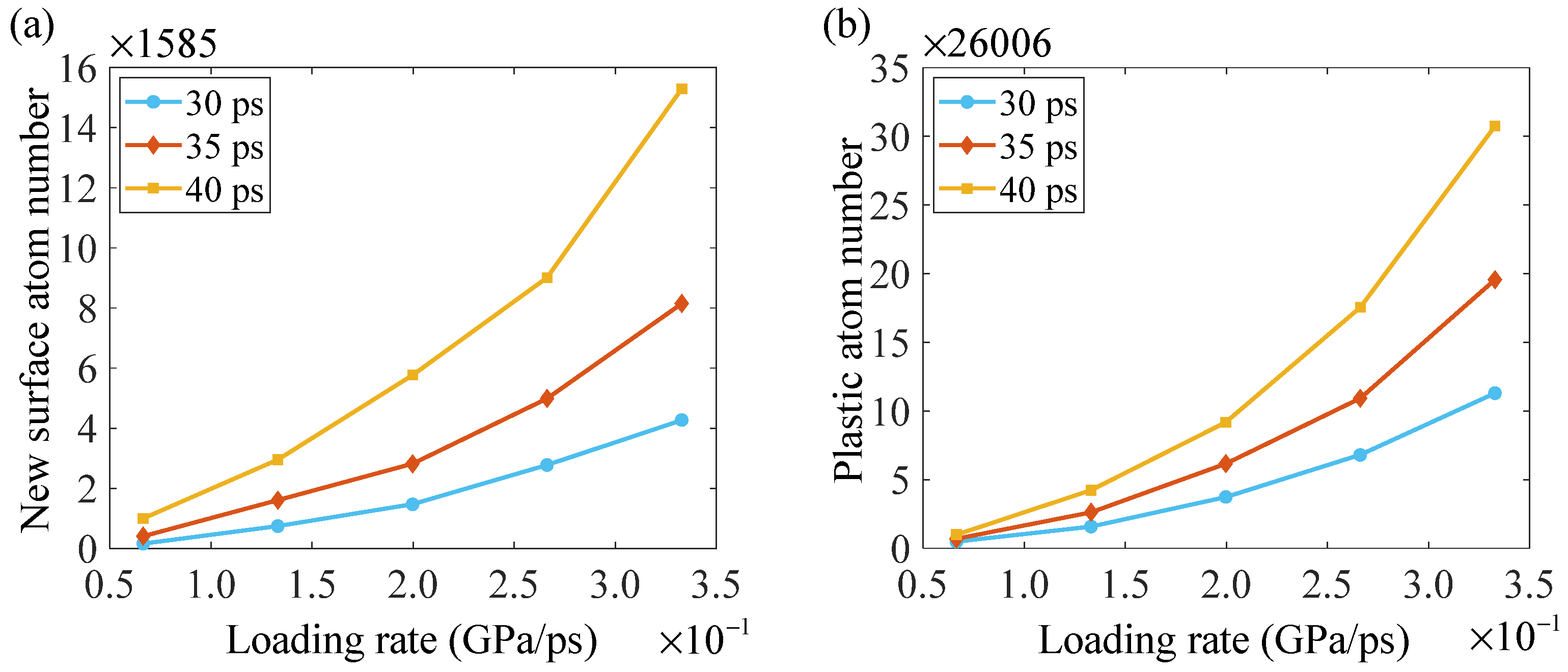
- The promoted grain boundary activities by the increase in loading rate cause an increase in the threshold energy for crack cleavage and enhance the resistance to the fracture of nanocrystalline bcc iron. After crack cleavage, both the new surface atom number and the plastic atom number grow with an increase in loading rate in a strong, nonlinear way, but the plastic atom number grows faster than the new surface atom number. The increase in loading rate can significantly increase the fracture ductility of nanocrystalline bcc iron.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, X.H.; Lu, J.; Lu, L.; Lu, K. Tensile properties of a nanocrystalline 316L austenitic stainless steel. Scr. Mater. 2005, 52, 1039–1044. [Google Scholar] [CrossRef]
- Liu, J.C.; Zhou, X.L.; Zheng, X.; Cui, H.; Zhang, J.S. Tribological behavior of cold-sprayed nanocrystalline and conventional copper coatings. Appl. Surf. Sci. 2012, 258, 7490–7496. [Google Scholar] [CrossRef]
- Azuma, D.; Ito, N.; Ohta, M. Recent progress in Fe-based amorphous and nanocrystalline soft magnetic materials. J. Magn. Magn. Mater. 2020, 501, 166373. [Google Scholar] [CrossRef]
- Fan, C.Z.; Xu, Z.J.; Han, Y.; Liu, Y.; Huang, F.L. Loading rate effect and failure mechanisms of ultra-high-strength steel under mode II fracture. Int. J. Impact Eng. 2023, 171, 104374. [Google Scholar] [CrossRef]
- Pandouria, A.K.; Yadav, K.; Tiwari, V. Compressive and tensile behavior of AA2014-T6 under different strain rates and different temperatures. Structures 2023, 49, 12–25. [Google Scholar] [CrossRef]
- Wang, G.Z.; Ren, X.C.; Chen, J.H. Effects of loading rate on fracture behavior of low-alloy steel with different grain sizes. Metall. Mater. Trans. A 2004, 35, 1765–1778. [Google Scholar] [CrossRef]
- Foster, J.T.; Chen, W.; Luk, V.K. Dynamic crack initiation toughness of 4340 steel at constant loading rates. Eng. Fract. Mech. 2011, 78, 1264–1276. [Google Scholar] [CrossRef]
- Chaudhari, V.V.; Kulkarni, D.M. Influence of loading rate on fracture behaviour of extra deep drawn steel sheets. Fatigue Fract. Eng. Mater. Struct. 2015, 38, 851–859. [Google Scholar] [CrossRef]
- Alfredsson, B.; Hazar, S.; Lai, J. Loading rate and temperature effects on the fracture toughness of a high strength bearing steel. Eng. Fract. Mech. 2021, 245, 107600. [Google Scholar] [CrossRef]
- Xu, S.; Eagleson, R.; Tyson, W.R.; Park, D.Y. Crack tunnelling and crack tip opening angle in drop-weight tear test specimens. Int. J. Fract. 2011, 172, 105–112. [Google Scholar] [CrossRef]
- Ambriško, Ľ.; Cehlár, M.; Marasová, D. The rate of stable crack growth (SCG) in automotive steels sheets. Metalurgija 2017, 56, 396–398. [Google Scholar]
- Zeng, Y.H.; Chen, J.H.; Ma, X.Y.; Zeng, Z.D.; Yang, D.R. Grown-in defects in heavily phosphorus-doped Czochralski silicon. Physica B 2009, 404, 4619–4621. [Google Scholar] [CrossRef]
- Swygenhoven, H.V.; Derlet, P.M.; Frøseth, A.G. Stacking fault energies and slip in nanocrystalline metals. Nat. Mater. 2004, 3, 399–403. [Google Scholar] [CrossRef] [PubMed]
- Frederiksen, S.L.; Jacobsen, K.W.; Schiøtz, J. Simulations of intergranular fracture in nanocrystalline molybdenum. Acta Mater. 2004, 52, 5019–5029. [Google Scholar] [CrossRef]
- Pan, Z.L.; Li, Y.L.; Wei, Q. Tensile properties of nanocrystalline tantalum from molecular dynamics simulations. Acta Mater. 2008, 56, 3470–3480. [Google Scholar] [CrossRef]
- Zhang, L.; Shibuta, Y.; Huang, X.X.; Lu, C.; Liu, M. Grain boundary induced deformation mechanisms in nanocrystalline Al by molecular dynamics simulation: From interatomic potential perspective. Comput. Mater. Sci. 2019, 156, 421–433. [Google Scholar] [CrossRef]
- Ma, K.; Sun, H.Y.; Qi, Y.; Ma, X. Grain size dependence of microstructure and mechanical properties of nanocrystalline TC4 alloy studied by molecular dynamic simulation. Phys. Lett. A 2023, 481, 129000. [Google Scholar] [CrossRef]
- Tucker, G.J.; Tiwari, S.; Zimmerman, J.A.; McDowell, D.L. Investigating the deformation of nanocrystalline copper with microscale kinematic metrics and molecular dynamics. J. Mech. Phys. Solids 2012, 60, 471–486. [Google Scholar] [CrossRef]
- Li, J.J.; Xian, Y.H.; Zhou, H.J.; Wu, R.N.; Hu, G.M.; Xia, R. Mechanical properties of nanocrystalline nanoporous gold complicated by variation of grain and ligament: A molecular dynamics simulation. Sci. China-Technol. Sci. 2018, 61, 1353–1363. [Google Scholar] [CrossRef]
- Jeon, J.B.; Lee, B.J.; Chang, Y.W. Molecular dynamics simulation study of the effect of grain size on the deformation behavior of nanocrystalline body-centered cubic iron. Scr. Mater. 2011, 64, 494–497. [Google Scholar] [CrossRef]
- Kumar, S.; Li, X.Y.; Haque, A.; Gao, H.J. Is stress concentration relevant for nanocrystalline metals? Nano Lett. 2011, 11, 2510–2516. [Google Scholar] [CrossRef]
- Shimokawa, T.; Nakatani, A.; Kitagawa, H. Grain-size dependence of the relationship between intergranular and intragranular deformation of nanocrystalline Al by molecular dynamics simulations. Phys. Rev. B 2005, 71, 224110. [Google Scholar] [CrossRef]
- Farkas, D.; Frøseth, A.; Swygenhoven, H.V. Grain boundary migration during room temperature deformation of nanocrystalline Ni. Scr. Mater. 2006, 55, 695–698. [Google Scholar] [CrossRef]
- Wu, C.D.; Li, H.X. Molecular dynamics simulation of strengthening of nanocrystalline Cu alloyed with Zr. Mater. Today Commun. 2021, 26, 101963. [Google Scholar] [CrossRef]
- Tang, Y.Z.; Bringa, E.M.; Meyers, M.A. Inverse Hall-Petch relationship in nanocrystalline tantalum. Mater. Sci. Eng. A 2013, 580, 414–426. [Google Scholar] [CrossRef]
- Paul, S.K.; Kumar, S.; Tarafder, S. Effect of loading conditions on nucleation of nano void and failure of nanocrystalline aluminum: An atomistic investigation. Eng. Fract. Mech. 2017, 176, 257–262. [Google Scholar] [CrossRef]
- Li, X.T.; Ma, W.T. Molecular dynamics simulation and theoretical modeling of free surface effect on nanocrack initiation induced by grain boundary sliding in nanocrystalline materials. Mater. Lett. 2021, 304, 130647. [Google Scholar] [CrossRef]
- Cao, A.J.; Wei, Y.G. Atomistic simulations of crack nucleation and intergranular fracture in bulk nanocrystalline nickel. Phys. Rev. B 2007, 76, 024113. [Google Scholar] [CrossRef]
- Bachurin, D.V. Influence of grain boundary misorientation on intergranular fracture of nanocrystalline palladium. Int. J. Fract. 2018, 214, 69–78. [Google Scholar] [CrossRef]
- Pei, L.Q.; Lu, C.; Tieu, K.; Zhu, H.T.; Zhao, X.; Cheng, K.Y.; Zhang, L. A molecular dynamics simulation of fracture in nanocrystalline copper. J. Nano Res. 2013, 23, 50–56. [Google Scholar] [CrossRef]
- Latapie, A.; Farkas, D. Molecular dynamics investigation of the fracture behavior of nanocrystalline α-Fe. Phys. Rev. B 2004, 69, 134110. [Google Scholar] [CrossRef]
- Li, Q.H.; Dong, Z.B.; Zhou, S.Z.; Han, F.; Li, C.K.; Chang, H.; Zhang, Z.P. Investigation of grain boundary content on crack propagation behavior of nanocrystalline Al by molecular dynamics simulation. Phys. Status Solidi B 2022, 259, 2100570. [Google Scholar] [CrossRef]
- Zhu, Y.H.; Hu, X.W.; Ni, Y.S. Molecular dynamics simulation of microstructure evolution during the fracture of nano-twinned Ag. Eng. Fract. Mech. 2021, 248, 107743. [Google Scholar] [CrossRef]
- Zhao, Z.F.; Chu, F.L.; Wei, Y.G. Atomistic scale behaviors of crack propagation in nanocrystalline bcc iron. Mater. Sci. Eng. A 2021, 809, 140948. [Google Scholar] [CrossRef]
- Qi, X.J.; You, J.H.; Zhou, J.F.; Qiu, K.Q.; Cui, X.L.; Tian, J.; Li, B.L. A review of fe-based amorphous and nanocrystalline alloys: Preparations, applications, and effects of alloying elements. Phys. Status Solidi A 2023, 220, 2300079. [Google Scholar] [CrossRef]
- Chang, L.; Zhang, Y.Q.; Dong, Y.Q.; Li, Q.; He, A.N.; Chang, C.T.; Wang, X.M. Enhanced magnetic properties of Fe-based nanocrystalline composites by addition of carbonyl iron powders. SN Appl. Sci. 2019, 1, 902. [Google Scholar] [CrossRef]
- Vetterick, G.; Baldwin, J.K.; Misra, A.; Taheri, M.L. Texture evolution in nanocrystalline iron films deposited using biased magnetron sputtering. J. Appl. Phys. 2014, 116, 233503. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Mendelev, M.I.; Han, S.; Srolovitz, D.J.; Ackland, G.J.; Sun, D.Y.; Asta, M. Development of new interatomic potentials appropriate for crystalline and liquid iron. Philos. Mag. 2003, 83, 3977–3994. [Google Scholar] [CrossRef]
- Swope, W.C.; Andersen, H.C.; Berens, P.H.; Wilson, K.R. A computer simulation method for the calculation of equilibrium constants for the formation of physical clusters of molecules: Application to small water clusters. J. Chem. Phys. 1982, 76, 637–649. [Google Scholar] [CrossRef]
- Sun, X.; Soulami, A.; Choi, K.S.; Guzman, O.; Chen, W. Effects of sample geometry and loading rate on tensile ductility of TRIP800 steel. Mater. Sci. Eng. A 2012, 541, 1–7. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO—The Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Helio, T.; Paulo, S.B.; Jose, P.R. Structural characterization of deformed crystals by analysis of common atomic neighborhood. Comput. Phys. Commun. 2007, 177, 518–523. [Google Scholar]
- Wolde, P.R.; Ruiz-Montero, M.J.; Frenkel, D. Numerical calculation of the rate of crystal nucleation in a Lennard-Jones system at moderate undercooling. J. Chem. Phys. 1996, 104, 9932. [Google Scholar] [CrossRef]
- Kelchner, C.L.; Plimpton, S.J.; Hamilton, J.C. Dislocation nucleation and defect structure during surface indentation. Phys. Rev. B 1998, 58, 11085. [Google Scholar] [CrossRef]
- Tanaka, M.; Wilkinson, A.J.; Roberts, S.G. Ductile–brittle transition of polycrystalline iron and iron–chromium alloys. J. Nucl. Mater. 2008, 378, 305–311. [Google Scholar] [CrossRef]
- Fan, Z.Y. The grain size dependence of ductile fracture toughness of polycrystalline metals and alloys. Mater. Sci. Eng. A 1995, 191, 73–83. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Z.; Wang, Z.; Bie, Y.; Liu, X.; Wei, Y. The Effect of Impact Load on the Atomistic Scale Fracture Behavior of Nanocrystalline bcc Iron. Nanomaterials 2024, 14, 370. https://doi.org/10.3390/nano14040370
Zhao Z, Wang Z, Bie Y, Liu X, Wei Y. The Effect of Impact Load on the Atomistic Scale Fracture Behavior of Nanocrystalline bcc Iron. Nanomaterials. 2024; 14(4):370. https://doi.org/10.3390/nano14040370
Chicago/Turabian StyleZhao, Zhifu, Zhen Wang, Yehui Bie, Xiaoming Liu, and Yueguang Wei. 2024. "The Effect of Impact Load on the Atomistic Scale Fracture Behavior of Nanocrystalline bcc Iron" Nanomaterials 14, no. 4: 370. https://doi.org/10.3390/nano14040370
APA StyleZhao, Z., Wang, Z., Bie, Y., Liu, X., & Wei, Y. (2024). The Effect of Impact Load on the Atomistic Scale Fracture Behavior of Nanocrystalline bcc Iron. Nanomaterials, 14(4), 370. https://doi.org/10.3390/nano14040370




